- Research Article
- Open access
- Published:
Secure Precise Clock Synchronization for Interconnected Body Area Networks
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 797931 (2011)
Abstract
Secure time synchronization is a paramount service for wireless sensor networks (WSNs) constituted by multiple interconnected body area networks (BANs). We propose a novel approach to securely and efficiently synchronize nodes at BAN level and/or WSN level. Each BAN develops its own notion of time. To this effect, the nodes of a BAN synchronize with their BAN controller node. Moreover, controller nodes of different BANs cooperate to agree on a WSN global and/or to transfer UTC time. To reduce the number of exchanged synchronization messages, we use an environmental-aware time prediction algorithm. The performance analysis in this paper shows that our approach exhibits very advanced security, accuracy, precision, and low-energy trade-off. For comparable precision, our proposal outstands related clock synchronization protocols in energy efficiency and risk of attacks. These results are based on computations.
1. Introduction
Body area networks (BANs) are receiving a lot of attention for civilian applications [1]. A BAN consists of wireless connected sensors nodes worn by or implated to a human body. Each BAN includes a controller node. The role of this node can be assigned either to a single sensor node or dynamically to any of the nodes of the BAN.
In this paper, we consider the interconnection of multiple BANs by means of the controller nodes. This setup enables quick, modular, and inexpensive deployment of a long range distributed wireless sensor network (WSN) for key applications, such as patient monitoring, for instance, for quick deployment of a medical WSN in a field hospital after disaster events. Each BAN collects vital parameters of a single patient. The cooperation between the different controllers allows for monitoring of multiple patients from a single central or remote location.
In the rest of the paper, we use WSN to refer to the long range wireless network formed by the interconnection of multiple BANs through the controller nodes.
The WSN can be formed in public or hostile areas, where wireless communications can be easily eavesdropped, deleted, and/or modified. In some applications, sensor nodes are left unattended (when detached from the monitored body), being then prone to capture and manipulation by an attacker. The monitored human itself may also be an intruder and, thus, may manipulate its body-attached nodes.
Time synchronization is a key service in WSNs for a diversity of purposes; including data fusion, power management, positioning, message integrity, coordination of future actions, and timestamping of sensed events. However, sensor node clocks have arbitrary starting offsets and nondeterministic fluctuating skews.
Moreover, the special nature of WSNs imposes challenging and intertwined requirements on secure time synchronization design. Firstly, time synchronization must be highly energy-efficient, since sensor nodes operate with batteries. Secondly, time synchronization must be accurate to the microsecond level as to fulfill time-critical BAN applications. Thirdly, time synchronization must be secure against passive, active, internal, and external attackers.
Existing secure pairwise time synchronization approaches are based either on receiver-receiver synchronization [2, 3] or on sender-receiver synchronization [3–6]. Based on pairwise time synchronization, secure global time synchronization is achieved by transferring global time from a source node to all the nodes of the network.
Security and accuracy cannot straightforward be provided in WSNs to the cost of sending a larger number of or more frequent synchronization messages for two reasons. Firstly, these solutions impose a high energy cost. Secondly, they do not guarantee that the synchronization of nodes will remain precise between two successive resynchronizations.
We propose a secure, accurate, precise, and energy-efficient time synchronization system for a WSN. We combine secure pairwise synchronization protocol (SPS) [4], rate adaptive time synchronization (RATS) [7], and μ TESLA [8]. SPS is used to achieve highly accurate and pairwise secure synchronization. RATS is used to maintain the accuracy achieved by SPS throughout a long period of time. μ TESLA is employed to enable efficient digital signatures for BAN-wide broadcast message synchronization.
The system can be used in WSN with extremely low-duty cycle nodes. The system achieves resiliency against compromised nodes without requiring repeating synchronization messages or continuous media sensing. The energy cost of the system is also very low.
The contributions of this paper are fivefold. Firstly, we derive the requirements for a secure time synchronization service for WSNs. Secondly, we exhaustively evaluate existing secure time synchronization proposals for WSN. Thirdly, we propose the SPS with sample exchange (SPS-SE) protocol, a SPS-based protocol for synchronizing two nodes and exchanging time observations for RATS. Fourthly, we propose a novel system for secure time synchronization in a WSN. Finally, we exhaustively evaluate the time synchronization proposal. These results are based on computations.
Temperature is a key parameter influencing clock skews. Therefore, we analyse our proposal for indoor and outdoor scenarios. A representative indoor scenario is a conventional hospital floor with a WSN. A representative outdoor scenario is a field hospital with a WSN.
The remainder of this paper is organized as follows. Section 2 derives the requirements for a secure time synchronization service and evaluates existing secure time synchronization proposals. In Section 3, we present the model of WSN for our system and we give important definitions and background. We describe our time synchronization system in Section 4. Sections 5 and 6, respectively, evaluate the security and performance level of the system. Finally, Section 7 concludes and discusses our future work.
2. Evaluation of Secure Time Synchronization Approaches
We first derive the requirements for a secure time synchronization service for WSNs. Secondly, we classify and evaluate existing secure time synchronization schemes against these requirements.
2.1. Requirements
A secure time synchronization service for WSNs must comply and trade off the following requirements: low cost, accurate, precise, secure, and periodically-scheduled.
Firstly, among all sensor node components, the radio consumes the most significant amount of energy [9, 10]. Therefore, the synchronization service must minimize the number of messages exchanged by sensor nodes. Secondly, the time synchronization service must enable applications with time accuracy demands at the tens of μ s level. Thirdly, time synchronization among nodes must be precise up to the hundreds of μ s for long periods. This requirement is particularly challenging to comply with for low-cost sensor nodes. Fourthly, WSNs are especially vulnerable to security attacks. Since sensor nodes use wireless communications, an external attacker may easily delete, forge, and modify time synchronization messages. Additionally, the attacker may launch pulse-delay [4] and/or wormhole [11] attacks, in which the adversary delays and/or rushes the authenticated synchronization messages, respectively. Since sensor nodes are not tamper-proof, an attacker may also compromise a (or a few) sensor node(s). Then, the attacker can use the sensor node(s) to inject false time synchronization messages. In addition, the attacker may instruct the sensor node(s) not to cooperate in the synchronization protocol. Finally, substantial clock drift during sleep periods requires fine scheduling of the time synchronization protocol.
2.2. Existing Techniques
Ganeriwal et al. [4] proposed several techniques for secure pairwise synchronization (SPS), multihop synchronization, and groupwise synchronization. The SPS adds timestamps and message integrity codes (MICs) to protect the synchronization messages. To remove the time uncertainty introduced by the MAC access waiting time, they propose to timestamp the message below the MAC layer. Their practical measurements show that SPS can synchronize two Mica2 motes with an accuracy of 10 μ s. An attacker can delay a time synchronization message only up to 20 μ s without being noticed. However, SPS exhibits no resiliency to compromised nodes.
Secure multi-hop synchronization [4] can be used to synchronize sensor nodes not within direct wireless communication range. Ganeriwal et al. propose three similar techniques: secure opportunistic multi-hop (SOM), secure direct multi-hop (SDM), and secure transitive multi-hop (STM). The three techniques extend SPS by using one or a set of intermediate trusted nodes. For five hops, SDM and STM provide a 25 μ s time synchronization accuracy and exhibit a pulse-delay attack vulnerability window of 50 μ s to 120 μ s, respectively. However, they exhibit no resiliency to compromised nodes. SOM can cope with compromised nodes but exhibits very poor accuracy and pulse-delay protection.
Group multi-hop synchronization [4] can be used to synchronize a group of sensor nodes of a wireless neighborhood. They first propose a lightweight secure group synchronization (L-SGS) that exploits multicast authentication to synchronize the neighborhood. This technique is also vulnerable to compromised nodes. To solve this vulnerability, Ganeriwal et al. propose secure group synchronization (SGS). SGS requires nodes to exchange and process messages after the initial multicast exchange to check time consistency. SGS and L-SGS provide 10 μ s accuracy and 20 μ s pulse-delay vulnerability window. The consistency check is inefficient, since it does not exploit the broadcast nature of the wireless neighborhood. Moreover, the consistency check can only tolerate one compromised node, and no provision is made to cope with a subset of compromised nodes. Moreover, they allow for whatever neighborhood member to anarchically start the (L-)SGS protocol, which can be exploited for battery depletion attacks.
Manzo et al. [2] discuss several internal attacks against and countermeasures for Reference Broadcast Synchronization (RBS) [12], Timing-sync Protocol for Sensor Networks (TPSN) [13], and Flooding Time Synchronization Protocol (FTSP) [14]. The internal attacks can be summarized as different flavors of injecting false information to disrupt the time synchronization protocol operation, for example, introducing false timestamps. To secure time synchronization protocols, they suggest to elect time root nodes probabilistically, to send time synchronization messages through alternate paths, and to use μ TESLA [8] to authenticate broadcast synchronization messages. Unfortunately, the strength and performance of these countermeasures is not analyzed. Moreover, they provide no mechanism to authenticate the timeliness of synchronization messages and thus no protection against pulse-delay and wormhole attacks.
Song et al. [3] investigated countermeasures for delay attacks against synchronization messages launched from compromised nodes. They proposed two methods for detecting and tolerating delay attacks: a generalized extreme studentized deviate (GESD) based and a threshold based. The general idea is to identify the malicious time offsets that are under delay attacks after collecting a set of time offsets from multiple involved nodes. The underlying assumption is that a malicious node magnifies its clock offset to accomplish the delay attack. Then, the GESD-based method filters out an outlier by applying the assumption that clock offsets from benign nodes follow the same (or similar) distribution or pattern. Similarly, the threshold-based method filters out outliers by rejecting clock offsets above an upper bound. They also show that these methods can be used to improve the accuracy of RBS in the presence of clock offset outliers. However, Song et al. do not provide arguments and/or proofs validating that benign clocks follow the same (or similar) distribution in practice. Moreover, both methods require each node to receive a sufficiently large number of messages to detect outliers, thus the accuracy improvement comes at a substantial energy cost.
Sun et al. [6] proposed to leverage SPS and μ TESLA to provide global time synchronization in multi-hop static WSNs. SPS is periodically and asynchronously employed to pairwise synchronize all the nodes of the WSN. Subsequently, global time is transferred from (set of) source nodes to the rest of sensor nodes. To improve the communication efficiency, authenticated global time synchronization messages are broadcasted locally in a wireless neighborhood (cf. L-SGS and SGS). To be resilient against compromised nodes, nodes already synchronized to global time rebroadcast synchronization messages. To tolerate up to t compromised neighbor nodes, the receiver must select among 2t + 1 clock differences through different neighbor nodes.
Sun et al. demonstrated experimentally that for a WSN with only 60 nodes and to tolerate up to 4 compromised nodes per neighborhood, their approach reaches an average global time accuracy below 52.08 μ s and a minimum accuracy below 121.52 μ s right after running the protocol. These numbers correspond to global time synchronization intervals of 5 to 10 seconds. Unfortunately, they do not discuss how this accuracy evolves through the 5- or 10-second interval. Since the clock drift of the CC2420 is 40 ppm [9], the time accuracy of two nodes can diverge up to 80 μ s per second after the synchronization. Then, in practice in 5 and 10 seconds the synchronization can loose precision up to 521.52 μ s and 921.52 μ s, respectively.
To avoid such poor accuracy, we can set up a lower global synchronization interval and, accordingly, also a lower pairwise synchronization interval. However, simple analysis shows that the effect is a substantial increase in energy consumption needed to send multiple re-synchronization messages.
The connectivity of the nodes with the rest of the network is not motivated or argued by Sun et al.'s proposal. In cases with cliquish neighborhoods the resiliency improving approach can turn out to be useless, since neighborhood nodes cannot get global time through different wireless paths to the rest of the WSN.
We identify a number of open issues in the previous proposals. Firstly, none of the above presented approaches analyze the period of time required to synchronize nodes with any of their proposed techniques, failing then to prove effective and efficient for low-duty cycle sensor nodes. For instance, if a WSN application requires nodes to sleep 99% of time, is 1% of time sufficient to synchronize time of sensor nodes? Which fraction of time out of that 1% is to be dedicated for time synchronization? Which is the maximum accuracy the sensor clocks will achieve? Yet more important, which accuracy will the sensor clocks maintain during each synchronization interval? and how much power needs a sensor to invest to achieve such accuracy level?
Secondly, none of these proposals discuss the scheduling of the time synchronization protocol. Unless we assume unsustainable 100% duty cycles, time synchronization cannot be completely asynchronous, but nodes need to prearrange well-delimited intervals of time to synchronize.
Finally, protection for time synchronization protocols against wormhole attacks is not analyzed. Sun et al. [6] propose to detect wormholes by detecting that the transmission delay is less than the maximum expected delay. However, this solution is at odds with the nature of a wormhole, since a wormhole attack decreases the latency of messages exchanged by two nodes at different locations in the WSN [15].
Hoepman et al. [16] consider an adversary that aims at tampering with the clock synchronization by intercepting messages, replaying intercepted messages, and capturing nodes (i.e., revealing their secret keys and impersonating them).
They present a clock sampling algorithm which tolerates attacks by this adversary, collisions, a bounded amount of losses due to ambient noise, and a bounded number of captured nodes that can jam, intercept, and send fake messages. The algorithm is self-stabilizing, so if these bounds are temporarily violated, the system can stabilize back to a correct state.
The core of their clock synchronization algorithm is a mechanism for sampling the clocks of neighboring nodes at reception of broadcasts called beacons. A beacon acts as a shared reference point.
3. Wireless Sensor Network Model
A BAN consists of wireless connected sensors nodes worn by or implated to a human body. A sensor node is a low-cost, low-power, wireless-enabled computing device. New sensor nodes can be incrementally added after the initial deployment. The BAN ranges a few meters around a human body.
Each BAN includes a controller node (CN) with routing, data fusion, and other functions. The role of this node can be assigned either to a single sensor node or dynamically to any of the nodes of the BAN. Let us assume that in average a BAN includes n sensor nodes. Two neighbour CNs are connected by a direct wireless link.
A WSN is the interconnection of multiple BANs by means of the controller nodes. The number of WSN nodes can range up to thousands of nodes. Therefore, the WSN can occupy a huge area.
The WSN can be formed in public or hostile areas, where wireless communications can be easily eavesdropped, deleted, and/or modified. In some applications, sensor nodes are left unattended (when detached from the monitored body), being then prone to capture and manipulation by an attacker. The monitored human itself may also be an intruder and, thus, may manipulate its body-attached nodes.
We also assume that nodes share pairwise keys [17]. Alternatively, each pair of nodes can directly derive a pairwise key [18, 19] just by knowing each node ID, without the need to exchange further messages.
Integrity-protected messages are timestamped below the MAC layer using existing techniques. Therefore, the period of uncertainty needed for the host to access the network interface card and to backoff is removed as demonstrated in [6].
Data sensed by sensor nodes is to be sent to a (small number of) base station(s) in a central or remote location.
3.1. Power Management
The WSN is provided of a power management service to save energy of sensor nodes. This service, in turn, guarantees the longest longevity for the WSN. The basic idea of the power management service is to put the radio of sensor nodes to sleep during idle times and wake it up right before message transmission and/or reception.
To allow communication in WSNs formed of low-duty cycle nodes, sensor nodes need to synchronize active and wake periods of time. This synchronization can be achieved synchronizing each sensor node to a common reference time. However, sensor nodes embed low-cost crystal oscillators which drift from the reference time. Consequently, sleep Tsleep and wake Twake periods are not equally measured by all the sensor nodes.
A time period of guard Tguard is defined to enable active periods from two sensor nodes to overlap despite their respective clock drift errors. The time of guard Tguard is a local time measure. During its time of guard, a sensor node can receive but cannot send data.
3.2. Definitions
In the rest of the paper we use the following definitions.
-
(i)
Pairwise Time. Pairwise time is the agreed synchronized time between two arbitrary sensor nodes u and v.
-
(ii)
BAN Time. BAN time is the agreed synchronized time among the sensor nodes of a BAN.
-
(iii)
WSN Time. WSN time is the agreed synchronized time among all the sensor nodes of the WSN.
-
(iv)
Coordinated Universal Time (UTC). This is the global synchronized time used by humans.
-
(v)
Clock Accuracy. Clock accuracy is the degree of closeness of a measured time value to that of a reference clock. For instance, let us consider a reference clock at 12:00:00. A clock c1 measuring 12:05:00 after 2 days of having been perfectly synchronized is considered to be inaccurate.
-
(vi)
Precision. Precision is the degree of closeness to which repeated measured time values agree with each other under unchanged conditions. Let us consider again the clock c1. During 10 consecutive days, we obtain time readings differing 10 seconds from each other and differing an average of 5 minutes from the reference clock. We consider c1 to be a precise yet inaccurate clock.
3.3. Prediction of Clock Skew
The time difference measured by two different clocks t u and t v depends on differences in phase and frequency of oscillation of each clock. The phase and the frequency oscillation variation of a clock is often referred in the literature to as clock offset and clock skew, respectively.
Initially, the offset counts the elapsed time from the time of start of t u in respect to t v or vice versa. Note that instantaneously correcting the offset between two clocks is relatively simple by running for instance a pairwise synchronization protocol. However, because of the effect of the clock skew, the two clocks drift after the initial synchronization. Therefore, to keep the clock drift under a required upper bound, all the related schemes in Section 2.2 propose to resynchronize frequently. Instead, to reduce the frequency of re-synchronization and, thus, the energy consumption of sensor nodes, we propose to predict the clock skew of each sensor node clock.
The variation of clock skew depends on different non-deterministic factors: including aging, noise, warmup, variations in temperature, atmospheric pressure, acceleration, voltage, radiation, and magnetic fields [20, 21].
We observe that temperature is the factor most influencing the frequency of the clocks. Temperature can cause variations up to several tens of ppm while the aggregated variation caused by other factors is far below 1 ppm [21].
We also observe that in typical WSN environments temperature changes smoothly. For instance, outdoors the temperature changes smoothly because of weather conditions. The temperature keeps relatively constant in normal circumstances in most indoor scenarios. In BANs, the effect of temperature change rate is even more negligible, since sensor nodes are separated just a few centimeters from each other.
Hereafter, a time period of no substantial temperature change is referred to as epoch. We assume that the clock skew for each sensor node and, thus, the relative clock skew for two nodes remain constant during an epoch [21].
Ganeriwal et al. [7] designed a prediction-based algorithm to model long-term clock skew between two sensor node clocks t u and t v . Wu et al. [21] and Elson et al. [12] developed similar concepts, demonstrating thus its suitability for WSNs.
After Ganeriwal et al. [7], the following P-degree polynomial represents the relative clock model between two nodes u and v:

where  is the prediction of of the actual t
v
measured with the clock of node u. The error
is the prediction of of the actual t
v
measured with the clock of node u. The error  includes both measurement errors and environmental factors that influence the clock stability. Over short timescales, there is the general agreement that a linear relative clock model (P = 1) is sufficient [7, 12–14].
includes both measurement errors and environmental factors that influence the clock stability. Over short timescales, there is the general agreement that a linear relative clock model (P = 1) is sufficient [7, 12–14].
Given a window of W past observations  ,
,  , the parameters β0 and β1 are the values which minimize the residual sum of squares (RSS):
, the parameters β0 and β1 are the values which minimize the residual sum of squares (RSS):

It is easy to see that finding the values β0 and β1 which minimize RSS is an extremely low-complexity problem. Then, the energy consumed by calculating these parameters can be neglected in comparison to the cost of sending a bit.
We define a sampling period S as the interval of time separating two consecutive observations  and
and  . Naturally, shorter values of S minimize the error of the prediction.
. Naturally, shorter values of S minimize the error of the prediction.
Given S, there exists an optimal window size W which minimizes the error of the prediction. For instance, Ganeriwal et al. [7] experimentally showed that W = 8 and S =60 seconds minimize the prediction error E p for indoor environment at a temperature range from 25 to 26°C.
In practice, each time we obtain new time observations, by using the low-cost rate adaptive time synchronization algorithm (RATS) [7], we can calculate two optimal values S and W which maintain the error of the prediction within a desired error bound for the calculated S.
3.4. Estimation of Prediction Error
Given a time window of W observations,  , the time at node v,
, the time at node v,  , can be predicted using time at node u, t
u
, with (1). Following standard regression theory, we can construct a
, can be predicted using time at node u, t
u
, with (1). Following standard regression theory, we can construct a  confidence interval for this prediction as
confidence interval for this prediction as

where

The first term of the product in (4) refers to an upper quantile of the t
vs
distribution with  degrees of freedom. The second term is the standard error (SE) of the predicted value.
degrees of freedom. The second term is the standard error (SE) of the predicted value.
3.5. The RATS Algorithm
The objective of RATS is to repeatedly calculate a new sampling period S so that the synchronization error remains bounded within the user specifications. The pseudocode for the RATS algorithm is as follows:
-
(1)
compute
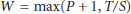 ,
, -
(2)
calculate (
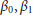 ) using a window of W samples in (2),
) using a window of W samples in (2), -
(3)
compute
 using (4),
using (4), -
(4)
compute
 ,
, -
(5)
if
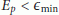 , then
, then 
else if  , then
, then  ,
,
-
(6)
if
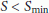 , then
, then 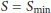
else if  , then
, then  .
.
RATS starts with calculating the optimal window size  using the optimal time window
using the optimal time window  for the given sampling period
for the given sampling period  . The relative clock model is estimated using a linear estimator on the sample history equal to
. The relative clock model is estimated using a linear estimator on the sample history equal to  . The estimation of the prediction error,
. The estimation of the prediction error,  , is then computed and scaled using the scaling factor
, is then computed and scaled using the scaling factor  .
.
If the error of the prediction  is below the lower threshold, we multiplicatively increase the sampling period. Conversely, if it is above the higher threshold, the sampling period is decreased multiplicatively. The sampling period remains unchanged if the error is between the two thresholds. At the end, we make sure that the new sampling period is within
is below the lower threshold, we multiplicatively increase the sampling period. Conversely, if it is above the higher threshold, the sampling period is decreased multiplicatively. The sampling period remains unchanged if the error is between the two thresholds. At the end, we make sure that the new sampling period is within  to avoid an unbounded increase/decrease of the sampling period.
to avoid an unbounded increase/decrease of the sampling period.
During a 2–4-hour learning phase, the nodes derive the values of the optimal time window  and scaling factor
and scaling factor  for a wide range of
for a wide range of  values. In [7], it is showed that this initial calibration is consistent with a great number of environments and for long periods of time. In deterministic WSN deployments, the initial calibration can be performed in factory to save postdeployment energy [7]. In random and mobile WSN deployments in factory calibration would not scale, since we ignore which sensor nodes will be neighbors after the deployment. Therefore, in these cases, the calibration must be performed autonomously by the nodes at the deployment site.
values. In [7], it is showed that this initial calibration is consistent with a great number of environments and for long periods of time. In deterministic WSN deployments, the initial calibration can be performed in factory to save postdeployment energy [7]. In random and mobile WSN deployments in factory calibration would not scale, since we ignore which sensor nodes will be neighbors after the deployment. Therefore, in these cases, the calibration must be performed autonomously by the nodes at the deployment site.
4. Secure WSN-Wise Synchronization
Our proposal consists of two periodic phases. In case the WSN needs to also synchronize to UTC time, we propose to add a third phase.
-
(1)
Secure CN Pairwise (Re-)synchronization. Each pair of neighbor CNs use the SPS-SE protocol to synchronize, initialize and maintain RATS, and schedule each subsequent time synchronization iteration. In this manner, a common time reference is set up for the WSN.
-
(2)
Secure BAN (Re-)synchronization. The CN uses the SPS-SE protocol to synchronize each BAN member. In this manner, a common time reference is set up for the BAN. RATS is accommodated to use it with multiple nodes.
-
(3)
UTC Synchronization. WSN time is translated to UTC time.
In the remainder of this paper, let us consider that at each period  a new controller node is elected in each BAN. Note that if the controller node is fixed, then R is the WSN lifetime.
a new controller node is elected in each BAN. Note that if the controller node is fixed, then R is the WSN lifetime.
We divide pairwise and BAN time in a number of variable time periods  and
and  , where
, where  complying
complying  and
and  complying
complying  , respectively. A period
, respectively. A period  or
or  can encompass one or more consecutive sleep plus wake intervals. In any case, we define the beginning of each period
can encompass one or more consecutive sleep plus wake intervals. In any case, we define the beginning of each period  or
or  right to coincide with the beginning of a wake interval.
right to coincide with the beginning of a wake interval.
The duration of a period  does not necessarily coincide with any
does not necessarily coincide with any  , for
, for  . The duration of a period
. The duration of a period  does not necessarily coincide with any
does not necessarily coincide with any  , for
, for  . The duration of a period
. The duration of a period  does not necessarily coincide with any
does not necessarily coincide with any  , for
, for  .
.
In the predeployment phase, that is, during manufacture, the sensor nodes are preconfigured with an initial default sampling period S d and an initial optimal window size W d . Once deployed, starting from the beginning of BAN existence, the nodes exchange W d time observations, each sample separated by S d seconds. The messages used to exchange these observations are protected by secure means.
After  seconds, the sensors derive the first estimate of their clocks using (1). If this estimation error is between the thresholds
seconds, the sensors derive the first estimate of their clocks using (1). If this estimation error is between the thresholds  , then the sensor nodes use the clock estimations for synchronizing. Otherwise, the sensors keep exchanging time observations each S
d
seconds till the estimation error is between the two thresholds. From this moment on, the sensors use the clock estimations for synchronizing.
, then the sensor nodes use the clock estimations for synchronizing. Otherwise, the sensors keep exchanging time observations each S
d
seconds till the estimation error is between the two thresholds. From this moment on, the sensors use the clock estimations for synchronizing.
During the rest of the BAN existence, the quality of the estimation is optimized to the particular conditions of each epoch. The nodes employ RATS to periodically calculate the optimal duration of  and
and  ,
,  , to maintain the precision of the clock estimations between the thresholds
, to maintain the precision of the clock estimations between the thresholds  . Moreover, a corresponding new optimal window size
. Moreover, a corresponding new optimal window size  and
and  ,
,  , is obtained. Additionally, after each interval
, is obtained. Additionally, after each interval  or
or  ,
,  , the nodes securely exchange a new time sample and recalculate the clock estimations.
, the nodes securely exchange a new time sample and recalculate the clock estimations.
These steps are repeated after each controller node re-election.
In the rest of the section, we thoroughly describe the SPS-SE protocol and each of the phases of the synchronization system.
4.1. Secure Pairwise Synchronization with Sample Exchange
We propose a protocol for secure pairwise synchronization and sample exchange that leverages SPS [4]. SPS is based on sender-receiver synchronization. It performs a handshake protocol between two nodes u and v.
The integrity and authenticity of SPS-SE messages are guaranteed using message integrity codes (MICs) and a shared key  . Moreover, the MIC provides resistance to pulse-delay attacks and external attackers.
. Moreover, the MIC provides resistance to pulse-delay attacks and external attackers.
The SPS-SE protocol consists of the following message exchanges (time samples between brackets denote message time of send (tos) or time of arrival (toa)):
-
(1)
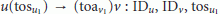 ,
, -
(2)
 , MIC2
, MIC2 -
(3)
 , MIC3,
, MIC3,
where  ,
,  , and
, and  is the key shared by u and v.
is the key shared by u and v.
At the end of the protocol, both nodes calculate the SPS message end-to-end delay  as specified in [4]:
as specified in [4]:

The end-to-end delay is used to detect pulse-delay attacks against SPS-SE.
The clock offset  is also calculated as follows:
is also calculated as follows:

Subsequently, u and v add the new time sample  to their respective sample repository.
to their respective sample repository.
For sensor nodes using crystal oscillators with stability up to 100 ppm, the duration of the protocol is to be bounded to a few hundred milliseconds. In such case, we can assume the clock drift to be negligible and accept the time observations accurate enough for the prediction.
4.2. Synchronization Method
The synchronization method allows two nodes to adapt their respective time measures. We distinguish two methods: short-lasting synchronization and long-lasting synchronization.
4.2.1. Short-Lasting Synchronization
Short-lasting synchronization is used during the initialization phase of RATS for the nodes to establish short-lasting accurate clock synchronization and for exchanging samples for a clock estimation with the required target precision.
Note that because of the low quality of clock crystals, this method cannot be used to maintain a high precision during a relative long time without an expensive energy cost. For instance, the CC2420 can drift up to 80 μ s per second, and in 60 seconds the clocks may drift up to 4810 μ s. To guarantee a precision below the 100 μ s, the nodes would need to synchronize each second.
The method works as follows. Firstly, by using the SPS-SE protocol, two nodes u and v calculate their relative clock offset. Subsequently, to synchronize a node's time measure, with another's clock measure the clock offset is added (or subtracted, as needed). For instance, if sensor u collects and timestamps a data sample at  ,
,  translates data collection time to
translates data collection time to  to get the time measure relative to its own notion of time.
to get the time measure relative to its own notion of time.
For subsequent message exchanges between u and v, the message delay d needs also to be taken into account to calculate the synchronized time. For messages timestamped below the MAC layer immediately prior to their transmission, the delay (d) adds the contribution of the transmission time, the propagation time, and the reception time. The transmission time is the time needed for the sender to transmit the message bit by bit at the physical layer. This time can be easily calculated by the receiver by knowing the length in bits of the message and the radio speed. The propagation time is the actual time taken by the message to traverse the wireless link from the sender to the receiver. In WSN, the distance among neighbor sensor nodes is of a few meters. Therefore, because radio waves move at the speed of light and the radio speed is up to a few Mbit/s, the propagation time is neglected compared to the rest of times. The reception time accounts for the time taken by the receiver in receiving the bits and passing them to the MAC layer. This time can also be easily calculated by the receiving node. Thus,

For instance, for a timestamped message that u sends at time  and reaches v at time
and reaches v at time  , v will interpret sent time as
, v will interpret sent time as  . For instance, v can check the time integrity of the message by verifying that the difference between
. For instance, v can check the time integrity of the message by verifying that the difference between  and
and  is below a certain threshold.
is below a certain threshold.
4.2.2. Long-Lasting Synchronization
Long-lasting synchronization is used to maintain precise clock synchronization with fine-tuned RATS.
Each new time sample (e.g., ( ,
,  )) exchanged with SPS-SE includes the offset but not the delay contribution, which is a particular measure of each exchanged message. Therefore, with estimated clocks, for a timestamped message that u sends at time
)) exchanged with SPS-SE includes the offset but not the delay contribution, which is a particular measure of each exchanged message. Therefore, with estimated clocks, for a timestamped message that u sends at time  and reaches v at time
and reaches v at time  , v will interpret sent time as
, v will interpret sent time as  . Furthermore, if sensor u collects and timestamps a data sample at
. Furthermore, if sensor u collects and timestamps a data sample at  , v translates data collection time to
, v translates data collection time to  to get the time measure relative to its own notion of time. Here
to get the time measure relative to its own notion of time. Here  is an estimation of the current offset between
is an estimation of the current offset between  and
and  .
.
4.3. Secure CN Pairwise (Re-)Synchronization
Secure CN pairwise (re-)synchronization is used to periodically synchronize two neighbor CNs. Each and every pair of neighboring CNs of the WSN is to synchronize following this method. In this manner, WSN time is established.
The interval of time  starts right after two newly elected CNs
starts right after two newly elected CNs  and
and  discover each other by physical and MAC layer means (the description of these means is out of the scope of this paper).
discover each other by physical and MAC layer means (the description of these means is out of the scope of this paper).
During time periods  ,
,  , BAN controller nodes use the short-lasting synchronization method. Additionally, this time is also employed to exchange the first
, BAN controller nodes use the short-lasting synchronization method. Additionally, this time is also employed to exchange the first  time samples. Right at the beginning of each time period
time samples. Right at the beginning of each time period  ,
,  , by using the SPS-SE protocol nodes
, by using the SPS-SE protocol nodes  and
and  synchronize and exchange a time sample
synchronize and exchange a time sample  ,
,  . To detect wormhole and pulse-delay attacks, each CN also measures the maximum SPS-SE expected message delay
. To detect wormhole and pulse-delay attacks, each CN also measures the maximum SPS-SE expected message delay  .
.
At the beginning of period  both CNs calculate the first clock estimations and initialize RATS for the first time. At the end of
both CNs calculate the first clock estimations and initialize RATS for the first time. At the end of  both CNs estimate their relative clock offset as follows:
both CNs estimate their relative clock offset as follows:

If  is below the required accuracy threshold
is below the required accuracy threshold  , then RATS is considered to be fine-tuned. Consequently, BAN controller nodes switch to the long-lasting synchronization method for the following BAN periods.
, then RATS is considered to be fine-tuned. Consequently, BAN controller nodes switch to the long-lasting synchronization method for the following BAN periods.
Otherwise, yet the synchronization method to be used is short-lasting synchronization for subsequent BAN periods  ,
,  , till the condition
, till the condition  is satisfied. Let us refer to the period when this condition is satisfied as
is satisfied. Let us refer to the period when this condition is satisfied as  . Typically,
. Typically,  .
.
During BAN periods  ,
,  , BAN controller nodes use the long-lasting synchronization methods. Right at the beginning of each of these periods,
, BAN controller nodes use the long-lasting synchronization methods. Right at the beginning of each of these periods,  and
and  exchange a new time sample (
exchange a new time sample ( ,
,  ) by using the SPS-SE protocol and add it to their respective sample repository. RATS is employed to periodically recalculate
) by using the SPS-SE protocol and add it to their respective sample repository. RATS is employed to periodically recalculate  (see Section 4.3.1). Additionally, the clock estimations are recalculated using (1). Finally, a real measure of the clock offset is calculated using the SPS-SE protocol to validate the estimation of the clock offset and, thus, to continuously monitor the quality of the clock estimations.
(see Section 4.3.1). Additionally, the clock estimations are recalculated using (1). Finally, a real measure of the clock offset is calculated using the SPS-SE protocol to validate the estimation of the clock offset and, thus, to continuously monitor the quality of the clock estimations.
Since the clocks of CN
u
and CN
v
drift throughout  ,
,  , the measure of
, the measure of  at the end of the period will likely be different at
at the end of the period will likely be different at  and
and  . To counter this relativistic effect, we define pairwise period-dependent time of guard. Despite the fact that clocks can get desynchronized, the time of guard guarantees that both CNs are ready to concurrently use the radio channel after long sleeping periods. In order to preserve energy of nodes the time of guard needs to be accurately minimized.
. To counter this relativistic effect, we define pairwise period-dependent time of guard. Despite the fact that clocks can get desynchronized, the time of guard guarantees that both CNs are ready to concurrently use the radio channel after long sleeping periods. In order to preserve energy of nodes the time of guard needs to be accurately minimized.
The pairwise period-dependent time of guard to be used at the beginning of  ,
,  , is calculated as follows:
, is calculated as follows:

During its  each CN is only allowed to receive messages. The first CN exhausting its
each CN is only allowed to receive messages. The first CN exhausting its  triggers the re-synchronization.
triggers the re-synchronization.
At the very end of each period  ,
,  , the offset
, the offset  is accurately predicted by using (8).
is accurately predicted by using (8).
The uncertainty included by the data rate  is just 4 ppm at 250 kbps. Because nodes of a WSN are separated at most a few tens of meters, the contribution by the propagation delay can be neglected.
is just 4 ppm at 250 kbps. Because nodes of a WSN are separated at most a few tens of meters, the contribution by the propagation delay can be neglected.
4.3.1. Calculation of Optimal Sample Period and Window Size
By using RATS, the two CNs calculate the optimal window size  for the current period
for the current period  . Additionally, the optimal duration for the the current period
. Additionally, the optimal duration for the the current period  is recalculated. The pseudocode for the RATS algorithm is as follows:
is recalculated. The pseudocode for the RATS algorithm is as follows:
-
(1)
compute
 ,
, -
(2)
calculate (
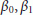 ) using a window of
) using a window of 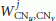 samples in (2),
samples in (2), -
(3)
compute
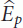 using (4),
using (4), -
(4)
compute
 ,
, -
(5)
if
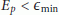 , then
, then 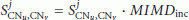
else if  , then
, then  ,
,
-
(6)
if
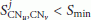 , then
, then 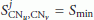
else if  , then
, then  .
.
4.3.2. Estimation of Relative Clock Skew
By using the time observations ( ,
,  ), where
), where  in (1) and (2), nodes
in (1) and (2), nodes  and
and  estimate
estimate  and
and  , respectively.
, respectively.
4.4. Secure BAN (Re-)Synchronization
Secure BAN (re-)synchronization is used to periodically synchronize BAN members with the CN. This, in turn, guarantees that each BAN member is synchronized to the same reference time. This process establishes BAN time without the need for each BAN member to pairwisely synchronize.
BAN wise synchronization can be scheduled in two different manners. First, we let each node to independently schedule its re-synchronization interval. That is, each node has an own measure of the BAN period  . At the beginning of each node-dependent BAN period, the node synchronizes with the CN. This manner requires the CN to be asleep each time a BAN member
. At the beginning of each node-dependent BAN period, the node synchronizes with the CN. This manner requires the CN to be asleep each time a BAN member  is to synchronize. Because of the independency of the length of each
is to synchronize. Because of the independency of the length of each  ,
,  , the requirement of low-duty cycling is hard to comply for the CN.
, the requirement of low-duty cycling is hard to comply for the CN.
A second manner consists of letting the CN to schedule a unique re-synchronization interval  for all the BAN members. At the beginning of each BAN period, a slot of time is reserved for each node to synchronize with the CN. This scheduling can be designed to accommodate for CN duty cycling requirements.
for all the BAN members. At the beginning of each BAN period, a slot of time is reserved for each node to synchronize with the CN. This scheduling can be designed to accommodate for CN duty cycling requirements.
Observe that to comply that clock estimations are below the required accuracy level during the period  , then the
, then the  must select as
must select as  the minimum duration for a BAN period required by all the nodes of the BAN.
the minimum duration for a BAN period required by all the nodes of the BAN.
To solve this issue, we have again two possible approaches. The first approach consists of letting each node  of the BAN,
of the BAN,  , calculate its own measure of
, calculate its own measure of  , that is,
, that is,  . Then, each node independently sends
. Then, each node independently sends  to the CN. Finally, the CN heads select
to the CN. Finally, the CN heads select  for all
for all  .
.
The second approach consists of the  calculating
calculating  for all
for all  ,
,  . Then, the CN heads select
. Then, the CN heads select  for all
for all  .
.
We favor the second approach because it does not require the nodes to send  to the CN. The need to send messages has implications of added energy consumption and delay both for the BAN members and the CN. The second approach requires much more computational effort in the CN than the first approach. However, the implied energy consumption and delay are neglected compared to the overhead of the first approach.
to the CN. The need to send messages has implications of added energy consumption and delay both for the BAN members and the CN. The second approach requires much more computational effort in the CN than the first approach. However, the implied energy consumption and delay are neglected compared to the overhead of the first approach.
The rest of the section describes the details of this second approach.
The interval of time  starts right after the BAN is formed. Right at its beginning the CN generates a BAN broadcast key chain of length
starts right after the BAN is formed. Right at its beginning the CN generates a BAN broadcast key chain of length  by repeatedly hashing a random value
by repeatedly hashing a random value  . The successive keys
. The successive keys  ,
,  , are to be used with μ TESLA to protect broadcast synchronization messages. We assume that the reader is familiar with μ TESLA [8].
, are to be used with μ TESLA to protect broadcast synchronization messages. We assume that the reader is familiar with μ TESLA [8].
The duration of the first  time periods
time periods  ,
,  , is fixed by default. The intervals
, is fixed by default. The intervals  ,
,  , are used to exchange the first
, are used to exchange the first  time samples that allow for RATS initialization and for the first clock estimations. At the beginning of each of these periods the
time samples that allow for RATS initialization and for the first clock estimations. At the beginning of each of these periods the  and each node
and each node  of the BAN,
of the BAN,  , synchronize and exchange a new time sample
, synchronize and exchange a new time sample  ,
,  , by using the SPS-SE protocol. In one of these SPE-SE exchanges, the CN sends the last value of the key chain
, by using the SPS-SE protocol. In one of these SPE-SE exchanges, the CN sends the last value of the key chain  for each BAN member.
for each BAN member.
Because the clocks are not yet estimated, during time periods  ,
,  , the CN and each node u of the BAN,
, the CN and each node u of the BAN,  , use the short-lasting synchronization method. Note that because of clock drifts, and each node u may need to re-synchronize multiple times during the duration of any period
, use the short-lasting synchronization method. Note that because of clock drifts, and each node u may need to re-synchronize multiple times during the duration of any period  ,
,  .
.
At the beginning of period  the CN calculates the first clock estimations
the CN calculates the first clock estimations  ,
,  , and initializes RATS for the first time. At the end of
, and initializes RATS for the first time. At the end of  the CN and each node u estimate their relative clock offset as follows:
the CN and each node u estimate their relative clock offset as follows:

If  is below the required accuracy threshold
is below the required accuracy threshold  , then RATS is considered to be fine-tuned for the CN and the corresponding node u. Consequently, the CN and the node u complying
, then RATS is considered to be fine-tuned for the CN and the corresponding node u. Consequently, the CN and the node u complying  switch to the long-lasting synchronization method for the following BAN periods.
switch to the long-lasting synchronization method for the following BAN periods.
The nodes not yet complying  are to use the short-lasting synchronization method for subsequent BAN periods
are to use the short-lasting synchronization method for subsequent BAN periods  ,
,  , till the condition
, till the condition  is satisfied.
is satisfied.
In this moment the BAN can have from 0 to n nodes synchronized with the long-lasting method. The remaining nodes, up to the n nodes still use the short-lasting method. This status exists till all the BAN members switch to long-lasting synchronization. For both groups of nodes the subsequent measure of  is different. The first adapts the measure of
is different. The first adapts the measure of  by using RATS. The second keep using the default value of
by using RATS. The second keep using the default value of  .
.
Let us refer to the period when one or more BAN members first switch to long-lasting synchronization as  . Typically,
. Typically,  . Let us use n′ to refer to the BAN members using long-lasting synchronization. In the rest of the section we describe the details of long-lasting synchronization.
. Let us use n′ to refer to the BAN members using long-lasting synchronization. In the rest of the section we describe the details of long-lasting synchronization.
Secure BAN long-lasting re-synchronization is performed at the beginning of each period  ,
,  . By using the SPS-SE protocol, nodes CN and u,
. By using the SPS-SE protocol, nodes CN and u,  , re-synchronize and exchange a new time sample
, re-synchronize and exchange a new time sample  and add it to their respective repository. Additionally, each node u calculates
and add it to their respective repository. Additionally, each node u calculates  . RATS is employed to periodically recalculate
. RATS is employed to periodically recalculate  (see Section 4.4.1).
(see Section 4.4.1).
When each and every pair (CN, u), for  , of the BAN is synchronized, then BAN time is established.
, of the BAN is synchronized, then BAN time is established.
Since the clocks of CN and u,  , drift throughout
, drift throughout  , the measure of
, the measure of  at the end of the period will likely be different at
at the end of the period will likely be different at  and
and  . To counter this relativistic effect, we define BAN period and node-dependent times of guard
. To counter this relativistic effect, we define BAN period and node-dependent times of guard  (see Figure 1) to be used at the beginning of
(see Figure 1) to be used at the beginning of  :
:

where  , is the local identifier of each BAN member and B is the time required to run the SPS-SE protocol in three steps. This method allocates a different time slot for SPS-SE-based synchronization between the CN and a node u.
, is the local identifier of each BAN member and B is the time required to run the SPS-SE protocol in three steps. This method allocates a different time slot for SPS-SE-based synchronization between the CN and a node u.
At the very end of each period  the CN calculates
the CN calculates  , for
, for  . Each node calculates
. Each node calculates  .
.
The CN does not need to contend to access the wireless media. After  and each subperiod
and each subperiod  are exhausted, the CN is the only node in the BAN allowed to start communication. After receiving an initial message from the CN, just the corresponding node u,
are exhausted, the CN is the only node in the BAN allowed to start communication. After receiving an initial message from the CN, just the corresponding node u,  , is allowed to answer.
, is allowed to answer.
4.4.1. Calculation of Optimal Sample Period
By leveraging RATS, the CN calculates the optimal duration for the current period  . The pseudocode for the RATS algorithm is as follows:
. The pseudocode for the RATS algorithm is as follows:
-
(1)
compute
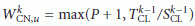 ,
, -
(2)
calculate (
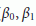 ,) using a window of
,) using a window of  samples in (2),
samples in (2), -
(3)
compute
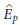 using (4),
using (4), -
(4)
compute
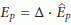 ,
, -
(5)
if
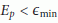 , then
, then 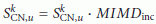
else if  , then
, then  ,
,
( 6) if  , then
, then 
else if  , then
, then  .
.
Finally,  for all u,
for all u,  .
.
Right after  , the CN broadcasts the current period
, the CN broadcasts the current period  in an integrity-protected message under key
in an integrity-protected message under key  . After
. After  seconds, for all u, the CN reveals
seconds, for all u, the CN reveals  (see Figure 2).
(see Figure 2).
In receiving  each node u first validates the authenticity of the key by hashing it and comparing it with the previous stored authentic value
each node u first validates the authenticity of the key by hashing it and comparing it with the previous stored authentic value  . If the validation is positive, then the node stores
. If the validation is positive, then the node stores  to be used in the next BAN time period. Subsequently, the integrity of the message containing
to be used in the next BAN time period. Subsequently, the integrity of the message containing  is verified. Finally, the value
is verified. Finally, the value  is stored for scheduling the next re-synchronization.
is stored for scheduling the next re-synchronization.
4.4.2. Estimation of CN Time
By leveraging RATS, each node u, for  , independently calculates
, independently calculates  with the same pseudocode the CN used (see Section 4.4.1). The node stores the obtained
with the same pseudocode the CN used (see Section 4.4.1). The node stores the obtained  but ignores the obtained
but ignores the obtained  . Instead, it will use
. Instead, it will use  as next sampling period.
as next sampling period.
By using the time observations  , where
, where  in (1) and (2), each node u estimates
in (1) and (2), each node u estimates  .
.
4.5. UTC Synchronization
We propose to securely pairwise synchronize the base station(s) with the CNs to which it is wireless connected using secure pairwise CN synchronization. Additionally, the base station is to be securely synchronized to UTC time by other means (the details of this synchronization means is out of the scope of this paper). Then, a correspondence WSN to UTC is then simple at the base station.
5. Security Analysis and Countermeasures
In this section, we identify threats and propose countermeasures to strengthen the security of our synchronization system. Because all the messages are integrity protected, confidentiality protection is provided when needed, and SPS is robust to pulse-delay attacks, the system is robust against external attackers.
In the rest of the section, we present threats and countermeasures for compromised nodes.
5.1. Coping with a Compromised CN
Because of their key mission in the synchronization system, CNs are an interesting target for attackers. In any case the effect of a compromised CN is bounded to the interval R.
A compromised CNc may fake (a subset of) the time samples  to be sent to v,
to be sent to v,  .
.
To detect this attack, we use the end-to-end delay. The end-to-end delay is bounded by the maximum and minimum expected delay dmax and dmin, respectively. After the SPS-SE protocol is run, v can confidently approximate  . If
. If  , then each faked time sample is rejected.
, then each faked time sample is rejected.
This method serves us to also detect wormhole and pulse-delay attacks. Recall that in pulse-delay and wormhole attacks the adversary delays and rushes the authenticated synchronization messages, respectively. To detect a pulse-delay, the sensor node checks if  . To detect a wormhole, the sensor node checks if
. To detect a wormhole, the sensor node checks if  .
.
In secure BAN re-synchronization, a compromised CN
c
can fake samples  and
and  for a given k. It may assign
for a given k. It may assign  a value substantially greater or lower than the actual
a value substantially greater or lower than the actual  . If
. If  , then the value of
, then the value of  for all u becomes expanded. If
for all u becomes expanded. If  , then the value of
, then the value of  for all u becomes contracted. Additionally, the nodes need to re-synchronize more frequently than the optimal re-synchronization period. In both situations, the effect is to increase the required duty cycle in nodes and, in turn, to consume more energy than the optimal.
for all u becomes contracted. Additionally, the nodes need to re-synchronize more frequently than the optimal re-synchronization period. In both situations, the effect is to increase the required duty cycle in nodes and, in turn, to consume more energy than the optimal.
To overcome this threat, when a CN broadcasts  , it must commit the identity of the node u
x
such that
, it must commit the identity of the node u
x
such that  . Node u
x
verifies that the released
. Node u
x
verifies that the released  corresponds to
corresponds to  .
.
Alternatively, especially to cope with scenarios where CN and node u
x
are compromised, lower and upper acceptable bounds for  can be calculated by each node.
can be calculated by each node.
5.2. Coping with Colluding CNs
A number of neighbor compromised CNs may collide together to create a delayed path through them.
We discuss this attack by assuming the BAN controller nodes in the path  collide, that is, in the moment of secure pairwise CN synchronization they introduced an additional delay in the links
collide, that is, in the moment of secure pairwise CN synchronization they introduced an additional delay in the links  and
and  .
.
To solve the attack we exploit a design property of WSNs for increased reliability and power-efficiency. We assume that there exist multiple routes connecting each pair of CNs.
We propose that a fourth legitimate BAN controller node CN4, which is connected to any of the colliding nodes, detects the delay attack. CN4 compares the delay introduced by the compromised path with the delay introduced by any or a number t of other paths. The countermeasure consists of adding  ,
,  and
and  to a blacklist of untrusted nodes and trigger re-election of controller node.
to a blacklist of untrusted nodes and trigger re-election of controller node.
5.3. Coping with Compromised BAN Members
A compromised node u
c
can fake (a number of) time samples  to be sent to its CN,
to be sent to its CN,  .
.
The CN can detect the attack by using the end-to-end delay, as in the case for a CN cheating a node.
To counter this attack, u c is added to the blacklist of untrusted nodes.
5.4. Temperature Attacks
In order to de-synchronize some nodes, an attacker may select a location and rapidly vary the temperature in the surroundings of one or group of BANs. For instance, in an indoor scenario, the attacker could increase the heating temperature or decrease the cooling temperature.
We believe this kind of attack to be unpractical in BAN applications since the users would quickly realise and stop the heating or cooling system.
6. Performance Analysis
In this section, we analyse the level of accuracy, precision, energy-efficiency, low-duty cycling, and communication overhead that the system can achieve for MICA2 motes.
The results of accuracy and precision are based on experimental findings borrowed from [4, 7]. We assume MAC layer time stamping and cryptographic computation to achieve a high degree of accuracy.
The rest of properties are derived theoretically.
The parameters on Table 1 are used for the performance evaluation of the proposed system.
For simplicity's sake, in the rest of the section, we consider the case with no compromised nodes.
6.1. Pairwise Accuracy and Precision of SPS-SE
The minimum pairwise clock precision (maximum error) of the SPS-SE protocol is 8.46 μ s. Therefore, right after two sensors run the SPS-SE protocol, the accuracy of their synchronized clocks ranges from 0 to 8.46 μ s.
This high level of accuracy can only be maintained at a expensive energy cost, since the node clocks can drift up to 80 μ s per second. For instance, in 60 seconds the clocks may drift up to 4810 μ s.
Therefore, SPS-SE clock synchronization is to be used uniquely to initially exchange the samples for RATS and/or to synchronize the clocks for application requirements.
6.2. Accuracy and Precision of BAN Time
The minimum precision of BAN time combines both the precision of SPS-SE and RATS.
The precision of BAN time depends on the values  and
and  . Figure 3 shows the minimum precision for a range of
. Figure 3 shows the minimum precision for a range of  values for three scenarios: Indoor with a temperature range of 25-26°C, Outdoor I with a temperature range of 17–21°C, and Outdoor II with a temperature range of 22–27°C. The value of
values for three scenarios: Indoor with a temperature range of 25-26°C, Outdoor I with a temperature range of 17–21°C, and Outdoor II with a temperature range of 22–27°C. The value of  used in the experiments is 2.
used in the experiments is 2.
Figure 3 shows that the sampling period  does not significantly affect precision of the clock prediction in Indoor and Outdoor II. Indoor achieves a precision of 20.96 μ s with
does not significantly affect precision of the clock prediction in Indoor and Outdoor II. Indoor achieves a precision of 20.96 μ s with  16 minutes. This result is a great achievement for BANs in terms of expected accuracy level and energy requirements.
16 minutes. This result is a great achievement for BANs in terms of expected accuracy level and energy requirements.
6.3. SPS-SE Duration
The length in time of the SPS-SE protocol can be approximated by the time needed to exchange three messages containing 6 node IDs, 6 timestamps, and 2 MICs. A sufficient number of nodes can be accommodated with 8-byte node IDs (such as in ZigBee networks). A length of 8 bytes is also a fair number for timestamps. A MIC of 16 bytes offers enough security for WSN applications. The physical and MAC layer add a minimum of 17 bytes per message [22]. Then, neglecting other sources of delay, at 250 kbps the SPS-SE protocol exchange lasts approximately 5,72 ms. Table 2 show the parameters used to compute the SPS packet length.
6.4. Minimum Accuracy and Precision of WSN Time
In the initial phase, while RATS is not yet tuned, CNs use SPS-SE for synchronization. Let us define as NCN the maximum number of CNs in the longest synchronization path of the WSN. When WSN time synchronization is triggered, the nodes of the path synchronize sequentially by consecutive pairs. The first pair of nodes synchronizes with minimum accuracy 8.46 μ s. While the second pair of nodes synchronize, the clock of the first two synchronized nodes may drift up to 40 ppm times the duration of SPS-SE. The SPS-SE is used  times after the initial one. Therefore, the minimum accuracy of WSN time can be approximated as
times after the initial one. Therefore, the minimum accuracy of WSN time can be approximated as  μ s.
μ s.
During the RATS phase, the precision of WSN time depends on the values  ,
,  and on the number of intermediate CNs. Figure 4 shows the minimum precision for
and on the number of intermediate CNs. Figure 4 shows the minimum precision for  and a range of
and a range of  values for three scenarios: Indoor with a temperature range of 25-26°C, Outdoor I with a temperature range of 17–21°C, and Outdoor II with a temperature range of 22–27°C. The value of
values for three scenarios: Indoor with a temperature range of 25-26°C, Outdoor I with a temperature range of 17–21°C, and Outdoor II with a temperature range of 22–27°C. The value of  used in the experiments is 2.
used in the experiments is 2.
Figure 4 (cf. Figure 3) demonstrates that the number of intermediate CNs NCN does not significantly affect precision of the clock prediction.
6.5. Applicability for Low-Duty Cycle Nodes
In this section we demonstrate applicability of the synchronization system for low-duty cycle nodes. Since CNs need to be active longer periods than BAN members and any node may become CN, we only analyze the minimum duty cycle required for a CN.
We use sampling window size  and period
and period  minutes, which allow a high level of precision in any scenario, as demonstrated in Figures 3 and 4.
minutes, which allow a high level of precision in any scenario, as demonstrated in Figures 3 and 4.
During the RATS phase, a CN needs to be active for each secure pairwise CN re-synchronization and for secure BAN re-synchronization. The initial synchronization is ignored in this analysis as it occurs when nodes need to otherwise increase their duty cycle for BAN formation purposes.
For BAN time synchronization, in each period  , a CN needs to be active a minimum of
, a CN needs to be active a minimum of  for all u seconds, where
for all u seconds, where  is given by (11). Again, we consider a worst case where the maximum clock skew during the re-synchronization period is the minimum BAN time precision:
is given by (11). Again, we consider a worst case where the maximum clock skew during the re-synchronization period is the minimum BAN time precision:
(i)Indoor:  μ s,
μ s,
(ii)Outdoor I:  μ s,
μ s,
(iii)Outdoor II:  μ s.
μ s.
Similarly, the period of activity of a CN is the time used for secure pairwise CN re-synchronization. Its value is  for all CN
u
seconds. Here ch accounts for the maximum number of neighboring CNs, and
for all CN
u
seconds. Here ch accounts for the maximum number of neighboring CNs, and  , so that WSN reliability and scalability is maximized.
, so that WSN reliability and scalability is maximized.
The value of  can be approximated by the time to send the largest message (in step (2)) of SPS-SE. This adds 2.34 ms. The optimal BAN size of a WSN is
can be approximated by the time to send the largest message (in step (2)) of SPS-SE. This adds 2.34 ms. The optimal BAN size of a WSN is  [23]. For this study, we consider the upper limit for a BAN size, that is, n = 8. We also assume that a CN may have up to ch = 8 neighbouring CNs.
[23]. For this study, we consider the upper limit for a BAN size, that is, n = 8. We also assume that a CN may have up to ch = 8 neighbouring CNs.
Table 3 shows the period of activity and the duty cycle for the CN. As it can be seen, the duty cycle is much below 1% (considering a sampling period  of 16 minutes).
of 16 minutes).
6.6. Communication Overhead
The maximum number of bytes a CN needs to send is  . This same CN receives
. This same CN receives  bytes. We use
bytes. We use  to denote the length of message i of the SPS - SE protocol.
to denote the length of message i of the SPS - SE protocol.
A BAN member sends  and receives
and receives  bytes.
bytes.
We can codify periods  of 16 minutes at the μ s precision with 4 bytes. A key length of 16 bytes is considered to be secure for WSNs. As in the previous section ch is bounded by n, and we consider n = 8.
of 16 minutes at the μ s precision with 4 bytes. A key length of 16 bytes is considered to be secure for WSNs. As in the previous section ch is bounded by n, and we consider n = 8.
Further considering the values for IDs, timestamps, and MICs of previous sections, the maximum number of bytes sent and received by a CN is 1580 and 1095, respectively.
6.7. Energy Efficiency
The number of Ah consumed by the CC2420 can be calculated according to the formulas in [10]. To send 1580 bytes, the radio module consumes 276.67 nAh, and, to receive 1095 bytes, consumes 169.36 nAh. The total battery consumption for a CN for synchronization is 446.03 nAh over 16 minutes.
Equipped with a 30 mAh cell battery, the node can assume the CN role for over 2 years. If the n = 8 nodes of the BAN, rotate the CN role, then the BAN will survive approximately 16 years (assuming that the nodes do nothing else but synchronizing).
7. Conclusions and Future Work
In this paper we have addressed the issue of secure, accurate, and precise synchronization in a WSN formed by the interconnection of multiple BANs.
We have exhaustively analyzed the related work and found a number of open issues for research. Additionally, we have proposed secure, accurate, and precise synchronization service for this particular kind of WSN. It can be used to provide secure pairwise, BAN-wise, and WSN-wise clock synchronization. We have also discussed a means to synchronize WSN time to UTC time.
We have analyzed both the performance and security of our proposal. We have presented very simple countermeasures to cope with compromised nodes. We have also shown that the synchronization service achieves minimal pairwise accuracy of 8.46 μ s.
We have obtained the BAN clock synchronization precision of our system in three scenarios for re-synchronization periods of up to 16 minutes:
-
(i)
indoor with a temperature range of 25-26°C: precision of 20.96 µ s,
-
(ii)
outdoor with a temperature range of 17–21°C: precision of 60.46 µ s,
-
(iii)
outdoor with a temperature range of 22–27°C: precision of 23.46 µ s.
The minimum precision of WSN time is 22.79 μ s, 68.46 μ s, and 31.34 μ s, for each aforementioned scenario, respectively. For these calculations, we considered a number of 10 consecutive BAN controller nodes and a re-synchronization period of 16 minutes.
Yet another interesting result is that sensor node equipped with a 30 mAh (low-resource) cell battery can assume the CN role and help BAN members to synchronize for over 2 years without changing batteries. If the n = 8 nodes of the BAN, rotate the CN role, then the BAN will survive approximately 16 years (assuming that the nodes do nothing else but synchronizing).
These results are based on computations.
References
Römer K, Mattern F: The design space of wireless sensor networks. IEEE Wireless Communications 2004, 11(6):54-61. 10.1109/MWC.2004.1368897
Manzo M, Roosta T, Sastry S: Time synchronization in networks. Proceedings of the 3rd ACM Workshop on Security of Ad Hoc and Sensor Networks (SASN '05), November 2005 107-116.
Song H, Zhu S, Cao G: Attack-resilient time synchronization for wireless sensor networks. Proceedings of the 2nd IEEE International Conference on Mobile Ad-Hoc and Sensor Systems (MASS '05), November 2005 765-772.
Ganeriwal S, Capkun S, Han C, Srivastava MB: Secure time synchronization service for sensor networks. Proceedings of the ACM Workshop on Wireless Security (WiSe '05), September 2005 97-106.
Sun K, Ning P, Wang C: Secure and resilient clock synchronization in wireless sensor networks. IEEE Journal on Selected Areas in Communications 2006, 24(2):395-408.
Sun K, Ning P, Wang C, Liu A, Zhou Y: TinySeRSync: secure and resilient time synchronization in wireless sensor networks. Proceedings of the 13th ACM Conference on Computer and Communications Security (CCS '06), November 2006, Alexandria, Va, USA 264-277.
Ganeriwal S, Ganesan D, Shim H, Tsiatsis V, Srivastava MB: Estimating clock uncertainty for efficient duty-cycling in sensor networks. Proceedings of the 3rd international Conference on Embedded Networked Sensor Systems, 2005 130-141.
Perrig A, Szewczyk R, Wen V, Culler D, Tygar JD: SPINS: security protocols for sensor networks. Proceedings of the 7th Annual International Conference on Mobile Computing and Networking (Mobicom '01), July 2001 189-199.
Chipcon : SmartRF CC2420 Datasheet (rev 1.3), 2005-10-03.
Sanchez D: Key management for wireless ad hoc networks, Ph.D. thesis. IKMZ BTU Cottbus; 2006.
Hu YC, Perrig A, Johnson DB: Packet leashes: a defense against wormhole attacks in wireless networks. Proceedings of the 22nd Annual Joint Conference on the IEEE Computer and Communications Societies (INFOCOM '03), April 2003 1976-1986.
Elson J, Girod L, Estrin D: Fine-grained network time synchronization using reference broadcasts. ACM SIGOPS Operating Systems Review 2002, 36: 147-163. 10.1145/844128.844143
Ganeriwal S, Kumar R, Srivastava MB: Timing-sync protocol for sensor networks. Proceedings of the 1st International Conference on Embedded Networked Sensor Systems (SenSys '03), November 2003 138-149.
Maróti M, Kusy B, Simon G, Lédeczi A: The flooding time synchronization protocol. Proceedings of the 2nd International Conference on Embedded Networked Sensor Systems (SenSys '04), November 2004 39-49.
Hu Y-C, Perrig A, Johnson DB: Packet leashes: a defense against wormhole attacks in wireless ad hoc networks. Proceedings of the 22nd Annual Joint Conference of the IEEE Computer and Communications Societies, April 2003
Hoepman J-H, Larsson A, Schiller EM, Tsigas P: Secure and self-stabilizing clock synchronization in sensor networks. In the proceedings of the 9th international symposium on self stabilization, safety, and security of distributed systems (SSS 2007). In Lecture Notes in Computer Science, 2007. Volume 4838. Springer; 340-356.
Çamtepe SA, Yener B: Combinatorial design of key distribution mechanisms for wireless sensor networks. Proceedings of 9th European Symposium on Research in Computer Security (ESORICS '04), 2004, Sophia Antipolis, France, Lecture Notes in Computer Science 3193: 293-308.
Blundo C, De Santis A, Herzberg A, Kutten S, Vaccaro U, Yung M: Perfectly secure key distribution for dynamic conferences. Information and Computation 1998, 146(1):1-23. 10.1006/inco.1998.2717
Sánchez D, Baldus H: A deterministic pairwise key pre-distribution scheme for mobile sensor networks. Proceedings of the 1st International Conference on Security and Privacy for Emerging Areas in Communications Networks (SecureComm '05), September 2005 277-288.
Vig JR: Introduction to quartz frequency standards. October 1992., (SLCET-TR-92-1 (Rev. 1)):
Wu Y, Fahmy S, Shroff NB: Optimal sleep/wake scheduling for time-synchronized sensor networks with QoS guarantees. Proceedings of the 14th IEEE International Workshop on Quality of Service (IWQoS '06), June 2006 102-111.
Gutierrez JA, Callaway E, Barrett R: Low-Rate Wireless Personal Area Networks: Enabling Wireless Sensors with IEEE 802.15.4. Institute of Electrical & Electronics Engineers; 2003.
Hwang J, Kim Y: Revisiting random key pre-distribution schemes for wireless sensor networks. Proceedings of the 2nd ACM Workshop on Security of Ad Hoc and Sensor Networks (SASN '04), October 2004 43-52.
Acknowledgment
This work has been funded by the Research Project COOLNESS (218163-FP7-PEOPLE-2007-3-1-IAPP).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sanchez, D., Alonso, L., Angelidis, P. et al. Secure Precise Clock Synchronization for Interconnected Body Area Networks. J Wireless Com Network 2011, 797931 (2011). https://doi.org/10.1155/2011/797931
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/797931
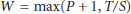 ,
,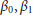 ) using a window of W samples in (2),
) using a window of W samples in (2), using (4),
using (4), ,
,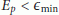 , then
, then 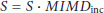
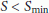 , then
, then 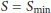
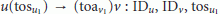 ,
, , MIC2
, MIC2 , MIC3,
, MIC3, ,
, ) using a window of
) using a window of 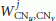 samples in (2),
samples in (2),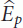 using (4),
using (4), ,
,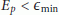 , then
, then 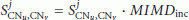
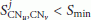 , then
, then 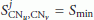
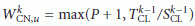 ,
,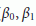 ,) using a window of
,) using a window of  samples in (2),
samples in (2),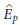 using (4),
using (4),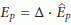 ,
,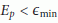 , then
, then 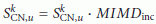



 .
.