- Research Article
- Open access
- Published:
A Family of Key Agreement Mechanisms for Mission Critical Communications for Secure Mobile Ad Hoc and Wireless Mesh Internetworking
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 807684 (2011)
Abstract
Future wireless networks like mobile ad hoc networks and wireless mesh networks are expected to play important role in demanding communications such as mission critical communications. MANETs are ideal for emergency cases where the communication infrastructure has been completely destroyed and there is a need for quick set up of communications among the rescue/emergency workers. In such emergency scenarios wireless mesh networks may be employed in a later phase for providing advanced communications and services acting as a backbone network in the affected area. Internetworking of both types of future networks will provide a broad range of mission critical applications. While offering many advantages, such as flexibility, easy of deployment and low cost, MANETs and mesh networks face important security and resilience threats, especially for such demanding applications. We introduce a family of key agreement methods based on weak to strong authentication associated with several multiparty contributory key establishment methods. We examine the attributes of each key establishment method and how each method can be better applied in different scenarios. The proposed protocols support seamlessly both types of networks and consider system and application requirements such as efficient and secure internetworking, dynamicity of network topologies and support of thin clients.
1. Introduction
Consider a disaster situation, such as an earthquake, a flood, or a terrorist attack, where the commercial network infrastructure is destroyed or out of order. The objective of the rescue workers is to set up quickly, efficiently, and easily a wireless network among them in order to help in a coordinated way the affected population. Their goal is to interconnect all their computing and communication devices, in a way that will enable them to share all necessary information securely, in a way that they could be sure that possible "high tech" terrorists/attackers in their range will not be able to disrupt or intercept the rescue efforts.
In real disaster scenarios, emergency response does not take place all at once. We usually observe an escalation in the presence of several groups of rescue workers and prioritized escalation of their efforts. In the beginning, we usually observe ad hoc groups working as independent teams that arrive at place independently. These teams gradually become part of coordinated action by a central disaster management entity, which requires more time to arrive at place, set up its infrastructure, and become operational. Approaching this scenario from a networking perspective, a sufficient approach would be the support of the initial groups of rescue workers by communication devices with mobile ad hoc networking capabilities. In this respect, an efficient networking solution for the support of the central disaster management entity would be the employment of adaptive, self-organized networks with advances networking capabilities, and redundant characteristics like wireless mesh networks. Seamless interworking of both types of networks would be a key requirement for such a scenario.
Security is a primary concern for providing protected communications in such environments where there is no available communication infrastructure and where networks of varying types and sizes must be established quickly and dynamically. Moreover, there might be situations where potentially large numbers of rescue workers, potentially from multiple government services or even nations must cooperate and coordinate their efforts in areas where natural or man-originated disasters have damaged or set temporarily out of order part or the entire telecommunication infrastructure. The unique nature and characteristics of mobile ad hoc Networks and wireless mesh networks make them ideal networking solution to the above situations. At the same time, their nature and characteristics pose a number of nontrivial challenges to their security design, architecture, and services.
In both MANETs and wireless mesh networks, like in any other type of network, trust cannot be created among the network nodes without the existence of predefined prior known information available to all nodes beforehand. This special kind of information is necessary in order to build trust between all participating nodes. A network is established among the existing nodes, if from this preexisting information known to all network nodes, we reach a state where a common session key is agreed among the nodes.
The technical goal is to make sure that no other entity outside the group should be able to gain access within the new network. However, since neither a certification authority nor a secure communication channel exists, potential attackers have the ability to eavesdrop and modify exchanged messages transmitted over the air. Additionally, since no central identification authority is present, group member impersonation is easy, jeopardizing the security of the whole system.
Considering all these issues, the main challenge that arises is the setting up of a wireless network where the legitimate members of a group will be able to establish a protected wireless network. Moreover, in the case where a new node arrives at place, desiring to become a member in an already established group, joining, without delaying or even intercepting the existing group, is also challenging. The case where a group member is captured by the enemy, and therefore the group key is compromised is also part of the considered scenario. All the above considerations become even more challenging for the mobile ad hoc/wireless mesh internetworking scenario examined in this work.
The rest of the paper is organized as follows. In Section 2, we describe the system model. In Section 3, we describe the adversary model, and in Section 4, we present the security requirements. In Section 5, we present a review of the related work concerning two-party and multiparty key agreements, and we give a brief introduction on weak to strong authentication and the elliptic curve theory. In Section 6, we describe specific multiparty key agreement protocols and particularly, the BCC, the FCC algorithms, and the tetrahedral approach and examine their properties. Finally, in Section 7, we conclude with suggestions for future work.
2. System/Network Model
In this section, we consider a system/network model as illustrated in Figure 1. It consists of both wireless mesh networks and mobile ad hoc networks. While several detailed surveys on mesh network architectures can be found in the literature [1, 2], the proposed system model is the similar to the one defined for the EU-MESH Project (http://www.eu-mesh.eu/) as far as wireless mesh networking is concerned. Accordingly, this model a mesh network consists of mesh routers that form a network with very similar networking attributes and characteristics of a static wireless ad hoc network. The mesh routers can function either as gateways to the wired Internet, or as wireless access points for mobile mesh clients.
We assume that the mesh routers belong to multiple operators, and they cooperate for providing aggregate networking services to all of their mesh clients. In the disaster management scenarios, we consider as different operators different teams of rescue workers (firemen, policemen, etc.). Their cooperation model, which falls out of the scope of this paper, can be based on simple on field agreements or on business agreements similar to roaming agreements in the case of cellular networks. Mesh clients are mobile computing devices (smart phones, PDAs, netbooks, etc.) operated by customers that can be associated with one or more operators by contractual means.
The mesh network provides various services to its clients like Internet access, real-time communications within the mesh network, and so forth. In this model, the mesh network is also designed to provide QoS applications with client mobility support. This way mobile mesh clients can perform seamless handovers between access points.
In parallel to the wireless mesh architecture, in our system model, we have the presence of independent mobile ad hoc networks as shown in red in Figure 1. A MANET is a type of network, which is typically composed of equal mobile hosts that we call nodes. When the nodes are located within the same radio range, they can communicate directly with each other using wireless links. This direct communication is employed in a distributed manner without hierarchical control. The absence of hierarchical structure introduces several problems, such as configuration advertising, discovery, maintenance, as well as ad hoc addressing, self-routing, and security [3].
In our internetworking model, a MANET node can be also considered as a mesh client and can perform seamless handovers between access points of the mesh network or between the MANET and the mesh network.
3. Adversary Model
As usual, the first step in the identification of security requirements is the understanding of the potential attacks against the system. This understanding is summed up in the following adversary model that describes the classes of attackers, their objectives and their means to attack the network.
Taking into account the system model of mobile ad hoc and wireless mesh internetworking, the following types of attackers are identified.
External Attackers
These are attackers that have no legitimate access to the MANET or the wireless mesh network but they have appropriate equipment to use the wireless medium and interfere with the operation of the network protocols.
Compromised Nodes/Clients
These are legitimate node devices that have legitimate access to the MANET and/or the wireless mesh network services and they have been compromised by attackers (e.g., by stealing a device or by capturing a legitimate user in the field). The attackers have the knowledge to modify the behavior of these nodes and try to take advantage of this in order to interfere with the operation of the network or to gain illegal access to its services.
Dishonest Network Nodes/Clients
They are misbehaving end users that while they have legitimate access to the wireless networks and some or all of the network services, they try to take advantage of this in order to gain illegal access to services that are not subscribed to, or to obtain higher QoS in services that they are already subscribed.
Dishonest Network Operators
They are operators of the mesh infrastructure that do not honestly keep to cooperation agreements.
Next, we identify the following main objectives of attacks.
Denial-of-Service (DoS)
The objective of this type of attack is to degrade the QoS provided by the mesh network and/or the MANET or even to completely disrupt the provided services. This is an objective of external adversaries.
Unauthorized Access to Services
This objective is mainly related to external adversaries and dishonest clients. Common services include internet access and real-time communications.
Unauthorized Access to Network Client Data and Meta-Data
Network client data are the messages exchanged in a service session and the corresponding objective is the violation of the confidentiality of the client whereas meta-data is information related to the client's location and service usage profile and the objective is the violation of the privacy of the client. Primarily, this objective is related to external adversaries and dishonest network operators.
Fraudulent Improvement of Operator Profile
This could be the objective of dishonest operators that may mount attacks on the mesh network or specific network operators/competitors participating in the network in order to gain some advantage over them. This can be achieved either by reducing or destroying the reputation of the competitors, or by spuriously increasing their own reputation.
There is a broad range of attack mechanisms that can be used and combined in order to reach the goals described above. However, most of these mechanisms fall into either one of the following two categories.
(i)attacks on wireless communications (including eavesdropping, jamming, replay, and injection of messages, and traffic analysis).
(ii)compromising existing nodes (typically by physical tampering or logical break-in). The behavior of the fake or compromised nodes can be arbitrarily modified in order to help to achieve specific attack objectives. In such a scenario, the underlying security depends on the size and the randomness of the chosen password. However, the larger the password gets the more difficult it is to memorize and use. Moreover, since the response time is vital during emergency operations, the use of large passwords can be proved inconvenient. Therefore, the use of short, user-friendly passwords is an essential requirement;
(iii)setting up fake mesh routers or compromising unattended existing mesh routers.
4. Security Requirements
It is broadly known that security mechanisms cannot create trust [4]. The members of a team that wish to establish a group know and trust one another physically. Otherwise, they would never be able to achieve mutual trust regardless of the authentication mechanism used. Our goal is to exploit the existing physical mutual trust and create a secure group of communication for both types of networks that would operate in a seamless manner.
An efficient solution to this direction, without adding new requirements like the use of dedicated hardware (i.e., smart cards), would be a password authentication mechanism. A simple approach of a password-based authentication scheme could be the use of sufficiently large and randomly generated data strings employed as passwords. In such a scheme, all nodes could agree on a password and achieve mutual authentication supported by a trivial authentication protocol.
In such a scenario, the underlying security depends on the size and the randomness of the chosen password. However, the larger the password gets the more difficult it is to memorize and use. Moreover, since the response time is vital during emergency operations, the use of large passwords can be proved inconvenient. Therefore, the use of short, user-friendly passwords is an essential requirement.
The use of short passwords provides weak authentication since the password selection set is quite limited, and thus the corresponding authentication procedure is vulnerable to dictionary attacks [5]. Therefore, we need an authentication protocol that will lead to a reasonable degree of security even if the authentication procedure has been initiated from a small, weak password.
Below, we outline the main security requirements of the proposed architecture.
Weak-to-Strong Password-Based Authentication
Use of an authentication scheme that will lead to a reasonable degree of security although the authentication procedure has been initiated from a small, weak password.
Secure Authentication
Only the entities that hold the correct password will eventually become members of the network.
Forward Authentication
Even if a malicious partner manages to compromise a network entity in a later phase, he will still be unable to participate in the already existing network.
Contributory Key Establishment
The network is established when a session key is generated and agreed among all network nodes. The session key should be generated throughout in a contributory manner, by all participating entities.
Security Architecture for Thin Clients
In both types of networks, there are mobile devices/clients with limited processing power and energy consumption. The cryptographic algorithms used for authentication and key agreement should add minimal computational overhead.
Rare Key Reestablishment
Session key refreshments should be performed as rare as possible, since during every new key reestablishment session the network is unavailable for node communications.
Unified Security Architecture for Combined MANET-Mesh Secure Internetworking
The proposed key agreement mechanisms should apply in both types of networks, without requiring any network-specific adjustments.
5. Background Theory
5.1. Password-Based Key Exchange
Typical cryptographic protocols based on keys chosen by the users, are weak to password guessing attacks. Bellovin and Merritt [6] proposed a protocol called Encrypted Key Exchange (EKE) where a strong shared key is derived from a weak one. The basic concept of the generic protocol is the following: there are two parties  ,
,  that share a password
that share a password  . Both parties use a suitable symmetric cryptosystem but entity
. Both parties use a suitable symmetric cryptosystem but entity  has also the ability to create a random asymmetric key pair, (
has also the ability to create a random asymmetric key pair, ( ). During the first step,
). During the first step,  generates a random public key
generates a random public key  and encrypts it symmetrically using key
and encrypts it symmetrically using key  in order to produce
in order to produce  (
( ). Then,
). Then,  sends it to
sends it to 

This message includes  's id in clear text.
's id in clear text.
Since  and
and  share the same password
share the same password  ,
,  decrypts the received message to obtain
decrypts the received message to obtain  . Node B generates a random secret key
. Node B generates a random secret key  and encrypts it in both asymmetric and symmetric cryptosystem using as an encryption key quantity
and encrypts it in both asymmetric and symmetric cryptosystem using as an encryption key quantity  and
and  , respectively. So,
, respectively. So,  produces
produces  and sends it to
and sends it to 

Entity  now decrypts the received message to obtain
now decrypts the received message to obtain  , generates a unique challenge
, generates a unique challenge  and encrypts it with
and encrypts it with  to produce
to produce and send it back to
and send it back to  ,
,

Then,  decrypts the message to obtain
decrypts the message to obtain  's challenge, generates a unique challenge
's challenge, generates a unique challenge  , and encrypts the two challenges with the secret key
, and encrypts the two challenges with the secret key  to obtain
to obtain . Node
. Node  is ready to transmit quantity
is ready to transmit quantity  to node
to node 

When  receives the message, it decrypts it to obtain
receives the message, it decrypts it to obtain and
and , and it compares it with the previous challenge. If there is a match,
, and it compares it with the previous challenge. If there is a match,  encrypts
encrypts with
with  to obtain
to obtain and sends it to
and sends it to 

If the challenge response protocol has been successfully deployed, then the authentication process is successfully accomplished and both parties proceed, using the symmetric cryptosystem and the quantity  as the session key. However, this protocol has a major drawback. That is, the creation of the common session key
as the session key. However, this protocol has a major drawback. That is, the creation of the common session key  has taking place with unilateral prospective, that is, only by the entity that first initiate the whole procedure. Thus, the key agreement scheme is not contributory.
has taking place with unilateral prospective, that is, only by the entity that first initiate the whole procedure. Thus, the key agreement scheme is not contributory.
In [7], Asokan and Ginzboorg proposed a contributory version of the above protocol for both two party and multiparty case. Their proposal is described as follows.
-
(1)
Two-party case
-
(i)
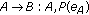 ,
, -
(ii)
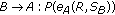 ,
, -
(iii)
 ,
, -
(iv)
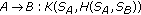 ,
, -
(v)
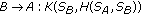 ,
,
where  are the random quantities generated from
are the random quantities generated from  ,
,  , respectively, and
, respectively, and  is the session key produced according the formula
is the session key produced according the formula , where
, where  is an one way function, and
is an one way function, and  is a public hash function.
is a public hash function.
-
(2)
Multiparty case
-
(i)
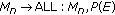 ,
, -
(ii)
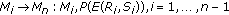 ,
, -
(iii)
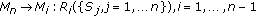 ,
, -
(iv)
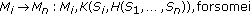 ,
,
where  is the Public key of
is the Public key of  .
.  is the random quantities generated from
is the random quantities generated from  , and
, and  is the session key produced according the formula
is the session key produced according the formula .
.  is an n-input one way function and
is an n-input one way function and  is a public hash function.
is a public hash function.
5.2. Password-Based Diffie-Hellman Key Exchange
5.2.1. Two Party Key Exchange
Diffie-Hellman is the first public key distribution protocol that opened new directions in cryptography [8]. In this important key distribution protocol, two entities  ,
,  after having agreed on a prime number
after having agreed on a prime number  and a generator
and a generator  of the multiplicative group
of the multiplicative group  , can generate a secret session key. In [6], Bellovin and Merritt proposed a password authenticated key exchange which operates in the following way.
, can generate a secret session key. In [6], Bellovin and Merritt proposed a password authenticated key exchange which operates in the following way.
-
(i)
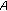 picks a random number,
picks a random number,  calculates
calculates 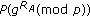 , and
, and  sends
sends 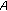 ,
, 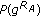 to
to  ; entity
; entity 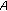 's id is sent in clear text.
's id is sent in clear text. -
(ii)
 picks a random number
picks a random number 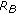 and calculates
and calculates 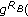 mod
mod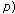 .
.  uses the shared password
uses the shared password  to decrypt
to decrypt 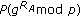 and calculates
and calculates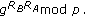 (6)
(6) -
(iii)
The session key
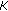 is derived from this value by selecting a certain number of bits. Finally, a random challenge,
is derived from this value by selecting a certain number of bits. Finally, a random challenge, 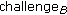 is generated. Then,
is generated. Then, 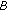 transmits
transmits (7)
(7) -
(iv)
 uses
uses 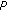 to decrypt
to decrypt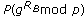 . From this, quantity
. From this, quantity  is calculated;
is calculated;  is in turn used to decrypt
is in turn used to decrypt .
. 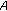 then generates a random challenge
then generates a random challenge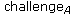 .
.  sends
sends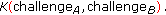 (8)
(8) -
(v)
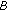 decrypts
decrypts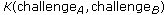 , and verifies that
, and verifies that  is correct.
is correct.  sends
sends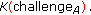 (9)
(9) -
(vi)
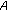 decrypts to obtain
decrypts to obtain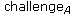 and verifies that it matches the original message.
and verifies that it matches the original message.
5.2.2. Elliptic Curve Diffie-Hellman
The original Diffie-Hellman algorithm is based on the multiplicative group modulo  . However, the elliptic curve Diffie-Hellman (ECDH) protocol is based on the additive elliptic curve group, and it is desribed below. We assume that two entities
. However, the elliptic curve Diffie-Hellman (ECDH) protocol is based on the additive elliptic curve group, and it is desribed below. We assume that two entities  ,
,  have selected the underlying field,
have selected the underlying field,  or
or , the elliptic curve
, the elliptic curve  with parameters
with parameters  ,
,  , and the base point
, and the base point  . The order of the base point
. The order of the base point  is equal to
is equal to  . Also, we ensure that the selected elliptic curve has a prime order, in order to comply with the appropriate security standards [9, 10].
. Also, we ensure that the selected elliptic curve has a prime order, in order to comply with the appropriate security standards [9, 10].
At the end of the protocol, the communicating parties end up with the same value  which represents a unique point on the curve. A part of this value can be used as a secret key to a secret-key encryption algorithm. We give a brief description of the protocol.
which represents a unique point on the curve. A part of this value can be used as a secret key to a secret-key encryption algorithm. We give a brief description of the protocol.
-
(i)
Entity
 selects an integer,
selects an integer,

-
(ii)
Entity
 selects an integer
selects an integer

-
(iii)
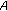 computes
computes 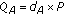 . The pair
. The pair  consists of
consists of  's public and private key.
's public and private key. -
(iv)
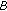 computes
computes 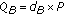 . The pair
. The pair 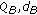 consists of
consists of  's public and private key.
's public and private key. -
(v)
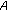 sends
sends 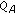 to
to 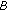

-
(vi)
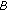 sends
sends  to
to 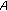

-
(vii)
 computes
computes

-
(viii)
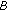 computes
computes

Quantity  is now the common shared key between
is now the common shared key between  and
and  . Moreover, it can also be used as a session key. Quantity
. Moreover, it can also be used as a session key. Quantity  is the order of the base point
is the order of the base point  .
.
5.2.3. Password-Based Elliptic Curve Diffie-Hellman
The efficiency of elliptic curves in terms of security and calculation efficiency has been extensively discussed [10, 11, 12, 9a, 14]. Therefore, their employment in the password-based Diffie-Hellman process would significantly accelerate the key establishment procedure. The importance of this enhancement becomes even greater in the case of an emergency situation, where all actions should be performed in the fastest and more secure possible way consuming limited computing power.
We assume there two entities  ,
, that have agreed on the underlying field
that have agreed on the underlying field on an elliptic curve
on an elliptic curve  with coefficients α, β defined over the selected field, on the base point
with coefficients α, β defined over the selected field, on the base point  and the password
and the password . The operation of the proposed protocol is as follows.
. The operation of the proposed protocol is as follows.
-
(i)
 picks a random number
picks a random number  , where
, where  is the order of the base point
is the order of the base point 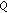 and calculates
and calculates 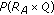
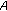 sends
sends  (16)
(16)
to  ; entity
; entity  's id is sent in clear.
's id is sent in clear.
-
(ii)
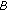 picks a random number
picks a random number 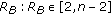 and calculates
and calculates  .
. 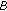 also uses the shared password
also uses the shared password 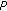 to decrypt
to decrypt 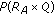 and calculates
and calculates

-
(iii)
The session key
 is derived from this value, perhaps by selecting certain bits. Finally, a random challenge
is derived from this value, perhaps by selecting certain bits. Finally, a random challenge  is generated.
is generated.  transmits
transmits

-
(iv)
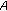 uses
uses 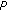 to decrypt
to decrypt . From this,
. From this, 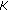 is calculated;
is calculated; 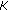 is in turn used to decrypt
is in turn used to decrypt .
.  then generates its own random challenge
then generates its own random challenge  .
.  sends
sends

-
(v)
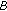 decrypts
decrypts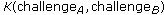 and verifies that
and verifies that 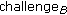 is correct.
is correct. 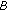 sends
sends

-
(vi)
 decrypts to obtain
decrypts to obtain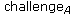 and verifies that it matches the original message.
and verifies that it matches the original message.
5.3. Efficient D-H-Based Multiparty Key Exchange
5.3.1. d-Cube Protocol Overview
For key establishment procedures in multiparty networks like MANETs and mesh networks, where several entities are involved, multiparty authentication protocols should be applied. A lot of research has been done in this direction. Becker and Wille [15] presented a method very efficient in terms of number of authentication rounds. According to this method, also known as  -cube protocol, all entities planning to participate in a network are initially arranged in a
-cube protocol, all entities planning to participate in a network are initially arranged in a  -dimensional hypercube. Each potential network entity is represented as a vertex in the
-dimensional hypercube. Each potential network entity is represented as a vertex in the  dimensional-cube, and it is uniquely assigned a
dimensional-cube, and it is uniquely assigned a  -bit address. The addresses are assigned in a way so that two vertices connected along the i th dimension differ only in the i th bit. There are
-bit address. The addresses are assigned in a way so that two vertices connected along the i th dimension differ only in the i th bit. There are  vertices each of which are connected to
vertices each of which are connected to  other vertices.
other vertices.
5.3.2. DH d-Cube
Assume that there are  entities seeking to establish an ad hoc non infrastructural network. During the first step, each entity is assigned to a vertex in the hypercube, and it is given a unique
entities seeking to establish an ad hoc non infrastructural network. During the first step, each entity is assigned to a vertex in the hypercube, and it is given a unique  -bit address. The deployment of the address arrangement is out of the scope of this paper and will not be examined. The key establishment protocol is illustrated within
-bit address. The deployment of the address arrangement is out of the scope of this paper and will not be examined. The key establishment protocol is illustrated within  rounds. In every single round the entities are paired together, according to a specific procedure, and the Diffie-Hellman key exchange is performed. These pairwise operations are performed in parallel during every round. For example, during the i th round of the protocol a node with address
rounds. In every single round the entities are paired together, according to a specific procedure, and the Diffie-Hellman key exchange is performed. These pairwise operations are performed in parallel during every round. For example, during the i th round of the protocol a node with address performs a two party Diffie-Hellman key exchange with the node whose address is
performs a two party Diffie-Hellman key exchange with the node whose address is . So, in the i th round there will be
. So, in the i th round there will be  pairs of groups, each group consisting of
pairs of groups, each group consisting of  nodes. By the time the d th is completed, a contributory session key will have be created. Next, we will present graphically the 2-d and 3-d cases.
nodes. By the time the d th is completed, a contributory session key will have be created. Next, we will present graphically the 2-d and 3-d cases.
In the 2-d case , there are four entities
, there are four entities  , and
, and  aiming to establish a common session key. Let us assume that the address that were assigned to them are
aiming to establish a common session key. Let us assume that the address that were assigned to them are  , respectively. Each entity contributes in order the common session key,
, respectively. Each entity contributes in order the common session key,  can be created, so let us also assume that the contribution of each entity is
can be created, so let us also assume that the contribution of each entity is  . During the first round, two pairs will be created,
. During the first round, two pairs will be created,  consisting of entities
consisting of entities  ,
,  and pair2 consisting of entities
and pair2 consisting of entities  ,
,  . The two pairs will be internally and in parallel perform a two party Diffie-Hellman yielding a pair of common keys
. The two pairs will be internally and in parallel perform a two party Diffie-Hellman yielding a pair of common keys  and
and  as shown in Figure 2.
as shown in Figure 2.
During the second round,  will perform a two-party Diffie-Hellman with the node
will perform a two-party Diffie-Hellman with the node  while node
while node  a two-party Diffie-Hellman with
a two-party Diffie-Hellman with  . Each node will use the common key computed during the previous round, (round 1), in order to create, during the current round, (round 2), the resulting common session key. So, by the end of the second round, all nodes will be sharing the same contributory key
. Each node will use the common key computed during the previous round, (round 1), in order to create, during the current round, (round 2), the resulting common session key. So, by the end of the second round, all nodes will be sharing the same contributory key  . This is presented graphically in Figure 3.
. This is presented graphically in Figure 3.
In [7], the authors incorporate the password-based authentication into the cube protocol. This is achieved by using the four-move two-party password authenticated Diffie-Hellman protocol for pairwise exchanges in each round of the  -cube protocol.
-cube protocol.
The method is also applicable in the case where the number of players is not a power of 2. The solution for this case is given thought the use of the  octopus proposed by Becker and Wille in [15]. This protocol manages to optimize the number of rounds performed. More precisely if the number of nodes
octopus proposed by Becker and Wille in [15]. This protocol manages to optimize the number of rounds performed. More precisely if the number of nodes  follows that
follows that  , then the first
, then the first  nodes act as the central controllers and the remaining ones
nodes act as the central controllers and the remaining ones  are distributed among them as their wards. The controllers execute a two-party Diffie-Hellman with their ward, and then they are engaged in a
are distributed among them as their wards. The controllers execute a two-party Diffie-Hellman with their ward, and then they are engaged in a  round cube protocol using information gathered from the previous stage. Finally, the derived key is distributed to the wards. Another important aspect that [7] introduced is the way that a node should behave when a two-party authentication procedure has failed. They propose an algorithm according which a node can select another potential partner until a nonfaulty one is found. For a single node
round cube protocol using information gathered from the previous stage. Finally, the derived key is distributed to the wards. Another important aspect that [7] introduced is the way that a node should behave when a two-party authentication procedure has failed. They propose an algorithm according which a node can select another potential partner until a nonfaulty one is found. For a single node  in a random round
in a random round  , there are at most
, there are at most  potential nodes and at most
potential nodes and at most  potential subrounds. Two basic requirements are set for node
potential subrounds. Two basic requirements are set for node .
.
-
(i)
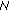 must not match two nodes to the same partner in a given subround.
must not match two nodes to the same partner in a given subround. -
(ii)
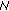 must not select the same partner twice.
must not select the same partner twice.
The work in [7] selects the closest partners before the more distant ones, in terms of Euclidean distance between the two corresponding address. The protocol depends on the current round performed, however each round can be consisted of several subrounds. A subround is executed when a two party key exchange with the appropriate partner node cannot be established. The operation of a player during a given subround is divided in
-
(i)
computation and transmission of all outgoing messages,
-
(ii)
reading of all waiting messages and state transition accordingly.
The proposed algorithm is best illustrated through a simple example which is depicted in Figures 4 and 5.
Every node has a three bit address  and a three bit mask, and it is labeled from
and a three bit mask, and it is labeled from  to
to  . Its key contribution is represented by the corresponding lowercase letter.
. Its key contribution is represented by the corresponding lowercase letter.
Labels next to the arrows indicate the nodes that have already contributed, directly or indirectly, to the key. Suppose that player  (with address 110) is unsuitable (unavailable or does not know the password). In round 1, player
(with address 110) is unsuitable (unavailable or does not know the password). In round 1, player  (111) will initiate the procedure of selecting as a partner the node whose address is 110 and mask 000.
(111) will initiate the procedure of selecting as a partner the node whose address is 110 and mask 000.
The exchange attempt with  fails and the mask is already $000$. So,
fails and the mask is already $000$. So,  does nothing in this round. In round 2,
does nothing in this round. In round 2, 
 $100$
$100$ will start with $110$ as candidate address and 001 as mask. The first recursive call will try $110$ as candidate address and $000$ as mask and will fail. The second recursive call will try $111$ as candidate address and $000$
will start with $110$ as candidate address and 001 as mask. The first recursive call will try $110$ as candidate address and $000$ as mask and will fail. The second recursive call will try $111$ as candidate address and $000$ as mask and will succeed. Similarly, in round 3 and Figure 4, node
as mask and will succeed. Similarly, in round 3 and Figure 4, node  ($010$) starts partner finding with $110$ as candidate. The work in [7] also considers the case, where the total number of nodes is not more than
($010$) starts partner finding with $110$ as candidate. The work in [7] also considers the case, where the total number of nodes is not more than  , while the number of the faulty nodes is
, while the number of the faulty nodes is  for some
for some  . The
. The  of them are located in a single
of them are located in a single  -cube
-cube  , and the rest of them in a
, and the rest of them in a  -cube
-cube  .
.
The number of subrounds required in rounds from  to
to  where
where  are at most
are at most  per round. This is because in each of those rounds, there is always one subround with
per round. This is because in each of those rounds, there is always one subround with  faulty partners. The same faulty node may select using
faulty partners. The same faulty node may select using  each of the
each of the  faulty partners in sequence before being able to complete its round exchange, thus resulting
faulty partners in sequence before being able to complete its round exchange, thus resulting  rounds. Since there is no other subcube with more faults,
rounds. Since there is no other subcube with more faults,  is the maximum number of subrounds required.
is the maximum number of subrounds required.
In round  , the number of faulty players in
, the number of faulty players in  , is
, is  , resulting that the maximum number of subrounds is
, resulting that the maximum number of subrounds is  . So the total number of subround for the first
. So the total number of subround for the first  rounds is therefore
rounds is therefore

Thus, the total number of communication rounds required to complete the exchange is  . This case incurs the maximum possible number of subrounds in the worst case during round 1 to
. This case incurs the maximum possible number of subrounds in the worst case during round 1 to  round.
round.
6. The Family of Key Agreement Protocols
In this section, we describe a family of key agreement protocols initially employed only in MANETs and the way that can be implemented in a MANET/mesh internetworking system.
In the approach described in Section 5, the only way to obtain a common session key when one or more nodes depart from the established MANET is to start over the algorithm from the very first step. Furthermore, there are no intermediate session keys stored between nodes that are still part of the network, which could be proven to be useful for node-to-node communication, when global session key is no longer valid due to network reform. Such approaches tend to be sufficient in relatively stable networks, where their topology does not change frequently. However, when network topology dynamicity increases, creating new global session keys very often is not the optimum solution.
The following algorithms propose efficient means for creation and use of intermediary session keys at the same time with the creation of the global network key, which can be used both for subgroup communications and as intermediate step for key refreshment of the global session key, without the obligation to restart the group key agreement.
6.1. The Body-Centered Cubic (BCC) Algorithm
The body-centered cubic algorithm [16] is a cryptographic key agreement algorithm that initiates from a tree-arrangement of 3-d cubes; it is based on the aggressive 3-d cube algorithm and employs the body-centered cubic (BCC) structure for the dynamic case. For simplicity purposes, in the rest of the paper, each bond in 2-d or 3-d space corresponds to a two-party password-based elliptic curve Diffie-Helman key exchange, as described in Section 5.2.3.
6.1.1. Initial Node Arrangement
The proposed system is based on the 3-d aggressive d-cube algorithm [17]. The initial key agreement procedure depends on the number of ad hoc nodes that wish to establish a MANET. We denote the number of nodes as n. In contrast to [17], in the proposed system, there is no need for d-dimension hyperspaces. The maximum order is the 3-d space. Nodes of the network are always arranged in the 3-d space, except the case that  where we can use the 2-d plane. Therefore, when we have a large number of nodes, they must be divided and arranged in 3-d cubes that each contains eight nodes. Each cube selects a leading node that will act as an intermediary between the corresponding cube nodes and the rest of the ad hoc network. The leading nodes constitute a new group; however, they follow the same rules for initial arrangement, that is, they are arranged in a new 3-d cube. In the case where the number of leading nodes is greater than eight (i.e., the number of all ad hoc nodes is greater than 64), they also need to elect leading nodes in their group that will act as their representatives to the ad hoc network. In such a case, the leading nodes elect higher level leaders in a tree model according to [18]. We consider the latter case as an extreme case since from a practical point of view typical ad hoc networks do not exceed 64 nodes. Figure 6 shows an initial arrangement of a 32-node network. Nodes are arranged in four independent cubes and each cube elects a leader (dashed annotation). Node arrangement and addressing can be performed in any way, as far as every simple-cube node has wireless connection with the rest of the seven nodes of the corresponding cube. This requirement must be also fulfilled by the leading nodes among themselves; therefore, it is an important criterion for the selection of a leading node within a simple cube.
where we can use the 2-d plane. Therefore, when we have a large number of nodes, they must be divided and arranged in 3-d cubes that each contains eight nodes. Each cube selects a leading node that will act as an intermediary between the corresponding cube nodes and the rest of the ad hoc network. The leading nodes constitute a new group; however, they follow the same rules for initial arrangement, that is, they are arranged in a new 3-d cube. In the case where the number of leading nodes is greater than eight (i.e., the number of all ad hoc nodes is greater than 64), they also need to elect leading nodes in their group that will act as their representatives to the ad hoc network. In such a case, the leading nodes elect higher level leaders in a tree model according to [18]. We consider the latter case as an extreme case since from a practical point of view typical ad hoc networks do not exceed 64 nodes. Figure 6 shows an initial arrangement of a 32-node network. Nodes are arranged in four independent cubes and each cube elects a leader (dashed annotation). Node arrangement and addressing can be performed in any way, as far as every simple-cube node has wireless connection with the rest of the seven nodes of the corresponding cube. This requirement must be also fulfilled by the leading nodes among themselves; therefore, it is an important criterion for the selection of a leading node within a simple cube.
6.1.2. Initial (Static) Key Agreement
Next, after the initial 3-d arrangement, BCC creates a common network key. In the proposed system this is done in two steps.
During the first step, the leading nodes perform a 3-d aggressive cube algorithm and they create a global session key. In the second step, every group performs a 3-d aggressive  -cube and establishes a simple-cube session key. During the simple-cube key generation, the leading nodes transmit the global session key that they have already established in step 1 to the remaining seven nodes of the group. After the second step, every node has a contributory simple-cube session key
-cube and establishes a simple-cube session key. During the simple-cube key generation, the leading nodes transmit the global session key that they have already established in step 1 to the remaining seven nodes of the group. After the second step, every node has a contributory simple-cube session key  for the cube that is part of, and the global session key of the entire network
for the cube that is part of, and the global session key of the entire network  .
.
In the first step, nodes  of cube
of cube  ,
,  of cube
of cube  ,
,  of cube
of cube  , and
, and  of cube
of cube  are elected as leading nodes of the corresponding cubes. Since they are four, they perform a 2-d aggressive algorithm, and they establish a global session key
are elected as leading nodes of the corresponding cubes. Since they are four, they perform a 2-d aggressive algorithm, and they establish a global session key  . If there are than four and equal or less than eight 3-d cubes, their leaders should perform a 3-d aggressive cube algorithm. In this case, the leading nodes can use the first two digits of their addressees as a 2-d address for the 2-d aggressive algorithm, that is,
. If there are than four and equal or less than eight 3-d cubes, their leaders should perform a 3-d aggressive cube algorithm. In this case, the leading nodes can use the first two digits of their addressees as a 2-d address for the 2-d aggressive algorithm, that is,  ,
,  , (10), and
, (10), and  . If other nodes are elected as cube leaders due to communication constraints, they should be addressed in a separate way than the one employed in their 3-d cube (second addressing is required).
. If other nodes are elected as cube leaders due to communication constraints, they should be addressed in a separate way than the one employed in their 3-d cube (second addressing is required).
Once the global session key of a group  is established the cubes perform a 3-d aggressive
is established the cubes perform a 3-d aggressive  -cube, and they establish the simple-cube session key
-cube, and they establish the simple-cube session key  . The final step is that each cube leader broadcasts the global key encrypted with the simple-cube key to the rest of the cube members. At the end of the protocol, every node has a simple-cube session key
. The final step is that each cube leader broadcasts the global key encrypted with the simple-cube key to the rest of the cube members. At the end of the protocol, every node has a simple-cube session key  for secure communications among nodes of simple-cubes, and a global session key
for secure communications among nodes of simple-cubes, and a global session key  , for the entire group (mesh or MANET).
, for the entire group (mesh or MANET).
6.1.3. BCC for the Dynamic Case
Above, we described the initial arrangement-addressing of nodes and the generation of a global and of simple-cube session keys. These keys are static, since if there is a need to add new nodes to the network, the key generation procedure must be repeated. Here, we describe an efficient method for dynamic key generation every time new nodes arrive to or depart from our network. The proposed dynamic algorithm is based on the body-centered cubic structure, and we call it BCC algorithm.
The body-centered cubic (bcc) structure is a cube with an additional node in the center. Figure 7(a) shows a typical cube while Figure 7(b) depicts a body-centered cube. If we consider the grid case, the bcc structure is a set of bcc cubes. The BCC algorithm for dynamic changing topologies is presented through two cases: addition of new nodes to an established network and extraction of network nodes.
Case 1 (Adding nodes to an established network).
The BCC algorithm operates in the following way: assume that a group has been established as previously described. Assume that one simple cube of this network is depicted in Figure 7(a). At some point of time, seven new nodes arrive and request to join the network. If the number of the new arriving nodes m is a multiple of 8, that is,  , then in groups of 8, they perform aggressive cube algorithms and each group elects a leader that will contact leaders of new groups and leaders from the established network in order to create a new global session key. If
, then in groups of 8, they perform aggressive cube algorithms and each group elects a leader that will contact leaders of new groups and leaders from the established network in order to create a new global session key. If  , then we will have
, then we will have  new groups of 8 nodes where
new groups of 8 nodes where  is the integer part of
is the integer part of  and
and  the number of the remaining nodes where
the number of the remaining nodes where  while the
while the  groups of 8 nodes will perform new aggressive cube algorithms, the remaining node will attach to an existing cube of the network in the following way.
groups of 8 nodes will perform new aggressive cube algorithms, the remaining node will attach to an existing cube of the network in the following way.
The first four new nodes are assigned addresses that correspond to the center of the existing cube the centers of the right, upper, and front cubes as shown in Figure 7(c) while the last three are assigned addresses that correspond to the centers of the left, back, and down cubes as shown in Figure 7(e). Keep in mind that the six neighboring cubes do not exist as network cubes; they are used as geometrical objects for demonstration purposes of the BCC algorithm. The first four new nodes (the body-centered cubic node and three central nodes of neighbor cubes) create a new cube with four nodes of the preexisting network cube as shown in Figure 7(d), and they perform a new aggressive cube algorithm. The latter 3 new nodes together with the body-centered cubic node (the node assigned to center of the existing cube of the network that has already participated in the previous new aggressive cube), and the remaining four nodes of the preexisting cube of the network perform a second new aggressive cube algorithm as shown in Figures 7(e) and 7(f).
The preexisting network nodes are colored black while the new arriving nodes are in gray color. Figure 8 demonstrates the BCC algorithm and the process that initiates with an existing network cube and concludes to two new cubes that both have the central node (body-centered cubic node) of the initial cube as common node.
Case 2 (Extracting nodes from an established network).
The process for extraction of nodes from an established network (MANET or mesh) is similar to the addition of new nodes to such a network. The remaining nodes of a simple cube find close cubes and perform the BCC algorithm. This process changes only the global session key of the network, since according to BCC algorithm cube leaders have to establish a new global key; however, the simple cube session keys of the rest of the MANET cubes remain unchanged. Figure 9 demonstrates the simple case where one node leaves an established cube (node 100 of the left cube of Figure 9(a)). The remaining seven nodes take place according to the BCC algorithm at the centers of the geometrically neighboring cubes of the right cube of Figure 9(a), as shown in Figure 9(b). The BCC algorithm concludes with the generation of two new cubes as shown in Figure 9(c).
6.2. The Face-Centered Cubic (FCC) Algorithm
The face-centered cubic algorithm is shown in Figure 10. The first 8 nodes (or less) are arranged in a 3-d cube as shown in the left side of Figure 3. They perform an aggressive 3-d cube algorithm and obtain a common session key. The first 6 nodes that will arrive in a later phase will be arranged in the centers of the six faces of the cube as shown in the central picture of Figure 3.
The 6 new nodes together, with nodes  and
and  that contributed to the initial cube, create a new cube and perform a new (second) aggressive 3-d cube algorithm. This way the inner cube creates a second common session key. After the setup of the second session, key nodes
that contributed to the initial cube, create a new cube and perform a new (second) aggressive 3-d cube algorithm. This way the inner cube creates a second common session key. After the setup of the second session, key nodes  and
and  hold both session keys corresponding to both cubes. This privilege makes nodes (
hold both session keys corresponding to both cubes. This privilege makes nodes ( and
and  leading nodes for the established network since any communication between black and grey nodes should pass through them. If we wish to avoid this hierarchy in our network, during the set up of the common session key within the inner cube, nodes
leading nodes for the established network since any communication between black and grey nodes should pass through them. If we wish to avoid this hierarchy in our network, during the set up of the common session key within the inner cube, nodes  and
and  propagate the common session key of the initial (black) cube to the new nodes. This way the first session key can be used by all nodes to communicate securely with each other, while the second can be used for the secure communication of the internal (grey) cube.
propagate the common session key of the initial (black) cube to the new nodes. This way the first session key can be used by all nodes to communicate securely with each other, while the second can be used for the secure communication of the internal (grey) cube.
The addressing of the new nodes is shown in Figure 11. We observe that the 2 old (black) nodes keep the same address with the one they had during the setup of the first session key. For the communication between nodes belonging to different cubes there is a separate metric (cube number) declaring the cube that the node is belonging to. In this example, black nodes are identified as cube 1 nodes, grey nodes are identified as cube 2 nodes, and nodes  and
and  have both identifiers since they belong to both cubes.
have both identifiers since they belong to both cubes.
In the hierarchical model, where every cube has its independent session key, key refreshment due to departing nodes is easy. As soon as a node is leaving the network, the rest nodes of the common cube, perform a new aggressive 3-d cube algorithm and create a new session key. In case the leaving node is belonging to two consecutive cubes, a new aggressive 3-d cube algorithm is performed automatically to both cubes.
In the case where the previous session keys belonging to previous cubes are forwardly distributed to the next cubes, the key renewal should be performed to all previous cubes. This appears not to be a desired feature, since if there is a departure in the last cube all previous stages/cubes will be affected. However, this can be also avoided if the set up is a combination of the two solutions. Periodically the key forwarding method is interrupted by the hierarchical solution. This way, we create isolated groups of concatenated cubes and any necessary key refreshment is bounded within these groups.
6.3. The Tetrahedral Approach
In the tetrahedral approach [19], in contrast to [16, 20] all intermediate two-party ECDH keys are stored by each node. This way, when a global session key has been created, every node in the d-dimensional cube maintains also a list of all the two-party ECDH keys that has created with every of her closest neighbors during the global key generation.
In the BCC and FCC approaches as described above, as soon as the initial phase of the proposed algorithm is completed, each node posses the global session key, and the two-party keys with her closest neighbors. At that point, if a node leaves the network, the global session key should be refreshed and in the meantime, secure communications would be only available between couples of closest neighbors that have already established two-party keys during the creation of the latest session key, which is no longer valid. This way, communication between distant neighbors, is only available through multihopping between nodes that, in couples, maintain valid two-party keys. This would add another requirement for routing metric information maintenance by all nodes, in order to serve each other to find the right secure path in the network. Solution to this direction is provided by the proposed integration of tetrahedral group key agreement in the existing cubes. The proposed structure covers both cases ( -cube and aggressive
-cube and aggressive  -cube) and takes place right after the creation of the global session key.
-cube) and takes place right after the creation of the global session key.
Below, the procedure is explained in detail.
As soon as the global session key has been created (round 3 in the 3-d example) all nodes establish two-party ECDH with their second level closer neighbors. There nodes are actually the ones based on the diagonal of each cubic surface. The algorithm is better demonstrated in Figure 12. Figure 12(a) describes the cube created after the global key agreement, while Figures 12(b) and 12(c) demonstrate the two-party ECDH key exchanges between the second order neighbors. All these additional two-party ECDH key exchanges form the two internal tetrahedrons inside the cube as shown in Figures 12(b) and 12(c). Figure 13 depicts the two internal tetrahedrons isolated by the cube. The process for the establishment of these tetrahedrons, in terms of two-party ECDH key agreements, is depicted in detail in Figure 14. We can observe that two-party ECDH key agreements take place on nonconnected segments. Although that after the second round the tetrahedrons have formed their global session keys, the algorithm has another final step, by covering all available segments.
This is due to two reasons: every node has a two party key with all nodes of the cube except the most distant node. For example,  has two party keys with every node of the cube except node
has two party keys with every node of the cube except node  . Besides the group session keys among every 4 nodes forming a square edge of the cube, the four triangles of each internal tetrahedron shares a common session key, since the ECDH key exchange this time is the party D-H key exchange instead of two-party in all other cases.
. Besides the group session keys among every 4 nodes forming a square edge of the cube, the four triangles of each internal tetrahedron shares a common session key, since the ECDH key exchange this time is the party D-H key exchange instead of two-party in all other cases.
Let us provide an example to demonstrate the attributes of the proposed algorithm. The reference node for this example will be node  . During the initial 3-d or aggressive 3-d algorithm, node
. During the initial 3-d or aggressive 3-d algorithm, node  creates three two-party keys with nodes
creates three two-party keys with nodes  ,
,  , and
, and  and the global session key of the cube. During the tetrahedral algorithm, node
and the global session key of the cube. During the tetrahedral algorithm, node  creates three two-party keys with nodes
creates three two-party keys with nodes  ,
,  and
and  . This way, node
. This way, node  maintains two-party keys with all nodes of the cube except
maintains two-party keys with all nodes of the cube except  .
.
If any of its first and second order closest neighbor leaves the network, during the global key renewal node  will be still able to communicate with all expect one of the remaining nodes. However, this distant node (in the example node
will be still able to communicate with all expect one of the remaining nodes. However, this distant node (in the example node  ) belongs to the other tetrahedron and has keys for communication with the remaining nodes.
) belongs to the other tetrahedron and has keys for communication with the remaining nodes.
In another case, if  decides to leave the network, its distant nodes, belonging to the left tetrahedron, do have keys for secure communications (a session key for the hole tetrahedron plus the two party keys among any pair of them), while the remaining three nodes
decides to leave the network, its distant nodes, belonging to the left tetrahedron, do have keys for secure communications (a session key for the hole tetrahedron plus the two party keys among any pair of them), while the remaining three nodes  ,
,  , and
, and  of the right tetrahedron, besides the two-party keys, they have a three-party key established among them during the last stage of the tetrahedral key agreement algorithm. Therefore, when a node leaves the network, the remaining nodes have all the two-party session keys, a four-party session key of the tetrahedron that did not change formation, and a three-party session key of the triangle composed of the three remaining nodes of the tetrahedron that the leaving node was part of.
of the right tetrahedron, besides the two-party keys, they have a three-party key established among them during the last stage of the tetrahedral key agreement algorithm. Therefore, when a node leaves the network, the remaining nodes have all the two-party session keys, a four-party session key of the tetrahedron that did not change formation, and a three-party session key of the triangle composed of the three remaining nodes of the tetrahedron that the leaving node was part of.
6.4. Analysis of the Algorithms
All proposed algorithms integrate elliptic curve cryptography together with the password-based DH key exchange protocols and extend this approach to the multiparty case where new network nodes arrive or existing network nodes depart from the network.
The static multiparty case is considered and after careful examination the aggressive  -cube algorithm is selected in the 3-d case. The algorithms are extended versions of the
-cube algorithm is selected in the 3-d case. The algorithms are extended versions of the  -cube algorithm proposed in [7], with additional features that enhance the resistance against the dictionary attacks [5]. The basic idea behind the algorithms' design is to isolate the faulty nodes in the earliest possible stage. We managed to reduce the interaction with the faulty nodes and therefore minimize the exposure to dictionary attacks and other types of attacks. However, the aggressive behavior of the algorithm may lead to isolation of even legitimate members due to reasons such as the loss of commutation signal or the typo errors of the initial password during the authentication procedure. To overcome these kind of problems and to provide a more dynamic and robust solution, we propose the body-centered cubic (BCC) as well as the face-centered cubic (FCC) and the tetrahedral algorithm.
-cube algorithm proposed in [7], with additional features that enhance the resistance against the dictionary attacks [5]. The basic idea behind the algorithms' design is to isolate the faulty nodes in the earliest possible stage. We managed to reduce the interaction with the faulty nodes and therefore minimize the exposure to dictionary attacks and other types of attacks. However, the aggressive behavior of the algorithm may lead to isolation of even legitimate members due to reasons such as the loss of commutation signal or the typo errors of the initial password during the authentication procedure. To overcome these kind of problems and to provide a more dynamic and robust solution, we propose the body-centered cubic (BCC) as well as the face-centered cubic (FCC) and the tetrahedral algorithm.
The BCC and the FCC algorithms can be considered as a series of different aggressive cube algorithms, each one performs for a different set of network nodes. In terms of two-party ECDH procedures, the BCC and FCC complexity is not higher than any of the single aggressive cube algorithms. This is because within a single two-party ECDH procedure of each algorithm, three ECDH procedures run simultaneously, each one corresponding to a different round of the aggressive cube algorithm.
The tetrahedral algorithm has significant differences compared with the BCC or the FCC algorithms. In this algorithm, all intermediate two-party keys are stored locally by the nodes and may be used during the network reformation process. Moreover, three-party keys are stored, providing the ability for secure subgroup communications among nodes that share the corresponding keys.
Depending on the mobility pattern and the reformation speed of the network, the aggressive  -cube algorithm is more efficient for almost static networks, the FCC approach would be more convenient for small-medium network reformation, BCC for medium-high network reformation and the tetrahedral algorithm would better facilitate high dynamicity in network reformation.
-cube algorithm is more efficient for almost static networks, the FCC approach would be more convenient for small-medium network reformation, BCC for medium-high network reformation and the tetrahedral algorithm would better facilitate high dynamicity in network reformation.
7. Conclusion
Our research was motivated by the need to establish fast, reliable, efficient, and secure group communications without relying on preexisting infrastructures. The actual operational environment and the varying nature of the established networks impose further key issues (e.g., the ability to add or subtract nodes depending on operational and security considerations) that need to be taken into account.
We have reviewed existing proposals around two-party or multiparty authentication and introduced new key establishment methods. Our proposal overcomes some of the main issues (such as rapid deployment, accuracy, and dynamic and robust behaviour) of existing solutions and operational environments. The proposed solutions introduce the use of elliptic curve cryptography in such a scenario. ECC computations require less storage, less power, less memory, and less bandwidth than other systems. This allows implementation of cryptography in constrained platforms such as wireless devices, handheld computers, smart cards, and thin-clients. For a given security level, elliptic curve cryptography raises computational speed and this is important in ad hoc networks, where the majority of the clients have limited resources.
The proposed algorithms meet all security requirements according the initial specification and provide differentiated solutions depending on the network reformation dynamicity. They are designed to support in a uniform approach both MANETs and wireless networks, taking into account a broad range of application requirements including secure internetworking and dynamicity of network topologies.
The proposed algorithms leave several open issues for future work. Formal analysis is necessary. The incorporation of several new password-based key agreement protocols, which do not require the use of asymmetric encryption, is a challenging consideration. Studying in detail the dynamic case, where the network topology is rapidly changing, would be very interesting, especially for indentifying the thresholds of network reformation that should be employed for algorithm switching.
References
Akyildiz IF, Wang X, Wang W: Wireless mesh networks: a survey. Computer Networks 2005, 47(4):445-487.
Bruno R, Conti M, Gregori E: Mesh networks: commodity multihop ad hoc networks. IEEE Communications Magazine 2005, 43(3):123-131.
Verikoukis C, Alonso L, Giamalis T: Cross-layer optimization for wireless systems: a European research key challenge. IEEE Communications Magazine 2005, 43(7):1-3.
Bonnefoi P-F, Sauveron D, Park JH: MANETS: an exclusive choice between use and security? Computing and Informatics 2008, 27(5):799-821.
Narayanan A, Shmatikov V: Fast dictionary attacks on passwords using time-space tradeoff. Proceedings of the 12th ACM Conference on Computer and Communications Security (CCS '05), November 2005, Alexandria, Va, USA 364-372.
Bellovin SM, Merritt M: Encrypted key exchange: password-based protocols secure against dictionary attacks. Proceedings IEEE Computer Society Symposium on Research in Security and Privacy, May 1992, Oakland, Calif, USA 72-84.
Asokan N, Ginzboorg P: Key agreement in ad hoc networks. Computer Communications 2000, 23(17):1627-1637. 10.1016/S0140-3664(00)00249-8
Diffie W, Hellman ME: New directions in cryptography. IEEE Transactions on Information Theory 1976, 22(6):644-654. 10.1109/TIT.1976.1055638
Johnson D, Vanstone S: The elliptic curve digital signature algorithm (ECDSA). International Journal on Information Security 2001, 1(1):36-63.
Cucker F, Smale S: Complexity estimates depending on condition and round-off error. Journal of the ACM 1999, 46(1):113-184. 10.1145/300515.300519
Koblitz N: Elliptic curve cryptosystems. Mathematics of Computation 1987, 4(8):203-209.
Menezes AJ, Okamoto T, Vanstone SA: Reducing elliptic curve logarithms to logarithms in a finite field. IEEE Transactions on Information Theory 1993, 39(5):1639-1646. 10.1109/18.259647
Menezes A, Teske E, Weng A: Weak fields for ECC. In Topics in Cryptology (CT-RSA '04), 2004, Lecture Notes in Computer Science. Volume 2964. Edited by: Okamoto T. Springer; 366-386.
Kalele A, Sule VR: Weak keys of pairing based Diffie-Hellman schemes on elliptic curves. Cryptology ePrint Archive 2005/30, 2005
Becker C, Wille U: Communication complexity of group key distribution. Proceedings of the 5th ACM Conference on Computer and Communications Security, November 1998, San Francisco, Calif, USA
Askoxylakis I, Sauveron D, Markantonakis K, Tryfonas T, Traganitis A: A body-centered cubic method for key agreement in dynamic mobile ad hoc networks. Proceedings of the 2nd International Conference on Emerging Security Information, Systems and Technologies, August 2008, Cap Esterel, France 193-202.
Askoxylakis IG, Kastanis DD, Traganitis AP: Elliptic curve and password based dynamic key agreement in wireless ad-hoc networks. Proceedings of the 3rd IASTED International Conference on Communication, Network, and Information Security (CNIS '06), October 2006, Cambridge, Mass, USA 50-60.
Liao L, Manulis M: Tree-based group key agreement framework for mobile ad-hoc networks. Future Generation Computer Systems 2007, 23(6):787-803. 10.1016/j.future.2007.01.001
Askoxylakis I, Tryfonas T, May J, Traganitis A: A dynamic key agreement mechanism for mission critical mobile ad hoc networking. Proceedings of the 2nd International Conference on Mobile Lightweight Wireless Systems, May 2010, Barcelona, Spain
Askoxylakis I, Markantonakis K, Tryfonas T, May J, Traganitis A: A face centered cubic key agreement mechanism for mobile ad hoc networks. Proceedings of the 1st International Conference on Mobile Lightweight Wireless Systems (MOBILIGHT '09), May 2009, Athens, Greece 103-113.
Acknowledgment
This work was supported in part by the European Commission in the 7th Framework Programme through project EU-MESH (Enhanced, Ubiquitous, and Dependable Broadband Access using MESH Networks), ICT-215320, http://www.eu-mesh.eu/.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Askoxylakis, I., Tryfonas, T., May, J. et al. A Family of Key Agreement Mechanisms for Mission Critical Communications for Secure Mobile Ad Hoc and Wireless Mesh Internetworking. J Wireless Com Network 2011, 807684 (2011). https://doi.org/10.1155/2011/807684
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/807684

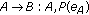 ,
,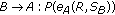 ,
, ,
,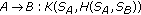 ,
,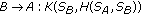 ,
,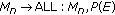 ,
,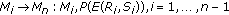 ,
,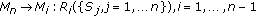 ,
,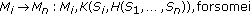 ,
,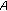 picks a random number,
picks a random number,  calculates
calculates 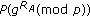 , and
, and  sends
sends 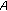 ,
, 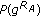 to
to  ; entity
; entity 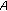 's id is sent in clear text.
's id is sent in clear text. picks a random number
picks a random number 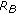 and calculates
and calculates 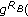 mod
mod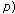 .
.  uses the shared password
uses the shared password  to decrypt
to decrypt 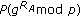 and calculates
and calculates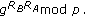
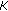 is derived from this value by selecting a certain number of bits. Finally, a random challenge,
is derived from this value by selecting a certain number of bits. Finally, a random challenge, 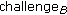 is generated. Then,
is generated. Then, 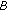 transmits
transmits
 uses
uses 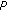 to decrypt
to decrypt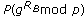 . From this, quantity
. From this, quantity  is calculated;
is calculated;  is in turn used to decrypt
is in turn used to decrypt .
. 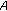 then generates a random challenge
then generates a random challenge .
.  sends
sends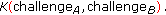
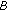 decrypts
decrypts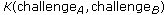 , and verifies that
, and verifies that  is correct.
is correct.  sends
sends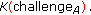
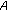 decrypts to obtain
decrypts to obtain and verifies that it matches the original message.
and verifies that it matches the original message. selects an integer,
selects an integer, selects an integer
selects an integer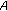 computes
computes 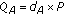 . The pair
. The pair  consists of
consists of  's public and private key.
's public and private key.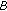 computes
computes 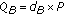 . The pair
. The pair 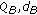 consists of
consists of  's public and private key.
's public and private key.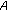 sends
sends 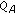 to
to 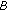
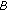 sends
sends  to
to 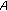
 computes
computes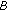 computes
computes picks a random number
picks a random number  , where
, where  is the order of the base point
is the order of the base point 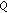 and calculates
and calculates 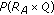
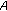 sends
sends 
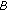 picks a random number
picks a random number 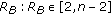 and calculates
and calculates  .
. 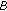 also uses the shared password
also uses the shared password 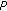 to decrypt
to decrypt 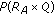 and calculates
and calculates is derived from this value, perhaps by selecting certain bits. Finally, a random challenge
is derived from this value, perhaps by selecting certain bits. Finally, a random challenge 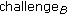 is generated.
is generated. 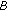 transmits
transmits uses
uses 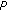 to decrypt
to decrypt . From this,
. From this, 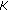 is calculated;
is calculated; 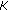 is in turn used to decrypt
is in turn used to decrypt .
.  then generates its own random challenge
then generates its own random challenge  .
.  sends
sends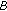 decrypts
decrypts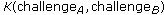 and verifies that
and verifies that 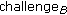 is correct.
is correct. 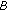 sends
sends decrypts to obtain
decrypts to obtain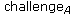 and verifies that it matches the original message.
and verifies that it matches the original message.

 must not match two nodes to the same partner in a given subround.
must not match two nodes to the same partner in a given subround. must not select the same partner twice.
must not select the same partner twice.









