- Research Article
- Open access
- Published:
Performance Analysis of Ad Hoc Dispersed Spectrum Cognitive Radio Networks over Fading Channels
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 849105 (2011)
Abstract
Cognitive radio systems can utilize dispersed spectrum, and thus such approach is known as dispersed spectrum cognitive radio systems. In this paper, we first provide the performance analysis of such systems over fading channels. We derive the average symbol error probability of dispersed spectrum cognitive radio systems for two cases, where the channel for each frequency diversity band experiences independent and dependent Nakagami- fading. In addition, the derivation is extended to include the effects of modulation type and order by considering M-ary phase-shift keying (
fading. In addition, the derivation is extended to include the effects of modulation type and order by considering M-ary phase-shift keying ( -PSK) and M-ary quadrature amplitude modulation
-PSK) and M-ary quadrature amplitude modulation  -QAM) schemes. We then consider the deployment of such cognitive radio systems in an ad hoc fashion. We consider an ad hoc dispersed spectrum cognitive radio network, where the nodes are assumed to be distributed in three dimension (3D). We derive the effective transport capacity considering a cubic grid distribution. Numerical results are presented to verify the theoretical analysis and show the performance of such networks.
-QAM) schemes. We then consider the deployment of such cognitive radio systems in an ad hoc fashion. We consider an ad hoc dispersed spectrum cognitive radio network, where the nodes are assumed to be distributed in three dimension (3D). We derive the effective transport capacity considering a cubic grid distribution. Numerical results are presented to verify the theoretical analysis and show the performance of such networks.
1. Introduction
Cognitive radio is a promising approach to develop intelligent and sophisticated communication systems [1, 2], which can require utilization of spectral resources dynamically. Cognitive radio systems that employ the dispersed spectrum utilization as spectrum access method are called dispersed spectrum cognitive radio systems [3]. Dispersed spectrum cognitive radio systems have capabilities to provide full frequency multiplexing and diversity due to their spectrum sensing and software defined radio features. In the case of multiplexing, information (or signal) is splitted into  data nonequal or equal streams and these data streams are transmitted over
data nonequal or equal streams and these data streams are transmitted over  available frequency bands. In the case of diversity, information (or signal) is replicated
available frequency bands. In the case of diversity, information (or signal) is replicated  times and each copy is transmitted over one of the available
times and each copy is transmitted over one of the available  bands as shown in Figure 1. Note that the frequency diversity feature of dispersed spectrum cognitive radio systems is only considered in this study.
bands as shown in Figure 1. Note that the frequency diversity feature of dispersed spectrum cognitive radio systems is only considered in this study.
Theoretical limits for the time delay estimation problem in dispersed spectrum cognitive radio systems are investigated in [3]. In this study, Cramer-Rao Lower Bounds (CRLBs) for known and unknown carrier frequency offset (CFO) are derived, and the effects of the number of available dispersed bands and modulation schemes on the CRLBs are investigated. In addition, the idea of dispersed spectrum cognitive radio is applied to ultra wide band (UWB) communications systems in [4]. Moreover, the performance comparison of whole and dispersed spectrum utilization methods for cognitive radio systems is studied in the context of time delay estimation in [5]. In [6, 7], a two-step time delay estimation method is proposed for dispersed spectrum cognitive radio systems. In the first step of the proposed method, a maximum likelihood (ML) estimator is used for each band in order to estimate unknown parameters in that band. In the second step, the estimates from the first step are combined using various diversity combining techniques to obtain final time delay estimate. In these prior works, dispersed spectrum cognitive radio systems are investigated for localization and positioning applications. More importantly, it is assumed that all channels in such systems are assumed to be independent from each other. In addition, single path flat fading channels are assumed in the prior works. However, in practice, the channels are not single path flat fading, and they may not be independent each other. Another practical factor that can also affect the performance of dispersed spectrum cognitive radio networks is the topology of nodes. In this context, several studies in the literature have studied the use of location information in order to enhance the performance of cognitive radio networks [8, 9]. It is concluded that use of network topology information could bring significant benefits to cognitive radios and networks to reduce the maximum transmission power and the spectral impact of the topology [10]. In [11], the effect of nonuniform random node distributions on the throughput of medium access control (MAC) protocol is investigated through simulation without providing theoretical analysis. In [12], a 3D configuration-based method that provides smaller number of path and better energy efficiency is proposed. In [13], 2D and 3D structures for underwater sensor networks are proposed, where the main objective was to determine the minimum numbers of sensors and redundant sensor nodes for achieving communication coverage. In [14–16], the authors represent a new communication model, namely, the square configuration (2D), to reduce the internode interference (INI) and study the impact of different types of modulations over additive white gaussian noise (AWGN) and Rayleigh fading channels on the effective transport capacity. Moreover, it is assumed that the nodes are distributed based on square distribution (i.e., 2D). Notice that the effects of node distribution on the performance of dispersed spectrum cognitive radio networks have not been studied in the literature, which is another main focus of this paper.
In this paper, performance analysis of dispersed spectrum cognitive radio systems is carried out under practical considerations, which are modulation and coding, spectral resources, and node topology effects. In the first part of this paper, the performance analysis of dispersed spectrum cognitive radio systems is conducted in the context of communications applications, and average symbol error probability is used as the performance metric. Average symbol error probability is derived under two conditions, that is, the scenarios when each channel experiences independent and dependent Nakagami- fading. The derivation for both cases is extended to include the effects of modulation type and order, namely, M-ary phase-shift keying (
fading. The derivation for both cases is extended to include the effects of modulation type and order, namely, M-ary phase-shift keying ( -PSK) and M-ary quadrature amplitude modulation (
-PSK) and M-ary quadrature amplitude modulation ( -QAM). The effects of convolutional coding on the average symbol error probability is also investigated through computer simulations. In the second part of the paper, the expression for the effective transport capacity of ad hoc dispersed spectrum cognitive radio networks is derived, and the effects of 3D node distribution on the effective transport capacity of ad hoc dispersed spectrum cognitive radio networks are studied through computer simulations [17].
-QAM). The effects of convolutional coding on the average symbol error probability is also investigated through computer simulations. In the second part of the paper, the expression for the effective transport capacity of ad hoc dispersed spectrum cognitive radio networks is derived, and the effects of 3D node distribution on the effective transport capacity of ad hoc dispersed spectrum cognitive radio networks are studied through computer simulations [17].
The paper is organized as follows. In Section 2, the system, spectrum, and channel models are presented. The average symbol error probability is derived considering different fading conditions and modulation schemes in Section 3. In Section 4, the analysis of the effective transport capacity for the 3D node distribution is provided. In Section 5, numerical results are presented. Finally, the conclusions are drawn in Section 6.
2. System, Spectrum, and Channel Models
The baseband system model for the dispersed spectrum cognitive radio systems is shown in Figure 2. In this model, opportunistic spectrum access is considered, where spectrum sensing and spectrum allocation (i.e., scheduling) are performed in order to determine the available bands and the bands that will be allocated to each user, respectively. Note that we assumed that these two processes are done prior to implementing dispersed spectrum utilization method. As a result, a single user that will use  bands simultaneously is considered in order to simplify the analysis in this study. The information of
bands simultaneously is considered in order to simplify the analysis in this study. The information of  is conveyed to the dispersed spectrum utilization system. In this stage, it is assumed that there are
is conveyed to the dispersed spectrum utilization system. In this stage, it is assumed that there are  available bands with identical bandwidths and dispersed spectrum utilization uses them. Afterwards, transmit signal is replicated
available bands with identical bandwidths and dispersed spectrum utilization uses them. Afterwards, transmit signal is replicated  times in order to create frequency diversity. Each signal is transmitted over each fading channel and then each signal is independently corrupted by AWGN process. At the receiver side, all the signals received from different channels are combined using Maximum Ratio Combining (MRC) technique.
times in order to create frequency diversity. Each signal is transmitted over each fading channel and then each signal is independently corrupted by AWGN process. At the receiver side, all the signals received from different channels are combined using Maximum Ratio Combining (MRC) technique.
Since there is not any complete statistical or empirical spectrum utilization model reported in the literature, we consider the following spectrum utilization model. Theoretically, there are four random variables that can be used to model the spectrum utilization. These are the number of available band ( ), carrier frequency (
), carrier frequency ( ), corresponding bandwidth (
), corresponding bandwidth ( ), and power spectral density (PSD) or transmit power (
), and power spectral density (PSD) or transmit power ( ) [18]. In the current study,
) [18]. In the current study,  is assumed to be deterministic. We also assume that PSD is constant and it is the same for all available bands, which results in a fixed SNR value. Additionally, since we consider baseband signal during analysis, the effect of
is assumed to be deterministic. We also assume that PSD is constant and it is the same for all available bands, which results in a fixed SNR value. Additionally, since we consider baseband signal during analysis, the effect of  such as path loss are not incorporated into the analysis. Ergo, the only random variable is the bandwidth of the available bands which is assumed to be uniformly distributed [18] with the limits of
such as path loss are not incorporated into the analysis. Ergo, the only random variable is the bandwidth of the available bands which is assumed to be uniformly distributed [18] with the limits of  and
and  , where
, where  and
and  are the minimum and maximum available absolute bandwidths, respectively. In addition, we assume perfect synchronization in order to evaluate the performance of dispersed spectrum cognitive radio systems. The analysis of the system is given as follows.
are the minimum and maximum available absolute bandwidths, respectively. In addition, we assume perfect synchronization in order to evaluate the performance of dispersed spectrum cognitive radio systems. The analysis of the system is given as follows.
The modulated signal with carrier frequency  is given by
is given by

where  denotes the real part of the argument,
denotes the real part of the argument,  is the carrier frequency, and
is the carrier frequency, and  represents the equivalent low-pass waveform of the transmitted signal.
represents the equivalent low-pass waveform of the transmitted signal.
For  .
. dispersed bands in Figure 1, the modulated signal waveform of the
dispersed bands in Figure 1, the modulated signal waveform of the  th band can be expressed as
th band can be expressed as

where we assume that there is not carrier frequency offset in any frequency diversity branch. Note that the same modulated signal is transmitted over  dispersed bands in order to create frequency diversity. The channel for
dispersed bands in order to create frequency diversity. The channel for  th band is characterized by an equivalent low-pass impulse response, which is given by
th band is characterized by an equivalent low-pass impulse response, which is given by

where  ,
,  , and
, and  are the gain, delay, and phase of the
are the gain, delay, and phase of the  th path at
th path at  th band, respectively. Slow and nonselective Nakagami-
th band, respectively. Slow and nonselective Nakagami- fading for each frequency diversity channel are assumed.
fading for each frequency diversity channel are assumed.
In the complex baseband model, the received signal for the  th band can be expressed as
th band can be expressed as

where  is the zero mean complex-valued white Gaussian noise process with power spectral density
is the zero mean complex-valued white Gaussian noise process with power spectral density  . The SNR from each diversity band (
. The SNR from each diversity band ( ) is combined to obtain the total SNR (
) is combined to obtain the total SNR ( ), which is defined as
), which is defined as

Notice from (5) that dispersed spectrum utilization method can provide full SNR adaptation by selecting required number of bands adaptively in the dispersed spectrum. This enables cognitive radio systems to support goal driven and autonomous operations.
The  can be expanded to be written in the form of SNR of
can be expanded to be written in the form of SNR of  th band with respect to the SNR of the first band. Hence, assume that the received power from the first band is equal to
th band with respect to the SNR of the first band. Hence, assume that the received power from the first band is equal to  and the AWGN experienced in this band has a power spectral density of
and the AWGN experienced in this band has a power spectral density of  . Assume that the received power from the
. Assume that the received power from the  th band is equal to (
th band is equal to ( ) and the AWGN experienced in this band has a power spectral density of (
) and the AWGN experienced in this band has a power spectral density of ( ). Thus, the total SNR can be expressed as
). Thus, the total SNR can be expressed as

where  and
and  . We assumed single-cell and single user case in this study. However, the analysis can be extended to multiple cells and multiuser cases, which is considered as a future work. At this point, we have obtained the total SNR, and in order to provide the performance analysis the average symbol error probability for two different cases, independent and dependent channels, are derived in the following section.
. We assumed single-cell and single user case in this study. However, the analysis can be extended to multiple cells and multiuser cases, which is considered as a future work. At this point, we have obtained the total SNR, and in order to provide the performance analysis the average symbol error probability for two different cases, independent and dependent channels, are derived in the following section.
3. Average Symbol Error Probability
In this section, we derive the average symbol error probability expressions of dispersed spectrum cognitive radio systems for both independent and dependent fading channel cases considering  -PSK and
-PSK and  -QAM modulation schemes. We selected these two modulation schemes arbitrarily. However, the analysis can be extended to other modulation types easily.
-QAM modulation schemes. We selected these two modulation schemes arbitrarily. However, the analysis can be extended to other modulation types easily.
3.1. Independent Channels Case
We assume Nakagami- fading channel for each band. In order to derive the expression of the average symbol error probability (
fading channel for each band. In order to derive the expression of the average symbol error probability ( ) for both
) for both  -PSK and
-PSK and  -QAM modulations, we utilize the Moment Generator Function (MGF) approach. By using (6), the MGF of the dispersed spectrum cognitive radio systems over Nakagami-
-QAM modulations, we utilize the Moment Generator Function (MGF) approach. By using (6), the MGF of the dispersed spectrum cognitive radio systems over Nakagami- channel is obtained, which is given by
channel is obtained, which is given by

where  is the fading parameter and
is the fading parameter and  , in which
, in which  is a function of modulation order
is a function of modulation order  . Therefore, for
. Therefore, for  -QAM and
-QAM and  -PSK modulation schemes,
-PSK modulation schemes,  is
is  and
and  , respectively.
, respectively.
3.1.1. M-QAM
 for dispersed spectrum cognitive radio systems is obtained by averaging the symbol error probability
for dispersed spectrum cognitive radio systems is obtained by averaging the symbol error probability  over Nakagami-
over Nakagami- fading distribution channel
fading distribution channel  , which is given by [19]
, which is given by [19]

3.1.2. M-PSK
By taking the same steps as in the  -QAM case,
-QAM case,  for
for  -PSK is obtained as follows [19]:
-PSK is obtained as follows [19]:

3.2. Dependent Channels Case
To show the effects of dependent case in our system, we just need to use the covariance matrix that shows how the  bands are dependent. To the best of our knowledge, unfortunately there is not empirical model or study on the dependency of dispersed spectrum cognitive radio or frequency diversity of channels, and determining such covariance matrix requires an extensive measurement campaign. However, there are studies on the dependency of space diversity channels [20, 21]. Therefore, we use two arbitrary correlation matrices for the sake of conducting the analysis here. These two arbitrary correlation matrices are linear and triangular, and they are referred to as Configuration A and Configuration B, respectively, in the current study.
bands are dependent. To the best of our knowledge, unfortunately there is not empirical model or study on the dependency of dispersed spectrum cognitive radio or frequency diversity of channels, and determining such covariance matrix requires an extensive measurement campaign. However, there are studies on the dependency of space diversity channels [20, 21]. Therefore, we use two arbitrary correlation matrices for the sake of conducting the analysis here. These two arbitrary correlation matrices are linear and triangular, and they are referred to as Configuration A and Configuration B, respectively, in the current study.
In our system, it is assumed that there are  correlated frequency diversity channels, each having Nakagami-
correlated frequency diversity channels, each having Nakagami- distribution. The basic idea is to express the SNR in terms of Gaussian distributions, since it is easy to deal with Gaussian distribution regardless of its complexity. The instantaneous SNR of parameter
distribution. The basic idea is to express the SNR in terms of Gaussian distributions, since it is easy to deal with Gaussian distribution regardless of its complexity. The instantaneous SNR of parameter  for each band can be considered as the sum of squares of
for each band can be considered as the sum of squares of  independent Gaussian random variables which means that the covariance matrix of the total SNR can be expressed by
independent Gaussian random variables which means that the covariance matrix of the total SNR can be expressed by  matrix with correlation coefficient between Gaussian random variables [22]. The MGF of Nakagami-
matrix with correlation coefficient between Gaussian random variables [22]. The MGF of Nakagami- fading for the dependent case is defined as [23]
fading for the dependent case is defined as [23]

where  , and
, and  are eigenvalues of covariance matrix for
are eigenvalues of covariance matrix for  .
.
The dimension of covariance matrix depends on  which means that there is always
which means that there is always  repeated eigenvalues with
repeated eigenvalues with  repeated eigenvalues per band. This is expected since the derivation depends on the facts that all the bands depend on each other. Thus, by using (10), the MGF for the dispersed spectrum cognitive radio systems in the case of dependent channels case can be expressed as
repeated eigenvalues per band. This is expected since the derivation depends on the facts that all the bands depend on each other. Thus, by using (10), the MGF for the dispersed spectrum cognitive radio systems in the case of dependent channels case can be expressed as

where  is the eigenvalue of covariance matrix for the
is the eigenvalue of covariance matrix for the  th band.
th band.
3.2.1. M-QAM
 for
for  -QAM modulation scheme is obtained using (8) and it is given by
-QAM modulation scheme is obtained using (8) and it is given by

3.2.2. M-PSK
Since fading parameters  and
and  are integers,
are integers,  for
for  -PSK modulation can be obtained using (9), and the resultant expression is
-PSK modulation can be obtained using (9), and the resultant expression is

4. Effective Transport Capacity
In the preceding sections, the analysis of dispersed spectrum cognitive radio network by obtaining the error probabilities for different scenarios and the MGF of the dispersed spectrum CR system over Nakagami-m channel is provided. Implementation of dispersed spectrum CR concept in practical wireless networks is of great interest. Therefore, in this section, we considered ad hoc type network for an application of dispersed spectrum CR discussed in the previous sections. The effective transport capacity performance analysis of conventional ad hoc wireless networks considering 2D node distribution is conducted in [14]. In the current section, this analysis is extended to ad hoc dispersed spectrum cognitive radio networks [3], where the nodes are distributed in 3D and they are communicated using the dispersed spectrum cognitive radio systems. In order to derive the effective transport capacity for the ad hoc dispersed spectrum cognitive radio networks, the following network communication system model is employed [14–16].
-
(i)
Each node transmits a fixed power of
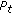 , and the multihop routes between a source and destination is established by a sequence of minimum length links. Moreover, no node can share more than one route.
, and the multihop routes between a source and destination is established by a sequence of minimum length links. Moreover, no node can share more than one route. -
(ii)
If a node needs to communicate with another node, a multihop route is first reserved and only then the packets can be transmitted without looking at the status of the channel which is based on a MAC protocol for INI: reserve and go (RESGO) [14]. Packet generation, with each packet having a fixed length of
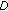 bits, is given by a Poisson process with parameter
bits, is given by a Poisson process with parameter  (packets/second).
(packets/second). -
(iii)
The INI experienced by the nodes in the network is mainly dependent on the node distribution and the MAC protocol.
-
(iv)
The condition
 , where
, where 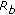 is transmission data rate of the nodes, needs to be satisfied for network communications.
is transmission data rate of the nodes, needs to be satisfied for network communications.
4.1. Average Number of Hops
In the 3D node configuration, there are  nodes, and each node is placed uniformly at the center of a cubic grid in a spherical volume
nodes, and each node is placed uniformly at the center of a cubic grid in a spherical volume  that can be defined as
that can be defined as

where  is the length of cube that a node is centered in. From (14), it can be shown that two neighboring nodes are at distance
is the length of cube that a node is centered in. From (14), it can be shown that two neighboring nodes are at distance  which is defined as
which is defined as

where  is the node volume density.
is the node volume density.
The maximum number of hops ( ) needs to be determined first in order to derive the expression for average number of hops (
) needs to be determined first in order to derive the expression for average number of hops ( ). The deviation from a straight line between the source and destination nodes is limited by assuming that the source and destination nodes lie at opposite ends of a diameter over a spherical surface, and a large number of nodes in the network volume are simulated [14]. It follows that
). The deviation from a straight line between the source and destination nodes is limited by assuming that the source and destination nodes lie at opposite ends of a diameter over a spherical surface, and a large number of nodes in the network volume are simulated [14]. It follows that  distribution can be defined for 3D configuration as
distribution can be defined for 3D configuration as

where  is the diameter of sphere and
is the diameter of sphere and  represents the integer value closest to the argument.
represents the integer value closest to the argument.
Since the number of hops is assumed to have a uniform distribution, the probability density function (PDF) can be defined as

therefore,

which agrees with the result in [14]. The average number of hops for 3D configuration can therefore be obtained as

The total effective transport capacity  is the summation of effective transport capacity for each route, and since the routes are disjointed, the
is the summation of effective transport capacity for each route, and since the routes are disjointed, the  is defined as [16]
is defined as [16]

where  is the number of disjoint routes and
is the number of disjoint routes and  is the average number of sustainable hops [16] which is defined as
is the average number of sustainable hops [16] which is defined as

where  and
and  are the bit error rate at the end of a single link and the maximum
are the bit error rate at the end of a single link and the maximum  can be tolerated to receive the data, respectively. The average
can be tolerated to receive the data, respectively. The average  at the end of a multihop route can therefore be expressed as [15]
at the end of a multihop route can therefore be expressed as [15]

According to (8),  is function of MGF, and the MGF of the dispersed spectrum CR system over Nakagami-m channel is given in (7) which is defined as the Laplace transform of the PDF of the SNR [19]. Let the SNR at the end of a single link in the case of conventional single band spectrum utilization be
is function of MGF, and the MGF of the dispersed spectrum CR system over Nakagami-m channel is given in (7) which is defined as the Laplace transform of the PDF of the SNR [19]. Let the SNR at the end of a single link in the case of conventional single band spectrum utilization be  . In addition, let us assume that there exists INI between the nodes, then
. In addition, let us assume that there exists INI between the nodes, then  can be expressed as [16]
can be expressed as [16]

where  is the transmitted power from each node,
is the transmitted power from each node,  is the noise figure and
is the noise figure and  is the Boltzmann's constant (
is the Boltzmann's constant ( J/K),
J/K),  is the room temperature (
is the room temperature ( K),
K),  is the fading envelope,
is the fading envelope,  b/s/Hz is the spectral efficiency (where
b/s/Hz is the spectral efficiency (where  is the transmission bandwidth),
is the transmission bandwidth),  is the INI power, and
is the INI power, and  can be expressed as
can be expressed as

where  and
and  are the transmitter and receiver antenna gains,
are the transmitter and receiver antenna gains,  is the carrier frequency,
is the carrier frequency,  is the speed of light, and
is the speed of light, and  is a loss factor. From (6) and (23),
is a loss factor. From (6) and (23),  for the dispersed spectrum cognitive radio networks can be expressed as
for the dispersed spectrum cognitive radio networks can be expressed as

Assuming that the destination node is in the center, we try to calculate all the interference powers transmitting from all nodes by clustering the nodes into groups in order to find out the general formula for  .
.
In the  th order tier of the 3D distribution, there are the following.
th order tier of the 3D distribution, there are the following.
-
(i)
The interference power at the destination node received from one of six nodes, at a distance
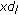 , is
, is  .
. -
(ii)
The interference power at the destination node received from one of eight nodes, at a distance
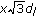 , is
, is 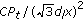 .
. -
(iii)
The interference power at the destination node received from one of twelve nodes, at a distance
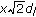 , is
, is  .
. -
(iv)
The interference power at the destination node received from one of twenty nodes, at a distance
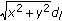 , where
, where  , and
, and  , is
, is 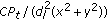 .
. -
(v)
The interference power at the destination node received from one of twenty nodes, at a distance
 , is
, is  .
. -
(vi)
The interference power at the destination node received from one of twenty nodes, at a distance
 , where
, where  ,
,  , is
, is  .
.
A maximum  and tier order
and tier order  exist since the number of nodes in the network is finite. Therefore,
exist since the number of nodes in the network is finite. Therefore,

For sufficiently large values of  , (26) leads to
, (26) leads to  . The probability of a single bit in the packet interfered by any node in the network is defined in [14, 16] as
. The probability of a single bit in the packet interfered by any node in the network is defined in [14, 16] as  which means that the overall interference power
which means that the overall interference power  using RESGO MAC protocol can be expressed as [14]
using RESGO MAC protocol can be expressed as [14]

where

5. Numerical Results
In this section, numerical results are provided to verify the theoretical analysis. Figure 3 illustrates the effect of frequency diversity order on the average symbol error probability performance of the dispersed spectrum cognitive radio systems. The results are obtained over independent Nakagami- fading channels considering 16-QAM modulation scheme and the same bandwidth for the frequency diversity bands. The performance of the conventional single band system (
fading channels considering 16-QAM modulation scheme and the same bandwidth for the frequency diversity bands. The performance of the conventional single band system ( ) is provided for the sake of comparison. In comparison to the conventional single band system, at
) is provided for the sake of comparison. In comparison to the conventional single band system, at  , the dispersed spectrum cognitive radio systems with two frequency diversity bands (
, the dispersed spectrum cognitive radio systems with two frequency diversity bands ( ) provide SNR gain of 8 dB. An additional 2 dB SNR gain due to the frequency diversity is achieved under the simulation conditions by adding yet another branch (
) provide SNR gain of 8 dB. An additional 2 dB SNR gain due to the frequency diversity is achieved under the simulation conditions by adding yet another branch ( ). It is clearly observed that the frequency diversity order is proportional to the performance. In the limiting case, if
). It is clearly observed that the frequency diversity order is proportional to the performance. In the limiting case, if  goes to infinity the performance converges to the performance of AWGN channel (see the appendix).
goes to infinity the performance converges to the performance of AWGN channel (see the appendix).
Figure 4 presents the performance comparison for the case of using 16-QAM and 16-PSK modulation schemes for independent and dependent cases with equal bandwidth. It is observed that the performance of 16-QAM is better than that of 16-PSK, and this result can be justified since the distance between any points in signal constellation of  -PSK is less than that in
-PSK is less than that in  -QAM. This figure shows the performance of the dispersed spectrum cognitive radio systems for the dependent channels case, where Configuration A and Configuration B are considered. It can be seen that the correlation degrades the performance of the system and it can also be noted that Configuration A case performs better than Configuration B case. This is due to the fact that Configuration B has lower correlation coefficients than those of Configuration A.
-QAM. This figure shows the performance of the dispersed spectrum cognitive radio systems for the dependent channels case, where Configuration A and Configuration B are considered. It can be seen that the correlation degrades the performance of the system and it can also be noted that Configuration A case performs better than Configuration B case. This is due to the fact that Configuration B has lower correlation coefficients than those of Configuration A.
In Figure 5, the effects of frequency diversity branches with different SNR values on the symbol error probability performance are shown. (The SNR value for each frequency diversity branch is given by  (e.g.,
(e.g.,  ).) These different SNR values for the diversity bands are assigned relative to the SNR value of the first band; for instance, for the SNR values of
).) These different SNR values for the diversity bands are assigned relative to the SNR value of the first band; for instance, for the SNR values of  , the SNR value of second band is three times the first band. It can be noted that the system performs better if the branch with the lowest fading severity has the highest SNR, since the symbol error probability mainly depends on the SNR proportionally, and fading parameter
, the SNR value of second band is three times the first band. It can be noted that the system performs better if the branch with the lowest fading severity has the highest SNR, since the symbol error probability mainly depends on the SNR proportionally, and fading parameter  .
.
The effects of coding on the performance of the system are also investigated. The convolutional coding with  code and
code and  generator matrices are considered. The bound for error probability in [24] is extended for our system and it is used as performance metric during the simulations. Finally, Nakagami-
generator matrices are considered. The bound for error probability in [24] is extended for our system and it is used as performance metric during the simulations. Finally, Nakagami- fading channel along with 16-QAM modulation is assumed. The result is plotted in Figure 6 which shows the effects of coding on the performance and it can be clearly seen that the performance is improved due to coding gain.
fading channel along with 16-QAM modulation is assumed. The result is plotted in Figure 6 which shows the effects of coding on the performance and it can be clearly seen that the performance is improved due to coding gain.
The results in Figures 7 and 8 are obtained using the following network simulation parameters:  ,
,  dB,
dB,  dB,
dB,  m3,
m3,  ,
,  μW, and
μW, and  . In order for the numerical results to be comparable to the results in [14], we choose the value of
. In order for the numerical results to be comparable to the results in [14], we choose the value of  for Nakagami-
for Nakagami- fading channels, which represents Rayleigh fading channels. The effects of 3D node distribution on the effective transport capacity of ad hoc dispersed spectrum cognitive radio networks are investigated through computer simulations considering
fading channels, which represents Rayleigh fading channels. The effects of 3D node distribution on the effective transport capacity of ad hoc dispersed spectrum cognitive radio networks are investigated through computer simulations considering  dispersed channels between two nodes, and the results are shown in Figure 7. In ad hoc model the dependency of
dispersed channels between two nodes, and the results are shown in Figure 7. In ad hoc model the dependency of  channels is assumed to be the same as dependent channels case in Section 3.2. This figure represents the relationship between the bit rate and the effective transport capacity considering 3D node distribution. It is shown that at low and high
channels is assumed to be the same as dependent channels case in Section 3.2. This figure represents the relationship between the bit rate and the effective transport capacity considering 3D node distribution. It is shown that at low and high  values, the effective transport capacity is low. However, at intermediate values, the effective transport capacity is saturated. This is due to the fact that the average sustainable number of hops is defined as the minimum between the maximum number of sustainable hops and the average number of hops per route. Full connectivity will not be sustained until reaching the average number of hops. Having reached the average number of hops, full connectivity will be sustained until the number of hops is greater than the threshold value as defined by an acceptable BER, since a low SNR value is produced by low and high
values, the effective transport capacity is low. However, at intermediate values, the effective transport capacity is saturated. This is due to the fact that the average sustainable number of hops is defined as the minimum between the maximum number of sustainable hops and the average number of hops per route. Full connectivity will not be sustained until reaching the average number of hops. Having reached the average number of hops, full connectivity will be sustained until the number of hops is greater than the threshold value as defined by an acceptable BER, since a low SNR value is produced by low and high  values. It can be seen that the correlation between fading channels degrades the performance of the system and it can also be noted that Configuration A case performs better than Configuration B case.
values. It can be seen that the correlation between fading channels degrades the performance of the system and it can also be noted that Configuration A case performs better than Configuration B case.
It is known that the deployment of an ad hoc network is generally considered as two dimensions (2D). Nonetheless, because of reducing dimensionality, the deployment of the nodes in a 3D scenario are sparser than in a 2D scenario, which leads to decrease of the internodes interference, thus increasing the effective transport capacity of the system. This can be observed by comparing Figures 7 and 8.
In addition, the 3D topology of dispersed spectrum cognitive radio ad hoc network can be considered in some real applications such as sensor network in underwater, in which the nodes may be distributed in 3D [13]. The 3D topology is more suitable to detect and observe the phenomena in the three dimensional space that cannot be observed with 2D topology [25].
6. Conclusion
In this paper, the performance analysis of dispersed spectrum cognitive radio systems is conducted considering the effects of fading, number of dispersed bands, modulation, and coding. Average symbol error probability is derived when each band undergoes independent and dependent Nakagami- fading channels. Furthermore, the average symbol error probability for both cases is extended to take the modulation effects into account. In addition, the effects of coding on symbol error probability performance are studied through computer simulations. We also study the effects of the 3D node distribution along with INI on the effective transport capacity of ad hoc dispersed spectrum cognitive radio networks. The effective transport capacity expressions are derived over fading channels considering
fading channels. Furthermore, the average symbol error probability for both cases is extended to take the modulation effects into account. In addition, the effects of coding on symbol error probability performance are studied through computer simulations. We also study the effects of the 3D node distribution along with INI on the effective transport capacity of ad hoc dispersed spectrum cognitive radio networks. The effective transport capacity expressions are derived over fading channels considering  -QAM modulation scheme. Numerical results are presented to study the effects of fading, number of dispersed bands, modulation, and coding on the performance of dispersed spectrum cognitive radio systems. The results show that the effects of fading, number of dispersed bands, modulation, and coding on the average symbol error probability of dispersed spectrum cognitive radio systems is significant. According to the results, the effective transport capacity is saturated for intermediate bit rate values. Additionally, it is concluded that the correlation between fading channels highly affects the effective transport capacity. Note that this work can be extended to the case where the number of available bands change randomly at every spectrum sensing cycle, which is considered as a future work.
-QAM modulation scheme. Numerical results are presented to study the effects of fading, number of dispersed bands, modulation, and coding on the performance of dispersed spectrum cognitive radio systems. The results show that the effects of fading, number of dispersed bands, modulation, and coding on the average symbol error probability of dispersed spectrum cognitive radio systems is significant. According to the results, the effective transport capacity is saturated for intermediate bit rate values. Additionally, it is concluded that the correlation between fading channels highly affects the effective transport capacity. Note that this work can be extended to the case where the number of available bands change randomly at every spectrum sensing cycle, which is considered as a future work.
Appendix
The MGF of Nakagami- fading channels of dispersed spectrum sharing system with
fading channels of dispersed spectrum sharing system with  available bands is given by
available bands is given by

For  (or
(or  ), we obtain the form of type
), we obtain the form of type  . The solution is given by introducing a dependant variable
. The solution is given by introducing a dependant variable

and taking the natural logarithm of both sides:

The limit  is an indeterminate form of type 0/0; by using L'Hôpital's rule we obtain
is an indeterminate form of type 0/0; by using L'Hôpital's rule we obtain

Since  as
as  or
or  , it follows from the continuity of the natural exponential function that
, it follows from the continuity of the natural exponential function that  or, equivalently,
or, equivalently,  as
as  (or
(or  ).Therefore,
).Therefore,

Since the MGF of the Gaussian distribution with zero variance is given by

we conclude that, when  , the channel converges to an AWGN channel under the assumption independent channel samples.
, the channel converges to an AWGN channel under the assumption independent channel samples.
References
Mitola J, Maguire GQ: Cognitive radio: making software radios more personal. IEEE Personal Communications 1999, 6(4):13-18. 10.1109/98.788210
Ekin S, Yilmaz F, Celebi H, Qaraqe KA, Alouini M, Serpedin E: Capacity limits of spectrum-sharing systems over hyper-fading channels. Wireless Communications and Mobile Computing. In press
Gezici S, Celebi H, Poor HV, Arslan H: Fundamental limits on time delay estimation in dispersed spectrum cognitive radio systems. IEEE Transactions on Wireless Communications 2009, 8(1):78-83.
Gezici S, Celebi H, Arslan H, Poor HV: Theoretical limits on time delay estimation for ultra-wideband cognitive radios. Proceedings of the IEEE International Conference on Ultra-Wideband (ICUWB '08), September 2008 2: 177-180.
Celebi H, Qaraqe KA, Arslan H: Performance comparison of time delay estimation for whole and dispersed spectrum utilization in cognitive radio systems. Proceedings of the 4th International Conference on Cognitive Radio Oriented Wireless Networks and Communications (CROWNCOM '09), June 2009 1-6.
Kocak F, Celebi H, Gezici S, Qaraqe KA, Arslan H, Poor HV: Time delay estimation in cognitive radio systems. Proceedings of the 3rd IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP '09), 2009 400-403.
Kocak F, Celebi H, Gezici S, Qaraqe KA, Arslan H, Poor HV: Time-delay estimation in dispersed spectrum cognitive radio systems. EURASIP Journal on Advances in Signal Processing 2010., 2010:
Chen T, Zhang H, Maggio GM, Chlamtac I: Topology management in CogMesh: a cluster-based cognitive radio mesh network. In Proceedings of the IEEE International Conference on Communications (ICC '07), 2007. Citeseer; 6516-6521.
Mähönen P, Petrova M, Riihijärvi J: Applications of topology information for cognitive radios and networks. Proceedings of the 2nd IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN '07), April 2007 103-114.
Chiganmi A, Sarac K, Prakash R: Variable power broadcasting in ad hoc networks. In Proceedings of the IEEE International Conference on Communications (ICC '06), 2006, Istanbul, Turkey. Citeseer;
Hoydis J, Petrova M, Mähönen P: Effects of topology on local throughput-capacity of ad hoc networks. Proceedings of the 19th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '08), September 2008 1-5.
Thomas RW, Komali RS, MacKenzie AB, DaSilva LA: Joint power and channel minimization in topology control: a cognitive network approach. Proceedings of the IEEE International Conference on Communications (ICC '07), June 2007 6538-6544.
Pompili D, Melodia T, Akyildiz IF: Three-dimensional and two-dimensional deployment analysis for underwater acoustic sensor networks. Ad Hoc Networks 2009, 7(4):778-790. 10.1016/j.adhoc.2008.07.010
Ferrari G, Baruffini B, Tonguz O: Spectral efficiency-connectivity tradeoff in ad hoc wireless network. Proceedings of the International Symposium on Information Theory and Its Applications (ISITA '04), October 2004, Parma, Italy
Ferrari G, Tonguz OK: MAC protocols and transport capacity in ad hoc wireless networks: Aloha versus PR-CSMA. Proceedings of the IEEE Military Communications Conference (MILCOM '03), October 2003, Boston, Mass, USA 1311-1318.
Tonguz O, Ferrari G: Ad Hoc Wireless Networks: A Communication Theoretic Perspective. John Wiley & Sons, New York, NY, USA; 2006.
Qaraqe KA, Mohammad M, Celebi H, El-Saigh A: The impacts of node distribution on the effective transport capacity of ad hoc dispersed spectrum cognitive radio networks. Proceedings of the 17th International Conference on Telecommunications (ICT '10), October 2010, Doha, Qatar 122-127.
Celebi H, Qaraqe KA, Arslan H: Performance analysis of TOA range accuracy adaptation for cognitive radio systems. Proceedings of the 70th IEEE Vehicular Technology Conference Fall (VTC '09), September 2009, Anchorage, Alaska, USA
Goldsmith A: Wireless Communciations. Cambridge University Press, Cambridge, UK; 2005.
Lee WCY: Mobile Communications Design Fundamentals. John Wiley & Sons, New York, NY, USA; 1993.
Zhang QT: Exact analysis of postdetection combining for DPSK and NFSK systems over arbitrarily correlated nakagami channels. IEEE Transactions on Communications 1998, 46(11):1459-1467. 10.1109/26.729390
Nakagami M: The m distribution—a general formula for intensity distribution of rapid fading. In Statistical Methods in Radio Wave Propagation. Edited by: Hoffman WG. Pergamon, New York, NY, USA; 1960:3-66.
Ghareeb I: Noncoherent MT-MFSK signals with diversity reception in arbitrarily correlated and unbalanced Nakagami- m fading channels. IEEE Journal on Selected Areas in Communications 2005, 23(9):1839-1850.
Lin S, Castello D: Error Control Coding. 2nd edition. Pearson, Prentice Hall, Upper Saddle River, NJ, USA; 1963.
Tiwari R, Dinh T, Thai M: On Approximation Algorithms for Interference-Aware Broadcast Scheduling in 2D and 3D Wireless Sensor Networks, Springer Wireless Algorithms, Systems, and Applications. Springer, New York, NY, USA; 2009.
Acknowledgment
This paper was supported by Qatar National Research Fund (QNRF) under Grant NPRP 08-152-2-043.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Qaraqe, K., Celebi, H., Mohammad, M. et al. Performance Analysis of Ad Hoc Dispersed Spectrum Cognitive Radio Networks over Fading Channels. J Wireless Com Network 2011, 849105 (2011). https://doi.org/10.1155/2011/849105
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/849105


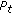 , and the multihop routes between a source and destination is established by a sequence of minimum length links. Moreover, no node can share more than one route.
, and the multihop routes between a source and destination is established by a sequence of minimum length links. Moreover, no node can share more than one route.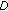 bits, is given by a Poisson process with parameter
bits, is given by a Poisson process with parameter  (packets/second).
(packets/second). , where
, where 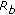 is transmission data rate of the nodes, needs to be satisfied for network communications.
is transmission data rate of the nodes, needs to be satisfied for network communications.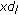 , is
, is  .
.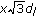 , is
, is 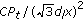 .
.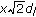 , is
, is  .
.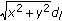 , where
, where  , and
, and  , is
, is 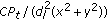 .
. , is
, is  .
. , where
, where  ,
,  , is
, is  .
.
 values and independent Nakagami-
values and independent Nakagami- fading channel (
fading channel ( ).
).
 -QAM and
-QAM and  -PSK signals (
-PSK signals ( ) with
) with  , Nakagami-
, Nakagami- fading channel (
fading channel ( ) for both independent and dependent channels cases.
) for both independent and dependent channels cases.
 for
for
 , respectively.
, respectively.

 , Nakagami-
, Nakagami-
 fading channel compared with the performance bound for convolutional codes.
fading channel compared with the performance bound for convolutional codes.

 versus
versus  for 16-QAM modulation with three Nakagami-
for 16-QAM modulation with three Nakagami- fading channels using 3D node distribution (
fading channels using 3D node distribution ( ,
,  ).
).
 versus
versus  for 16 QAM modulation with three Nakagami-
for 16 QAM modulation with three Nakagami- fading channels using 2D node distribution
fading channels using 2D node distribution  .
.