- Research Article
- Open access
- Published:
Efficient Public Key Certificate Management for Mobile Ad Hoc Networks
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 935457 (2011)
Abstract
Mobile ad hoc networks involve communications over a shared wireless channel without any centralized infrastructure. Consequently, in an optimal solution, management and security services depend exclusively on network members. The main contribution of this paper is an efficient public key management scheme that is suitable for fully self-organized mobile ad hoc networks where all nodes play identical roles. Our approach implies that the operations of creating, storing, distributing, and revoking nodes' public keys are carried out locally by the nodes themselves. The goal of the presented methods is the improvement in the process of building local certificate repositories of nodes. In order to do it, an authentication solution based on the web of trust concept is combined with an element of routing based on the multipoint relay concept introduced in the optimized link state routing protocol. Our proposal leads to a good tradeoff among security, overhead, and flexibility. Experimental results show a considerable decrease in resource consumption while carrying out the certificate verification process.
1. Introduction
A Mobile Ad hoc NETwork (MANET) is a highly dynamic wireless network with no fixed infrastructure and heavy constraints in node capabilities. Such characteristics unable the use of the classical public key management paradigm based on a centralized Certification Authority (CA).
Research on the deployment of a Public Key Infrastructure (PKI) in MANETs has been mainly two tiered so far. In particular, the two main approaches we can find in the bibliography are a distributed certification model and a self-organized scheme.
The methods here described and evaluated are aimed at improving the process of building the local certificate repository associated to each node in the self-organized model, which leads to a significant improvement in the efficiency of the whole model. Particularly, a considerable decrease in resource consumption while undertaking the verification process associated to authentication is obtained from the experiments. In order to achieve such improvement, we face the problem by combining typical authentication elements with common ideas used in routing protocols in MANETs. In particular, the Optimised Link State Routing (OLSR) protocol from which some ideas regarding the use of the MultiPoint Relay (MPR) technique have been borrowed to design the proposed algorithm for updating repositories.
The structure of this paper is as follows. Section 2 is devoted to the description of the background, including the description of the MPR technique. Since our proposal is specifically designed to be deployed in the self-organized public-key management model, Section 3 deals with the details of the graph-based version of such an approach. A complete algorithmic description of the proposed method is provided in Section 4. Section 5 describes the results of several computational experiments while several conclusions are included in the last section.
2. Background
In order to improve the construction of certificate repositories for the key management scheme when adopting the web of trust model and the self-organized approach to implement a PKI, we use certain elements of the routing protocol known as OLSR. This section contains an introductory description of such a protocol, paying special attention to the MPR technique embedded in it.
Routing in MANETs has been one of the research areas with more activity [1]. A first basic classification used when talking about routing protocols distinguishes between proactive and reactive protocols. Protocols in the first category are characterized by the fact that each node stores a route for each reachable member of the network, although such a path may not be required at that precise moment; while in reactive protocols only when a request for communication between two nodes is required, a route discovery procedure is initiated. Due to this feature, reactive protocols are referred to as on-demand routing protocols. Proactive algorithms are also known as table-driven routing protocols since local routing information defining the different paths is organized according to a table stored by each node. The information contained in such a table defines an entry associated to each reachable node containing the next node in the path to the destination, and a metric or distance, among other data. The metric can be defined in function of several criteria such as the hop distance, the total delay, or the cost of sending messages.
In general, when comparing proactive and reactive protocols, we have that in the first case certain overload is originated in the network due to the continuous updates produced in routing information, while in the second case, certain delay is produced by the execution of routing discovery procedures any time a new path is defined. In networks with high mobility, reactive routing protocols have a better behaviour since the paths are recalculated as soon as a link state change is detected. Building an accurate topological map of the network requires exchange of information among nodes on a regular basis, which can lead to certain network overloading on the network, unless network traffic is sporadic. On the other hand, when dealing with delay-sensitive networks (such as Vehicular Ad hoc NETworks or VANETs) proactive protocols outperform better [2].
In this work, we use certain elements of the Optimized Link State Routing protocol (OLSR) [3], which is one of the four basic protocols adopted for MANETs. OLSR is a proactive protocol because local routing information defining the different paths is organized according to a table stored by each node.
The OLSR routing procedure has been extensively analyzed in the bibliography, and currently OLSRv2 is under consideration [4]. Some works devoted to improve it by integrating security tools [5] have been also developed. In the OLSR proactive routing two stages can be clearly differentiated. Firstly, a reliable map of the network is built. In order to obtain such an accurate map, all the network nodes must exchange messages regarding the state of their connections links. In the second stage, and based on the built map, the optimum route among the nodes is generated. The main obstacle this protocol has to skip is the high number of messages to be exchanged among nodes. However, thanks to these messages the network configuration is known by all its members.
In order to reduce the overhead and message redundancy and to avoid the storm problem [6], a specific technique, named the MultiPoint Relay technique, was defined in OLSR. In this technique each node selects a particular neighbour subset (nodes at one-hop distance with bidirectional links) whose members will be in charge of broadcasting the information. By doing so, the number of messages exchanged is considerably reduced [7].
The MPR technique was originally deployed for reducing the duplicity of messages at local level when broadcasting information in a proactive MANET. In general, the number of redundant packets received by a node may be equal to the number of neighbours a node has. Roughly speaking, it can be said that the MPR allows determining the minimum number of nodes needed for reaching the whole network when it is recursively applied. This approach obtains better results regarding optimization in large and dense networks. The way we use the basics of the MPR in the proposed key management for MANETs, as well as its relationship with Graph Theory problems is included below.
2.1. OLSR Description and Notation
In the OLSR protocol only a subset of nodes will be in charge of retransmitting the received packets. In this way, every node  must define among its direct neighbours a set of transmitters (here denoted by
must define among its direct neighbours a set of transmitters (here denoted by  ) that will be the only ones in charge of retransmitting the messages emitted by the initial node. This means that control packets are retransmitted by a node belonging to
) that will be the only ones in charge of retransmitting the messages emitted by the initial node. This means that control packets are retransmitted by a node belonging to  only when the packet was sent by
only when the packet was sent by  and it is the first time it is received. According to this method, each router chooses independently the set
and it is the first time it is received. According to this method, each router chooses independently the set  among its symmetric 1-hop neighbours such that all symmetric 2-hop neighbours are reachable via at least one symmetric 1-hop neighbour belonging to
among its symmetric 1-hop neighbours such that all symmetric 2-hop neighbours are reachable via at least one symmetric 1-hop neighbour belonging to  .
.
In routing models, the network is usually represented with a graph whose vertex set  symbolizes the set of nodes of the network. In this way, for any node
symbolizes the set of nodes of the network. In this way, for any node  ,
,  denotes the set of
denotes the set of  's symmetric neighbours in an
's symmetric neighbours in an  -hop distance from
-hop distance from  . It is assumed that
. It is assumed that  . Consequently,
. Consequently,  stands for
stands for  's direct neighbours and the cardinality
's direct neighbours and the cardinality  corresponds to
corresponds to  's degree. These sets are defined by using the shortest path and in such a way that
's degree. These sets are defined by using the shortest path and in such a way that  and
and  are disjoint sets. Computation of these shortest paths may be accomplished as stated in [8].
are disjoint sets. Computation of these shortest paths may be accomplished as stated in [8].
Following the notation defined in [9] jointly with the one previously introduced in this paper, it is feasible to formally define the set MPR for a vertex  as
as  .
.
Through this definition, decision and optimization problems associated to the MPR construction may be defined. According to the Computational Complexity hierarchy the associated decision problem may be reduced in polynomial time to the Dominating Set problem, which belongs to the NP-complete class. Therefore a heuristic approach is adequate for computing the MPR set. The description of OLSR [3] includes a particular heuristic for solving this problem (although in [4] it is stated that "Routers can freely interoperate whether they use the same or different MPR selection algorithms") as example. The heuristic defined there uses a greedy approach handling, among other parameters, the willingness of nodes to participate in the routing process and the vertex degree. A complete description and analysis of this heuristic may be found in [10]. Next we include a brief description of such a heuristic.
Step 1.
Begin with an empty MPR set.
Step 2.
Select those one-hop neighbour nodes of  that are the only neighbour of some two-hop neighbours of
that are the only neighbour of some two-hop neighbours of  , and add them to
, and add them to  .
.
Step 3.
Add to  the neighbour node of
the neighbour node of  that covers the largest number of two-hop neighbours of
that covers the largest number of two-hop neighbours of  that are not yet covered by the current
that are not yet covered by the current  set.
set.
Repeat Step 3 until all two-hop neighbours are covered.
Using the notation introduced so far we may describe the greedy heuristic distinguishing two main stages as follows. In the first one those vertices  in
in  with a unique neighbour
with a unique neighbour  in
in  are examined in order to include in
are examined in order to include in  the vertex
the vertex  . If there are remaining nodes without covering in
. If there are remaining nodes without covering in  , in the second stage, those vertices in
, in the second stage, those vertices in  covering more vertices in that situation are also included in
covering more vertices in that situation are also included in  . A graphic explanation of how the algorithm works is included in Figure 2.
. A graphic explanation of how the algorithm works is included in Figure 2.
In order to clarify the proposal we need to define several vertex subsets that are specified below. First, for each node  in a one-hop distance from
in a one-hop distance from  it is required to consider a new vertex subset
it is required to consider a new vertex subset  formed by those vertices that simultaneously belong to the order 2
formed by those vertices that simultaneously belong to the order 2  's neighbourhood and are direct neighbours of
's neighbourhood and are direct neighbours of  (see Figure 1(a)). This set may be calculated by the following intersection
(see Figure 1(a)). This set may be calculated by the following intersection  . Vertices in this set have in common the fact that they are candidates to be covered by vertex
. Vertices in this set have in common the fact that they are candidates to be covered by vertex  .
.
A second vertex subset  is defined for each vertex
is defined for each vertex  belonging to
belonging to  's two-hop neighbourhood. In this case, such a subset may be obtained through the intersection
's two-hop neighbourhood. In this case, such a subset may be obtained through the intersection  (Figure 1(b)). This new set gathers those vertices in
(Figure 1(b)). This new set gathers those vertices in  that may cover vertex
that may cover vertex  . When transferring this computation to the self-organized PKI model,
. When transferring this computation to the self-organized PKI model,  is computed by using the set of predecessors of vertex
is computed by using the set of predecessors of vertex  denoted by
denoted by  .
.
3. PKI Approaches in MANETs
In this section the main characteristics of the public-key infrastructure models used in MANETs are described before introducing some new ideas that conform our proposal. We may find two main alternatives for the deployment of PKIs in MANETs in the bibliography: distributed certification authorities, and self-organized public-key management.
In the first case, the certification process is underpinned by distributed CAs, which use a threshold digital signature scheme and are in charge of issuing and renewing certificates of nodes [11–13]. One of the first schemes following this approach was proposed in [14], where a group of special nodes, acting as a coalition, are responsible for certification tasks. There the authors put forward that the CA's functions should be the responsibility of a set of special servers set included in the network. These servers will sign the public key of the nodes trough a  threshold signature scheme [15]. Therefore, each time a node in the network
threshold signature scheme [15]. Therefore, each time a node in the network  wishes to communicate with one of his peers
wishes to communicate with one of his peers  , he should contact with
, he should contact with  servers in advance in order to obtain
servers in advance in order to obtain  's public key signed with the CA's secret key. One of the servers included in the previous coalition will be in charge of playing the combiner's role. This means that once he receives the shares from its peers in the coalition, he generates the signature of the requested public key. However, there are some general drawbacks associated to this alternative. First, the combiner figure and the servers acting as certification authorities produce system overload as all the communications requesting certification issuance and validation should be attended for them. Additionally, introducing special servers does not guarantee the elimination of vulnerabilities to DoS attacks. Another question to take into account is the need for additional storage requirements since the public keys of all the members of the network must be stored by the servers. When the network is sparse or during its first deployment stages finding
's public key signed with the CA's secret key. One of the servers included in the previous coalition will be in charge of playing the combiner's role. This means that once he receives the shares from its peers in the coalition, he generates the signature of the requested public key. However, there are some general drawbacks associated to this alternative. First, the combiner figure and the servers acting as certification authorities produce system overload as all the communications requesting certification issuance and validation should be attended for them. Additionally, introducing special servers does not guarantee the elimination of vulnerabilities to DoS attacks. Another question to take into account is the need for additional storage requirements since the public keys of all the members of the network must be stored by the servers. When the network is sparse or during its first deployment stages finding  servers available in its transmission range may become a handicap.
servers available in its transmission range may become a handicap.
The methods included in [16, 17] solve some of the previous problems by establishing that any node may act as a member of a distributed CA. Consequently in both references any group of  nodes without distinction may act as servers at the moment of issuing certificates. Hence, one of the mayor advantages of this strategy is the balance reached in the distribution of the computational load. Even though this characteristic is truly important in the scenario of MANETs, there are still disadvantages associated to this proposal. For instance, a distributor in charge of providing credentials to the first nodes should be considered during the bootstrapping stage. Also finding a valid coalition each time a certificate needs to be verified may result infeasible depending on the network actual topology and conditions. Besides, the methods in [16] do not provide any instrument to protect against malicious nodes when they send fake shares.
nodes without distinction may act as servers at the moment of issuing certificates. Hence, one of the mayor advantages of this strategy is the balance reached in the distribution of the computational load. Even though this characteristic is truly important in the scenario of MANETs, there are still disadvantages associated to this proposal. For instance, a distributor in charge of providing credentials to the first nodes should be considered during the bootstrapping stage. Also finding a valid coalition each time a certificate needs to be verified may result infeasible depending on the network actual topology and conditions. Besides, the methods in [16] do not provide any instrument to protect against malicious nodes when they send fake shares.
A general drawback of those methods based on distributed CA's is the computational intensive operations required by the threshold application when signing a certificate, and the definition of additional procedures such as share refreshing [18].
Other proposals related to this paradigm may be found in the more recent bibliography, but in this work we have opted by the second type of solutions, based on the self-organized paradigm, which has been also used for node authentication [19].
Such a self-organized version of public-key management was chosen as base for this paper in order to guarantee identical roles for all MANET nodes. This approach involves the relocation of the responsibility for creating, storing, distributing, and revoking public keys among the members of the network.
3.1. Describing the Self-Organized Approach
The self-organized model in MANETs was initially described in [20]. Its authors put forward the substitution of the centralized certification authority by a self-organized scenario where certification is carried out through chains of certificates which are issued by the nodes themselves. Such a scheme is based on the information stored by each node and the trust relationship among neighbour nodes.
In this work we decided to follow the self-organized key management model based on the web of trust approach. Several are the reasons that justify the choice of this option. First, this model demands less maintenance overhead. Secondly, it is well worth remarking that on the one hand the self-organized approach eases the use of a simple bootstrap mechanism, and on the other hand all the nodes perform equal roles.
In this model, public keys and certificates are represented as a directed graph  , known as certificate graph. Each vertex
, known as certificate graph. Each vertex  in this graph defines a public key of a node, and each arc
in this graph defines a public key of a node, and each arc  denotes a certificate associated to
denotes a certificate associated to  's public key, signed with
's public key, signed with  's private key. Each node
's private key. Each node  has a public key, a private key, and two certificate repositories, the updated and the nonupdated repositories, denoted, respectively,
has a public key, a private key, and two certificate repositories, the updated and the nonupdated repositories, denoted, respectively,  and
and  . Initially the updated certificate repository contains the list of certificates on which each node trusts (out-bound list) and the list of certificates of all the nodes that trust on
. Initially the updated certificate repository contains the list of certificates on which each node trusts (out-bound list) and the list of certificates of all the nodes that trust on  (in-bound list). A sequence
(in-bound list). A sequence  of certificates where the vertices are all different is called a certificate chain from
of certificates where the vertices are all different is called a certificate chain from  to
to  .
.
The tasks that any member of the network has to develop in this public-key management scheme are:
-
(1)
Certificate Management:
-
(a)
Key generation: the node generates its keys by itself.
-
(b)
Certificate issuance: each node issues certificates that bind public keys of other nodes to their identities.
-
(c)
Certificate exchange: each node exchanges certificates with other nodes and builds its non-updated repository.
-
(d)
Updated certificate repository construction: the node builds its updated repository.
-
(a)
-
(2)
Public-Key Verification:
-
(a)
Finding a certificate chain.
-
(b)
Verifying the certificates in the chain.
-
(a)
Although the self-organized methodology for PKI deployment has been extensively analyzed [21–23], there are still open questions that needs further research. One of this pending questions is how to encourage node's participation in the tasks related to certification issuance or certification exchange. Since many resources are limited in MANETs the cooperation issue is a major issue when dealing with many node tasks, and PKI management is one of the crucial ones.
In the following we describe how certificate management and public-key verification are carried out in the self-organized model.
Each node  generates by itself the pair formed by its public key and its secret key. Then a request for signing the generated public key is sent to
generates by itself the pair formed by its public key and its secret key. Then a request for signing the generated public key is sent to  's neighbours. Since these nodes are in a one-hop distance from
's neighbours. Since these nodes are in a one-hop distance from  , they can use any trusted mechanisms such as side channels in order to assure the binding established between the corresponding public key and the node's identity.
, they can use any trusted mechanisms such as side channels in order to assure the binding established between the corresponding public key and the node's identity.
Apart from that, in order to ease certificate revocation, each certificate issued will be valid for a certain period of time. This parameter may be chosen depending on the mobility characteristics of the underlying MANET.
Since the certificates issued by a node are stored in its local repository, one of the tasks that a node may perform during idle periods is the renewal of certificates issued by it to those nodes that might still be considered as trusted. Otherwise, certificate renewal may be developed on demand. It means that when an expired certificate is included in the non-updated repository of a node, such a node should request a renewal for that certificate. When a certificate for a node  is issued by a node
is issued by a node  the edge
the edge  is added to the certificate graph and each node
is added to the certificate graph and each node  and
and  stores it in its in-bound and outbound list, respectively.
stores it in its in-bound and outbound list, respectively.
Note that the speed in the creation of the certificate graph and its density depend on the willingness of users for distributing certificates, and on nodes' mobility. In particular, the more mobility the nodes have, the more complete the repositories will be. The same happens with other aspects related to MANET cooperation.
As in any PKI-based system, certificate revocation should be also taken into account. When revocation is initiated due to key compromise or misbehaviour of the corresponding node, the certificate issuer sends a message to all nodes stating that such a certificate has been revoked. This can be accomplished because each node maintains a list containing the members of the network that have contacted it to request updates of the certificates it had issued. Hence, in fact it is not necessary to send the revocation message to all the members of the network. The last proposals related to revocation policies in MANETs defend the creation of schemes based in reputation systems [24, 25]. When revocation is due to the fact that the expiration time has been reached, such a revocation can be deduced directly by all nodes since the expiration date is contained in the certificate. The work in [26] describes a method to update expired certificates by using probabilistic multicast. The importance of this method is that nodes different from the actual issuer of the certificate can update it once it has expired.
Certificate exchange can be considered a low-cost procedure because it only involves one-hop distance nodes. It allows to share and to distribute the issued and stored certificates. A description of this procedure is as follows.
-
(1)
Every node
 retransmits the hash values of the certificates stored in the repositories
retransmits the hash values of the certificates stored in the repositories  and
and  to its neighbours. The recipient nodes answer with the hash values of the certificates contained in their repositories.
to its neighbours. The recipient nodes answer with the hash values of the certificates contained in their repositories. -
(2)
Every node compares the received value with the one it already has and requests to its neighbours only the certificates that are new.
-
(3)
If the local memory of a node is not large enough, the expired certificates are deleted from the non-updated repository, starting by the oldest ones.
-
(4)
In this way, after a short period of time the non-updated repository
 contains almost all the certificate graph
contains almost all the certificate graph 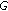 . Afterwards, the only task to be carried out by the nodes is to exchange the new certificates.
. Afterwards, the only task to be carried out by the nodes is to exchange the new certificates.
In the original proposal two ways of building the updated certificate repository  of a node
of a node  were described.
were described.
-
(1)
Node
 communicates with its neighbours in the certificate graph.
communicates with its neighbours in the certificate graph. -
(2)
Node
 applies over
applies over  an appropriate algorithm in order to generate
an appropriate algorithm in order to generate 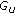 after checking the validity of every single certificate.
after checking the validity of every single certificate.
One of the crucial issues in the self-organized scheme that may influence the correct behaviour of the whole scheme is the selection of the certificates stored by each node in its repository. The method specified with this objective should satisfy two requirements at the same time: limitation in storing requirements, and performance of the updated repository in terms of ability to find chains for the largest possible number of nodes. This problem, known as certification chain discovery problem, has received particular attention in the bibliography related to MANETs [21–23, 27].
Since the algorithm used in the construction of the updated repositories will influence the efficiency of the scheme, it should be carefully designed. The simplest algorithm for that construction is the so-called Maximum Degree Algorithm (MDA) [20] (see Algorithm 1), where the criterion followed in the selection of certificates is mainly the degree of the vertices in the certificate graph.
Algorithm 1: –
–  heuristic.
heuristic.
input:  ,
,  ,
,  ,
, 
Output: 
 Initialization
Initialization
-
(1)

-
(2)

-
(3)

-
(4)
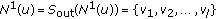
-
(5)

-
(6)

-
(7)

-
(8)

-
(9)
while
 do
do -
(10)
while
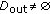 do
do -
(11)
if
 then
then -
(12)
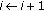
-
(13)
end
-
(14)
else
-
(15)
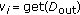
-
(16)

-
(17)

-
(18)
while
 and
and  do
do -
(19)
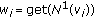
-
(20)
if
 then
then -
(21)

-
(22)
end
-
(23)
else
-
(24)
if
 then
then -
(25)
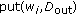
-
(26)
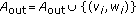
-
(27)
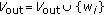
-
(28)
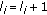
-
(29)

-
(30)
end
-
(31)
end
-
(32)
end
-
(33)
end
-
(34)
if
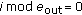 then
then -
(35)

-
(36)
end
-
(37)
end
-
(38)
end
There is another more sophisticated algorithm, called Shortcut Hunter Algorithm, in which certificates are chosen taking into account that when they are deleted, the length of the minimum path between the nodes connected through that certificate is increased in more than 2.
When using the MDA, every node  builds two subgraphs, the out-bound subgraph and the inbound subgraph, which when joined generate the updated certificate repository
builds two subgraphs, the out-bound subgraph and the inbound subgraph, which when joined generate the updated certificate repository  . The outbound subgraph is formed by several disjoint paths with the same origin vertex
. The outbound subgraph is formed by several disjoint paths with the same origin vertex  while in the in-bound subgraph
while in the in-bound subgraph  is the final vertex. In the description of the MDA algorithm, the starting node is
is the final vertex. In the description of the MDA algorithm, the starting node is  and
and  ,
,  stands for the in-degree and the out-degree of node
stands for the in-degree and the out-degree of node  , respectively. The number of paths to be found is represented by
, respectively. The number of paths to be found is represented by  .
.
A bound on the number of disjoint paths starting at  as well as a bound on the number of disjoint paths to be built with
as well as a bound on the number of disjoint paths to be built with  as final node are given by
as final node are given by  and
and  , respectively.
, respectively.
Another important input parameter is  , which represents the maximum number of vertices to be included in the subgraph generated when the in-bound and the out-bound subgraphs are combined. This parameter may be also controlled by defining as
, which represents the maximum number of vertices to be included in the subgraph generated when the in-bound and the out-bound subgraphs are combined. This parameter may be also controlled by defining as  the length of the chains generated when building the out-bound subgraph and
the length of the chains generated when building the out-bound subgraph and  for the in-bound one.
for the in-bound one.
In order to apply the greedy criterion,  and
and  , where
, where  consists of a set of vertices, include the sorted vertices of
consists of a set of vertices, include the sorted vertices of  into descending order according to
into descending order according to  and
and  , respectively.
, respectively.
Note that the process to build the in-bound subgraph is equivalent to it except for the fact that in this case the edges to be chosen are always incoming edges.
In the first stage of the MDA,  outgoing arcs from
outgoing arcs from  are included. The final vertices of these arcs are then included in
are included. The final vertices of these arcs are then included in  . This set is implemented as a typical queue where the insertion (put) and the extraction (get)operations are used. Henceforth,
. This set is implemented as a typical queue where the insertion (put) and the extraction (get)operations are used. Henceforth,  arcs are chosen in such a way that the formed paths are disjoint. This is accomplished by selecting their origin belonging to
arcs are chosen in such a way that the formed paths are disjoint. This is accomplished by selecting their origin belonging to  and checking that neither the origin nor the final vertices were previously used in another path.
and checking that neither the origin nor the final vertices were previously used in another path.
4. Proposed Algorithm
The main contribution of this paper consists in substituting the MDA algorithm proposed for the updated repository construction by a new algorithm that uses the MPR technique described in Section 2 (see Algorithm 2). In this way, for each vertex in the certificate graph we have to define a re-transmitter set.
Algorithm 2: heuristic.
heuristic.
input:  ,
, 
output: 
 Initialization
Initialization
-
(1)

 Stage 0
Stage 0
-
(2)

-
(3)
for
 to
to  do
do
(4) 
(5) if  then
then
(6) 
(7) end
-
(8)
end
-
(9)
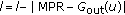
-
(10)

 Stage 1
Stage 1
-
(11)
for
 to
to  do
do
(12) 
(13) if  then
then
(14) for  to
to  do
do
(15) 
(16) 
(17) if  then
then
(18) 
(19) 
(20) end
(21) end
(22) end
-
(23)
end
-
(24)
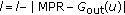
-
(25)

 Stage 2
Stage 2
-
(26)
While
 do
do
(27) for  to
to  do
do
(28) 
(29) 
(30) 
(31) end
(32) 
-
(33)
for
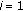 to
to  do
do
(34) if  then
then
(35) 
(36) 
-
(37)
end
-
(38)
end
(39) 
-
(40)
end
The MPR heuristic adapted to the certificate graph is described below. First, node  starts by calculating
starts by calculating  . Then, these vertices are included in
. Then, these vertices are included in  together with the edges
together with the edges  . Henceforth, nodes
. Henceforth, nodes  in
in  apply recursively the same procedure of retransmitting backwards the result
apply recursively the same procedure of retransmitting backwards the result  .
.
In order to extend the notation used in the introduction of the MPR greedy heuristic described in Section 2, which is required to be used in the certificate graph, we denote by  the set of predecessors of node
the set of predecessors of node  that may be found in an i-hop distance. This means that the smallest number of certificate chains required in order to reach the remaining nodes will be obtained as well. The algorithm proposed is an iterative scheme that may be described in the following way.
that may be found in an i-hop distance. This means that the smallest number of certificate chains required in order to reach the remaining nodes will be obtained as well. The algorithm proposed is an iterative scheme that may be described in the following way.
-
(1)
Every vertex
 locally determines its re-transmitter set (
locally determines its re-transmitter set (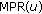 ), which include the certificates associated to the corresponding edges.
), which include the certificates associated to the corresponding edges. -
(2)
This vertex contacts all the nodes in
 . At this stage, every node
. At this stage, every node 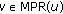 has previously obtained its retransmitters set
has previously obtained its retransmitters set  , and consequently it may send to node
, and consequently it may send to node  the certificates associated to such a set.
the certificates associated to such a set.
Since each node knows from whom is a re-transmitter, the  subgraph is generated by applying first the reverse process and then adding in-going arcs. The certificate chains required in the authentication are built by using the arcs
subgraph is generated by applying first the reverse process and then adding in-going arcs. The certificate chains required in the authentication are built by using the arcs  . After that, for all
. After that, for all  and for all
and for all  the arcs
the arcs  are also added after having checked that they have not been added in previous updates.
are also added after having checked that they have not been added in previous updates.
Note that the procedure every node  has to develop in order to build
has to develop in order to build  takes
takes  steps when no bound is defined on the length of the chains to be built. Otherwise, the number of iterations to be carried out is given by the number of hops to explore in the certificate graph. As for the definition of the aforementioned bound, it has to be remarked that such a parameter may be dynamically adjusted in function of the changes experienced by the certificate graph. This may be justified by the fact that as the network evolves, the information contained in each node's repository is more complete. Thanks to this substitution the generated procedure is easier and more efficient, guaranteeing in this way that each node has a set of neighbours that allows it to reach the biggest number of public keys.
steps when no bound is defined on the length of the chains to be built. Otherwise, the number of iterations to be carried out is given by the number of hops to explore in the certificate graph. As for the definition of the aforementioned bound, it has to be remarked that such a parameter may be dynamically adjusted in function of the changes experienced by the certificate graph. This may be justified by the fact that as the network evolves, the information contained in each node's repository is more complete. Thanks to this substitution the generated procedure is easier and more efficient, guaranteeing in this way that each node has a set of neighbours that allows it to reach the biggest number of public keys.
One of the main advantages of the proposal is that all the information gathered for the construction of the chains is locally obtained by each node. After obtaining the in-bound and out-bound subgraphs, both subgraphs are merged and the initial repository is generated so that the authentication process may start. When a node  needs to check the validity of the public key of another node
needs to check the validity of the public key of another node  , it has to find a certificate chain
, it has to find a certificate chain  from itself to
from itself to  in the graph that results from combining its own repository with
in the graph that results from combining its own repository with  's repository. If this chain is not found there, the search is extended to
's repository. If this chain is not found there, the search is extended to  , what implies the inclusion of
, what implies the inclusion of  's nonupdated repository in the search. If this second exploration is successful,
's nonupdated repository in the search. If this second exploration is successful,  should request the update of those certificates that belong exclusively to
should request the update of those certificates that belong exclusively to  . When no path is found, the authentication fails. Once the path
. When no path is found, the authentication fails. Once the path  is determined,
is determined,  should validate every certificate included in it. This is done as follows.
should validate every certificate included in it. This is done as follows.
-
(1)
The first certificate in the chain
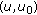 is directly checked by
is directly checked by  since it was signed by
since it was signed by  himself.
himself. -
(2)
Each one of the remaining certificates
 in the chain may be checked using the public key of the previous node
in the chain may be checked using the public key of the previous node 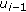 .
. -
(3)
The last arc
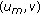 corresponds to the certificate issued by
corresponds to the certificate issued by 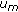 that binds
that binds  with its public key.
with its public key.
The proposal described in this work will allow us to integrate information obtained and used by the routing process into the PKI management tasks. This approach will simplify the certification procedures. This idea of combining routing information within authentication procedures was also put forward in [21]. One of the main differences between our proposal and the scheme described there is the routing scheme used as base. We make use of the OLSR proactive scheme (more specifically we use the MPR technique used there), while the reactive AODV routing protocol is used by the other proposal. The main idea behind this alternative is to build a binary tree of trust connecting all the nodes in the network claiming that this structure will simplify certificate path discovery and certificate issuance. The main difficulties behind the use of such a global structure is that network partition may occur easily since each node only has direct trusted connections with its parent and two-child nodes. Depending on the mobility pattern associate to member nodes this number of connections may be inadequate.
There is a characteristic in the designed algorithm that is shared with the proposal described at [22]. It is possible to adapt the number of certificate chains to be built as well as their length depending on the characteristics of the MANET where the proposal must be implemented.
5. Experimental Results
This work proposes the application of the MPR technique in the computation of certificate repositories included in the self-organized public-key management model. Our proposal is supported by the good results obtained when using the MPR procedure in the OLSR routing algorithm in MANETs as well as computational experiments. A detailed description of the implementation and the results provided by it are presented in the current section. The main goal of the experiments was showing that applying the MPR technique when building certificate repositories in the self-organized approach instead of using the MDA heuristic provides the public-key management scheme with simplicity and efficiency.
5.1. Implementation Characteristics
The implementation has been carried out using Java and the open source library JUNG 2.0 (Java Universal Network/Graph Framework) which provides the basic tools for representing and dealing with graphs.
One of the reasons why JUNG was selected was having the possibility of working with random graphs with the small-world property. When a graph follows the small-world model, it is assumed that its paths have a small average length and a high Clustering Coefficient (CC). The CC corresponds with the average of the fraction of pairs of  's neighbours (taken over all the network nodes
's neighbours (taken over all the network nodes  ) which are at the same time direct neighbours of each other.
) which are at the same time direct neighbours of each other.
This characteristic is supported by certificate graphs as it was shown in [28]. When a graph holds this feature, most nodes may be reached by a small number of hops from any source node. This kind of graphs has received special attention in several scientific disciplines [29]. In [30], an extended small-world model with applications in different MANET scenarios was introduced.
The small-world model used in the simulation developed was proposed by Kleingberg [31]. When generating a graph with  vertices according to this model, the first step is to create an
vertices according to this model, the first step is to create an  toroidal lattice. Then each node
toroidal lattice. Then each node  is connected to four local neighbours, and in addition one long range connection to some node
is connected to four local neighbours, and in addition one long range connection to some node  , where
, where  is chosen randomly, according to a probability proportional to
is chosen randomly, according to a probability proportional to  .
.  denotes the lattice distance between
denotes the lattice distance between  and
and  and
and  stands for the CC. Generating the graphs following this model guarantees that the shortest paths may be determined using local information, what makes them particularly interesting for the networks we are dealing with.
stands for the CC. Generating the graphs following this model guarantees that the shortest paths may be determined using local information, what makes them particularly interesting for the networks we are dealing with.
5.2. Computational Results
Some of the data gathered from the first computational experience are shown below (see Table 1). The number of nodes in the graph ( ), the rate of certificates contained in the repository (
), the rate of certificates contained in the repository ( ), the clustering coefficient (
), the clustering coefficient ( ), the maximum length in the chains generated (
), the maximum length in the chains generated ( ), and the time consumption while the execution (
), and the time consumption while the execution ( ) expressed in seconds are the parameters that have been measured. From this experience, it may be remarked that the certificate rate finally contained in the local repository increases as the size of the graph increases as well as the clustering coefficient increases. This phenomenon may be better appreciated in Figure 3. Additionally, the maximum lengths in the obtained chains are kept at reasonable values, that is what makes the chain verification process lighter. Finally, the rate of certificates stored in the repository surpasses 95% in more than 75% of the executions while time consumption corresponds to sensible values. These first experiments showed promising results.
) expressed in seconds are the parameters that have been measured. From this experience, it may be remarked that the certificate rate finally contained in the local repository increases as the size of the graph increases as well as the clustering coefficient increases. This phenomenon may be better appreciated in Figure 3. Additionally, the maximum lengths in the obtained chains are kept at reasonable values, that is what makes the chain verification process lighter. Finally, the rate of certificates stored in the repository surpasses 95% in more than 75% of the executions while time consumption corresponds to sensible values. These first experiments showed promising results.
Another computational experience consisted of generating random graphs according to the Kleingberg's model where the size of the graphs  ranges in the interval [9,441], the Clustering Coefficient (CC) takes values between
ranges in the interval [9,441], the Clustering Coefficient (CC) takes values between  . For these parameters, the Certificate Rate obtained by MPR (
. For these parameters, the Certificate Rate obtained by MPR ( ) jointly with time consumption (
) jointly with time consumption ( expressed in seconds were measured.
expressed in seconds were measured.
For analyzing the MDA alternative, it is applied over the same input graphs using as specific parameters the maximum number of chains to built ( ) and their maximum length (
) and their maximum length ( ) is bounded by 7. In this case, the Certificate Rate in the repository (
) is bounded by 7. In this case, the Certificate Rate in the repository ( ) and time consumption (
) and time consumption ( ) were also obtained.
) were also obtained.
From this experience, there are some general conclusions that may be remarked. The certificate rate  finally contained in the local repository increases as the size of the graph increases. However, the behaviour of the certificate rate is not affected by the growth of the Clustering Coefficient. This phenomena may be better appreciated in Figure 4. Additionally, the maximum length in the chains obtained by MPR are kept at reasonable values, what makes the chain verification process lighter.
finally contained in the local repository increases as the size of the graph increases. However, the behaviour of the certificate rate is not affected by the growth of the Clustering Coefficient. This phenomena may be better appreciated in Figure 4. Additionally, the maximum length in the chains obtained by MPR are kept at reasonable values, what makes the chain verification process lighter.
The most important fact when comparing the certificate rates  and
and  is that only in the 3.95% of the executions the MDA algorithm outperforms MPR, and it only occurs when the input certificate graph is small. Although, in the previous figure it seems that the difference between both certificates rates is reduced as the size of the graph increases, it should be taken in mind that MANETs have a limited number of nodes. Furthermore, in the 45.83% percent of the problems the difference between the certificate rates
is that only in the 3.95% of the executions the MDA algorithm outperforms MPR, and it only occurs when the input certificate graph is small. Although, in the previous figure it seems that the difference between both certificates rates is reduced as the size of the graph increases, it should be taken in mind that MANETs have a limited number of nodes. Furthermore, in the 45.83% percent of the problems the difference between the certificate rates  and
and  is in the interval [50%,75%] (see Figure 5).
is in the interval [50%,75%] (see Figure 5).
Hence, it may be concluded that the repository built by MPR provides further information to facilitate the authentication process. Finally, another result that illustrates the positive characteristics of MPR to solve the problem of updating the certificate repository is that in the 82.45% of the executions the repository built by MPR contains more than the 75% of the whole certificate set.
6. Conclusion
The application of the Multipoint Relay Technique in the update process of public key certificate repositories in MANETs has been evaluated in this work. For the assessment of this proposal, several experiments with an implementation developed in JAVA have been carried out. According to these experiments the presented alternative outperforms the original graph-based and self-organized model in several aspects. The most relevant improvements of the proposed MPR-based method are a higher certificate rate included in the repository and the shorter generated certificate chains. They result in a less need of interaction among nodes during the building process of an authentication chain and lead to a more efficient verification procedure.
Our immediate goal is to adapt the developed implementation to a network simulator in order to evaluate the behaviour of the method with different mobility models.
References
Ilyas M (Ed): The Handbook of Ad Hoc Wireless Networks. CRC Press, Boca Raton, Fla, USA; 2003.
Haerri J, Filali F, Bonne C: Performance comparison of AODV and OLSR in VANETs urban environments under realistic mobility patterns. Proceedings of the 5th IFIP Mediterranean Ad-Hoc Networking Workshop (Med-Hoc-Net '06), 2006, Lipari, Italy
Clausen T, Jacquet P: RFC 3626: Optimized Link State Routing Protocol. (OLSR), 2003
Clausen T, Dearlove C, Jacquet P: The optimized link state routing protocol version 2 draft-ietf-manet-olsrv2-11. IETF Internet-Draft, April 2010
Vilela JP, Barros J: A feedback reputation mechanism to secure the optimized link state routing protocol. In Proceedings of IEEE Communications Society/CreateNet International Conference on Security and Privacy for Emerging Areas in Communication Networks (Securecomm'07), 2007. IEEE Computer Society;
Ni SY, Tseng YC, Chen YS, Sheu JP: The broadcast storm problem in a mobile ad hoc network. Proceedings of the 5th Annual ACM/IEEE International Conference on Mobile Computing and Networking (MobiCom '99), 1999 151-162.
Laouti A, Mhlethaler P, Najid A, Plakoo E: Simulation results of the OLSR routing protocol for wireless network. Proceedings of the 1st Mediterranean Ad-Hoc Networks workshop (Med-Hoc-Net '02), 2002, Sardegna, Italy
Baccelli E, Jacquet P, Nguyen D, Clausen T: Ospf multipoint relay (mpr) extension for ad hoc networks. IETF Request for Comments: 5449, February
Mans B, Shrestha N: Performance evaluation of approximation algorithms for multipoint relay selection. Proceedings of the 3rd Annual Mediterranean Ad Hoc Networking Workshop, 2004
Härri J, Bonnet C, Filali F: OLSR and MPR: mutual dependences and performances. IFIP International Federation for Information Processing 2006, 197: 67-71. 10.1007/0-387-31173-4_8
Saxena N, Tsudik G, Yi JH: Threshold cryptography in P2P and MANETs: the case of access control. Computer Networks 2007, 51(12):3632-3649. 10.1016/j.comnet.2007.03.001
Wu B, Wu J, Fernandez EB, Ilyas M, Magliveras S: Secure and efficient key management in mobile ad hoc networks. Journal of Network and Computer Applications 2007, 30(3):937-954. 10.1016/j.jnca.2005.07.008
Joshi D, Namuduri K, Pendse R: Secure, redundant, and fully distributed key management scheme for mobile ad hoc networks: an analysis. EURASIP Journal on Wireless Communications and Networking 2005, 2005(4):579-589.
Zhou L, Haas ZJ: Securing ad hoc networks. IEEE Network 1999, 13(6):24-30. 10.1109/65.806983
Gennaro R, Jarecki S, Krawczyk H, Rabin T: Robust threshold DSS signatures. Information and Computation 2001, 164(1):54-84. 10.1006/inco.2000.2881
Kong J, Zerfos P, Luo H, Lu S, Zhang L: Providing robust and ubiquitous security support for mobile ad-hoc networks. Proceedings of the International Conference on Network Protocols (ICNP '01), November 2001 251-260.
Kaliaperumal S: Securing authentication and privacy in ad hoc partitioned networks. In Proceedings of the Symposium on Applications and the Internet Workshops (SAINT-W '03), 2003, Washington, DC, USA. IEEE Computer Society; 354.
Narasimha M, Tsudik G, Yi J: On the utility of distributed cryptography in P2P and MANETs: the case of membership control. Proceedings of the 11th IEEE International Conference on Network Protocols (ICNP '03), 2003 336-345.
Caballero-Gil P, Hernández-Goya C: Self-organized authentication in mobile ad-hoc networks. Journal of Communications and Networks 2009, 11(5):509-517.
Capkun S, Buttyan L, Hubaux JP: Self-organized public key management for mobile ad hoc networks. Mobile Computting and Communication Review 2002., 6(4):
Kambourakis G, Konstantinou E, Douma A, Anagnostopoulos M, Fotiadis G: Efficient certification path discovery for MANET. EURASIP Journal on Wireless Communications and Networking 2010, 2010:-16.
Satizábal C, Hernández-Serrano J, Forné J, Pegueroles J: Building a virtual hierarchy to simplify certification path discovery in mobile ad-hoc networks. Computer Communications 2007, 30(7):1498-1512. 10.1016/j.comcom.2006.12.024
Li R, Li J, Liu P, Chen H-H: On-demand public-key management for mobile ad hoc networks. Wireless Communications and Mobile Computing 2006, 6(3):295-306. 10.1002/wcm.396
Arboit G, Crépeau C, Davis CR, Maheswaran M: A localized certificate revocation scheme for mobile ad hoc networks. Ad Hoc Networks 2008, 6(1):17-31. 10.1016/j.adhoc.2006.07.003
Moore T, Clulow J, Nagaraja S, Anderson R: New strategies for revocation in ad-hoc networks. Proceedings of the 4th European Workshop on Security and Privacy in Adhoc and Sensor Networks (ESAS '07), 2007
Xie D, Zhou H: A probabilistic certificate updating protocol for manet. Proceedings of the 20th International Conference on Advanced Information Networking and Applications (AINA '06), 2006, Washington, DC, USA 2: 147-154.
Jung E, Elmallah ES, Gouda MG: Optimal dispersal of certificate chains. IEEE Transactions on Parallel and Distributed Systems 2007, 18(4):474-484.
Capkun S, Buttyan L, Hubaux JP: Small worlds in security systems: an analysis of the PGP certificate graph. Proceedings of the ACM New Security Paradigms Workshop, September 2002, Norfolk, Va, USA 8.
Liu C, Wu J: Scalable routing in delay tolerant networks. Proceedings of the 8th ACM International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc '07), September 2007 51-60.
Wu J, Yang S-H: Small world model-based polylogarithmic routing using mobile nodes. Journal of Computer Science and Technology 2008, 23(3):327-342. 10.1007/s11390-008-9136-9
Kleinberg J: Small-world phenomenon: an algorithmic perspective. Proceedings of the 32nd Annual ACM Symposium on Theory of Computing, May 2000 163-170.
Acknowledgments
This research was supported by the Ministerio Español de Educación y Ciencia and the European FEDER Fund under TIN2008-02236/TSI project and by the Agencia Canaria de Investigación, Innovación y Sociedad de la Información under PI2007/005 project.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Caballero-Gil, P., Hernández-Goya, C. Efficient Public Key Certificate Management for Mobile Ad Hoc Networks. J Wireless Com Network 2011, 935457 (2011). https://doi.org/10.1155/2011/935457
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/935457




 are analyzedStage 2: Nodes of maximum degree are included in
are analyzedStage 2: Nodes of maximum degree are included in 
 retransmits the hash values of the certificates stored in the repositories
retransmits the hash values of the certificates stored in the repositories  and
and  to its neighbours. The recipient nodes answer with the hash values of the certificates contained in their repositories.
to its neighbours. The recipient nodes answer with the hash values of the certificates contained in their repositories. contains almost all the certificate graph
contains almost all the certificate graph 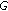 . Afterwards, the only task to be carried out by the nodes is to exchange the new certificates.
. Afterwards, the only task to be carried out by the nodes is to exchange the new certificates. communicates with its neighbours in the certificate graph.
communicates with its neighbours in the certificate graph. applies over
applies over  an appropriate algorithm in order to generate
an appropriate algorithm in order to generate 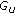 after checking the validity of every single certificate.
after checking the validity of every single certificate.


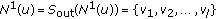




 do
do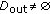 do
do then
then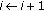
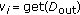


 and
and  do
do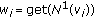
 then
then
 then
then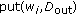
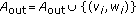
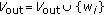
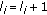

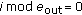 then
then


 to
to  do
do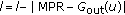

 to
to  do
do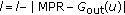

 do
do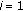 to
to  do
do locally determines its re-transmitter set (
locally determines its re-transmitter set (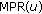 ), which include the certificates associated to the corresponding edges.
), which include the certificates associated to the corresponding edges. . At this stage, every node
. At this stage, every node 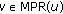 has previously obtained its retransmitters set
has previously obtained its retransmitters set  , and consequently it may send to node
, and consequently it may send to node  the certificates associated to such a set.
the certificates associated to such a set.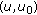 is directly checked by
is directly checked by  since it was signed by
since it was signed by  himself.
himself. in the chain may be checked using the public key of the previous node
in the chain may be checked using the public key of the previous node 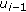 .
.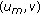 corresponds to the certificate issued by
corresponds to the certificate issued by 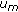 that binds
that binds  with its public key.
with its public key.

