- Research Article
- Open access
- Published:
Amplitude PDF Analysis of OFDM Signal Using Probabilistic PAPR Reduction Method
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 983915 (2011)
Abstract
To reduce the peak-to-average power ratio (PAPR) of an orthogonal frequency division multiplexing (OFDM) modulation scheme, one class of methods is to generate several OFDM symbols (candidates) carrying the same information and to select for transmission the one having the lowest PAPR. We derive a theoretical amplitude probability density function (PDF) of the selected OFDM symbol using order statistics. This amplitude PDF enables one to derive the signal-to-noise-plus-distortion ratio (SNDR) as a function of the number of candidates. Based on the SNDR derivation, theoretical error performance and statistical channel capacity are provided for this class of methods. The results match the simulations and make the system design easier.
1. Introduction
Orthogonal frequency division multiplexing (OFDM) is a multicarrier multiplexing technique, where data is transmitted through several parallel frequency subchannels at a lower rate. It has been popularly standardized in many wireless applications such as Digital Video Broadcasting (DVB), Digital Audio Broadcasting (DAB), High Performance Wireless Local Area Network (HIPERLAN), IEEE 802.11 (WiFi), and IEEE 802.16 (WiMAX). It has also been employed for wired applications as in the Asynchronous Digital Subscriber Line (ADSL) and power-line communications.
A significant drawback of the OFDM-based system is its high Peak-to-Average Power Ratio (PAPR) at the transmitter, requiring the use of a highly linear amplifier which leads to low power efficiency [1]. Moreover, when an OFDM signal level works on the nonlinear area of amplifier, the OFDM signals go through nonlinear distortions and degrade the error performance.
The various approaches to alleviate this problem in OFDM-based systems can be classified into five categories: clip effect transformation [2], coding [3], frame superposition using reserved tones [4], expansible constellation point: tone injection [4] and active constellation extension [5], and probabilistic solutions [6–13].
The principle of probabilistic methods is to reduce the probability of high PAPR by generating several OFDM symbols (multiple candidates) carrying the same information and by selecting the one having the lowest PAPR. The probabilistic method can also be classified into two strategies: subblock partitioning strategy and entire block strategy. The subblock partitioning strategy, such as partial transmit sequence (PTS) [6–8], divides frequency domain signals into several subblocks. On the other hand, the entire block strategy, such as selected mapping (SLM) [8–10] and interleaving [11–13], considers the entire block for generating multiple candidates.
In this paper, we consider the entire block strategy of the probabilistic methods to generate multiple candidates. First, the probability density function (PDF) for the multiple candidate system is analyzed. When the candidate having the lowest PAPR is selected, the PDF of the amplitude of a selected OFDM symbol becomes the function of the number of candidates  . We apply the analyzed PDF (as a function of
. We apply the analyzed PDF (as a function of  ) to Ochiai's method [13] for obtaining the signal-to-noise-plus-distortion ratio (SNDR) as a function of
) to Ochiai's method [13] for obtaining the signal-to-noise-plus-distortion ratio (SNDR) as a function of  . Then, the SNDR (as a function of
. Then, the SNDR (as a function of  ) can be used for analytical error performance. Note that in [13], the authors used the Rayleigh PDF (single candidate) for obtaining the error performance of multiple candidate cases. However, we suggest using our PDF (multiple candidates) to obtain the theoretical error performance and also the statistical channel capacity for the multiple candidate system.
) can be used for analytical error performance. Note that in [13], the authors used the Rayleigh PDF (single candidate) for obtaining the error performance of multiple candidate cases. However, we suggest using our PDF (multiple candidates) to obtain the theoretical error performance and also the statistical channel capacity for the multiple candidate system.
The paper is organized as follows: in Section 2, we describe the multiple candidate OFDM system, and analyze the PDF for the system. In Section 3, we derive the theoretical performance, such as the SNDR (as a function of  ), and error rate, and also statistical channel capacity. In Section 4, an extension of the results to an oversampled SLM model, implementing the "clipping and filtering" technique [14], is tackled. Finally, we conclude this paper in Section 5.
), and error rate, and also statistical channel capacity. In Section 4, an extension of the results to an oversampled SLM model, implementing the "clipping and filtering" technique [14], is tackled. Finally, we conclude this paper in Section 5.
2. Multiple Candidate System
2.1. Description
In this section, we describe the multiple candidate solution for reduction of PAPR. Figure 1 describes the multiple candidate system and our PDF notation for several variables.  candidates (frequency domain signal) are generated by the candidate generator, where this candidate generator represents a class of probabilistic methods such as the SLM method [8–10] or the interleaving method [11–13]. After the
candidates (frequency domain signal) are generated by the candidate generator, where this candidate generator represents a class of probabilistic methods such as the SLM method [8–10] or the interleaving method [11–13]. After the  -point Inverse Discrete Fourier Transform (IDFT), we get the
-point Inverse Discrete Fourier Transform (IDFT), we get the  OFDM candidates (time domain signal),
OFDM candidates (time domain signal),  . When we define
. When we define  , then
, then

and the peak detector selects the  th candidate, where
th candidate, where  for
for  and
and  . Then, the selected (
. Then, the selected ( th) OFDM signal candidate is clipped by a nonlinear amplifier, where we consider the soft clipping model [13] as follows:
th) OFDM signal candidate is clipped by a nonlinear amplifier, where we consider the soft clipping model [13] as follows:

where  is the maximum permissible amplitude for the clipping model.
is the maximum permissible amplitude for the clipping model.
The clipped  th candidate is transmitted to the receiver with its side information, where the side information contains the information of
th candidate is transmitted to the receiver with its side information, where the side information contains the information of  and it is used for recovering the original data. The side information protection depends on the various protection strategies, such as no side information method [9, 10] or coded side information method [12].
and it is used for recovering the original data. The side information protection depends on the various protection strategies, such as no side information method [9, 10] or coded side information method [12].
However, in this paper, for analyzing the pure effect of increasing  for the multiple candidate system, we assume that the side information is sent without errors.
for the multiple candidate system, we assume that the side information is sent without errors.
Throughout this paper, the following are also assumed: according to the central limit theorem, the complex OFDM signal, which consists of a number of independent orthogonal subcarriers, is modeled as a complex Gaussian process with Rayleigh envelope distribution. In addition, since the OFDM modulation is strictly band limited, we consider only in-band distortion.
2.2. PDF Analysis
Based on the assumption that the OFDM signal  for
for  and
and  is complex Gaussian distributed with mean 0 and variance 1, the envelope
is complex Gaussian distributed with mean 0 and variance 1, the envelope  is Rayleigh distributed with PDF
is Rayleigh distributed with PDF  given by
given by

According to the largest order statistics [15], the distribution of the maximum of the amplitude values  is given by
is given by

When we select the candidate having a minimum peak amplitude among  candidates, according to the smallest order statistics [15], we obtain the PDF of the peak amplitude of the selected candidate
candidates, according to the smallest order statistics [15], we obtain the PDF of the peak amplitude of the selected candidate  , using
, using  :
:

where  and
and  .
.
We now want to know the PDF of amplitude of the selected candidate  . In (5), we have obtained
. In (5), we have obtained  from
from  using the smallest order statistics. Furthermore, since
using the smallest order statistics. Furthermore, since  , we can also express
, we can also express  as a function of
as a function of  using the largest order statistics. Then,
using the largest order statistics. Then,

where  . From (6), we can obtain
. From (6), we can obtain

So, the PDF of the amplitude of the selected candidate is given by

where  .
.
Figure 2 gives a comparison between the analytical and the simulation PDF in logarithm scale. Notice that the analytical line fits the simulation points.
3. Theoretical Performance
3.1. 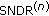 for Multiple Candidate System
for Multiple Candidate System
Now, we apply (8) to obtaining the signal-to-noise-plus-distortion ratio (SNDR) as a function of  , by using Ochiai's method [13]. The authors in [13] used the Rayleigh PDF,
, by using Ochiai's method [13]. The authors in [13] used the Rayleigh PDF,  , to obtain the SNDR of a multiple candidate system. However, as shown in Figure 2, the PDF of amplitude of the selected candidate is not Rayleigh PDF anymore, being the function of
, to obtain the SNDR of a multiple candidate system. However, as shown in Figure 2, the PDF of amplitude of the selected candidate is not Rayleigh PDF anymore, being the function of  . Therefore, we use the PDF of (8),
. Therefore, we use the PDF of (8),  , to obtain the SNDR of multiple candidate system, and hereafter we will use
, to obtain the SNDR of multiple candidate system, and hereafter we will use  as a function of
as a function of  , instead of SNDR.
, instead of SNDR.
For that, the PAPR threshold for clipping  is defined as
is defined as  , where the input power
, where the input power  and
and  is the maximum permissible amplitude for the multiple candidate system.
is the maximum permissible amplitude for the multiple candidate system.
Then, based on  in (8), the total output power for the multiple candidate solution after clipping is obtained as
in (8), the total output power for the multiple candidate solution after clipping is obtained as

and the signal distortion rate,  , is given by
, is given by

Then,  , total attenuation factor, is the following:
, total attenuation factor, is the following:

Finally,  for the multiple candidate technique is given by
for the multiple candidate technique is given by

3.2. Error Rate
Since we assume that the side information is transmitted without errors, the BER of QPSK-modulated signal over the AWGN channel is given by  . Furthermore, QPSK symbol error rates (SER) are as follows:
. Furthermore, QPSK symbol error rates (SER) are as follows:  .
.
For the frequency-nonselective slowly (constant attenuation during one OFDM symbol) Rayleigh-fading channel [16], the BER is given by

where  is the channel attenuation which is Rayleigh distributed with
is the channel attenuation which is Rayleigh distributed with  .
.
Figure 3 shows the error performance comparison over AWGN channel and frequency-nonselective slowly fading channel, where the analytical approach and the simulation results are compared. For the simulations, 1024-point FFT pairs are considered and the signals are modulated by QPSK. At the transmitter, the OFDM signals are clipped at  dB. In the figure, we can see that the simulated SER is well matched on the analytical line, and an error floor appears at large SNR because of the clipping noise. In addition, we can see better error performance, when
dB. In the figure, we can see that the simulated SER is well matched on the analytical line, and an error floor appears at large SNR because of the clipping noise. In addition, we can see better error performance, when  increases.
increases.
Symbol Error Rate (SER) comparison between the analytical approach (line) and the simulation results (marker) over AWGN channel (red) and frequency-nonselective slowly fading channel (blue), where the data is QPSK modulated, and 1024-point FFT pairs are considered. The OFDM symbols are clipped at  dB. In the figure, the lines represent our analytical approach, such as solid line (
dB. In the figure, the lines represent our analytical approach, such as solid line ( ), dash line (
), dash line ( ), dot line (
), dot line ( ), and dash-dot line (
), and dash-dot line ( ). The markers represent the simulation results, such as
). The markers represent the simulation results, such as  (
( ), □ (
), □ ( ), ∆ (
), ∆ ( ), × (
), × ( ).
).
Since our theoretical analysis matches well the simulations, we can estimate the analytical frame error floor as a function of the PAPR threshold  (see Figure 4). We can see that the error floor level can decrease, by increasing
(see Figure 4). We can see that the error floor level can decrease, by increasing  and/or
and/or  . Our analytical approach makes it possible to foresee the expected level of the error rate without a time-consuming simulation.
. Our analytical approach makes it possible to foresee the expected level of the error rate without a time-consuming simulation.
3.3. Channel Capacity
We consider the channel capacity of selected and clipped OFDM symbols for a multiple candidate system. For this, we take into consideration the M-ary Input AWGN channel models [17]. Suppose that the receiver knows the exact information about which candidate has been transmitted. Then, the channel capacity of transmitted symbols is  , where
, where  is the received symbol, and from which we may write
is the received symbol, and from which we may write

where  is the two-dimensional PDF of received symbol with the Gaussian noise variance
is the two-dimensional PDF of received symbol with the Gaussian noise variance  in each dimension.
in each dimension.
Figure 5 illustrates the channel capacity for 16-QAM case (up) and 64-QAM case (down) over M-ary Input AWGN channel. The figure implies that, due to the clipped symbol, it is impossible to achieve error-free performance. However, as the number of candidate increases, we can obtain theoretical capacity gains as long as  increases. In particular, the channel symbols of M-QAM, where
increases. In particular, the channel symbols of M-QAM, where  , are so sensitive to the clipping noise that the multiple candidate system can attain additional channel capacity gains effectively. When SNR = 45 dB, the measured capacity gain is 0.1284 bits/channel symbol with 16 candidates (64-QAM symbols clipped at
, are so sensitive to the clipping noise that the multiple candidate system can attain additional channel capacity gains effectively. When SNR = 45 dB, the measured capacity gain is 0.1284 bits/channel symbol with 16 candidates (64-QAM symbols clipped at  dB).
dB).
4. Application: Oversampling and Filtering
We present an extension of the multiple candidate system: combination with an oversampling and filtering technique [14]. For the single-candidate system, an OFDM symbol with a large  is usually assumed to have a Gaussian PDF in the real and imaginary parts. However, for the multiple candidate system, this Gaussian assumption no longer holds. In this section, we show mathematical non-Gaussian PDF for the multiple candidate system.
is usually assumed to have a Gaussian PDF in the real and imaginary parts. However, for the multiple candidate system, this Gaussian assumption no longer holds. In this section, we show mathematical non-Gaussian PDF for the multiple candidate system.
4.1. Presentation of Extended Model
The multiple candidate system in the presence of the soft limiter can be extended to the oversampling and filtering technique [14]. In this case,  frequency domain OFDM symbols
frequency domain OFDM symbols  are zero-padded, and
are zero-padded, and  -times oversampled IDFT processes are performed, generating
-times oversampled IDFT processes are performed, generating  candidates
candidates  in the time domain, where the
in the time domain, where the  -times oversampled IDFT operation is denoted as
-times oversampled IDFT operation is denoted as

Then, the candidate  with the minimum PAPR is selected, and clipped by the soft limiter, where
with the minimum PAPR is selected, and clipped by the soft limiter, where  ,
,  , as in (8). The clipped signal
, as in (8). The clipped signal  goes through a band pass filter (BPS) which removes out-of-band frequency components, yielding a filtered signal
goes through a band pass filter (BPS) which removes out-of-band frequency components, yielding a filtered signal  which will be converted into an analog signal
which will be converted into an analog signal  .
.
Let  be the SNDR of the
be the SNDR of the  th subcarrier for
th subcarrier for  candidate system, then its inverse can be expressed as [14]
candidate system, then its inverse can be expressed as [14]

where SNR denotes the signal-to-noise ratio for the channel, and  denotes the signal-to-distortion ratio of the
denotes the signal-to-distortion ratio of the  th subcarrier for
th subcarrier for  candidate system.
candidate system.
In (16),  can be expressed as [14]
can be expressed as [14]

where  is given in (9) and
is given in (9) and  is the autocorrelation function of the clipped signal.
is the autocorrelation function of the clipped signal.
Let  and
and  , then the clipped signals are given by
, then the clipped signals are given by  and
and  , and the autocorrelation function
, and the autocorrelation function  is given by
is given by

where  denotes the expectation operation.
denotes the expectation operation.
4.2. Inaccuracy of Gaussian Assumption
For the single candidate case, since  are assumed to be Gaussian distributed,
are assumed to be Gaussian distributed,  is expressed as a joint Gaussian PDF [14, 18]. However, for the multiple candidate case
is expressed as a joint Gaussian PDF [14, 18]. However, for the multiple candidate case  , since the amplitude of the selected candidate is not Rayleigh distributed, such as (8), this Gaussian assumption no longer holds. In the rest of this paper, we consider the PDF of
, since the amplitude of the selected candidate is not Rayleigh distributed, such as (8), this Gaussian assumption no longer holds. In the rest of this paper, we consider the PDF of  for the multiple candidate case.
for the multiple candidate case.
Without loss of generality, we consider  and
and  , where
, where  and
and  are assumed to be independent and identically distributed. Then, the amplitude is defined as
are assumed to be independent and identically distributed. Then, the amplitude is defined as

where  is given by (8).
is given by (8).
Defining a power variable  , its characteristic function [15] is given by
, its characteristic function [15] is given by

and let  and
and  , such that
, such that  . Since
. Since  and
and  are independent and have an identical PDF
are independent and have an identical PDF  , we get
, we get

Then,  is given by
is given by

Now, we consider the case  with the PDF of
with the PDF of  . Notice that a negative value of
. Notice that a negative value of  will have its symmetrical PDF. The characteristic function of
will have its symmetrical PDF. The characteristic function of  is given by
is given by

Finally, by using (22) and (23), we get

which denotes the mathematical non-Gaussian PDF of  or
or  .
.
5. Conclusion
We study the probability density function (PDF) analysis and the signal-to-noise-plus-distortion ratio (SNDR) of a multiple candidate system for reducing the PAPR in OFDM modulation system. Since the selected OFDM symbol (candidate) has an amplitude PDF which is function of the number of candidates  , the derived
, the derived  is also the function of
is also the function of  , and it can be used for estimation of theoretical error performance and statistical channel capacity.
, and it can be used for estimation of theoretical error performance and statistical channel capacity.
In this paper, the side information is assumed not to be erroneous for analyzing the pure effect of multiple candidates. The analytical estimation matches well the simulation results, and with this study, we conclude that the more the candidates, not only the better PAPR reduction performance, but also the better error performance and the more gain of channel capacity, under the assumption of side information transmission without error, and at the expense of computational complexity for  IFFT circuits.
IFFT circuits.
Furthermore, the amplitude PDF analysis enables one to apply to a probabilistic PAPR reduction system jointly with "oversampling and filtering" technique. In this application, since the selected candidate is not complex Gaussian distributed, more investigation for SNDR is required.
Our analytical approach to obtaining the  implies that the estimation of error rate is achievable without time-consuming simulation, making system level design easier. Note that the error floor level is usually decreased by implementing channel coding techniques. In our future work, we will take channel coding into account for error performance analysis.
implies that the estimation of error rate is achievable without time-consuming simulation, making system level design easier. Note that the error floor level is usually decreased by implementing channel coding techniques. In our future work, we will take channel coding into account for error performance analysis.
References
Sari H, Svensson A, Vandendorpe L: Multicarrier systems. EURASIP Journal on Wireless Communications and Networking 2008., 2008:
Saeedi H, Sharif M, Marvasti F: Clipping noise cancellation in OFDM systems using oversampled signal reconstruction. IEEE Communications Letters 2002, 6(2):73-75. 10.1109/4234.984699
Jones AE, Wilkinson TA: Combined coding for error control and increased robustness to system nonlinearities in OFDM. Proceedings of the 46th IEEE Vehicular Technology Conference (VTC '96), May 1996, Atlanta, Ga, USA 904-908.
Tellado J, Cioffi J: Peak power reduction for multicarrier transmission. Proceedings of the IEEE Communications Theory Mini-Conference (CTMC '98), IEEE Global Communications Conference (GLOBECOM '98), 1998, Sydney, Australia
Krongold BS, Jones DL: PAR reduction in OFDM via active constellation extension. IEEE Transactions on Broadcasting 2003, 49(3):258-268. 10.1109/TBC.2003.817088
Xiao Y, Lei X, Wen Q, Li S: A class of low complexity PTS techniques for PAPR reduction in OFDM systems. IEEE Signal Processing Letters 2007, 14(10):680-683.
Siegl C, Fischer RFH: Partial transmit sequences for peak-to-average power ratio reduction in multiantenna OFDM. EURASIP Journal on Wireless Communications and Networking 2008., 2008:
Muller SH, Huber JB: Comparison of peak power reduction schemes for OFDM. Proceedings of the IEEE Global Communications Conference (GLOBECOM '97), November 1997 1-5.
Bäuml RW, Fischer RFH, Huber JB: Reducing the peak-to-average power ratio of multicarrier modulation by selected mapping. Electronics Letters 1996, 32(22):2056-2057. 10.1049/el:19961384
Knoo BK, Le Goff SY, Tsimenidis CC, Sharif BS: OFDM PAPR reduction using selected mapping without side information. Proceedings of the IEEE International Conference on Communications (ICC '07), June 2007 4341-4345.
Jayalath ADS, Tellambura C: Reducing the peak-to-average power ratio of orthogonal frequency division multiplexing signal through bit or symbol interleaving. Electronics Letters 2000, 36(13):1161-1163. 10.1049/el:20000822
Jayalath ADS, Tellambura C: Peak-to-average power ratio reduction of an OFDM signal using data permutation with embedded side information. Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS' 01), April 2000 562-565.
Ochiai H, Imai H: Performance of the deliberate clipping with adaptive symbol selection for strictly band-limited OFDM systems. IEEE Journal on Selected Areas in Communications 2000, 18(11):2270-2277. 10.1109/49.895032
Ochiai H, Imai H: Performance analysis of deliberately clipped OFDM signals. IEEE Transactions on Communications 2002, 50(1):89-101. 10.1109/26.975762
Papoulis A, Pillai SU: Probability, Random Variables and Stochastic Processes. 4th edition. McGraw-Hill, New York, NY, USA; 2002.
Proakis JG: Digital Communications. 4th edition. McGraw-Hill, New York, NY, USA; 2001.
Ryan WE, Lin S: Channel Codes Classical and Modern. Cambridge University Press, Cambridge, UK; 2009.
Banelli P, Cacopardi S: Theoretical analysis and performance of OFDM signals in nonlinear AWGN channels. IEEE Transactions on Communications 2000, 48(3):430-441. 10.1109/26.837046
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yoo, H., Guilloud, F. & Pyndiah, R. Amplitude PDF Analysis of OFDM Signal Using Probabilistic PAPR Reduction Method. J Wireless Com Network 2011, 983915 (2011). https://doi.org/10.1155/2011/983915
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/983915

 , and the peak detector selects the
, and the peak detector selects the  th candidate, where
th candidate, where  for
for  and
and  .
.
 corresponding to
corresponding to  .
.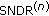 for Multiple Candidate System
for Multiple Candidate System

 . In the case,
. In the case,  and the QPSK modulation is considered.
and the QPSK modulation is considered.
 and M-ary Input AWGN channel (MI-AWGN) is considered.
and M-ary Input AWGN channel (MI-AWGN) is considered.