- Research Article
- Open access
- Published:
A Conjugate-Cyclic-Autocorrelation Projection-Based Algorithm for Signal Parameter Estimation
EURASIP Journal on Wireless Communications and Networking volume 2006, Article number: 086026 (2006)
Abstract
A new algorithm to estimate amplitude, delay, phase, and frequency offset of a received signal is presented. The frequency-offset estimation is performed by maximizing, with respect to the conjugate cycle frequency, the projection of the measured conjugate-cyclic-autocorrelation function of the received signal over the true conjugate second-order cyclic autocorrelation. It is shown that this estimator is mean-square consistent, for moderate values of the data-record length, outperforms a previously proposed frequency-offset estimator, and leads to mean-square consistent estimators of the remaining parameters.
References
Gardner WA: Statistical Spectral Analysis: A Nonprobabilistic Theory. Prentice-Hall, Englewood Cliffs, NJ, USA; 1988.
De Angelis V, Izzo L, Napolitano A, Tanda M: Performance analysis of a conjugate-cyclic-autocorrelation projection-based algorithm for signal parameter estimation. Proceedings of 6th International Symposium on Wireless Personal Multimedia Communications (WPMC '03), October 2003, Yokosuka, Kanagawa, Japan
Ciblat P, Loubaton P, Serpedin E, Giannakis GB: Performance analysis of blind carrier frequency offset estimators for noncircular transmissions through frequency-selective channels. IEEE Transactions on Signal Processing 2002,50(1):130–140. 10.1109/78.972489
Gini F, Giannakis GB: Frequency offset and symbol timing recovery in flat-fading channels: a cyclostationary approach. IEEE Transactions on Communications 1998,46(3):400–411. 10.1109/26.662646
Napolitano A, Tanda M: Blind estimation of amplitudes, phases, time delays, and frequency shifts in multiuser communication systems. Proceedings of IEEE 51st Vehicular Technology Conference (VTC '00), May 2000, Tokyo, Japan 2: 844–848.
Napolitano A, Tanda M: Blind parameter estimation in multiple-access systems. IEEE Transactions on Communications 2001,49(4):688–698. 10.1109/26.917775
Napolitano A, Tanda M: A non-data-aided cyclic-autocorrelation-based algorithm for signal parameter estimation. Proceedings of 4th International Symposium on Wireless Personal Multimedia Communications (WPMC '01), September 2001, Aalborg, Denmark
Napolitano A, Tanda M: Performance analysis of a Doppler-channel blind identification algorithm for noncircular transmissions in multiple-access systems. Proceedings of 7th IEEE International Symposium on Signal Processing and Its Applications (ISSPA '03), July 2003, Paris, France 2: 307–310.
Napolitano A, Tanda M: Doppler-channel blind identification for noncircular transmissions in multiple-access systems. IEEE Transactions on Communications 2004,52(12):2073–2078. 10.1109/TCOMM.2004.838716
Streight DA, Lott GK, Brown WA: Maximum likelihood estimates of the time and frequency differences of arrival of weak cyclostationary digital communications signals. Proceedings of 21st Century Military Communications Conference (MILCOM '00), October 2000, Los Angeles, Calif, USA 2: 957–961.
Napolitano A: Cyclic higher-order statistics: input/output relations for discrete- and continuous-time MIMO linear almost-periodically time-variant systems. Signal Processing 1995,42(2):147–166. 10.1016/0165-1684(94)00124-I
Dandawaté AV, Giannakis GB: Asymptotic theory of mixed time averages and
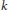 th-order cyclic-moment and cumulant statistics. IEEE Transactions on Information Theory 1995,41(1):216–232. 10.1109/18.370106
th-order cyclic-moment and cumulant statistics. IEEE Transactions on Information Theory 1995,41(1):216–232. 10.1109/18.370106Hasan T: Nonlinear time series regression for a class of amplitude modulated cosinusoids. Journal of Time Series Analysis 1982,3(2):109–122. 10.1111/j.1467-9892.1982.tb00333.x
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
De Angelis, V., Izzo, L., Napolitano, A. et al. A Conjugate-Cyclic-Autocorrelation Projection-Based Algorithm for Signal Parameter Estimation. J Wireless Com Network 2006, 086026 (2006). https://doi.org/10.1155/WCN/2006/86026
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/WCN/2006/86026
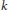 th-order cyclic-moment and cumulant statistics. IEEE Transactions on Information Theory 1995,41(1):216–232. 10.1109/18.370106
th-order cyclic-moment and cumulant statistics. IEEE Transactions on Information Theory 1995,41(1):216–232. 10.1109/18.370106