- Research
- Open access
- Published:
Distributed wireless information flow allocation in multiple access networks
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 14 (2011)
Abstract
We present a general framework for distributed wireless information flow allocation problem in multiple access networks, where the end users (EUs) can seek wireless flows from multiple access points (APs). We aim to minimize the power consumption while satisfying each EU's minimum data rate requirement but not violating peak power constraint of each AP and interference constraint monitored by regulatory agents. Toward this end, we model the flow allocation problem as a game which is proved to be a best-response potential game. Then based on potential game theory, we show the existence and uniqueness of Nash equilibrium in the formulated game. Moreover, we demonstrate that the Nash equilibrium is actually the globally optimal solution to our problem. Besides, we propose two distributed algorithms along with convergence analysis for the network to obtain the Nash equilibrium. Meanwhile, we reveal the interesting layered structure of the problem in question. Extensive numerical results are conducted to demonstrate the benefits obtained by flow allocation, as well as the effectiveness of our proposed algorithms.
Introduction
During the past two decades, we have witnessed an ever increasing demand of high data rate services in wireless communications. An end user (EU) is normally just associated with one access point (AP) in today's wireless networks such as Wireless Local Area Networks (WLANs) to access the Internet. However, researchers realize that the performance of this classic scheme may be unsatisfactory to meet the demand of high data rate services from EUs. Besides, this single-AP based scheme may be prone to suffer from fading due to the single link between EU and the corresponding AP [1]. As a result, more flexible WLANs, where EUs can be associated with multiple APs to get access to the Internet, are drawing increasingly interests from both academia and industry (see, e.g., [2] and references therein).
Another practical motivation comes from the recent interests in femtocell networks, in which consumers can install home base stations (BSs) for better indoor wireless voice and data communications [3]. However, an EU in femtocell networks tends to suffer from low throughput due to the limited capacity of backhaul connection to legacy cellular networks. Therefore, allowing the EUs to simultaneously access different home BSs in femtocell networks becomes a natural solution to aggregate sum rates of different backhaul links and thus avoid traffic bottleneck [4]. For simplicity, we also refer to this multiple home BSs access scheme in femtocell networks as multi-AP based scheme.
In spite of the potentials of multi-AP based scheme, the resource allocation problem in such scenarios is challenging. In particular, how the resources at APs can be used efficiently while satisfying the rate requirements from EUs? On the one hand, each EU can be connected to multiple APs and each AP may also need to serve multiple EUs, making the resource allocation problem (especially distributed implementation) seemingly prohibitively difficult. On the other hand, interference is a severe issue in multi-AP based scheme due to the simultaneous transmission from multiple APs to EUs, which often makes the resource allocation problem non-convex and thus hard to solve [5].
In [4], the authors formulated a general game-based framework for the multi-AP based scheme to develop self-organizing femtocell networks. Specifically, the APs send independently coded information to multiple EUs over orthogonal channels. In such a scenario, they focused on how individual AP independently decides its transmit power over several orthogonal channels, each of which has been allocated to one EU, to maximize its own data rate.
However, there exist several issues in the approach adopted in [4]. The first problem lies in the non-convexity nature of their formulation. It is well known that this non-convexity issue of maximizing the total achievable rate over the available parallel orthogonal channels in multi-user scenario makes the problem generally NP-hard [6]. That is, this problem is at least as hard as the hardest problems in NPa. Indeed, according to [6], this problem is already NP-hard even in a two-user communication system with arbitrary number of available channels. Thus, globally optimal performance cannot be obtained efficiently adopting the approach in [4]. Moreover, [4] assumed that an EU simply treats all the other APs' signals as noises when decoding a particular AP's signal. In spite of the low complexity, the achievable rate region by this decoding scheme is a strict subset of the capacity region of multiple access channel (MAC) [7]. This further degrades the achievable date rate of the framework proposed in [4].
In contrast, as it will become clear later, we adopt a reverse approach in this article which avoids the difficulty caused by the non-convexity. In particular, unlike [4], we study the power allocation problem from the EUs' point of view, though we also adopt a game-based approach. In our model, each EU individually decides its flow rate distribution from different APs to minimize the total power it consumes while guaranteeing its own quality-of-service (QoS) requirement (in terms of aggregate flow rate). Note that EUs need to competitively access the power resources of APs, resulting in a coupled strategy space among EUs. Furthermore, rather than treating the interference from other APs as noises when decoding some AP's signal, we adopt successive interference cancellation (SIC) at the EUs (decoders) to avoid performance loss (or equivalently to achieve the capacity) [1]. Practical implementation scheme of SIC in MAC has already been proposed (see, e.g., [8]). Besides, to make our approach more generally applicable, we impose additional interference temperature constraints. These constraints are of practical interests. For example, they can be applied in cellular networks so that the wireless signals generated in a particular cell would not cause too much interference to adjacent cells. Also, interference temperature constraints are commonly adopted by cognitive radio (CR) networks [9]. For convenience, we will refer to these interference temperature constraints as they are applied in CR networks in this article.
Interestingly, this reverse approach helps us investigate the resource allocation problem in question as a convex one. As a result, we are able to show that the Nash equilibrium (NE) of our formulated resource allocation game not only exists but also is unique. What is more, the unique NE in our formulation also turns out to be the globally optimal solution though NE is often known as an inefficient operating point [10]. Hence, the two proposed distributed algorithms can converge not only to the unique NE but in fact a globally optimal solution.
The rest of this article is organized as follows. Section II describes the specific system model and presents a game formulation for the problem in question. In Sect. III, we characterize the relevant properties of NE in the studied game. We propose two distributed algorithms which can satisfy different requirements in real implementation in Sect. IV. Section V presents extensive numerical results for performance evaluation, and is followed by our conclusions in Sect. VI.
System model and problem formulation
System model
We consider a radio network as shown in Figure 1, where N APs denoted by ℕ = {1, 2, ..., N } simultaneously transmit information to I EUs denoted by  over I orthogonal channels. Each EU receives signals over its pre-assigned channel which is orthogonal to other EUs' channels. We assume all the channels have equal bandwidth W but note that extension of our work to unequal bandwidth case is straightforward. Without loss of generality, we assume channel i is assigned to EU i. Besides, there are K monitoring devices (MDs) denoted by
over I orthogonal channels. Each EU receives signals over its pre-assigned channel which is orthogonal to other EUs' channels. We assume all the channels have equal bandwidth W but note that extension of our work to unequal bandwidth case is straightforward. Without loss of generality, we assume channel i is assigned to EU i. Besides, there are K monitoring devices (MDs) denoted by  , which regulates the interference caused by transmission from APs to EUs. The maximum interference level that MS k can tolerate over channel i is denoted by T
k, i
.
, which regulates the interference caused by transmission from APs to EUs. The maximum interference level that MS k can tolerate over channel i is denoted by T
k, i
.
We denote by  the channel power gain from AP n to EU i, and
the channel power gain from AP n to EU i, and  , the channel power gain from AP n to MD k over channel i. The power AP n allocates for transmission to EU i is denoted by
, the channel power gain from AP n to MD k over channel i. The power AP n allocates for transmission to EU i is denoted by  . AP n has a total power constraint
. AP n has a total power constraint  , i.e.,
, i.e.,  . Besides, due to the interference temperature constraints regulated by MDs, the transmit powers of APs also need to satisfy
. Besides, due to the interference temperature constraints regulated by MDs, the transmit powers of APs also need to satisfy  .
.
Unlike most previous works (see, e.g., [11–13]) which applied low complexity decoding scheme that simply treats other signals as noises when decoding a particular signal, we adopt SIC at the EUs to achieve the capacity of Gaussian multiple access channels. Besides, it is assumed that the zero-mean additive white Gaussian noise (AWGN) at EU i has spectral density N i .
As for the availability of channel state information (CSI), network nodes can obtain their desired information through training sequences and channel feedback. In particular, EU i is assumed to be aware of its local CSI, i.e.,  , ∀n ∈ ℕ by measuring the received power of the training sequences, and
, ∀n ∈ ℕ by measuring the received power of the training sequences, and  , by feedback from MDs. However, EU i may or may not know other EUs' CSI.
, by feedback from MDs. However, EU i may or may not know other EUs' CSI.
Problem formulation
Before we formally formulate our problem, we define for EU i the following self-mapping function

such that  . In other words, "π
i
(n) = m" implies that the channel power gain between EU i and AP m is the n-th largest of all the links connecting EU i to APs. We denote by
. In other words, "π
i
(n) = m" implies that the channel power gain between EU i and AP m is the n-th largest of all the links connecting EU i to APs. We denote by  the transmit signal-to-noise ratio (SNR) of EU i where
the transmit signal-to-noise ratio (SNR) of EU i where  is the total power of APs use for EU i's information flow. We further denote by
is the total power of APs use for EU i's information flow. We further denote by  the information flow rate from AP π
i
(n) to EU i. We then group the information flow rates of EU i into a column vector R
i
, i.e.,
the information flow rate from AP π
i
(n) to EU i. We then group the information flow rates of EU i into a column vector R
i
, i.e.,  . Then we have the following lemma.
. Then we have the following lemma.
Lemma 1: Given the information flow rate vector R
i
, the minimum required  is given by
is given by

where  is the transmit SNR of the link between AP π
i
(n) and EU i.
is the transmit SNR of the link between AP π
i
(n) and EU i.
Lemma 1 can be derived by studying the capacity region  of Gaussian multiple access channels. In particular,
of Gaussian multiple access channels. In particular,  can be characterized by [7]:
can be characterized by [7]:

To obtain the minimum required  for rate vector R
i
, we can consider a linear programming (LP) problem:
for rate vector R
i
, we can consider a linear programming (LP) problem:

Then we can show that the optimal value of the above LP problem is given by Lemma 1. For a more detail derivation of Lemma 1, we refer interested readers to [14].
Lemma 1 implies that EU i would require more power resource from APs that have better links to EU i. Clearly, this flexible multi-AP based scheme allows the power resource to be used more efficiently by taking advantage of the multi-user diversity in the networks.
Now we model EU i's QoS requirement in terms of minimum rate requirement  . In particular, EU i's total flow rate R
i
should satisfy
. In particular, EU i's total flow rate R
i
should satisfy

where  denotes the inverse function of
denotes the inverse function of  defined in (2), i.e.,
defined in (2), i.e.,  , and
, and  denotes the n-th coordinate of vector
denotes the n-th coordinate of vector  , i.e.,
, i.e.,  .
.
To appreciate the EUs' flow distributions, let us now consider a special scenario, where only one EU exists and interference constraints are relaxed. Under this setting, we have the following proposition.
Proposition 1: Suppose only EU i exists and interference constraints are relaxed in the network. Without loss of generality, let n0 be the index such that  is the first zero element in a rate vector
is the first zero element in a rate vector  . If
. If  can satisfy EU i's QoS, i.e.,
can satisfy EU i's QoS, i.e., , then
, then  minimizes its required transmit SNR
minimizes its required transmit SNR  (c.f. equation (2)) if and only if
(c.f. equation (2)) if and only if

where  .
.
Proof: See Appendix A. ■
Proposition 1 describes how an EU should allocate its flow requirement over different APs. Roughly speaking, an EU always first tries to seek flows from the AP whose link to that EU is the best for the moment. If the best AP fails to satisfy that EU's QoS requirement, it continues seeking flows from its second best AP. This process continues until the EU's QoS is satisfied. Interestingly, this process resembles (but is not the same as) the well known waterfilling power allocation strategy [1]. Hence, we regard it as a pseudo-waterfilling strategy. We further illustrate this pseudo-waterfilling process in Figure 2, as well as by numerical results provided in Sect. V.
Nevertheless, due to the limited power resource of each AP and interference constraints, EUs compete with each other to meet their respective minimum rate requirements. Thus, Proposition 1 is not sufficient to characterize collective behaviors of EUs. Instead, we further resort to game theory to analyze the competitive behaviors between EUs. Toward this end, EU i is associated with a utility function given by

Note that EU i with utility function J
i
(R
i
) aims to minimize its total required transmit SNR from APs. This formulation is not directly equivalent to minimizing the power resource EU i consumes. Indeed, the total power resource p
i
required by EU i equals  . Hence, our formulation can be viewed as a weighted power minimization problem, where EU
. Hence, our formulation can be viewed as a weighted power minimization problem, where EU  is weighted by
is weighted by  .
.
The strategy set of EU i is given by

where  denotes the non-negative orthant of N-dimensional Euclidean space, R
−i
represents the rate allocation of all EUs except EU i. In (7), the first constraint implies the minimum rate required by EU i, the second set of constraints denotes the maximum interference levels regulated by each MD over every channel, and the last set of constraints imposes a total power constraint to each AP. For later use, we also define the set value mapping
denotes the non-negative orthant of N-dimensional Euclidean space, R
−i
represents the rate allocation of all EUs except EU i. In (7), the first constraint implies the minimum rate required by EU i, the second set of constraints denotes the maximum interference levels regulated by each MD over every channel, and the last set of constraints imposes a total power constraint to each AP. For later use, we also define the set value mapping

and the global flow rate allocation strategy set

For a particular EU i, given the flow rate vectors of other EUs, i.e., R −i , it aims at solving the following optimization problem to decide its own flow rate allocation vector R i :

whose optimal solution set is denoted by  , i.e., EU i's best response function.
, i.e., EU i's best response function.
Now we are in a position to formulate the following non-cooperative game to characterize the interaction between EUs:

where  is the set of players, i.e., EUs, Φ
i
(R
−i
) is EU i's strategy space, and J
i
(R
i
) is EU i's utility function. Clearly, the concept of Nash equilibrium (NE) plays a fundamental role in characterizing the non-cooperative game
is the set of players, i.e., EUs, Φ
i
(R
−i
) is EU i's strategy space, and J
i
(R
i
) is EU i's utility function. Clearly, the concept of Nash equilibrium (NE) plays a fundamental role in characterizing the non-cooperative game  [15]. In particular, no EU can increase its utility by unilaterally changing its flow rate allocation strategy at an NE state. We formally define the NE in game
[15]. In particular, no EU can increase its utility by unilaterally changing its flow rate allocation strategy at an NE state. We formally define the NE in game  as follows.
as follows.
Definition 1: Flow rate allocation  is called Nash equilibrium of the non-cooperative game
is called Nash equilibrium of the non-cooperative game  if and only if, for any EU
if and only if, for any EU 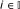 , the following condition holds:
, the following condition holds:

It should be pointed out that game  differs from many conventional non-cooperative game models where players' utilities couple with each other but strategy spaces are independent (see, e.g., [16]). In contrast, it is interesting to note that players in game
differs from many conventional non-cooperative game models where players' utilities couple with each other but strategy spaces are independent (see, e.g., [16]). In contrast, it is interesting to note that players in game  have coupled strategy spaces but their associated utilities are independent. Therefore, the approach used in [16] cannot be directly applied in this article. Instead, we resort to other approaches to tackle game
have coupled strategy spaces but their associated utilities are independent. Therefore, the approach used in [16] cannot be directly applied in this article. Instead, we resort to other approaches to tackle game  , especially in distributed algorithms design, as shown in the forthcoming sections.
, especially in distributed algorithms design, as shown in the forthcoming sections.
A careful reader may be concerned with the increasing hardware complexity of EUs' equipments since we formulate the flow allocation game  from EUs' point of view. We would like to stress that players in game
from EUs' point of view. We would like to stress that players in game  are just normative. They may or may not be the real decision makers. Indeed, if a central decision maker exists, it can compute the NE and then implements the NE in the network. Likewise, the APs in our model can also serve as decision makers. So our proposed scheme will not necessarily increase the EUs' hardware complexity. Besides, wireless networks in the future might be user-centric. That is, EUs with enhanced hardware in future wireless networks would be intelligent and cognitive. Then EUs in game
are just normative. They may or may not be the real decision makers. Indeed, if a central decision maker exists, it can compute the NE and then implements the NE in the network. Likewise, the APs in our model can also serve as decision makers. So our proposed scheme will not necessarily increase the EUs' hardware complexity. Besides, wireless networks in the future might be user-centric. That is, EUs with enhanced hardware in future wireless networks would be intelligent and cognitive. Then EUs in game  could be the true decision makers without difficulties even if they were incapable of implementing our proposed scheme for the time being.
could be the true decision makers without difficulties even if they were incapable of implementing our proposed scheme for the time being.
Characterization of NE
The NE state represents a steady state which is central to the understanding of distributed wireless information flow allocation in this article. The first question arising in game  is the existence of NE since lack of such equilibrium implies the instability of a distributed system. Moreover, the uniqueness of NE is also desirable for network operators to predict the distribution of wireless information flow and thus adjust the network parameters accordingly. Besides, it is of great significance to develop (possibly distributed) algorithms to reach the NE from initially non-equilibria states [10]. We will address these issues in this and next section.
is the existence of NE since lack of such equilibrium implies the instability of a distributed system. Moreover, the uniqueness of NE is also desirable for network operators to predict the distribution of wireless information flow and thus adjust the network parameters accordingly. Besides, it is of great significance to develop (possibly distributed) algorithms to reach the NE from initially non-equilibria states [10]. We will address these issues in this and next section.
Feasibility assumption
Note that the strategy space Φ may be empty. As an extreme case, MDs set  . Then it cannot be guaranteed that EUs can meet their minimum flow rate requirements. Therefore, determining the non-emptiness of strategy space Φ is also of interest. An admission control scheme aiming at identifying EUs who require infeasible minimum flow rate requirements may also be needed. This feasibility identification problem is interesting and will be our future work. In this article, we make the following assumption.
. Then it cannot be guaranteed that EUs can meet their minimum flow rate requirements. Therefore, determining the non-emptiness of strategy space Φ is also of interest. An admission control scheme aiming at identifying EUs who require infeasible minimum flow rate requirements may also be needed. This feasibility identification problem is interesting and will be our future work. In this article, we make the following assumption.
Assumption 1: There exists a feasible information flow rate allocation  such that
such that  , and
, and 
We remark that Assumption 1 should not be regarded as a stringent one. In fact, it is just the notable Slater condition with minor modification which is commonly assumed and required in optimization problems [17]. Note that we do not require  , to be inactive at R0 while Slater condition requires all inequality constraints to be inactive at some point. This is not a contradiction since
, to be inactive at R0 while Slater condition requires all inequality constraints to be inactive at some point. This is not a contradiction since  , can be recast as equality constraints without any performance loss as demonstrated in the following proposition.
, can be recast as equality constraints without any performance loss as demonstrated in the following proposition.
Proposition 2: Suppose the NE set ℝ of game  is not empty. Then any
is not empty. Then any  satisfies that
satisfies that

In other words, for any EU  , we can replace the "≥" in
, we can replace the "≥" in  by "=" while retaining the same NE set ℝ.
by "=" while retaining the same NE set ℝ.
Proof: See Appendix B. ■
Existence and uniqueness of NE
In this section, we investigate the existence and uniqueness of NE in game  . Before we state the main results in this section, we remark that, though the existence of NE in a game can often be readily verified, it is generally more involved to establish the uniqueness of NE. In fact, many realistic models do not possess the uniqueness property, motivating the investigation of the sufficient conditions for the uniqueness of NE case by case [10]. Nevertheless, by identifying game
. Before we state the main results in this section, we remark that, though the existence of NE in a game can often be readily verified, it is generally more involved to establish the uniqueness of NE. In fact, many realistic models do not possess the uniqueness property, motivating the investigation of the sufficient conditions for the uniqueness of NE case by case [10]. Nevertheless, by identifying game  as a best-response potential game, we show that a unique NE exists in game
as a best-response potential game, we show that a unique NE exists in game  [18]. We summarize this result in the following proposition.
[18]. We summarize this result in the following proposition.
Proposition 3: Game  possesses a unique NE R* .
possesses a unique NE R* .
Proof: See Appendix C. ■
Note that NE in general is inefficient and the price of anarchy can even be unbounded (see, e.g., [19]). Nevertheless, from the proof of Proposition 3, it is interesting to note that the unique NE R* in fact maximizes  . This is a very desirable result which implies that the social optimum can be obtained if we can find a scheme to reach the unique NE R* by playing game
. This is a very desirable result which implies that the social optimum can be obtained if we can find a scheme to reach the unique NE R* by playing game  , which is the very topic of the next section.
, which is the very topic of the next section.
Now we know that the unique NE R* maximizes  , or equivalently, minimizes
, or equivalently, minimizes  . We are now in a position to point out that minimizing the weighted power
. We are now in a position to point out that minimizing the weighted power  , to some extent, is equivalent to minimizing the network outage probability. To make this point explicitly, assuming for the time being a uniform QoS requirement, i.e.,
, to some extent, is equivalent to minimizing the network outage probability. To make this point explicitly, assuming for the time being a uniform QoS requirement, i.e.,  , we normalize the total SNR as
, we normalize the total SNR as  , which can be interpreted as total additional SNR required to combat against fading compared to the AWGN channel with channel gain g and the same rate requirement R. The network outage probability is defined as
, which can be interpreted as total additional SNR required to combat against fading compared to the AWGN channel with channel gain g and the same rate requirement R. The network outage probability is defined as  , where
, where  is the optimal normalized SNR under the unique NE R*,
is the optimal normalized SNR under the unique NE R*,  is the normalized SNR supported by the network under limited power resource at the APs. Under this interpretation, it becomes clear that, compared to the single-AP based scheme, the main advantage of multi-AP based scheme is the diversity gain. This diversity gain will also be demonstrated in the numerical results.
is the normalized SNR supported by the network under limited power resource at the APs. Under this interpretation, it becomes clear that, compared to the single-AP based scheme, the main advantage of multi-AP based scheme is the diversity gain. This diversity gain will also be demonstrated in the numerical results.
Distributed algorithms design
In this section, we propose two distributed algorithms for EUs to reach NE along with the corresponding theoretical convergence analysis. The design idea of the first algorithm is directly based on sequential best-response path (referred to as D-SBRA) [20]. However, as shown later, D-SBRA may be inconvenient due to its inherent drawbacks. Hence, we propose another algorithm to resolve the difficulties in D-SBRA by further resorting to partial dual decomposition (referred to as P-SBRA) [21]. Nevertheless, it will become clear later that P-SBRA requires the participation of APs while interaction only occurs among EUs in D-SBRA. Therefore, network operators can choose either D-SBRA or P-SBRA in practical implementation according to specific network situations.
D-SBRA
To begin with, we recite the relevant concepts of sequential best-response path from [20]. In particular, a sequence  in strategy space Φ is a sequential best-response path if EUs response one by one according to best-response strategy. A sequential best-response path is admissible if all I EUs have taken their best-response strategies at least once whenever I successive periods have passed. We now state the favorable convergent property of game
in strategy space Φ is a sequential best-response path if EUs response one by one according to best-response strategy. A sequential best-response path is admissible if all I EUs have taken their best-response strategies at least once whenever I successive periods have passed. We now state the favorable convergent property of game  in the following proposition which also justifies the convergence of D-SBRA.
in the following proposition which also justifies the convergence of D-SBRA.
Proposition 4: Every admissible sequential best-response path played in game  converges to the unique NE R*.
converges to the unique NE R*.
Proof: See Appendix D. ■
Proposition 4 implies that there exist infinite ways to reach the NE in game  as long as the sequential best-response path is admissible. However, we only provide an ordered-version for D-SBRA here due to limited space. We formally summarize D-SBRA for the distributed wireless information flow allocation problem in Algorithm 1.
as long as the sequential best-response path is admissible. However, we only provide an ordered-version for D-SBRA here due to limited space. We formally summarize D-SBRA for the distributed wireless information flow allocation problem in Algorithm 1.
Algorithm 1 D-SBRA
-
1:
Step 1: Initialization:
EUs exchange channel power gain information and start with an arbitrarily feasible flow rate allocation, i.e., R(0) Φ. Set t := 0; i := 1.
-
2:
Step 2: Computation:
-
3:
EU i calculates its strategy space:
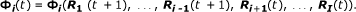 (14)
(14) -
4:
EU i computes its current flow rate allocation R i (t + 1) by solving the following best response problem:
 (15)
(15) -
5:
EU i broadcasts its new flow rate allocation R i (t + 1).
-
6:
Set i := i + 1. If i ≤ I, go to Step 2; otherwise, go to Step 3.
-
7:
Step 3: Convergence Verification:
If stopping criteria are satisfied, then stop; otherwise, set t := t + 1; i := 1, and go to Step 2.
Note that each EU needs to know the global CSI and other EUs' strategies in each response to compute its own strategy space and obtain best response in D-SBRA. This requirement may cause unacceptable level of communication overhead for some wireless networks. Worse still, some EUs may take advantage of other EUs by telling false information. In this scenario, a mechanism guaranteeing truth-telling is the dominant strategy for every EU may be required to achieve the global optimum. Therefore, we propose P-SBRA to overcome these drawbacks of D-SBRA.
P-SBRA
Recall that EU i's strategy space Φ i (R −i ) are constrained in two aspects. In particular, R i is constrained by both individual constraints that are independent of other EUs' strategies, i.e., the first two set of constraints in (7), and coupling constraints that depend on other EUs' strategies, i.e., the last set of constraints in (7). The main cause for the inconveniences in D-SBRA comes from the coupling issue among EUs' strategy spaces. To resolve this problem, we relax the coupling constraints by resorting to partial dual decomposition approach [21].
To begin with, let us introduce some notations for ease of exposition. In particular, we denote  , where Ψ
i
is EU i's own independent strategy space given by
, where Ψ
i
is EU i's own independent strategy space given by

We further define

We group all the fl (R) into a column vector f(R), i.e., f(R) = [f1(R), f2(R), ..., fN (R)] T .
Now let us introduce the Nash game (NG) (denoted by  ) cost function
) cost function  defined as [21]:
defined as [21]:

Here note that we write  as a function of R
−i
and x
i
for consistency though it in fact does not depend on R
−i
. Since a unique NE R* exists in game
as a function of R
−i
and x
i
for consistency though it in fact does not depend on R
−i
. Since a unique NE R* exists in game  by Proposition 3, based on Lemma 1 in [21], R* satisfies
by Proposition 3, based on Lemma 1 in [21], R* satisfies

Construct the following constrained optimization problem

where  . Then it is clear that R* is a solution to (20) with optimal NG cost
. Then it is clear that R* is a solution to (20) with optimal NG cost  . That is, we can solve (20) to obtain the NE of game
. That is, we can solve (20) to obtain the NE of game  . Toward this end, we relax the coupled constraints and obtain the corresponding partial Lagrangian function given by
. Toward this end, we relax the coupled constraints and obtain the corresponding partial Lagrangian function given by

where  , and λ is the corresponding Lagrangian multiplier vector. Then the following proposition that follows directly from Theorem 2 in [21] comes into handy.
, and λ is the corresponding Lagrangian multiplier vector. Then the following proposition that follows directly from Theorem 2 in [21] comes into handy.
Proposition 5: R* is the NE of game  if only if there exists corresponding dual variable λ* such that
if only if there exists corresponding dual variable λ* such that




We then resort to a decomposition approach to solve the above set of equations to achieve the NE R*. Consider the associated dual function given by

Where  is an NE of NG
is an NE of NG  with the same player set as game
with the same player set as game  but different utility function
but different utility function  ,
,  , and decoupled strategy space Ψ
i
,
, and decoupled strategy space Ψ
i
,  . That is, we can solve game
. That is, we can solve game  to obtain g(λ). In fact, this new game
to obtain g(λ). In fact, this new game  is trivial since there are no coupling issues in both the utilities and strategy spaces among players. In other words, given λ, EU i,
is trivial since there are no coupling issues in both the utilities and strategy spaces among players. In other words, given λ, EU i,  , only needs to solve the following convex optimization problem:
, only needs to solve the following convex optimization problem:

Besides, the best-response  in (27) is unique since Ψ
i
is a nonempty bounded convex set and
in (27) is unique since Ψ
i
is a nonempty bounded convex set and  is strictly concave with respect to R
i
on Ψ
i
. Hence, given λ, as long as all the EUs take their associated best response once, we can obtain the trivial NE R†(λ) of game
is strictly concave with respect to R
i
on Ψ
i
. Hence, given λ, as long as all the EUs take their associated best response once, we can obtain the trivial NE R†(λ) of game  .
.
The next key step is to update λ iteratively, making NE R†(λ) of game  converge to the unique NE R* of the original game
converge to the unique NE R* of the original game  . Indeed, the dual variable λ in the dual problem
. Indeed, the dual variable λ in the dual problem

can be updated by applying iterative subgradient method, i.e.,

where t is the iteration index, β(t) is the positive iteration step size, and [·]+ denotes the projection onto the set of non-negative numbers. Now we are in a position to summarize P-SBRA in Algorithm 2.
Algorithm 2 P-SBRA
-
1:
Step 1: Initialization:
EUs start with an arbitrarily feasible flow rate allocation, i.e., R(0) ∈ Φ. Set λ:= 0; t := 1.
-
2:
Step 2: Computation:
-
3:
Each EU
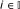 computes its current flow rate allocation R
i
(t + 1) by solving the following problem:
computes its current flow rate allocation R
i
(t + 1) by solving the following problem: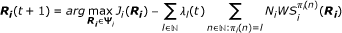 (30)
(30)and obtains the associated required
 , according to (2).
, according to (2). -
4:
Each EU
 notifies AP π
i
(n),∀n ∈ ℕ, its required SNR
notifies AP π
i
(n),∀n ∈ ℕ, its required SNR  .
. -
5:
Step 3: Subgradient Update:
Each AP l ∈ ℕ updates its dual variable λ l (t + 1) as follows:
 (31)
(31) -
6:
Step 4: Convergence Verification:
If stopping criteria are satisfied, then stop; otherwise, set t := t + 1, and go to Step 2.
By Proposition 5, we note that the iteration process in Algorithm 2 continues until the following complementary conditions are satisfied:

Besides, the convergence of subgradient updating process in Algorithm 2 can be guaranteed by certain choices of step sizes, such as  , β0> 0, which satisfies the diminishing step size rule [17].
, β0> 0, which satisfies the diminishing step size rule [17].
Furthermore, given the Lagrangian variable λ, each EU only needs to know its local CSI to carry out its best response in P-SBRA, resulting in less communication overhead than that of D-SBRA. However, this advantage comes with the requirement of the participation of APs. Therefore, D-SBRA is desirable when APs may not be able to play such a coordination role.
Before ending this section, we point out that the Lagrangian variable λ in Algorithm 2 has a nice economic interpretation. In fact, we can view λ
l
, ∀l ∈ ℕ, as a price that EUs need to pay for the violation of AP l's total power constraint. In particular, if  , then λ
l
in the next run will be increased according to (29). Then EUs will experience a higher price when asking for flows from AP l and may try to seek flows from other APs. As a result, the violation of AP l's total power constraint may be alleviated in the next run. This dynamic process continues until the unique NE R* is reached. However, it should be noted that no real payment needs to be carried out in the implementation of P-SBRA.
, then λ
l
in the next run will be increased according to (29). Then EUs will experience a higher price when asking for flows from AP l and may try to seek flows from other APs. As a result, the violation of AP l's total power constraint may be alleviated in the next run. This dynamic process continues until the unique NE R* is reached. However, it should be noted that no real payment needs to be carried out in the implementation of P-SBRA.
Best response and layered structure
In this section, we study how the best responses (15) in Algorithm 1 and (30) in Algorithm 2 can be obtained. Note that best response problem (15) and (30) are both convex and thus can be solved very efficiently using standard convex optimization methods (interior point method, for one) [17]. Nevertheless, we here resort to subgradient method to help us further appreciate the implicit layered structure in our studied problem. Since best response problem (15) and (30) are similar, we only discuss problem (30) and the layered structure of P-SBRA here for brevity. D-SBRA can be analyzed in a similar fashion.
To begin with, we denote the objective function in problem (30) by  , which can be explicitly written as
, which can be explicitly written as

Then consider the Lagrangian function for EU i:

where u
i
= [u1, i, ..., u
K, i
] and v
i
are the associated non-negative Lagrange multipliers. We then resort to subgradient method to obtain the optimal solution  . Toward this end, let us further consider the associated dual function given by
. Toward this end, let us further consider the associated dual function given by

The corresponding dual problem

can be solved via subgradient method. In particular, with initial feasible (u
i
(0), v
i
(0)), the sequence (u
i
(s),  obtained from the subgradient method is given by
obtained from the subgradient method is given by


where s is the iteration index, α
i
(s) is the positive iteration step size. Then the primal solution  during the s th iteration is given by
during the s th iteration is given by

Now we are in a position to describe the inherent layered structure of P-SBRA as shown in Figure 3.
In particular, this layered structure can be viewed as a Stackelberg game with APs being the leaders and EUs being the followers [10]. On the leader side, based on the current SNR requirement  from the EUs, the APs set the corresponding power price λ to guarantee that their power resources are not over utilized. Then on the follower side, given current λ, each EU
from the EUs, the APs set the corresponding power price λ to guarantee that their power resources are not over utilized. Then on the follower side, given current λ, each EU  chooses its flow rate allocation vector R
i
to maximize its utility
chooses its flow rate allocation vector R
i
to maximize its utility  .
.
Note that, given λ, there also exists internal layered structure of EU  . Specifically, u
i
denotes interference price at the physical layer that EU i needs to pay for its violation of the interference constraints set by the MDs. Meanwhile, v
i
denotes QoS guarantee price at the transport layer that EU i needs to pay if it cannot satisfy the corresponding QoS request. Given u
i
and v
i
, EU i adjusts its flow rate allocation R
i
accordingly, and vice versa. After all EUs decide their flow rate allocation strategies, the corresponding required SNR
. Specifically, u
i
denotes interference price at the physical layer that EU i needs to pay for its violation of the interference constraints set by the MDs. Meanwhile, v
i
denotes QoS guarantee price at the transport layer that EU i needs to pay if it cannot satisfy the corresponding QoS request. Given u
i
and v
i
, EU i adjusts its flow rate allocation R
i
accordingly, and vice versa. After all EUs decide their flow rate allocation strategies, the corresponding required SNR  can be fed back to the leaders, i.e., APs. Then APs can update their power price λ accordingly, initiating a new round adjustment. This dynamic process continues until convergence or stopping criteria are satisfied.
can be fed back to the leaders, i.e., APs. Then APs can update their power price λ accordingly, initiating a new round adjustment. This dynamic process continues until convergence or stopping criteria are satisfied.
We remark that the layered structure of P-SBRA differs from those revealed in the context of cross layer optimization, in which layered structure exists only in individual user's protocol stack (see, e.g., [22, 23], and references therein). In particular, the layered structure of P-SBRA includes not only the internal layered structure in individual user's protocol stack but also an external layer due to the coordination of APs.
So far, we can see that SIC plays a fundamental role in our proposed scheme. A careful reader might be concerned with practical issues in applying SIC in wireless networks. Indeed, current receivers generally treat interference as noise though substantial research works have been carried out on interference-aware receivers. Nevertheless, it is widely accepted that current adopted receiving technique is increasingly sub-optimal when the number of interferers grows. Therefore, it is believed that the application of interference cancellation including SIC, which brings dramatic capacity gain (also shown in the next section), will become popular in the future interference-limited wireless networks [24]. Another interesting issue is how inexact SIC affects the performance of our proposed scheme. A satisfactory answer to this question requires a careful modeling of the inexactness of SIC, which is beyond the scope of this article. Nevertheless, we are positive about the potentials of SIC. Indeed, [25] shows that, compared to no interference cancellation, SIC still doubles the system capacity even with 50% channel estimation error which causes inexact SIC.
Performance evaluation
Protocol evaluation
We investigate the gain obtained by multi-AP based scheme compared to single-AP based scheme in this section. As suggested in the end of Section III, we use outage probability, which is defined as the probability that the minimum required powerb by EUs to guarantee the QoS is greater than a given power threshold of APs, as the performance metric [16]. For clarity, we assume a uniform QoS requirement, i.e.,  . Without loss of generality, we set R = 1 and g = 1 here. Accordingly, all the channel gains in our model are simulated as experiencing Rayleigh fading and thus follow exponential distribution, the mean of which is set to be 1.
. Without loss of generality, we set R = 1 and g = 1 here. Accordingly, all the channel gains in our model are simulated as experiencing Rayleigh fading and thus follow exponential distribution, the mean of which is set to be 1.
We set the number of APs and EUs to be the same, i.e., I = N, so that each EU can be associated with an AP exactly in single-AP based scheme. We plot the results for 2-AP 2-EU scenario and 3-AP 3-EU scenario in Figures 4 and 5, respectively. Here, direct transmission denotes the single-AP based scheme, and multiple access denotes the multi-AP based scheme. As expected, multiple access transmission brings a diversity order of 2 in Figure 4 and 3 in Figure 5. In contrast, the diversity order of direct transmission is only 1 in both scenarios. This evidently demonstrates the benefits brought by multi-AP based scheme over that of single-AP based scheme.
It should be pointed out that the above setting I = N does not lose generality. Indeed, this setup can be readily extended to the scenario accommodating the case of any individual AP serving multiple EUs. Let us take a specific example to make this point more explicitly. Suppose there is an AP serving two EUs. The AP cannot serve the two EUs in the same channel. Now we can imagine there are two virtual APs taking the place of the original actual AP. These two APs serve the two EUs over the two orthogonal channels, separately. Following this construction, we can always make I = N.
Note that we do not impose peak power constraint at the APs and interference temperature constraint at the MDs in this simulation since it is not clear how we should define the outage probability while incorporating these additional constraints. Instead, we just impose a total power threshold for the APs in this simulation. Nevertheless, if we could find an appropriate definition for the outage probability to take into account these additional constraints, we argue that the extra diversity order obtained by multiple access scheme will be maintained though a deteriorated outage performance might be observed.
Convergence and performance
We provide some numerical results in this section to illustrate the convergence behaviors of the two proposed algorithms. Simulation parameters are chosen as follows. The number of EUs, the number of APs, and the number of MDs are set to be 16, 8, and 4, respectively. Note that all the channel power gains are exponentially distributed. We set the mean of  to be 1, ∀n ∈ ℕ,
to be 1, ∀n ∈ ℕ,  while the mean of
while the mean of  is 0.2, ∀n ∈ ℕ,
is 0.2, ∀n ∈ ℕ,  . For clarity, we set the peak power constraint at each AP to be the same, i.e.,
. For clarity, we set the peak power constraint at each AP to be the same, i.e.,  , ∀n ∈ ℕ, and also a uniform interference temperature constraint at each MD over every channel, i.e., T
k, i
= 8,
, ∀n ∈ ℕ, and also a uniform interference temperature constraint at each MD over every channel, i.e., T
k, i
= 8,  , and a uniform QoS requirement, i.e.,
, and a uniform QoS requirement, i.e.,  .
.
We plot the results in Figure 6 which shows the evolutions of power allocation of APs associated with D-SBRA and P-SBRA as a function of iteration index. For clarity, we only show the evolutions of power allocation of AP1, AP4, and AP8 in Figure 6. The initial price vector λ for P-SBRA is randomly generated. We can see both algorithms converge relatively fast. Similar fast convergent behaviors of D-SBRA and P-SBRA can be observed with other simulation parameters. The fast convergence behaviors of two proposed algorithms are desirable for practical implementation. Moreover, as expected, the convergent speed of P-SBRA is greater than that of D-SBRA. This is understandable since each EU under D-SBRA needs to wait for the responses of all the other EUs before updating its own flow allocation while EUs under P-SBRA can update their responses simultaneously.
To further appreciate the performance, we compare our proposed scheme with the popular iterative water-filling algorithm (IWFA) which treats interference as noise when decoding. We choose IWFA as it has been extensively studied and advocated by many researchers for distributed resource allocation in wireless networks (see, e.g., [4, 12, 13] and references therein). For fair comparison, we relax the interference constraint for the time being. There are 5 APs with peak power  which ensures feasibility. We adopt the widely used metric defined as the ratio of the total energy consumption to the sum flow rates, which represents the amount of energy needed for each unit flow rate. This performance metric is appropriate for designing power efficient wireless networks, which is also the very objective of our article. We refer to [26] for a more detail discussion on this performance metric.
which ensures feasibility. We adopt the widely used metric defined as the ratio of the total energy consumption to the sum flow rates, which represents the amount of energy needed for each unit flow rate. This performance metric is appropriate for designing power efficient wireless networks, which is also the very objective of our article. We refer to [26] for a more detail discussion on this performance metric.
The numerical results are shown in Figure 7 in which SICA denotes our proposed SIC-based algorithms. As illustrated, SICA has a remarkable performance improvement over IWFA. These performance gains are due to two unique features in SICA. One the one hand, the SIC technique used in our scheme archives the capacity of multiple access channels while the performance of IWFA is suboptimal since IWFA simply treats interference as noises when decoding. On the other hand, APs in our scheme use their powers more wisely than those in IWFA. Indeed, APs in IWFA are selfish and only care about maximizing their own flow rates to EUs, resulting in excessive interference and unnecessary power waste. In contrast, APs in our scheme use their powers only when EUs require flows from them. Thus, network powers are wisely used and interference are kept to the minimum in our rate-on-demand (RoD) scheme.
Flow distribution
To better understand the pseudo-waterfilling strategy in Proposition 1, we provide some numerical results in a scenario with just one EU present, i.e., I = 1. Common simulation parameters are chosen as follows. The number of APs, and the number of MDs are 8 and 2, respectively. The channel power gains and the peak power constraint at each AP are the same as those in previous section.
We plot the results in Table 1 where T
k
= 10,  . In fact, with such a high interference tolerance level, the unique EU can choose flows from any APs while still satisfying the interference constraint. In particular, as shown in the table, the EU can satisfy its flow rate requirement 1 served by its "best" AP7. However, as flow rate requirement Rmin increases to 2.5, AP7 cannot satisfy the EU's QoS even when its peak power 8 is used. As a result, the EU seeks flows from its second "best" AP2. Similar behaviors can be observed when Rmin further increases to 3 and 3.5, respectively.
. In fact, with such a high interference tolerance level, the unique EU can choose flows from any APs while still satisfying the interference constraint. In particular, as shown in the table, the EU can satisfy its flow rate requirement 1 served by its "best" AP7. However, as flow rate requirement Rmin increases to 2.5, AP7 cannot satisfy the EU's QoS even when its peak power 8 is used. As a result, the EU seeks flows from its second "best" AP2. Similar behaviors can be observed when Rmin further increases to 3 and 3.5, respectively.
However, this flow seeking behavior largely depends on the simulation parameters and might not always be true. In particular, we plot the results in Table 2 where T
k
= 2,  . In fact, with such a low interference tolerance level, the EU cannot freely choose flows from any APs since now the transmission behaviors of APs are regulated and may not be able to transmit at their peak powers. This situation can be observed in Table 2. In the previous simulation results shown in Table 1, the flow rate requirement Rmin = 3 can be satisfied by AP7, AP2, AP3 with power 8, 8, 1.474, respectively. However, this flow rate allocation violates the interference constraint in this simulation. In fact, as shown in Table 2, the flow rate requirement Rmin = 3 now needs to be satisfied by AP7, AP2, AP5, AP3 with power 8, 8, 1.757, 0.316, respectively. Note that the flow allocation problem becomes infeasible when Rmin increases to 3.5 shown in Table 2.
. In fact, with such a low interference tolerance level, the EU cannot freely choose flows from any APs since now the transmission behaviors of APs are regulated and may not be able to transmit at their peak powers. This situation can be observed in Table 2. In the previous simulation results shown in Table 1, the flow rate requirement Rmin = 3 can be satisfied by AP7, AP2, AP3 with power 8, 8, 1.474, respectively. However, this flow rate allocation violates the interference constraint in this simulation. In fact, as shown in Table 2, the flow rate requirement Rmin = 3 now needs to be satisfied by AP7, AP2, AP5, AP3 with power 8, 8, 1.757, 0.316, respectively. Note that the flow allocation problem becomes infeasible when Rmin increases to 3.5 shown in Table 2.
It is also of interest to see the network flow distribution from the APs' perspective. Additional numerical results are provided in Table 3 and 4 with two EUs present for this purpose. In these two tables, the entry (x, y) at the intersection of EU i's row and AP j's column indicates that AP j which is EU i's y-th best AP allocates x units of power for the transmission between AP j and EU i. Table 3 where T k = 10 shows that AP6, EU1's best AP, can satisfy EU1's flow rate requirement 1. The same is true for EU2's best AP, i.e., AP8. However, as flow rate requirement Rmin increases to 3, AP6 cannot satisfy EU1's QoS, and so does AP8. As a result, AP3, which happens to be the second best AP of both EU1 and EU2, splits its power resource and provides the additional required flows for EU1 and EU2, respectively.
The network flow distribution changes in Table 4 where T k = 2. In particular, when the flow rate requirement Rmin = 3, AP3 now cannot transmit with power 1.875 to EU 2 as in Table 3 due to the low interference tolerance level. In this scenario, additional AP is needed to satisfy EU2's QoS. Indeed, AP3 now just transmits with power 1.166 to EU2. The remaining flows are provided by EU2's 4-th best AP, i.e., AP7, with power 5.875. Interestingly, AP6, EU2's third best AP, remains silent in this scenario.
A grid network simulation
To further verify the various arguments mentioned above, we carry out simulation for a 9 × 9 grid network as shown in Figure 8, where 30 EUs denoted by green dots randomly locate within the network, 9 APs denoted by magenta boxes locate at (1.5·i, 1.5·j) where i, j ∈ {1, 2, 3}, and 4 MDs denoted by red stars locate at the four corners, respectively. The channel gain  where d
ij
denotes the Euclidean distance between node i and node j. In such a network, we are interested in how the random distributed EUs allocate their information flows based on the proposed algorithms.
where d
ij
denotes the Euclidean distance between node i and node j. In such a network, we are interested in how the random distributed EUs allocate their information flows based on the proposed algorithms.
We plot the simulation results in Figure 8 where an information flow exists if there is a line between an EU and an AP. To be more specific, if an EU are connected to more than one AP, then the connection is denoted by a red line; otherwise, the corresponding connection is denoted by a blue line. The three subfigures are associated with either different peak power constraint at APs or different interference temperature constraints at MDs. However, we assume a uniform rate requirement Rmin = 1 which remains the same in all the three subfigures.
In the first subfigure, the peak power  , ∀n ∈ ℕ and the interference temperature T
k, i
= 10,
, ∀n ∈ ℕ and the interference temperature T
k, i
= 10,  . Under such abundant power resource at every AP and high interference tolerance level at every MD over each channel, every EU can satisfy its flow rate requirement by just seeking flow from its "best" AP. However, this is not true in the second subfigure where the peak power
. Under such abundant power resource at every AP and high interference tolerance level at every MD over each channel, every EU can satisfy its flow rate requirement by just seeking flow from its "best" AP. However, this is not true in the second subfigure where the peak power  is the same but interference temperature T
k, i
is set to be 1. Although the power resource is still abundant, some EUs may need to seek flows from more than one AP since their corresponding "best" APs cannot transmit at a high power level which violates the interference constraint. As expected, there are 4 EUs seeking flows from more than one AP shown in the second subfigure. Similar outcome can be observed in the third subfigure where the peak power
is the same but interference temperature T
k, i
is set to be 1. Although the power resource is still abundant, some EUs may need to seek flows from more than one AP since their corresponding "best" APs cannot transmit at a high power level which violates the interference constraint. As expected, there are 4 EUs seeking flows from more than one AP shown in the second subfigure. Similar outcome can be observed in the third subfigure where the peak power  is only 20 and the interference temperature T
k, i
is still 10. Now though MDs have a high interference tolerance level, some EUs may need to seek flows from more than one AP since their corresponding "best" APs may not have enough power resources to satisfy the QoS requirements. This situation is shown in the third figure where 5 EUs seek flows from more than one AP.
is only 20 and the interference temperature T
k, i
is still 10. Now though MDs have a high interference tolerance level, some EUs may need to seek flows from more than one AP since their corresponding "best" APs may not have enough power resources to satisfy the QoS requirements. This situation is shown in the third figure where 5 EUs seek flows from more than one AP.
Nevertheless, we can see only a few (0, 4, and 5 in the three subfigures, respectively) EUs out of total 30 EUs seek flows from more than one AP. As mentioned, this result is favorable. On the one hand, only a few EUs in the network need to carry out SIC in decoding, which reduces the average decoding complexity in a network setting. On the other hand, it also reduces the implementation complexity of flow splittingc in the wired network which is carried out for only a few EUs. This implies that the multi-AP based transmission scheme using the proposed algorithms brings considerable gains with a moderate cost in complexity.
Conclusion
In this article, we address the distributed wireless information flow allocation problem in multiple access networks. We model the flow allocation problem within the game-theoretical framework. The formulated game turns out to be a potential game, whose NE exists and is unique. Moreover, this unique NE is shown to be the globally optimal solution to the studied problem. Two distributed algorithms along with convergence analysis are proposed for EUs to reach NE. The layered structure of the problem is revealed too. The benefits of multi-AP based scheme and the effectiveness of our proposed algorithms are verified by extensive numerical results.
As for the future work, we will address the feasibility issue discussed in Sect. III. Besides, extending current work to the mobile networks where channel gains are time varying is also interesting and challenging.
Appendix A
Proof of Proposition 1
Proof: It is equivalent to show that the rate vector  is the optimal solution to the following optimization problem:
is the optimal solution to the following optimization problem:

We prove the only if part first. Toward this end, we note that the necessary condition for optimality is that  should satisfy the Karush-Kuhn-Tucker (KKT) conditions [17]. Consider the Lagrangian:
should satisfy the Karush-Kuhn-Tucker (KKT) conditions [17]. Consider the Lagrangian:

where γ, η, and ζ are the corresponding Lagrange multipliers. Then the KKT conditions are given by




where

Now we claim that  . If this claim is not true,
. If this claim is not true,  such that
such that  . Then it follows that the corresponding Lagrangian multiplier
. Then it follows that the corresponding Lagrangian multiplier  and
and  by complementary slackness conditions in (43) and (44), respectively. Thus,
by complementary slackness conditions in (43) and (44), respectively. Thus,

where the first two equalities follow from (42), the third equality follows from the facts that  and thus
and thus  by complementary slackness conditions in (44) and
by complementary slackness conditions in (44) and  and
and  , the fourth equality follows from (46), and the inequality follows from the assumption
, the fourth equality follows from (46), and the inequality follows from the assumption  and the non-negativeness of
and the non-negativeness of  in (43). Clearly, (47) gives us the desired contradiction.
in (43). Clearly, (47) gives us the desired contradiction.
We further claim that  , ∀n > n0 - 1. If this claim is not true,
, ∀n > n0 - 1. If this claim is not true,  such that
such that  . It follows that
. It follows that  by complementary slackness conditions in (44). We also have
by complementary slackness conditions in (44). We also have

which implies that ζ = 0 by complementary slackness conditions in (45). Thus,

resulting in a contradiction.
Hence, we conclude that  is the unique solution satisfying the KKT conditions given at the beginning of this proof. This completes the proof of only if part.
is the unique solution satisfying the KKT conditions given at the beginning of this proof. This completes the proof of only if part.
Note that problem (40) is a convex optimization problem since it can be readily checked that the associated objective function and the inequality constraints are continuously differentiable convex functions. Then it follows that KKT conditions are also sufficient for the optimality [17]. This completes the proof of if part. ■
Appendix B
Proof of Proposition 2
Proof: For any R* ∈ ℝ, suppose there exists some  such that
such that  . Given
. Given  , it can be readily checked that EU i's utility J
i
(R
i
) is a strictly monotone decreasing function of R
i
. Thus if
, it can be readily checked that EU i's utility J
i
(R
i
) is a strictly monotone decreasing function of R
i
. Thus if  , EU i can choose another feasible flow rate allocation strategy
, EU i can choose another feasible flow rate allocation strategy  such that
such that

with the corresponding utility  . This contradicts the assumption that R* is an NE. In fact, we can repeat this argument until (13) holds. This completes the proof. ■
. This contradicts the assumption that R* is an NE. In fact, we can repeat this argument until (13) holds. This completes the proof. ■
Appendix C
Proof of Proposition 3
Proof: We first claim that the function  given by
given by

is a potential function of game  . Indeed, we have
. Indeed, we have

where Φ
−i
(R
i
) denotes the global strategy space given EU i's flow rate allocation R
i
. Since (52) holds for any EU  , game
, game  by definition is a best-response potential game [18]. In other words, we have an associated coordination game
by definition is a best-response potential game [18]. In other words, we have an associated coordination game  , where all players share a common utility
, where all players share a common utility  such that the best response
such that the best response  of each player
of each player  in game
in game  is the same as its best response in game
is the same as its best response in game  .
.
We denote by  the set of maxima of
the set of maxima of  on the domain Φ which is nonempty by Assumption 1. Since
on the domain Φ which is nonempty by Assumption 1. Since  is a real-valued continuous function on a nonempty compact (i.e., closed and bounded) set Φ,
is a real-valued continuous function on a nonempty compact (i.e., closed and bounded) set Φ,  is always nonempty according to the Weierstrass Theorem [17]. Besides, Φ is a convex set, and
is always nonempty according to the Weierstrass Theorem [17]. Besides, Φ is a convex set, and  is continuously differentiable on the interior of Φ and strictly concave on Φ. Then, based on Theorem 3 in [27], we conclude that the NE of game
is continuously differentiable on the interior of Φ and strictly concave on Φ. Then, based on Theorem 3 in [27], we conclude that the NE of game  is unique.
is unique.
Appendix D
Proof of Proposition 4
Proof: To show Proposition 3, we need the following lemma that follows directly from Theorem 2 in [20].
Lemma 2: If game  has continuous best-response functions, compact strategy sets, and a unique NE R*,
has continuous best-response functions, compact strategy sets, and a unique NE R*,  is a best-response potential game if and only if every admissible sequential best-response path converges to R*.
is a best-response potential game if and only if every admissible sequential best-response path converges to R*.
Clearly, best-response function ℬ
i
(R
−i
),  , is continuous on the strategy set Φ
i
(R
−i
). Besides, Φ
i
(R
−i
),
, is continuous on the strategy set Φ
i
(R
−i
). Besides, Φ
i
(R
−i
),  , is a compact strategy set. Note that we have shown the existence and uniqueness of NE in game
, is a compact strategy set. Note that we have shown the existence and uniqueness of NE in game  in Proposition 2. Hence, Proposition 3 follows by Lemma 2. This completes the proof. ■
in Proposition 2. Hence, Proposition 3 follows by Lemma 2. This completes the proof. ■
End notes
aNP, abbreviated for "nondeterministic polynomial time", is a fundamental complexity class in computational complexity theory. We refer interested readers to [28] for more details.
bFor simplicity, we normalize N i and W throughout all the simulation results. Thus, our scheme aiming at minimizing the total transmit SNR also minimizes the total power consumption in this scenario.
cFor the flow splitting technique, we refer readers to [29] and references therein.
Abbreviations
- AP:
-
access point
- AWGN:
-
additive white Gaussian noise
- BSs:
-
base stations
- CR:
-
cognitive radio
- CSI:
-
channel state information
- EU:
-
end user
- IWFA:
-
iterative water-filling algorithm
- LP:
-
linear programming
- MAC:
-
multiple access channel
- MDs:
-
monitoring devices
- NE:
-
Nash equilibrium
- NG:
-
Nash game
- QoS:
-
quality-of-service
- RoD:
-
rate-on-demand
- SNR:
-
signal-to-noise ratio
- SIC:
-
successive interference cancellation
- WLANs:
-
Wireless Local Area Networks.
References
Tse D, Viswanath P: Fundamentals of Wireless Communication. Cambridge University Press, Cambridge; 2005.
Zhu Y, Zhang Q, Niu Z, Zhu J: Leveraging multi-AP diversity for transmission resilience in wireless networks: Architecture and performance analysis. IEEE Trans Wireless Commun 2009, 8(10):5030-5040.
Chandrasekhar V, Andrews J, Gatherer A: Femtocell networks: a survey. IEEE Commun Mag 2008, 46(9):59-67.
He G, Cottatellucci L, Debbah M: The waterfilling game-theoretical framework for distributed wireless network information flow. EURASIP J Wireless Commun Netw 2010, Article ID 482975. 13 pages (2010)
Han Z, Liu KJR: Resource Allocation for Wireless Networks: Basics, Techniques, and Applications. Cambridge University Press, Cambridge; 2008.
Luo ZQ, Zhang S: Dynamic spectrum management: complexity and duality. IEEE J Select Top Signal Process 2008, 2(1):57-73.
Cover TM, Thomas JA: Elements of Information Theory. Wiley-Interscience, New York; 1991.
Wang X, Poor H: Iterative (turbo) soft interference cancellation and decoding for coded CDMA. IEEE Trans Commun 1999, 47(7):1046-1061. 10.1109/26.774855
FCC: Establishment of an interference temperature metric to quantify and manage interference and to expand available unlicensed operation in certain fixed, mobile and satellite frequency bands. ET Docket no. 03-237 2003.
Altman E, Boulogne T, El-Azouzi R, Jiménez T, Wynter L: A survey on networking games in telecommunications. Comput Oper Res 2006, 33(2):286-311. 10.1016/j.cor.2004.06.005
Yates R: A framework for uplink power control in cellular radio systems. IEEE J Select Areas Commun 1995, 13(7):1341-1347. 10.1109/49.414651
Scutari G, Palomar D, Barbarossa S: Optimal linear precoding strategies for wideband noncooperative systems based on game theory-- Part I: Nash equilibria. IEEE Trans Signal Process 2008, 56(3):1230-1249.
Wu Y, Tsang D: Distributed power allocation algorithm for spectrum sharing cognitive radio networks with QoS guarantee. IEEE International Conference on Computer Communications (INFOCOM 2009) 2009, 981-989.
Tam WP, Lok TM, Wong TF: Flow optimization in parallel relay networks with cooperative relaying. IEEE Trans Wireless Commun 2009, 8(1):278-287.
Osborne MJ, Rubinstein A: A Course in Game Theory. MIT Press, Cambridge; 1994.
Ng CY, Lok TM, Wong TF: Pricing games for distributed cooperative transmission. IEEE Trans Veh Technol 2010, 59(7):3393-3406.
Stephen B, Lieven V: Convex Optimization. Cambridge University Press, Cambridge; 2004.
Voorneveld M: Best-response potential games. Econ Lett 2000, 66(3):289-295. 10.1016/S0165-1765(99)00196-2
Etkin R, Parekh A, Tse D: Spectrum sharing for unlicensed bands. IEEE J Select Areas Commun 2007, 25(3):517-528.
Jensen MK: Stability of pure strategy Nash equilibrium in best-reply potential games. University of Birmingham, Birmingham, United Kingdom, Technical Report; 2009.
Pavel L: An extension of duality to a game-theoretic framework. Automatica 2007, 43(2):226-237. 10.1016/j.automatica.2006.08.027
Chiang M, Low S, Calderbank A, Doyle J: Layering as optimization decomposition: a mathematical theory of network architectures. Proc IEEE 2007, 95(1):255-312.
Gatsis N, Ribeiro A, Giannakis G: A class of convergent algorithms for resource allocation in wireless fading networks. IEEE Trans Wireless Commun 2010, 9(5):1808-1823.
Andrews JG: Interference cancellation for cellular systems: a contemporary overview. IEEE Wireless Commun Mag 2005, 12(2):19-29. 10.1109/MWC.2005.1421925
Andrews JG, Meng T: Optimum power control for successive interference cancellation with imperfect channel estimation. IEEE Trans Wireless Commun 2003, 2(2):375-383. 10.1109/TWC.2003.809123
Saraydar C, Mandayam N, Goodman D: Efficient power control via pricing in wireless data networks. IEEE Trans Commun 2002, 50(2):291-303. 10.1109/26.983324
Scutari G, Barbarossa S, Palomar D: Potential games: a framework for vector power control problems with coupled constraints. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2006) 2006, 4: 14-19.
Papadimitriou C: Computational complexity. John Wiley and Sons Ltd., New York; 2003.
Kandula S, Katabi D, Sinha S, Berger A: Dynamic load balancing without packet reordering. SIGCOMM Comput Commun Rev 2007, 37(2):51-62. 10.1145/1232919.1232925
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lin, X., Lok, T.M. Distributed wireless information flow allocation in multiple access networks. J Wireless Com Network 2011, 14 (2011). https://doi.org/10.1186/1687-1499-2011-14
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1499-2011-14


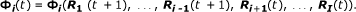

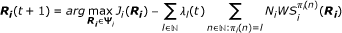
 , according to (2).
, according to (2). .
.






 , T
k, i
= 10.
, T
k, i
= 10.