- Research
- Open access
- Published:
Preamble and pilot symbol design for channel estimation in OFDM systems with null subcarriers
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 2 (2011)
Abstract
In this article, design of preamble for channel estimation and pilot symbols for pilot-assisted channel estimation in orthogonal frequency division multiplexing system with null subcarriers is studied. Both the preambles and pilot symbols are designed to minimize the l2 or the l∞ norm of the channel estimate mean-squared errors (MSE) in frequency-selective environments. We use convex optimization technique to find optimal power distribution to the preamble by casting the MSE minimization problem into a semidefinite programming problem. Then, using the designed optimal preamble as an initial value, we iteratively select the placement and optimally distribute power to the selected pilot symbols. Design examples consistent with IEEE 802.11a as well as IEEE 802.16e are provided to illustrate the superior performance of our proposed method over the equi-spaced equi-powered pilot symbols and the partially equi-spaced pilot symbols.
I. Introduction
Orthogonal frequency division multiplexing (OFDM) is an effective high-rate transmission technique that mitigates inter-symbol interference (ISI) through the insertion of cyclic prefix (CP) at the transmitter and its removal at the receiver. If the channel delay spread is shorter than the duration of the CP, ISI is completely removed. Moreover, if the channel remains constant within one OFDM symbol duration, OFDM renders a convolution channel into parallel flat channels, which enables simple one-tap frequency-domain equalization.
To obtain the channel state information (CSI), training OFDM symbols or pilot symbols embedded in each OFDM symbol are utilized. Training OFDM symbols or equivalently OFDM preambles are transmitted at the beginning of the transmission record, while pilot symbols (complex exponentials in time) are embedded in each OFDM symbol, and they are separated from information symbols in the frequency-domain [1–3]. If the channel remains constant over several OFDM symbols, channel estimation by training OFDM symbols may be sufficient for symbol detection. But in the event of channel variation, training OFDM symbols should be retransmitted frequently to obtain reliable channel estimates for detection. On the other hand, to track the fast varying channel, pilot symbols are inserted into every OFDM symbol to facilitate channel estimation. This is known as pilot-assisted (or -aided) channel estimation [2, 4, 5]. The main drawback of the pilot-assisted channel estimation lies in the reduction of the transmission rate, especially when larger number pilot symbols are inserted in each OFDM symbol. Thus, it is desirable to minimize the number of embedded pilot symbols to avoid excessive transmission rate loss.
When all subcarriers are available for transmission, training OFDM preamble and pilot symbols have been well designed to enhance the channel estimation accuracy, see e.g., [6] and references therein. If all the subcarriers can be utilized, then pilot symbol sequence can be optimally designed in terms of (i) minimizing the channel estimate mean-squared error [1, 3]; (ii) minimizing the bit-error rate (BER) when symbols are detected by the estimated channel from pilot symbols [7]; (iii) maximizing the lower bound on channel capacity with channel estimates [8, 9]. It has been found that equally spaced (equi-distant) and equally powered (equi-powered) pilot symbols are optimal with respect to several performance measures.
In practice, not all the subcarriers are available for transmission. It is often the case that null subcarriers are set on both the edges of the allocated bandwidth to mitigate interferences from/to adjacent bands [10, 11]. For example, IEEE 802.11a has 64 subcarriers among which 12 subcarriers, one at the center of the band (DC component) and at the edges of the band are set to be null, i.e., no information is sent [12]. The presence of null subcarriers complicates the design of both the training preamble for channel estimation and pilot symbols for pilot-aided channel estimation over the frequency-selective channels. Null subcarriers may render equi-distant and equi-powered pilot symbols impossible to use in practice.
In the literature, several pilot symbols design techniques for OFDM systems with null subcarriers have been studied [11, 13–16]. In [11], a method that assigns equal power to all pilot subcarriers and utilizes the exhaustive search method to obtain the optimal pilot set is proposed. However, the approach in [11] optimizes only pilot placements of the equally powered pilot symbols. The design of pilot symbols should take into account the placements as well as power loading. Moreover, the exhaustive search becomes intractable for large number of pilot symbols and/or active subcarriers even if the search process is carried out during the system design phase. To address the exhaustive search problem, the partially equi-spaced pilot (PEP) scheme, which will be referred as PEP in this article, is discussed in [13]. The algorithm in [13] is novel as it can be employed to design pilot symbols for both the MIMO-OFDM as well as SISO-OFDM systems. Furthermore, the design considers both the placements and power distribution to the pilot symbols. However, the method does not guarantee better performance for some channel/subcarriers configuration.
In [14], equi-powered pilot symbols are studied for channel estimation in multiple antennas OFDM system with null subcarriers. However, they are not always optimal even for point-to-point OFDM system. Also in [15], a proposal was made that employs cubic parameterizations of the pilot subcarriers in conjunction with convex optimization algorithm to design pilot symbols. However, the accuracy of cubic function-based optimizations in [15] depends on many parameters to be selected for every channel/subcarriers configuration which complicates the design. Pilot sequences designed to reduce the MSE of the channel estimation in multiple antenna OFDM system are also reported in [13, 16] but they are not necessarily optimal.
In this article, we optimally allocate power to the preamble as well as design pilot symbols to estimate the channel in OFDM systems with null subcarriers. Even though there is no closed form expression relating pilot placement with the MSE, we propose an algorithm that takes into account both the pilot placements and power distribution. Our design criteria are the l2 norm as well as the l∞ norm of the MSE of channel estimation in frequency-domain. Contrary to [15], where it is stated that l∞ is superior over l2, we verify that there is no significant difference in performance between the two norms.
To find the optimal power allocation, we first show that the minimization problem can be casted into a semidefinite programming (SDP) problem [17]. With SDP, the optimal power allocation to minimize our criterion can be numerically found. We also propose an iterative algorithm that uses the designed optimal preamble as an initial value to determine the significant placement of the pilot symbols and power distribution.
Finally, we present design examples under the same setting as IEEE 802.11a and IEEE 802.16e to show the improved performance of our proposed design over the PEPs and the equi-spaced equi-powered pilot symbols. We also made comparisons between our proposed design, PEP, and the design proposed by Baxley et al. in [15] for IEEE 802.16e. We demonstrated that our proposed design can be used as a framework to design pilot symbols for different channel/subcarriers configurations, and it is crucial to optimally allocate power to the pilot symbols to improve the MSE and BER performances. It is also verified that, the conventional preamble of IEEE 802.11a is comparable to the optimally designed preamble.
II. Preamble and pilot symbols for channel estimation
We consider point-to-point wireless OFDM transmissions over frequency-selective fading channels. We assume that the discrete-time baseband equivalent channel has FIR of maximum length L, and remains constant in at least one block, i.e., is quasi-static. The channel impulse response is denoted as {h0, h1,..., hL-1}. Since we basically deal with one OFDM symbol, we omit the index of the OFDM symbol for notational simplicity.
Let us consider the transmission of one OFDM symbol with N number of subcarriers. At the transmitter, a serial symbol sequence {s0, s1,..., sN-1} undergoes serial-to-parallel conversion to be stacked into one OFDM symbol. Then, an N-points inverse discrete Fourier transform (IDFT) follows to produce the N dimensional data, which is parallel-to-serial converted. A CP of length Ncp is appended to mitigate the multipath effects. The discrete-time baseband equivalent transmitted signals u n can be expressed in the time-domain as

Assume that Ncp is greater than the channel length L so that there is no ISI between the OFDM symbols. At the receiver, we assume perfect timing synchronization. After removing CP, we apply DFT to the received time-domain signal y n for n ∈ [0, N - 1] to obtain for k ∈ [0, N - 1]

where H k is the channel frequency response at frequency 2πk/N given by

and the noise W
k
is assumed to be i.i.d. circular Gaussian with zero mean and variance  .
.
For simplicity of presentation, we utilize a circular index with respect to N where the index n of a sequence corresponds to n modulo N. Let  be a set of active subcarriers (i.e., non-null subcarriers), then the cardinality of a set
be a set of active subcarriers (i.e., non-null subcarriers), then the cardinality of a set  can be represented as
can be represented as  .
.
Take WLAN standard (IEEE 802.11a), for example, where 64 subcarriers (or slots) are available in the OFDM symbol during data transmission mode. Out of which 48 are utilized as information symbols, 4 as pilot symbols, while the rest except for the DC subcarrier serves as spectral nulls to mitigate the interferences from/to OFDM symbols in adjacent bands. Thus,  = {1,2,..., 26, 38, 39, ..., 63} and
= {1,2,..., 26, 38, 39, ..., 63} and  .
.
The detailed structure of the OFDM packet in a time-frequency grid is shown in Figure 1. At the beginning of the transmission, two long OFDM preambles are transmitted to obtain CSI (see [[18], p. 600]). In IEEE 802.11a standard, the first part of the preamble consists of 10 short pilot symbols in 12 subcarriers equally spaced at 4 subcarriers interval, which is not shown in Figure 1. The second part of the preamble initiation, which corresponds to the first two OFDM symbols of Figure 1, requires the transmission of two columns of pilot symbols in all active subcarriers in order to make precise frequency offset estimation and channel estimation possible [18].
For channel estimation, we place  pilot symbols
pilot symbols  at subcarriers
at subcarriers  , which are known at the receiver. We assume that N
p
≥ L so that the channel can be perfectly estimated if there is no noise, and we denote the index of pilot symbols as
, which are known at the receiver. We assume that N
p
≥ L so that the channel can be perfectly estimated if there is no noise, and we denote the index of pilot symbols as  .
.
Let diag(a) be a diagonal matrix with the vector a on its main diagonal. Collecting the received signals having pilot symbols as

we obtain

where  is a diagonal matrix with its n th diagonal entry being
is a diagonal matrix with its n th diagonal entry being  such that
such that

and p is a pilot vector defined as

From  , we would like to estimate channel frequency responses for equalization and decoding. (In this article, we consider only channel estimation by one OFDM symbol but the extension to multiple OFDM symbols could be possible). Let us define
, we would like to estimate channel frequency responses for equalization and decoding. (In this article, we consider only channel estimation by one OFDM symbol but the extension to multiple OFDM symbols could be possible). Let us define  as an index set specifying the channel frequency responses to be estimated. In other words, H
k
for
as an index set specifying the channel frequency responses to be estimated. In other words, H
k
for  have to be estimated from
have to be estimated from  .
.
In a long training OFDM preamble, all subcarriers in  can be utilized for pilot symbols so that
can be utilized for pilot symbols so that  . On the other hand, in pilot-assisted modulation (PSAM) [4], a few known pilot symbols are embedded in an OFDM symbol to facilitate the estimation of unknown channel. Thus, for PSAM, we have
. On the other hand, in pilot-assisted modulation (PSAM) [4], a few known pilot symbols are embedded in an OFDM symbol to facilitate the estimation of unknown channel. Thus, for PSAM, we have  where\represents set difference.
where\represents set difference.
If we can adopt equally spaced (equi-distant) pilot symbols with equal power for channel estimation and symbol detection, then it can be analytically shown that the channel mean-squared estimation error [1, 3] as well as the BER [7] are minimized, while the lower bound on channel capacity [8, 9] is maximized. But the optimality of equi-distant and equi-powered pilot symbols does not necessarily hold true when there are null subcarriers.
In this article, for a given  , we use convex optimization technique to optimally distribute power to these subcarriers. Then, we propose an algorithm to determine pilot set
, we use convex optimization technique to optimally distribute power to these subcarriers. Then, we propose an algorithm to determine pilot set  with significant power to be used for PSAM.
with significant power to be used for PSAM.
III. Mean-squared channel estimation error
Let us define F as an N × N DFT matrix, the (m + 1, n + 1)th entry of which is e-j 2πmn/N. We denote an N × L matrix

consisting of N rows and first L columns of DFT matrix F, where  is the complex conjugate transpose operator. We also define an N
p
× L matrix F
p
having
is the complex conjugate transpose operator. We also define an N
p
× L matrix F
p
having  for
for  as its n th row. Then, we can express (5) as
as its n th row. Then, we can express (5) as

where the diagonal matrix D p and channel vector h are respectively defined as

and

Let a vector having channel responses to be estimated, i.e., H
k
for  , be
, be

Similar to F
p
, we define a  matrix F
s
having
matrix F
s
having  for
for  as its n th row, where k
n
< k
n'
if n < n'. Then, we obtain
as its n th row, where k
n
< k
n'
if n < n'. Then, we obtain

We assume that the mean of the channel coefficients is zero, i.e., E{h} = 0 and the channel correlation matrix is

where E{·} stands for the expectation operator. Then, since (9) is linear, the minimum mean-squared error (MMSE) estimate Ĥ s of H s is given by [19]

It follows from (9) and (13) that

and

We utilize the notation  (or A≻ 0) for a symmetric matrix A to indicate that A is positive semidefinite (or positive definite). Let us assume R
h
≻ 0 for the simplicity of presentation.
(or A≻ 0) for a symmetric matrix A to indicate that A is positive semidefinite (or positive definite). Let us assume R
h
≻ 0 for the simplicity of presentation.
If we define the estimation error vector E s as

then, the correlation matrix R e of E s can be expressed as [19]

where Λ p is a diagonal matrix given by

with  for
for  .
.
On the other hand, the least squares (LS) estimate of H
s
is found to be F
s
(D
p
Fp)† , where (·)† stands for the pseudo-inverse of a matrix. The LS estimate does not require any prior knowledge on channel statistics and is thus widely applicable. In contrast, the second order channel statistics
, where (·)† stands for the pseudo-inverse of a matrix. The LS estimate does not require any prior knowledge on channel statistics and is thus widely applicable. In contrast, the second order channel statistics  and the noise variance
and the noise variance  are essential to compute the MMSE estimate. When the signal-to-noise ratio (SNR) gets larger, i.e.,
are essential to compute the MMSE estimate. When the signal-to-noise ratio (SNR) gets larger, i.e.,  gets smaller for a given signal power, the MMSE estimate converges to the LS estimate. In general, the LS estimate can be easily obtained from the MMSE design by setting R
h
= 0 and
gets smaller for a given signal power, the MMSE estimate converges to the LS estimate. In general, the LS estimate can be easily obtained from the MMSE design by setting R
h
= 0 and  . Thus, to avoid possible duplications in the derivations, we only consider the MMSE estimate.
. Thus, to avoid possible duplications in the derivations, we only consider the MMSE estimate.
In place of the channel frequency responses, one may want to estimate the channel coefficient h directly. Similar to (15) and (19), the MMSE estimate  of and h the error correlation matrix are found to be
of and h the error correlation matrix are found to be

and

If  for a non-zero constant c, then from (19),
for a non-zero constant c, then from (19),  where ||·|| denotes the Euclidean norm. The equation
where ||·|| denotes the Euclidean norm. The equation  is attained if all pilot symbols have the same power and are uniformly distributed in an OFDM symbol. But, this is not always possible if there are null subcarriers in the OFDM symbol. As shown later, even with null subcarriers, the minimization of
is attained if all pilot symbols have the same power and are uniformly distributed in an OFDM symbol. But, this is not always possible if there are null subcarriers in the OFDM symbol. As shown later, even with null subcarriers, the minimization of  becomes possible.
becomes possible.
Now, our objective is to find the optimal pilot symbols that minimize a criterion function. Two important criteria are considered. One is the l2 norm of the mean-squared channel estimation errors  at data subcarriers, which is defined as
at data subcarriers, which is defined as

Where

The other is the maximum of {r k } defined as

which is the l∞ norm of  . It should be remarked that
. It should be remarked that  if
if  . To differentiate them, we call the former the frequency-domain channel MSE and the latter the time-domain channel MSE.
. To differentiate them, we call the former the frequency-domain channel MSE and the latter the time-domain channel MSE.
In the long preamble of IEEE 802.11a standard, equi-powered pilot symbols are utilized but may not be optimal due to the existence of null subcarriers. Equi-powered pilot symbols are also investigated for channel frequency response estimation in multiple antenna OFDM system with null subcarriers [14]. To reduce the sum of channel MSE for multiple antenna OFDM system, pilot symbol vector p has been designed to satisfy  in [16]. However, such pilot sequence does not always exist. In addition, the necessary and sufficient condition for its existence within the active subcarrier band has not yet been fully established.
in [16]. However, such pilot sequence does not always exist. In addition, the necessary and sufficient condition for its existence within the active subcarrier band has not yet been fully established.
IV. Pilot power distribution with SDP
For any prescribed energy to be utilized for channel estimation, we normalize the sum of pilot power such that

Then, our problem is to determine the optimal

that minimizes η2 in (23) or η∞ in (25) under the constraint (26).
We first consider the minimization η2. The optimal power distribution can be obtained by minimizing the squared η2 in (23) with respect to λ under the constraints that

where  (or a≻ 0) for a vector signifies that all entries of a are equal to or greater than 0 (or strictly greater than 0). As stated in the previous section, analytical solutions could not be found in general. As in [20], we will resort to a numerical design by casting our minimization problem into a SDP problem.
(or a≻ 0) for a vector signifies that all entries of a are equal to or greater than 0 (or strictly greater than 0). As stated in the previous section, analytical solutions could not be found in general. As in [20], we will resort to a numerical design by casting our minimization problem into a SDP problem.
The SDP covers many optimization problems [17, 21]. The objective function of SDP is a linear function of a variable x∈ RMsubject to a linear matrix inequality (LMI) defined as

where Am ∈ RM × M. The complex-valued LMIs are also possible, since any complex-valued LMI can be written by the corresponding real-valued LMI. Since the constraints defined by the LMI are convex set, the global solution can be efficiently and numerically found by the existing routines.
By re-expressing the n th row of F
p
as  , our MSE minimization problem can be stated as
, our MSE minimization problem can be stated as

where  . This problem possesses a similar form as the transceiver optimization problem studied in [22], which is transformed into an SDP problem. Similar to the problem in [22], our problem can be transformed into an SDP form. Now let us introduce an auxiliary Hermite matrix variable W and consider the following problem:
. This problem possesses a similar form as the transceiver optimization problem studied in [22], which is transformed into an SDP problem. Similar to the problem in [22], our problem can be transformed into an SDP form. Now let us introduce an auxiliary Hermite matrix variable W and consider the following problem:


It is reasonable to assume that the number of data carriers is greater than the channel length, i.e.,  , so that R ≻ 0. For R ≻ 0, if
, so that R ≻ 0. For R ≻ 0, if  , then
, then  [[23], p. 470]. From [[23], p. 471] it can be shown that
[[23], p. 470]. From [[23], p. 471] it can be shown that

Which is equivalent to

It follows that the minimization of trace(W R) is achieved if and only if  , which proves that the minimization of trace (W R) in (31) is equivalent to the original minimization problem in (30). Similarly, it has been proved in [[23], p.472] that
, which proves that the minimization of trace (W R) in (31) is equivalent to the original minimization problem in (30). Similarly, it has been proved in [[23], p.472] that

is positive definite if and only if  and
and  Thus, the constraint (32) can be rewritten as shown in (36) below. Finally, we reach the following minimization problem which is equivalent to the original problem:
Thus, the constraint (32) can be rewritten as shown in (36) below. Finally, we reach the following minimization problem which is equivalent to the original problem:


This is exactly an SDP problem where the cost function is linear in W and λ, and the constraints are convex, since they are in the form of LMI. Thus, the global optimal solution can be numerically found in polynomial time [17, 21].
We have discussed the design of pilot symbols minimizing the frequency-domain channel estimate MSE and are in general more preferable than pilot symbols minimizing the time-domain channel estimate MSE. Pilot symbols minimizing the time-domain channel estimate MSE can be obtained by just replacing R with I in (30) (cf. (23) and (22)), and apply the same design procedure used for the pilot symbols minimizing the frequency-domain channel estimate MSE.
Next, we consider the minimization of η∞ in (25), that is,

The minimization is equivalent to

subject to (28) and

It follows from (19) that

By using Schur's complement, (39) can be written as

Since (41) is convex, the minimization problem in (38) is also a convex optimization, and can be solved numerically. Compared to the minimization of the l2 norm, the minimization of the l∞ norm have  constraints, which lowers the speed of numerical optimization.
constraints, which lowers the speed of numerical optimization.
V. Pilot design
As we have seen, for a given set of subcarriers, the optimal pilot symbols are obtained by resorting to numerical optimization. In the OFDM preamble, all active subcarriers can be utilized for channel estimation so that we have  . On the other hand, in a pilot-assisted OFDM symbol, we have to select pilot subcarriers and allocate power to pilot and data subcarriers.
. On the other hand, in a pilot-assisted OFDM symbol, we have to select pilot subcarriers and allocate power to pilot and data subcarriers.
To determine the optimal set  having N
p
entries, i.e., the optimal location of N
p
pilot symbols, we have to enumerate all possible sets, then optimize the pilot symbols for each set and compare them. This design approach becomes infeasible as
having N
p
entries, i.e., the optimal location of N
p
pilot symbols, we have to enumerate all possible sets, then optimize the pilot symbols for each set and compare them. This design approach becomes infeasible as  gets larger. In [15], the pilot location is characterized with a cubic function, and an iterative pilot symbol design for LS channel estimation has been developed by using the cubic function. The cubic parameterization can also be applicable to our optimization. However, the parameterization depends on several parameters to be selected for every channel/subcarriers configuration, and for each set of parameters, the objective function has to be iteratively optimized which complicates the design. In [20], another pilot selection scheme has been proposed and is reported in [15] that for some special cases, it does not work well.
gets larger. In [15], the pilot location is characterized with a cubic function, and an iterative pilot symbol design for LS channel estimation has been developed by using the cubic function. The cubic parameterization can also be applicable to our optimization. However, the parameterization depends on several parameters to be selected for every channel/subcarriers configuration, and for each set of parameters, the objective function has to be iteratively optimized which complicates the design. In [20], another pilot selection scheme has been proposed and is reported in [15] that for some special cases, it does not work well.
In this article, we improve the method of [20] by introducing an iterative algorithm as follows. Let 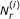 be a positive even integer. First, we use a designed optimal preamble with SDP and denote its λ
k
as
be a positive even integer. First, we use a designed optimal preamble with SDP and denote its λ
k
as  , then, we remove
, then, we remove  subcarriers with minimum power symmetrically about the center (DC) subcarrier, i.e.,
subcarriers with minimum power symmetrically about the center (DC) subcarrier, i.e.,  on every side of the central DC subcarrier. Then, we optimize the remaining pilot symbols. Similarly, for the i th iteration, after removing subcarriers corresponding to
on every side of the central DC subcarrier. Then, we optimize the remaining pilot symbols. Similarly, for the i th iteration, after removing subcarriers corresponding to 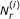 minimum power, we optimize pilot power for the remaining set again with SDP. When the iterative algorithm is completed, we will remain with only
minimum power, we optimize pilot power for the remaining set again with SDP. When the iterative algorithm is completed, we will remain with only  subcarrier indexes and its corresponding optimal power.
subcarrier indexes and its corresponding optimal power.
Our design procedure is as outlined by the pseudo-code algorithm below:
-
1)
Set i = 0.
-
2)
Obtain the optimal preamble using convex optimization and initialize temporary set
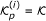 .
. -
3)
If
 , remove from
, remove from  ,
, 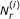 subcarriers with minimum power symmetrically with respect to the DC subcarrier, else go to step 5.
subcarriers with minimum power symmetrically with respect to the DC subcarrier, else go to step 5. -
4)
Optimize the power of the remaining subcarriers using SDP and go to step 3 after updating i ← i + 1.
-
5)
Exit.
The value of  is not fixed. The number of iterations can be reduced by increasing the value of
is not fixed. The number of iterations can be reduced by increasing the value of 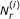 . However, when the number of removed subcarriers
. However, when the number of removed subcarriers 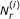 is large, the proposed scheme may not work well for some channel/subcarriers configuration as in [20], where the significant N
p
subcarriers of the optimized preamble are selected at once.
is large, the proposed scheme may not work well for some channel/subcarriers configuration as in [20], where the significant N
p
subcarriers of the optimized preamble are selected at once.
To obtain a better pilot set for any channel/subcarriers configuration, the number of removed subcarriers 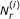 should be kept smaller. There is a tradeoff between the computational complexity and the estimation performance of the resultant set. Since we can design pilot symbols off-line, we can set the minimum for
should be kept smaller. There is a tradeoff between the computational complexity and the estimation performance of the resultant set. Since we can design pilot symbols off-line, we can set the minimum for 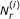 such as
such as 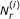 = 2.
= 2.
VI. Design examples
In this section, we demonstrate the effectiveness of our proposed preamble and pilot symbols designs through computer simulations. The parameters of the transmitted OFDM signal studied in our design examples are as in the IEEE 802.11a and IEEE 802.16e (WiMaX) standards. For IEEE 802.11a, an OFDM transmission frame with N = 64 subcarriers is considered. Out of 64 subcarriers, 52 subcarriers are used for pilot and data transmission while the remaining 12 subcarriers are null subcarriers [[18], p. 600]. For IEEE 802.16e standard, an OFDM transmission frame in [[24], p. 429] is considered. In a data-carrying symbol 200 subcarriers of the N = 256 subcarrier window are used for data and pilot symbols. Of the other 56 subcarriers, 28 subcarriers are null in the lower-frequency guard band, 27 subcarriers are nulled in the upper frequency guard band, and one is the central null (DC) subcarrier. Of the 200 used subcarriers, 8 subcarriers are allocated as pilot symbols, while the remaining 192 subcarriers are used for data transmission.
In the simulations, the total power of each OFDM frame is normalized to one, but power distribution among pilot symbols is not constrained to be uniform. The diagonal element of channel correlation matrix is set to be  for m, n ∈ [0, L - 1], where δ(·) stands for Kronecker's delta, and c is selected such that trace R
h
= 1.
for m, n ∈ [0, L - 1], where δ(·) stands for Kronecker's delta, and c is selected such that trace R
h
= 1.
A. Preamble design
First, we start with the design of preamble where all active subcarriers are considered as pilot symbols. For a given channel length L, to design an OFDM preamble, we optimize all active subcarriers by minimizing the l2 norm or the l∞ norm of MSEs  using convex optimization package in [25]. Figure 2 depicts the optimal power distribution to the IEEE 802.11a preamble designed by l2 norm when the SNR is 10 dB and the channel length L = 4. We omit the power distribution by l∞ norm, since it is nearly identical to that of the l2 norm-based design. Unlike the standard preamble where equal power is allocated to all the subcarriers, our optimized preamble distribute power to the subcarriers such that the channel estimate MSE is minimized.
using convex optimization package in [25]. Figure 2 depicts the optimal power distribution to the IEEE 802.11a preamble designed by l2 norm when the SNR is 10 dB and the channel length L = 4. We omit the power distribution by l∞ norm, since it is nearly identical to that of the l2 norm-based design. Unlike the standard preamble where equal power is allocated to all the subcarriers, our optimized preamble distribute power to the subcarriers such that the channel estimate MSE is minimized.
We also consider a case when the channel length L = 8. The results in Figure 3 show the optimized preamble at 10 dB. Again, there is no significant difference between the design with l2 norm and the design with l∞ norm. However, the computational complexity of the design with l2 norm is quite lower than the computational complexity of the design with l∞ norm, thereby making the former more preferable to the latter. Even though the design process is usually done in off-line, such minor advantage may be an important factor when designing preambles and pilot symbols for an OFDM frame with a large number of subcarriers.
Figures 2 and 3 show that the designed preambles are symmetric around 0. This is due to the symmetric nature of our objective function and its constraints. There are differences in power distribution to the designed preambles when L = 4 and L = 8, this suggests that in the preamble design, equi-powered subcarriers may not necessarily be optimal when there are null subcarriers. This may not be well encapsulated in the overall channel estimate MSE. However, when considering the channel estimate in each subcarrier, there is a slight difference between the proposed designs and the standard preamble especially at the edges of the active band.
To verify this, we compare frequency-domain channel MSE η2 obtained by the l2 and l∞ norm-based design with the standard IEEE 802.11a preamble. By varying the channel length L, from 1 to 16, we numerically obtain the channel estimate MSE for each L. Figure 4 presents the frequency-domain channel MSE η2, against channel length L at 10 dB. From the plot, it is obvious that there is no significant difference between the three designs, which suggests that the standard preamble is almost optimal in the l2 sense even if there are null subcarriers. This is not so surprising since in the absence of null subcarriers, equi-powered preamble is optimal. Through our design approach, we numerically corroborate that for IEEE 802.11a, the standard preamble is nearly optimal.
To demonstrate the versatility of our method, we minimize the LS channel estimate MSE to design preambles for the IEEE 802.16e standard. Figure 5 shows the designed preamble of IEEE 802.16e for L = 16. Similar to 802.11a, the distribution of power to the active subcarriers is not uniform. This further suggests that equi-powered preambles are not necessarily optimal for the OFDM systems with null subcarriers.
B. Pilot design
We employ the algorithm developed in Section V to design pilot symbols for PSAM. Similar to the preamble design, total power of the pilot symbols are normalized to one. First, we consider an OFDM symbol with 64 subcarriers and 4 pilot symbols, i.e., N p = 4. This complies with the IEEE 802.11a standard pilot symbols, where four equi-spaced and equi-powered pilot symbols are adopted.
In general, within an OFDM symbol, the number of pilot symbols in frequency domain should be greater than the channel length (maximum excess delay), which is related to the channel delay spread (i.e., N p ≥ L) [2]. When N p > L, the MSE performance will be improved as long as the power of pilot symbols is optimally distributed, but the capacity (or data rate) will be degraded. Thus, in our simulations, we use N p = L. However, it should be remarked that except for some special cases, it still remains unclear what value of N p is optimal.
Figure 2 shows the pilot symbols designed by l2 norm at 10 dB when N
p
= L = 4. The designed pilot symbols are almost equi-spaced ( = {±8, ±24)}, and the existing standard allocates the equi-powered pilot symbols at (
= {±8, ±24)}, and the existing standard allocates the equi-powered pilot symbols at ( = {±7, ±21}). For OFDM systems with null subcarriers, equi-spaced pilot symbols having the same power are not necessarily optimal. In our proposed design, the optimized power allocated to the pilot symbols is not uniformly distributed, which suggests that in the presence of null subcarriers, equi-powered pilot symbols may not necessarily be optimal. This may not be well encapsulated in the total channel estimate MSE, but is more clearer when considering the channel estimate in each subcarrier.
= {±7, ±21}). For OFDM systems with null subcarriers, equi-spaced pilot symbols having the same power are not necessarily optimal. In our proposed design, the optimized power allocated to the pilot symbols is not uniformly distributed, which suggests that in the presence of null subcarriers, equi-powered pilot symbols may not necessarily be optimal. This may not be well encapsulated in the total channel estimate MSE, but is more clearer when considering the channel estimate in each subcarrier.
We also illustrate the performance of our proposed algorithm by designing pilot symbols for N
p
= L = 8. Figure 3 presents the power distribution to the designed pilot symbols at 10 dB. The pilot power distribution is found to be symmetric around 0. This is due to the symmetric nature of our objective functions and the fact that pilot positions are obtained by removing the minimum power subcarriers symmetrically. The eight pilot symbols are located at the subcarriers  = {±4, ±12, ±19, ±26}. Pilot symbols are well distributed within the in-band region, which ensures nearly constant estimation in all subcarriers.
= {±4, ±12, ±19, ±26}. Pilot symbols are well distributed within the in-band region, which ensures nearly constant estimation in all subcarriers.
We make a comparison of our proposed design, the PEPs scheme and the equi-spaced equi-power design which we will refer to it as a reference design. Figure 6 shows the designed pilot set for each of the three methods. Both of the proposed and PEP design allocate some pilot subcarriers close to the edges. For the reference design, the equi-spaced and equi-powered pilot symbols are allocated at ±3, ±9, ±15, and ±21. There are no pilot subcarriers close to the edges of the active band. The lack of the pilot subcarriers at the edges of the OFDM symbol may lead to higher channel estimation errors for the active subcarriers close to the null subcarriers.
To demonstrate the effectiveness of the pilot symbols in Figure 6, we plot the channel estimate MSE for each active subcarrier. The total power allocated to the pilot symbols is the same for all three designs. Figure 7 shows the channel estimate MSE of the three designs. From the results, it is clear that, both of our proposed and the PEP design outperform the reference design, and there is no significant difference between the proposed design and the PEP design. The reference (equi-spaced equi-powered) design does a poor job of estimating channel close to the null subcarriers, this is due to the lack of pilot subcarriers at the edges of the OFDM symbol. Channel estimation via extrapolation results into higher errors at the edges of the OFDM symbols if there is no pilot subcarriers with significant power at the edges of the OFDM symbols. This suggests that both the pilot power and the placements need to be carefully considered in the design.
We also compare the average channel estimate MSE of our proposed design with the PEP design for different channel length L. We evaluate the channel estimate MSE of our proposed designs as well as the PEP scheme, by varying the channel length L, from 1 to 16. Figure 8 presents the average channel MSE against channel length L at 10 dB. The proposed designs, (l2 and l∞) exhibit lesser channel MSE than the PEP symbols except for the trivial case when L = 1. This verifies the potential of our proposed designs over the PEP scheme.
Figure 8 shows that the two design criteria (l2 and l∞) exhibit nearly the same η2 for different channel lengths L. This is contrary to [15], where it is stated that the l∞ norm-based design outperforms the l2 norm-based design. Our results suggest that any of the two design criteria can be used to design pilot symbols. However, it should be noted that l2 norm-based design has less computational complexity as compared with the l∞. Since the results obtained by the two proposed methods are almost similar for both the preamble and the pilot symbol design, then it is reasonable to adopt the l2 norm-based design for the preamble as well as for the pilot symbol design.
Next, we consider pilot symbol design for IEEE 802.16e by minimizing the LS channel estimate MSE. Figure 5 shows the designed pilot symbols for L = N p = 16. Similarly, the pilot symbols are well distributed within the active subcarrier band, and the power distribution to the pilot symbols is not uniform. The result emphasizes on adopting non-uniform power distribution for an OFDM frame with null subcarriers. Furthermore, the result underlines the potential of our proposed scheme in designing pilot symbols for OFDM systems with different number of subcarriers, channel length, and dedicated number pilot subcarriers. We have provided the results based on the LS estimator to verify that, in designing pilot power and placement, minimization of both the LS and the MMSE channel estimate MSE, perform almost equally well.
Figure 9 illustrates the power distribution to the pilot symbols for the PEP, the method in [15], which we will refer to it as Baxley and the proposed designs. Similar to the results in Figure 6 for IEEE 802.11a, the placement of pilot symbols for the PEP and our proposed design are almost same. However, there is a noticeable difference in power distribution between the PEP and the proposed design for L = N p = 16. This suggests that the MSE performance of the two designs will be different. For Baxley's method, both the pilot placement and the power distribution are comparable to our proposed design. The design in [15], uses exhaustive grid search to obtain pilot set with minimum channel estimate MSE. The placement of the pilot symbols depends on the searching granularity over the predetermined domain of some optimizing parameters. The main challenge in [15] lies in the adjustment of several parameters to obtain reasonable pilot positions. With the proper selection of the optimizing parameters of the cubic function, the performance of Baxley's method is comparable to our proposed design.
The prominence of optimal power distribution to the pilot symbols is further depicted in Figure 10, where for the designed pilot symbols in Figure 9, we plot the normalized channel estimate MSE for each active subcarrier. The total power allocated to the pilot symbols is the same for all the three designs. Figure 10 depicts the channel estimate MSE of the three designs. From the results, it is clear that, both of our proposed and the Baxley designs outperform the PEP design, and there is no significant difference between the proposed design and the Baxley design. Unlike the results depicted in Figure 7, where the performance of the PEP design are comparable to our proposed method, here the PEP design does a poor job of estimating the channel close to the null subcarrier zone. This is not due to the lack of pilot subcarriers at the edges of the OFDM symbol, but due to insignificant power allocated to the pilot symbols close to the null subcarriers. The results suggest that, considerable MSE performance improvements can be realized by the proper distribution of power to the pilot symbols.
Similarly, we make a comparison of the frequency-domain channel MSE between the PEP, the Baxley method, and our pilot symbol designs for IEEE 802.16e. Figure 11 presents the channel estimate MSE of the IEEE 802.16e for N p = 16. From the results, it is clear that there is a significant improvement in MSE performance between our proposed and the PEP designs. This further substantiates the superior performance of our proposed method over PEP for different channel/subcarriers configurations. The Baxley method performs equally well as our proposed design, which suggests that the method in [15] can be used for pilot symbol designs as well. However, the cubic parameterization technique adopted in the Baxley method obtains pilot placement for a given set of successive active subcarriers. Thus, for the case where some subcarriers within the active band are reserved for other applications, the method cannot be easily adopted. For example, to avoid the cubic parameterization from selecting the central DC subcarrier, additional constraint is introduced. This implies that, cubic parameterization techniques call for some modifications whenever active subcarriers are not consecutive. Unlike [15], our proposed design can be easily employed to obtain significant pilot set for any given set of active subcarriers.
A good example is in [26, 27], where tone reservation (TR) technique is adopted for peak-to-average power ratio (PAPR) reduction. For a system that utilizes TR method to mitigate PAPR, the transmitter sends dummy symbols in some selected subcarriers within the active band [26, 27]. These reserved subcarriers change the orientation of the data subcarriers in the active band and thereby limit direct application of the cubic parameterization techniques in designing pilot symbols. Unlike cubic parameterization method, PEP as well as our proposed method can be easily adopted even when some subcarriers within the active band are restricted. Another example is in [13], where PEP scheme is used to design pilot symbols for both the MIMO-OFDM as well as the SISO-OFDM systems. Like PEP, our proposed method can be easily adopted in the design of the disjoint pilot symbols for MIMO-OFDM systems. For MIMO-OFDM systems that utilizes pilot symbols, to reduce interference between the pilot symbols transmitted from different antennas, it is necessary for the pilot symbols to be orthogonal. The orthogonality of the pilot sequences for MIMO-OFDM can be established by ensuring that the pilot symbols of one transmit antenna are disjoint from the pilot symbols of any other transmit antenna or by using phase-shift (PS) codes. Baxley method cannot be directly applied to design disjoint pilot sets for MIMO-OFDM systems while our method be can easily applied.
In the following, we explore the BER performance gains that could be realized if the pilot symbols in IEEE 802.16e are designed to conform with the proposed method. We demonstrate the efficacy of our proposed method by comparing the BER performance of the proposed, PEP, the Baxley and the reference design. The frequency-selective channel with L = N
p
taps is considered. Each channel tap is i.i.d. complex Gaussian with zero mean and the exponential power delay profile is given by the vector ρ= [ρ0 ⋯ ρL - 1] where  , and
, and  is a constant selected such that
is a constant selected such that  .
.
Figures 12 and 13 depict the BER performance of the OFDM system when using PSK modulation. For N p = 8, we made a comparison between the proposed design, PEP, the Baxley, and the reference design. It is noted that conventional standard utilizes equi-spaced equi-powered pilot symbols. Figure 12 depicts the BER performance of the four designs for QPSK modulation. The PEP, the Baxley, and the proposed design outperform the reference design. The results show that, at high SNR, there is a slight improvement in BER performance of the proposed design over the PEP and the Baxley design.
To demonstrate the flexibility of our proposed design, we provide two comparable BER curves, Proposed 1 and Proposed 2, where the former is the BER performance of our designed pilot symbols and the latter is the BER performance of our pilot symbols optimized when we reserve subcarriers  = {±100, ±76, ±47, ±14} for TR. This verifies that, even for discontinuous data subcarriers, our proposed design can still be used to design significant pilot symbols, while the Baxley design cannot be directly applicable to this configuration.
= {±100, ±76, ±47, ±14} for TR. This verifies that, even for discontinuous data subcarriers, our proposed design can still be used to design significant pilot symbols, while the Baxley design cannot be directly applicable to this configuration.
For N p = 16, we only consider PEP, the Baxley, and the proposed design as it is impossible to have 16 equally spaced pilot symbols within 200 active subcarriers. Figure 13 depicts the BER performance for QPSK, 16-PSK, and 64-PSK. The results verify that the proposed design provides improved BER performance over the PEP design. This performance gap is a result of the PEP design having insignificant power distribution to the pilot symbols at the edges of the active subcarrier band that leads to poor estimate of the channels. The performance of the Baxley design is similar to the proposed design for QPSK-modulated data. However, for 16-PSK and 64-PSK modulation, our proposed design outperforms the Baxley design. Also, for 16-PSK and 64-PSK modulation, there is a slight improvement in BER performance of the Baxley method over the PEP design. The gain attained by our proposed method over the PEP and the Baxley design together with the flexibility of the proposed technique in designing pilot symbols for different channel/subcarriers configurations promotes our proposed design to be a candidate for pilot symbols design in OFDM systems with null subcarriers.
VII. Conclusion
We have addressed the design of optimal preamble as well as suboptimal pilot symbols for channel estimation in OFDM systems with null subcarriers. First, we have formulated the channel estimate MSE minimization problem for a determined subcarrier set as an SDP, then we have employed convex optimization techniques to obtain near optimal power distribution to a given subcarrier set. Design examples consistent with IEEE 802.11a standard show that in terms of channel estimate MSE, the long OFDM preamble with equi-powered active subcarriers is nearly optimal.
In designing the pilot symbols, we have considered pilot placement as well as power allocation. We have proposed an iterative algorithm to determine pilot placements and then distribute power to the selected pilot symbols by using convex optimization techniques. Several examples consistent with IEEE 802.11a and IEEE 802.16e have been provided which show that the proposed methods can be used to design preamble as well as pilot symbols for channel estimation in OFDM systems with different frame size. We have also verified that our proposed method is superior over the equi-spaced equi-powered pilot symbols as well as the PEP and slightly outperforms the Baxley design.
Note
† The material in this article was presented in part at Asia-Pacific Conference on Communications 2008.
Abbreviations
- CP:
-
cyclic prefix
- CSI:
-
channel state information
- IDFT:
-
inverse discrete Fourier transform
- ISI:
-
inter-symbol interference
- LMI:
-
linear matrix inequality
- MMSE:
-
minimum mean-squared error
- MSE:
-
mean-squared errors
- OFDM:
-
orthogonal frequency division multiplexing
- PAPR:
-
peak-to-average power ratio
- PEP:
-
partially equi-spaced pilot
- PSAM:
-
pilot-assisted modulation
- SDP:
-
semidefinite programming
- SNR:
-
signal-to-noise ratio
- TR:
-
tone reservation.
References
Negi R, Cioffi J: Pilot tone selection for channel estimation in a mobile OFDM system. IEEE Trans Consumer Electron 1998, 44: 1122-1128. 10.1109/30.713244
Ozdemir MK, Arslan H: Channel estimation for wireless OFDM systems. IEEE Commun Surv Tutor 2007, 9(2):18-48.
Sandell M, Edfors O: A comparative study of pilot-based channel estimators for wireless OFDM. Technical report, Research Report TULEA 1996, Lulea University of Technology 1996.
Cavers JK: Pilot symbol assisted modulation and differential detection in fading and delay spread. IEEE Trans Inf Theory 1995, 43: 2206-2212.
Li YG: Pilot-symbol-aided channel estimation for OFDM in wireless systems. IEEE Trans Vehic Technol 2000, 49(4):1207-1215. 10.1109/25.875230
Tong L, Sadler BM, Dong M: Pilot-assisted wireless transmissions: general model, design criteria, and signal processing. Signal Process Mag 2004, 21(6):12-25. 10.1109/MSP.2004.1359139
Ohno S, Giannakis GB: Optimal training and redundant precoding for block transmissions with application to wireless OFDM. IEEE Trans Commun 2002, 50(12):2113-2123. 10.1109/TCOMM.2002.806547
Adireddy S, Tong L, Viswanathan H: Optimal placement of training for frequency-selective block-fading channels. IEEE Trans Inf Theory 2002, 48(8):2338-2353. 10.1109/TIT.2002.800466
Ohno S, Giannakis GB: Capacity maximizing MMSE-optimal pilots for wireless OFDM over frequency-selective block Rayleigh-fading channels. IEEE Trans Inf Theory 2004, 50(9):2138-2145. 10.1109/TIT.2004.833365
Sari H, Karam G, Jeanclaude I: Transmission techniques for digital terrestrial TV broadcasting. IEEE Commun Mag 1995, 33: 100-109.
Song S, Singer AC: Pilot-aided OFDM channel estimation in the presence of the guard band. IEEE Trans Commun 2007, 55(8):1459-1465.
Nee RV, Prasad R: OFDM for Wireless Multimedia Communications. Artech House Publishers; 2000.
Huang Q, Ghogho M, Freear S: Pilot design for MIMO OFDM systems with virtual carriers. IEEE Trans Signal Process 2009, 57(5):2024-2029.
Larsson EG, Li J: Preamble design for multiple-antenna OFDM-based WLANs with null subcarriers. IEEE Signal Process Lett 2001, 8(11):325-327.
Baxley R, Kleider J, Zhou GT: Pilot design for OFDM with null edge subcarriers. IEEE Trans Wirel Commun 2009, 8: 396-405.
Hu D, Yang L, Shi Y, He L: Optimal pilot sequence design for channel estimation in MIMO OFDM systems. IEEE Commun Lett 2006, 10(1):1-3. 10.1109/LCOMM.2006.1576550
Vandenberghe L, Boyd S: Semidefinite programming. SIAM Rev 1996, 38: 49-95. 10.1137/1038003
IEEE Standard for Information Technology---Telecommunications and Information Exchange Between Systems---Local and Metropolitan Area Networks--Specific Requirement Part 11: Wireless Medium Access Control (MAC) and Physical Layer (PHY) Specifications, IEEE Std 2007.
Kay SM: Fundamentals of Statistical Signal Processing. Prentice Hall; 1993.
Ohno S: Preamble and pilot symbol design for channel estimation in OFDM. Proceedings of the International Conference on ASSP 2007, 281-284.
Boyd S, Vandenberghe L: Convex Optimization. Cambridge University Press; 2004.
Luo ZQ, Davidson TN, Giannakis GB, Wong KM: Transceiver optimization for block-based multiple access through ISI channels. IEEE Trans Signal Process 2004, 52(4):1037-1052. 10.1109/TSP.2004.823502
Horn RA, Johnson CR: Matrix Analysis. Cambridge University Press; 1990.
IEEE Standard for Local and Metropolitan Area Networks Part 16: Air Interface for Fixed Broadband Wireless Access Systems, IEEE Std 2004.
Gahinet P, Nemirovski A, Laub AJ, Chilali M: LMI Control Toolbox. The Math Works, Inc; 1995.
Cavalcante R, Yamada IA: Flexible peak-to-average power ratio reduction scheme for OFDM systems by the adaptive projected subgradient method. IEEE Trans Signal Process 2009, 57: 1456-1468.
Erdogan AT: A low complexity multicarrier PAR reduction approach based on subgradient optimization. Signal Process 2006, 86(12):3890-3903. 10.1016/j.sigpro.2006.03.030
Author information
Authors and Affiliations
Corresponding author
Additional information
IX. Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ohno, S., Manasseh, E. & Nakamoto, M. Preamble and pilot symbol design for channel estimation in OFDM systems with null subcarriers. J Wireless Com Network 2011, 2 (2011). https://doi.org/10.1186/1687-1499-2011-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1499-2011-2

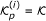 .
. , remove from
, remove from  ,
, 










