On the achievable rates of multiple antenna broadcast channels with feedback-link capacity constraint

Abstract

In this paper, we study a MIMO fading broadcast channel where each receiver has perfect channel state information while the channel state information at the transmitter is acquired by explicit channel feedback from each receiver through capacity-constrained feedback links. Two feedback schemes are considered, i.e., the analog and digital feedback. We analyze the achievable ergodic rates of zero-forcing dirty-paper coding (ZF-DPC), which is a nonlinear precoding scheme inherently superior to linear ZF beamforming. Closed-form lower and upper bounds on the achievable ergodic rates of ZF-DPC with Gaussian inputs and uniform power allocation are derived. Based on the closed-form rate bounds, sufficient and necessary conditions on the feedback channels to ensure nonzero and full downlink multiplexing gain are obtained. Specifically, for analog feedback in both AWGN and Rayleigh fading feedback channels, it is sufficient and necessary to scale the average feedback link SNR linearly with the downlink SNR in order to achieve the full multiplexing gain. While for the random vector quantization-based digital feedback with angle distortion measure in an error-free feedback link, it is sufficient and necessary to scale the number of feedback bits B per user as where M is the number of transmit antennas and 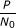is the average downlink SNR.

Introduction

The multiple antenna broadcast channels, also called multiple-input multiple-output (MIMO) downlink channels, have attracted great research interest for a number of years because of their spectral efficiency improvement and potential for commercial application in wireless systems. Initial research in this field has mainly focused on the information-theoretic aspect including capacity and downlink-uplink duality [1–4] and transmit precoding schemes [5–9]. These results are based on a common assumption that the transmitter in the downlink has access to perfect channel state information (CSI). It is well known that the multiplexing gain of a point-to-point MIMO channel is the minimum of the number of transmit and receive antennas even without CSIT [10]. On the other hand, in a MIMO downlink with single-antenna receivers and i.i.d. channel fading statistics, in the case of no CSIT, user multiplexing is generally not possible and the multiplexing gain is reduced to unity [11]. As a result, the role of the CSI at the transmitter (CSIT) is much more critical in MIMO downlink channels than that in point-to-point MIMO channels.

The acquisition of the CSI at the transmitter is an interesting and important issue. For time-division duplex (TDD) systems, we usually assume that the channel reciprocity between the downlink and uplink can be exploited and the transmitter in the downlink utilizes the pilot symbols transmitted in the uplink to estimate the downlink channel [12]. The impact of the channel estimation error and pilot design on the performance of the MIMO downlink in TDD systems has been studied in [13–18]. For frequency-division duplex (FDD) systems, no channel reciprocity can be exploited, and thus it is necessary to introduce feedback links to convey the CSI acquired at the receivers in the downlink back to the transmitter.

There are generally two kinds of CSI feedback schemes applied for MIMO downlink channels in the literature. The first scheme is called the unquantized and uncoded CSI feedback or analog feedback (AF) in short, where each user estimates its downlink channel coefficients and transmits them explicitly on the feedback link using unquantized quadrature-amplitude modulation [12, 19–21]. The performance of the downlink linear zero-forcing beamforming (ZF-BF) scheme with AF was evaluated through simulations in [19], and analytical results were given later in [20] and [21]. The second feedback scheme is called the vector quantized CSI feedback or digital feedback (DF) in short, where each user quantizes its downlink channel coefficients using some predetermined quantization codebooks and feeds back the bits representing the quantization index [20–27]. The MIMO broadcast channel with DF has been considered in [20, 21, 24–27]. In [24], a linear ZF-BF-based multiple-input single-output (MISO) system is firstly considered with random vector quantization (RVQ) limited feedback link, in which the closed-form expressions for expected SNR, outage probability, and bit error probability were derived. Then the vector quantization scheme based on the distortion measure of the angle between the codevector and the downlink channel vector was adopted in [20, 21, 25], and a closed-form expression of the lower and upper bound on the achievable rate of ZF-BF was derived. The results there also showed that the number of feedback bits per user must increase linearly with the logarithm of the downlink SNR to maintain the full multiplexing gain. Further, the authors in [26] pointed out that in the scenario where the number of users is larger than that of the transmit antennas, with simple user selection, having more users reduces feedback load per user for a target performance.

However, the aforementioned literatures [20, 21, 25] both focus on the linear ZF-BF scheme, which is not asymptotically optimal compared with nonlinear schemes, such as zero-forcing dirty-paper coding (ZF-DPC) [1]. So, it is necessary to investigate the limiting performance for MIMO downlink channels with limited digital feedback link. In [27], the authors analyzed both the linear ZF-BF and nonlinear zero-forcing dirty-paper coding (ZF-DPC) and derived loose upper bounds of the achievable rates with limited feedback. But different from the distortion measure of the angle in [20, 21, 25], another vector quantization approach based on the distortion measure of mean-square error (MSE) between the codevector and the downlink channel vector was adopted in [27]. Simultaneously, the exact lower bounds of the achievable rates with limited feedback for ZF-DPC are not given in [27].

In this paper, we consider both analog and digital feedback schemes and study the achievable rates of a MIMO broadcast channel with these two feedback schemes, respectively. Different from [21, 25] focusing on the ZF-BF, the ZF-DPC is analyzed in our work which is inherently superior to the ZF-BF due to its nonlinear interference precancelation characteristic and is asymptotically optimal [1] as [27]. Specially, for DF, we adopt the vector quantization distortion measure of the angle between the codevector and the downlink channel vector, and perform RVQ [20, 21, 25] for analytical convenience. Our main contributions and key findings in this paper are as follows:

• A comprehensive analysis of the achievable rates of ZF-DPC with either analog or digital feedback is presented, and closed-form lower and upper bounds on the achievable rates are derived. For fixed feedback-link capacity constraint, the downlink achievable rates of ZF-DPC are bounded as the downlink SNR tends to infinity, which indicates that the downlink multiplexing gain with fixed feedback-link capacity constraint is zero.

• In order to achieve full downlink multiplexing gain, it is sufficient and necessary to scale the average feedback link SNR linearly with the downlink SNR for AF in both AWGN and Rayleigh fading feedback channels. While for DF in an error-free feedback link, it is sufficient and necessary to scale the feedback bits per user as where M is the number of transmit antennas and 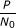is the average downlink SNR.

We note that although the ZF-DPC with DF has been considered in [27], our work also differs from it in several aspects. First, a different distortion measure for channel vector quantization is applied in our work compared to that in [27] as stated earlier. Actually, for RVQ-based DF, the angle distortion measure in [20, 21, 25] seems more reasonable than the MSE distortion measure in [27], which will be discussed in this paper. Second, a more thorough analysis about the downlink achievable rates (including upper and lower bounds) and multiplexing gain is presented in this paper than that in [27] (only upper bounds are given), covering both AF and DF.

The remainder of this paper is organized as follows. We give a brief introduction to the ZF-DPC with perfect CSIT in Section 2. Comprehensive analysis of achievable rates and multiplexing gain for both AF and DF are presented in Sections 3 and 4, respectively. A rough comparison of AF and DF is also given in Section 4. Finally, conclusions and discussions for future work are given in Section 5.

Throughout the paper, the symbols (·) ^T , (·)* and (·) ^H represent matrix transposition, complex conjugate and Hermitian, respectively. [·] _{m, n} denotes the element in the m th row and the n th column of a matrix. ||·|| represents the Euclidean norm of a vector. |·| and ∠(·) denote the magnitude and the phase angle of a complex number, respectively. represents expectation operator. Var(·) is the variance of a random variable. denotes a circularly symmetric complex Gaussian random variable with mean of a and variance of b.

Zero-forcing dirty-paper coding with perfect CSIT

Consider a multiple antenna broadcast channel composed of one base station (BS) with M transmit antennas and K users each with a single receive antenna. Assuming the channel is at and i.i.d. block fading, the received signal at user i in a given block is

(1)

where h _i ∈ ℂ^{1 × M}is the complex channel gain vector between the BS and user i, x ∈ ℂ^{M × 1}is the transmitted signal with a total transmit power constraint P, i.e., , and v _i is the complex white Gaussian noise with variance N₀. For analytical convenience, we assume spatially independent Rayleigh fading channels between the BS and the users, i.e., the entries of h _i are i.i.d. , and h _i, i = 1, ..., K are mutually independent. Under the assumption of i.i.d. block fading, h _i is constant in the duration of one block and independent from block to block. By stacking the received signals of all the users into y = [y₁⋯ y _K ] ^T , the signal model is compactly expressed as

(2)

where and v = [v₁v₂ ⋯ v _k ]^T.

In this paper, we focus on the case K = M. If K < M, there will be a loss of multiplexing gain. The case K > M will introduce multi-user diversity gain and we will leave it for future work.

We first give a brief introduction of ZF-DPC under perfect CSIT in this section.

In the ZF-DPC scheme, the BS performs a QR-type decomposition to the overall channel matrix H denoted as H = GQ, where G is an M × M lower triangular matrix and Q is an M × M unitary matrix. We let x = Q^Hd and the components of d are generated by successive dirty-paper encoding with Gaussian codebooks [1], then the resulting signal model with the precoded transmit signal can be written as:

(3)

From Equation 3 the received signal at user i is given by

(4)

where g _ij = [G] _{i, j} and d _i , the i th entry of d, is the output of dirty-paper coding for user i treating the term as the ∑_{j < i}g _ij d _j noncausally known interference signal.

From the total transmit power constraint , we have . If the transmit power is uniformly allocated to each user, i.e., , then for i.i.d. Rayleigh flat fading channel, the closed-form expression of the achievable ergodic sum rate using the ZF-DPC is given by [1, 27]:

(5)

and

(6)

where is the exponential integral function of order n[28].

The multiplexing gain [10] of ZF-DPC under perfect CSIT is M, i.e.,

(7)

which is the full multiplexing gain of the downlink [1, 25].

Achievable rates of ZF-DPC under analog feedback

In this section, we consider the analog feedback (AF) scheme, where each user estimates its downlink channel coefficients and transmits them explicitly on the feedback link without any quantization or coding. In order to focus on the impact of feedback link capacity constraint, we assume perfect CSI at each user's receiver (CSIR), and no feedback delay, i.e., the downlink CSI is fed back instantaneously in the same block as the subsequent downlink data transmission. For ease of analysis, we also impose two restrictions on the transmission strategy: (1) the total transmit power is equally allocated to the users and (2) independent Gaussian encoding is applied for each user at the transmitter side.

In order to compare the impact of different feedback channels for AF scheme, we first consider the AWGN feedback channels from Sections 3.1 to 3.4, then extend the analysis to the Rayleigh fading channels in Section 3.5.

Analog feedback in AWGN feedback channels

The M users estimate and feed back their complex channel coefficients using orthogonal feedback channels. A simplifying assumption of our work is firstly to consider the AWGN feedback channels, i.e., no fading in the feedback links. Each user takes β _fb M (β _fb ≥ 1 and β _fb M is an integer) channel uses to feed back its M complex channel coefficients by modulating them with a group of orthonormal spreading sequences where s _m is a 1 × β _fb M vector and , m = 1, ..., M, ∀ m ≠ n[12]. Then the received signals of the feedback channel from user i over β _fb M channel uses can be written in a compact form:

(8)

where denotes the downlink channel gain from the m th transmit antenna of the BS to user i, the 1 × β _fb M vector with i.i.d. entries each distributed as denotes the additive white Gaussian noise on the feedback channel and SNR _fb represents the average transmit power (and also the average SNR in the feedback channel).

After despreading, the sufficient statistic for estimating h _{i, m} is obtained as written below:

(9)

where n _{i, m} is the equivalent noise distributed as . MMSE estimation is performed to estimate h _{i, m} . We denote the MMSE estimate of h _{i, m} as and the corresponding estimation error as δ_{i, m}. Since , and δ_{i, m}are also circularly symmetric complex Gaussian random variables with zero mean, and their variances are:

(10)

(11)

Moreover, and δ_{i, m}are independent from each other.

The vector quantization scheme using the distortion measure of MSE in [27] leads to the same statistics of the channel error as the AF scheme introduced above, so it is equivalent to the AF scheme. Therefore, the following analysis framework developed for AF can be readily applied to the case studied in [27].

Lower bound on the achievable rate of ZF-DPC with AF in AWGN feedback channels

The BS collects the channel estimates (i, m = 1, ..., M) to form the estimated channel matrix , then simply we have the following relationship between H and :

(12)

where and [Δ]_{i, m}= δ_{i, m}. Obviously, and Δ are mutually independent.

The BS performs ZF-DPC treating the estimated channel matrix as the true one. The QR decomposition of can be written as , where is a lower triangular matrix and is a unitary matrix. The received signal is modeled as:

(13)

From the above equation, we can extract the received signal at user i as listed below:

(14)

where and Δ _i is the i th row of Δ.

We have the following theorem that gives a lower bound on the achievable ergodic rate of ZF-DPC under AF.

Theorem 1. If the downlink channel is i.i.d. Rayleigh fading and the feedback channels are AWGN channels, then the achievable ergodic rate of ZF-DPC with AF is lower bounded as:

(15)

where

Proof. We first consider the lower bound on the achievable rate under given . Recall Equation 14 and introduce three notations: , and . Then we have the following signal model:

(16)

With uniform power allocation among the M users and independent Gaussian encoding , d _i and d _j (i ≠ j) are independent of each other. So x _i and s _i are mutually independent, but n _i is no longer Gaussian and is not independent of x _i , so we cannot directly apply the result of dirty-paper coding in [29] to derive the capacity of this channel.

As s _i is still known at the transmitter, from [30], we know that the achievable rate of this kind of channel can be formulated in the form of mutual information as shown below:

(17)

where u _i is an auxiliary random variable. Let u _i = x _i + αs _i where α is called the inflation factor, then

(18)

where the first "≥" follows from the fact that the entropy is larger than the conditional entropy, and the second "≥" follows from the fact that a Gaussian random variable has the largest differential entropy when the mean and variance of a random variable are given.

Since , we have and h(x _i ) = log₂ (πe · var(x _i )). As and Then we can get

(19)

(20)

Substituting Equation 19 into Equation 18, we have

(21)

Choosing maximizes the right-hand side (RHS) of the inequality in Equation 21, and thus, we get

(22)

The above inequality shows the lower bound on the achievable rate of user i under given . In the following paragraph, we derive closed-form expression for the lower bound on the achievable ergodic rate under fading downlink channel.

Since , can be decomposed as where the entries of are i.i.d. and is a diagonal matrix. Denote the QR decomposition of as , then . Therefore, and where ^. From Lemma 2 in [1] we know that where denotes the central chi-square distribution with 2k degrees of freedom, whose pdf is f(z) = z^{k- 1}e^-z/(k - 1)! Then by taking the means of both sides of the inequality in Equation 22, the achievable ergodic rate of user i is lower bounded as follows:

(23)

where

(24)

and E _j (x) is the exponential integral function of order j. The closed-form expression of the expectation in Equation 23 follows from the results in [31].

Thus, we have completed the proof.

Upper bound on the achievable rate of ZF-DPC with AF in AWGN feedback channels

An upper bound of the achievable rate is derived by assuming a genie who can provide the encoders at the BS and the decoders at the users with some extra information. This upper bound is referred to as the genie-aided upper-bound.

Recall Equation 14 and rewrite it as follows:

(25)

where is the i th column of , and . Assume there is a genie who knows the values of and and tells these values to the encoder and decoder for user i, then with i.i.d. channel inputs , n _i is Gaussian distributed with zero mean and variance and is independent of x _i . Hence the channel for user i in Equation 25 will be recognized as a standard dirty-paper channel and its capacity is log₂ (1 + Var(x _i )/Var(n _i )) [29]. Finally the downlink achievable ergodic rate can be upper bounded by the genie-aided upper bound as given in the following theorem.

Theorem 2. If the downlink channel is i.i.d. Rayleigh fading and the feedback channels are AWGN channels, the achievable ergodic rate of ZF-DPC is bounded by a genie-aided upper-bound as follows:

(26)

It is difficult to derive a closed-form expression for the right-hand side (RHS) in Equation 26, so we use Monte Carlo simulations to obtain this upper bound.

We plot the lower and upper bounds on the achievable ergodic sum rates obtained in Theorems 1 and 2 with fixed feedback-link capacity constraint in Figure 1. We set M = 4, β _fb = 1 and SNR _fb = 10, 15, 20 dB. Achievable rate of ZF-DPC with perfect CSIT is also plotted. An important observation from Figure 1 is that there is a ceiling effect on the achievable rate of ZF-DPC under AF if the feedback-link capacity constraint is fixed, i.e., the achievable rate is bounded as the downlink SNR tends to infinity. This can be explained intuitively that the power of the interference caused by imperfect CSIT always scales linearly with the signal power. A more rigid explanation is given in the following corollary:

Figure 1

Lower and upper bounds on the achievable ergodic sum rate of ZF-DPC with AF in AWGN feedback channels.

Corollary 1. The achievable ergodic rate of ZF-DPC with AF and fixed feedback-link capacity is upper bounded for arbitrary downlink SNR:

(27)

where γ is the Euler-Mascheroni constant [32] and .

The proof of the corollary is in Appendix 1. Although this upper bound is quite loose, it does predict the ceiling effect on the achievable rate with fixed feedback-link capacity.

Achievable downlink multiplexing gain with AF in AWGN feedback channels

From Corollary 1, it is obvious that the downlink multiplexing gain with fixed feedback-link capacity is zero. In order to maintain a nonzero multiplexing gain, the feedback channel quality should improve at some rate as the downlink SNR increases, which is given in detail in the following theorem:

Theorem 3. For AF and AWGN feedback channels, and β _fb SNR _fb scales as , then a sufficient and necessary condition for achieving the multiplexing gain of M (0 < b₀ < 1) is that b = b₀; a sufficient and necessary condition for achieving the full multiplexing gain of M is that b ≥ 1. Moreover, for b > 1, the asymptotic rate gap between the achievable rate of ZF-DPC with perfect CSIT and that under AF is zero as the downlink SNR goes to infinity.

The proof of the theorem is in Appendix 2. Figure 2 illustrates the conclusions in Theorem 3. We set M = 4, β _fb = 1, a = 0.5 and b = 0.5, 1 and 1.5. The curves coincide with the analytical results in Theorem 3. Note that increasing the value of a can further reduce the rate gap between the perfect CSIT case and the AF case.

Figure 2

Illustration of the achievable downlink multiplexing gain of ZF-DPC with AF in AWGN feedback channels.

Achievable rates and multiplexing gain with AF in Rayleigh fading feedback channels

In this subsection, we will further consider the effects of Rayleigh fading feedback channels to the achievable rates and multiplexing gain with AF. From Equation 11, we notice that D _i is the function of the feedback channel . If the feedback channel is a fading channel, then D _i will become a random variable and thus the lower bound we have obtained in Equation 15 is also random. So we need to take the mean of the RHS of the inequality in Equation 15 with respect to to get the new lower bound for the fading feedback channel case.

First, we introduce a lemma to help us derive the lower bound.

Lemma 1. f(x) = e^xE _n (x) (n ≥ 1) is a convex and monotonically decreasing function.

The proof of this lemma is in Appendix 3. Then we have the following closed-form lower bound on the downlink achievable ergodic rate in the Rayleigh fading feedback channels.

Theorem 4. If both the downlink channel and the feedback channels are i.i.d. Rayleigh fading, then the achievable ergodic rate of ZF-DPC with AF and uniform power allocation is lower bounded as:

(28)

where

(29)

Proof: Taking the mean of the RHS of the inequality in Equation 15 with respect to , we get the lower bound for fading feedback channel:

(30)

where . The second "≥" in Equation 30 follows from Lemma 1 and the Jensen inequality for convex functions.

Substituting Equation 11 into Equation 24, we have the following expression for β _i :

(31)

Given that the entries of are i.i.d. , we have . Then γ _i can be calculated in a closed form:

(32)

This finishes the proof.

The upper bound of the achievable ergodic rate with fading feedback channels can also be derived from Equation 26 as the following corollary, and simulations are still needed to calculate the upper bound:

Corollary 2. The achievable ergodic rate of ZF-DPC with AF and Rayleigh fading feedback channels is upper bounded for arbitrary downlink SNR:

(33)

where γ is the Euler-Mascheroni constant.

The proof is similar to that of Corollary 2 and thus omitted due to the page limit. From this corollary, we also have the observation for the fading feedback channel that when the downlink SNR goes to infinity while keeping the parameters of the feedback channel constant, there is also a ceiling effect on the achievable ergodic rate of ZF-DPC.

Figure 3 illustrates the lower and upper bounds on the achievable ergodic sum rates of ZF-DPC with AF in Rayleigh fading feedback channels. We set M = 4, SNR _fb = 5, 10, 15 dB. The curves verify the analytical results in Theorem 4 and Corollary 2.

Figure 3

Lower and upper bounds on the achievable ergodic sum rate of ZF-DPC with AF in Rayleigh fading feedback channels.

Figures 4 and 5 compare the achievable ergodic sum rates between ZF-DPC and ZF-BF schemes, in which we set M = 4, β _fb = 1. In Figure 4, the achievable rates under fixed SNR _fb = 5 dB and SNR _fb = 15 dB are compared for ZF-DPC and ZF-BF schemes over different downlink SNR P/N 0, respectively. Here, the achievable ergodic sum rates of ZF-BF are obtained by Monte Carlo simulations as in [19]. From Figure 4 it can be seen that the ZF-DPC can outperforms the ZF-BF in terms of achievable rates at the same settings of feedback channels. Figure 5 shows the achievable rates comparison under fixed downlink SNR P/N₀ = 20 dB, from which the same conclusion can be drawn as Figure 4 shows.

Figure 4

Achievable rate comparison between ZF-DPC and ZF-BF with AF in Rayleigh fading feedback channels-I: fixed SNR _fb .

Figure 5

Achievable rate comparison between ZF-DPC and ZF-BF with AF in Rayleigh fading feedback channels-II: fixed P/N ₀ = 20 dB.

From Corollary 2 we can see that the upper bound also tends to a constant. So the multiplexing gain is zero, which is the same as the AWGN feedback channel case. In order to maintain a multiplexing gain of M, the SNR of the feedback channel should scale with the downlink SNR, as shown in the following corollary:

Corollary 3. For AF and i.i.d. Rayleigh fading feedback channel, let β _fb SNR _fb scales as , a, b > 0, then if b ≥ 1, the multiplexing gain of the downlink will maintain as M;

if b < 1, the multiplexing gain of at least bM can be achieved. Moreover, for b > 1, the asymptotic rate gap between the achievable rate of ZF-DPC with perfect CSIT and that under AF is zero as the downlink SNR goes to infinity.

The proof is quite similar to that of Theorem 3 and thus omitted here for brevity. We also notice that the results are the same as those for AWGN feedback channels, so no more simulation results are given here.

Achievable rates of ZF-DPC under digital feedback

We now consider digital feedback (DF), where the downlink CSI are estimated and quantized into several bits using a vector quantization codebook at each user and the quantization bits are fed back to the BS. The feedback channel is assumed to be capacity-constrained and error-free, i.e., as long as the number of feedback bits does not exceed the feedback-link capacity in terms of the maximum feedback bits per fading block, the feedback transmission will be error-free [23]. We also assume perfect CSIR and no feedback delay as in Section 3. Moreover, the same restrictions are imposed on the transmission strategy as in Section 3.

Digital feedback

The downlink channel vector h _i of user i can be expressed as , where is the amplitude of h _i and is the direction of h _i. Under the assumption that the entries of h _i are i.i.d. , we have and is uniformly distributed on the M dimensional complex unit sphere [24]. Moreover, λ _i and are independent of each other [24].

The Random Vector Quantization (RVQ) [24, 25] is adopted in our analysis due to its analytical tractability and close performance to the optimal quantization. The quantization codebook is randomly generated for each quantization process, and we analyze performance averaged over all such choices of random codebooks, in addition to averaging over the fading distribution. At the receiver end of user i, is quantized using RVQ. First, a random vector codebook is generated for user i by selecting each of the N vectors independently from the uniform distribution on the M dimensional complex unit sphere, i.e., the same distribution as . The codebooks for different users are also independently generated to avoid the case that multiple users quantize their channel directions to the same quantization vector. The BS is assumed to know the codebooks generated each time by the users. Then the code vector that has the largest absolute square inner product with is picked up as the quantization result, mathematically formulated as follows:

(34)

Then the B = log₂N quantization bits are fed back to the BS.

We note that Equation 34 is actually based on the distortion measure of the angle between the codevector and the downlink channel vector, which is equivalent to (2) in [25] and (51) in [21]. It is obviously different from the distortion measure of MSE adopted in [27]. We also find out that the MSE distortion measure in [27] is similar to the distortion measure (Equation 12) used in AF in our work; therefore, the analysis based on MSE distortion measure in [27] can be easily incorporated into our AF analysis framework.

Define and , then we introduce two lemmas that are useful for further discussion.

Lemma 2. [24]: The cumulative distribution function of ν _i is

(35)

Lemma 3. [33]: θ _i is uniformly distributed in the interval (-π, π] and independent from ν _i .

In the next subsection, we will find that the information of θ _i is necessary for phase compensation at user i's receiver. Therefore, we need to store the value of θ _i at user i's receiver. Notice that the norm information of the channel vectors is not conveyed to the BS.

Lower bound on the achievable rate of ZF-DPC with DF

Under the assumption that the feedback channel is error free, the B bits conveyed by each user can be received by the BS correctly. The BS reconstructs the quantized channel vector using the B bits fed back from user i and treats as the true channel vector. Then the BS performs ZF-DPC using the reconstructed channel matrix as did in Section 3.2. The QR decomposition of can be written as , where is a lower triangular matrix and is a unitary matrix. The received signal is modeled as:

(36)

where is a diagonal matrix, and .

At each user's receiver, a phase compensation operation is carried out by multiplying to the received signal of user i, written in a compact form as follows:

(37)

where is a diagonal matrix, has the same statistics as v.

Denote , then we can rewrite it in a compact form, i.e., , where . Equation 37 can be rewritten as:

(38)

From the above equation we can extract the received signal at user i as listed below:

(39)

We first give three lemmas useful for deriving the lower bound of the achievable rate of ZF-DPC under DF.

Lemma 4. .

Lemma 5. in which

(40)

where N = 2 ^B , and .

Lemma 6. f(x) = e^xE _n (x) (n ≥ 1) is a monotonically decreasing function.

The proofs of these three lemmas are in Appendices 4-6, respectively. Then we have the following theorem on the lower bound of the achievable ergodic rate of ZF-DPC under DF.

Theorem 5. If the downlink channel is i.i.d. Rayleigh fading and the feedback channels are error-free, then the achievable ergodic rate of ZF-DPC with DF is lower bounded as:

(41)

where ψ(x) is the Euler psi function [28] and is given in Lemma 5.

Proof: Since λ _i is known by the receiver of user i, the signal model in Equation 39 can be transformed into:

(42)

where and . Using the same methodology as in Section 3.2, we arrive at the following inequality for the downlink achievable rate of user i under fixed and Λ:

(43)

With Gaussian inputs and uniform power allocation, , then .

In the digital feedback scheme, the channel norm information is not conveyed back to the BS, i.e., λ _i is not known at the BS, so we are not able to adjust α according to Var(x _i ) and Var(n _i ). We just simply choose α = 1, then is lower bounded by:

(44)

Since , then

(45)

Substituting Equation 45 into Equation 44 we finally get the following lower bound under fixed and Λ:

(46)

Based on the above results, we can derive the lower bound for the achievable ergodic rate in the Rayleigh fading downlink channel. Taking the mean of both sides of the inequality in Equation 46, we have

(47)

where the second "≥" follows from the Jensen inequality of the concave function.

From Lemma 4, we can calculate the closed-form expression for :

(48)

where ψ(x) is the Euler psi function [28].

Since , the closed-form expression for the third term in Equation 47 can be calculated as shown below:

(49)

where the closed-form expression of has been obtained in Lemma 5.

Substituting Equations 48 and 49 into Equation 47, we finally get the conclusion.   ■

Remark: From the above theorem and the monotony of e^xE _n (x) shown in Lemma 6, we can see that decreasing will raise the lower bound on the achievable rate. Now we give an explanation on the necessity of the phase compensation operation at each receiver. In the absence of the phase compensation, the channel error vector would be . Then

(50)

From Lemma 3, θ _i is independent from ν _i and , then

(51)

and thus, the same lower bound remains no matter how many bits are used to quantize . Therefore, the information of θ _i and phase compensation plays an important role in the DF scheme, which is different from the case in [25] where no phase compensation is needed.

Upper bound on the achievable rate of ZF-DPC with DF

The upper bound on the achievable rate of ZF-DPC with DF can be obtained in a similar way as in Section 3.3.

Recall Equation 42 and rewrite it as follows:

(52)

where is the i th column of , and . We also assume there is a genie who knows the values of λ _i , and , then following the methodology in Section 3.3, we can see that the channel for user i is also recognized as a standard dirty-paper channel. Therefore, the downlink achievable ergodic rate can be upper bounded by the genie-aided upper bound as shown below:

Theorem 6. The achievable ergodic rate of ZF-DPC with DF is bounded by a genie-aided upper-bound, i.e.,

(53)

Simulations are also necessary to calculate the upper bound given in Theorem 6.

The lower and upper bounds on the achievable ergodic sum rate obtained in Theorems 5 and 6 with fixed feedback-link capacity constraint are plotted in Figure 6. We set M = 4 and calculate three groups of curves where the number of feedback bits per user, i.e., B, is 12, 16 and 20, respectively. Achievable rate of ZF-DPC with perfect CSIT is also plotted. The curves in Figure 6 reveal the ceiling effect on the achievable rate which is just the same as the AF case.

Figure 6

Lower and upper bounds on the achievable ergodic sum rate of ZF-DPC with DF in error-free feedback channels.

From Theorem 6, we also derive a closed-form upper bound for the achievable rate with DF as shown below.

Corollary 4. The achievable ergodic rate of ZF-DPC with DF and a fixed number of feedback bits per user B is upper bounded for arbitrary downlink SNR:

(54)

The proof is similar to those of Corollaries 1 and 2, and thus omitted due to the page limit. Although this upper bound is quite loose, it does also predict the ceiling effect on the achievable rate with fixed feedback bits per user.

Achievable downlink multiplexing gain with DF

The multiplexing gain of the downlink with DF and fixed feedback bits per user is zero due to the ceiling effect. In order to maintain nonzero multiplexing gain, the feedback bits per user should scale with the downlink SNR. With Theorem 5 and Corollary 4, we can derive the following sufficient and necessary conditions on the scaling to ensure nonzero and full multiplexing gain:

Theorem 7. For DF and error-free feedback channels, assume that the number of feedback bits per user scales according to:

(55)

then we have the following conclusions:

• (1) A sufficient and necessary condition for achieving the downlink multiplexing gain of α ₀ M (0 < α ₀ < 1) is that α = α ₀.

• (2) A sufficient and necessary condition for achieving the full downlink multiplexing gain of M is that α ≥ 1.

• (3) If α > 1, then

  

  (56)

The proof of Theorem 7 is similar to that of Theorem 3 and thus omitted due to the page limit here. Note that the same conclusion has been drawn for ZF-BF in [25]. Figure 7 illustrates the conclusions in Theorem 7. We set M = 4 and α = 0.5, 1, 1.5. The curves coincide with the analytical results in Theorem 7.

Figure 7

Illustration of the achievable downlink multiplexing gain of ZF-DPC with DF in error-free feedback channels.

Comparison of AF and DF

In order to compare DF with AF, we need to relate the number of feedback bits B per user with SNR _fb and the number of channel uses in the feedback link, or equivalently β _fb . In this paper, we make an idealistic assumption that the AWGN feedback link can operate error-free at its capacity, i.e., it can reliably transmit log2 (1 + SNR_fb) bits per channel use. This assumption describes the maximum possible number of bits that can ever be conveyed correctly through the AWGN feedback channel. In [21], the authors have pointed out that for fair comparison, β _fb M feedback channel uses in AF should correspond to β _fb (M - 1) feedback channel uses in DF, since no channel norm information is fed back in DF and a system using DF could use one feedback channel symbol to transmit the norm information. Thus, the number of feedback bits per user in the AWGN feedback channel is B = β _fb (M - 1) log₂ (1 + SNR_fb).

Now we can make a comparison about the performance of AF and DF. Assume for DF, the feedback bits per user scale as , then from Theorem 7, we know that the multiplexing gain of M can be achieved. Using the relationship between B and SNR _fb obtained above, we can derive the connection of SNR _fb to the downlink SNR:

(57)

Then from Theorem 3, we can see that as long as β _fb > 1, only a multiplexing gain of less than M can be achieved for AF. This means the DF scheme is asymptotically superior to the AF scheme when β _fb > 1. Figure 8 compares the achievable rates under AF and DF for β _fb = 1 and 2. As analyzed above, the asymptotic performance of DF is superior to AF when β _fb = 2. The conclusion is, however, somewhat optimistic since we assume the AWGN feedback channel can operate error-free at its capacity. The true performance of DF may degrade when some specific coding scheme is used. A thorough comparison when using practical coding schemes for DF, such as uncoded QAM modulation discussed in [21], is for future work.

Figure 8

Comparison of AF and DF with β _fb = 1 and 2.

Conclusion and future work

We have investigated the performance of ZF-DPC in the multiuser MIMO downlink of a FDD system where the CSIT is obtained through capacity-constrained feedback channels. Two CSI feedback schemes, i.e., the analog and digital feedback schemes, are considered in our work. Closed-form expressions for lower and upper bounds on the achievable ergodic rates of ZF-DPC with Gaussian inputs and uniform power allocation are derived. Based on the closed-form rate bounds, sufficient and necessary conditions on the feedback channels to ensure nonzero and full downlink multiplexing gain are obtained. Our primary results show that for AF in both AWGN and Rayleigh fading feedback channels, it is both sufficient and necessary to scale the average feedback link SNR linearly with the downlink SNR in order to achieve full downlink multiplexing gain. While for the RVQ-based DF with angle distortion measure in an error-free feedback link, it is both sufficient and necessary to scale the feedback bits per user as where M is the number of transmit antennas and 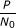is the average downlink SNR.

We also mention that there are several issues not considered in our current work. In this paper, we have assumed perfect CSI at the users' receivers. In a practical system, however, there are always channel estimation errors due to finite number of training symbols, which will further degrade the performance of ZF-DPC. The impact of the feedback delay of the downlink CSI on the achievable rates is also not considered, which could be significant when the downlink channel is fast fading. For DF scheme, we apply the RVQ for quantization of the channel vector in order to make the analysis easier. Generalization to arbitrary vector quantization codebooks is an interesting issue and we expect the same conclusions could be drawn. In the analysis of DF scheme, we made an optimistic assumption that the AWGN feedback link can operate error-free at its capacity. This assumption can be removed by considering practical feedback transmission schemes, such as the uncoded QAM modulation discussed in [21]. Throughout the paper, we have assumed that the number of users is equal to the number of transmit antennas. We conjecture that when the number of users is larger than that of transmit antennas and we properly design the user selection scheme, the feedback link quality (average feedback SNR for AF and the number of feedback bits for DF) per user could be less stringent while keeping the same performance. Finally, the analysis of the achievable ergodic rates are carried out with the restrictions of Gaussian inputs and uniform power allocation. Determining whether Gaussian input is optimal and the optimal power allocation scheme under imperfect CSIT is a challenging problem.

Appendix 1: Proof of Corollary 1

From Theorem 2 we have:

From the proof of Theorem 1, we know that

(A-2)

Since Δ is independent of , Δ _i is also independent of and , so

(A-3)

As for the term , because the entries of Δ _i are i.i.d. as and , we have and thus where . Then we have:

(A-4)

where γ is the Euler-Mascheroni constant [32]. Substituting Equations A-2, A-3 and A-4 into Equation A-1, we arrive at the conclusion.

Appendix 2: Proof of Theorem 3

Sufficient Condition

Denote the RHS of the inequalities in Theorem 1 and Corollary 1 as and respectively, then we have:

(B-1)

Let , a, b₀ > 0. Then the expression of β _i is expanded as:

(B-2)

Then we can find out that if 0 < b₀ < 1 and β _i ~ O(N₀/P) if b₀ ≥ 1.

We now introduce two results about the exponential integral functions in [34]:

(B-3)

(B-4)

where γ is the Euler-Mascheroni constant. From Theorem 1 and Equations B-3 and B-4, the lower bound of will have the following asymptotic behavior:

(B-5)

Therefore,

(B-6)

From Corollary 1 we have:

(B-7)

Substitute Equations B-6 and B-7 into Equation B-1 and notice that the downlink multiplexing gain cannot exceed M, then the following holds:

(B-8)

For the case b₀ > 1, the following holds:

(B-9)

Therefore, the asymptotic rate gap, i.e., the limit of is:

(B-10)

Necessary Condition

If where 0 < b₀ ≤ 1, then

(B-11)

Let , a, b > 0. From Equations B-6, B-7 and B-11, we have min(b, 1) ≤ b₀ ≤ b. So for the case 0 < b₀ < 1, we have b ≤ b₀ ≤ b and thus b = b₀; while for the case b₀ = 1, we have b ≥ 1.   ■

Appendix 3: Proof of Lemma 1

Using the fact that [28], we can calculate the first-order derivative as shown below:

(C-1)

Using the definition of E _n (x), we can expand the term E _n (x) - E_{n - 1}(x) as:

(C-2)

And thus f'(x) < 0 which indicates that f(x) = e^xE _n (x) is a monotonically decreasing function.

Further, the second-order derivative is calculated as follows:

(C-3)

Since f"(x) > 0, we can conclude that f(x) is convex.   ■

Appendix 4: Proof of Lemma 4

Since we use RVQ, has the same distribution as , i.e., . Therefore, , i.e., the entries of are i.i.d. . Note that is the QR decomposition of where is a lower triangular matrix and is a unitary matrix. Since is the i th diagonal element of , then from [1] we can conclude that .

Appendix 5: Proof of Lemma 5

From the definition of Δ _i, we have

(E-1)

where ℜ(·) stands for the real part of a complex number. We also have

(E-2)

Therefore, the following holds:

(E-3)

Using Lemma 2, we can derive the closed-form expressions for as follows:

(E-4)

Let x = 1 - ν, then

(E-5)

(1 - x^{M - 1}) ^N can be expanded as . Moreover, we have the following integral [28]:

(E-6)

Substituting the above results into Equation E-4, we finally get

(E-7)

Thus, we have completed the proof.   ■

Appendix 6: Proof of Lemma 6

Using the fact that [28], we can calculate the first-order derivative as shown below:

(F-1)

Using the definition of E _n (x), we can expand the term E _n (x) - E_{n - 1}(x) as:

(F-2)

So f'(x) < 0 which indicates that f(x) = e^xE _n (x) is a monotonically decreasing function.