- Research
- Open access
- Published:
A utility-based approach for secondary spectrum sharing
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 32 (2011)
Abstract
This paper provides a social welfare framework for coexistence of secondary users of spectrum in the presence of static primary users. We consider a formulation that captures spatial differences in available spectrum while considering general system topologies and utility functions: a collection of wireless sessions is considered under an arbitrary conflict graph that indicates the sessions which cannot transmit simultaneously on a common channel. It is assumed that each session has a utility associated with its spectrum utilization. A carrier sense multiple access-based randomized channel selection technique is considered to maximize the resulting sum of utilities. A measurement-based gradient ascent method is used to improve the channel selection performance and to achieve local maxima of the social welfare. Distributed versions of the method are discussed and shown to outperform previously published work in a variety of simulation scenarios that study effects of primary user presence, varying secondary user density, varying total channel availability.
1 Introduction
Recent regulatory proceedings in wireless telecommunications offer tremendous potential for efficient spectrum usage via novel operational models of spectrum access. An important legislative development in the US, for an example, is the FCC's recent release [1] of a part of VHF/UHF band for fixed broadband access systems to address the problem of spectrum scarcity. This development introduces the concept of secondary spectrum users that are allowed to use the spectrum while avoiding conflicts with primary users, which, in this particular case, are TV broadcast services. Similar primary - secondary usage scenarios are also likely to arise due to regulatory reforms that grant full property rights to spectrum licensees, thereby allowing them to provide services in secondary markets.
While isolation of primary users is challenging due to the cognitive capabilities imposed on the secondary users, yet another technical challenge arises in how the available spectrum can be shared among secondary users. This latter issue is closely related to the concept of wireless coexistence. However, it poses further complications due to the spatial variability of available spectrum in the presence of primary users, and due to possible heterogeneity of secondary users. Resolution of spectrum access can be addressed by cooperative techniques that are based on coordinative messaging, or by non-cooperative techniques that are based on an etiquette [2]. The former approach requires over-the-air messaging or exchange through a backhaul network and it is suitable for homogenous systems. Examples of this approach can be found in [3] that describes a distributed handshake mechanism to share time-spectrum blocks, and in [4, 5] that propose spectrum sharing techniques for OFDM-based air interfaces. In addition, self-coexistence in the IEEE 802.16 WiMax standard [6] and the developing cognitive radio-based IEEE 802.22 standard [7] are based on this approach. Such protocols require tight network synchronization and capability of direct message exchange between parties to coordinate spectrum sharing activities. These assumptions do not hold for heterogeneous systems of technologically incompatible spectrum users. In heterogeneous systems treating all interference as noise or applying a listen-before-talk (LBT) technique are often the only available options for spectrum sharing [8].
A common goal in distributed channel selection is to achieve minimal collaborative communication among secondary users. A game-theoretic view-point is employed in [9, 10] to address the problem of non-cooperative multi-radio channel allocation. Chen et al. [11] employ distributed interference measurements to improve overall network throughput amid limited cooperation. Seferoglu et al. [12] elaborate on a slotted Aloha model to implement a dynamic decentralized multi-channel multiple access algorithm. Opportunistic spectrum access is studied in [13] to minimize the collisions between cooperating secondary spectrum users and non-cooperating primary users. Bao et al. [14] present collision-free mechanism for distributed channel access based on local neighborhood discovery.
It is well-recognized that in spatially dispersed systems channel selection is closely related to graph coloring. This abstraction relies on representing possible conflicts in spectrum access via a graph and interpreting each channel as a distinct "color" [15]. Earlier work [16] analyzes channel assignment problem as a graph coloring problem for special topologies. Computational complexity of such application of graph coloring problem is addressed in [17–19], where distributed coloring algorithms are introduced that do not guarantee optimal coloring but can be applied in a decentralized manner.
The coloring approach is overly rigid for cognitive radio systems for two main reasons: (1) presence of primary users lead to variability of available colors for each secondary user, and therefore suggests list coloring problems that are generally harder than graph coloring, and (2) if secondary users are not active continuously, assigning each user a dedicated channel may lead to considerable inefficiency. In that case, channels can be time-shared among multiple conflicting users, and it is natural to seek a basis to determine the allocation among different users, and mechanisms to implement such an allocation.
In this work, we adopt a utility-based perspective to determine channel allocations in systems of general topology, and a combination of randomized channel selection and carrier sense multiple access (CSMA)-based techniques to implement such allocations. CSMA has been considered by Ni et al. [20], Jiang and Walrand [21], and Marbach and Eryilmaz [22] in similar settings but for systems that have a single common channel. The main goal in the single channel case is to tune backoff timers of users so as to achieve throughput optimality. In setting of this paper, the additional optimization dimension due to multiple channels will be shown to lead a nontrivial problem. We will address that problem by fixing the backoff rates but dynamically tuning certain channel access probabilities.
In related work, randomized channel access techniques were considered in similar settings by Leith and Clifford [23] and Kauffmann and Bacelli [24]. The mechanism presented in [23] ensures that a successful channel choice remains unchanged and provides a distributed algorithm that converges to dedicated channel assignments with no conflicts, provided such assignment is feasible. Yet, performance of the algorithm remains unclear if the number of available channels is less than the chromatic index of the conflict graph. In [24], a distributed Gibbs-sampling methodology is employed to optimize the channel selection probabilities, where each user autonomously updates its operating channel based on interference measurements on all available channels.
The contribution of the present paper is: (1) a utility-based formulation of spectrum sharing among secondary users is presented. The formulation accounts for the presence of static primary users, and provides a spectrum allocation principle that is applicable to all system topologies and channel availabilities. (2) a CSMA-based dynamic channel selection technique is presented as an implementation of the solution. The channel selection technique is a gradient ascent method to adaptively converge to local maxima of the utility function. Distributed versions of the method are discussed and justified. (3) extensive numerical experiments indicate that the presented method outperforms the existing algorithms significantly in a variety of considered scenarios. These experiments address the issues of primary user presence, varying secondary user density, and varying total channel availability.
The rest of this paper is organized as follows: Section 2 provides the considered model of secondary spectrum usage and formulates a social welfare optimization problem that is based on channel utilizations of involved parties. This problem is re-parameterized in Section 3 in a manner that is suitable for CSMA-based randomized channel access methods. Although the original problem is convex, the re-parameterization is not, and local maxima of the latter problem are also characterized in this section. Section 4 provides a novel gradient ascent algorithm to improve the randomized channel access towards local maxima, and it identifies distributed approximations of these algorithms. A detailed numerical and comparative study of the proposed principles are provided in Section 5. The paper concludes with final remarks in Section 6.
2 Utility-based spectrum sharing
We consider a system of M wireless sessions that interact through the interference they generate on each other. This system is represented by an undirected graph G = (V, E) where V is the set of nodes and E is the set of edges. Each node in G represents a wireless session; hence, there are exactly M nodes in V. An edge in G indicates that its incident nodes correspond to sessions that interfere with each other due to geographical proximity of transmitters and receivers. This results in the operational constraint that two such sessions cannot actively use a narrowband channel at the same instant.
We shall consider that coexistence of M wireless sessions on a spectrum band comprised C narrowband channels. Generally, only a subset of these channels may be available to each session. This scenario implicitly reflects the presence of primary users that hold channels on a static basis: for example, a TV broadcast in the vicinity of a given session renders a number of channels unavailable for that session, while these channels may be available to far away sessions. Let  denote the entire set of channels available in the shared spectrum band. We shall further denote the set of channels available to node i by
denote the entire set of channels available in the shared spectrum band. We shall further denote the set of channels available to node i by  . In visualizing the interference relations for each channel c ∈ {1, 2,..., C}, it may be helpful to consider the subgraph Gc (V c , Ec ) that is induced by nodes i for which channel c is available. Figure 1 illustrates these subgraphs for a sample topology with a total of C = 3 channels. The scope of this paper is general and no assumptions are imposed on the subgraphs Gc . To avoid trivialities we focus on the case in which there is at least one channel available for each node. We shall also assume that each node can transmit on one channel at a time.
. In visualizing the interference relations for each channel c ∈ {1, 2,..., C}, it may be helpful to consider the subgraph Gc (V c , Ec ) that is induced by nodes i for which channel c is available. Figure 1 illustrates these subgraphs for a sample topology with a total of C = 3 channels. The scope of this paper is general and no assumptions are imposed on the subgraphs Gc . To avoid trivialities we focus on the case in which there is at least one channel available for each node. We shall also assume that each node can transmit on one channel at a time.
Illustration of an interference graph G with six nodes and three channels. (a) Nodes of G(V, E) are connected if their transmissions conflict on the same channel. Not all channels are available to all nodes, due to presence of static primary users. The interferences graphs associated with each one of the three channels: (b) G1(V1, E1), (c) G2(V2, E2), (d) G3(V3, E3).
For each node i ∈ V and channel  we define the quantity
we define the quantity  as
as

With this definition, it follows that the sum  is the fraction of time that session i accesses the entire spectrum, or equivalently, it is the spectrum utilization of session i.
is the fraction of time that session i accesses the entire spectrum, or equivalently, it is the spectrum utilization of session i.
The numbers  depend on the adopted channel allocation scheme that determines how the spectrum is shared among the M sessions. However, they have three invariant properties:
depend on the adopted channel allocation scheme that determines how the spectrum is shared among the M sessions. However, they have three invariant properties:
-
1.
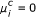 if
if  ; since channel c is then not available to session i.
; since channel c is then not available to session i. -
2.
 ; since a node can transmit only on one channel at a time.
; since a node can transmit only on one channel at a time. -
3.
For each channel, c let
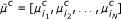 where i 1, i 2,..., i
N
represent the nodes in the subgraph Gc . That is, i 1, i 2,..., i
N
are the nodes for which channel c is available. Let
where i 1, i 2,..., i
N
represent the nodes in the subgraph Gc . That is, i 1, i 2,..., i
N
are the nodes for which channel c is available. Let 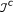 denote the collection of independent setsa of the subgraph Gc , and let co
denote the collection of independent setsa of the subgraph Gc , and let co  denote the convex hull of (i.e. all convex combinations of the elements in) the set
denote the convex hull of (i.e. all convex combinations of the elements in) the set 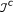 . Then
. Then 
This property is inherited from single-channel systems and it can be verified from [21].
In this paper we consider spectrum sharing so as to achieve channel access rates  that solve the following optimization problem:
that solve the following optimization problem:

Here each, U i is a generic utility function and the sum of the utility functions amount to social welfare. Particular choice of the utility functions is dictated by the specific criteria adopted in spectrum sharing. For example, choosing U i (x) = x amounts to maximization of total spectrum utilization in the entire system. Achieving this goal may require starving some of the sessions. If fairness is also a criterion in addition to efficiency, then the utility functions can be chosen strictly concave, such as U i (x) = log(x).
The objective function  is concave in
is concave in  , and the constraints of Problem STATIC identify a convex domain for
, and the constraints of Problem STATIC identify a convex domain for  . Therefore, the problem can be solved using standard optimization methods and optimal
. Therefore, the problem can be solved using standard optimization methods and optimal  can thereby be obtained. However, such a solution is descriptive rather than prescriptive: it characterizes, the optimal spectrum utilizations for sessions but it does not offer a dynamic perspective that can serve as a basis to develop MAC layer algorithms that achieve such optimality. In the following section, we consider a re-parametrization of this problem that provides insight on dynamics of optimal, CSMA-based medium access algorithms.
can thereby be obtained. However, such a solution is descriptive rather than prescriptive: it characterizes, the optimal spectrum utilizations for sessions but it does not offer a dynamic perspective that can serve as a basis to develop MAC layer algorithms that achieve such optimality. In the following section, we consider a re-parametrization of this problem that provides insight on dynamics of optimal, CSMA-based medium access algorithms.
3 CSMA-based utility optimization
CSMA is a fundamental medium access method that is built on the concept of listen-before-transmit. In this concept, a transmitter probes the medium at locally determined instances. Probing the medium entails detecting the possible ongoing transmission activity by other sessions. If there is such activity, then transmission is deferred, otherwise a packet is transmitted. In either case, the channel is probed at a later instant under the same rules.
In the present setting, we shall consider the case when each node adopts CSMA for medium access and probes the spectrum at random times. It is assumed that each node i probes the spectrum r
i
> 0 times per second, on average. The node also maintains a probability vector  that determines which channel to probe at each probing instant. Here it is understood that
that determines which channel to probe at each probing instant. Here it is understood that  only if channel c is available to node i; that is, only if
only if channel c is available to node i; that is, only if 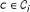 . Our goal in this e ort is twofold: (1) to identify optimal probability vectors p
i
for all nodes i, to maximize the social welfare objective, and (2) to characterize dynamic algorithms that update these probability vectors so as to drive them towards their optimal values in time. To keep the focus on the multi-channel aspect of the problem, we shall assume that propagation delays are negligible and that no hidden terminals exist.
. Our goal in this e ort is twofold: (1) to identify optimal probability vectors p
i
for all nodes i, to maximize the social welfare objective, and (2) to characterize dynamic algorithms that update these probability vectors so as to drive them towards their optimal values in time. To keep the focus on the multi-channel aspect of the problem, we shall assume that propagation delays are negligible and that no hidden terminals exist.
A flow chart of the medium-access algorithm at (the transmitter of) each node is sketched in Figure 2. Here, we assume that transmitters have infinite backlog of packets so that they transmit whenever they probe an idle channel. Transmission of a packet may take certain time that may be different from packet to packet. Each node sets up a timeout upon completing transmission of a packet or upon sensing another transmission on the probed channel. At the expiration of the timeout, the node randomly chooses a channel 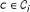 according to the probability distribution
according to the probability distribution  Then, the transmitter senses the chosen channel c and immediately starts transmission of a packet if none of the neighbors currently use this channel. Otherwise, the transmitter backs off until another timeout expires.
Then, the transmitter senses the chosen channel c and immediately starts transmission of a packet if none of the neighbors currently use this channel. Otherwise, the transmitter backs off until another timeout expires.
We shall analyze the resulting system-wide behavior using Markovian models. Towards this end, we impose the following statistical assumptions on packet transmission times and on timeouts: (1) transmission time of each packet is exponentially distributed with mean 1, and (2) each timeout period at node i is exponentially distributed with mean  . We shall assume that packet transmission times and timeout values are independent random variables. This assumption implies that each node i probes the medium at instants of a Poisson clock with rate r
i
.
. We shall assume that packet transmission times and timeout values are independent random variables. This assumption implies that each node i probes the medium at instants of a Poisson clock with rate r
i
.
Let us proceed further with describing the possible states of the overall system. Let  be the binary value that is defined as
be the binary value that is defined as

Clearly,  is a binary random process whose value fluctuates according to the probing decisions taken by nodes. For a fixed choice of probability distributions p
i
, i ∈ V, the collection of all such binary variables
is a binary random process whose value fluctuates according to the probing decisions taken by nodes. For a fixed choice of probability distributions p
i
, i ∈ V, the collection of all such binary variables  is an ergodic Markov process. The state space of this process is S
G
where
is an ergodic Markov process. The state space of this process is S
G
where

A closer inspection of S
G
yields that for each channel c the vector  of transmission activity on channel c is an independent set of Gc .
of transmission activity on channel c is an independent set of Gc .
We define the parameter P= {p1, p2,..., p M } as the collection of all individual probability distributions adopted at different nodes. For a fixed choice of probability distributions P, we denote the equilibrium distribution of the process s by π. Standard state-space truncation arguments [25] can be employed to determine an explicit expression for π for any state s∈ S G . Namely,

Note that expected fraction of time a node i transmits on channel 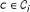 can be expressed in terms of π as:
can be expressed in terms of π as:

The equilibrium probability  is the fraction of time node i transmits on channel c, measured over a time interval that is long enough to allow the process s to settle to equilibrium. In turn, it can be obtained through sufficiently long measurements of channel utilization by every node for every available channel. We shall use
is the fraction of time node i transmits on channel c, measured over a time interval that is long enough to allow the process s to settle to equilibrium. In turn, it can be obtained through sufficiently long measurements of channel utilization by every node for every available channel. We shall use  as a proxy to
as a proxy to  , and thereby re-parametrize Problem STATIC in terms of P. This gives rise to Problem OPT that is defined as:
, and thereby re-parametrize Problem STATIC in terms of P. This gives rise to Problem OPT that is defined as:

3.1 Necessary conditions for optimality in OPT
While the objective of Problem STATIC is concave in  , the objective of Problem OPT is not necessarily concave in P. Perhaps the easiest way to verify this is to consider the case when G has two nodes connected by an edge, and there are C = 2 channels both of which are available to the two nodes. As each utility function U
i
(·) is increasing, it follows that W (P) is maximized if P is such that the two nodes deterministically choose different channels at all times. That is, choosing either p1 = [1,0], p2 = [0,1] or p1 = [0,1], p2 = [1,0] maximizes the social welfare; however, convex combinations of these two points yield strictly smaller utility since the two nodes would then start blocking each other's access to the medium.
, the objective of Problem OPT is not necessarily concave in P. Perhaps the easiest way to verify this is to consider the case when G has two nodes connected by an edge, and there are C = 2 channels both of which are available to the two nodes. As each utility function U
i
(·) is increasing, it follows that W (P) is maximized if P is such that the two nodes deterministically choose different channels at all times. That is, choosing either p1 = [1,0], p2 = [0,1] or p1 = [0,1], p2 = [1,0] maximizes the social welfare; however, convex combinations of these two points yield strictly smaller utility since the two nodes would then start blocking each other's access to the medium.
We therefore turn to the locally optimal solutions of OPT. Lagrange multiplier method [26] can be utilized to define candidates for local optimality of the objective function in Equation 4. The Lagrangian function L(P, λ, η , x ) for the problem Equation 4 with Lagrange multipliers λ, η , ≥ 0 and a slack variable x is:

Here, the slack variable x ensures that  , i ∈ V,
, i ∈ V, 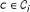 . After taking partial derivatives with respect to P, λ, η , x, equating the result to zero and discarding the slack variable x one gets.
. After taking partial derivatives with respect to P, λ, η , x, equating the result to zero and discarding the slack variable x one gets.

for all i ∈ V; 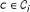 . These relations are the well-known Karush-Kuhn-Tucker conditions specifying necessary conditions of optimality for Problem OPT. The following theorem presents another representation of these conditions that is particularly helpful in the consideration of dynamic optimization algorithms.
. These relations are the well-known Karush-Kuhn-Tucker conditions specifying necessary conditions of optimality for Problem OPT. The following theorem presents another representation of these conditions that is particularly helpful in the consideration of dynamic optimization algorithms.
Theorem 1 If solves OPT, then it must satisfy
solves OPT, then it must satisfy

for every node i ∈ V ; and  .
.
Proof 1 If then due to the last relation in Equation 5
then due to the last relation in Equation 5 and according to the first relation in Equation 5:
and according to the first relation in Equation 5:

By the same argument applied to , the following is true
, the following is true


Combining Equation 7 and Equation 8 immediately yields the first statement of the theorem. Since in (5), combining (7) and (9) results in the second statement of the theorem.
in (5), combining (7) and (9) results in the second statement of the theorem.
4 Updating channel access probabilities
The randomized channel selection technique presented in the previous section needs to be supplied with an adaptation mechanism to update P in a way to solve problem OPT and maximize its objective. For this task, we shall mimic evolution of the entire collection of channel selection probabilities P via differential systems of the form

Here,  represents the time derivative of P. In such an expression, probability distributions P are interpreted to be updated according to a certain rule f to be determined. This rule depends on the equilibrium distribution π of the system under the current value of P. Hence, implementing the update rule entails measuring the system state s over time interval that is long enough to allow equilibrium probabilities to settle in. In turn, we seek update rules that are measurement-based and that do not require explicit communication of channel probabilities among nodes.
represents the time derivative of P. In such an expression, probability distributions P are interpreted to be updated according to a certain rule f to be determined. This rule depends on the equilibrium distribution π of the system under the current value of P. Hence, implementing the update rule entails measuring the system state s over time interval that is long enough to allow equilibrium probabilities to settle in. In turn, we seek update rules that are measurement-based and that do not require explicit communication of channel probabilities among nodes.
The goal of this section is to determine update rules f based on a gradient ascent method. The idea of this method is to change distributions P in the direction of the gradient of objective function W (P) in order to reach a local maximum of W (P). A standard gradient ascent algorithm in the present context can be characterized by

However, this differential system cannot be applied to Problem OPT because it violates the constraint in Equation 4 that each vector p i should be a probability vector. For every node i ∈ V entries of p i must sum up to one; and therefore, the following must be maintained:

We therefore modify the expression Equation 10 in the following manner:

Note that in this case

Hence if  then equality Equation 11 is satisfied. In addition, since
then equality Equation 11 is satisfied. In addition, since  when
when  , the value
, the value  never changes its sign. This implies that if the initial choice of p
i
is a probability vector, then that property is satisfied at all future times.
never changes its sign. This implies that if the initial choice of p
i
is a probability vector, then that property is satisfied at all future times.
The following theorem proves that, in addition, P converges to a local maximum of the objective function in Equation 4. We note that since P is varying so is W (P); and we denote by  the time derivative of W (P).
the time derivative of W (P).
Theorem 2 Suppose P is updated according to Equation 12. Then for any P and the equality holds if P satisfies conditions Equation 6.
for any P and the equality holds if P satisfies conditions Equation 6.
Proof 2 The proof is done by expanding time derivative using chain rule and by substituting time derivatives
using chain rule and by substituting time derivatives with the right-hand side of the equality Equation 12.
with the right-hand side of the equality Equation 12.

Since , for all i and
, for all i and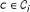 , then Equation 13 is always nonnegative. Note that any point that makes the right-hand side of Equation 13 equal to zero necessarily satisfies the Karush-Kuhn-Tucker conditions Equation 6. This completes the proof.
, then Equation 13 is always nonnegative. Note that any point that makes the right-hand side of Equation 13 equal to zero necessarily satisfies the Karush-Kuhn-Tucker conditions Equation 6. This completes the proof.
The second statement of Theorem 2 shows that if differential system Equation 12 is initialized at either a saddle point or a local maximum of problem Equation 4, then the value of P never changes from this point. However, the first statement of the theorem practically ensures that saddle points of problem Equation 4 are not stable points and rule Equation 12 converges only to local maxima. In practice, an implementation of a differential system Equation 12 is perturbed due to presence of computational error noise and limited time frame over which equilibrium probabilities π are estimated. Therefore, if initialized at a saddle point, any infinitesimal change of P will cause the differential system to further increase the value of the objective function and, thus, to move away from the saddle point.
4.1 Distributed approximations of the method
Although gradient ascent method Equation 12 provides a way to converge to a local maxima of Problem OPT, it is not yet clear how it can be applied in a decentralized fashion. A distributed solution should operate successfully without global view on measurements in the network. In our interpretation of the evolution Equation 12, exact distributed implementation would be feasible if for each node i the partial derivatives

can be obtained via local measurements made by node i.
We start by expressing these partial derivatives in an explicit form that sheds light on the implementation aspects of the update rule Equation 12. For clarity of presentation, we shall restrict attention to the specific objective of maximizing system-wide spectrum utilization. That is, we consider the case when U i (x) = x for all nodes i. The discussion can be readily generalized to other utility functions. The following theorem identifies the quantities that should be estimated by each node for strict implementation of Equation 12:
Theorem 3 Suppose that U i (x) = x for all i. Then

where i ∈ V, and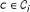 ,
,  .
.
Proof 3 Let us express the objective function W(P) by using explicit expressions for equilibrium distributions π in Equation 2:

Therefore,

If , then
, then

The theorem follows by substituting the right-hand side of this expression for the partial derivatives in Equation 15, and then by recognizing the fractions in the resulting expression in terms of the equilibrium probabilities Equation 2.
We point out that the expression

that arises in equality Equation 14 is the covariance of the two random variables  ,
,  (recall that
(recall that  indicates transmission of node i on channel c) with respect to the equilibrium distribution π, which is itself induced by P.
indicates transmission of node i on channel c) with respect to the equilibrium distribution π, which is itself induced by P.
Every node i ∈ V that implements system Equation 12 has to estimate partial derivatives of W(P) in Equation 12 according to equality Equation 14. However, it is practically inconvenient for every node to know its correlation terms with the rest of the network because, under such a scenario, nodes would require exhaustive information exchange to yield global view of the network at every node. Rather, it is desirable to have each node operate with regard to only local information. As a possible solution, we propose a distributed version of Equation 12 that estimates partial derivatives Equation 14 based on covariance terms between immediate neighbors.
To justify this approach, let us illustrate decay of covariance Equation 16 as nodes i and j get more distant from each other. Consider a rectangular 11-11 grid and the channels C = 2 for all nodes. The central node of the grid has an index 61. Correlation terms between the central node and the whole network are presented in Figure 3, where the varying node index is mapped on the actual grid location of the corresponding node. This result is obtained using a simulation framework described in Section 5. Probabilities P are chosen at random, medium probing rate r
i
is equal to 10 for all nodes i, and 100 experiments are performed to obtain average values. As one can notice, correlation between the central node and itself has the highest value, followed by correlation between the central node and its immediate neighbors. It quickly declines as we move further away from the central node. This observation encourages one to limit computations of the double sum in Equation 14 only to the neighborhood N(i) of node i and yet get a potentially close approximation of the precise value of partial derivatives  .
.
Under the proposed distributed implementation, channel access probabilities are updated as

for i ∈ V and 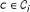 . This update rule is inspired by Equation 12, but it is obtained by approximating each partial derivative Equation 14 by a sum that is restricted to a subset N(i) of nodes associated with each node i. The set N(i) defines two different versions of distributed implementation:
. This update rule is inspired by Equation 12, but it is obtained by approximating each partial derivative Equation 14 by a sum that is restricted to a subset N(i) of nodes associated with each node i. The set N(i) defines two different versions of distributed implementation:
-
Local: N(i) is the set of all nodes j such that (i, j) ∈ E, and additionally node i,
-
Greedy: N(i) is comprised only node i.
In practice, the update rule Equation 17 can be implemented through periodic exchange of estimated correlation terms between immediate neighbors. To calculate these quantities, a node keeps a time log of channel utilization in its immediate neighborhood that also includes the node itself. A sufficiently long measurement interval would allow the equilibrium probabilities to be estimated by using the time log. To have a flavor of the required length of this interval, we note that each probability to be estimated is between 0 and 1; so its variation is at most 0.25. Hence, if the samples are taken sufficiently apart in time so that they are roughly independent, Chebyshev's inequality implies that (4ε2)-1 samples would be enough to estimate each probability within an error margin of ε, with probability at least max(0, 1-ε). Once the measurement interval expires, the node exchanges its measurements of π-terms in Equation 17 with its immediate neighbors and changes probabilities P according to Equation 17. Then, the node starts its time log over to get new measurements of correlation terms. Similarly, the greedy version of Equation 17 would require a node to keep a log of only its own channel utilization without local information exchange.
How well these distributed versions perform against each other and centralized Equation 12 version for random topologies can be seen through extensive numerical simulations. The results of practical application of the gradient ascent method are presented in the next section.
5 Numerical study
Performance of the CSMA-based channel selection technique presented in Section 3 and now equipped with gradient ascent method Equation 12 and Equation 17 can be tested to optimize W(P) in a variety of scenarios. In this section, we choose

for each node i, and thereby aim to maximize the aggregate spectrum utilization in system. Main objective of this simulation study is to see how different versions of this method perform against each other and against most relevant published algorithms [23, 24] in the common setting. Such comparison is conducted while varying graph connectivity, changing total channel availability and also introducing spatial variability in available channel sets due to presence of primary spectrum users. Although providing exhaustive experiments seem difficult in view of the arbitrariness of possible topologies of G, the reported experimental results expose important aspects of cognitive radio setup and can serve as benchmarks for practical performance comparison.
5.1 Simulation framework
To start, let us first describe a simulation framework that was implemented to test performance of gradient ascent-based methods (12) and (17) and algorithms [23, 24] operating within the channel selection technique described in Section 3.
As mentioned earlier, the channel selection technique is based on iterative estimation of equilibrium probability distributions π followed by changing probability distributions P. Let us describe one such iteration in more detail:
-
1.
Initialize the channel selection technique with initial choice of probability distributions P. To limit effect of this step on results, every node has uniform initial probability of choosing every of its available channels.
-
2.
Simulate the technique for current P by successfully transmitting enough packets.
-
3.
Estimate π by using temporal statistics of channel usage by every node. By using π calculate full partial derivatives Equation (12) or partial sums Equation (17).
-
4.
Update P according to:
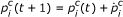 , where
, where 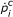 is either Equation 12 or Equation (17).
is either Equation 12 or Equation (17). -
5.
Obtain a new value of the objective function W(P) according to the new estimate of π.
-
6.
Terminate the simulation if improvement of the objective is below a predetermined threshold.
-
7.
Otherwise, proceed to step 2.
Medium probing rate r i is 10 for every node i. For fair comparison purposes, channel selection methods in [23, 24] need to be embedded in the same simulation framework as described next.
5.2 Benchmark algorithms
To be clear, the work [23] does not pursue optimization of an objective function. Rather, it attempts to settle every node for a deterministic channel choice through a randomized mechanism. In this study, we treat this mechanism in [23] as a way of changing P and we fit it into the Step 4 of the algorithm in Section 5.1. Namely, at this step, every node i ∈ V chooses a channel 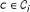 according to current P. Then, all neighbors compare their choices. This comparison is used as an interference measure that [23] do not specify. (Any alternative should be chosen considerably to ensure convergence of [23].) If any of neighbors of i happen to choose the same channel c then
according to current P. Then, all neighbors compare their choices. This comparison is used as an interference measure that [23] do not specify. (Any alternative should be chosen considerably to ensure convergence of [23].) If any of neighbors of i happen to choose the same channel c then  and
and  for all other channels
for all other channels  . Otherwise,
. Otherwise,  and
and  for all other z ≠ c. The algorithm in Section 5.1 is then performed based on the updated P. Let us refer to this modification as "Leith-Clifford" for convenience.
for all other z ≠ c. The algorithm in Section 5.1 is then performed based on the updated P. Let us refer to this modification as "Leith-Clifford" for convenience.
The algorithm [24] requires a measure of interference  in the neighbor-hood of every on every of its available channels
in the neighbor-hood of every on every of its available channels 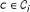 . For such measure, we used
. For such measure, we used  . Below is a complete procedure that replaces Step 4:
. Below is a complete procedure that replaces Step 4:
-
Compute parameter T = T0/log2(2+t), where T0 = 100 in this studyb.
-
By using estimated π, compute
 for every channel
for every channel 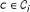 .
. -
For all
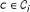 compute probability distribution
compute probability distribution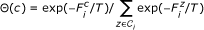
-
Sample channel k according to Θ and assign
 and
and  for c ≠ k,
for c ≠ k, 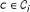
Unlike gradient ascent methods and Leith-Clifford, every node here transmits on a fixed channel that can be switched only at Step 4. This algorithm is referred to as "Gibbs".
5.3 Experiments
5.3.1 Effect of secondary user density
In practical scenarios, secondary users can face varying degree of competition for limited spectrum in their neighborhood. In completely connected topologies a user will need to share all of its available channels. In disconnected topologies, however, a user never has to share its channels. This experiment studies the effect of such competition by changing connectivity of graph G(V, E). To test this scenario, we fix the number of channels to 11 (due to wide use of IEEE 802.11 hardware in channel selection literature) and randomly place 30 nodes on a unit square. There are 100 different realizations of node placements. Interference radius is introduced to generate topologies with varying connectivity. If any two nodes are within the rapdius, then they are connected on a graph. The radius varies from 0 to  to ensure having a completely connected graph in 30 steps. Thus, every node placement yields 30 topologies with different connectivity. Figure 4 illustrates the performance of gradient ascent-based methods against Leith-Clifford and Gibbs. In general, it is observed that overall channel utilization declines as competition for 11 channels increases in dense neighborhoods. The gradient ascent-based algorithms are seen to clearly outperform Leith-Clifford and Gibbs, especially for moderately connected topologies. Performance of Leith-Clifford deteriorates compared with the gradient-based algorithms when high node density makes it impossible to assign channels in a non-conflicting way. The three gradient ascent-based algorithms perform closely to each other in the given setup.
to ensure having a completely connected graph in 30 steps. Thus, every node placement yields 30 topologies with different connectivity. Figure 4 illustrates the performance of gradient ascent-based methods against Leith-Clifford and Gibbs. In general, it is observed that overall channel utilization declines as competition for 11 channels increases in dense neighborhoods. The gradient ascent-based algorithms are seen to clearly outperform Leith-Clifford and Gibbs, especially for moderately connected topologies. Performance of Leith-Clifford deteriorates compared with the gradient-based algorithms when high node density makes it impossible to assign channels in a non-conflicting way. The three gradient ascent-based algorithms perform closely to each other in the given setup.
Performance of the gradient ascent-based methods against Leith-Clifford and Gibbs for different densities of 30 nodes. C = 11 channels are considered. The "centralized", "local", and "global" versions of the proposed algorithm are represented by the top curve and their performances are hardly distinguishable. 95% confidence intervals are also displayed.
5.3.2 Effect of varying spectrum availability
Decreasing the total number of available channels also increases competition for limited spectrum. Figure 4 indicates that Leith-Clifford and Gibbs significantly underperform the rest, for example, at interference radius equal to 0.5852. For this radius, 100 different topologies are generated. For each topology, a total number of channels available in the network C is changed from 1 to 20. Simulations indicated the absence of competition for channels when C > 20 and thus corresponding results are omitted. Figure 5 summarizes the results for algorithms under consideration. Leith-Clifford performs on par with the gradient ascent-based methods when the number of channels available is high relative to moderate node density resulting from the given interference radius. Leith-Clifford's performance deteriorates for decreasing channel availability compared with the gradient ascent-based methods which again display close performance between each other. Gibbs algorithm underperforms the others.
Performance of the gradient ascent-based methods against Leith-Clifford and Gibbs for varying number of channels C under a moderate node density. The "centralized", "local", and "global" versions of the proposed algorithm are represented by the top curve and their performances are hardly distinguishable. 95% confidence intervals are displayed.
5.3.3 Effect of primary spectrum user presence
The goal of this experiment is to test a scenario when the presence of primary channel users affect channel availability throughout the network. Number of ways exists to model such situations. In this particular case, we generate the same number of topologies in the same way as in the first experiment for 30 secondary users. Now, a generated topology is combined with 30 fixed primary users, each of them is assigned one of 11 channels uniformly and at random. Initially, homogeneous channel availability for the secondary users is now affected by primary users. If a primary user and a secondary user are within an interference radius, then the primary user's channel is excluded from possible channel choices available to the secondary user. A topology is not simulated if it contains a secondary user with no channels to choose from, caused by the presence of a high number of primary users in its neighborhood. The results of this experiment are displayed in Figure 6 which demonstrates the versatility of gradient ascent-based methods (12) and (17) in spectrum sharing problems with spatial spectrum inequality between secondary users. The methods presented in this work outperform Leith-Clifford and Gibbs algorithms, especially when connectivity of a topology increases.
6 Conclusion
This work presented a randomized channel selection technique suited for distributed implementation in cognitive radio systems. The technique adaptively converges to a local maximum of a performance objective by using the gradient ascent method. Decentralized versions of the method were also presented. Reported numerical tests reveal that the proposed gradient ascent-based methods outperform benchmark algorithms amid high competition for limited spectrum resources or when primary users are present. For the whole range of topology connectivity, performance of greedy and local versions of the proposed gradient ascent method matches performance of the centralized version that utilizes all information available in the network. This result strongly encourages further research in applications of such decentralized methods to spectrum sharing in cognitive radio systems.
Endnotes
aAn independent set of a graph is a subset of nodes that does not include any neighbors in the graph. We shall represent each independent set with a binary vector that has a 1 for each node included in the set, and a 0 for each of the remaining nodes. Hence convex combinations of independent sets are defined accordingly. bThe parameter T represents agility of the algorithm and provides a tradeoff between long term performance (convergence to a global maximum) and short term performance (avoiding getting stuck at local maxima). The reader is referred to [24] for further details and other applications of such parameters.
Abbreviations
- CSMA:
-
carrier sense multiple access
- LBT:
-
listen-before-talk.
References
The Federal Communications Commission, Secondary Markets Initiative[http://wireless.fcc.gov/licensing/secondarymarkets/]
Shellhammer S, Sadek A, Zhang W: Technical challenges for cognitive radio in the TV white space spectrum. Proceedings of the ITA Workshop, USCD, USA 2009.
Yuan Y, Bahl P, Chandra R, Moscibroda T, Wu Y: Allocating dynamic time-spectrum blocks in cognitive radio networks. Proceedings of the MobiHoc, Montreal, QC, Canada 2007.
Geirhofer S, Tong L, Sadler B: Interference-aware OFDMA resource allocation: a predictive approach. Proceedings of the MILCOM, San Diego, CA, USA 2008.
Shen D, Li V: Stabilized multi-channel ALOHA for wireless OFDM networks. Proceedings of the GLOBECOM, Taipei, Taiwan 2002.
IEEE 802.16 License-Exempt (LE) Task Group (802.16h)[http://www.ieee802.org/16/le]
Stevenson C, Choinard G, Lei Z, Hu W, Shellhammer S, Caldwell W: IEEE 802.22: the first cognitive radio wireless regional area network standard. IEEE Commun. Magazine 2009, 47(1):130-138.
Sadek A, Zhang W, Shellhammer S: Listen-before-talk versus treating interference as noise for spectrum sharing. Proceedings of the DySPAN, Chicago, IL, USA 2008.
Wu F, Zhong S, Qiao C: Globally optimal channel assignment for non-cooperative wireless networks. Proceedings of the INFOCOM, Phoenix, AZ, USA 2008.
Fálegyházi M, Čagalj M, Saeedi Bidokhti S, Hubaux J: Non-cooperative multi-radio channel allocation in wireless networks. Proceedings of the INFOCOM, Anchorage, AK, USA 2007.
Chen J, de Veciana G, Rappaport T: Improved measurement-based frequency allocation algorithms for wireless networks. Proceedings of the GLOBECOM, Washington, DC, USA 2007.
Seferoglu H, Lakshmikantha A, Ganesh A, Key P: Dynamic decentralized multi-channel MAC protocols. Proceedings of the ITA Workshop, USCD, USA 2008.
Huang S, Liu X, Ding Z: Opportunistic spectrum access in cognitive radio networks. Proceedings of the INFOCOM, Phoenix, AZ, USA 2008.
Bao L, Garcia-Luna-Aceves J: Distributed dynamic channel access scheduling for Ad Hoc networks. J. Parallel Distrib. Comput 2003, 63(1):3-14. 10.1016/S0743-7315(02)00039-4
Yang L, Cao L, Zheng H: Physical interference driven dynamic spectrum management. Proceedings of the DySPAN, Chicago, IL, USA 2008.
Khanna S, Kumaran K: On wireless spectrum estimation and generalized graph coloring. Proceedings of the INFOCOM, San Francisco, CA, USA 1998.
Mishra A, Banerjee S, Arbaugh W: Weighted coloring based channel assignment for WLANs. Mobile Comput. Commun. Rev 2005, 9(3):19-31. 10.1145/1094549.1094554
Moscibroda T, Wattenhofer R: Coloring unstructured radio networks. Proceedings of the SPAA, Las Vegas, NV, USA 2005.
Peng C, Zheng H, Zhao B: Utilization and fairness in spectrum assignment for opportunistic spectrum access. Mobile Netw. Appl 2006, 11(4):555-576. 10.1007/s11036-006-7322-y
Ni J, Tan B, Srikant R: Q-CSMA: queue-length based CSMA/CA algorithms for achieving maximum throughput and low delay in wireless networks. Proceedings of the INFOCOM, San Diego, CA, USA 2010.
Jiang L, Walrand J: A distributed csma algorithm for throughput and utility maximization in wireless networks. Proceedings of the Allerton Conference, Allerton House, IL, USA 2008.
Marbach P, Eryilmaz A: A backlog-based CSMA mechanism to achieve fairness and throughput-optimality in multihop wireless networks. Proceedings of the Allerton Conference, Allerton House, IL, USA 2008.
Leith D, Clifford P: Convergence of distributed learning algorithms for optimal wireless channel allocation. Proceedings of the CDC, San Diego, CA, USA 2006.
Kauffmann B, Bacelli F, Chaintreau A: Measurement-based self organization of interfering 802.11 wireless access networks. Proceedings of the INFOCOM, Anchorage, AK, USA 2007.
Kelly F: Reversibility and Stochastic Networks. Wiley; 1979.
Rao S: Engineering Optimization: Theory and Practice. Wiley-Interscience; 1996.
Acknowledgements
This work was supported in part by NSF through grants CCF-0964652 and CNS-1018154.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Dashouk, M., Alanyali, M. A utility-based approach for secondary spectrum sharing. J Wireless Com Network 2011, 32 (2011). https://doi.org/10.1186/1687-1499-2011-32
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1499-2011-32

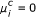 if
if  ; since channel c is then not available to session i.
; since channel c is then not available to session i. ; since a node can transmit only on one channel at a time.
; since a node can transmit only on one channel at a time.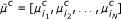 where i 1, i 2,..., i
N
represent the nodes in the subgraph Gc . That is, i 1, i 2,..., i
N
are the nodes for which channel c is available. Let
where i 1, i 2,..., i
N
represent the nodes in the subgraph Gc . That is, i 1, i 2,..., i
N
are the nodes for which channel c is available. Let 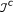 denote the collection of independent setsa of the subgraph Gc , and let co
denote the collection of independent setsa of the subgraph Gc , and let co  denote the convex hull of (i.e. all convex combinations of the elements in) the set
denote the convex hull of (i.e. all convex combinations of the elements in) the set 


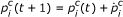 , where
, where 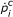 is either Equation
is either Equation 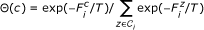
 and
and 

