- Research
- Open access
- Published:
Performance analysis of distributed cluster-based MAC protocol for multiuser MIMO wireless networks
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 34 (2011)
Abstract
It is known that multiuser multiple-input multiple-output (MIMO) communication can enhance the performance of wireless networks. It can substantially increase the spectral efficiency of wireless networks by utilising multiuser interference rather than avoiding it. This paradigm shift has most impact on the medium access control (MAC) protocol because most existing MAC protocols are designed to reduce the interference. In this article, we propose a novel cluster-based carrier sense multiple access with collision avoidance (CB-CSMA/CA) scheme. The proposed scheme enables multiuser MIMO transmissions in wireless local area networks (WLANs) by utilising the multiuser interference cancellation capability of the physical layer. In this article we focus on the performance analysis of CB-CSMA/CA. We investigate saturation throughput applying optimum backoff parameters and in the presence of synchronisation errors. Furthermore, we study the impact of different clustering methods on non-saturation throughput. We show that CB-CSMA/CA improves throughput significantly compared to the CSMA/CA scheme used in the IEEE 802.11 system. It is a promising approach for a variety of network configurations including typical infrastructure WLANs as well as many other wireless cooperative networks.
I. Introduction
Multiuser multiple-input multiple-output (MIMO) communication is an effective approach to improve the performance of a wireless system by realising distributed spatial multiplexing and/or diversity gains. However, the current WLAN MIMO standard, IEEE 802.11n, supports only point-to-point MIMO links [1]. The IEEE 802.11n specifies the medium access control (MAC) and physical (PHY) layers to enhance the data rate of wireless local area networks (WLANs) using MIMO techniques. The main channel access method of the IEEE 802.11 MAC protocol, i.e. the distributed coordination function (DCF), is based on carrier sense multiple access with collision avoidance (CSMA/CA) [2]. While multiuser MIMO techniques can provide spatial multiplexing gains even in networks with single-antenna stations (STAs), DCF prevents this by a collision avoidance mechanism. Therefore, in order to realise distributed spatial multiplexing gains, the interference avoidance scheme should be modified to facilitate controlled interference.
Contribution of this work
First we briefly devise a novel cluster-based MAC as extension of CSMA/CA to utilise the multiuser interference mitigation capability of PHY. The proposed scheme is simple and can be applied to different infrastructure or ad hoc networks with or without relays. According to the proposed cluster-based CSMA/CA (CB-CSMA/CA) scheme, nodes in a network, including stations (STAs) and access point (AP) or relays, are allocated to different clusters. The nodes belonging to the same cluster are allowed to transmit at the same time, provided that there are enough degrees of freedom [3] available to efficiently decode the desired stream at the destination.
In this article, we focus on the MAC performance analysis. We investigate the performance bounds of CB-CSMA/CA for a representative application: a network which consists of a multiple-antenna AP and several single-antenna STAs. We present comprehensive performance results of the considered application and of a reference system, which is based on the IEEE 802.11n standard. As it will be explained in Section III, in a network with an AP which has four antennas the uplink throughput of CB-CSMA/CA is about 2.5 times higher than that of IEEE 802.11n.
In order to find out how the proposed protocol performs in realistic scenarios we investigate the throughput in different situations. We estimate performance bounds of the CB-CSMA/CA protocol under different conditions. We study the maximum throughput, which can be obtained by properly adjusting the backoff parameters. Then we focus on performance analysis in realistic scenarios where for example the protocol fails to meet its basic requirements due to synchronisation errors. We denote this problem by the term event-synchronisation error. We evaluate the impact of event-synchronisation errors on the network throughput under saturation condition analytically and by simulations. Furthermore, we evaluate the non-saturation throughput and investigate impact of different clustering methods on throughput. In addition to the IEEE 802.11 reference, we compare the results with another multiuser protocol which has been proposed in [4].
Related Work
Several papers consider the MAC enhancement to support concurrent multiuser transmissions [4–8] or to resolve collisions [9, 10]. However, as it will be explained in more detail in the following paragraphs, the proposed CB-CSMA/CA differs from the existing methods in several ways, including the backoff procedure.
Park et al. [5] have proposed a MAC protocol mitigating interference by using multiple antennas at the receivers. In [8], the authors proposed a MAC protocol which considers the spatial correlation between the signal and interference to decide whether multiple links should transmit simultaneously or not. In their proposal, links are allowed to contend for the channel sequentially while transmitting data packets simultaneously. The throughput of the multipacket reception in a WLAN has been investigated in [4], where the authors consider an uplink scenario with a multiple-antenna AP. In their scenario simultaneous multiuser transmissions up to a certain number can be decoded by the AP and hence are not considered as collision. However, in their work, contrary to CB-CSMA/CA, there is no systematic way to exploit multiuser transmissions.
A MAC protocol with antenna arrays is suggested for ad hoc networks in [6]. The antenna array is used to null the interference from neighbours. In this scheme, bandwidth is divided into two orthogonal channels: a data and a control channel. The nodes use a CSMA/CA-based scheme on the control channel to acquire the channel and learn about ongoing transmissions by monitoring this channel. Similarly, concurrent transmissions from different users may be allowed by applying the busy-tone medium access [7]. In this method, out of band busy-tones on control channels are used to notify nodes about the number of actual streams and hence, avoid collisions.
In [9], the authors suggest a MAC protocol with the ability to resolve collisions. According to this protocol, when collisions occur, the collided packets have to be buffered. In the subsequent time slots, a set of nodes behave as non-regenerative relays and forward the signal they have received during the collision slot one by one. This method has been extended and applied to a large-scale wireless sensor network by dividing the network into several clusters [10]. In [10] each cluster has a clusterhead, and the nodes in a cluster only communicate with the clusterhead. Collisions within a cluster are resolved as in [9], while the clusterhead acts like a base station. Contrary to [9] and [10], in which the authors focus on the diversity techniques, we focus on utilising the spatial multiplexing gain in CSMA/CA-based systems.
In [11], we have presented the basic idea of CB-CSMA/CA and applied it to an ad hoc scenario where several amplify-and-forward relays performed multiuser interference cancellation. This has been done by choosing appropriate relay gain allocations. However, in [11] we have only considered a simple scenario where all STAs where perfectly event-synchronised and always had packets ready to be transmitted.
The CB-CSMA/CA scheme has some distinct advantages compared to existing proposals: it requires neither sequential contention per node for the data transmission as it is needed in [5] and [8], nor a control channel as in [6, 7], or [9]. Besides, by grouping nodes into clusters, the collision probability of the CB-CSMA/CA depends on the number of contending clusters rather than the total number of contending stations. As it has been shown in [11], the CB-CSMA/CA collision probability is considerably reduced compared to the standard IEEE 802.11 MAC. Furthermore, in contrast to [4] where there is a multipacket transmission only if accidentally more than one STA transmit in a time slot, the CB-CSMA/CA is designed such that each transmission attempt contains as many data packets as possible.
Outline
In Section II, we present the proposed CB-CSMA/CA scheme. In Section III we describe a representative application which is considered throughout this article as well as reference systems. Furthermore, we briefly present the model on which our analysis is based. We investigate the CB-CSMA/CA performance bounds in Section IV in which we analyse throughput for optimum backoff window parameters, asynchronous case, where STAs in a cluster transmit independently, and non-saturation scenarios where different clustering methods are applied. Conclusions are drawn in Section V.
II. Cluster-based CSMA/CA protocol
Assume a network where multiple users can transmit independent data streams simultaneously and the destination nodes can efficiently decode the desired signal out of multiple streams. This is possible if there are enough degrees of freedom available at the destinations, e.g. each destination has enough antennas, or appropriate cooperation exists among nodes. In such a network, to enhance the spectral efficiency, multiple nodes should be able to transmit simultaneously. In order to do so, we classify the nodes in a network into clusters. The nodes belonging to the same cluster access the channel at the same time. Similarly, nodes belonging to the same cluster may receive simultaneous streams provided that the intended stream at each destination can be decoded. Consequently, the spectral efficiency for the given system improves.
Similar to multiple transmissions from a cluster, a cluster may receive several simultaneous streams if the multiuser interference can be cancelled, either directly at the destination, or for example by setting proper gain factors at the transmitters or at the amplify-and-forward (AF) relays. Hence, from the MAC layer point of view, the clusters replace the individual nodes, and the nodes belonging to the same cluster look like a single entity. Consequently, the probability of collision in the network can be substantially reduced.
We consider three types of clusters: source-, destination- and relay-clusters. In a system with V clusters in total, we denote the v th cluster by C
v
, where v ∈ {1, 2, ..., V }. A cluster which generates the data packets is called the source-cluster and denoted by  . The size of the source-cluster is limited by the maximum number of concurrent streams which can be efficiently decoded. A cluster which includes the target receivers is a destination-cluster and denoted by
. The size of the source-cluster is limited by the maximum number of concurrent streams which can be efficiently decoded. A cluster which includes the target receivers is a destination-cluster and denoted by  . Even though forming a destination-cluster is not always necessary, for simplicity we assume that the destinations of a given source-cluster belong to a single destination-cluster. It should be noted that a source-cluster and its destination-cluster may interchange their functions at different time slots. A relay-cluster, denoted by
. Even though forming a destination-cluster is not always necessary, for simplicity we assume that the destinations of a given source-cluster belong to a single destination-cluster. It should be noted that a source-cluster and its destination-cluster may interchange their functions at different time slots. A relay-cluster, denoted by  , is a cluster of relays which receives and forwards data to other clusters without private benefit.
, is a cluster of relays which receives and forwards data to other clusters without private benefit.
Clusters can be formed based on a certain application or a given structure. For example, in an infrastructure network with a multiple-antenna AP, the AP forms clusters of STAs such that it can decode multiple streams in the uplink (for example by successive interference cancellation), or separates them in downlink transmissions (for example by performing zero-forcing). Since in the infrastructure mode all STAs associate with the AP, it is aware of each new STA entering its network or any STA leaving it. The AP can cluster nodes such that neighboured STAs belong to a single cluster or as it will be explained in Section IV-C adaptively allocate STAs which have packets ready to be transmitted to one cluster. The maximum size of the clusters is determined by the number of antennas at the AP.
The AP itself constitutes a single-member cluster Cr. Figure 1 depicts a scenario where the AP has four antennas and each source- and destination-cluster consists of four single-antenna STAs.
Throughout this article we consider a wireless network where STAs belong to the same basic service set (BSS).a Furthermore, for practical reasons, we consider only half-duplex nodes which are not able to transmit and receive simultaneously. We focus on the data transmission phase and assume that clusters are defined a priori.
A. Basics of CB-CSMA/CA
According to the CB-CSMA/CA, the nodes in a cluster behave similar to a single node, i.e. they access the channel at the same time and transmit simultaneously. Therefore, assuming the DCF access method is used, we need to consider two major modifications to the current backoff procedure: (i) having the same initial backoff duration for all cluster members and (ii) updating this value at the same time. The first requirement can be achieved for example by having the same random generator seed in each cluster, so that the same pseudo-random numbers are generated. In infrastructure networks the AP informs STAs in a cluster about the initial value of the contention window (CW) and, as explained in Section II-C, informs STAs in case they need to update it. As a second requirement, the STAs within a cluster should be event-synchronous.b This is necessary since according to the IEEE 802.11, the CW doubles after any unsuccessful transmission up to a maximum value [2]. Thus, after a transmission, STAs in a cluster should all know whether they need to increase the CW or not, as explained in the next subsection. In this way, each node in a cluster contends only with other clusters and not with other nodes in the same cluster. We assume that the clusters are constructed in a way that the destinations are able to decode the intended message. Consequently, simultaneous transmissions of the STAs within a cluster are resolved and do not lead to collisions.
The clusters access the channel one after the other in a similar way as single nodes act in the current CSMA/CA systems. As it will be shown in the next section, the event-synchronisation error leads to a throughput loss but the CB-CSMA/CA is relatively robust to such errors. In the worst case scenario, when all cluster members are not synchronous anymore, the CB-CSMA/CA performance gets close to that of the standard CSMA/CA.c
In a single-input single-output (SISO) WLAN system, the header of each transmitted frame can be ideally decoded by any node which is in the communication range of the transmitter. Accordingly nodes within a WLAN learn about an ongoing transmission by decoding the headers which include the duration field. However, the situation changes in a CB-CSMA/CA system, where several frames might be transmitted in parallel. The system is structured in such a way that each destination is able to decode its intended packet's header as well as its payload. However, other nodes in the network may not be able to do so. In order to solve this problem, a cluster common preamble should be sent prior to the data transmission.
The common preamble, which is sent at the lowest rate, could have a similar format as that of the legacy preamble of the PLCP header used in the IEEE 802.11n mixed format [1].d It additionally includes the address of the source-cluster and its LENGTH field should be set to the maximum length of all concurrent packets. The maximum value can be either set to the value specified by the standard for all transmissions or adaptively set by the AP according to the actual traffic and cluster structure for each cluster. In the latter case the AP informs the STAs about this value once it forms the cluster.
B. PHY layer requirements
The existing IEEE 802.11n supports only MIMO point-to-point links. However advanced signal processing techniques have enabled distributed multiuser MIMO transmissions. In order to efficiently decode an intended data packet in the presence of multiuser transmissions, the interference from other nodes has to be cancelled out. This can be done similar to point-to-point MIMO networks by successive or parallel interference cancelation. The main difference is that here individual nodes participate in each transmission and form some sort of a virtual antenna array.
In the current WLAN, the receivers estimate the channels by receiving the training sequence in the PLCP preamble of each frame. In CB-CSMA/CA, each transmission attempt may consist of several simultaneous streams. Therefore, orthogonal training sequences are allocated to different STAs within a source-cluster. The orthogonal training sequences can be designed as proposed in the IEEE 802.11n for MIMO transmissions, where for each transmit chain, the training field is cyclically shifted [1].
It should be noted that in OFDM systems, as long as the sum of the maximum delay offset and the channel delay spread is shorter than the cyclic prefix, both the multiuser interference and the inter-symbol interference can be mitigated. Since we focus on indoor scenarios the maximum channel delay spread and distances between nodes are quite small. As, in this article, our main goal is to analyse the performance of MAC layer, we assume an ideal PHY layer with perfect time and frequency synchronisation and no channel or decoding errors.
C. Collision detection
In WLANs, packets may fail due to collisions and channel errors. The cause of failure, however, cannot be distinguished in current WLAN systems [12, 13]. Hence, in both cases, the backoff interval increases exponentially up to a maximum value which is specified by the standard. However, in the event of a channel error, the binary exponential backoff may reduce efficiency and cause unfairness. An inherent advantage of our proposed CB-CSMA/CA is its ability to differentiate between these losses in practical SNR regimes. As explained in the next paragraph, this feature can be optionally used to enhance the performance.
We assume that all nodes in a BSS are in the radio range of each other. At each transmission attempt a common preamble is transmitted by all members of the source-cluster. The common preamble is included in the frame header. It is short and transmitted at the lowest data rate. Therefore, it is assumed that it is error-free. However, as different clusters send different common preambles, the common preambles collide if more than one cluster transmits in a time slot. Accordingly, upon reception of the frame, collisions can be post-detected as explained in the following paragraph.
If the common preamble cannot be decoded, it can be assumed that a collision has occurred. However, if the common preambles collide, the information about involved clusters may not be obtained. Hence, a short packet, called contention window update request (CWUR) packet, should be broadcasted to all clusters. In infrastructure networks this is performed by the AP. Upon reception of CWUR all source-clusters enter the next backoff process. However, only the source-clusters which have been involved in the pending transmission increase their CW unless the maximum CW value has already been reached. In the latter case they keep the maximum CW for the upcoming transmission.
Figure 2 shows the uplink transmission in an infrastructure network, where the AP has two antennas and STA1 and STA2 belong to cluster Cs1, while STA3 is a member of cluster Cs2. In Figure 2(a) an example of a successful transmission is shown, where STAs in Cs1 have a shorter backoff than STAs in Cs 2, hence they transmit first. In Figure 2(b) both clusters begin to transmit at the same time and hence a collision occurs. In this figure superscript c i above the data indicates the source-cluster from which the data packet is originated while subscript j below the data or ACK specifies the respective STA.
CB-CSMA/CA access mechanism in an infrastructure network with a multiple-antenna AP as the receiver. In (a) an example of a successful transmission is shown, where STA1 and STA2 in  have a shorter backoff than that of STAs in
have a shorter backoff than that of STAs in  and they transmit first. In (b) both clusters begin to transmit at the same time and hence collision occurs.
and they transmit first. In (b) both clusters begin to transmit at the same time and hence collision occurs.
III. Outline of representative applications and the analytical model
In this section first we introduce a CB-CSMA/CA application which is considered throughout this article. Furthermore, we explain the reference application, operating based on the standard, and another multiuser transmission protocol. Then we briefly review the existing model for calculating the throughput of a CSMA/CA-based network and point out the modifications which have to be considered for CB-CSMA/CA applications.
A. Applications
The proposed CB-CSMA/CA has wide applicability to different cooperative wireless networks. Appropriate applications include cooperative scenarios like multiuser zero-forcing relaying (MUZFR) [14] and two-way relaying [15], which require multiple STAs to transmit simultaneously and are not supported by the current WLAN MAC. Besides, any multiuser WLAN scenario that is supported by the standard MAC, is more efficient under the CB-CSMA/CA if multiuser interference can be cancelled.
In this article we focus on infrastructure networks where the AP is equipped with multiple antennas. For the analysis we only consider uplink transmissions. Hence, the AP acts as the receiver and all other STAs transmit to the AP. The ad hoc case where several relays assist the communication between sources and destinations is explained in [11].
1) CB-CSMA/CA application
In this article we use a representative application to quantify the performance of the CB-CSMA/CA scheme. This application is an uplink scenario in an infrastructure network with a multiple-antenna AP. The system consists of an AP with Na antennas and n STAs, each equipped with a single antenna. Hence, at each transmission attempt Na STAs should be able to transmit in parallel. In order to do so, sources are grouped into clusters and operate based on CB-CSMA/CA as explained in Section II. Although we only focus on uplink in this article, multiple transmissions in downlink can be supported by the CB-CSMA/CA protocol in a similar way.
2) Reference 1--IEEE 802.11 MAC Protocol
As a first reference system, we consider the above-mentioned infrastructure network which operates based on the IEEE 802.11 DCF. Therefore, in this reference system, at each time instant at most one node is allowed to access the channel.
3) Reference 2--a multiuser MIMO protocol
In addition to the standard CSMA/CA, we compare the results with those of a multipacket reception protocol described in [4]. In [4] and [16] the authors have proposed a multipacket reception (MPR) protocol and investigated its performance for various types of networks and parameters. In [4], uplink transmissions in an infrastructure network are considered, where the AP has Na antennas. STAs compete for the channel according to the DCF request to send/clear to send (RTS/CTS) mechanism. However, if accidentally more than one STA transmits in a time slot and the AP can decode the RTS frames, it sends the CTS frame to all senders. This can be done as long as the number of concurrent transmissions are less or equal to Na. Afterwards the transmitters send their data packets simultaneously to the AP. The suggested MAC closely follows the standard MAC, however, some modifications are required. For example, as the AP does not have any a priori knowledge about the transmitters and their channels, it should apply blind techniques to decode the RTS frames. Furthermore, it has to allocate orthogonal training sequences to the transmitters once it sends the CTS frames [4].
B. Throughput analysis
Throughput is defined by the average payload bits which are transmitted successfully in a time slot divided by the duration of the time slot, i.e. Tslot. We mainly consider saturation throughput where there is always a packet in the buffer of each station ready for transmission. However, in Section IV-C non-saturation throughput and impact of the presence of packets in buffers on the throughput are studied.
In this article we use Bianchi's model [17] as the basis for calculating the collision and transmission probabilities. In [17] an ideal channel with no channel errors, hidden nodes or capture is assumed. All nodes operate in saturation condition. Furthermore, no retransmission limit is considered. The model has been validated in [17] for IEEE 802.11b parameters. In [18] the authors have considered the IEEE 802.11a parameters and showed that the results using the original model are very close to the results obtained from a more accurate model introduced in [18].
As shown in [17], analysis of the Markov chain model leads to the following equations which have to be solved numerically to obtain the transmission and conditional collision probability (collision probability given that a STA transmits) in a network with n competing stations:


where W and m can be calculated from the minimum and maximum contention window sizes, denoted by CWmin and CWmax, respectively, as follows: W = CWmin + 1 and CWmax = 2 mW - 1
For the CB-CSMA/CA application we need to adapt the basic model. For scenarios where all members of clusters are perfectly event-synchronised we just need to replace the number of STAs in the original model by the number of clusters, Nc. However, as it will be shown in the next section, further changes are required for cases where one or more STAs are not event-synchronous anymore.
For the reference model and the MPR we can directly apply the equations given in [17] and [4], respectively, to calculate transmission and collision probability. Due to space limit we do not repeat those equations here and refer the interested reader to [17] and [4].
Saturation throughput for Na = 4 for both CB-CSMA/CA and the standard CSMA/CA are depicted in Figure 3. A link rate of 19.5 Mb/s (PHY rate of 26 Mb/s and a coding rate of 3/4) is assumed for CB-CSMA/CA application. This is one of the IEEE 802.11n possible data rates. Since there are four antennas at the AP, in the reference system at each transmission attempt there is a 1 × 4 single-input multiple-output (SIMO) link. Compared to a SISO link, for the reference system the maximum spectral efficiency gain of log(4) = 2 b/s/Hz (or 40 Mb/s for a system with 20 MHz bandwidth) can be expected [19]. Here as an extreme case (in favour of the reference system), we have increased the data rate of the reference system compared to the CB-CSMA/CA application to the next higher rate of IEEE 802.11n (58.5 Mb/s which can be achieved by a PHY rate of 78 Mb/s and coding rate of 3/4).
For both systems control packets are transmitted at the lowest data rate, i.e. 6.5 Mb/s. As it can be observed in this figure, CB-CSMA/CA can improve the throughput significantly. The results are verified by computer simulations. The simulation results are also plotted in the same figure. As it is expected simulated results follow the analytical results closely and the results become more accurate as the network size grows. The parameters which are used for numerical investigations throughout this article are given in Table 1.
IV. Performance bounds
In this section we analyse throughput upper and lower bounds of the CB-CSMA/CA application under different conditions. First we calculate the maximum saturation throughput and compare the results with the throughput of the reference system and that of the MPR protocol. Then the performance of the CB-CSMA/CA protocol in non-ideal conditions, e.g. where STAs in a cluster cannot transmit simultaneously or some of them may not have packets to transmit, is considered. The former is achieved by taking the impact of event-synchronisation error on the network throughput into consideration. The latter is done by considering non-saturation throughput and impact of different clustering methods on the network throughput. In practice, throughput of a CB-CSMA/CA application may vary between the calculated bounds.
A. Maximum saturation throughput
First we estimate the upper bound of the throughput by varying the transmission probability τ and finding the maximum throughput for a network with n STAs. In order to do so we can either calculate throughput results for different values of τ and find the τ* which maximises the throughput or find τ* as explained in [13] by applying the following equation:

where ω = Tc/σ with Tc being the time duration when the channel is sensed busy due to collision and σ being the duration of a time slot which is 9 μ s according to IEEE 802.11n [1].
The maximum throughput for CB-CSMA/CA and MPR versus the number of antennas at the AP are plotted in Figure 4. The throughput of the reference system is also plotted for comparison. In the CB-CSMA/CA application the cluster size increases with the number of antennas at the AP, Na. In the MPR application the maximum number of simultaneous transmissions which can be supported by the AP is increased with Na. While a constant rate per link of 58.5 Mb/s is assumed for all CB-CSMA/CA and MPR setups, link data rate of the reference system has been increased logarithmically with the number of antennas at the AP.e This is done since in the CB-CSMA/CA application, the antennas at the AP are used to cancel the multiuser interference but in the reference system we have SIMO links where at each time instant the antennas at the AP are only used for a single transmission. In all setups number of STAs is set to n = 60.
For the CB-CSMA/CA application two types of training sequences have been considered. As explained in Section II, time-orthogonal training sequences per cluster-members can be used to make channel estimation possible at the AP. In this way, the header length increases as the cluster size becomes larger. In Figure 4 the results for this case are denoted as variable header. However, training sequences may be orthogonalised in other domains such as frequency. In this way duration of the header does not change with the cluster size, cf., CB-CSMA/CA constant header curve in Figure 4. In this figure constant headers are assumed for the MPR application.
As we can observe in Figure 4, CB-CSMA/CA gains more than other applications from increasing Na. However, note that for very large cluster sizes, overhead increases as long as orthogonal training sequences in time are applied. It should be noted that the results in Figure 4 are the upperbound of throughput. In practice where the CW parameters are fixed, the throughput of the considered applications are below the values shown here.
B. Impact of event-synchronisation errors on CB-CSMA/CA performance
So far we have assumed perfect event-synchronisation in all clusters. Consequently, each time when a cluster accesses the medium, all of its members transmit concurrently. However, in practice members of a cluster may become event-asynchronous when for example one or more of them cannot receive or decode the CWUR packet. This may happen if any of the members are in a deep fade. In this section we study the impact of event-synchronisation errors on the throughput performance of the CB-CSMA/CA. However, to quantify the MAC layer performance again PHY channels are assumed to be perfect.
An event-synchronisation error can originate from different types of errors, including decoding errors on control frames and hidden nodes. In this chapter we assume that event-synchronisation errors occur due to decoding errors. Hence, the original backoff model can still be applied.
In the presence of an event-synchronisation error a subset of STAs in a cluster may be silent while the others are transmitting. Consequently, the number of parallel streams is not the same as the cluster size anymore.
In CB-CSMA/CA even if all STAs in all clusters become event-asynchronous, the conditional collision probability is reduced compared to the CSMA/CA case. This is due to the fact that simultaneous transmissions from the same cluster can still be decoded. It should be noted that in CB-CSMA/CA the preambles are defined in such a way that multiple streams originated from a single cluster can be decoded. On the other hand, if for example two STAs, each from one cluster, begin to transmit simultaneously, the training sequences may not be orthogonal any more and hence the receiver cannot estimate the channel and decode the packets. This happens even if the receiver has multiple antennas. Therefore, it is assumed that collision occurs if at least two stations which belong to different clusters begin to transmit at the same time regardless of the number of parallel streams.
We begin the analysis by considering a symmetric scenario where all clusters suffer from synchronisation errors in the same way. Then we extend the scenario to a general case in which each STA
i
has an event-synchronisation probability of  . For all scenarios, we investigate the throughput equations as a function of Pse.
. For all scenarios, we investigate the throughput equations as a function of Pse.
Again we consider the uplink of an infrastructure network where the AP has four antennas and each source-cluster contains four single-antenna STAs. We assume that all clusters can support a link data rate of 58.5 Mb/s regardless of the number of parallel streams. This could be the case in the high SNR regime where this rate could be supported on individual links.
First we consider a simple symmetric scenario, where all Nc clusters have the same number of asynchronous STAs. Assuming each cluster has a total number of Nnc STAs from which, k STAs are event-asynchronous. In this way, in the worst case scenario all STAs are asynchronous, i.e. k = Nnc and each cluster sees k(Nc - 1) = Nnc(Nc - 1) contending units at each transmission attempt.
1) Worst case scenario, k= Nnc
First we assume that all STAs in clusters encounter synchronisation errors. We study an extreme case where Pse is assumed to be equal to 1, (i.e. all members of clusters are with probability one asynchronous). Taking the MAC layer into account, this is the worst case which can happen and hence the throughput values in this case give the lower bound of the CB-CSMA/CA throughput.
In this case, a collision happens if one or more STAs in a cluster transmit while any other STA from any other cluster transmits at the same time. It should be noted that even in this case simultaneous transmissions of multiple STAs within a cluster can be resolved and hence do not lead to collisions. The collision probability given that at least one STA transmits can be calculated by taking into account the collision probability in an equivalent CSMA/CA, with n = NcNnc STAs, and then subtracting the probability that any other node from the same cluster transmits while other clusters are silent:

Pcol can also be directly obtained by taking into account the total number of contenders, i.e. the number of contending STAs which belong to other clusters:

As expected, for identical parameters, Equations 4 and 5 lead to the same result.
Since all members of clusters are asynchronous, the aggregate throughput of all clusters is defined by:

where k = Nnc and Tslot is the duration of the time window which can be obtained using:

where Pid, Ps and Pe are the probabilities that the slot is idle, contains a successful transmission and channel error, respectively. Ts, Tc and Te are the average time required for successful data transmission, collision and channel error. Ps and Pid can be calculated from the following equations:

where Pt is the probability that at least one STA in a cluster transmits in a slot:  .
.
Throughout this article we focus on MAC layer features and we set Pe to 0. For the CB-CSMA/CA application T s and T c can be obtained from:

where TData and TACK are the duration of the data (including the common preamble) and the ACK transmission, respectively, and TCWUR is the duration of the CWUR frame. The duration of the data and a control frames in an OFDM-based WLAN can be obtained as follows [20]:


where  ,
,  and Tsym are the durations of the PHY layer convergence protocol preamble (PLCP), PLCP SIGNAL and one OFDM symbol, respectively. The number of bytes per OFDM symbol for a given modulation M and the payload size are denoted by BpS(M) and L, respectively.
and Tsym are the durations of the PHY layer convergence protocol preamble (PLCP), PLCP SIGNAL and one OFDM symbol, respectively. The number of bytes per OFDM symbol for a given modulation M and the payload size are denoted by BpS(M) and L, respectively.
As it is expected by setting Nnc to 1 and Nc to be equal to the number of STAs, n, (6) reduces to the throughput equation in the standard case, i.e. Eq. (13) in [17].
The normalised throughput of the worst case scenario, where all STAs encounter synchronisation errors with probability one, is plotted in Figure 5. Normalised throughput is a unitless parameter which is defined by the time used for payload transmission divided by the total time needed for that transmission, i.e. Tslot. We also depict the throughput of a reference system based on the standard CSMA/CA. It is assumed that both systems transmit at the same data rate. This is a sensible assumption since even for CB-CSMA/CA with high probability only one node transmits at each transmission attempt. In this section we, furthermore, focus on the high SNR regime where CB-CSMA/CA can also operate at the highest PHY data rate defined by the standard regardless of the number of parallel streams.
Comparison of normalised throughput results obtained using the model with those from simulations, P se = 1. Solid lines show the analytical results and the symbols show the simulated results. For CB-CSMA/CA simulations have been performed for a second setup where the impact of orthogonal training sequence has been considered when calculating the collision probability.
For the CB-CSMA/CA applications, it has been assumed that multiple transmissions from more than one cluster always lead to collisions. This is the worst case as in practice different frames from different clusters may still have orthogonal training sequences and hence the AP can decode those frames as long as the number of streams does not exceed the number of antennas at the AP.
It can be observed that in the worst case scenario, when all STAs are event-asynchronous, the CB-CSMA/CA throughput is reduced to that of the reference system. It should be noted that even in this scenario the collision probability of the CB-CSMA/CA is smaller than that of the standard CSMA/CA, however, the headers in CB-CSMA/CA are longer than that in the reference system due to the common preamble and the orthogonal training sequences. For large network size, this leads to slightly smaller throughput in CB-CSMA/CA as compared to that of the standard CSMA/CA, cf., Figure 5.
In order to validate the results obtained from the model, we have simulated the same scenario in MATLAB. The normalised throughput obtained from simulations are compared with those obtained from the analytical model in Figure 5. As it can be observed, results from the model match the simulation. The model becomes more accurate as the network size increases.
For the CB-CSMA/CA application, in addition to the worst case scenario, a second set of the results is shown in Figure 5. In this case, we have assumed that there are totally Nnc = Na groups of orthogonal training sequences and collisions occur only when either more than Na STAs transmit at the same time or two or more STAs with non-orthogonal training sequences transmit concurrently. The simulated results for this case are also depicted in Figure 5. As it has been expected the second setup has higher throughput than the first one.
2) Asymmetric scenario
In practice different clusters may have different channel conditions and hence we extend the study to cover asymmetric scenarios. In this section, we consider an asymmetric scenario where only one cluster suffers from synchronisation errors. In this case we need to distinguish between two different categories of clusters: (i) Category i which has only one cluster, i.e. C i . Each STA in C i has a non-zero Pse. (ii) The second category includes all other clusters with Pse = 0. We denote the clusters in this category by C j where j ≠ i.
Since the clusters in the latter category are all perfectly event-synchronised, the members of C i face collisions only when any STA of C i begins to transmit while any other cluster transmits at the same time. Therefore, the collision probability of C i when k of its members are asynchronous is defined by:

where superscript (k) indicates dependency on k.

On the other hand, for any C j in the second category, a collision happens if it transmits and at the same time any other cluster from the same category or any of the STAs in C i begin to transmit. Accordingly, for this category collisions occur with different probabilities, depending on the number of clusters as well as the number of asynchronous STAs within the C i , see (12) above.
In this scenario again we can use (2) to calculate τ i . For each k, Equations 2, 11 and 12 can be solved numerically.
For each transmission attempt of C
i
, there are different numbers of parallel streams. The number of parallel streams depends on the number of asynchronous STAs within C
i
and whether they transmit by chance at the same time or not. To calculate the throughput of cluster C
i
we first need to determine the probability that k STAs out of  STAs in C
i
are asynchronous, i.e.
STAs in C
i
are asynchronous, i.e.

For a given k, the STAs in C i are divided into two groups:
-
(i)
the first group consists of
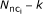 synchronised STAs, these nodes access the channel at the same time and act as a single unit. The transmission probability of this group is denoted by
synchronised STAs, these nodes access the channel at the same time and act as a single unit. The transmission probability of this group is denoted by 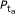 .
. -
(ii)
the second group consists of k asynchronous members, these STAs access the channel individually, however, some of them may by chance transmit at the same time. We denote the transmission probability of this group by
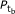 .
.
For a given k we have:

The probability that only STAs in C i transmit is:

The probability that only one of the clusters from the second category transmits is:

Hence, throughput of cluster C i and aggregate throughput of all other clusters are, respectively, expressed as:

where Tslot is equal to:

where Pid and Pc, i.e. probability that collisions occur in a slot, are, respectively, given by:

The throughput of each cluster category is shown in Figure 6(a). As the number of clusters increases, the throughput of C
i
improves with increase in  . when
. when  increases, with high probability there are more asynchronous STAs in C
i
. However, as simultaneous transmissions from C
i
can be resolved and hence are not considered as collisions, this only increases the collision probability of other clusters. Consequently, C
i
may transmit with higher probability and thus benefit from longer backoff durations at other clusters. For the same reason the throughput of any other cluster degrades when
increases, with high probability there are more asynchronous STAs in C
i
. However, as simultaneous transmissions from C
i
can be resolved and hence are not considered as collisions, this only increases the collision probability of other clusters. Consequently, C
i
may transmit with higher probability and thus benefit from longer backoff durations at other clusters. For the same reason the throughput of any other cluster degrades when  increases.
increases.
The aggregate throughput versus the number of clusters for different values of  has been depicted in Figure 6(b). As it is expected, an event-synchronisation error leads to throughput loss and the aggregate throughput decreases when
has been depicted in Figure 6(b). As it is expected, an event-synchronisation error leads to throughput loss and the aggregate throughput decreases when  increases. However, the throughput values for different
increases. However, the throughput values for different  get close to each other for a large number of clusters. The impact of a single cluster C
i
almost disappears once the number of clusters becomes very large.
get close to each other for a large number of clusters. The impact of a single cluster C
i
almost disappears once the number of clusters becomes very large.
3) General scenario
In this section, we will consider a general and more realistic case, where members of each cluster may suffer from synchronisation errors with a certain probability. It is assumed that each cluster C
i
has  STAs out of which k
i
are asynchronous. For each cluster, the collision probability depends on the number of total units, i.e. asynchronous and synchronous STAs, in other clusers. Consequently, for
STAs out of which k
i
are asynchronous. For each cluster, the collision probability depends on the number of total units, i.e. asynchronous and synchronous STAs, in other clusers. Consequently, for  where
where  we have:
we have:

For any number of asynchronous STAs in each cluster the transmission probability can be obtained by solving the set of equations given in (20) and (2). Accordingly, the transmission probability of synchronous and asynchronous STAs in each C i can be calculated as follows:

Here and in the following, for simplicity we denote the superscript  by
by  . The probability that k
i
out of
. The probability that k
i
out of  STAs are asynchronous can be obtained from (13), however, here k may take different values in different clusters. In this scenario, the probability that only members of one cluster transmit also depends on
STAs are asynchronous can be obtained from (13), however, here k may take different values in different clusters. In this scenario, the probability that only members of one cluster transmit also depends on  and can be obtained as follows:
and can be obtained as follows:


The throughput of each cluster is given by:

where Tslot can be calculated from the following equations:



Applying the above equations, we evaluate the throughput of the general scenario where  of each cluster is chosen uniformly from the interval [0, 1]. Each time the throughput of each cluster and the aggregate throughput are calculated. Then
of each cluster is chosen uniformly from the interval [0, 1]. Each time the throughput of each cluster and the aggregate throughput are calculated. Then  values are set to new random numbers. The results are shown in Figure 7. Although the throughput is degraded compared to the case where all STAs are event-synchronous, it is still much higher than that of the CSMA/CA system.
values are set to new random numbers. The results are shown in Figure 7. Although the throughput is degraded compared to the case where all STAs are event-synchronous, it is still much higher than that of the CSMA/CA system.
C. Impact of clusterings on CB-CSMA/CA non-saturation throughput
In unsaturated conditions STAs may or may not have a packet to transmit, depending on the traffic arrival rate. In order to calculate the transmission probability under unsaturated condition, we can apply the Markov chain model as proposed in [21]. In this model, compared to the saturation model, a new state is introduced, which indicates the probability that there is at least one packet to be transmitted in the buffer. This probability is denoted by q. As it is shown in [21], in this case the transmission probability can be obtained from:

Assume λ as the average packet arrival rate at each STA. For a traffic model with Poisson packet arrival process and for a small buffer size the probability q can be calculated from [22]:

where Tslot can be obtained from (7).
In non-saturation scenarios, grouping different STAs into a cluster can impact the network throughput. This happens since STAs in a cluster may or may not have a packet to send. Here we distinguish between two types of clusterings: non-adaptive clustering where clusters are formed regardless of the presence of queued packets and adaptive clustering where STAs which have packets to transmit are allocated to the same clusters. Adaptive clustering can for instance be achieved by using the polling information in the contention-free (CF) period. The AP can adaptively change clusters based on the information obtained during the contention-free period. According to IEEE 802.11e [23], STAs which do not have any queued packet to send, reply the CF-Poll by a Null frame. As a result, the hybrid-coordinator (here the AP) can form clusters by taking only STAs with queued packets into account. As each CF period is followed by a contention period, the clusters can be formed during CF period and can remain the same during the contention period.
1) CB-CSMA/CA with non-adaptive clustering
First we consider a scenario where clusters are defined independently of the presence of packets in their queues. Let us assume a worst case scenario where a cluster begins to compete for the channel as soon as all of its members have packets ready to send. Although in practice members of a cluster should be able to transmit even if other members remain idle, this scenario shows an extremely inefficient way of clustering under unsaturated condition. Accordingly, for the CB-CSMA/CA throughput analysis we have to replace q in (28) by  .
.
Non-saturation throughput of CB-CSMA/CA protocol with the considered non-adaptive clustering is depicted in Figure 8. For the purpose of comparisons, the throughput of the MPR as well as that of the IEEE 802.11n DCF basic access mechanism are also shown. At q = 1 each STA has a non-empty buffer with probability one and the system is saturated. It can be observed that the CB-CSMA/CA achieves higher throughput above a certain threshold. For very low values of q, CB-CSMA/CA throughput is below that of the other systems. This happens since clusters are defined independently of the packet arrival rate and each cluster transmits only if all of its members have packets to transmit. The results in Figure 8 are calculated for n = 24.
CSMA/CA achieves slightly higher throughput for very low value of q as compared to MPR. While MPR is performed using RTS/CTS handshake, the CSMA/CA is based on the basic access mechanism. Hence, in the region where the collision probability is small CSMA/CA benefits from smaller overheads.
2) CB-CSMA/CA with adaptive clustering
In this part we assume an adaptive clustering method. According to this method, for each transmission attempt, we select STAs which have packets in their buffer and put them together in clusters. In this way, assuming n STAs and Nnc = 2, we can form a cluster with two members as soon as there are at least two STAs which have packets in their buffer. This happens with the probability  .
.
Throughput results for this scenario with n = 24 are depicted in Figure 8. It can be observed that the CB-CSMA/CA protocol with adaptive clustering outperforms both the MPR and CSMA/CA for most values of q.
V. Conclusion
In this article we proposed a novel cluster-based CSMA/CA scheme which supports multiuser streams and reduces the collision probability in a network.
The CB-CSMA/CA protocol showed a promising throughput improvement compared to a reference system based on IEEE 802.11. The analysis of event-synchronisation errors shows that the CB-CSMA/CA is relatively robust to the event-synchronisation error and in the worst case it performs similar to the standard CSMA/CA.
The CB-CSMA/CA outperforms both MPR and CSMA/CA in saturation as well as unsaturation mode with medium and high probability of non-empty buffers. However, to benefit from CB-CSMA/CA for low packet arrival rates, we should apply an adaptive clustering. The adaptive clustering takes the presence of packets in the STAs into account and it can be performed by using the information obtained in the polling phase.
Endnotes
aThe BSS is defined as the basic building block of an IEEE 802.11 network [2]. It is assumed that the stations within a BSS are in the communication range of each other.
bWe denote all errors which cause different backoff window values at nodes within a same cluster, as event-synchronisation error.
cEven in this case concurrent transmissions from each cluster, which may still happen accidentally, do not lead to collision. Hence, the CB-CSMA/CA has lower collision probability than that of CSMA/CA.
dIt consists of the short and the long training sequences and a SIGNAL field. The SIGNAL field includes a RATE and a LENGTH field, one reserved bit, a parity bit and 6 tail bits and is one OFDM symbol long.
eIt should be noted that due to the wide range of values on the y-axis, variation of the reference curve with N a is not visible.
Abbreviations
- AP:
-
access point
- AF:
-
amplify-and-forward
- BSS:
-
basic service set
- CF:
-
contention-free
- CW:
-
contention window
- CWUR:
-
contention window update request
- DCF:
-
distributed coordination function
- MIMO:
-
multiple-input multiple-output
- MPR:
-
multipacket reception
- MUZFR:
-
multiuser zero-forcing relaying
- PHY:
-
physical
- RTS/CTS:
-
request to send/clear to send
- STAs:
-
stations
- SISO:
-
single-input single-output
- SIMO:
-
single-input multiple-output
- WLANs:
-
wireless local area networks.
References
Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications, Amendment 5: Enhancements for Higher Throughput, IEEE Std. 802.11n. 2009.
Wireless (LAN) Medium Access Control (MAC) and Physical Layer (PHY) Specifications, IEEE Std. 802.11, 1999 Edition (ISO/IEC 8802-11:1999).
Tse D, Viswanath P: Fundamentals of wireless communication. 1st edition. Cambridge, UK: Cambridge University Press; 2005.
Zheng P, Zhang Y, Liew S: Multipacket reception in wireless local area networks. IEEE International Conference on Communications, ICC 2006, 3670-3675.
Minyoung P, Heath RW, Nettles S: Improving throughput and fairness for MIMO ad hoc networks using antenna selection diversity. IEEE Global Communications Conference, Globecom 2004, 1: 3363-3367.
Mundarath J, Ramanathan P, Veen BV: Nullhoc: A MAC protocol for adaptive antenna array based wireless ad hoc networks in multipath environments. IEEE Global Communications Conference, Globecom 2004, 5: 2765-2769.
Wang D, Tureli U: Joint MIMO-OFDM and MAC design for broadband multihop ad hoc networks. EURASIP journal on Wireless Communications and Networking 2006, 2006: 1-9.
Ke B, Zhang Y, Liew S: Media access control with spatial correlation for MIMO ad hoc networks. IEEE International Conference on Communication, ICC 2007, 3660-3665.
Lin R, Petropulu A: A new wireless network medium access protocol based on cooperation. IEEE Transactions on Signal Processing 2005, 53(12):.4675-4684.
Dong L, Elanchezian A, de Oliveira JC, Petropulu A: Multicluster ALLIANCES: A high throughput and energy efficient approach for wireless sensor networks. Asilomar conference on Signals, Systems and Computers 2006, 300-304.
Ettefagh A, Kuhn M, Eşli C, Wittneben A: Performance of a cluster-based MAC protocol in multiuser MIMO wireless LANs. International ITG Workshop on Smart Antennas, WSA 2010.
Pang Q, Liew SC, Leung V: Design of an effective loss-distinguishable MAC protocol for 802.11 WLAN. IEEE Communications Letters 2005, 9: 781-783. 10.1109/LCOMM.2005.1506701
Medepalli K, Tobagi FA: On optimization of CSMA-CA based wireless LANs-part I-impact of exponential backoff. IEEE International Conference on Communication, ICC 2006, 2089-2094.
Wittneben A, Rankov B: Distributed antenna systems and linear relaying for gigabit MIMO wireless. IEEE Vehicular Technology Conference, VTC Fall 2004, 3624-3630.
Rankov B, Wittneben A: Spectral efficient protocols for half-duplex fading relay channels. IEEE Journal on Selected Areas in Communication 2007, 25(2):379-389.
Zhang YJ, Cheng PX, Liew SC: How does multiple-packet reception capability scale the performance of wireless local area networks? IEEE Transactions on Mobile Computing 2009, 8(7):923-935.
Bianchi G: Performance analysis of the IEEE 802.11 distributed coordination function. IEEE Journal on Selected Areas in Communication 2000, 18: 535-547. 10.1109/49.840210
Tinnirello I, Bianchi G: Refinements on IEEE 802.11 distributed coordination function modeling approaches. IEEE Transactions on Vehicular Technology 2010, 59(3):1055-1067.
Paulraj A, Nabar R, Gore D: Introduction to space-time wireless communications. 1st edition. Cambridge, UK: Cambridge University Press; 2003.
Qiao D, Choi S, Shin KJ: Goodput analysis and link adaptation for IEEE 802.11a wireless LANs. IEEE Transactions on Mobile Computing 2002, 1(4):278-292. 10.1109/TMC.2002.1175541
Daneshgaran F, Laddomada M, Mesiti F, Mondin M: Unsaturated throughput analysis of IEEE 802.11 in presence of non ideal transmission channel and capture effects. IEEE Transactions on Wireless Communications 2008, 7(4):1276-1286.
Malone D, Duffy K, Leith D: Modeling the 802.11 distributed coordination function in nonsaturated heterogeneous conditions. IEEE/ACM Transactions on Networking 2007, 15(1):159-172.
Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) specifications, Amendment 8: Medium Access Control (MAC) Quality of Service Enhancements, IEEE Std. 802.11e. 2005.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ettefagh, A., Kuhn, M., Eşli, C. et al. Performance analysis of distributed cluster-based MAC protocol for multiuser MIMO wireless networks. J Wireless Com Network 2011, 34 (2011). https://doi.org/10.1186/1687-1499-2011-34
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1499-2011-34





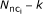 synchronised STAs, these nodes access the channel at the same time and act as a single unit. The transmission probability of this group is denoted by
synchronised STAs, these nodes access the channel at the same time and act as a single unit. The transmission probability of this group is denoted by 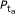 .
.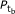 .
.

