- Research
- Open access
- Published:
Profit optimization in multi-service cognitive mesh network using machine learning
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 36 (2011)
Abstract
Cognitive technology enables licensed users (primary users, PUs) to trade the surplus spectrum and to transfer temporarily spectrum usage right to the unlicensed users (secondary users, SUs) to get some reward. The rented spectrum is used to establish secondary network. However, the rented spectrum size influences the quality of service (QoS) for the PU and the gained rewards. Therefore, the PU needs a resource management scheme that helps it to allocate optimally a given amount of the offered spectrum among multiple service classes and to adapt to changes in the network conditions. The PU should support different classes of SUs that pay different prices for their usage of spectrum. We propose a novel approach to maximize a PU reward and to maintain QoS for the PUs and for the different classes of SUs. These complex contradicting objectives are embedded in our reinforcement learning (RL) model that is developed to derive resource adaptations to changing network conditions, so that PUs' profit can continuously be maximized. Available spectrum is managed by the PU that executes the optimal control policy, which is extracted using RL. Performance evaluation of the proposed RL solution shows that the scheme is able to adapt to different conditions and to guarantee the required QoS for PUs and to maintain the QoS for a multiple classes of SUs, while maximizing PUs profits. The results have shown that cognitive mesh network can support additional SUs traffic while still ensuring PUs QoS. In our model, PUs exchange channels based on the spectrum demand and traffic load. The solution is extended to the case in which there are multiple PUs in the network where a new distributed algorithm is proposed to dynamically manage spectrum allocation among PUs.
Introduction
In conventional spectrum management schemes, spectrum assignment decisions are often static, with spectrum allocated to licensed users (PUs) on a long term basis for large geographical regions. Under these schemes, PUs hold exclusive rights to access the spectrum. Unfortunately, recent spectrum utilization measurements have shown that the usage of spectrum is concentrated on certain portions of the spectrum while significant amounts are severely underutilized. As a result, spectrum scarcity problem occurs due to the static and rigid nature of these schemes [1]. Moreover, these schemes prevent spectrum owners to trade the unused spectrum in secondary markets. Spectrum scarcity problem motivates developing new communication paradigms to exploit the unused spectrum efficiently and meet the exponential growth of spectrum demand nowadays.
Wireless mesh technology (WMN) is a first step toward providing high-bandwidth network over a specific coverage area. Thus, WMNs are predicted to be a key technology that provides ubiquitous connectivity to the end user. Although WMNs improve performance (with flexible network architectures, easy deployment and configuration, and fault tolerance), spectrum scarcity problem, large fluctuation of radio spectrum, and the inefficiency in the spectrum usage lower the network capacity. There will be a significant need for more spectrum due to a dramatic increase in the access to the limited bandwidth [1–3].
To overcome spectrum scarcity problem, Federal Communications Commission (FCC) has already started work on the concept of spectrum sharing where SUs can use licensed spectrum if their usage do not harm PUs [1]. Dynamic spectrum access (DSA) is proposed to solve the spectrum scarcity problem, which enables users to adjust communication parameters, such as operating frequency, transmission power, and modulation scheme, in response to the changes in the radio environment [1–3]. DSA enables implementation of cognitive radio (CR) that brings a promise to increase spectrum at a minimum cost by using licensed spectrum whenever spectrum owners do not use it. CR enables SUs to access the unused licensed spectrum using underlay, overlay or spectrum trading approaches [1, 3, 4]. In overlay and underlay approaches, SUs access the licensed spectrum without paying any usage charge to PUs. Their access is allowed as long as their usages do not harm the PUs. For example, in IEEE 802.22, SUs can access to TV bands. Although these approaches help in solving a spectrum scarcity problem, it is not likely to be accepted in the current market since the PUs do not have any financial incentive from SUs usage of spectrum.
CR applications range from public to commercial network. In our work, we will focus on commercial applications of CR. Spectrum Broker (e.g., FCC in USA) sells radio spectrum through an auction process to the PUs. The PUs transfer their spectrum rights temporarily to SUs for some revenue [3]. Hence, CR presents tremendous opportunities for widely spread wireless commercial to generate more revenues through renting the unused spectrum. Despite of obvious advantages of using CR in WMNs, there are still several issues that require more investigation such as economic factors that include PUs revenues, maintaining QoS for the PUs and SUs satisfaction. Moreover, spectrum trading presents the challenge of sharing spectrum among PUs.
In this article, we consider a CR environment where PUs can temporarily rent their spectrum to SUs to get some reward by charging for spectrum usage. For example, we can imagine a HotSpot located at popular public sites (e.g., coffee shops, airports, hotels) as a PU that owns the spectrum and provides users Internet access over a wireless local area network. The PU offers its prices for accessing unused spectrum and customers set up a short term contract with the PU. In the primary network, PUs may borrow channels from other PUs based on spectrum demand. Our design objective is to improve spectrum utilization (among PUs) and maximize revenue for spectrum owners (spectrum trading), while meeting some defined constraints.
PUs are expected to support various kinds of applications defined by their different QoS requirements. This need for the next generation of networks complicate designing their architecture and protocols. Even in the case of wired networks, no agreement has emerged and the proposed solutions are constantly challenged by the emerging services.
In this article, we propose to use adaptive, machine-learning based approach to develop an intelligent radio that is able to deal with conflicting objectives in radio environment. We formulate the spectrum trading problem as a revenue maximization problem. Reinforcement learning (RL) [5], a subfield of artificial intelligence (AI), is an attractive solution for spectrum trading problem in WMNs for a number of reasons. It provides a way of finding an optimal solution purely from experience and it requires no specific model of the environment; the learning agent builds up its own environment model by interacting with environment. It can provide real time control while it is in the process of learning without any supervision. The agent adapts to the environment through ongoing learning [5].
The rest of this article is organized as follows. First, related work and our contributions to the paper are introduced in 'Background' section. Next, our cognitive wireless mesh network is presented in 'Network overview' section. We describe spectrum sharing among PUs in 'On-demand spectrum sharing between PUs' section. 'Spectrum sharing between PUs and SUs using trading' section formulates the spectrum trading problem among PUs and SUs and describes our model for solving the problem using RL. Then we illustrate its implementation and how we optimize the obtained PUs' revenues using RL algorithm in 'Resource adaptation using cognitive network' section. Next, we present some of the performed tests and show the behavior of the implemented system under different conditions in 'Performance evaluation' section. Finally, the article is concluded in 'Conclusion' section.
Background
Related work
Previous work addressing the ability of cognitive networks to support SUs' requirements concentrated on using information theory to analyze the capacity of CRs. In [6], a new transmission model for CR channels is defined and information theory is used to analyze the capacity of CR. In [7], the information theory framework is used to characterize the capacity of the secondary network.
Several studies address the issue of spectrum sharing among PUs. PUs are competing for the spectrum in [8]. An auction theory was used to analyze the dynamic spectrum allocation of the unused spectrum bands to PUs. The problem was formulated as a multi-unit sealed-bid sequential and concurrent auction. In [9], PUs dynamically compete for portions of available spectrum. They are charged by the spectrum server for the amount of bandwidth used. The competition problem is formulated as a non-cooperative game and a new iterative bidding scheme that achieves Nash equilibrium of the operator game is proposed. Two spectrum brokers offer a spectrum for PUs in [10]. The key objective of the broker is maximizing its own revenue. The revenues are modeled as the payoffs that they gain from the game. On the other hand, PUs attempts to meet their QoS as much as they can with minimum expense. Centralized regional spectrum broker manages the spectrum in [11] and allocates spectrum for PUs. In [12], users adjust their spectrum usage based on a defined threshold called poverty-line. A PU can borrow from its neighbors if the neighbors have number of idle channels greater than a poverty-line. However, this scheme (poverty-line scheme) does not consider the availability of channels and the load of PU. It is possible that the neighbors have a number of idle channels less than their poverty line and these channels remain unused.
Many studies tackled the interplay among PUs and SUs for a spectrum in CRs. Game theory was used in [4] to model the competition among the PUs to sell free spectrum to SUs. Game theory was also used in [13] where SUs select the provider according to their preferences. In [14], an optimal bidding scheme mechanism was presented. The objective was defined to maximize the PUs' revenues while satisfying SUs. However, the equilibrium among multiple PUs and the stability of bidding in a competitive environment were neglected. A new framework was proposed in [15] to model the competition among multiple SUs to access the radio spectrum. Multiple SUs buy spectrums from multiple owners in [16]. A game theoretic framework is used to model the dynamic spectrum sharing in multi-owners and multi-users cognitive radio networks. In [17] SUs compete for the spectrum offered by a single PU. The willingness of PUs and SUs to trade the available spectrum is modeled using demand and supply functions in [12]. The market-equilibrium was considered as the solution and a distributed algorithm was proposed to obtain the solution.
All of these works concentrated on spectrum sharing for a single class of service. None of these works try to balance the PUs' revenues and the QoS for multiple classes. Moreover, the dynamic behavior to adapt to the network conditions was ignored in these strategies [4, 14–17].
Contribution
We address the problem of maximizing the PUs revenues in a commercial network by controlling the price and the size of the offered spectrum using RL. To the best of our knowledge, this is the first attempt to jointly optimize the PUs revenues and maintain QoS for PUs and SUs. In the game-theory based approach [4, 14–17], users make decisions based on other user's strategies and do not interact with the changes in the network conditions. Moreover, none of these schemes consider the following:
-
Utilizing the entire spectrum efficiently. Most of previous work assumes competition among PUs to maximize their revenues. However, cooperation among PUs to utilize the whole spectrum efficiently is neglected.
-
Maximizing total revenues of PUs through exchanging spectrum among PUs.
-
Using a machine learning method to extract the optimal control policy for managing PUs resources.
-
Heterogeneity of the SUs. All of the above studies consider one class of the SUs while maximizing the PUs revenue. Multiple class of services for SUs are not considered. Previous studies do not attempt to find a trade-off between PUs revenue and QoS for the PUs and SUs.
The contributions of our article are as follows:
-
A new distributed spectrum management scheme is proposed that manages spectrum sharing among PUs.
-
A computationally feasible solution to the spectrum trading problem is obtained using RL.
-
An extensive numerical evaluation, based on analysis and simulation, of the RL-based method for spectrum trading is presented.
We show using simulations our scheme's ability to utilize spectrum efficiently. We compare its performance with the poverty-line scheme. Moreover, we conduct experiments to show how our scheme can adapt to different network conditions such as traffic load.
Network overview
In this section, we present our cognitive wireless mesh network (CWMN) where the secondary network consisting of SUs is overlaid on a PU's primary network. This new network relays SUs traffic to the destinations using the rented spectrum from PUs. A CWMN has several mesh routers (MRs) and each MR serves several mesh clients (MCs) under it and these jointly form a cluster. The network architecture consists of several such clusters as seen in Figure 1.
Mesh routers have fixed locations whereas mesh clients are moving and changing their places arbitrarily. The algorithm proposed in [18] is used to form and maintain clusters. Moreover, the proposed signaling protocol in [18] is used to manage communication among the PUs and the SUs. The spectrum is divided into non-overlapping channels which is the basic unit of allocation. The network consists of W PUs and N SUs. We define a PU as a spectrum owner that may rent a spectrum to other users. PUs are allowed to borrow spectrum from each other in our system. Each PU has K channels assigned to it in advance and it offers an adaptable number of these channels to MRs (SUs). The total capacity of the network is given as:

MRs use the rented channels to serve different classes of MCs. Each PU y , y = 1, 2,....,W, specifies S y the spectrum size for renting, its QoS requirements (blocking probability), and the price of spectrum. We assume that these parameters are changed over time corresponding to the network conditions, such as traffic load, spectrum demand, and spectrum cost. A PU therefore needs to change the price and the size of the offered spectrum when needed. We use RL in our network to extract an optimal control policy for managing spectrum size and price for all SUs classes. SUs can access a licensed spectrum if they rent the spectrum from a PU. From PUs point of view, the optimal resource management scheme is the one which maximizes their revenue. However, some constraints prevent PUs from maximizing its profit such as resource constraint and QoS for PUs. In this article, we address the problem of optimizing spectrum trading in the secondary spectrum market for satisfying both QoS for multiple classes of services for SUs and for PUs and maximizing the revenue of PUs. Our network is multi-service cognitive network where multiple classes of SUs pay the PUs for their spectrum usage based on short term contract. PUs serve different classes of SUs to maximize their profits while considering the trading constraints.
Since spectrum access charges differ between user classes, serving new SUs whenever there is available spectrum may not maximize the PU's revenue. The PU has to compute the gained reward and decide whether to serve the request or reject it and wait till a user with worthy reward arrives. Therefore, the optimal resource management scheme is mandatory in our system. A policy for maintaining the QoS for the PUs plays an important role in protecting the right of the PUs to access the spectrum exclusively. Since PUs are given priority over SUs, PUs protection is achieved by a properly organized price and the size of the offered spectrum.
For SUs, we assume that spectrum request arrival follow Poisson distribution and each SU class i has arrival rate λ i . The service time μ i for each request of i th class is assumed to be exponentially distributed. These assumptions capture some reality of wireless applications such as phone call traffic [19–21]. Each SU of i th class pay a price p i for a spectrum unit.
The problem of optimal resource allocation for satisfying QoS for multiple classes of SUs is a challenging problem in the design of our network. The main motivation for the research in this problem is to adapt the services to the changes in the structure of the spectrum secondary market. Most of the research that has been conducted in this field assumes one class of SUs and one type of service. Nowadays, with an explosion in the diversity of real-time services a better and more reliable communication is required. Moreover, some of these applications require firm performance guarantees from the PUs.
On-demand spectrum sharing between PUs
In this section, we show how PUs share free spectrum to maximize the total profits based on the spectrum demand and interference constraint. Spectrum sharing among PUs is based on borrowing from each other which improves spectrum utilization significantly. In our model, we define the following components for primary user y (PU y ):
-
Spectrum allocation vector SP y :
We model a channel as an ON/OFF where the ON period indicates the duration of PUs' activities. SP y = {SP y (m)|SP y (m) ε{0,1}}is a vector of spectrum status. If SP y (m) = 1, channel m is not available currently.
-
Interference vector I y :
I y = {I y (i)|I y (i) ε{0,1}}is a vector that represents the interference among PU y and other PUs; if I y (i) = 1 then PU y and PU i cannot use the same channel at the same time because they would interfere with each other.
-
Borrowable channel set BC y :
Our scheme allows two neighbors to exchange channels to maximize their reward while complying with conflict constraint from set of the neighbors. We define that two PUs are neighbors if their transmission coverage area is overlapped with each other. The set of channels that PU y can borrow from PU j should not interfere with PU y neighbors. We refer to these channels as BC y (PU y , PU j ):

Where L gives the set of channels assigned to the given user(s) (e.g., L(PU j ) represents the list of PU j channels), G(PU y ) is a list of neighbors of a primary user PU y .
In our sharing scheme, PUs can exchange channels if the borrowed channels do not interfere with the channels of its neighbors. After serving a request, the PU returns back borrowed channels to the owner users. PUs adjust their spectrum usage based on demand. As a result, the PU decides to borrow channels if the spectrum is not available to accommodate SUs requests and it is profitable to serve new SUs in terms of revenue. In our scheme, spectrum is shared among PUs as follows:
-
Step 1: PU computes the revenue of serving new SUs based on the reward function as described in 'Reinforcment learning formulation for spectrum trading' section.
-
Step 2: If the revenue is positive and worthy, a PU requests neighboring PUs for a spectrum through a 'borrowing frame' that is broadcast to all neighbors. The request frame specifies the size of required spectrum.
-
Step 3: Each neighboring PU receives a 'borrowing frame', checks its idle channel list and if there are idle channels, the PU temporarily gives up a certain amount of idle spectrum for a specific period of time, and sends an 'accept frame' that includes channel IDs. If all channels are busy then the request is ignored.
-
Step 4: After receiving 'accept frame(s)', the PU specifies a borrowable channel set BC and ranks its elements based on their capacity. If the PU does not receive any 'accept frame', it queues the requests.
-
Step 5: After selecting channels, the PU informs the owners of the selected channels.
-
Step 6: After the PU finish serving SUs, it returns the borrowed channels.
Our scheme guarantees high utilization by using all system channels provided that the interference constraint is met. This is shown in the result section 'Performance evaluation'.
Spectrum sharing between PUs and SUs using trading
We consider spectrum sharing based on trading between SUs and PUs in a multi-service network. PUs serve different classes of SUs to maximize their profits while considering the trading constraints. We first give a brief overview of RL, and then explain how RL is used to extract the optimal policy for trading the free spectrum to SUs. The model takes into account the reward of PUs and the cost of renting the spectrum.
An overview about reinforcement learning
The revenue maximization at each PU faces a unique challenge due to time-varying spectrum availability. Therefore, a PU should jointly consider serving SUs requests and maintain QoS for itself to maximize its profit. We formulate RL by accounting for time-varying spectrum demand and spectrum availability. The basic and essential components of the RL are derived by considering system states and the possible actions to be taken for revenue optimization at each state.
Let Z = {Z0, Z1, Z2, Z3...Z
t
} be the set of possible states an environment may be in, and A = {a
0
,a
1
,a2...a
t
} be a set of actions a learning agent may take. In RL, a policy is any function: π : Z→A that maps states to actions. Each policy gives a sequence of states when executed as follows:Z0→Z1→Z2... →Zt, where Z
t
represents the system state at time t and a
t
is the action at time t. Given the state Z
t
, the learning agent interacts with the environment by choosing an action a
t
, then the environment gives a reward R(Z
t
,a
t
) and the system transits to the new state Z
t+1
according to the transition probability  and the process is repeated. The goal of the agent is to find an optimal policy π*(Z) that maximizes the total reward over time. We apply a Q-learning algorithm to find an optimal policy. For a policy π the Q value is defined as [5]:
and the process is repeated. The goal of the agent is to find an optimal policy π*(Z) that maximizes the total reward over time. We apply a Q-learning algorithm to find an optimal policy. For a policy π the Q value is defined as [5]:

where Qπ (Z t ,a t ) is the expected discounted reward for executing action a t in state Z t , γ is the discount revenue and R(Z t ,a t ) is the reward received at time t when taking action a t in state Z t . Let:

Then, we can define the optimal policy π* as follows [5]:

As learning agent interacts with environment it updates the state-action value Q(Z, a) based on the gained reward it receives using the following Q-learning rules:

where  and ∞ is the learning rate. In order to utilize RL, we need to identify the system states, actions, and rewards.
and ∞ is the learning rate. In order to utilize RL, we need to identify the system states, actions, and rewards.
Reinforcment learning formulation for spectrum trading
The agent developed provides the trading functionality at the PU level of CWMN in a distributed manner. Each agent uses its local information and makes a decision for the events occurring in the PU in which it is located. In our system, an event can occur in a PU (agent) when a new request for spectrum arrives or a SU releases its assigned spectrum. These events are modeled as stochastic variables with appropriate probability distribution. In this section, we introduce the basic elements for RL model.
State and action space
At any time the PU is in a particular configuration defined by the size, the price of the offered spectrum and the number of admitted SUs of each class. In our work, the state is indicated by the set Z t = {Z i } where Z i is the number of accepted requests for i th class. All possible states are limited by the following constraints:

where S y is the size of PU y rented spectrum for SUs and F is a set of SUs classes. From a state, the system cannot make a transition if the constraints conditions are not met. When an event occurs, a PU has to decide among all possible actions. In our work, when a request from SU arrives, a PU either serves the request or rejects it. The action space is given by:

where a t = 0 denotes request rejection, a t = 1 indicates that the PU accepts serving new SU.
Reward function
Spectrum demand is changing over time. Since the size and the price of the rented spectrum should be adapted from time to time; PUs need a mechanism that can indicate when and how to adapt the spectrum size to maximize its revenues while guaranteeing QoS for a PU. A PU y (PU y ) incurs cost C y of obtaining its spectrum from the spectrum broker, which is computed as follows:

where δ is the cost of one spectrum unit and S y is the size of spectrum that PU y would rent to the SUs at a price p i for each class i. The average reward for PU y is given by:

where  is the average rate of accepting SUs request of class i. The PU
y
average net revenue is computed as follows:
is the average rate of accepting SUs request of class i. The PU
y
average net revenue is computed as follows:

At state Z t , the received revenue is computed as follows:

where μ
i
is the service rate of i th class. We assume the key objective for the PU is the maximization of revenue R
y
(Z
t
,a
t
) with respect to S
t
, under the condition that the blocking probabilities for a PU
y
(B
y
) does not exceed  . Then, revenue maximization problem can be formulated as follows:
. Then, revenue maximization problem can be formulated as follows:


The first constraint states that the capacity of the secondary network (size of spectrum) should be less than or equal the capacity of the primary network (PUs' network). The second constraint reveals that PU y and PU j cannot assign the same channel (m) for their clients simultaneously because they will interfere with each other. Finally, third constraint defines that blocking probability for a PU y should not exceed the blocking constraint for a PU y applications. In this formulation, the maximization of revenue can be achieved by adapting the size and the price of the spectrum periodically based on (11) and the blocking probability of PUs. Our goal of RL is to choose a sequence of actions that maximize the total value of the received revenue for a PU y :

where T y indicates the total net revenue of PU y when policy π is executed and D represents the time horizon. At each state Z t , e t (Z t ) is the dynamic cost of serving new requests of class i. It is used to decide the new admitted requests. A PU chooses the requests with maximum positive gain as follows:

If there is no request with positive gain, all requests are neglected. The average net gain for class i requests under policy π can be defined as follows:

where p(Z t ) denotes the states probability, and g i (Z t ) is the gain of accepting class i requests.
Theorem 1: Average reward for a PU y is sensitive to the arrival rate of class i and this sensitivity can be calculated as follows:

Proof: the net gain for class i at state Z t under policy π can be expressed as follows:

where (Z t + Δ t ) denotes the new state of the system after accepting the i th class requests. The right-hand side of Equation 16 can be written as [22]:

where R y (Z t+1 ,a t ) denotes the reward rate after taking the action a t of accepting new request of i th class at time t. By using Equation 17 it can be shown that (18) is equivalent to:

Analogous proof holds if one request is served. This analysis is helpful for a PU to decide if a request is to be admitted or rejected based on the sensitivity of reward to arrival rates of different classes.
Using RL to find an optimal policy π*
In our work, a lookup table is used to store the Q values as each state-action pair Q(Z, a). Each action is executed a large number of times at each state to guarantee the convergence of the Q-learning algorithm. In a trading process, when an event occurs at time t, a PU senses the environment (such as spectrum price, available spectrum size, and SU class). Then, the state of the system Z t is specified. After that, the PU can find the possible actions at this state. Next, the PU looks up the aggregated Q value table and finds a set of Q values corresponding to state Z t and the possible action. Then, the action a t with the maximum Q value is selected. According to the selected action the environment will transit to the next state Z t-1 and the PU adapts its resources in the new state (such as spectrum price, and size of the offered spectrum). Finally, the Q value is updated using Equation 6. In the next section, we show how the PU adjusts its resources to meet the network blocking probability constraint and maximizes its revenue.
Resource adaptation using cognitive network
Spectrum size adaptation in radio environment
The conditions of the system are changing randomly. These conditions include traffic level, spectrum demand from SUs and the size of available spectrum. Therefore PUs should adapt its resources to achieve its objectives. Several parameters can be tuned by PU to adapt to the new conditions. These parameters include price and the size of the offered spectrum. Revenue maximization can be achieved by spectrum size adaptation. In this case, the necessary condition for optimal solution can be formulated as a requirement of having the network revenue gradient with respect to PUs offered spectrum equal to zero vector:

In our model, the PUyrevenues sensitivity to the number of the offered spectrum size can be derived from equation (10):

We assume the average reward sensitivity to the offered spectrum size can be approximated by the average spectrum price of the SUs class with unit spectrum requirement, . As a result, Equation 21 can be written as:
. As a result, Equation 21 can be written as:

where  is the average spectrum price and it is computed as follows:
is the average spectrum price and it is computed as follows:

The PU's revenue is maximized when spectrum size equals the root of:

We used Newton's method of successive linear approximations to find the root of Equation 24. The new spectrum size S n+1 (PU index is omitted in the notation) at each iteration step n is computed as follows:

Approximating the derivative in equation (25) at step n:

and substituting (26) in (25), the new spectrum size will be:

Spectrum size adaption is then realized using the following algorithm:
AdaptSpectrumSize

begin
if ((Abs

return

else
{
S n = S n+1 ;
compute

AdaptSpectrumSize

}
end;
where ε is the tolerable error.
QoS support for PUs and SUs in CWMNs
The presented solution for revenue maximization does not take into account the QoS for PUs. A spectrum request is blocked if it arrives while PU y is already using its entire spectrum. Therefore, the probability of blocking for PU y is computed as follows [23]:

where p is computed as follows:

The blocking probabilities of PUs may exceed their constraints in some scenarios. The offered price in the secondary network is adapted to meet the blocking constraints for the PUs. It is clear when a PU increase the prices the arrival rates of SUs classes will be decreased. Hence, the spectrum demand at the secondary network will be decreased. The surplus spectrum can be used to serve the PUs applications. The arrival rate of SUs classes depends on the offered price. The new arrival rate of i th class is calculated as follows [24]:

where τ is the maximum number of users arriving at a PU, ω
i
represents the rate of decrease of the arrival rate as spectrum price increases and it is related to the degree of competition between the PUs and  is the new price for the i th class. Here we assume ω
i
is given a prior. There is an inverse relationship between the price and the demand of the spectrum. A PU has to meet its blocking probability constraint
is the new price for the i th class. Here we assume ω
i
is given a prior. There is an inverse relationship between the price and the demand of the spectrum. A PU has to meet its blocking probability constraint  , which is a function of the number of available channels and the traffic load. PU continues increasing the prices in the secondary market till its blocking probability is satisfied. PUs tries to minimize the price increment as much as possible to keep the PUs revenues positive. A PU calculates the new revenue as follows:
, which is a function of the number of available channels and the traffic load. PU continues increasing the prices in the secondary market till its blocking probability is satisfied. PUs tries to minimize the price increment as much as possible to keep the PUs revenues positive. A PU calculates the new revenue as follows:

This leads to the following problem formulation:

subject to: 

In our proposed adaptation scheme the new values of spectrum prices reflect the amount of spectrum required by a PU. Due to competition in the market, a price increment is limited due to the possibility of losing customers. If the blocking constraint of a PU is not met, a PU increases the values of all service prices by applying a common multiplier γ to all spectrum prices. After each increment, a PU computes its blocking probability and if it is not met it continues to increase the prices till a blocking constraint is met. If a blocking constraint for a PU is met then it tries to meet the blocking constraint for SUs. If some of the SUs blocking constraints are not met, it decreases the service prices while increasing those of SUs classes for which blocking probability are smaller than their constraints, in such a way that total offered spectrum price is maintained.
Revenue optimization for multiple PUs
In our work, an iterative gradient approach is used for revenue maximization in (20), where a successive projection of the revenue gradient is performed to converge  to 0. We use a step-size factor φ to scale the projected spectrum size changes ΔO = (ΔS1, ΔS2,..., ΔS
W
) at each iteration step to improve the convergence. We use Newton successive projection to find ΔS
W
approximating the solution to
to 0. We use a step-size factor φ to scale the projected spectrum size changes ΔO = (ΔS1, ΔS2,..., ΔS
W
) at each iteration step to improve the convergence. We use Newton successive projection to find ΔS
W
approximating the solution to 
Assume O
n
and  denote the vector of offered spectrum sizes and the average revenue at iterationn, respectively, and let ψ
y
be the vector of size W with 1 in the y position and 0 in all other positions. The first and second derivative with respect to the PU
y
offered spectrum,
denote the vector of offered spectrum sizes and the average revenue at iterationn, respectively, and let ψ
y
be the vector of size W with 1 in the y position and 0 in all other positions. The first and second derivative with respect to the PU
y
offered spectrum,  and
and  can be approximated by the following differentials:
can be approximated by the following differentials:

Using these approximations we compute ΔS y as follows:

We apply the following adaptation algorithm to find the optimal offered spectrum size at each PU within a specified relative accuracy ε:
n = 0;
initialize O n to any arbitrary spectrum size vector
compute

do
for each PU y
compute

end for
search for the scalar size
 such that:
such that:

if


returnO n+1 ;
end if
else
n = n+ 1;
while

Performance evaluation
In this section, we show simulation results to demonstrate the ability of our spectrum scheme to adapt to different network conditions. The system of PUs and SUs is implemented as a discrete event simulation. The simulation is written by using matlab. We uniformly distribute 4 PUs and each PU is randomly assigned 20 channels. For the mesh network, 100 MCs are distributed uniformly in the transmission region of the MRs. The results presented are for several system settings scenarios in order to show the effect of changing some of the control parameters. The network parameters chosen for evaluating the algorithm and the methodology of the simulation are shown in Table 1. Simulation results are found to closely match the analytical results.
Note that some of these parameters are varied according to the evaluation scenarios.
Performance of on-demand sharing scheme
We compare the performance of our on-demand based spectrum sharing scheme with the poverty-line heuristic [12] through simulations. For PU y , the poverty-line is computed as follows:

The performance metrics considered are:
-
(1)
throughput, which is the average rate of successful message delivery over a communication channel.
-
(2)
spectrum utilization, which is the percentage of busy spectrum at time t and is computed as follows:
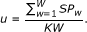 (36)
(36)
We examine the performance under different parameter settings. Throughput comparison of the two schemes is shown in Figure 2. The figure shows that the throughput increases as the number of total channels increases. This is due to more spectrum that can be employed. Our scheme utilizes the unused spectrum resourcefully because there is no limit to channels borrowing among PUs. For poverty-line heuristic [12], a PU cannot exceed a certain number of channels that can be borrowed from its neighbors even if the neighbors have idle channels.
We further present the results of spectrum utilization with different spectrum sizes in Figure 2. Our scheme performs better than the poverty-line heuristic. Our scheme utilizes the whole spectrum because PUs can have access to neighbor's channels based on availability of channels and on-demand. This improves the cognitive network throughput and overall spectrum utilization. However, some unused spectrum is not utilized under poverty-line heuristic because of the threshold constraint.
It is clear from Figure 2 that our scheme is not sensitive to the number of channels in the network. However, the only constraint that prevents our scheme from full utilization of spectrum is the interference factor. In the poverty-line based scheme, spectrum sharing is limited by the poverty-line that depends on the number of idle channels. From the figure, we can see that as the number of channels increases the utilization of channels decreases because of an increment in idle channels.
Supporting QoS for SUs in CWMNs
Figure 3 presents the offered traffic using on-demand and poverty-line scheme for all SUs classes in the secondary network. In this experiment the arrival rate for all classes are equal (λ i = 1). It is clear from the figure that the on-demand scheme supports much higher traffic than poverty-line. The main reason is utilization of the entire spectrum in the on-demand scheme. Moreover, we can see the offered traffic for class 1 is higher than other classes flow. Because class 1 pays more than other classes, the PUs assign more spectrum for this class. The results stress our scheme ability to support QoS for SUs classes.
Figure 4 measures the average delay for the two schemes (e.g., the delay of a network specifies how long it takes for a packet to travel from one sender to the receiver).
For the poverty-line scheme, because it does not utilize the entire free spectrum, the reported delay is higher than our scheme. Class 1 has the minimum time delay in our scheme because it gets more spectrum than other classes. The figure shows that the resulting performance of all schemes depends on both the spectrum demand at the PUs. The result emphasis that as the demand of spectrum increases at PUs the performance at the secondary network is degraded. Each PU needs a spectrum for its usage and to support the QoS for classic traffic. If an additional network overlaid its traffic over the unused spectrum it should not affect the  of the PU
y
. Figure 5 displays the blocking probability for the two classes under the two schemes. The reported blocking probability for the on-demand scheme is less than the poverty-line. Because it gives the higher reward, the PU assigns the largest amount of spectrum to the class 1. As a result, the proportion of rejecting its requests is less than other classes.
of the PU
y
. Figure 5 displays the blocking probability for the two classes under the two schemes. The reported blocking probability for the on-demand scheme is less than the poverty-line. Because it gives the higher reward, the PU assigns the largest amount of spectrum to the class 1. As a result, the proportion of rejecting its requests is less than other classes.
Figure 6 displays the spectrum size for each class of SUs. The on-demand scheme allocates more spectrum for trading in the secondary network. The entire free spectrum is offered for trading if it is worthy to trade the spectrum. For commercial reasons, PU allocates more spectrum for class 1. Figure 7 shows how the PU satisfies the QoS for SUs classes. Figure 7a shows that PU increases the spectrum price for class 1 to assign more spectrum for class 2. Increasing a spectrum price will reduce the demand for a spectrum and it give the PU advantage of taking the surplus spectrum and assign it to other classes whose blocking probability are not met. In Figure 7a, the PU continues increasing the price for class 1 while it blocking probability is met. For class 2, we notice from Figure 7b how a PU meets the blocking probability by allocating the extra spectrum that is resulted from increasing the price for class 1.
Tradeoffs between a PU revenue and QoS constraints
Figure 8 plots the tradeoff between a PU revenue and its QoS. To show the relationship between the two, we vary the blocking probability constraint for a PU (the QoS requirement for a PU). From the figure, we notice when the blocking constraint becomes stricter, PUs offer less spectrum for all SUs classes to maintain its QoS. As a result, the rejection ratio for SUs requests is increased especially for class 2. However, as this constraint is relaxed, a PU offers more spectrum for all classes of SUs. For large values of blocking probability, a PU can easily maintain a QoS for its applications and therefore it increases the spectrum for all classes but class 1 get the largest part of the offered spectrum. The gained revenue for PU is increased when it becomes less strict.
Figure 9 plots the reported average revenue for PUs under different blocking probability constraints and spectrum demand. The results show that the revenue is increased under large value of blocking probability constraints and spectrum demand. Because our scheme adapt to these changes by computing the revenue at each state, it allocates more spectrum to trade for large values of arrival rates of SUs and PUs blocking probability constraints. The figure stresses the adaptability of our scheme to the changes in the spectrum demand. We notice from the figure when spectrum demand is increased and blocking probability does not surpass  , PU
y
increases the size of the offered spectrum to generate more revenue. However, when the demand decreases, PU reduces the size of the offered spectrum to avoid a waste of spectrum. When the spectrum demand for SUs classes increases, blocking probabilities at PUs normally increase beyond their constraints because of willing of PU to generate more revenue from trading. It is clear as the spectrum demand increases (arrival rate), PUs increases the size of offered spectrum especially for class 1.
, PU
y
increases the size of the offered spectrum to generate more revenue. However, when the demand decreases, PU reduces the size of the offered spectrum to avoid a waste of spectrum. When the spectrum demand for SUs classes increases, blocking probabilities at PUs normally increase beyond their constraints because of willing of PU to generate more revenue from trading. It is clear as the spectrum demand increases (arrival rate), PUs increases the size of offered spectrum especially for class 1.
Spectrum size adaptation for profit maximization
If the blocking probability for a PU is met then it tries to increase the size of the offered spectrum for SUs to generate more revenue and vice versa. Figure 10 displays the offered spectrum sizes for trading in a network which consists of 4 PUs. From the figure, we can see that PUs continue to increase the offered size as there is a chance to maximize the revenues and its QoS is maintained. However, offering more spectrum induces more revenue and less reimbursement cost due to more room available to accommodate user arrivals, but the profit will eventually be saturated due to the bounded SUs customers. Moreover, the blocking probability constraint of a PU prevents it from continuing to increase the size of offered spectrum. Hence, leasing more channels than necessary becomes unproductive in term of revenue and QoS for PUs.
Maintaining QoS for PUs
A PU with well dimensioned spectrum size and correctly chosen spectrum price provides the desired QoS and maintains blocking probabilities in acceptable range. While our adaptation scheme try to maximize PUs' revenues by increasing spectrum size when the spectrum demand increase, it maintains QoS by bringing blocking probabilities back to its constrained range by increasing the spectrum price. Figure 11 shows the spectrum prices adaptation for all classes when the blocking probability surpasses blocking constraint. PU increases the price of spectrum to decrease spectrum demand for each SUs class and maintain QoS for PUs. The results show our scheme's ability to bring blocking probabilities back to their constrained range by adapting spectrum price.
Conclusion
The main objective of this paper is to analyze the ability of CWMNs to maximize PUs revenues, maintain QoS for PUs and serve the maximum number of SUs. CWMNs use the rented spectrum from PUs to overlay their traffic. The resulting CWMN has been modeled, analyzed and simulated. We propose a new scheme for the PUs to control spectrum trading for the emerging spectrum secondary market. PUs can employ the proposed scheme to choose the optimal price and size of the offered spectrum. The objective is to adapt the size and price of spectrum in order to continuously maximize PUs' net revenues while maintaining PUs' QoS.
Simulations were also conducted and demonstrated the ability of our algorithm to support SUs requirements and obtain the potential performance gains by applying cognitive radio. It has been verified that cognitive technology can support additional users without deteriorating the QoS for the PUs. Moreover, the results demonstrated our scheme's ability to maintain QoS for users by adapting the size and price of the offered spectrum under different conditions.
We also propose a new distributed spectrum sharing scheme among primary users. PUs share spectrum based on demand whereby they can borrow spectrum from their neighbors while complying with interference rules. The benchmark in our experiments is the poverty-line heuristic which was proposed in [12]. Because it utilizes the unused spectrum efficiently for trading to the poverty-line heuristic, our scheme achieves higher net revenues. The poverty-line heuristic restricts borrowing by a threshold called poverty line which los the chance of using this spectrum for trading.
Abbreviations
- AI:
-
artificial intelligence
- CR:
-
cognitive radio
- CWMN:
-
cognitive wireless mesh network
- DSA:
-
dynamic spectrum access
- FCC:
-
Federal Communications Commission
- MRs:
-
mesh routers
- MCs:
-
mesh clients
- Pus:
-
primary users
- QoS:
-
quality of service
- RL:
-
reinforcement learning
- SUs:
-
secondary users
- WMN:
-
wireless mesh technology.
References
Akyildiz IF, Lee W-Y, Vuran MC, Mohanty S: NeXt generation/dynamic spectrum access/cognitive radio wireless networks: a survey. Comput Netw 2006, 50: 2127-2159. 10.1016/j.comnet.2006.05.001
Akyildiz IF, Wang X: Wireless Mesh Networks. John Wiley and Sons Ltd, United kingdom; 2009.
Hossain E, Niyato D, Han Z: Dynamic Spectrum Access and Management in Cognitive Radio Networks. Cambridge University Press, United kingdom; 2009.
Niyato D, Hossain E, Le LB: Competitive spectrum sharing and pricing in cognitive wireless mesh networks. In IEEE WCNC. Las Vegas, USA; 2008.
Sutton RS, Barto AG: Reinforcement Learning: An Introduction. The MIT Press, USA; 1998.
Devroye N, Mitran P, Tarokh V: Achievable rates in cognitive radio channels. IEEE Trans Inform Theory 2006, 52(5):1813-1827.
Jafar SA, Srinivasa S: Capacity limits of cognitive radio with distributed and dynamic spectral activity. IEEE J Sel Areas Commun 2007 2007, 25(3):529-537.
Sengupta S, Chatterjee M: Sequential and concurrent auction mechanisms for dynamic spectrum access. In Proceedings of CROWNCOM. Florida, USA; 2007:498-515.
Ileri O, Samandzija D, Sizer T, Mandayam N: Demand responsive pricing and competitive spectrum allocation via a spectrum server. In Proceedings of IEEE DYSPAN. Baltimore, USA; 2005:194-202.
Isiklar G, Bener A: Brokering and pricing architecture over cognitive radio wireless networks. In Proceedings of IEEE CCNC. Las Vegas, USA; 2008:1004-1008.
Buddhikot MM, Kolody P, Miller S, Ryan K, Evans J: DIMSUMNet: new directions in wireless networking using coordinated dynamic spectrum access. In Proceedings of IEEE WoWMoM. Taormina - Giardini Naxos; 2005:78-85.
Lili C, Haitao Z: Distributed rule-regulated spectrum sharing. IEEE J Sel Areas Commun 2008, 26: 130-145.
Li Y, Wang M X: Guizani, A spatial game for access points placement in cognitive radio networks with multi-type service. In IEEE Globecom. Florida, USA; 2010.
Giupponi L, Agustí R, Pérez-Romero J, Sallent O: An economic-driven joint radio resource management with user profile differentiation in a beyond 3G cognitive network. In IEEE Globecom. San Francisco, USA; 2006.
Niyato D, Hossain E: Equilibrium and disequilibrium pricing for spectrum trading in cognitive radio: a control-theoretic approach. In IEEE Globecom. Washington, USA; 2007:4852-4856.
Li D, Xu Y, Liu J, Wang X: A market game for dynamic multiband sharing in cognitive radio networks. In Proceedings of IEEE ICC. Capetown, South Africa; 2010.
Raoof O, Al-Banna Z, Al-Raweshidy HS: Competitive spectrum sharing in wireless networks: a dynamic non-cooperative game approach. In Wireless and Mobile Networking, IFIP Advances in Information and Communication Technology. Volume 308. Springer, Berlin, Heidelberg; 2009.
Alsarhan A, Agarwal A: Cluster-based spectrum management using cognitive radios in wireless mesh network. In ICCCN. San Francisco, USA; 2009.
Ren W, Zhao Q, Swami A: Power control in cognitive radio networks: how to cross a multi-lane highway. IEEE J Sel Areas Commun 2009, 27: 1283-1296.
Kushwaha H, Xing Y, Chandramouli R, Heffes H: Reliable multimedia transmission over cognitive radio networks using fountain codes. Proc IEEE 2008, 96: 155-165.
Avidor D, Mukherjee S, Onat F: Transmit power distribution of wireless ad-hoc networks with topology control. IEEE Trans Wireless Commun 2008, 7: 1111-1116.
Reiman MI, Simon B: Open queueing systems in light traffic. Math Oper Res 1989, 14: 26-59. 10.1287/moor.14.1.26
Beckmann P: Elementary Queuing Theory and Telephone Traffic. In A Volume in a Series on Telephone Traffic. Lee's ABC of the Telephone, Geneva, IL; 1977.
Gallego G, Ryzin Gv: Optimal dynamic pricing of inventories with stochastic demand over finite horizons. Manage Sci 1994, 40: 999-1020. 10.1287/mnsc.40.8.999
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Alsarhan, A., Agarwal, A. Profit optimization in multi-service cognitive mesh network using machine learning. J Wireless Com Network 2011, 36 (2011). https://doi.org/10.1186/1687-1499-2011-36
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1499-2011-36