- Research
- Open access
- Published:
Resource allocation for maximizing outage throughput in OFDMA systems with finite-rate feedback
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 56 (2011)
Abstract
Previous works on orthogonal frequency division multiple access (OFDMA) systems with quantized channel state information (CSI) were mainly based on suboptimal quantization methods. In this paper, we consider the performance limit of OFDMA systems with quantized CSI over independent Rayleigh fading channels using the rate-distortion theory. First, we establish a lower bound on the capacity of the feedback channel and build the test channel that achieves this lower bound. Then, with the derived test channel, we characterize the system performance with the outage throughput and formulate the outage throughput maximization problem with quantized channel state information (CSI). To solve this problem in low complexity, we develop a suboptimal algorithm that performs resource allocation in two steps: subcarrier allocation and power allocation. Using this approach, we can numerically evaluate the outage throughput in terms of feedback rate. Numerical results show that this suboptimal algorithm can provide a near optimal performance (with a performance loss of less than 5%) and the outage throughput with a limited feedback rate can be close to that with perfect CSI.
1 Introduction
Orthogonal frequency division multiplexing (OFDM) is a promising technique for the next-generation wireless communication systems. OFDM divides the frequency-selective fading channel into N orthogonal flat-fading subcarriers to provide a high data rate. Orthogonal frequency division multiple access (OFDMA) adds multiple access to OFDM by allowing a number of users to use different subcarriers. One aim of the OFDMA technique is to find an optimal allocation of resources to users using channel adaptive techniques [1]. It implies that the channel state information (CSI) of users should be known to the base station (BS). However, in the frequency division duplexing (FDD-) OFDMA systems, the BS only obtains the quantized CSI. For downlink transmissions, the BS requires the CSI with the minimum distortion to maximize the transmission rate; for the feedback channel, given a feedback rate constraint, the minimum distortion of the downlink CSI can be characterized by the rate-distortion theory [2]. Thus, the maximum throughput of the OFDMA systems will be achieved, if the feedback CSI is optimized in terms of the rate-distortion function (RDF) [2]. However, existing research works, such as [3–5], mainly focused on simple but suboptimal quantization methods, and did not shown the best performance of OFDMA systems.
In this paper, we focus on the performance limit of the OFDMA system with finite feedback rate. As typically done in the literature (e.g., [3–5]), we assume independent Rayleigh downlink channels over subcarriers, i.e., the channel power gain |H|2 on each subcarrier is exponentially distributed. We use the RDF to characterize the lower bound on the required feedback channel's capacity for a given mean quantization error under OFDMA downlink channels [2]. The author in [6] investigated the optimal encoding of the exponential inter-arrival time of a Poisson process. The RDF of the exponentially distributed time was evaluated with a distortion equal to the absolute error between the quantized arrival time and the actual arrival time. This approach, however, does not result in closed-form results. Here, we consider the alternative approach where the quantized channel gain is less than or equal to the actual channel gain. This constraint applies to the situation in which the truncation quantization method is employed, and enables us to derive the analytical expression for RDF. Once the relation between the distortion (mean magnitude error associated with channel quantization) and rate (capacity of feedback channel) has been established, the resource allocation problem with quantized CSI can be formulated under feedback capacity constraints.
We introduce the outage throughput as the performance measure for the downlink throughput. Here, we define the outage throughput as the maximum expected rate of information delivered to users in non-outage states, where the data rate is lower than the channel capacity. Clearly, the definition of outage throughput is different from that of the ergodic throughput, which is defined as a long-term achievable throughput averaged over all fading blocks [7]. The performance measure of the ergodic throughput is suitable for applications insensitive to delay, but not suitable for delay-sensitive applications. For the latter ones, the outage probability has been considered as a valid performance measure [8–10]. It is desirable to minimize the outage probability for the given quantized CSI. However, low outage probability results in low throughput. There exists a tradeoff between minimizing the outage probability and maximizing the throughput. Outage throughput, which can be regarded as a measure of the expected reliably decodable rate at the user side, provides this tradeoff between transmission rate and outage probability [11, 12].
We investigate the resource allocation problem to maximize the outage throughput. We show that the algorithm that achieves the optimum could have an exponential time complexity. Thus, to reduce the complexity, we propose a suboptimal algorithm that separates the resource allocation into two steps: subcarrier allocation and power allocation. This suboptimal approach has a linear complexity in the number of users and subcarriers and achieves optimality gaps of less than 5%. With the suboptimal approach, the achieved throughput in the rate-distortion limit is more than twice of the throughput achieved under the threshold-based quantization approach, when the feedback rate is low.
Notations: Bold letters denote vectors and matrices, and BT denotes the transpose of B. Also, E[·] denotes the statistical expectation, and in particular, E X [·] denotes that with respect to X.
1.1 Overview
We continue the introduction with a brief review of related work in Section 1.2. Section 2 outlines the downlink channel model and derives the RDF for the downlink CSI. Section 3 presents the expression of outage throughput, formulates the outage throughput maximization problem with quantized CSI, and proposes the resource allocation algorithm that achieves a suboptimal solution. Numerical results are given in Section 4 to illustrate the performance of the outage throughput using the proposed algorithm. Conclusions are drawn in Section 5.
1.2 Related work
In practice, it is difficult for the transmitter to obtain perfect CSI due to feedback delay (for both FDD and time division duplexing (TDD)), channel estimation error (for both FDD and TDD), and quantization error (for FDD) [13]. The impact of imperfect CSI for OFDM systems has been an active research area in recent years. The effect of feedback delay was addressed in [14]. The author considered a minimum square error channel prediction scheme to overcome the detrimental effect of feedback delay and proposed resource allocation algorithms to maximize the downlink throughput. The works in [15–17] focused on the imperfect CSI resulting from channel estimation error and proposed power loading algorithms for the single user OFDM system. Resource allocation with quantized CSI was investigated in [3–5]. The authors in [3] assumed uniform power distribution over subcarriers and derived closed-form expressions for the downlink throughput. In [4, 5], the design parameters related to imperfect CSI, such as quantization levels and the feedback period, were optimized to reduce the feedback overhead with a guaranteed system performance for OFDMA systems. However, most previous research works, such as [3–5], were based on suboptimal quantization method. Recently, the authors in [18] proposed OFDMA throughput maximization algorithm under the assumption that quantization for CSI feedback is optimized in terms of the rate-distortion theory point of view. In [18], the feedback of CSI is assumed to be the Gaussian channel gain H. However, in resource allocation for OFDMA systems, we only need the real value of |H|2 instead of the complex value of H. Thus, it could be more efficient to feed back |H|2 than H to minimize the CSI feedback rate. In this paper, we consider the quantization of |H|2.
The aforementioned research works in [3–5, 14] take the ergodic throughput as the performance measure. For applications insensitive to delay, the ergodic throughput is a suitable performance measure [7]. On the other hand, the outage throughput is more appropriate to characterize the downlink throughput for real-time applications [8]. In this work, we discuss the outage throughput maximization with imperfect CSI.
2 System model
We consider a one-cell OFDMA system with N subcarriers (or orthogonal channels) that will be shared by K users. The system model is depicted in Figure 1. We assume that each subcarrier is assigned to one user exclusively and the system employs FDD. It is assumed that each user perfectly estimates the CSI of the downlink channel (from the BS to the user), which is simply referred to as downlink CSI in this paper. Each user quantizes his/her estimated downlink CSI and sends it (actually an index of quantized downlink CSI) to the BS through a dedicated feedback channel. The BS receives the downlink CSI from all users and utilizes this information to assign subcarriers to users and adjust transmit power for each subcarrier.
Denote by H k, n the channel gain of user k at subcarrier n. Throughout the paper, we assume that the channel gains are independent over subcarriers and the probability density function of the channel power gain α k, n = |H k, n |2 is given by

where u(·) denotes the unit step function, and λ k, n = E[α k, n ]. Here, the channel power gain α k, n is exponentially distributed, α k, n ~ exp(λ k, n ), where exp(m) denotes the exponential distribution with mean m. Due to the assumption of independent channels, we may not be able to take the spatial correlation of frequency-selective fading channels. However, if subcarriers are discontinuously allocated to a user, the spatial correlation can be ignored.
Now, we consider the quantization of downlink CSI and determine the capacity of the feedback channel required to deliver the quantized CSI using the rate-distortion theory. From this, we can characterize the minimum distortion of the quantized CSI for a given capacity of the feedback channel.
User k describes his/her knowledge of downlink CSI A
k
= (αk,1, ..., α
k, N
)T by an index I
k
and feeds the index I
k
back to the BS. The BS reproduces  from the index I
k
, where
from the index I
k
, where  is the quantized description of α
k, n
. The quantized power gain
is the quantized description of α
k, n
. The quantized power gain  is assumed to be not greater than the actual power gain
is assumed to be not greater than the actual power gain  .
.
To measure the accuracy of the quantized CSI, we introduce the distortion measure function with the magnitude error criterion:

Then, we can define the information RDF of A k as

where D k denotes the upper bound of the mean quantization error and I(·;·)denotes the mutual information. By the rate-distortion theory [2], this RDF gives a minimum number of bits for the index I k that can describe the channel power gain A k without exceeding the mean quantization error D k . The RDF of A k is given by the following theorem:
Theorem 1. Let A k = (αk,1, ..., α k, N )T be a vector source with uncorrelated components that are exponentially distributed given by Equation 1. Then,
-
1.
the RDF of A k is given by
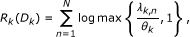
where θ k is chosen such that

-
2.
the test channel that achieves the RDF is given by

where Z k = (zk,1, ..., z k, N ) is independent of
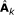 and has uncorrelated components with Z
k, n
~ exp (min{θ
k
, λ
k, n
}).
and has uncorrelated components with Z
k, n
~ exp (min{θ
k
, λ
k, n
}).
Proof: See Appendix Appendix 1.
Remark 1. In downlink throughput maximization with imperfect CSI, we require the probability density function of the actual power gain conditioned on the quantized power gain. By the second part of Theorem 1, for a given  , the probability density function of α
k, n
is
, the probability density function of α
k, n
is

where v k, n = min {θ k , λ k, n }. Here, the variable v k, n can be regarded as the mean quantization error for the channel power gain α k, n .
Remark 2. There are two special cases. By setting θ
k
= 0, from Theorem 1, we have D
k
= 0, R
k
(D
k
) = +∞ and z
k, n
= 0. In this case, the CSI is perfectly known to the BS. On the other hand, by setting θ
k
= +∞, we have  and R
k
(D
k
) = 0, which implies that no CSI is fed back to the BS.
and R
k
(D
k
) = 0, which implies that no CSI is fed back to the BS.
3 Outage throughput maximization with quantized CSI
3.1 Problem formulation
For a given capacity of the feedback channel, we have characterized the distortion in Section 2. With the quantized downlink CSI, the resource allocation can be carried out for a given performance measure. From this, we can formulate the resource allocation with capacity constraints of the feedback channels. Toward this end, in this subsection, we introduce the outage throughput as the performance measure.
Given the quantized CSI, the outage probability on the n-th subcarrier to the k-th user is defined as

where γ n is the input signal error ratio (SNR) of the n-th subcarrier and R is the transmission rate. From Equation 3, the maximum transmission rate R that can maintain the outage probability ε is

where  . Thus, the expected rate of information successfully decoded at user k on subcarrier n is
. Thus, the expected rate of information successfully decoded at user k on subcarrier n is

It is possible to maximize  by choosing ε,
by choosing ε,

Here, the throughput  is termed as the outage throughput. Setting
is termed as the outage throughput. Setting  , we obtain
, we obtain

where  . Substituting Equation 2 yields
. Substituting Equation 2 yields

The optimal x that maximizes  is given by the following theorem:
is given by the following theorem:
Theorem 2. There exists a unique globally optimal x that maximizes  in Equation 6, which is given by
in Equation 6, which is given by

where W(x) is the Lambert-W function, which is the solution to the equation W(x)e W(x)= x.
Proof See Appendix Appendix B.
Thus, for each given transmit power γ
n
, quantized power gain  and quantization error v
k, n
, we can evaluate the outage throughput of the k-th user on the n-th subcarrier
and quantization error v
k, n
, we can evaluate the outage throughput of the k-th user on the n-th subcarrier  in Equation 5 by Theorem 2. The overall outage throughput conditioned on the quantized CSI
in Equation 5 by Theorem 2. The overall outage throughput conditioned on the quantized CSI  is represented as
is represented as

where ρ
k, n
is the subcarrier allocation indicator: if the n-th subcarrier is assigned to the k-th user, then ρ
k, n
= 1; otherwise ρ
k, n
= 0. Here, the BS decides γ
n
and ρ
k, n
with the knowledge of quantized CSI  . To emphasize this, we denote the input SNR and the allocation indicator as functions of
. To emphasize this, we denote the input SNR and the allocation indicator as functions of  by
by  and
and  , respectively. The average outage throughput is thus given by
, respectively. The average outage throughput is thus given by

Now, we can formulate the outage throughput maximization under feedback capacity constraints:

where the first constraint is the feedback capacity constraint, the second constraint ensures that each subcarrier is assigned to one user exclusively, and the third constraint is for total transmit power, denoted by γ T .
By Theorem 1, for each R
k
(D
k
), there exists a test channel that achieves R
k
(D
k
). Thus, maximizing the downlink throughput under feedback capacity constraints is equivalent to maximizing the downlink throughput under the corresponding test channel. It can also be observed that to maximize T°, we can maximize the conditional outage throughput  for each realization of
for each realization of  under the conditional probability density function
under the conditional probability density function  given in Equation 2. That is,
given in Equation 2. That is,

To make the problem in Equation 10 tractable, we consider a suboptimal solution by breaking the problem into two steps: subcarrier allocation and power allocation. In the first step, subcarriers are assigned to users under the assumption that the transmit power is identical over all subcarriers; in the second step, power is loaded on the subcarriers assigned in the first step.
3.2 Subcarrier allocation
Under the assumption of γ n = γ T /N, the optimization problem in Equation 10 reduces to

It implies that the subcarriers should be assigned based on the following criterion:

The above criterion requires to evaluate KN values of the rate given in Equation 5. However, we can simplify this criterion in the case where on subcarrier n, the mean quantization error v k, n is identical among all users k. We state the following theorem:
Theorem 3. For any given v
k, n,
, the throughput  defined Equation 5 is monotonically increasing in
defined Equation 5 is monotonically increasing in  if
if  in Equation 5 is monotonically increasing in
in Equation 5 is monotonically increasing in  .
.
Proof By assumption, we have  for
for  . Thus,
. Thus,

It follows that

It can be shown that  given in Equation 6 is monotonically increasing in
given in Equation 6 is monotonically increasing in  . Thus, by Theorem 3, in the case of v
k', n
= v
k, n
for k ≠ k', the subcarrier allocation reduces to
. Thus, by Theorem 3, in the case of v
k', n
= v
k, n
for k ≠ k', the subcarrier allocation reduces to

When a tie occurs, we can select users in random fashion.
3.3 Power allocation
Denote by k n the selected user on the n-th subcarrier, i.e., k n = arg max k ρ k, n . Given the subcarrier allocation, the problem 10 becomes

From the Equations 6 and 7, we can observe that  is not concave in γ
n
. Hence, the problem 12 is not a convex optimization problem. However, we can employ a dual approach to obtain a suboptimal solution.
is not concave in γ
n
. Hence, the problem 12 is not a convex optimization problem. However, we can employ a dual approach to obtain a suboptimal solution.
The dual problem is

where

where μ is the Lagrangian multiplier of the first constraint in Equation 12. Given μ, the optimal power allocation on the n-th subcarrier is

We can use a derivative-free line search method, such as the golden section method to find the γ n for a given Lagrangian multiplier μ [19].
The Lagrangian dual problem 13 has been shown to be a convex optimization problem in μ [20]. Thus, we can use the bisection method to find the optimal global multiplier μ [19]. The bisection method requires to evaluate the first derivative of g(μ) with respect to μ. Although g(μ) is not continuously differentiable due to the max function, we can use the subgradient instead [21],

where γ n is obtained from Equation 14.
Using the dual optimization approach, it is possible that the final power allocation  may not satisfy
may not satisfy  . We can multiply the final power allocation on each subcarrier
. We can multiply the final power allocation on each subcarrier  by a constant
by a constant  to arrive a feasible solution.
to arrive a feasible solution.
Complexity: in the first step, assigning subcarriers requires to find the maximum  among K users for each subcarrier n, and thereby, the complexity of subcarrier allocation is O(KN). In the power allocation, in each iteration for μ in Equation 13, we need to compute N power allocation values given by Equation 14. Each power allocation value requires a search routine, which is assumed to converge within I
γ
iterations. Assuming that I
μ
iterations are required to find the optimal μ, the overall complexity of the suboptimal algorithm is O(KN + I
μ
I
γ
N). Ignoring the constants I
μ
and I
γ
, the complexity is just O(KN).
among K users for each subcarrier n, and thereby, the complexity of subcarrier allocation is O(KN). In the power allocation, in each iteration for μ in Equation 13, we need to compute N power allocation values given by Equation 14. Each power allocation value requires a search routine, which is assumed to converge within I
γ
iterations. Assuming that I
μ
iterations are required to find the optimal μ, the overall complexity of the suboptimal algorithm is O(KN + I
μ
I
γ
N). Ignoring the constants I
μ
and I
γ
, the complexity is just O(KN).
4 Numerical results
We present several numerical results to demonstrate the performance of OFDMA systems using the proposed algorithms. We assume an OFDMA system with the average channel power gain E[α k, n ] = 1. Furthermore, the feedback capacities of all users are assumed to be identical. That is, C K = C K' for all k ≠ k'. By Theorem 1, it implies that the mean quantization errors of all users on each subcarrier n are identical, v k, n = v k', n
First, for the problem 10, we compare the proposed suboptimal algorithm with a full-searching algorithm. This full-searching algorithm considers all possible subcarrier allocations, and for each subcarrier allocation, it assigns transmit power based on the dual optimization approach as proposed in Section 3.3 without projecting the final power allocation back to the feasible region. Thus, this algorithm gives an upper bound on the optimal solution to the problem in 10 [20].
Figure 2 plots both the suboptimal results and the upper bound of the optimal results for an OFDMA system with N = 8 subcarriers and K = 2 users. In Figure 2, as the capacity of the feedback channel increases from C k = 1.6 bps/Hz to C k = 64 bps/Hz, the performance gap between the suboptimum and the upper bound of the optimum gets larger. However, in both scenarios, the difference between the optimum and suboptimum is within 5%.
Next, we consider an OFDMA system with N = 1,024 subcarriers and K = 8 users. We compare the outage throughput achieved in the rate-distortion limit using the proposed suboptimal algorithm with the threshold-based quantization method considered in [4, 22]. In the threshold-based quantization method, the channel power gain α
k, n
on each subcarrier n of each user k is quantized in intervals with  thresholds T
q
with q = 0, ..., W, where T0 = 0, T
W
= + ∞, and N
Q
is the number of quantization bits per subcarrier. Here, we assume that all users have identical N
Q
on all subcarriers. The thresholds T
q
for q = 1, ..., W - 1 are determined by partitioning the probability density function of α
k, n
into W equiprobable intervals. It implies that T
q
= F-1(q/W), where F(·)is the cumulative density function (cdf) of α
k, n
. The decoded channel power gain at the BS side is assumed to be
thresholds T
q
with q = 0, ..., W, where T0 = 0, T
W
= + ∞, and N
Q
is the number of quantization bits per subcarrier. Here, we assume that all users have identical N
Q
on all subcarriers. The thresholds T
q
for q = 1, ..., W - 1 are determined by partitioning the probability density function of α
k, n
into W equiprobable intervals. It implies that T
q
= F-1(q/W), where F(·)is the cumulative density function (cdf) of α
k, n
. The decoded channel power gain at the BS side is assumed to be

Then, the BS assigns subcarriers and transmit power with the knowledge of the power gain  : the user with the highest power gain
: the user with the highest power gain  is chosen on each subcarrier, and the transmit power on each subcarrier is determined using the water-filling method [23]. This method gives the maximum throughput when
is chosen on each subcarrier, and the transmit power on each subcarrier is determined using the water-filling method [23]. This method gives the maximum throughput when  [23].
[23].
Figure 3 shows the rate-distortion curves for the two schemes. In this figure, for a wide range of the average distortion, the required capacity of the feedback channel in the rate-distortion limit is about 50-80% of the threshold-based quantization scheme. However, when the capacity of the feedback channel is zero (no CSI is fed back to the BS), both schemes result in the average distortion of NE[α k, n ] = 1,024.
Figure 4 depicts the outage throughput in terms of the capacity of the feedback channel. When no CSI is available at the BS, according to Sections 3.2 and 3.3, the proposed scheme tends to assign subcarriers randomly to users and allocate equal transmit power γ
n
on each subcarrier n. In this case, the outage throughput is N max
x
log(1+xγ
T
/N)Pr(α
k, n
≥ x). For the threshold-based method, since the decoded power gain  is equal to the knowledge of the lower bound on the actual power gain as given by Equation 15, the BS can only set
is equal to the knowledge of the lower bound on the actual power gain as given by Equation 15, the BS can only set  . In this case, no signal is transmitted on subcarriers. At C
k
< 400 bps/Hz, the achieved outage throughput in the rate-distortion limit is more than twice of the threshold-based method. The difference between the two schemes decreases for larger capacity of the feedback channel. When the feedback channel's capacity of each user reaches 6,144 bps/Hz, the throughput is saturated regardless of any type of the schemes (could happen when the perfect CSI is available at the BS). It can also be noted that at γ
T
/N = 30 dB and C
k
= 1,024 bps/Hz, the performance gap between the outage throughput in the rate-distortion limit and that in the perfect CSI case is within 6%. Thus, it implies that with limited feedback rate, the system performance can be close to that of the perfect CSI one.
. In this case, no signal is transmitted on subcarriers. At C
k
< 400 bps/Hz, the achieved outage throughput in the rate-distortion limit is more than twice of the threshold-based method. The difference between the two schemes decreases for larger capacity of the feedback channel. When the feedback channel's capacity of each user reaches 6,144 bps/Hz, the throughput is saturated regardless of any type of the schemes (could happen when the perfect CSI is available at the BS). It can also be noted that at γ
T
/N = 30 dB and C
k
= 1,024 bps/Hz, the performance gap between the outage throughput in the rate-distortion limit and that in the perfect CSI case is within 6%. Thus, it implies that with limited feedback rate, the system performance can be close to that of the perfect CSI one.
5 Conclusions
In this paper, we investigated the outage throughput maximization for an OFDMA system with finite feedback rate over independent Rayleigh fading channels. First, we derived the RDF for the downlink CSI. This RDF gives a lower bound on the capacity of the feedback channel according to the rate-distortion theory. Meanwhile, we obtained the test channel that achieves this RDF. The derived test channel enabled us to formulate the resource allocation problem that maximizes the outage throughput with capacity constraints of feedback channels. For this problem, we proposed a low-complexity suboptimal algorithm. This algorithm divides the problem into two subproblems, namely subcarrier and power allocation problems. Through numerical results, we found that the proposed suboptimal algorithm has performance close to the optimum. We also observed that the outage throughput in the rate-distortion limit outperforms that with the threshold-based quantization method, and with limited feedback rate, the system performance can be close to that with perfect CSI.
Appendix A Proof of Theorem 1
First, we show that the exponential distribution maximizes the entropy over all distributions with non-negative support.
Lemma 1. Let the non-negative random variable x have the mean E[x] = m. Then, the differential entropy of x is upper bounded by , and the equality is achieved iff x is exponentially distributed, x ~exp(m).
, and the equality is achieved iff x is exponentially distributed, x ~exp(m).
Proof Let f(x) be the probability density function of a non-negative random variable x satisfying  . Let y be an exponentially distributed random variable with the Probability Density Function g(y) = exp (-y/m)/m. Then,
. Let y be an exponentially distributed random variable with the Probability Density Function g(y) = exp (-y/m)/m. Then,

where (Appendix A.1a) follows from  , and (Appendix A.1b) follows from the concavity of the function log.
, and (Appendix A.1b) follows from the concavity of the function log.
Then, we derive the RDF for an one-dimensional exponentially distributed source x ~ exp(m).
Lemma 2. Define the RDF of an exponentially distributed source x ~ exp(m) as

where  is the quantized description of x. Then, the RDF is given by
is the quantized description of x. Then, the RDF is given by

and the test channel that achieves this RDF is

where z is independent of  with z ~ exp(min{D, m}).
with z ~ exp(min{D, m}).
Proof In the case D > m , the quantizer need not transmit any information since the the decoded information can be chosen as

This ensures that the constraints  and
and  are satisfied. In this case,
are satisfied. In this case,  and z ~ exp(m). Henceforth, we assume 0 ≤ D ≤ m. We observe that
and z ~ exp(m). Henceforth, we assume 0 ≤ D ≤ m. We observe that

where (Appendix A.2a) follows from the fact that conditioning reduces entropy, and (Appendix A.2b) follows from Lemma 1. The equality in (Appendix A.2a) is achieved iff  independent of
independent of  , and the equality in (Appendix A.2b) is achieved iff z ~ exp(D).
, and the equality in (Appendix A.2b) is achieved iff z ~ exp(D).
Now, we are able to prove Theorem 1.
Proof [Proof of Theorem 1] We have

where  , (Appendix A.3a) follows from the fact that the components of A
k
are uncorrelated, (Appendix A.3b) from the fact that conditioning reduces entropy, and (Appendix A.3c) follows from Lemma 2. The equality (Appendix A.3c) is achieved iff
, (Appendix A.3a) follows from the fact that the components of A
k
are uncorrelated, (Appendix A.3b) from the fact that conditioning reduces entropy, and (Appendix A.3c) follows from Lemma 2. The equality (Appendix A.3c) is achieved iff  with z
k, n
~ exp(min{λ
k, n
, D
k, n
}) is independent of
with z
k, n
~ exp(min{λ
k, n
, D
k, n
}) is independent of  , and the equality in (Appendix A.3b) is achieved iff
, and the equality in (Appendix A.3b) is achieved iff  . From this, it also implies that Z
k
= (zk,1, ..., z
k, N
)T has uncorrelated components.
. From this, it also implies that Z
k
= (zk,1, ..., z
k, N
)T has uncorrelated components.
The problem of finding the RDF of A k now reduces to

The Lagrangian of the problem is

where μ is the Lagrangian multiplier. We can find the optimal D k, n that minimizes L by differentiating L with respect to D k, n ,

Thus, we conclude the optimal D k, n is

where θ = log e/μ.. Recalling the constraint ∑ n D k, n = D k , we obtain the result of the Theorem 1.
Appendix B Proof of Theorem 2
Proof First, we show that ln  in Equation 6 is concave in x ∈ (0, + ∞). From Equation 6, we express ln
in Equation 6 is concave in x ∈ (0, + ∞). From Equation 6, we express ln  as
as

Since log(1 + xγ
n
) is concave in x and log(1 + xγ
n
) > 0 for x > 0, γ
n
≥ 0, lnlog(1 + xγ
n
) is concave in x for i > 0, γ
n
≥ 0 [[20], p.86]. Since non-negative weighted sum and pointwise infimum preserve the concavity [[20], Section 3.2], ln  is concave in x.
is concave in x.
Also, note that  in Equation 6 satisfies
in Equation 6 satisfies  , and
, and  . Thus, there exists a globally unique x that maximizes
. Thus, there exists a globally unique x that maximizes  .
.
Differentiating  with respect to x for
with respect to x for  and setting equal to zero, we have
and setting equal to zero, we have

That is,

For  ,
,  is maximized when
is maximized when  . Thus, we have the solution in 7.
. Thus, we have the solution in 7.
References
Wong CY, Cheng R, Lataief K, Murch R: Multiuser OFDM with adaptive subcarrier, bit, and power allocation. IEEE J Select Areas Commun 1999, 17(10):1747-1758. 10.1109/49.793310
Berger T: Rate Distortion Theory: A Mathematical Basis for Data Compression. Prentice-Hall Englewood Cliffs, New Jersey, USA; 1971.
Kuehne A, Klein A: Adaptive subcarrier allocation with imperfect channel knowledge versus diversity techniques in a multi-user OFDM-system. Proceedings of the IEEE PIMRC '07 2007, 1-5.
Agarwal R, Majjigi V, Han Z, Vannithamby R, Cioffi J: Low complexity resource allocation with opportunistic feedback over downlink OFDMA networks. IEEE J Select Areas Commun 2008, 26(8):1462-1472.
Chen J, Berry RA, Honig ML: Performance of limited feedback schemes for downlink OFDMA with finite coherence time. Proceedings of the IEEE ISIT '07 2007, 2751-2755.
Rubin I: Information rates and data-compression schemes for poisson processes. IEEE Trans Inform Theory 1974, 20(2):200-210. 10.1109/TIT.1974.1055195
Goldsmith AJ, Varaiya PP: Capacity of fading channels with channel side information. IEEE Trans Inform Theory 1997, 43(6):1986-1992. 10.1109/18.641562
Bettesh I, Shamai S: Outages, expected rates and delays in multiple-users fading channels. Proceedings of the Conference on Information Science and Systems 2000., 1:
Biglieri E, Proakis J, Shamai S: Fading channels: information-theoretic and communications aspects. IEEE Trans Inform Theory 1998, 44(6):2619-2692. 10.1109/18.720551
Cover T: Broadcast channels. IEEE Trans Inform Theory 1972, 18(1):2-14. 10.1109/TIT.1972.1054727
Kim T, Skoglund M: On the expected rate of slowly fading channels with quantized side information. IEEE Trans Commun 2007, 55(4):820-829.
Effros M, Goldsmith A: Capacity definitions and coding strategies for general channels with receiver side information. Proceedings of the IEEE ISIT '98 1998, 39.
Isukapalli Y, Annavajjala R, Rao B: Performance analysis of transmit beamforming for miso systems with imperfect feedback. IEEE Trans Commun 2009, 57(1):222-231.
Wong IC, Evans B: Optimal resource allocation in the OFDMA downlink with imperfect channel knowledge. IEEE Trans Commun 2009, 57(1):232-241.
Yao Y, Giannakis G: Rate-maximizing power allocation in OFDM based on partial channel knowledge. IEEE Trans Wireless Commun 2005, 4(3):1073-1083.
Sukumar C, Merched R, Eltawil A: Joint power loading of data and pilots in OFDM using imperfect channel state information at the transmitter. Proceedings of the IEEE Globecom '08 2008, 1-5.
Choi E, Choi W, Andrews J, Womack B: Power loading using order mapping in OFDM systems with limited feedback. IEEE Signal Process Lett 2008, 15: 545-548.
Chen C, Bai L, Wu B, Choi J: Downlink throughput maximization for OFDMA systems with feedback channel capacity constraints. IEEE Trans Signal Process 2011, 59(1):441-446.
Press WH, Flannery BP, Teukolsky SA, Vetterling WT: Numerical Recipes in C: The Art of Scientific Programming. Cambridge University Press, Cambridge, England; 1992.
Boyd S, Vandenberghe L: Convex Optimization. Cambridge University Press, Cambridge, England; 2004.
Bertsekas DP: Nonlinear Programming. 2nd edition. Athena Scientific, Belmont, USA; 2004.
Agarwal R, Hwang C-S, Cioffi J: Opportunistic feedback protocol for achieving sum-capacity of the mimo broadcast channel. Proceedings of the IEEE VTC '07-Fall 2007, 606-610.
Jang J, Lee KB: Transmit power adaptation for multiuser OFDM systems. IEEE J Select Areas Commun 2003, 21(2):171-178. 10.1109/JSAC.2002.807348
Acknowledgements
This work has been supported by the China Postdoctoral Science Foundation and the China National 973 project under the grant No. 2009CB320403.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wu, B., Bai, L., Chen, C. et al. Resource allocation for maximizing outage throughput in OFDMA systems with finite-rate feedback. J Wireless Com Network 2011, 56 (2011). https://doi.org/10.1186/1687-1499-2011-56
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1499-2011-56

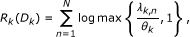


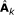 and has uncorrelated components with Z
k, n
~ exp (min{θ
k
, λ
k, n
}).
and has uncorrelated components with Z
k, n
~ exp (min{θ
k
, λ
k, n
}).

