- Research
- Open access
- Published:
Selective sensing and transmission for multi-channel cognitive radio networks
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 7 (2011)
Abstract
In this article, we consider a continuous time Markov chain (CTMC) modeled multi-channel CR network, where there are multiple independent primary users and one slotted secondary user (SU) who can access multiple channels simultaneously. To maximize SU's temporal channel utilization while limiting its interference to PUs, a selective sensing and selective access (SS-SA) strategy is proposed. With SS strategy, each channel is sensed almost periodically with different periods according to parameter Tc, which reflects the maximal period that each channel should be probed. The effect of sensing period is also considered. When the sensing period is suitable, the SA strategy can be regarded as greedy access strategy. Numerical simulations illustrate that Tc is a valid measurement to indicate how often each channel should be sensed, and with SS-SA strategy, SU can effectively utilize the channels and consume less energy and time for sensing than adopting reference strategies.
Introduction
Recently, people have made great progress on cognitive radio (CR) technology [1, 2]. The basic idea of CR is to allow secondary user (SU) to search and utilize instantaneous spectrum opportunities left by primary user (PU), while limiting its interference to PU. Therefore, SU's sensing and access strategy is very important to its performance, especially for multi-channel CR networks. To discover and utilize the spectrum opportunities timely and efficiently, SU should first model PU's behavior. There are mainly two models, namely, discrete-time model and continuous-time model.
In discrete-time model, PU's time behavior is slotted and SU adopts the same slot size as PU. In [3], the authors show that intuitive sensing (IS) strategy (i.e., descending order of channel's available probability) is not optimal when adaptive modulation is used, and then propose a dynamic programming approach to search for the optimal sensing order. However, the computational complexity is high. In [4], the authors propose an opportunistic MAC protocol with random and negotiation-based sensing policies for ad hoc networks. In [5], the authors derive the optimal sensing and access strategy under the formulation of finite-horizon partially observable Markov decision process (POMDP). For this model, the synchronization of all primary and secondary users is necessary, which increases more overhead. And the time offset may be fatal for SU's access strategy.
In continuous-time model, PU is not time-slotted but SU is still slotted mostly. Since PU's state may change at any time, this model is more difficult to analyze. The authors of [6] derive the optimal access strategy with periodic sensing (PS) for one slotted SU overlapping a CTMC modeled multi-channel primary network. Although PS is easy to implement, it is not efficient. Furthermore, the access strategy, which allows SU access only one channel in each slot, is also not efficient for multi-channel network. In [7, 8], the authors obtain the optimal access strategy with fully sensing. However, on the one hand, the frequency of channel's state changes is different generally, thus, how often each channel should be probed is distinct. On the other hand, if SU senses all channels simultaneously, it takes much energy and time to probe channels, process the received signals and judge the channels' states. Therefore, in each slot, SU has no need to probe all channels, instead, it could only sense part of channels, by which SU could save more energy and time for transmission. If so, SU needs a sensing strategy to decide which channels should be detected first. Furthermore, none of these works study the magnitude of sensing period, which also affects the design of sensing and access strategy. Obviously, the sensing period could not be very large especially for the channels whose state changes quickly, and excessive tiny sensing period is also not necessary, which makes SU consume much energy and time for sensing. Thus, suitable sensing period should also be considered. In [9–11], the optimal sensing period is derived for the simplest single-channel model. In [12], a theoretical framework is proposed for jointly optimizing sensing and transmission time for each channel. And then a spectrum selection and sensing scheduling method is proposed to exploit multiple channels. However, the authors do not analyze the optimal sensing period and only adopt the minimum time unit of sensing time and transmission time.
In our previous study [11], we investigate the simplest single-channel continuous-time model and proposed two access policies under interference constraint and energy consumption constraint. Finally, the optimal sensing period and transmission time are derived. In this article, we will consider a more general situation, namely, multi-channel CR network. For this multi-channel network, we investigate SU's sensing and access strategies. Furthermore, the magnitude of sensing period is also considered. Particularly, we assume that each channel is assigned to one PU and each channel's time behavior is modeled by a two-state (ON/OFF) first-order continuous time Markov chain. Furthermore, we assume all PUs' activities are independent. Meanwhile, SU employs a time slotted communication protocol and adopts a "Listen-Before-Talk" strategy, according to which SU senses these channels before transmission. Furthermore, SU can access these available channels simultaneously. We assume that SU senses only one channel in each slot (the proposed sensing strategy can be easily generalized to the case when SU probes n channels each time). Therefore, at the beginning of each slot, SU should decide which channel should be sensed first, and then decide if and in which channels to transmit according to the current and historic sensing results.
The main contributions of this article are as follows. To maximize SU's temporal channel utilization while limiting its interference to PUs, we propose a selective sensing and selective access (SS-SA) strategy for one slotted SU overlaying a non-time-slotted ON/OFF CTMC modeled multi-channel primary network. And the proposed SS-SA strategy is simple and easy to implement. With the proposed SS strategy, each channel will be detected almost periodically with different periods according to the parameter Tc. The parameter Tc, which is related to channel's characteristic parameters and interference tolerance, is a valid measurement to indicate how often each channel should be sensed. If SU's sensing period is suitable, the proposed SA strategy can be regarded as greedy access strategy. The greedy access strategy is also appropriate for SU adopting PS or IS strategy with suitable sensing period. With SS-SA strategy, SU can effectively utilize these channels and adopt larger sensing period than PS-SA and IS-SA strategies, which means SU could consume less energy and time for sensing.
The rest of the article is organized as follows. After introducing the system model and problem formulation, the periodic sensing and selective access (PS-SA) strategy and SS-SA strategy are studied, followed by the simulation results. Finally, conclusions are drawn.
System model and problem formulation
In this section, we will first introduce system model and time behaviors of PU and SU, and then we will focus on the problem formulation.
System model
We consider a multi-channel CR network which has multiple channels available for transmissions by primary and secondary users. Particularly, we assume there are N channels and each channel is assigned to one PU. Furthermore, we assume there is only one SU, who can access these available channels simultaneously, and its transmission on one channel will not interfere with other channels. To achieve this, we can simply adopt D-OFDM as the physical layer technique with a single radio equipment [13, 14]. The SU can be regarded as one node of an ad hoc network, which communicates with another one in multiple channels, or a CR base station, who can serve multiple SUs at the same time.
We assume that all PUs exhibit a non-time-slotted ON/OFF behavior and their activities are independent, while SU employs a time-slotted communication protocol with period Ts. Furthermore, SU adopts a "Listen-Before-Talk" strategy. Take PS for example, the time behaviors of primary and secondary users are shown in Figure 1.
The channel model
As mentioned above, PU's behavior is not time slotted and switches between ON and OFF states. Furthermore, we model each channel's time behavior by a two-state (ON/OFF) first-order CTMC, which arises from [7]. Such a CTMC model is not always justified, of course, but experimental studies on the IEEE 802.11 Wireless LAN (WLAN) support a semi-Markovian model for various traffic patterns (ftp, http, and VoIP) [15–19]. The CTMC assumption strikes a good tradeoff between model accuracy and the facility of theoretical analysis. And this modeling approach has been used in lots of related publications [6, 20].
Based on stochastic theory [21], for arbitrary channel i, the holding times in both ON and OFF states are exponentially distributed with parameters μi,ONand μi,OFF, respectively. The transition matrix of ON and OFF states is given by (1). The transition diagram of ON/OFF model is shown in Figure 2.

Since channel's parameters μi,ONand μi,OFFare statistical parameters, SU can obtain them by historical information. Thus, we assume these parameters are available to SU.
SU's sensing and access model
Generally, the frequency of different channels' states change is different, thus, how often each channel should be probed will be distinct. For example, if the channel's ON/OFF states switch slowly, the last sensing result will still be trustworthy for a long time, thus, sensing period could be large, or else sensing period should be small. On the other hand, if SU senses all channels simultaneously, it takes more energy and time to probe channels, process received signals and judge channels' states. Therefore, in each slot, SU has no need to probe all of these N channels, instead, it could only sense part of the channels, by which SU will consume less energy and time. It is noteworthy that the state of the system at any time will be only partially observed, therefore, the interference between PU and SU is unavoidable. For example, in Figure 1, SU collides with PU2 in slot 4.
Particularly, we assume that SU senses only one channel in each slot (the proposed sensing strategy can be easily be generalized to the case when SU probes n(≤ N) channels each time). To perceive all channels' states well, at the beginning of each slot, SU should decide which channel should be sensed first. And then, to increase its spectrum utilization and meanwhile limit its interference to each PUs, SU should decide if and in which channels to transmit according to the current and historic sensing results.
Besides, for ease of analysis, we assume perfect sensing and the sensing time is short enough to be ignored. However, we provide the simulation results when the sensing time cannot be ignored.
Problem formulation
We focus on the problem of maximizing SU's total channel utilization while limiting its interference perceived by PUs. Particularly, the interference between PU and SU is modeled by the average temporal overlap, namely, interference time divided by total time, which is also adopted in some related publications [7, 10]. Mathematically, the interference I i between SU and PU i is1

where 1{·} is the indicator function of the event enclosed in the brackets; A i (τ) and B i (τ) denote the event that PU i and SU access channel i at time τ, respectively.
Similarly, channel utilization is defined by SU's temporal utilization ratio, namely, transmission time divided by total time.
Mathematically, SU's channel utilization U i on channel i is

Therefore, this leads to the problem P:


where C i ∈ 0[1] is the maximum interference level tolerable by PU i. Generally, C i is very small, e.g., C i = 1%.
It is obvious that SU's sensing and access strategy will jointly affect its interference to PUs and the channel utilization. For example, assume that under some sensing strategy, if one channel whose state changes quickly has not been sensed for a long time, then SU will not forecast this channel's state accurately. If SU accesses this channel, the probability of collision (interference) will increase; otherwise, SU's channel utilization will decrease. Therefore, the rapidly the channel's ON/OFF state varies, the frequently the channel should be sensed.
It is remarkable that sensing strategy for the SU who can access only one channel at a time is different from the one who can access multiple channels simultaneously. This is because if SU can access only one channel at a time, then it will tend to sense the channel whose idle probability is high, for the purpose of channel utilization, or the channel whose idle duration is large, for the purpose of less spectrum mobility.
Furthermore, the magnitude of sensing period Ts will also affect this problem. Obviously, Ts could not be very large especially for these channels whose state change quickly, and excessive tiny sensing period is also not necessary, which will make SU consume more energy and time to sense the channels. Thus, suitable sensing period should be chosen.
Therefore, to maximize SU's channel utilization while limiting its interference to PUs, we will study the sensing and access strategy for one SU overlaying multi-channel primary networks. At the same time, the effect of sensing period Ts will also be taken into account.
PS-SA strategy
In this section, we will first focus on the optimal access strategy while SU senses these channels periodically. The PS strategy facilitates the theoretical analysis. And we will discover the disadvantage of PS strategy, which will help us to propose the better SS strategy in the next section.
Sub-problem of the original problem P
Figure 1 illustrates the sensing and transmission structure under PS strategy for a case of N = 4. At the beginning of each slot, SU detects the N channels in turn. Thus, for each channel, the sensing protocol is also periodic with period NT s . However, the access strategy is not periodic, which depends on the sensing results.
Before studying the access strategy, we will first simplify the problem P, which facilitates the access strategy design.
From the perspective of time, in each slot, SU should decide how to access N channels according to the current and historical sensing results. However, since PUs' activities are independent, thus, the interferences between SU and each PU do not interact with each other. Therefore, the original problem P can be decoupled into N independent sub-problems P i :


That is to maximize SU's temporal channel utilization on channel i while limiting its interference perceived by PU i. Therefore, from the perspective of each channel, SU should decide how to access the N slots between two adjacent sensing events. For example, in Figure 1, SU probes the channel 1 at the beginning of the first slot, and the next probing will not be carried out until slot 4. Thus, SU should determine how to access channel 1 from slot 1 to slot 4, according to the sensing result of slot 1.2
If all these N sub-problems P i achieve optimal synchronously, then the original problem P will be optimal.
SA strategy
In this section, we will first focus on the optimal access strategy for each sub-problem P i , and then we will give the SA strategy for the original problem P.
Since SU's access strategy will influence its interference to PUs, we will first analyze the property of interference caused by SU's transmission. Without loss of generality, we assume SU senses the channel i at time t = 0, and wants to access the following m th slot. It is obvious that the interference to PU i will depend on the sensing result at time t = 0. Therefore, according to transition matrix (1), if sensing result is "OFF," the expected time overlap ϕ0(m) is

where Pr (·) denotes the probability and μ i = μi,OFF+ μi,ON. If sensing result is "ON", the expected time overlap ϕ1(m) is

Therefore, similar to [11], we can obtain the following lemma.
Lemma 1: The interference caused by SU's transmission in one slot (i.e., the expected time overlap ϕ0(m) and ϕ1(m)) has the following properties. That is, ∀n, m ∈ ℕ,
-
1)
ϕ 0(n) <ϕ 1(m);
-
2)
If n < m, then ϕ 0(n) < ϕ 0(m) and ϕ 1(n) > ϕ 1(m).
Proof: See the Appendix A. ■
Remark: For the facility of discussion, we define the terms "OFF slot" and "ON slot" first. For any channel i, if the sensing result is "OFF," then the subsequent slots before channel i being sensed next time are called "OFF slot," otherwise, these slots are called "ON slot." For example, in Figure 1, for channel 3, the slots 3, 4, 5, and 6 are "OFF slot" and slots 7 and 8 are "ON slot." It is noteworthy that the "OFF slot" does not means that the PU is always "OFF" in these slots, and so does "ON slot."
The first property of Lemma 1 means transmitting in "ON slot" will always cause more interference than transmitting in "OFF slot." The second property means if the sensing result is "OFF," transmitting in the former slot will cause less interference than transmitting in the latter slot, and if the sensing result is "ON," the conclusion is just the opposite. Furthermore, it is noteworthy that with PS strategy, we always have 1 ≤ n, m ≤ N, however, Lemma 1 shows that ∀n, m ∈ ℕ the above two properties always hold true, even though the sensing event is not periodic under some sensing strategy. It is very important for us to design the SS and access strategy in the next section.
Therefore, based on lemma 1, we can obtain the optimal access strategy directly.
Theorem 1: To maximize SU's temporal utilization on channel i while limiting its interference to PU i , the optimal access strategy for SU to access channel i is
-
1)
If the sensing result is "OFF," SU should transmit consecutively in the relatively earlier slots (i.e., during [0, ρ 0,i NT s], where
 );
); -
2)
If the sensing result is "ON," SU should transmit consecutively in the relatively latter slots (i.e., during [(1 - ρ 1,i)NT s, NT s], where
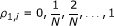 );
); -
3)
SU can access the "ON slots" if and only if all "OFF slots" have been utilized, i.e., ρ 1,i> 0 iff ρ 0,i= 1.
Based on the optimal access strategy, SU can know how to access the channel qualitatively, but not quantitatively. In other words, the ratios ρ0,iand ρ1,iare unknown. Apparently, ρ0,iand ρ1,idepend on the magnitude of period T (= NTs). Next, we will focus on the relationship between ρ0,i(ρ1,i) and T.
According to Theorem 1, the expected time overlap in "OFF slots" and "ON slots" are

and

respectively, where T = NTs.
Therefore, the sub-problem P i is equivalent to




where  is the probability of the sensing result being "OFF."
is the probability of the sensing result being "OFF."
This sub-problem is very similar to our previous work [11], in which ρ0,iand ρ1,iare continuous variables. In [11], we have proved and obtained the relationship between ρ0,i(ρ1,i) and T, which can be illustrated in Figure 3.
-
1)
ρ 0,i: when period T is small, ρ 0,i= 1, which means SU can access all the "OFF slots" and its interference to PU i will not exceed threshold C i . When
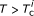 , the optimal ρ 0,i will decrease. It is easy to understand. When T is small, during [0, T], the probability that PU's state ("OFF") changes is very small, thus, SU can utilize all of the N slots (i.e., during [0, T]) and will not cause much interferences; and as T increases, the probability that PU's state changes will increase, especially at the end of duration [0, T], thus in this case, SU should reduce its transmission time.
, the optimal ρ 0,i will decrease. It is easy to understand. When T is small, during [0, T], the probability that PU's state ("OFF") changes is very small, thus, SU can utilize all of the N slots (i.e., during [0, T]) and will not cause much interferences; and as T increases, the probability that PU's state changes will increase, especially at the end of duration [0, T], thus in this case, SU should reduce its transmission time. -
2)
ρ 1,i: from Figure 3, we can observe that ρ 1,i> 0 if and only if ρ 0,i= 1, which is consistent with Lemma 1. Furthermore, when
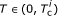 , ρ 1,idecreases as T increases. This is because when T is very small, transmitting in "OFF slot" will cause only a few interference, then SU can use part of the "ON slot." And as T increases, the interference caused by transmitting in "OFF slot" will increase, thus, the transmission time in "ON slot" should be reduced.
, ρ 1,idecreases as T increases. This is because when T is very small, transmitting in "OFF slot" will cause only a few interference, then SU can use part of the "ON slot." And as T increases, the interference caused by transmitting in "OFF slot" will increase, thus, the transmission time in "ON slot" should be reduced. -
3)
U i : SU's channel utilization U i , which is the weighted average of ρ 0,iand ρ 1,i, decreases as T increases. And the maximal U i is obtained when T approaches to zero under the assumption that sensing time can be ignored.
When ρ0,iand ρ1,iare continuous variables, the maximal U
i
is obtained when T approaches to zero. However, generally it is not suitable for discrete cases. Generally, PU's interference tolerance C
i
is very small, especially far less than the probability of PU being "ON" (i.e., 1- k
i
). For example, assume C
i
= 1% and 1 - k
i
= 0.5, thus, the maximal  . That is to say SU cannot access any "ON slot" unless there are more than 50 available channels. Generally, that is not realistic.
. That is to say SU cannot access any "ON slot" unless there are more than 50 available channels. Generally, that is not realistic.
Therefore in this case, SU cannot access any "ON slot" at all and the maximal channel utilization U i = k i . On the other hand, even though SU could access part of "ON slots," the increment of channel utilization caused by transmitting in "ON slot" is very small (namely, C = 1%) and meanwhile the sensing period should be very small.
Based on the above discussion, we learn that (i) when  , all the "OFF slots" can be utilized; (ii) generally, SU can only access none or only a few of the "ON slots"; and (iii) transmitting in "ON slots" has only a little contribution to the channel utilization and meanwhile the sensing period must be very small, which means SU has to take more time and energy to sensing the channels.
, all the "OFF slots" can be utilized; (ii) generally, SU can only access none or only a few of the "ON slots"; and (iii) transmitting in "ON slots" has only a little contribution to the channel utilization and meanwhile the sensing period must be very small, which means SU has to take more time and energy to sensing the channels.
Thus, if we give up the opportunity of transmitting in "ON slots" and select appropriate sensing period (i.e.,  ), then SU could make full use of the "OFF slots" and the channel utilization will have no or only a little degradation. Based on this idea, we propose the following SA strategy, which can be regarded as greedy access.
), then SU could make full use of the "OFF slots" and the channel utilization will have no or only a little degradation. Based on this idea, we propose the following SA strategy, which can be regarded as greedy access.
Theorem 2: With PS strategy, if the sensing period  , SU can greedily access channel i:
, SU can greedily access channel i:
-
1)
If sensing result is "OFF," SU can access all subsequent slots before channel i being sensed next time;
-
2)
If sensing result is "ON," SU should stand by (i.e., does not access) until channel i being sensed next time.
In [11], we have obtained that

where  (when C
i
< k
i
(1- k
i
)) and
(when C
i
< k
i
(1- k
i
)) and  denotes the Lambert's W function [22], which solves the equation w exp(w) = x for w as a function of x. When x is real and satisfies
denotes the Lambert's W function [22], which solves the equation w exp(w) = x for w as a function of x. When x is real and satisfies  , there are two possible real values of
, there are two possible real values of  . The branch satisfying
. The branch satisfying  is called the principle branch, while the other branch satisfying
is called the principle branch, while the other branch satisfying  is called the negative branch. Since 0 < C
i
< k
i
(1- k
i
), we have
is called the negative branch. Since 0 < C
i
< k
i
(1- k
i
), we have  . Obviously,
. Obviously,  is one of the solutions, which located on the negative branch. However, it will result in
is one of the solutions, which located on the negative branch. However, it will result in  . Thus, we are only interested in the value obtained from the principle branch, which will result in
. Thus, we are only interested in the value obtained from the principle branch, which will result in  .
.
According to (16), if μi,OFF and μi,ONare big (i.e., channel's state changes fast) or C
i
is small (i.e., interference constraint is strict), then  is small. It is in accord with intuition.
is small. It is in accord with intuition.
If  , then the greedy access strategy can be adopted for all channels. Therefore, we obtain the PS-SA strategy, as shown in Algorithm 1.
, then the greedy access strategy can be adopted for all channels. Therefore, we obtain the PS-SA strategy, as shown in Algorithm 1.
Algorithm 1 Periodic sensing and selective access (PS-SA) strategy
1: Initialization. Obtain N, μi,OFF, μi,ONand C i (∀i);
2:  ;
;
3: Calculate  using Eq. (16), i = 1, ... N;
using Eq. (16), i = 1, ... N;
4:  ;
;
5: t ← 1;
6: repeat
7: At the beginning of slot t(∈ ℕ), SU senses channel n (n = (t -1) mod N + 1), and saves the sensing result ("ON" or "OFF") into RESULT[n];
8: for i = 1 to N do
9: if RESULT[i] = "OFF" then
10: SU accesses channel i in slot t;
11: else
12: SU doesn't access channel i in slot t;
13: end if
14: end for
15: t ← t + 1;
16: until SU doesn't want to transmit anymore.
According to Algorithm 1, for any channel i, since all of the "OFF slots" have been access and none of the "ON slots" can be utilized by SU, we have that ρ0,i= 1 and ρ1,i= 0. Thus, SU's temporal channel utilization on channel i is k i , which equals to channel i's idle probability. That means SU can "almost" utilize all of the spectrum holes under the proposed PS-SA strategy. However, under PS strategy all channels are treated equally, and most sensing opportunities are wasted on these channels that do not need to be sensed yet. For example, for a case of N = 2 and Tc = [0.1, 1] (s), under PS strategy, Ts = 50 (ms) and each channel will be probed every 100 ms. This is suitable to channel 1, but is not necessary for channel 2. Therefore, a SS strategy, which makes SU first sense the channel that needs to be probed the most, is required.
SS-SA strategy
In the previous section, we analyze and obtain the SA strategy with PS strategy. With PS-SA strategy, SU can make full use of each channel, however, the PS strategy is not efficient, which make SU waste most sensing opportunities on these channels that do not need to be sensed yet. Thus, in this section, we will try to propose a more efficient strategy, namely, SS-SA strategy.
SS strategy
Based on the former discussion, we find that  , which is related to channel's characteristic parameters (μi,ONand μi,OFF) and interference tolerance (C
i
), reflects the frequency that channel i should be probed. Thus naturally, we propose a SS strategy, which makes all channels almost be probed periodically with their favorite period
, which is related to channel's characteristic parameters (μi,ONand μi,OFF) and interference tolerance (C
i
), reflects the frequency that channel i should be probed. Thus naturally, we propose a SS strategy, which makes all channels almost be probed periodically with their favorite period  . Particularly, at the beginning of each slot, SU senses the channel, whose "age" of last sensing result is closest to its favorite period
. Particularly, at the beginning of each slot, SU senses the channel, whose "age" of last sensing result is closest to its favorite period  . Mathematically, this SS strategy leads to3
. Mathematically, this SS strategy leads to3

where a
i
∈ ℕ is the "age" (in terms of number of slots) of last sensing result of channel i and p ∈ (0, 1) is a constant coefficient. From Figure 3, we can see that if the sensing time interval is greater than  , the SU's temporal utilization will degrade sharply, otherwise, interference will exceed the threshold if SU insists on transmitting in all "OFF slots." Thus, the parameter p is introduced, to make SU sense the channel in advance before the age of sensing result close to
, the SU's temporal utilization will degrade sharply, otherwise, interference will exceed the threshold if SU insists on transmitting in all "OFF slots." Thus, the parameter p is introduced, to make SU sense the channel in advance before the age of sensing result close to  . According to the simulation results (Figure 4), we obtain that when p > 1, the sensing period decreases sharply, and when p = 0.9, the sensing period is the maximal. Through further simulation, p = 0.9 is suitable for most situations. Thus, we choose p = 0.9.
. According to the simulation results (Figure 4), we obtain that when p > 1, the sensing period decreases sharply, and when p = 0.9, the sensing period is the maximal. Through further simulation, p = 0.9 is suitable for most situations. Thus, we choose p = 0.9.
It is apparent that the proposed SS strategy is not strict periodic generally. However, since each channel will be sensed when the age of sensing result is close to  , therefore, each channel is probed almost periodically.
, therefore, each channel is probed almost periodically.
SA strategy
Similar to the discussion in the previous section, with the proposed SS strategy, the problem P can also decoupled into N independent sub-problems. And for each sub-problem P i , the interference model remain the same; i.e., Equations 8) and (9) do not change, thus, Lemma 1 holds true. That is to say, transmitting in "OFF slot" is always better than transmitting in "ON slot." And furthermore, transmitting in "ON slot" has little or no contribution to increase channel utilization.
Therefore, the greedy access strategy (Theorem 2) is also suitable for the SS strategy. That is to say, if sensing period Ts is suitable, namely, all the channels are probed in time, SU can access all "OFF slots" and give up all "ON slots." It is noteworthy that unlike the PS-SA strategy, we could not give the accurate mathematical formulation of sensing period Ts. However, the approximate Ts can be obtain by simple simulation. Given channels' parameters (μ i , λ i ), we can generate all channels' states and simulate the SS-SA strategy for different Ts. Then, we can obtain SU's channel utilization and its interference to each PU. The approximate Ts is the maximal Ts that makes the interference to each PU not exceed the threshold C i .
Since the SS strategy can be regarded as periodic approximately for any channel i, with SS-SA strategy, SU's temporal channel utilization on channel i is k
i
, which equals to the one with PS-SA strategy. On the other hand, with PS strategy, each channel will be probed every N slots and the maximal Ts should satisfy  . However, with the SS strategy, the average sensing period K
i
(in terms of number of slots) for each channel i will no longer be the same. If
. However, with the SS strategy, the average sensing period K
i
(in terms of number of slots) for each channel i will no longer be the same. If  is small, then the channel i will be probed frequently, thus K
i
will be smaller, otherwise, K
i
will be larger. For channel i, the maximal sensing period Ts can be nearly regarded as
is small, then the channel i will be probed frequently, thus K
i
will be smaller, otherwise, K
i
will be larger. For channel i, the maximal sensing period Ts can be nearly regarded as  , therefore, with the proposed SS strategy, sensing period Ts for each channel will be almost the same and more larger than PS strategy.
, therefore, with the proposed SS strategy, sensing period Ts for each channel will be almost the same and more larger than PS strategy.
Therefore, with SS-SA strategy, SU could achieve the same channel utilization as the case with PS-SA strategy, and meanwhile consume less time and energy to sense the channels. Furthermore, according to the following simulation results, with SS-SA strategy, SU's channel utilization is much bigger when the sensing time cannot be ignored.
SS-SA strategy for single-channel CR network
In our previous study [11], we considered the simplest single-channel CR model and proposed two access policies (i.e., π1 and π2) for a slotted SU overlaying an non-slotted ON/OFF CTMC modeled primary network under constraints of interference and energy consumption. Policy π1 allows SU to transmit only in "OFF slot," which is similar to the proposed SS-SA strategy, but policy π2 allows SU to utilize both "OFF slot" and "ON slot." Next, we will compare SS-SA strategy with policy π1 for the single-channel CR model.
According to the definition of SS-SA strategy, SU senses the only channel at the beginning of each slot and then access the whole slot if and only if the sensing result is OFF. The optimal slot size is Tc and SU's channel utilization equals to this channel's idle probability. In [11], we consider the energy consumption constraint, which is not considered in this article. Thus, we release this constraint by setting the parameter P (Equation 6 in [11]) to infinite. Therefore, according to Theorem 5 of [11], we could obtain that the optimal slot size Ts ∈ (0, Tc] and SU's channel utilization is k × 1, which in accordance with SS-SA strategy.
Therefore, SS-SA strategy coincides with policy π1 without consideration of energy consumption constraint.
Simulation Results
In this section, we will first introduce an intuitive strategy, i.e., intuitive sensing and selective access (IS-SA) strategy, for the purpose of comparison. And then, simulation results for different situations are presented.
IS-SA strategy
We consider an IS strategy: SU first senses the channel whose state (ON/OFF) is most likely to change. Particularly, we assume that channel i was last sensed at the beginning of slot t i (∈ ℕ), then at the beginning of slot t > t i , the age of last sensing result is a i = t - ti. Thus, during the period of ((t i - 1)Ts, (t - 1)Ts), channel i's state varying is equivalent to the holding time being less than a i Ts. Since the holding times in both ON and OFF state are exponentially distributed, thus, during the period of ((t i - 1)Ts, (t -1)Ts), the probability P i that channel i's state changes is

where

Thus, we can obtain the IS strategy:

Similarly, if there are multiple channels with the same maximal value, SU will randomly choose one channel among them. With the IS strategy, if the "age" of sensing result (i.e., a i ) is large or channel's state changes fast (i.e., θ i is larger), the channel will be probed first. This is the same as intuition. However, it is apparent that the IS strategy does not consider the effect of PU's interference tolerance, which make this strategy be invalid for different interference thresholds.
Similar to the case of PS and SS, the greedy access strategy (i.e., SU accesses all "OFF slots" and gives up all "ON slots") is also suitable here if the sensing period is suitable. Therefore, SU's channel utilization with IS-SA strategy will be the same as PS-SA and SS-SA strategies, but the maximal sensing period will be different generally.
In the following simulations, to find the suitable sensing period Ts for each sensing strategies, the greedy access strategy will be adopted no matter the sensing period Ts is suitable or not. And then, if Ts is suitable, the interference to each PU will be less than or equal to the threshold C i . Furthermore, we assume that the SU will consume constant energy Es to sense one channel every time. Thus per unit time, the energy used for sensing is Es/Ts. Therefore, the larger is the sensing period Ts, the less energy will be used for sensing the channels.
Example 1: performance comparison for different holding times
In this example, we study the case that the idle probabilities of each channel are the same, but the holding times for each channel are different, namely, μi,OFF= μi,ON(∀i) but μi,ON≠ μj,ON(∀i ≠ j). Particularly, we focus on the case N = 5 and λ-1 = μ-1 = [1, 2, 5, 10, 20] (s). Thus, the holding time of channel 1 is shorter, while the holding time of channel 5 is longer. Furthermore, we assume C i = 5% (∀i) and p = 0.9. Therefore, according to (16), we have Tc = [0.232, 0.464, 1.161, 2.321, 4.642] (s).
The temporal channel utilization for PS-SA, SS-SA, and IS-SA strategy is shown in Figure 5. From Figure 5, we can see that SU's total channel utilization is 2.5, and SU's channel utilization on each channel i is 50%, which equals to channel i's idle probability. That is to say, SU could make full use of each channel. It is noteworthy that SU's channel utilization is the same for the three strategies regardless of interference tolerance. If the sensing period is not suitable, the interferences to some PUs will be greater than their tolerances and SU has to limit its transmission time on these channels, therefore, the total channel utilization will be less than 2.5.
Figures 6, 7, and 8 show the interference with PS-SA, SS-SA, and IS-SA strategy, respectively. As shown in Figure 6, when Ts ≤ 46.6 (ms), the interference to each PU is less than the threshold (5%), and when Ts > 46.6 (ms), the interference to PU 1 is not tolerable. Thus, if the sensing period Ts > 46.6 (ms), SU has to reduce its transmission time on channel 1 and the channel utilization will degrade. Furthermore, in theory, the maximal sensing period for PS-SA strategy is  . Therefore, the simulation result demonstrates the validity of our theoretical analysis.
. Therefore, the simulation result demonstrates the validity of our theoretical analysis.
As shown in Figures 7 and 8, the maximal sensing periods for SS-SA and IS-SA strategies are 116 (ms) and 118.5 (ms), respectively, which are approximately the same in this case. Since the maximal sensing period of either IS-SA or SS-SA is larger than the one of PS-SA strategy, SU could consume less time and energy for sensing by adopting SS-SA or IS-SA strategy.
Furthermore, as shown in Figure 7, the curves are not smooth. This is because according to (17), the sensing period Ts will affect the sensing order of each channel. Therefore, each channel's priority may change for different sensing periods. For example, when Ts = 100, 110, 120 (ms), we assume that channel i is probed every 5, 6, and 5 slots (i.e., every 500, 660, and 600 ms), respectively. Therefore, when Ts = 110, the interference to PU i is larger than the cases of Ts = 100 and Ts = 120.
Example 2: performance comparison for different interference tolerances
In this example, we will study the case that each channel's parameters (μi,OFFand μi,ON) are the same, but the interference tolerances (C i ) for each PU are different. And we will find that the proposed SS-SA strategy is better than IS-SA and PS-SA strategies.
Particularly, we focus on the case N = 5 and for each channel i,  . Furthermore, we assume the interference tolerances for each PU are 2%, 4%, 6%, 8% and 10%, respectively. Therefore, Tc = [254, 539, 865, 1242, 1689] (ms). And similar to Example 1, since the idle probability of each channel is 50%, SU's total channel utilization is also 2:5.
. Furthermore, we assume the interference tolerances for each PU are 2%, 4%, 6%, 8% and 10%, respectively. Therefore, Tc = [254, 539, 865, 1242, 1689] (ms). And similar to Example 1, since the idle probability of each channel is 50%, SU's total channel utilization is also 2:5.
Figure 9 shows the interference with IS-SA strategy. Since μi,OFFand μi,ONare the same, with IS-SA strategy, all channels will be regarded as the same. Therefore, IS-SA strategy is the same as PS-SA strategy and the five curves in Figure 9 overlap each other. Due to the minimal interference tolerance is only 2%, the maximal sensing period Ts ≈ 51 (ms), which is in accord with the theoretical value. However, this sensing period is not necessary for other PUs.
With SS-SA strategy, SU considers both channel's characteristic parameters (μi,ONand μi,OFF) and interference tolerance (C i ). Therefore, with SS-SA strategy, these channels will not be regarded as the same any more. The interference with SS-SA strategy is illustrated in Figure 10. As shown in this figure, the maximal sensing period is about 108 (ms), which is twice as much as IS-SA strategy, and the sensing period is suitable for all channels. Therefore, the proposed SS-SA strategy is better than IS-SA and PS-SA strategies.
Example 3: performance comparison for different available channels

In this example, we will study more general cases that the number of channel, channel's parameters, and interference tolerances are different. Particularly, we assume there are totally six available channels (as shown in Table 1), from which SU chooses N(≤ 6) channels to access.
The simulation results are shown in Table 2. In cases 1 and 2, since only one channel is selected, three strategies are the same and the optimal sensing period equals to Tc, which is in accordance with theoretical analysis. In cases 3, 4, and 5, the channels with different parameters but the same interference tolerances are selected. According to the results, we can obtain that SS-SA strategy is better than IS-SA and PS-SA strategies. In cases 6 and 7, more general situation is investigated and the SS-SA strategy is still efficient.
Therefore, the SS-SA strategy is better than PS-SA and IS-SA strategies for different available channels.
Example 4: performance comparison while sensing time cannot be ignored
In this example, we take into account the effect of sensing time, i.e, the sensing time cannot be ignored. We use the same parameters as Example 1 and assume that the sensing time τ = 20 (ms). Furthermore, we assume that SU cannot sense and transmit simultaneously. Therefore, in each slot, during [0,τ], SU chooses one channel to sense, and then decides decide if and in which channels to transmit during [τ, Ts].
Since Tc is obtained without regarded to the sensing time, thus it will not correct here. However, it is comprehensible that the maximal sensing period for greedy access strategy will be larger than Tc, since SU will not cause interference while it senses the channel. And furthermore, if Tc is large, the channel need not be probed frequently, thus, the total sensing time between two adjacent sensing events for the channel with larger Tc will be greater than the channel with smaller Tc. For example, assume  and channel i and j will be sensed every 10 and 2 slots, respectively. Then, the total sensing time for channel i and j are 10τ = 200 and 2τ = 40 (ms). Therefore, we modify the SS strategy (Equation 17) as
and channel i and j will be sensed every 10 and 2 slots, respectively. Then, the total sensing time for channel i and j are 10τ = 200 and 2τ = 40 (ms). Therefore, we modify the SS strategy (Equation 17) as

Figure 11 shows the temporal channel utilization for three strategies. Since the sensing time cannot be ignored, the channel utilization will degrade badly, especially when Ts is small. And as Ts increases, the proportion of sensing time (i.e.,  ) will decrease, thus, in each slot, SU has more opportunity to transmit and then SU's channel utilization will increase.
) will decrease, thus, in each slot, SU has more opportunity to transmit and then SU's channel utilization will increase.
Figure 12 shows the interference while SU adopts PS-SA strategy. From Figure 12, we can obtain that while SU adopts PS-SA strategy, the maximal sensing period is about 70 (ms), and meanwhile, as shown in Figure 11, the total channel utilization is only 1.788. Thus, SU can only make use of 35.8% (i.e., 1.788/5) of the time for each channel, which is far less than the spectrum opportunity (i.e., k = 50%). This is because for each channel i, if the last sensing result is "OFF," SU has only Ts - τ = 50 ms to transmit in each slot, therefore, the temporal channel utilization on channel i is  , which is in accordance with the simulation result. Thus, the PS-SA strategy is inefficiency while the sensing period cannot be ignored.
, which is in accordance with the simulation result. Thus, the PS-SA strategy is inefficiency while the sensing period cannot be ignored.
Figures 13 and 14 illustrate the interference while SU adopts the SS-SA and IS-SA strategy, respectively. With these strategies, the maximal sensing period is about 142 (ms) and the total channel utilization is about 2.146. And then, SU can make use of 42.9% of the time for each channel. Thus, in this case, by adopting SS-SA strategy, SU's channel utilization can rise about 20% than PS-SA strategy, and meanwhile SU consumes less time and energy to sense the channels.
Conclusion
In this article, we propose a SS-SA strategy for one slotted SU overlaying a non-time-slotted ON/OFF CTMC modeled multi-channel primary network. With SS strategy, each channel will be detected almost periodically with different periods according to the parameter Tc, which reflects the maximal period that each channel should be detected. The effect of sensing period is also considered in this article. And if the sensing period is suitable, SA strategy can be regarded as greedy access strategy.
We also give two reference sensing strategies, namely, PS and IS strategy. With PS strategy, SU senses the channels one by one, and with IS strategy, SU first senses the channel whose state is most likely to change. The proposed SA strategy is also appropriate for SU adopting PS or IS strategy if the sensing period is suitable. Numerical simulations illustrate that Tc is a valid measurement to indicate how often the channel should be sensed, and with SS-SA strategy, SU can effectively utilize the spectrum holes and consume less energy and time for sensing than PS-SA and IS-SA strategies.
Proof of the Lemma 1
According to Equation 8, we have

where k i = μi,ON/μ i .
Since ∀τ > 0,  . Furthermore, due to 0 < k
i
< 1 and the sensing period Ts is always larger than zero, we have
. Furthermore, due to 0 < k
i
< 1 and the sensing period Ts is always larger than zero, we have
that

And then, ϕ0(m) < 1 - k i will hold true for arbitrary m ∈ ℕ.
Similarly, from Equation 9 we have

and ϕ1(m) > 1 - k i will hold true for arbitrary m ∈ ℕ.
Therefore, for arbitrary n, m ∈ ℕ, we have

Furthermore, since as τ increases,  will decrease. Thus, if n < m, we have
will decrease. Thus, if n < m, we have

Therefore, if n < m, we have


Note
1If we focus on the proportion of interference time in PU's busy time, the interference model can be easily modified only by divided by the probability of PU being "ON" (i.e.,  ).
).
2This is because due to the first-order CTMC model, the channel state is only related to the last sensing result and has nothing to do with earlier sensing results. Thus, those earlier sensing results have not been taken into account.
3If there are multiple channels with the same minimal value, SU will randomly choose one channel among them.
Abbreviations
- CR:
-
cognitive radio
- CTMC:
-
continuous time Markov chain
- IS:
-
intuitive sensing
- IS-SA:
-
intuitive sensing and selective access
- POMDP:
-
partially observable Markov decision process
- PS:
-
periodic sensing
- PS-SA:
-
periodic sensing and selective access
- PU:
-
primary user
- SU:
-
secondary user
- SS-SA:
-
selective sensing and selective access
- WLAN:
-
Wireless LAN.
References
Mitola J, Maguire GQ Jr: Cognitive radio: making software radios more personal. IEEE Pers Commun 1999, 6(4):13-18. 10.1109/98.788210
Akyildiz IF, Lee WY, Vuran MC, Mohanty S: NeXt generation/dynamic spectrum access/cognitive radio wireless networks: a survey. Comput Netw 2006, 50(13):2127-2159. 10.1016/j.comnet.2006.05.001
Jiang H, Lai L, Fan R, Poor HV: Optimal selection of channel sensing rrder in cognitive radio. IEEE Trans Wirel Commun 2009., 8(1):
Su H, Zhang X: Cross-layer based opportunistic MAC protocols for QoS provisionings over cognitive radio mobile wireless networks. IEEE J Sel Areas Commun 2008, 26(1):118-129.
Zhao Q, Tong L, Swami A, Chen Y: Decentralized cognitive MAC for opportunistic spectrum access in ad hoc networks: A POMDP framework. IEEE J Sel Areas Commun 2007., 25(3):
Zhao Q, Geirhofer S, Tong L, Sadler BM: Opportunistic spectrum access via periodic channel sensing. IEEE Trans Signal Process 2008., 56(2):
Geirhofer S, Tong L, Sadler BM: Interference-aware OFDMA resource allocation: A predictive approach. Proceedings of the IEEE Military Communications Conference 2008 (MILCOM 2008) 2008.
Geirhofer S, Tong L, Sadler BM: A sensing-based cognitive coexistence method for interfering infrastructure and ad-hoc systems. Wirel Commun Mob Comput 2010, 10(1):16-30. 10.1002/wcm.896
Pei Y, Hoang AT, Liang Y: Sensing-throughput tradeoff in cognitive radio networks: how frequently should spectrum sensing be carried out? Proceedings of 18th IEEE PIMRC, Athens, Greece 2007.
Xu Y, Li Y, Zou H, Yang X: Joint sensing period optimization and transmission time allocation for cognitive radio networks. The 2009 International Conference on Wireless Communications and Signal Processing (WCSP 2009), Nanjing, China 2009.
Xu Y, Sun Y, Li Y, Zhao Y, Zou H: Joint sensing period and transmission time optimization for energy-constrained cognitive radios. EURASIP J Wirel Commun Netw 2010., 2010:
Lee WY, Akyildiz IF: Optimal spectrum sensing framework for cognitive radio networks. IEEE Trans Wirel Commun 2008., 7(10):
Poston J, Horne W: Discontiguous OFDM considerations for dynamic spectrum access in idle TV channels. IEEE DySPAN 2005, 607-610.
Jia J, Zhang J, Zhang Q: Cooperative relay for cognitive radio networks. IEEE INFOCOM 2009, 2304-2312.
Geirhofer S, Tong L, Sadler BM: A measurement-based model for dynamic spectrum access in WLAN channels. Proceedings of the IEEE Military Commununication Conference (MILCOM), Washington, DC 2006.
Sondik E: The optimal control of partially observable Markov processes over the infinite horizon: Discounted costs. Oper Res 1978, 26(2):282-304. 10.1287/opre.26.2.282
Yu H: Approximation solution methods for partially observable Markov and semi-Markov decision processes. In Ph.D. Dissertation. Massachusetts Inst. Technol., Cambridge, MA; 2007.
Geirhofer S, Tong L, Sadler BM: Dynamic spectrum access in the time domain: Modeling and exploiting whitespace. IEEE Commun Mag 2007, 45(5):66-72.
Jones S, Merheb N, Wang I: An experiment for sensing-based opportunistic spectrum access in CSMA/CA networks. Proceedings of the 1st IEEE International Symposium on New Frontiers Dynamic Spectrum Access Networks 2005, 593-596.
Geirhofer S, Tong L, Sadler BM: Cognitive medium access: Constraining interference based on experimental models. IEEE J Sel Areas Commun 2008, 26(1):95-105.
Resnick SI: Adventures in Stochastic Processes Birkhauser, Boston. 1992.
Corless RM, Gonnet GH, Hare DEG, Jeffrey DJ, Knuth DE: On the Lambert W function. Adv Comput Math 1996, 5(1):329-359. 10.1007/BF02124750
Acknowledgements
The authors would like to thank the anonymous referees for providing comments that have considerably improved the quality of this article. This work was supported by National Basic Research Program of China (2007CB310608), National Natural Science Foundation of China (60832008), National Science and Technology Pillar Program (2008BAH30B09), National S&T Major Project (2009ZX03002-002), Tsinghua University Initiative Scientific Research Program (20101082055), NCET, PCSIRT and Datang Mobile Communications Equipment Co., Ltd.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xu, Y., Li, Y., Zhao, Y. et al. Selective sensing and transmission for multi-channel cognitive radio networks. J Wireless Com Network 2011, 7 (2011). https://doi.org/10.1186/1687-1499-2011-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1499-2011-7


 );
);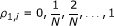 );
);
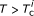 , the optimal ρ 0,i will decrease. It is easy to understand. When T is small, during [0, T], the probability that PU's state ("OFF") changes is very small, thus, SU can utilize all of the N slots (i.e., during [0, T]) and will not cause much interferences; and as T increases, the probability that PU's state changes will increase, especially at the end of duration [0, T], thus in this case, SU should reduce its transmission time.
, the optimal ρ 0,i will decrease. It is easy to understand. When T is small, during [0, T], the probability that PU's state ("OFF") changes is very small, thus, SU can utilize all of the N slots (i.e., during [0, T]) and will not cause much interferences; and as T increases, the probability that PU's state changes will increase, especially at the end of duration [0, T], thus in this case, SU should reduce its transmission time.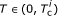 , ρ 1,idecreases as T increases. This is because when T is very small, transmitting in "OFF slot" will cause only a few interference, then SU can use part of the "ON slot." And as T increases, the interference caused by transmitting in "OFF slot" will increase, thus, the transmission time in "ON slot" should be reduced.
, ρ 1,idecreases as T increases. This is because when T is very small, transmitting in "OFF slot" will cause only a few interference, then SU can use part of the "ON slot." And as T increases, the interference caused by transmitting in "OFF slot" will increase, thus, the transmission time in "ON slot" should be reduced.









