- Research
- Open access
- Published:
Uplink interference mitigation for heterogeneous networks with user-specific resource allocation and power control
EURASIP Journal on Wireless Communications and Networking volume 2014, Article number: 55 (2014)
Abstract
This paper investigates interference mitigation for an uplink heterogeneous network (HetNet) with universal frequency reuse. In this study, we propose a user-specific resource allocation as well as a power control scheme for the uplink HetNet. With this scheme, the mobile users are grouped into two different groups according to their evaluated signal-to-leakage-plus-noise ratio (SLNR) metric. By dividing users into two groups, the primal nonconvex resource allocation problem can be casted to two subproblems. For the ‘good users’ with high SLNR value, the formulated nonconvex optimization problem which focuses on maximizing the system capacity is transformed into a standard geometric programming (GP) convex power optimization problem. For the other ‘interfering users’ with low SLNR values, we develope a semiorthogonal resource block (RB) allocation strategy for interference control. Simulation results show that most of the severe inter-cell interference can be removed by the semiorthogonal RB allocation scheme and the optimal power allocation of interfering users contributes to a better overall system capacity.
1 Introduction
The spectrum efficiency is significantly improved in long-term evolution (LTE)/LTE Advanced by exploiting universal frequency reuse with multiple-input multiple-output (MIMO) and orthogonal frequency division multiplexing (OFDM). However, facing the explosive data demands, pure macro coverage can hardly meet the increasing requirements. A latest evolution of cellular networks, namely heterogeneous networks (HetNet), has been well acknowledged as an effective way of balancing the high-data rate requirements with low complexity. A HetNet consists of a large number of small cells, including microcells, picocells, and femtocells underlaying regular macrocells [1, 2]. As macrocells and small cells share the same frequency resource, mobile users who dynamically associate with macro-/small cell stations can benefit a lot from small cell deployments.
As the aggressive frequency reuse is used, even in homogeneous LTE cellular systems, inter-cell interference has been a major factor that limits the entire network performance. A number of ways have been proposed for inter-cell interference coordination (ICIC) in different systems [3]. In current homogeneous cellular systems, the third-generation partnership project (3GPP) has proposed to balance the network performance and inter-cell interference by exploiting proper frequency reuse patterns, instead of the universal frequency reuse strategy. Two popular frequency assignment patterns are known as fractional frequency reuse (FFR) [4] and soft frequency reuse (SFR) [5].
HetNet has been a promising technique for future wireless cellular networks. Unfortunately, unplanned small cell deployments lead to the unprecedented challenges in terms of inter-cell interference control [6]. In a downlink HetNet, for instance, a picocell station causes severe interference to a macrocell user (MUE) in the proximity of the picocell coverage. Similarly for an uplink HetNet, the co-channel interference between macro- and small cells also exists, and it becomes an essential concern which limits the entire network performance. In order to deal with the more severe and complicated interference problems, enhanced inter-cell interference coordination (eICIC) techniques have been proposed by both industrial and academic researchers. In [7], cell range expansion (CRE) is developed for balancing the macro- and picocell performance without any new spectrum available. However, the users associated with the picocell in the expanded region suffer severe downlink interference from the macro base station (BS). To mitigate this problem, a specific subframe called almost blank subframe (ABS) is introduced in [8, 9] at the macrocell transmission durations. The duration of ABS is left for picocell stations to schedule its cell-edge users; hence, the picocell users (PUE) is rarely affected by the macrocell interference. It is obvious that the benefits of PUEs are obtained at a cost of MUE performance. Moreover, in order to maintain the macrocell performance, carrier aggregation (CA)-based interference control strategies are proposed by exploiting a new spectrum resource [10].
Most of the above-mentioned techniques are specified for downlink HetNets. In a traditional uplink system, fractional power control (FPC) [11] is a typical scheme for uplink channels. However, the FPC is usually applied in homogeneous networks while it is shown not effective enough in HetNets. In [12], a cell-specific power control strategy was proposed for a special kind of uplink HetNet composing of a macrocell and a femtocell. It adaptively chose specified reference power P0 for femto stations near or far from the macro station. Differently in [13], opportunistic power control schemes were proposed with both centralized sensing and distributed sensing strategies in order to maintain the outage requirements. The performance was evaluated under different settings of user outage requirements. Both studies [12] and [13] assumed a closed subscriber group which allows access only to a limited number of authorized terminals. For an open accessed uplink HetNet, a closed-loop power control scheme as well as cell range expansion was considered in [14] with performance evaluation under different CRE offsets and P0 values for FPC.
With the above-mentioned works, however, few has considered designing adaptive interference control for different users. This could be an essential problem especially for HetNets. In a HetNet, users generally experience a large variety of interference levels depending on their associations, locations, and adjacent traffic loads for the uplinks. Therefore, it is natural to consider user-specified interference control strategies for an uplink HetNet. In this paper, we study a user-specific resource allocation as well as power control scheme based on user grouping to mitigate uplink interference in HetNets. With this method, all users in each cell are divided into groups according to a signal-to-leakage-plus-noise ratio (SLNR) metric [15, 16], that is, the users are labelled as cell-center users and cell-edge users. The power control optimization problem for cell-center users is transformed to a geometric program (GP) formulation. While for the cell-edge users from different cells, they share a δ-semiorthogonal resource blocks (RBs) assignment with fixed power control. A system level simulator is constructed to verify the proposed scheme. This user-specific resource allocation as well as power control scheme is shown effective in mitigating the inter-cell interference and improving the entire network performance.
The remainder of this paper is organized as follows: Section 2 briefly reviews the existing mechanism of FPC for uplink power control. Section 3 describes the HetNet under consideration, and then Section 4 presents the proposed power control and resource allocation strategy. In Section 5, computer simulation results are provided. Finally, conclusions are drawn in Section 6.
2 Review of FPC mechanism
In current uplink cellular systems, the FPC strategy has been considered as a primitive guideline for uplink users to adjust their transmit power. Generally, the FPC compensates the long-term path loss as well as the shadowing effect in order to guarantee an acceptable strength of receive power at the BS. Mathematically, the FPC strategy at user k is determined by the following formula [17]:
where Pmax is the maximum transmit power allowed at user k, P0 is a target UE received power, α is the path loss compensate factor, Ploss,k is the estimated downlink path loss from the user k to its serving BS, and N l is the number of RBs assigned to the k-th uplink user in a cell l. According to [18], P0 is an integral value selected from the set {−126,…,24 dBm} and a typical value of α is within the set of {0.4,0.5,0.6,0.7,0.9,1.0}.
The FPC has been proven effective in conventional uplink homogeneous networks. In an uplink HetNet, however, the FPC strategy is not always suitable due to the randomly deployed small cells underlaying the macro coverage. If an MUE at the cell edge adjusts its transmit power according to the FPC rule, the users associated with nearby small cells can be severely influenced due to the increased co-channel interference. Moreover, since the CRE is used in HetNet for a balanced user association, the FPC does not work well for all users due to their cell associations with different tiers of cells and respective CRE bias values. Therefore, to enhance the throughput performance of the uplink HetNet, in the following, we will consider the uplink interference control by developing a user-specific resource allocation as well as power control strategy.
3 System model and problem formulation
We consider a HetNet of macrocell and picocell coexistence as illustrated in Figure 1. There are a number of picocells indexed by number {1,…,L} overlay on the top of a macrocell referred to as cell {0}. Without loss of generality, a number of users are randomly dropped within the cell coverage, and the cell association is determined according to the downlink reference signal received power (RSRP) of each individual user. Note that the usage of CRE with arbitrary bias values does not change the following proposed strategy in the HetNet. In the network, all cells in the macro or pico tier share the same frequency spectrum available for the system. Within each single cell, we restrict an RB allocated to a single user in order to avoid intra-cell interference. In the system, there are overall N RBs available for data transmission. The number of users associated with the macrocell and the l-th picocell are K0 and K l , respectively. Since RB is the smallest resource assignment granularity as specified by LTE, in this work, we only consider the resource and power control across different RBs while assuming simple equal power allocation across subcarriers within each RB.
Let be the signal channel from the macrocell (for l=0) or the l-th picocell (for l=1,...,L) to the k-th user. Denote as the interference channel from the user i associated with the j-th cell to the l-th one. We can characterize the received SINR at the macro BS for MUE k at the n-th RB as
where is the uplink transmit power of user i at the n-th RB in cell l, is the cell association index with values {0,1}, and σ2 represents the variance of the additive white Gaussian noise (AWGN) at the receiver side. Note that indicates that user i is associated with the l-th cell on the n-th RB, otherwise means that the n-th RB of cell l is assigned to other users. Similarly, the received SINR at the n-th RB of the l-th picocell for the k-th PUE is
In the HetNet, the problem of RB allocation and uplink power control of all users is formulated as a weighted sum rate maximization problem. From (2) and (3), the problem of resource allocation and power control is formulated as follows:
where w l is the weighting factor with respect to the achievable rate corresponding to different cells and N l =⌈N/K l ⌉, ∀l∈{0,1,…,L} is the maximum allowed number of RBs allocated to each user in the l-th cell. Note that the first constraint of problem (4) assumes for simplicity that the maximum power spectrum of a single user is uniformly constrained with across the allocated RBs. We let so that the total power constraint of Pmax is always satisfied.
Although with the above assumption, the problem (4) is inherently a nonconvex problem with integer constraints. Generally, it is not easy to handle the integer constraints with globally optimal solution using linear complexity. Moreover, the sum rate maximization object depends on a complex variable in terms of the SINR. The SINR as shown in (2) and (3) is a coupled function with respect to not only the power and RB allocation to the user itself but the resources allocated to other users. In order to make the problem tractable with reasonably good solutions, in the following, we will simplify the problem by presenting a user-specific power and RB allocation algorithm for the HetNet.
4 User-specific resource allocation and power control
It has been stated that the primal problem of (4) is difficult to solve with efficient approaches, especially in large-scale HetNet with both macrocells and a number of pico-/femtocells. To deal with the problem, the main job is to handle the inter-cell interference and to find a balance between the complexity of interference control and entire network performance. In this section, we resort to solving (4) via decomposing the problem into two subproblems under different user experiences. Then, we can address the uplink interference problem via designing a user-specific power and resource allocation strategy.
As for the users suffering severe interference from adjacent cells, the power control itself with full frequency reuse may not be suitable for well controlling the interference. Meanwhile, if the user’s uplink transmission causes severe interference to other user channels, the interfering user may also need to use an orthogonal frequency band instead of sharing with others. Otherwise, if the user is in the proximity of its serving cell station, it can share the allocated frequency band with other users since the mutual interference could be ignorable. The basic idea of our proposed algorithm is outlined as follows:
-
In the HetNet, each user is specified with both the interference it suffers and its caused interference to others. According to the evaluation, the users will be classified as ‘good users’ and ‘interfering users’.
-
For the good users, a specified power allocation scheme is presented via using geometric programming (GP) [19] as well as a universal frequency reuse strategy.
-
For the interfering users, frequency reuse may not be able to achieve better performance than regular frequency partition approach, especially when there are a large number of interfering users around. A δ-semiorthogonal RB assignment is thus presented for these interfering users while letting them use an aggressive maximum transmit power.
With the above strategy applied, all users are classified into two groups referred to as good users and interfering users. This kind of user classification is different from the user classification in homogeneous multicell networks in that both its suffered interference and the interference it caused to other users are taken into account. In the following, the metric and procedure of the user grouping are firstly detailed, and then the details of the user-specific resource allocation and power control strategy are elaborated.
4.1 User classification under HetNet
In traditional homogeneous networks, the users are usually classified as either ‘cell-center user’ or ‘cell-edge user’ based on the received SINR for coordinated multicell joint processing. In the heterogeneous network, however, the SINR metric can be ineffective in user classification. Due to the unplanned and arbitrary topology of the pico-/femtocell deployment, each user should not only consider its received SINR but also suppress the interference caused to other users. Hence, we present to utilize the SLNR measurement for user classification. Although SLNR has been widely used for beamforming design in multi-antenna [15] and multi-cell systems [16], to the best of our knowledge, it has not been considered for resource allocation under the HetNet scenario. Here, the SLNR at the macro/pico BS for a single user k in cell l is defined by
Note that when we evaluate the SLNR metric for a user k associated with cell l, the initially allocated power can be chosen by the conventional uplink power control formula or just simply . Given a predetermined value ε l as the SLNR threshold for users in the l-th cell, users are then classified into two different groups.
-
For users with : All these users can be treated as good users within the l-th cell. The good users have good enough signal power while causing very limited inter-cell interference, hence resulting in a large SLNR value. Specifically for the good users, we let all cells share the same RBs for them due to their low inter-cell interference and relatively large signal strength. Note that we set different SLNR thresholds for different kinds of cells, i.e., macro- and picocells. This configuration is reasonable and necessary for a practical HetNet because the transmit power and user topology of users are quite different for a macrocell user and a pico-/femtocell user.
-
For users with : These users are treated differently as interfering users. The low SLNR evaluation implies that the users have either or both of the two characterizations: (1) experiencing low useful signal strength due to large distance between the user and its associated cell station; (2) causing severe interference to adjacent cells.
4.2 User-specific heuristic RB allocation
Given the users have been classified as two groups, we divide the entire frequency band into two orthogonal parts dedicated for the user groups. More specifically, the first part of the overall spectrum is reserved for the good users, while the rest part of the spectrum is reserved for the interfering users. Specified for the good users, the dedicated frequency spectrum in terms of RBs is equally assigned to the users within each cell. Meanwhile for the interfering users, the users from different cells will be paired as a δ-element group which has no more than δ users sharing the same RB among all, and the RBs will be allocated to the δ-element user group in a sequential way.
Since the RB allocation for good users is easy to implement, here in the following, we present a detailed description on how the RB allocation for ‘interfering users’, that is, to determine the ‘ δ-element group’ with proper RB assignments. Different from orthogonal RB allocation for all users, this strategy allows a small number of users, say δ instead of all users, to share an RB for transmission. We hence in this study referred to it as the ‘ δ-element semiorthogonal RB allocation’ scheme in the following. The detailed steps of the algorithm are described as follows:
-
1.
Initialize , where N l is the average number of RBs assigned to a single user, i.e., the number of RBs reserved for interfering users divided by the number of interfering users in the l-th cell.
-
2.
For each cell l, we first select a subset of users which have the least number of assigned RBs in the l-th cell, and this user subset may have one or more users according to the selection criterion. Subsequently, we choose the user with the maximum SLNR value from the user subset. The user is denoted by k l. Initialize the user group with ; the corresponding cells with users selected in
 is initialized by .
is initialized by . -
3.
Calculate the current achievable rate as
-
4.
If the cardinality or equivalently , find the least interfered cell c according to
where represents the complementary set of cells in
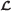 , and denotes the interference channel from user u to cell c. Else, stop.
, and denotes the interference channel from user u to cell c. Else, stop. -
5.
For each user u in cell c, calculate the updated achievable rate with user u involved in the group. It gives
-
6.
If R u ≥R M for any user u in cell c, update , the corresponding
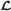 , and the achievable rate R
M
=R
u
. Else, stop.
, and the achievable rate R
M
=R
u
. Else, stop. -
7.
Go back to step 4.
4.3 User-specific power control under fixed RB allocation
As discussed in the previous subsection, the RB allocation is carried out according to the user classification. With this method, universal frequency spectrum reuse is deployed for all good users in different cells, while a δ-element semiorthogonal RB allocation strategy is proposed for interfering users. Given the fixed RB allocation, we look back at the primal resource allocation problem in (4). Once the RB assignment labels are fixed with {0,1}, the optimization problem reduces to a power control problem for the HetNet uplink channels. It follows
where the uplink received SINR for each user becomes
where the user index k corresponds to the assigned user in cell l at the n-th RB. From the above formulation, it is readily observed that the problem is still difficult to solve due to its non-convexity. Actually, even the problem of power control for a simple single-cell interference channel has not been well investigated with efficient solution. In order to make the problem tractable, we recall the above design philosophy with user-specific power control strategies.
First, we consider the power control for good users which generally have a much better achieved SINR than average. Fortunately, with high SNR assumption, the power control problem can be approximately casted to a typical GP problem which admits a globally optimal solution by using efficient algorithms [20]. Without loss of generality, let C l denote the number of good users in the l-th cell. With several steps of manipulations as detailed in the Appendix, the problem is finally casted to a standard form of GP. It gives
Thus far, the above problem is a standard GP which definitely is a convex optimization problem. Hence, it is easy to achieve the optimal power control solution via efficient computations like interior point method [21]. Note that some popular optimization tools including cvx [22] and sedumi [23] can be directly utilized for solving the convex optimization problems GP very efficiently.
After the power control for good users has been solved, we subsequently discuss the power control strategy for interfering users. Recall that most of the severe inter-cell interference has been removed by semiorthogonal RB allocation among interfering users. It is intuitively true to let the interfering users transmit with their maximum power. Since the semiorthogonal RB assignment guarantees marginal interference to adjacent cells, the high transmit power will obviously contribute to a better received signal power, resulting in a higher achievable throughput. To sum up, a flow chart of the proposed algorithm is illustrated in Figure 2.
5 Simulation results
In this section, we constructed a system level simulator for evaluating the performance of our proposed resource allocation as well as power control strategy for the uplink HetNet. Detailed system parameters of our simulator is summarized in Table 1. Moreover, for comparison, we tested four different strategies as follows:
-
Scheme (1): With this scheme, all cells share the entire frequency band and each user transmits with its maximum allowed power Pmax. It is referred to as ‘Pmax’.
-
Scheme (2): This is a benchmark scheme for our study, namely the traditional uplink power control referred to as ‘FPC’.
-
Scheme (3): In order to focus on the advantage of our proposed resource allocation scheme. We tested the third scheme as our proposed RB allocation strategy while using the traditional FPC for the uplink power control of all users. This scheme is referred to as ‘Proposed-FPC’.
-
Scheme (4): This scheme is our proposed interference control strategy in this work. User-specific resource allocation strategy is presented with GP-based power control. The scheme is referred to as ‘Proposed-GP’.
Before presenting the simulation results, we first give a brief elaboration on system level simulation. For simplicity, we focused on the performance of a macrocell with four pico stations randomly located within the macro coverage. Generally, in order to evaluate the average user performance, the simulation results are collected from 20 drops and averaging over 500 loops within each drop. For each drop test, a number of users (10 users or 20 users as specified) are uniformly located within the cell coverage. Under this circumstance of a single drop, the user performance is evaluated using four different resource allocation and power control schemes for comparison. The user performance is obtained via Monte-Carlo simulation for 500 channel realizations, commonly say 500 loops. In particular for each loop, we generate channel coefficients according to the Rayleigh fading distribution for each and every link between UE terminals and macro/pico stations. Note that the user performance is averaged over 500 channel realizations to remove the fluctuation due to fast fading. Finally, the user CDF is evaluated for all PUEs and MUEs for 20 drops. In this way, the performance by different schemes can be fairly compared under different user locations.
In Table 2, the performance comparisons between four different schemes are summarized in terms of both cell average performance and the cell edge performance. Notice that the cell average performance is evaluated as the average throughput of all users in both macro- and picocells of the observed macro coverage. The cell edge performance is widely utilized to characterize the quality of the cell coverage, and it is given by the average value of the 5 percentile user throughput. From Table 2, we find that our proposed scheme with different power control strategies outperforms the existing schemes including the Pmax and FPC. The FPC proposed by 3GPP is more effective than the naive scheme (1) with all Pmax by about 5% gain. Our proposed scheme (4) achieves over 12% gain in terms of the cell average performance than the existing scheme. It is also interesting to observe from Table 2 that the macrocell capacity decreases slightly from scheme (3) to scheme (4), whereas the pico capacity increases noticeably. This is because of the centralized power control nature in scheme (4) compared with the distributed power control strategy in scheme (3). Given both schemes (3) and (4) that share the same RB allocation, the centralized GP-based power control in scheme (4) aims at an overall cell capacity maximization. As the PUEs generally experience a lower path loss effect, scheme (4) finds it more effective to allocate power to PUEs than to the MUEs in the macrocell. This leads to a higher picocell capacity increase at an expense of slight degradation in macrocell capacity. For scheme (3), the fractional power control is utilized in a distributed way. It may not be able to outperform the performance of scheme (4) in terms of the overall network performance, although scheme (3) can also balance the power and interference between the macrocell and picocell. Scheme (3) to a large extend improves the overall network performance compared with the existing schemes (1) and (2) while not achieving the optimal balance of the macro and pico performance tradeoffs. With respect to scheme (4), it obtains a slight macrocell performance gain while it lost the chance of achieving a considerable gain in terms of picocell, hence resulting in a lower overall system performance. Moreover, the cumulative distribution functions (CDF) of the user throughput by different schemes are compared in Figure 3. For clarification and comparison, the user throughputs of macro users and pico users are separately depicted in the figure. From this figure, the advantages of our proposed schemes are also evidenced especially for the pico users.
The scenario with 20 picousers is also tested in our simulator with different resource allocation and power control schemes. Table 3 summarizes the performance comparison of the four schemes. Similar observations can be found as in Table 2. Moreover, by comparing the results in Tables 2 and 3, it shows a more significant performance gain by our proposed scheme in Table 3 as there are more users in the picocell. This is reasonable that our proposed scheme aims at interference mitigation in the uplink HetNet. For the system with more users, the interference control becomes more necessary and complicated in the system. In this case, the proposed user-specific scheme is able to perform much better than the conventional schemes. Moreover, when we focus on the uplink transmission in a single picocell, with more users communicating to the station, there is a bigger chance for the RB to pick up a user with good channel condition, hence improving the system performance. This phenomenon is well-known as ‘multiuser diversity gain’ which has already been discovered in [24] for performance enhancement. From Table 3, a performance gain over 20% in average throughput can be achieved compared to the naive Pmax scheme and at least 10% gain over the 3GPP FPC scheme. In Figure 4, the CDF of the user throughput evaluated under this scenario with 20 PUEs is also provided. The performance gain by our proposed scheme is shown promising especially for the pico users.
In the above results, we fixed good-to-interfering user ratio as 70%/30%. Here, for comparison, the performance of different ratio values is also presented. Figure 5 illustrates the empirical CDF of user SLNRs which equivalently illustrates the empirical SLNR thresholds for different choices of the good-to-interfering user ratio. From the performance comparison in Table 4, it shows as expected that the performances by schemes (1) and (2) do not change due to their nature of treating all users homogeneously. For the proposed schemes (3) and (4), it shows that low/high choices of the SLNR threshold lead to different MUE and PUE performances. The table tested different good-to-interfering user ratios from a higher value of 90%/10% to a low value of 50%/50%. It can be found that there is a tradeoff between the MUE/PUE performance over the choices of the SLNR threshold. The MUE performance improves as the ratio value increases because more users who may suffer severe interferences are properly treated. While for the PUEs, an increasing value of the ratio implies orthogonal resource allocation for more users which results in a lower PUE performance. From the viewpoint of the entire network performance maximization, the choice of 70%/30% appears to be a proper choice. Moreover, from this result, we find the performance is robust to the ratio value. A different choice at 80%/20% generates almost the same performance in terms of the entire network performance as 70%/30%.
6 Conclusions
In this paper, an uplink interference mitigation with user-specific power control and RB allocation scheme is presented for uplink heterogeneous networks. The entire user pool is classified as two groups, and each group of users is specified with optimized RB allocation as well as power control strategy for interference control. Simulation results verify that the proposed scheme can achieve a better performance in terms of both the entire network throughput and the cell edge performance. Our proposed scheme is effective in noticeably improving the picocell performance especially when there are a large number of users suffering severe mutual interference.
Appendix
Concerning the original problem (6) for good users, we let C l denote the number of good users in the l-th cell and then apply the approximation log (1+x)≈ logx for these users with large x. It casts the power control optimization problem (6) to
Given that the RB allocation is fixed with given pairs (k,n), the above problem can be rewritten with further simplified notations as
where γn,l represents the in (9) as k is automatically determined with fixed RB allocation at a given n-th RB in the l-th cell. To further reformulate the above problem, we invoke a new variable
By substituting the above new variable in (10), the problem is equivalent to
At this step, by applying some basic manipulations, the above problem can be finally casted to a standard form of GP which is readily (8) as desired.
References
A Damnjanovic: A survey on 3GPP heterogeneous networks. IEEE Wireless Commun 2011, 18(3):10-21.
V Chandrasekhar: Femtocell networks: a survey. IEEE Commun. Mag 2008, 46(9):59-67.
B Soret: CRS interference cancellation in heterogeneous networks for LTE-advanced downlink. In Proceedings of the IEEE International Conference on Communications (ICC). IEEE, Piscataway 2012; June 2012:6797-6801.
M Al-Shalash: Interference constrained soft frequency reuse for uplink ICIC in LTE networks. In Proceedings of the IEEE International Symposium on Personal Indoor and Mobile Radio Communications (PIMRC). IEEE, Piscataway; 2010:1882-1887.
F Wamser: Soft frequency reuse in the uplink of an OFDMA network. In Proceedings of the IEEE Vehicular Technology Conference (VTC-Spring). IEEE, Piscataway; 2010:1-5.
V Pauli: Heterogeneous LTE networks and inter-cell interference coordination. Nomor Research Whitepapers Dec 2010 . Accessed 1 June 2013 http://www.nomor.de/uploads/a4/81/a4815c4dc585be33c81f0ec7a15deed7/2010-12-WhitePaper_LTE_HetNet_ICIC.pdf
İ Güvenc: Capacity and fairness analysis of heterogeneous networks with range expansion and interference coordination. IEEE Commun. Lett 2011, 15(10):1084-1087.
J Pang: Optimized time-domain resource partitioning for enhanced inter-cell interference coordination in heterogeneous networks. In Proceedings of the IEEE Wireless Communication and Networking Conference (WCNC). IEEE Piscataway; 2012:1613-1617.
G de la Roche, D López-Pérez: Enhanced intercell interference coordination challenges in heterogeneous networks. IEEE Wireless Commun. Mag 2011, 18(3):22-30.
GX Yuan: Carrier aggregation for LTE-advanced mobile communication systems. IEEE Commun. Mag 2010, 48(2):88-93.
A Simonsson: Uplink power control in LTE - overview and performance, subtitle: principles and benefits of utilizing rather than compensating for SINR variations. In Proceedings of the IEEE Vehicular Technology Conference (VTC-Fall). IEEE, Piscataway; 2008:1-5.
J Gora: Cell-specific uplink power control for heterogeneous networks in LTE. In Proceedings of the IEEE Vehicular Technology Conference (VTC-Fall). IEEE Piscataway; 2010:1-5.
MS Jin: Per cluster based opportunistic power control for heterogeneous networks. In Proceedings of the IEEE Vehicular Technology Conference (VTC-Spring). IEEE, Piscataway; 2011:1-5.
A Morimoto: Investigation on transmission power control in heterogeneous network employing cell range expansion for LTE-Advanced uplink. In European Wireless Conference. Poznan: IEEE, Piscataway; 2012.
M Sadek: A leakage-based precoding scheme for downlink multi-user MIMO channels. IEEE Trans. Wireless Commun 2007, 6(5):1711-1721.
H Shen: Joint transmit and receive beamforming for MIMO downlinks with channel uncertainty. IEEE Trans. Veh. Tech 2013, PP(99):1.
3GPP: E-UTRA-physical layer procedures. TS 36.213 v8.8.0., European Telecommunications Standards Institute 2009, 1-78.
3GPP: E-UTRA–MAC protocol specification. TS 36.321 v9.0.0., European Telecommunications Standards Institute 2009, 1-48.
S Boyd: A tutorial on geometric programming. Optim. Eng 2007, 8: 67-127. 10.1007/s11081-007-9001-7
M Chiang: Power control by geometric programming. IEEE Trans. Wireless Commun 2007, 6(7):2640-2651.
S Boyd: Convex Optimization. Cambridge: Cambridge University Press; 2004.
M Grant: Matlab software for disciplined convex programming, v2.0 beta, Sep 2013. 2013.http://cvxr.com/cvx . Accessed 1 Oct
JF Sturm: Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones Optimization Methods Softw. 11–12. 1999, 625-653.http://sedumi.ie.lehigh.edu/
P Viswanath: Opportunistic beamforming using dumb antennas. IEEE Trans. Inform. Theory 2002, 48(6):1277-1294. 10.1109/TIT.2002.1003822
Acknowledgements
The authors would like to thank the reviewers for their helpful comments which have greatly improve the quality of this paper. This work was supported by the 973 Program under 2013CB329204, the NSFC under 61101087, the SRFDP under 20110092120011, and the Important National Science & Technology Specific Projects 2013ZX03003016.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xu, W., Zhang, H. Uplink interference mitigation for heterogeneous networks with user-specific resource allocation and power control. J Wireless Com Network 2014, 55 (2014). https://doi.org/10.1186/1687-1499-2014-55
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1499-2014-55

 is initialized by .
is initialized by .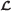 , and denotes the interference channel from user u to cell c. Else, stop.
, and denotes the interference channel from user u to cell c. Else, stop.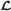 , and the achievable rate R
M
=R
u
. Else, stop.
, and the achievable rate R
M
=R
u
. Else, stop.


