Self-coordination of parameter conflicts in D-SON architectures: a Markov decision process framework

Abstract

We consider a distributed SON (D-SON) architecture where the interaction of different self-organizing network (SON) functions negatively affect the performances of the system. This is referred to in 3rd Generation Partnership Project (3GPP) as a SON conflict, which needs to be handled by means of a self-coordination framework. We focus on a functional architecture and a theoretical framework based on the theory of Markov decision process (MDP) for the self-coordination of different actions taken by different SON functions. In order to cope with the complexity of the overall SON problem, we subdivide the global MDP modeling the long-term evolution (LTE)-enhanced node base station (eNB) onto simpler subMDPs modeling the different SON functions. Each sub-problem is defined as a subMDP and solved independently by means of reinforcement learning (RL), and their individual policies are combined to obtain a global policy. This combined policy can execute several actions per state but can introduce policy conflicts. We focus on the specific SON conflict generated by the concurrent execution of coverage and capacity optimization (CCO) and inter-cell interference coordination (ICIC) SON functions, which may require to update the same parameter, i.e., the transmission power level. The coordination among the different actions selected by the conflicting use cases is achieved by means of a coordination game where the players are the subMDPs and the actions and rewards are those provided by means of a RL approach. Performance evaluation is carried out in a ns3 release 8 compliant LTE system simulator, and it shows that our self-coordination approach provides satisfying solutions in terms of system performances for both the conflicting SON functions.

1 Introduction

A promising approach, which is receiving significant interest from industrial and research communities, to maximize total performance in cellular networks, is to bring into them intelligence and autonomous adaptability. This is referred to as self-organizing network (SON). This concept has been introduced by 3rd Generation Partnership Project (3GPP) in release 8 and it has been expanding across subsequent releases. The main objective of SON is to reduce the costs associated with network operations, by diminishing human involvement, while enhancing network performance, in terms of network capacity, coverage, and service quality. The main motivation behind the increasing interest in the introduction of SON is twofold. On the one hand, from the technical perspective, the complexity and large scale of future radio access technologies imposes significant operational challenges due to the multitude of tuneable parameters and the intricate dependencies among them. In addition, the advent of new heterogeneous kind of nodes like femto, pico, relays, etc., is expected to make tremendously increase the number of nodes in this new ecosystem, so that traditional network management activities based on, e.g., classic manual and field trial design approaches are not viable anymore.

Different architectural solutions have been designed, ranging from a centralized SON (C-SON), where the self-organizing algorithms reside in the network management system, in the operation and maintenance center (OMC) or in the network management systems (NMS), to a distributed SON (D-SON) solution, where the SON functions are distributed, in the control plane, across the edges of the network, typically in the enhanced node base stations (eNB). C-SON can take into consideration data from all nodes in the network to identify and address network-wide issues. However, centralized systems may respond too slowly in the emerging world of small cells that experience very transitory traffic loads. On the other hand, D-SON functionalities are designed for near real-time response in seconds or milliseconds, which makes the SON functions highly dynamic and enables the network to adapt to local changes more rapidly. The main challenge in a D-SON implementation is that, it is more vulnerable than C-SON against network instabilities caused by the concurrent operation of SON functions with conflicting objectives. In particular, multiple SON functions, or instances of the same function running in neighboring cells, can be executed in parallel and may then interact such that the originally intended operation from one function is affected, and the related system performance may be different from what was intended to be. In 3GPP, this kind of negative interactions, which affect the system performances, is referred to as SON function conflict, and the general framework to solve them is referred to as self-coordination. The literature on SON mainly focuses on individual SON function design, [1-3] while some initial work on self-coordination functions can be found in [4-6] and [7] where the authors focused on the identification and classification of different conflict types. Algorithmic solutions [8,9] and implementation challenges [10] have been recently discussed in literature.

In this paper, we target the self-coordination problem in a small cell network. As a result, in the context of a D-SON architecture, we propose a theoretical framework and a functional architecture, which can be easily implemented for self-coordination in 3GPP networks. We propose to map the multiple eNBs in the scenario onto a multiagent system, where each entity is a self-organized agent capable of making autonomous decisions. The multiple agents interact among each other through their actions and operate within an environment, which in our case is the wireless setting. We propose that the theoretical model behind each agent is the theory of Markov decison process (MDP), able to model a dynamic process which evolves through stages, as a result of stochastic actions. In each stage, the MDP chooses one of several actions, and the system stochastically evolves to a new state based on the current state and the chosen action. The solution to a MDP determines a policy which specifies the action to be selected at each time step, such that a certain objective function is maximized. The eNBs have to be capable of executing the multiple standardized SON functions, each one resulting in a different action, e.g., increasing transmission power, modifying the antenna tilt, altering the handover parameters, etc. While in [8], the authors focus on the interactions of two SON functions and on the solution of the MDP obtained as the result of their concurrent execution, we consider that this approach is not scalable, when more SON functions and their instances across multiple cells are running in parallel. The global SON problem including all the standardized SON functions and related instances would become extremely complex. To solve it, we should rely on multi-objective optimization frameworks, which do not allow real-time solutions [11]. As a result, we propose to subdivide the proposed Markov decision problem into several simpler subproblems represented by the different SON functions and their instances. This results in a MDP organized onto multiple tasks which are theoretically modeled by different Markov decision sub-processes (subMDP). Each subMDP can be solved independently through the theory of reinforcement learning (RL), which has already been proposed in the literature of self-organization and heterogeneous networks (HetNets) as a valid solution [12], and which allows to make decisions taking into account the past experience. The solution to each subMDP provides a local policy. The multiple solution policies are then combined to obtain a global solution, such that the actions of each subMDP can be executed concurrently. In MDP literature, this approach is referred to as concurrent actions model [13,14].

As a particular case, in this paper, we focus on the coordination of two specific SON functions, the coverage and capacity optimization (CCO) and the ICIC, and we model them through two subMDPs, which are solved independently through RL. We consider that focusing on only two functions does not result in a loss of generality to our approach, as also other SON functions, considering their automatic characteristic, can be solved through RL, e.g., [8,12], so that our theoretical model can be extended to N _SON SON functions. The generality of our solution for 3GPP SON architecture is proven later in the paper. The two selected SON functions incur in the so-called output parameter SON conflict [15] when, e.g., the CCO function increases the transmission power levels to decrease the outage probability at the cell edge, while the inter-cell interference coordination (ICIC) decreases the power transmission levels to minimize interference. These two policies may generate a resource conflict as each one requires modifying the eNB transmission power in a way that may cancel the actions that the other one intends to take. We propose then a self-coordination approach modeled by means of a coordination game [16], where the players are the conflicting SON functions, the actions are the solutions to the specific subMDPs, i.e., the output of the actor critic algorithm, and the rewards are those provided by the solution of the individual subMDPs. Coordination games have been proven to correctly model the coordination problems that arise when there is a conflicting interest, i.e., when two or more persons prefer different equilibrium outcomes. This is why we consider that they are appropriate to model the problems that the self-coordination function has to face. The self-coordination framework aims then at founding a Nash equilibrium through the coordination game, maximizing the average reward. The proposed approach is validated through system level simulations based on the release 8 compliant platform LTE-EPC network simulator (LENA), available in ns3.

The outline of the paper is organized as follows. Section 2 discusses the work related to this paper from standardization, market, and academic perspectives. Section 3 provides the details of the system model. Section 4 describes the MDP framework for the execution of concurrent SON functions. Section 5 presents a functional architecture for the solution of SON conflicts. Section 6 defines the global SON problem modeling it through a MDP, and its decomposition through subMDPs modeling the different SON functions. Section 7 describes the CCO and ICIC conflict case study. Section 8 describes the details of the simulation platform and scenarios, as well as meaningful simulation results. Finally, Section 9 concludes the paper.

2 Related work

SON functionalities are often designed as stand-alone functionalities, by means of control loops. When they are executed concurrently in the same or different network elements, the impact of their interactions is not easy to be predicted, and unwanted effects may occur. The risk of unacceptable oscillations of configuration parameters or undesirable performance results increase with the number of SON functions, so that it is considered necessary to define and implement a self-coordination framework [3,4,8].

3GPP has proposed different architectures for SON implementation, ranging from centralized C-SON to distributed D-SON, as it is shown in Figures 1 and 2, and the choice of the architecture has a strong impact on the efficiency of the self-coordination framework. If C-SON is used, SON functions are implemented in the OMC or in the NMS, as part of the operation and support system (OSS). This implementation benefits from global information about metrics and key performance indicators (KPIs), as well as computational capacity to run powerful optimization algorithms involving multiple variables or cells. However, it suffers from long timescales. In order to avoid oscillations of decision parameters, 3GPP requires [17] that each SON function asks for permission before changing any configuration parameter. This means that a request must be sent from the SON function to the SON coordinator and a response has to be returned. In C-SON, all these requests must pass through the interface-N, which is not suitable for real-time communication, so that there is no possibility to give priority to SON coordination messages over other operations, administration, and maintenance (OAM) messages. If in turn, distributed coordination is used, the interaction between the SON function and the local SON coordinator will be over internal vendor-specific interfaces, with much lower latency characteristics. This makes the D-SON architecture much more flexible and adequate for small cell networks, which experience very transitory traffic loads, thus requiring high reactivity to propagation and traffic conditions. Market implementations of C-SON are offered by vendors like Celcite (acquired by AMDOCS), Ingenia Telecom, and Intucell (acquired by Cisco), while D-SON solutions have traditionally been more challenging to implement and vendor specific, not allowing for easy interaction of products from different vendors, so that a supervisory layer is commonly still needed to coordinate the different instances of D-SON across a much broader scope and scale. Only recently, vendors like Qualcomm or Airhop have started proposing D-SON as a SON mainstream, as small cells and HetNets require the millisecond response times of D-SON.

Figure 1

C-SON self-coordinator implementation.

Figure 2

D-SON self-coordinator implementation.

The topic of conflicts resolution and coordination has been receiving growing interest also from academic community. In [6,7,15], the authors focus on the classification of potential SON conflicts and on discussing the valid tools and procedures to implement a solid self-coordination framework. Examples of centralized and distributed implementations of SON coordination are offered in [18] and [19], respectively. A preventive coordination mechanism that uses policy-based decision-making has been proposed in [10]. Guard functions have been proposed in [4] to detect undesirable network behaviors and trigger countermeasures. Decision trees have been proposed in [20] for properly adjusting remote electrical tilt (RET) and transmission power. Q-learning, as a RL method, has been proposed in [8] to take advantage of experience gained in past decisions, in order to reduce the uncertainty associated with the impact of the SON coordinator decisions when picking an action over another to resolve conflicts.

3 System model

We consider a heterogeneous wireless network composed of a set of macrocells that coexist with small cells. The $M\,{=}\,|\mathcal {M}|$ macrocells form a regular hexagonal network layout with inter-site distance D and provide coverage over the entire network, comprising both indoor and outdoor users. The $F\,{=}\,|\mathcal {F}|$ small cells are placed indoors within the macro-cellular coverage area following the 3GPP dual strip deployment model. Both macro and small cells operate in the same frequency band, which allows to increase the spectral efficiency per area through spatial frequency reuse.

An orthogonal frequency division multiple access (OFDMA) downlink is considered, where the system bandwidth BW is divided into B resource blocks (RBs). A RB represents one basic time-frequency unit that occupies the bandwidth B W _RB over time T. In particular, in LTE systems, each frame has a duration of 10 ms, divided into equally sized transmission time interval (TTI), which have a duration of 1 ms. The bandwidth B is divided into B _RB=180 kHz physical RBs which are grouped in resource block group (RBG) of different sizes determined as a function of the transmission bandwidth configuration in use. Associated with each macro and small cell base station (BS) are U ^M macro and U ^F small cell users, respectively. The multiuser resource assignment that distributes the B RB among the U ^M macro and U ^F femto users is carried out by a proportional fair scheduler.

We denote by $\textbf {p}^{n}_{t}=\left (p_{1,t}^{n},\ldots,p_{B,t}^{n}\right)$ the transmission power vector of BS n at time t, with $p_{r,t}^{n}$ denoting the downlink transmission power of RB r. The maximum transmission power for small and macro BSs are $P_{\text {max}}^{\mathrm {F}}$ and $P_{\text {max}}^{\mathrm {M}}$, with $P_{\text {max}}^{\mathrm {F}{\ll }}P_{\text {max}}^{\mathrm {M}}$, such that $\sum _{r=0}^{B}p_{r,t}^{m} \leq P_{\text {max}}^{\mathrm {M}}, m{\in }\mathcal {M}$ and $\sum _{r=0}^{B}p_{r,t}^{f} \leq P_{\text {max}}^{\mathrm {F}}, f{\in }\mathcal {F}$.

We analyze the system performance under different perspectives. First of all, we consider the signal-to-interference and noise ratio (SINR). Assuming perfect synchronization in time and frequency, the SINR of macrouser u ^m who is allocated RB b of macrocell $m{\in }\mathcal {M}$ amounts to:

$$ \gamma_{b,t}^{m}=\frac{p_{b,t}^{m}h_{b,t}^{mu}}{\sum\limits_{n\in\mathcal{M},n\neq m}p_{b,t}^{n}h_{b,t}^{nu} + \sum\limits_{f\in\mathcal{F}}p_{b,t}^{f}h_{b,t}^{fu} + \sigma^{2}} $$

((1))

where $h_{b,t}^{mu}$ accounts for the link gain between the transmitting macro BS m and its macrouser u ^m; while $h_{b,t}^{nu}$ and $h_{b,t}^{fu}$ represent the link gain of the interference that BSs n and f imposes on macrouser u ^m, respectively. Finally, σ ² denotes the thermal noise power.

Likewise, the SINR of small cell user v ^f who is allocated in RB b by small cell $f{\in }\mathcal {F}$ is in the form:

$$ \gamma_{b,t}^{f}=\frac{p_{b,t}^{f}h_{b,t}^{fv}}{\sum\limits_{m\in\mathcal{M}}p_{b,t}^{m}h_{b,t}^{mv} + \sum\limits_{n\in\mathcal{F},n\neq f}p_{b,t}^{n}h_{b,t}^{nv} + \sigma^{2}} $$

((2))

where $h_{b,t}^{nv}$ and $h_{b,t}^{mv}$ indicate the link gain between BSs n and m and small cell user v ^f, respectively.

We also use as a meaningful indicator of quality perceived by users the channel quality indicator (CQI). This is computed based on the spectral efficiency per user, using the mapping function as indicated in [21], where the block error rate (BLER) $\text {BLER}=1-\exp \left (\text {log}\frac {(1-\text {BLER})}{\text {TBS}}\right)$, should be smaller or equal to 10%, and the transport block size (TBS) for the estimated CQI is calculated as reported in [21]. As a system metric, we also use the reference signal received quality (RSRQ) from the serving cells, which is defined as the number of RBs multiplied by the reference signal received power (RSRP) over the system bandwidth BW multiplied by reference signal strength indication (RSSI). Finally, the throughput per user is achieved by user data protocol (UDP) client application.

4 Theoretical model of SON conflicts: a Markov decision process framework

We propose a framework where the decision makers are the 3GPP eNBs. The learner or decision maker is called agent, and it interacts continuously with the so-called environment. The agent selects actions and the environment responds to those actions and evolves into new situations. In particular, the environment responds to the actions through rewards, i.e., numerical values that the agent tries to maximize over time.

The agent has to exploit what it already knows in order to obtain a positive reward, but it also has to explore in order to take better actions in the future. We assume that the environment is the wireless cellular scenario, with all its realistic characteristics, in terms of mobility of users, channel variations, and users’ activity patterns. The problem is then defined by means of a Markov decision process $\left \{ \mathcal {S}, \mathcal {A}, \mathcal {T}, \mathcal {R} \right \}$, where , is the set of possible states of the environment $\mathcal {S}=\left \{s_{1},s_{2},\ldots,s_{n}\right \}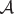$, is the set of possible actions $\mathcal {A}=\{a_{1},a_{2},\ldots,a_{q}\}$ that each decision maker may choose, is the probability of moving to state s+1 when action a is taken in state s, and 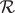is a reward function $\mathcal {R}(s,a)$, which specifies the immediate return when taking action a in state s. The interactions between the multi-agent system and the environment at each time instant t consist of the following sequence.

• Agent i senses the state ${s^{i}_{t}}=s \in \mathcal {S}$.

• Based on s, agent i selects an action ${a^{i}_{t}}=a \in \mathcal {A}$.

• As a result, the environment makes a transition to the new state $s^{i}_{t+1}=v \in S$.

• The transition to the state v generates a reward ${r^{i}_{t}}=r \in \mathfrak {R}$.

• The reward r is fed back to the agent and the process is repeated.

In the following, we remove the notation indicating the specific agent i, for the sake of simplicity. The solution to a MDP is based on the RL framework [22]. At each time step, the agent implements a mapping from states to probabilities of selecting each possible action. This mapping is the agent’s policy. The objective of each learning process is to find an optimal policy $\pi ^{*}(s) \in \mathcal {A}$ for each s, to maximize some cumulative measure of the reward r received over time. Almost all RL algorithms are based on estimating a so-called value function, which is a function of the states estimating how good it is for an agent to be in a given state. The quantification of this is defined based on the expected future rewards. Of course, the rewards that an agent can expect to receive in the future depend on what actions it will take. As a result, the value of a state s under a policy π, and denoted V _π (s), is the expected return when starting in s and following π thereafter:

$$ V_{\pi}(s)=\mathbb{E}_{\pi} \left[ \sum\limits^{\infty}_{k=0} \gamma^{k} r_{t+k+1} \middle | s_{t}=s \right] $$

((3))

where stands for the expectation operator, t is any time step, and 0≤γ≤1 is a discount factor.

The literature of MDPs offers two methods to solve this kind of problems in a closed form: value iteration and policy iteration [23]. The first one is used to find ε-optimal policies for discounted MDPs, the second one works by constructing a sequence of policies with increasing rewards. Both of them require an explicit representation of states and actions and need to explore the entire state space during each iteration. As a result, the temporal complexity of these solution methods can be very large when they are applied to complex problems represented by big state-action spaces. In order to reduce the complexity of MDPs, the literature proposes three approaches: factorization [24], abstraction [25], and decomposition [26]. The idea behind the factorization approach is to address the complexity of the problem by identifying variables, which determine the state of the environment and the specific actions which have an effect on them, under certain conditions. In this framework, a state is implicitly described by an assignment to a set of state variables X={x ₁,...,x _n }, where the state at time t is now represented as a vector X _t ={x _1,t ,...,x _n,t }, where X _i,t denotes the ith state variable at time t [27]. Furthermore, the rewards can often also be decomposed as a sum of rewards related to individual variables. The abstraction approach, in turn, creates an abstract model that aims at generating an equivalent simplified MDP by mapping a group of states, sharing a local behavior, onto a single state. Finally, the decomposition approach subdivides the complex problem into smaller tasks. Each task is modeled by means of a subMDP and the value function and optimal policy for the MDP associated to each subtask are computed and then combined.

We rely then on the so-called decomposition approach [13], which subdivides the autonomous decision making process into multiple tasks represented by the individual SON functions. This results in a MDP organized onto multiple tasks which are theoretically modeled by different subMDPs. Each subMDP is solved independently through actor critic (AC), as described in the next section, and the resulting policies are combined to obtain a global solution.

4.1 Learning the optimal policy

We have modeled the eNBs as decision makers through a MDP, which we propose to factor onto as many subMDPs as SON functions the eNB needs to execute in parallel. The solution of a MDP passes through the theory of RL, which offers different alternatives depending on the peculiarities of the problem to solve. A possible solution could be based on the theory of dynamic programming. However, in the complex wireless environment where the decision makers are operating, it is not possible to evaluate the probabilities of transition from one state to another, as a result of a given set of actions, as it would be necessary to apply this kind of solutions. Another group of potential solutions is based on time-difference learning methods, which allow to make decisions online and self-adapting to the natural evolution of the wireless environment as a function of the mobility of users, traffic patterns, propagation characteristics, etc. Numerous embodiments of temporal difference (TD) learning exist (Q-learning, SARSA, actor critic, etc.), where we concentrate on the actor critic approach, which in its very nature is suited for dynamical wireless systems, for its capability of learning from experience and its computational complexity. These kinds of methods are able to learn directly from experience, without a model of the environment’s dynamics.

RL solutions based on time difference algorithms such as Q-learning [28] or some actor critic approaches [29] can be proven to converge to the optimal policy when only one agent/decision maker is present in the scenario. It is worth mentioning, anyway, that the eventual convergence to the optimal is reassuring in theory, but could be useless in practical terms, as an agent that quickly reaches the 99% of optimality is preferable in most applications compared to another agent guaranteed of eventual optimality, but with a very low learning rate [30]. When more agents are present in the scenario, as it is the case in our setting, the standard convergence proof of time difference algorithms does not hold anymore, as the Markov transition models depend also on the unknown policies of the other learning agents. However, in practice, these learning schemes have been shown to provide successful results also in multiagent scenarios [31]. The generalization of the MDP problem to a multiagent system is a stochastic game. In this case, we cannot prove the eventual optimality, but we can prove the existence of a Markov perfect equilibrium [32], which also is a challenging problem in decentralized wireless networks.

AC methods are TD methods that have a separate memory structure to represent the policy independently of the value function. The policy structure is known as the actor, since it is used to select the actions, while the estimated value function is known as the critic. The critic learns and critiques whatever policy is currently being followed by the actor and takes the form of a TD error δ, which is used to determine if a _t was a good action or not. δ is a scalar signal, which is the output of the critic and drives the learning procedure. After each action selection, the critic evaluates the new state to determine whether things have gone better or worse than expected, as it is defined by the TD error:

$$ \delta_{t}=r_{t}+ \gamma V_{t}(s_{t+1})-V_{t}(s_{t}) $$

((4))

where V is the current value function implemented by the critic to evaluate the action a _t taken in s _t . If the TD error is positive, it suggests that the tendency to select a _t should be strengthened for the future, whereas if the TD error is negative, it suggests that the tendency should be weakened. We identify this tendency with a preference function P(s _t ,a _t ), which indicates the tendency or preference to select a certain action in a certain state. Then, the strengthening or weakening described above can be implemented by increasing or decreasing P(s _t ,a _t ) by:

$$ P(s_{t},a_{t})\leftarrow P(s_{t},a_{t})+\beta\; \delta_{t} $$

((5))

where β is a positive learning parameter. This is the most simple implementation of a AC algorithm. The variation that we consider for implementation is to add different weights to different actions, for example, based on the probability of selecting action a _t in state s _t , i.e., π(s _t ,a _t ), which results in the following update rule:

$$ P(s_{t},a_{t})\leftarrow P(s_{t},a_{t})+\beta\; \delta_{t}(1-\pi(s_{t},a_{t})) $$

((6))

In this implementation, AC directly implements the Boltzmann exploration method to select actions as follows:

$$ \pi(s_{t},a_{t})=\frac{e^{P(s_{t},a_{t})}}{\sum_{a_{t}\in\mathcal{A}}e^{P(s_{t},a_{t})/\tau}} $$

((7))

This means that the probability to select an action a in state s at time t depends on the temperature parameter τ and on the preference values P(s _t ,a _t ) at time t. In this kind of exploration, actions that seem more promising, because of higher preference values, have a higher probability of being selected.

5 Functional architecture

We model the self-organized decision-making process of the eNB, characterized by the multiple parallel SON functions, by means of a MDP. The problem, involving all the radio access autonomous functions, is so complex that it cannot be handled by means of classical approaches. We rely on the decomposition approach, which subdivides the autonomous decision-making process into multiple tasks represented by the simpler SON functions’ decision-making processes. This results in a MDP organized onto multiple tasks which are theoretically modeled by different subMDPs. Each subMDP is solved independently, and their policies are combined to obtain a global solution, such that the actions of each subMDP can be executed. This is illustrated in Figure 3.

Figure 3

General architecture.

If the tasks are independent, the policies can be executed without incurring into conflicts. However, if it is not the case, and the selected actions for each task are executed concurrently and not serially, conflicts among local policies may arise, which may result in undesirable behaviors. In order to solve SON conflicts, we propose a functional architecture based on two main functions:

• Functional decomposition: It is the function in charge of breaking the complex problem into tasks. The complex MDP is subdivided into k subMDPs, which are solved locally. k optimal policies $\pi ^{\ast }_{1},\ldots,\pi ^{\ast }_{k}$ are obtained so that at each time step t actions a ₁,…,a _k can be selected.

• Resolution of policy conflicts: It is the function in charge of detecting and solving potentially conflicting policies, which are to be executed concurrently. The resource conflict detector entity, represented in Figure 3, evaluates whether two or more of the actions a ₁,…,a _k aim at modifying the same parameter. In this case, the conflict is detected and the self-coordinator entity is activated to solve the conflict. The result is the execution of the global solution $a^{\prime }_{1},\ldots, a^{\prime }_{k}$.

The next sections describe these two functions with further details.

5.1 Functional decomposition

This module is responsible for breaking the global MDP $\{\mathcal {S}, \mathcal {A}, \mathcal {T}, \mathcal {R}\}$ into k tasks. Each task is characterized by a specific objective and is modeled by a subMDP, which is solved independently to find a policy π that maps states to actions to maximize the expected reward. Each subMDP i is characterized by its own state, action set, transition probability, and reward functions and is denoted by $\text {subMDP}_{i}=\{\mathcal {S}_{i}, \mathcal {A}_{i}, \mathcal {T}_{i}, \mathcal {R}_{i}\}$.

The set $\mathcal {S}=\left \{s_{1},s_{2},\ldots,s_{n}\right \}$ of states of the global problem is modeled by means of a set of m variables of possible states of the environment X={x ₁,x ₂,…,x _m }. For each subMDP, we consider a decomposed representation, so that the subMDP state space is modeled by a set of v state variables: X _i ={x ₁,x ₂,…,x _v }, where v<m. The state space of the global problem is fully modeled when the k subMDPs include all the m variables, i.e., $X=\cup _{i=1}^{k} X_{i}$. If the global problem is not modeled in a decomposed representation, the union of all space states of the subMDPs must be equal to the state space of the global problem, i.e., $\mathcal {S}=\left \{\mathcal {S}_{1} \cup \mathcal {S}_{2} \cup, \ldots, \cup \mathcal {S}_{k}\right \}$. Each subMDP is solved independently to obtain the value function $V^{\ast }_{i}$ for any $\pi ^{\ast }_{i}$. The global problem is then defined by k subMDPs, subMDP₁,subMDP₂,…,subMDP_k, such that:

• The global state space is modeled in a decomposed form, in such a way that the total state variable X is the union of the k sets of state variables X=X ₁∪X ₂∪,…,∪X _k .

• The action space $\mathcal {A}=\{\mathcal {A}_{1},\mathcal {A}_{2},\ldots,\mathcal {A}_{k}\}$.

• The transition function $\mathcal {T}=\{\mathcal {T}_{1}, \mathcal {T}_{2},\ldots,\mathcal {T}_{k}\}$

• The reward function $\mathcal {R}=\{R_{1}+R_{2} +, \ldots,+ R_{k}\}$

5.2 Resolution of policy conflicts

In this section, we deal with the conflicts, which may arise from the combination of local solutions of individual subMDPs. We focus on the parameter conflict generated by different subMDPs, which occurs when two or more subMDPs may request different values for the same parameter. If there are no conflicts, the set of actions to be selected in a generic state s, $\mathbb {A}=\{\pi ^{\ast }_{1}(s)=a_{1}, \pi ^{\ast }_{2}(s)=a_{2}, \ldots, \pi ^{\ast }_{k}(s)=a_{k}\}$ is executed simultaneously and the solution is optimal. Otherwise, the subMDPs with conflicts are detected and solved. In the following, we propose a solution based on the theory of coordination games, which have already been proven in literature good to solve coordination problems which arise when there is a conflicting interest. The classic example of application is the ‘battle of the sexes’ game, where the man prefers to attend a baseball game and the woman prefers to attend an opera, but both would rather do something together than go to separate events. The question is, if they cannot communicate, where they would go. We consider that this game perfectly fits our coordination game in case of conflicting interests between two SON functions. This game has two pure strategy Nash equilibria, one where both go to the opera and another where both go to the football game. There is also a mixed strategies Nash equilibrium, where the players go to their preferred event more often than the other.

For the sake of simplicity, we model the conflict between two subMDPs, subMDP₁ and subMDP₂, by means of a two-player coordination game. However, the conflict between n subMDPs is scalable to a n-player coordination game.

• S is the set of possible states of the environment, which is the same as the one defined for the global MDP $\mathcal {S}=\left \{s_{1},s_{2},\ldots,s_{n}\right \}$.

• A={α,β} is the action set, where α and β are the actions selected by subMDP₁ and subMDP₂, respectively, and they belong to the corresponding action sets, i.e., $\alpha \in \{a_{\text {subMDP}{_{11}}},\ldots,a_{\text {subMDP}{_{1q1}}}\} \phantom {\dot {i}\!}$ and $\beta \in \{a_{\text {subMDP}{_{21}}},\ldots,a_{\text {subMDP}{_{2q2}}}\} \phantom {\dot {i}\!}$.

• The reward matrix associated with each state at time t is denoted by R.

The self-coordinator module receives as input the actions selected by each subMDP, and based on that, the possible situations to face are the following:

• The subMDPs choose the same action (α=β).

• The subMDPs choose different actions, with different rewards, i.e., α≠β with r _α ≠r _β .

• The subMDPs choose different actions, but with the same reward, i.e., α≠β with r _α =r _β .

If the actions are the same, the coordinator just executes the action, otherwise, the conflict is solved by mixed strategies through the reward matrix depicted inside the coordination box in Figure 4, where A, a, are the rewards of subMDP₁ and subMDP₂, respectively, when executing for both subMDP α; B, b, are the rewards of subMDP₁ and subMDP₂, respectively, when executing action α for subMDP₂ and action β for subMDP₁; C, c, are the rewards of subMDP₁ and subMDP₂, respectively, when executing action α for subMDP₁ and action β for subMDP₂; D, d, are the rewards of subMDP₁ and subMDP₂, respectively, when executing for both subMDPs action β.

Figure 4

Self-coordination based on coordination game.

This game has mixed strategy Nash equilibria given by probabilities p=(d−b)/(a+d−b−c) to play α and 1−p to play β for player 1 (rows) and q=(D−C)/(A+D−B−C) to play α and 1−q to play β for player 2 (columns). Hence, each player is not actually choosing α,β directly, but choosing a probability with which a player will play α. A given number p means that player 1 will play α with probability p and β with probability 1−p. Similar considerations can be done for player 2. Since d>b and d−b<a+d−b−v, p and q are always between 0 and 1, so the existence is assured.

The algorithm for solving resource conflict is described in Algorithm 1.

6 Functional decomposition of the general 3GPP self-optimization use case

In this section, we provide an example about how the proposed functional architecture can be used to deal with the conflicts generated by the concurrent execution of multiple SON functions. The objective of this section is to show that the proposed approach is general enough to model all the SON functions and their derived conflicts. For this purpose, we focus on the self-optimization functionality and on all the associated SON functions, as defined in [15] and [21], i.e., mobility load balancing (MLB), mobility robustness optimisation (MRO), CCO, ICIC, cell outage compensation (COC), energy saving (ES), and random access channel (RACH) optimization. We first introduce these SON functions in the context of the general SON architecture, together with high-level examples of how they may interfere. Then, we define the state and action spaces of the global MDP that models the self-optimization procedure of the overall radio access network (RAN) segment. Finally, we show that the global self-optimization problem can be decomposed onto as many subMDPs as SON functions. We define the different subMDPs, with state and action spaces and tentative proposals for reward functions. References in literature will show that these self-optimization problems can be solved using reinforcement learning functionalities. We consider that this demonstrates the generality of our approach to solve conflicts in 3GPP SON architectures.

6.1 Overview of 3GPP self-optimization functions

In the following, we quickly describe the main self-optimization functions. We describe the main information these functions rely on and the main parameters they aim to tune.

The MLB is a SON function where cells with congestion can transfer load to other cells. The main objective is to improve end-user experience and achieve higher system capacity by distributing user traffic across system radio resources. The implementation of this function is generally distributed and supported by the load estimation and resource status exchange procedure. The messages containing useful information for this SON function (resource status request, response, failure, and update) are transmitted over the X2 interface [33]. MLB can be implemented by tuning the cell individual offset (CIO) parameter. The CIO contains the offsets of the serving and the neighbor cells that all UEs in this cell must apply in order to satisfy the A3 handover condition [21].

The MRO is a SON function designed to guarantee proper mobility, i.e., proper handover in connected mode and cell re-selection in idle mode. Among the specific goals of this function, we have the minimization of call drops, the reduction of radio link failure (RLF), the minimization of unnecessary handovers and ping pongs due to poor handover parameters settings, and the minimization of idle problems. Its implementation is commonly distributed. The messages containing useful information are, e.g., the S1AP handover request or X2AP handover request, the handover report, and the RLF indication/report. MRO operates over connected mode and idle mode parameters. In connected mode, it tunes meaningful handover trigger parameters, such as the event A3 offset (when referring to intra-RAT, intra-carrier handovers), the time to trigger (TTT), or the layer 1 and layer 3 filter coefficients. In idle mode, it tunes the offset values, such as the Qoffset for the intra-RAT, intra-carrier case. CCO is a SON function, which aims to provide capacity and coverage optimization. The targets that can be optimized may be vendor dependent and include coverage, cell throughout, edge cell throughput, or a weighted combination of the above.

CCO reacts to changes in the environment depending on diverse origins: seasonal changes, changes in the surrounding infrastructures, changes in the network planning, daily variations of traffic, etc. It can be implemented in both centralized (in the network manager or element manager) and distributed architectures. Useful information is generally extracted from UE measurements. Parameters that may be tuned are the transmission power, the pilot power, and antenna parameters (azimuth and tilt).

ICIC is a SON function, which aims to minimize interference among cells using the same spectrum. It involves the coordination of physical resources between neighboring cells to reduce interference from one cell to another. ICIC can be done in both uplink and downlink for the data channels physical downlink shared channel (PDSCH) and physical uplink shared channel (PUSCH) or uplink control channel physical downlink control channel (PDCCH). ICIC can be static, semi-static, or dynamic. Dynamic ICIC relies on frequent adjustments of parameters, supported by signaling among cells over X2 interface. To support proactive coordination among cells, the high interference indicator (HII) and the relative narrowband transmit power (RNTP) indicators have been defined, while to support reactive coordination, the overload indicator (OI) has been introduced [33]. Parameters that may be tuned are the transmission power, the pilot power, antenna parameters (azimuth and tilt), and the support of coordinated almost blank subframes (ABS).

COC is applied to alleviate the outage caused by the loss of a cell from service. For this use case, an adequate reaction is vital for the continuity of the service so vendor-specific cell outage detection (COD) schemes have to be designed. Parameters to tune to try to compensate the outages are the transmission power and antenna parameters of the cells neighboring the fault.

ES aims at providing the quality of experience to end users with minimal impact on the environment; the objective is to optimize the energy consumption by designing network element (NE)s with lower power consumption and temporarily shutting down unused capacity when not needed. The most common action is to switch on/off the appropriate cells.

RACH optimization aims at optimizing the random access channels in the cells based on UE feedback and knowledge of its neighboring eNBs RACH configuration. RACH optimization can be done by adjusting the power control (Pc) parameter or change the preamble format to reach the set target access delay.

The independent execution of these individual SON functions affects parameters or performances that can end up in conflict. For example, the ICIC may decide to reduce the transmission power to reduce inter-cell interference, while the CCO may decide on increasing it to improve coverage. These conflicting actions affect the borders of the cell and consequently the performances of the MLB function of the same cell and its neighbors. To compensate for the actions taken by ICIC and CCO, the MLB may decide to modify some handover parameters, which then have impact on the handover and MRO performances, etc.

6.2 Definition of the global MDP and of the decomposed subMDPs

We consider a heterogeneous wireless network composed by M+F 3GPP (H)eNBs, as defined in Section 3. Each eNB has to be capable of executing the N standardized SON functions, where N _SON is the number of implemented SON functions. As an example, in this paper, we will consider the following functions: CCO, COC, ICIC, MLB, MRO, ES, RACH. We can model the global self-optimization problem defined by the N _SON SON functions through a MDP, as it consists of a multi-objective, multi-parameter decision-making/optimization process where the outcomes are partly random and partly under the control of the decision maker. The global problem is then defined by:

• State. The state space is defined by a set of state variables X defined, among others, by: (1) the allocation of users to RBs, (2) the values of CQI, (3) UE measurements in terms of RSRP and the values of RSRQ, (4) resource status information, (5) handover and RLF statistics and information, and (6) interference coordination information in terms of HII, OI, and RNTP.

• Actions. The action set 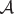consists of all the possible actions that can be taken by tuning, among others, the following parameters: (1) transmission power, (2) pilot power, (3) antenna parameters, in terms of tilt and azimuth, (4) CIO, (5) handover parameters in terms of event offsets, TTT, Qoffset, etc.

• Reward. The reward 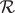is defined based on the following rationale. If the combination of the selected actions gives, e.g., an intercell interference below a threshold or an outage probability above a threshold, RLF statics above a threshold or throughput performances below objectives, or pilot pollution above threshold, etc., the reward is negative; otherwise, the reward is weighted function of multiple objectives, such as the network throughput and the users fairness.

The global MDP including the N _SON SON functions is extremely complex. To solve it, we should rely on multi-objective optimization frameworks, which do not provide real-time solutions [11]. As a result, the global SON problem is subdivided into multiple tasks represented by the simpler N=7 SON functions described before. Other functional decomposition approaches may be possible but they would not be aligned with the 3GPP SON architecture, and consequently, they are not interesting for our problem. Here, each subMDP _i is characterized by its own state, action set, transition probability, and reward functions and is denoted by $\text {subMDP}_{i}=\{\mathcal {S}_{i},\mathcal {A}_{i}, \mathcal {T}_{i},\mathcal {R}_{i}\}$.

We define the state and action spaces, together with one of the possible reward functions of each subMDP as follows:

• 1. CCO

  • State: The state $\mathcal {S}_{1}$ is defined based on the result of the scheduling scheme, which defines (1) the allocation of users to RBs, (2) the values of CQI of each user in the corresponding RB, and (3) UE measurements (e.g., RSRP, RSRQ, etc.)

  • Actions: The action set $\mathcal {A}_{1}$ is based on (1) the set of eligible actions that are a finite set of downlink transmission power levels, which can be allocated to the RBs assigned to the users, and (2) the finite set of available tilt, and azimuth values, which can be assigned to the gain of the vertical plane of the antenna model.

  • Reward: If the CQI is greater or equal than 1, the reward will be positive, otherwise, will be negative. The threshold is set in order to support the SINR values for multiple-input multiple-output (MIMO) transmissions.

  The subMDP representing this SON function can be solved through reinforcement learning, as for example has been done before in [34].

• 2. ICIC

  • State: The state $\mathcal {S}_{2}$ is defined based on the result of the scheduling scheme, which defines (1) the allocation of users to RBs, (2) the values of SINR of each user in the corresponding RB, and (3) UE measurements (e.g., RSRP, RSRQ, etc.)

  • Actions: The set of eligible actions $\mathcal {A}_{2}$ are defined based on (1) the finite set of downlink transmission power levels, which can be allocated to the RBs assigned to the users and (2) the finite set of available tilt and azimuth values, which can be assigned to the gain of the vertical plane of the antenna model.

  • Reward: If the SINR is greater or equal than 0 dB, the reward will be positive, otherwise will be negative. The threshold is set in order to support the SINR values for MIMO transmissions.

  Also, the subMDP modeling this SON function can be solved through reinforcement learning as it is done for example in [35].

• 3. COC

  • State: The state $\mathcal {S}_{3}$ is defined based on the result of the scheduling scheme, which defines (1) the allocation of users to RBs and (2) UE measurements (e.g., RSRP, RSRQ, etc.)

  • Actions: The set of eligible actions $\mathcal {A}_{3}$ are defined based on (1) the finite set of downlink transmission power levels, which can be allocated to the RBs assigned to the users and (2) the finite set of available tilt and azimuth values, which can be assigned to the gain of the vertical plane of the antenna model.

  • Reward: If the SINR is greater or equal than 6 dBs, the reward is positive, otherwise is negative. The threshold is set in order to support the lowest modulation and coding scheme (MCS).

  A complete solution for COC by adjusting the gain of the antenna due to the electrical tilt and the downlink transmission power of the surrounding eNBs can be founded in [36], and this solution is based on reinforcement learning tools.

• 4. ES

  • State: The state $\mathcal {S}_{4}$ is defined based on (1) the resource status information of the cell and its neighbors, (2) the expected demand of traffic, and (3) the energy available to the network element.

  • Actions: The action set $\mathcal {A}_{4}$ consists of switching on/off the cell.

  • Reward: If the resource usage and the energy available for consumption (in case we are in an energy constrained system) are below a certain threshold, the reward is negative, otherwise it is positive.

  The subMDP modeling this use case can also be solved through reinforcement learning, as it is demonstrated in [37].

• 5. MLB

  • State: The state $\mathcal {S}_{5}$ is defined based on the resource status information of each cell and of that of its neighbors.

  • Actions: The action set $\mathcal {A}_{5}$ is defined based on the update of the CIO value, by a finite set of fixed values.

  • Reward: If the change of CIO removes overload with minimal negative handover (HO) effects the reward will be positive, otherwise will be negative.

  A solution for the subMDP modeling, this function can also be based on reinforcement learning tools [8].

• 6. MRO

  • State: The state $\mathcal {S}_{6}$ is defined based on handover and RLF reports and statistics.

  • Actions: The action set $\mathcal {A}_{6}$ is defined based on the update of the cell’s handover event offsets, TTT, and layer 1/layer 3 filter coefficients.

  • Reward: If the users affected by the RLF in the cell after the HO parameter setting is completed are lower than a threshold, the reward will be positive, otherwise will be negative.

  A solution for the subMDP modeling this function can also be based on reinforcement learning tools [8].

• 7. RACH optimization

  • State: The state $\mathcal {S}_{7}$ is defined based on the resource status information.

  • Actions: The action set $\mathcal {A}_{7}$ is defined based on the update of the power control parameter or of the preamble format to reach the set target access delay.

  • Reward: If the users achieve lower data rate than the agreed guaranteed bit rate (GBR), the reward will be negative, otherwise, will be positive.

  This can also be solved through reinforcement learning strategies, as shown in [38].

If n polices are in conflict, the coordination is handled through a n-player coordination game, as discussed in Section 5.2.

7 Case study: self-coordination for ICIC and CCO function conflict

Among the different SON functions defined by 3GPP, we focus our attention on CCO and ICIC. The CCO is in charge of optimizing the capacity and coverage of the area of influence of the particular eNB. As a result, it aims to decrease the outage probability at the border of the cell. The ICIC is in charge of minimizing the interference among different cells. We will focus on the conflict generated by ICIC and CCO SON functions, as both of them aim at modifying the transmission power. In particular, while the CCO may decide to increase the power, e.g., to improve the coverage or the capacity, the ICIC may decide to decrease the power to reduce the interference. Figure 5 shows the actions taken by the two different SON functions, in the D-SON architecture implemented in a heterogeneous scenario. The impact of the concurrent execution of two conflicting actions is highlighted for cell boundaries of one cell. In this section, we describe how to solve the independent subMDPs characterizing the ICIC and CCO functions through TD learning and the actor critic algorithm in particular. Once each SON function has found the optimal policy by means of the AC algorithm, if the actions are different, ICIC and CCO play a game with conflicting interests. We define a two-player game G={N,A,R}, where the N=2 players are the SON functions, A={α,β} is the action set consisting of the actions selected by CCO, $\alpha =\{p_{\text {CCO}{_{1}}},\ldots,p_{\text {CCO}{_{R}}}\} \phantom {\dot {i}\!}$, and ICIC, $\beta =\{p_{\text {ICIC}{_{1}}}, \ldots, p_{\text {ICIC}{_{R}}}\} \phantom {\dot {i}\!}$. The reward matrix associated with each state is denoted by R, represented in Figure 4, inside the coordination game box. Here, the rows correspond to the ICIC and the columns to the CCO.

Figure 5

Impact of ICIC and CCO parameter conflict.

7.1 AC-based solution for CCO function

The CCO SON function aims to provide capacity and coverage optimization. In this scenario, the uncovered planned cell area is the coverage holes that need to be optimized by the coverage and capacity optimization [39]. We measure this by decreasing the outage probability. As an indicator, we consider the CQI, which is a measurement of the communication quality of wireless channels. We define the state and action spaces and the reward function as follows.

• State: The state is defined based on the result of the scheduling scheme, which defines: (1) the allocation of users to RBs (RB₁,RB₂,…,RB _R ) to the N users, (2) the values of CQI of each user in the corresponding RB.

• Actions: The set of eligible actions are the finite set of downlink transmission power levels, which can be allocated to the RBs assigned to the users. The selected values are 0 to 46 dBm per RB with 0.5 dBm granularity.

• Reward:

  $$ r(s_{t},a_{t})=\left\{ \begin{array}{cc} 1 \;,\;\; & \text{if} \; \text{CQI}\geq 1\\ 0 \;, \;\;& \text{otherwise} \end{array}\right.\ $$

  The threshold is set based on the CQI. The reason behind this value is that one of the possible causes of bad BLER is bad coverage. This one should be smaller or equal than 10%, which is the requirement from the LTE standard. As for the particular CQI values associated to the modulation schemes and channel coding rates, we refer to [21].

7.2 AC-based solution for ICIC function

The ICIC SON function aims to minimize interference among cells using the same spectrum. In this scenario [39], we define the state and action spaces and the reward function as follows.

• State: The state is defined based on the result of the scheduling scheme, which defines: (1) the allocation of users to RBs (RB₁,RB₂,…,RB _R ) to the N users and (2) the values of SINR measured for each user in the corresponding RB.

• Actions: The set of eligible actions are the finite set of downlink transmission power levels, which can be allocated to the RBs assigned to the users. The selected values are 0 to 46 dBm per RB with 0.5 dBm granularity.

• Reward:

  $$ r(s_{t},a_{t})=\left\{ \begin{array}{cc} 1 \;,\;\; & \text{if}\; \text{SINR} \geq 0\\ 0 \;, \;\;& \text{otherwise} \end{array}\right.\ $$

  Where the threshold is set in order to support the SINR values for multiuser MIMO transmission mode [21]. MIMO can be used to increase the SINR, i.e., the capacity increases logarithmically with the SINR.

8 Simulation platform, scenario, and results

The proposed algorithms have been evaluated on the ns3 LENA platform based on LTE release 8 [40]. The self-coordinator framework given in Figure 4 is executed every time a new action is selected by one of the functions, i.e., every time a CQI or the UE measurements are reported to the (H)eNB. This happens, in periodic reporting, every 2 to 160 ms for the CQI and every 120 ms - 160 ms for the UE measurements [41]. The parameters used in the simulations for CCO and ICIC are given in Table 1.

Table 1 Simulation parameters

The scenario that we set up consists of 2 eNBs, each one with three sectors, which results in 6 cells and 38 UEs. The small cell network is based on the dual stripe scenario with one block of two buildings. Each building has one floor, with 20 apartments, which results in 40 apartments per block, as depicted in Figure 6. The number of blocks is equal to 5. The HeNB activation factor is 0.5 and the deployment ratio is 0.2, which results in 20 HeNBs, each one located in an independent apartment. Each HeNB provides service to one user in the scenario, which results in 20 HeNB users.

Figure 6

Scenario.

In the scenario, users are randomly distributed, and after the related IP traffic session ends, the UE appears in another location and starts a new session. In addition, in order to test the quality of service (QoS) performance, we use a UDP client application, which takes care of the generation of radio link control (RLC) protocol data units (PDUs) allowing multiple flows belonging to different QoS classes. The parameters used in the simulations, for both the cellular scenario and the learning algorithm, are given in Table 1.

We first show in Figure 7 the time evolution of the average SINR reported by UEs when the two SON functions are executed independently and for different values of the CQI and UE measurements reporting periodicity (i.e., CQI feedback every 2/120/160 ms and RSRQ feedback every 120 ms). We observe that both the AC algorithms implementing the two SON functions after a first training phase converge in a stable manner to a situation where no user is in outage. This is achieved even if the proposed scenario is characterized by the dynamism typical of realistic wireless networks; as the UEs move around, the HeNBs are characterized by random activation factors, the channel model includes shadow and fading effects, etc. We observe as well that the time of convergence depends on the periodicity of feedback to the (H)eNBs from the users.

Figure 7

Time evolution of the average SINR of UEs in the scenario. Considering different values of reporting periodicity for the CQI and the UE measurements.

In Figure 8, we compare performances in terms of time evolution of the SINR provided by the proposed coordination game framework and by the approach that is suggested by 3GPP in [17]. Here, it is proposed that every time that a SON function is willing to modify a transmission parameter, it asks for permission to the self-coordination entity, which handles the queues of requests for parameter modifications. We consider then an implementation of ICIC and CCO characterized by similar reporting periodicity, i.e., 120 ms, for each SON function. We observe in Figure 8 that while the self-coordination framework based on the proposed coordination game actually selects the most appropriate action to execute based on a compromise between conflicting interests, the 3GPP-proposed approach handles the conflict by properly scheduling in time the different actions. In this case, due to the execution of both actions, the 3GPP scheme generates unnecessary oscillations and poorer performances in terms of average-achieved SINR for the UEs in the scenario.

Figure 8

Time evolution of the average SINR of UEs in the scenario. For the self-coordination frameworks based on coordination game and 3GPP approaches.

We now further analyze the results provided by the independent implementation of ICIC and CCO, in comparison to the results obtained when the self-coordination framework is active. Figure 9 represents the cumulative distribution function (CDF) of the SINR of the UEs at the end of simulation time. We observe that when performing the SON functions independently, the CCO offers better performances than the ICIC for low values of SINR, i.e., at the border of the cell, as it aims at optimizing the capacity and coverage features of the scenario. On the other hand, the ICIC function performs better than the CCO for higher values of SINR, as it aims at minimizing the effect of inter-cell interference in the whole scenario, thus improving interference performances for all users. When executing the two SON functions in parallel, conflicts may arise, so we need the support of a self-coordination function. When implementing it, we achieve a compromise between the conflicting objectives of the two SON functions. On the one hand, at the cell edge, we are reducing the outage probability with respect to the results obtained by ICIC, while we are maintaining the outage with respect to results obtained by CCO. On the other hand, inside the cell, the self-coordination framework obtains better performances in terms of outage, compared to previous results of the CCO, while it increases the outage compared to ICIC independent results. The reason behind this behavior is to be found in the compromise achieved by means of the mixed strategy equilibrium, which consists in an equilibrium where there is a percentage of time during which ICIC gets less reward than CCO and the rest of the time when the CCO achieves a higher reward than ICIC.

Figure 9

CDF of the SINR of UEs in the scenario.

Figure 10 shows the RSRQ from the serving cell, which is one of the UE measurements periodically reported by the same UE indicating its performance rate. We observe a similar behavior as discussed for Figure 9. However, here, the self-coordinator performs more similarly to ICIC inside the cell and more similarly to CCO at the cell edge, thus managing to get the best out of each SON function. Finally, the same desirable behavior is also confirmed in Figure 11, which depicts the CDF of each UE average throughput. The considered traffic uses a RLC saturation mode (SM), which takes care of the generation of RLC PDUs allowing multiple flows belonging to different QoS classes.

Figure 10

CDF of the RSRQ from the UEs in the scenario.

Figure 11

CDF of the UE average throughput.

9 Conclusions

In this paper, we have discussed the challenging problem that arises when multiple concurrent SON functions are executed by the same node, or different instances of the same or different SON functions are executed in neighboring cells. Without loss of generality, we have focused on the conflicts between two different SON functions, which aims at updating the same (H)eNB transmission parameter in a D-SON architecture, more suitable for a small cell scenario. We have proposed then a general framework to support the modeling of SON functions and their conflicts when they are executed in parallel. We have shown that the global SON problem can be modeled through a MDP, which can be organized onto simpler subproblems to favor scalability and modeled by means of subMDP. Due to the dynamic nature of the wireless environment and to the autonomous characteristic of the SON functions, we solve the subMDPs by means of RL. RL algorithms provide solution policies to the different SON functions which can be in conflict, so that these require a self-coordinator framework. We have shown that this framework can be modeled by means of a coordination game, where the subMDPs are the players and their solution policies the actions. Simulation results obtained in a release 8 compliant LTE network simulator which demonstrates that the proposed scheme provides a convenient compromise among conflicting actions, taking the best result among the conflicting solution policies.