- Research
- Open access
- Published:
Network-coded primary-secondary cooperation in OFDM-based cognitive multicast networks
EURASIP Journal on Wireless Communications and Networking volume 2015, Article number: 144 (2015)
Abstract
This paper investigates resource allocation for network-coded primary-secondary cooperation in orthogonal frequency division multiplexing (OFDM)-based cognitive multicast networks, in which cognitive radio (CR), network coding (NC), multicast, and OFDM are effectively combined toward the spectrum efficient fifth generation (5G) wireless communication systems. Different from the conventional one-to-one/one-to-more primary-secondary cooperation, the paper concentrates on two-to-one primary-secondary cooperation, in which one secondary user (SU) cooperates with two primary users (PUs) to gain more spectrum access opportunities. To accomplish the cooperation, an agreement is established between the SU and PUs. Meanwhile, to alleviate spectrum bands consumed for PUs’ data transmission, network coding is employed at the SU transmitter. Subject to per-primary-user minimum rate requirement and the total power budget at the secondary transmitter, the investigated primary-secondary cooperation strategy is formulated as a mixed integer optimization problem with the aim of maximizing the average multicast transmission rate. The formulated problem is non-convex and difficult to solve directly. In this paper, a stepwise optimization algorithm is proposed in which the subcarrier assignment and power allocation are executed separately to reduce the computation complexity. The simulation results show that compared to existing schemes, the achieved secondary multicast transmission rate in the proposed scheme is greatly improved. The presented network-coded primary-secondary cooperation is a promising paradigm to improve the spectrum efficiency for the future 5G systems.
1 Introduction
The dramatic growth of mobile data services driven by wireless Internet and smart devices has triggered the investigation of fifth generation (5G) for the next generation of terrestrial mobile telecommunications [1]. Facing great challenges of future mobile networks, the essential requirements for 5G which mainly include higher traffic volume, spectrum, energy, and cost efficiency are pointed out. Therein, cognitive radio (CR) technology, which provides the authorized spectrum of primary users (PUs) to various unlicensed users also called secondary users (SUs) in an opportunistic (time-limited), interference-limited, or paid way [2], handles flexibly the predicament of spectrum underutilization and spectrum shortage resulting from the surging wireless requirements and applications and, thus, has been regarded as the inevitable option for 5G to improve spectrum efficiency [3,4]. Particularly, cognitive cooperation, not only allowing SUs in cognitive radio networks (CRNs) to share authorized spectrum but also inheriting the unique advantages of cooperative communications that promise significant capacity and multiplexing gain increase through distributed transmission/processing, has been becoming an appealing communication paradigm [5,6].
Meanwhile, due to its high spectrum utilization, multicast transmission has become an indispensable part of mobile communication systems nowadays [7]. In this paper, cognitive cooperation and multicast are joint considered. For the primary-secondary cooperation in cognitive multicast networks (CMNs), the secondary source (SS) with limited transmit power needs to broadcast message to multiple secondary destinations (SDs), and hence, the transmission data rate is confined to the worst channel condition among all SDs. Thus, the quality of service (QoS) of the SU suffers severely, and the spectrum accessed by the SU might not be able to afford satisfactory communication services for the SU. One effective protection countermeasure is that the SU assists simultaneously multiple PUs to gain more spectrum access opportunities. Moreover, the SU turns to spend least power and spectrum on transmission data for PUs and scrambles to save resources any way for multicast members. Wireless network coding (NC), which mixes the data from different sessions before signal forwarding to increase per-transmission information content, has been a promising approach [8,9]. Motivated by all these profits, NC technique is adopted by the SU. Furthermore, to enhance the spectrum efficiency, orthogonal frequency division multiplexing (OFDM) [10] is considered in this paper. Combining these technologies mentioned above, this paper investigates the resource allocation strategy for the one-secondary-user and two-primary-user (1S2P) cooperation with NC in OFDM modulated CMNs.
In this paper, first of all, the essential conditions for 1S2P cooperation is analyzed. Secondly, PU 1 and PU 2 separately commit to listen for signal from each other and SU, in exchange for safeguarding their minimum transmission rate requirements. Meanwhile, the SU can access both PUs’ authorized spectrum on the premise that the SU assists PUs in their data transmission with corresponding minimum rate requirements for PUs. Thirdly, the SU switches adaptively between NC mode and decode-and-forward (DF) mode and performs subcarrier assignment and power allocation to maximize its own benefits. Fourthly, the cooperation strategy problem for the SU is formulated as a mixed integer optimization problem, in which the subcarrier assignment and power allocation for NC-based data forwarding, DF-based data forwarding, and SU’s data transmission are tightly coupled and hard to search the optimal solution. And finally, we present a stepwise subcarrier and power optimization algorithm with a low computational complexity.
The rest of this paper is organized as follows: in Section 2, we introduce the related work about cognitive cooperation and summarize the current work related to network coding-based cooperation in cognitive radio system. In Section 3, the system model and 1S2P cooperation are introduced. In Section 4, formulation for the profit-driven 1S2P cooperation strategy problem is presented. The stepwise optimization algorithm is derived in Section 5. Section 6 lists evaluation results and Section 7 concludes our study.
2 Related works
Most researches focus on non-NC cognitive cooperation [11], which from the perspective of profit-driven collaborators, can fall into three categories: selfless relay cooperation (SLRC), profit-driven equal-priority user cooperation (PEPC), and profit-driven unequal-priority primary-secondary user cooperation (PUPSC). In the SLRC, one or more relays put all resources into assisting PUs or SUs to forward data [12-15]. This kind of research is established on the assumption that all relays are selfless. However, in the future cooperation networks, the relay nodes deployed probably by different service providers or individuals have self-serving features and heterogeneous resource requirements. Hence, effective profit-driven mechanism becomes an inevitable development trend for cognitive cooperative transmission. In the PEPC, cognitive users with equal priority collaborate with each other to share resources such as spectrum sensing information and antennas to decrease inter-cell interference and the interference to PUs [16-19]. On the other hand, in the PUPSC, the SUs assists PUs to forward data in exchange for obtaining more spectrum access opportunities to achieve the most benefit, such as transmission rate maximization and transmit power minimization [19-21].
In the current literature, the researches on NC in cognitive cooperation spring up for its satisfactory performance gain. Comparatively speaking, there are a few researches on network-coded cognitive cooperation which mainly focus on non-primary-secondary cooperation [22,23]. In [22], Jin et al. present an optimization framework for multicast scheduling in CRNs, where secondary base station opportunistically utilizes ‘spectrum holes’ to multicast data to SUs and SUs help with each other with network coding in a local neighborhood to reduce overhead and perform error control and recovery. Chun et al. in [23] consider network-coded cooperation for cognitive relay networks, in which SUs communicate to the secondary destination through multiple relay nodes in underlay way while some relay nodes generate the network-encoded packet using linear combination.
At last, researches related to cognitive primary-secondary cooperation can be classified into the following two sides: on one hand, most studies in the literature focus on one-secondary-user and one-primary-user cooperation or multi-secondary-user and one-primary-user cooperation model [24,25], where one PU selects one or multiple SUs to assist it in data communication, while one-secondary-user and multi-primary-user cooperation, in which one SU assists two or more primary transmissions simultaneously, can provide more spectrum access opportunities for the SU. On the other hand, there are only a few researches on NC-based cognitive primary-secondary cooperation. Zou et al. [26,27] study resource allocation problem at the PU side in NC-based cognitive cooperative networks, in which PUs assist in the transmission of SUs, and in exchange for this concession, PUs receive payments from SUs for the spectrum and cooperative transmit power being used in cooperation. In their study, one PT combines together its own data sent in the first phase and the data overheard from the secondary transmitter in the second phase and sends the additive data out with network coding. Then, both PR and secondary receiver extract their desired data from the combined data by subtracting the data they overheard.
Based on the research [28], which demonstrates that the NC noise received at each session’s destinations increases along with the number of sessions increasing, it is unfavorable to employ NC blindly in cooperation. In our previous work [29], the power and spectrum allocation at the SU side is researched for network-coded 1S2P cooperation in CRNs. However, to the best of our knowledge, there are few literature concentrating on profit-driven PUPSC strategy problem at the SU side with NC in OFDM-modulated CMNs. Therefore, in this paper, 1S2P cooperation for network-coded OFDM-modulated CMNs will be studied in which one SU assists the data transmission of two PUs and utilizes NC to save the spectrum resource used for PUs’ data transmission.
Compared with the recent researches, the main contributions of the paper are summarized as follows.
-
Essential condition and content of agreement for network-coded 1S2P cooperation is analyzed. It contains objective environmental factors of the SU and two PUs, their respective transmission requirements and resource constraints, and their respective responsibilities that should be performed.
-
The resource allocation strategy for network-coded 1S2P cooperation is modeled as a mixed integer optimization problem. The problem mainly covers adaptive cooperative mode switch between NC and DF, the assignment of each subcarrier, and the power allocation on each subcarrier.
-
The stepwise subcarrier and power allocation optimization algorithm is derived for the formulated problem, and extensive simulations verify the effectiveness and superiority of the proposed cooperation scheme compared with existing schemes.
3 System model and analysis for cooperation
3.1 System model
Consider an OFDM-modulated cognitive multicast cooperation network with one SU and two PUs, i.e., PU 1 and PU 2. As shown in Figure 1, the SU in the secondary network is composed of a SS and G secondary multicast groups (SMGs) \(\mathcal {K}_{g},~g\in \mathcal {G}=\{1,\cdots,G\}\) with K g SDs. The PU i,i=1,2 in the primary network is composed of a primary transmitter (PT) i and a primary receiver (PR) i. The OFDM technology is adopted in the system to facilitate fine-grained spectrum management. The whole spectrum band is divided into multiple subcarriers (SCs), and the occupied SC set of PT i is denoted as Ω i . The transmit power on the SC l at the PT i is \(P^{l}_{\text {PT}i}, l\in \Omega _{i}\), and the minimum transmission rate requirement at the PR i is r i . Assume that SC set 1 and SC set 2 have different elements, i.e., Ω 1∩Ω 2=∅.
Focusing on network-coded 1S2P cooperation in OFDM-modulated cognitive multicast network, as shown in Figure 1, two PTs that intend to send data to their corresponding PRs cannot communicate directly and ask for assistance from the SU.
Meanwhile, the SS which assists the data transmission of these two PUs can access their licensed spectrum bands and multicasts data to its different SMGs at different rates. To assist the traffic of PT 1 and PT 2 with fewer spectrum bands and save more for its own multicast transmission, the SS acts as a relay to assist PTs’ transmissions by the NC and DF relaying protocol. Thus, for the sake of favorable cooperation, PU 1 (PT 1 →PR 1), PU 2 (PT 2 →PR 2), and SU (SS →SDs) reach a tripartite cooperation agreement: 1) The SD assists both PUs in data transmission. As a reward, SS can access both the spectrum bands of PUs and reallocate it for both the data relaying of PUs and its own multicast data delivery. 2) The PU 1(2) overhears the data of PU 2(1) as auxiliary information for decoding coded data from SS and both PRs are able to operate and receive signals on the whole spectrum bands.
Remark.
In the network-coded 1S2P cooperation scheme, for simplicity, we focus on the scenario of no direct link from each PT to its corresponding PR, i.e., both PTs cannot communicate directly with their corresponding PRs and the direct transmission between each PT and its corresponding PR is not available [30-32]. The case with direct links between the PT and its corresponding PR involves many complicated problems such as the maximum ratio combination of network-coded data and direct transmitted data and is beyond the focus of the paper. In addition, due to the long distance or the shielding effect caused by some barrier between each PT and its corresponding PR, the PR is not within the communication range of the PT, and thus, the assumption that there is no direct link between the source and destination is reasonable for some practical applications [33-35].
Before analyzing the network-coded 1S2P cooperation and resource allocation for the SU, we first introduce the essential condition for cooperation among two PUs and one SU in OFDM-modulated CMNs.
3.2 Essential condition of network-coded 1S2P cooperation
In order to achieve cooperation among PU 1, PU 2, and SU, some essential conditions should be satisfied.
On one hand, the SS must be located within both the transmission ranges of PT 1 and PT 2. Otherwise, as depicted in Figure 2a, if the location of SS is not within PT 2’s transmission range, then the SS cannot receive the signal of PT 2 and assist the data transmission of PT 2. On the other hand, each PR should be located within the transmission range of its cooperative PU member for the decoding of its own data from the coded data transmitted by the SU. If one PR, for example, PR 2 shown in Figure 2b, is not located within the transmission range of PT 1, PR 2 cannot listen the data from PT 1 and decode the needed data after it receives the mixed data of PT 1 and PT 2 transmitted by the SS.
Location-based necessary condition sketch for tripartite cooperation.(a) Node SS is not located within the intersection transmission range of PT 1 and PT 2. (b) One primary receiver is not located within the transmission range of its cooperative primary member. (c) Both conditions are satisfied and necessary condition of 1S2P cooperation for further progress is guaranteed.
Only when both these sides are satisfied, as shown in Figure 2c, their own benefits of the three members for network-coded 1S2P cooperation can be guaranteed, and the network-coded 1S2P cooperation among them can be meaningful. Therefore, the essential conditions for the network-coded 1S2P cooperation are summarized as follows:
-
 (SS) ∈ Υ(PT 1)\(~\bigcap \Upsilon \)(PT 2);
(SS) ∈ Υ(PT 1)\(~\bigcap \Upsilon \)(PT 2); -
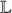 (PR 2) ∈ Υ(PT 1), and
(PR 2) ∈ Υ(PT 1), and 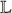 (PR 1) ∈ Υ(PT 2).
(PR 1) ∈ Υ(PT 2).
where Υ(PT i) (i=1,2) denotes the transmission range of PT i and  (X) denotes the location of X.
(X) denotes the location of X.
4 Problem formulation for network-coded 1S2P cooperation
Concentrating on the resource allocation problem at the SS in network-coded 1S2P cooperation, the SS reallocates SCs in the set \(\mathcal {S}=\Omega _{1}\cup \Omega _{2}\) into G+3 SC sets \(\mathcal {S}_{k}, ~k\in \Pi =\{1,\cdots,G+3\}\), as depicted in Figure 3. The SCs in set \(\mathcal {S}_{k}, ~k=1,\cdots,G\) are used for broadcasting SU’s data to \(\mathcal {K}_{g},~g=1,\cdots,G\). The SCs in set \(\mathcal {S}_{G+i}, ~i=1,2\) are used for assisting transmission of PT i’s data using DF protocol. The SCs in set \(\mathcal {S}_{G+3}\) are used for forwarding transmission of the XOR-ed data from PT 1 and PT 2. Next, we start with the cooperation transmission analysis for network-coded 1S2P cooperation.
4.1 Cooperation transmission analysis
As sketched in Figure 3, two time slots are applied in each cooperation transmission. In the first time slot, PTs broadcast their data, respectively, and hence, the time slot is called as primary user broadcast phase. In the second time slot, the SS communicates with PRs and multicasts data to SMGs, and hence, the time slot is also referred as secondary user relay and multicast phase.
4.1.1 4.1.1 Primary user broadcast phase
In the broadcast phase, two PTs broadcasts their symbols simultaneously. Specially, PT i,i=1,2 sends signals on subcarrier l in SC set Ω i . The received signals at the SS and PR i can be expressed, respectively, as
where \(x^{l}_{\text {PT}i}\) is the transmitted symbol with unit power from PT i on subcarrier l, \(p^{l}_{\text {PT}i}\) is the transmit power for PT i on subcarrier l, and n SS and \(\phantom {\dot {i}\!}n_{\text {PR}i'}\) are the additive white Gaussian noise at the SS, PR i ′, respectively. We assume that \(n_{\text {SS}},n_{\text {PR}i} \sim \mathcal {CN}(0,N_{0})\). \(h^{l}_{\text {PT}i,\text {SS}} \left (h^{l}_{\text {PT}i,\text {PR}i'}\right)\) denotes the channel coefficients from PT i to the SS (PR i ′) on the subcarrier l.
The transmission rate of the first hop on the subcarrier l for PT i, i=1,2, l∈Ω i is
where the spanning bandwidth of each subcarrier is Δ f Hz, and coefficient \(\frac {1}{2}\) is derived from the time-division transmission as depicted in Figure 3.
4.1.2 4.1.2 Secondary user relay and multicast phase
In the secondary user relay and multicast phase, the SU reallocates SCs in  into SC sets \(\mathcal {S}_{k}~(k\in \Pi)\). Therein, the SC sets \(\mathcal {S}_{k}~(k\in \{1,\cdots,G\})\) are used for transmitting its own multicast data to SDs belonging to SMGs \(\mathcal {K}_{k}\), respectively. The SC sets \(\mathcal {S}_{k}~(k=G+i,i\in \{1,2\})\) are allocated for transmitting the received signal from PT i using DF protocol, respectively. The SC set \(\mathcal {S}_{k}~(k=G+3)\) is assigned for transmitting the XOR-ed data of received data from both PTs. Define the indicator functions \({\delta _{k}^{l}}\) that
into SC sets \(\mathcal {S}_{k}~(k\in \Pi)\). Therein, the SC sets \(\mathcal {S}_{k}~(k\in \{1,\cdots,G\})\) are used for transmitting its own multicast data to SDs belonging to SMGs \(\mathcal {K}_{k}\), respectively. The SC sets \(\mathcal {S}_{k}~(k=G+i,i\in \{1,2\})\) are allocated for transmitting the received signal from PT i using DF protocol, respectively. The SC set \(\mathcal {S}_{k}~(k=G+3)\) is assigned for transmitting the XOR-ed data of received data from both PTs. Define the indicator functions \({\delta _{k}^{l}}\) that
Accordingly, the received signals at SDs and PRs on each SC can be expressed, respectively, as
where \(x^{l}_{\text {SS}}\) is the transmitted symbol with unit power by the SS on the SC l for SDs, \(\widetilde {x}^{~\!l}_{\text {PT}i}\) is the symbol from PT i transmitted by the SS with unit power on the SC l using DF protocol for PR i, \(P_{\mathrm {s}}^{l}\) denotes the power loaded on the SC l by the SS, \(h^{l}_{\text {SS},\text {PR}i}\) denotes the channel coefficients from the SS to the PR i on the SC l, \(h^{l}_{\text {SS},\text {PR}3}=\min \left \{h^{l}_{\text {SS},\text {PR}1},h^{l}_{\text {SS},\text {PR}2}\right \}\), \(h^{l}_{\text {SS},\text {SD}u}\) is the channel coefficient from the SS to the SD u belonging to the SMG \(\mathcal {K}_{g}\), we denote that \(h^{l}_{\text {SS},\text {SG}g}=\min \left \{h^{l}_{\text {SS},\text {SD}u}|u\in \mathcal {K}_{g}\right \}\) which means the received signal at the SD of multicast group g is limited by the minimum channel gain among members of the group g, n SDu is the additive white Gaussian noise at the SD u, and we also assume that \(n_{\text {SD}u}\sim \mathcal {CN}(0,N_{0})\).
Denote that
Owing to signal transmission uniqueness for each subcarrier, mathematically, we have the following constraints \(\mathcal {C}1\) and \(\mathcal {C}2\).
4.2 Formulation for network-coded 1S2P cooperative resource allocation
According to the description above and network coding constraint that the receiver terminal needs enough information to decode its desired data by XORing the received data with its own data or auxiliary data [8,33,36], the achievable transmission rate for coded data at the second hop is limited by the minimum transmission rate R 3 of data transmitted by both PTs from the first hop, i.e.,
and we have
where \(C^{l}_{\text {sp},3}\left (\gamma ^{l}_{\text {sp},3},P^{l}_{\mathrm {s}}\right)=\frac {1}{2}\Delta f\log _{2}\left (1+\gamma ^{l}_{\text {sp},3}P^{l}_{\mathrm {s}}\right)\) denotes the achievable transmission rate of network coded data transmitted by the SS on the subcarrier l if \(l\in \mathcal {S}_{G+3}\).
If \(l\in \mathcal {S}_{G+i},i=1,2\), the achievable transmission rate of data to the PU i transmitted by the SS according to DF protocol on the subcarrier l can be denoted as \(C^{l}_{\text {sp},i} \left (\gamma ^{l}_{\text {sp},i},P^{l}_{\mathrm {s}}\right)=\frac {1}{2}\Delta f\log _{2}\left (1+ \gamma ^{l}_{\text {sp},i}P^{l}_{\mathrm {s}}\right)\). To achieve the cooperation agreement, the SS need to guarantee both PUs’ minimum transmission rate requirements r i ,i=1,2. Mathematically, the following constraint should be satisfied
It should be noticed that the total achieved transmission rate for PU i is limited by the transmission data rate R i from PU i during the first hop, i.e., \({\sum \nolimits }_{l\in \mathcal {S}}\left (\delta ^{l}_{G+3}C^{l}_{\text {sp},3} \left (\gamma ^{l}_{\text {sp},3},P^{l}_{\mathrm {s}}\right)+\delta ^{l}_{G+i}C^{l}_{\text {sp},i} \left (\gamma ^{l}_{\text {sp},i},P^{l}_{\mathrm {s}}\right)\right)\leq R_{i},~\forall ~i=1,2\), where \(R_{i} = {\sum \nolimits }_{l\in \Omega _{i}}C_{\mathrm {p},i}^{l}\). If R i <r i , then the conditions (12) cannot be satisfied, and hence the network-coded 1S2P cooperation cannot guarantee the minimum rate requirements of PRs, and the cooperation agreement cannot be achieved. Thus, cooperation members for the network-coded 1S2P cooperation should be reselected based on the essential conditions mentioned in Section 3.2 and the criterion R i ≥r i for PU i involved in the collaboration. Considering the power budget P th at the SS and the maximum power P high that can be loaded on each SC, the power loaded on the SCs should be constrained as
The achievable transmission rate of data for the SMG \(\mathcal {K}_{g},g\in \mathcal {G}\) on the subcarrier l, if \(l\in \mathcal {S}_{g}\), is \(C^{l}_{\text {ss},g}\left (\gamma ^{l}_{\text {ss},g},P^{l}_{\mathrm {s}}\right)=\frac {1}{2}\Delta f\log _{2}\left (1+ {\gamma ^{l}_{g}}P^{l}_{\mathrm {s}}\right)\). To maximize the achieved transmission rate of the SS to all SDs, the network-coded 1S2P cooperative resource allocation problem can be formulated as the following model \(\mathcal {OP}_{1}\).
5 Subcarrier assignment and power allocation for network-coded 1S2P cooperation problem
In the section, the solution for problem \(\mathcal {OP}_{1}\) is investigated. First of all, in order to facilitate problem solving, the reformulation of problem \(\mathcal {OP}_{1}\) is implemented and the transformation method has been mentioned in our previous work [29]. It is found that in order to save power and SCs resource and to maximize the achievable transmission rate of the SS to all SDs, the SS would give priority to network-coded data forward transmission for satisfying the minimum rate requirements of both PRs. Therefore, the power and SCs allocated for network-coded data forward transmission must make full use of the given resource R 3, i.e.,
where W 3= min{R 3,r 1,r 2}, which is to say that if R 3≥ min{r i }, then W 3= min{r i }; otherwise, W 3=R 3.
Meanwhile, due to the different rate requirements and channel conditions for two PUs, the surplus rate requirements of PRs should be provided by the SS with respective cooperation with each PU. Thus, the constraints \(\mathcal {C}4\) can be reformulated as
Denote that W i =r i −W 3,∀ i=1,2, the constrains \(\mathcal {C}3'\sim \mathcal {C}4'\) can be jointly expressed as
Therefore, problem \(\mathcal {OP}_{1}\) can be reformulated as \(\mathcal {OP}_{2}\) described below
Specifically, we present some basic analysis for the equivalence of problem \(\mathcal {OP}_{1}\) and \(\mathcal {OP}_{2}\): If R 3≥ min{r i }, without loss of generality, assume r 1≥r 2, which means that the resource R 3 can afford the QoS of the PT 2 and the constraint \(\mathcal {C}4\) for the PT 2 becomes loose, then the constraints \(\mathcal {C}3\) and \(\mathcal {C}4\) in the problem \(\mathcal {OP}_{1}\) can be converted as \({\sum \nolimits }_{l\in \mathcal {S}}\delta ^{l}_{G+3}C^{l}_{\text {sp},3} \left (\gamma ^{l}_{\text {sp},3},P^{l}_{\mathrm {s}}\right)\geq r_{2}\) and \({\sum \nolimits }_{l\in \mathcal {S}}\delta ^{l}_{G+1}C^{l}_{\text {sp},1} \left (\gamma ^{l}_{\text {sp},1},P^{l}_{\mathrm {s}}\right)\geq r_{1}-r_{2}\) with \(\delta ^{l}_{G+2}=0\), which are in accordance with problem \(\mathcal {OP}_{2}\). Other situations suffer the similar analysis omitted to avoid wordiness.
Next, the solution algorithm for problem \(\mathcal {OP}_{2}\) is derived.
5.1 Stepwise optimization problem presentation
The allocation issue of joint subcarrier and power has high computational complexity, and it is even intractable when subcarrier number and secondary multicast group number are very large. In the section, we try to present a low-complexity and efficient solution by dividing the problem \(\mathcal {OP}_{2}\) into two separate subproblems \(\mathcal {OP}_{2a}\) and \(\mathcal {OP}_{2b}\) as follows. \(\mathcal {OP}_{2a}\): Optimize the sum rate by varying SC assignment \(\mathrm {\delta }^{l}_{k}\) when fixing power allocation \(P_{\mathrm {s}}^{l}\) denoted as \(\tilde {P}_{\mathrm {s}}^{l}\).
where \(\tilde {C}^{l}_{\text {ss},g}=C^{l}_{\text {ss},g}\left (\gamma ^{l}_{\text {ss},g},\tilde {P}^{l}_{\mathrm {s}}\right)\) and \(\tilde {C}^{l}_{\text {sp},j}=C^{l}_{\text {sp},j}\left (\gamma ^{l}_{\text {sp},j},\tilde {P}^{l}_{\mathrm {s}}\right)\). \(\mathcal {OP}_{2b}\): Optimize the sum rate by varying power allocation \(P_{\mathrm {s}}^{l}\) when fixing SC assignment \(\mathrm {\delta }^{l}_{k}\) denoted as \(\left ({\delta ^{l}_{k}}\right)^{*}\), respectively.
Through the division of problem \(\mathcal {OP}_{2}\), suboptimal power and subcarrier allocation is obtained. However, it has been shown that the stepwise low-complexity suboptimal allocation scheme can achieve the similar performance with the optimal one [33,37].
5.2 The heuristic solving method for \(\mathcal {OP}_{2a}\)
To solve the subproblem \(\mathcal {OP}_{2a}\), a heuristic solving method is applied. The main idea of the heuristic solving method is elaborated as follows.
On one hand, let set J={1,2,3} denote the current unsatisfied minimum constraint item set for the \(\mathcal {C}3^{\prime \prime }\) in the subproblem \(\mathcal {OP}_{2a}\). One top priority is to assign the SCs for \(\mathcal {S}_{G+j},j\in J\) to guarantee the minimum rate requirements.
Specifically, for rate transmission targets W
j
,j∈J, find the maximum W
j
and the corresponding j, and select the first best channel, the second best one, etc. from current unassigned subcarrier set \(\mathcal {S}_{0}\) which is initialized to  in turn until the constraint \({\sum \nolimits }_{l\in \mathcal {S}}\delta ^{l}_{G+j}\tilde {C}^{l}_{\text {sp},j}\geq W_{j}\) is satisfied. The point is that the SC l in set \(\mathcal {S}_{0}\) is removed from \(\mathcal {S}_{0}\) once it is selected, and l is assigned to \(\mathcal {S}_{G+j}\). Another point is that once the target W
j
is guaranteed, the J is updated as J∖{j}.
in turn until the constraint \({\sum \nolimits }_{l\in \mathcal {S}}\delta ^{l}_{G+j}\tilde {C}^{l}_{\text {sp},j}\geq W_{j}\) is satisfied. The point is that the SC l in set \(\mathcal {S}_{0}\) is removed from \(\mathcal {S}_{0}\) once it is selected, and l is assigned to \(\mathcal {S}_{G+j}\). Another point is that once the target W
j
is guaranteed, the J is updated as J∖{j}.
On the other hand, each remaining unassigned SC \(l\in \mathcal {S}_{0}\) is assigned in turn to the SMG \(\mathcal {K}_{g}\) that maximizes the value of \(K_{g}\tilde {C}^{l}_{\text {ss},g}\), where \(g\in \mathcal {G}\).
The heuristic SC assignment (HSCA) sub-algorithm is provided as shown in Algorithm 1.

5.3 The dual method for \(\mathcal {OP}_{2b}\)
Based on the SC assignment \(\left ({\delta _{k}^{l}}\right)^{*}\) determined through solving the subproblem \(\mathcal {OP}_{2a}\), the subproblem \(\mathcal {OP}_{2b}\) can be solved by the dual method.
By introducing lagrangian multipliers λ j ,j=1,2,3 and μ for the constraints C3″ and C4 of the subproblem \(\mathcal {OP}_{2b}\) respectively, the lagrangian function \(\mathcal {L}\left (\left \{{P_{s}^{l}}\right \},\{\lambda _{j}\},\mu \right)\) can be expressed as
To obtain necessary conditions for optimal solution, differentiating \(\mathcal {L}\left (P_{\mathrm {s}}^{l},\lambda _{j},\mu \right)\) with respect to \(P_{\mathrm {s}}^{l}\) provides the following Karush-Kuhn-Tucker (KKT) conditions [38] as
Since for each l, only one \(({\delta ^{l}_{k}})^{*},k\in \Pi \) is non-zero. Associating with the constraints \(\mathcal {C}6\) of subproblem \(\mathcal {OP}_{2b}\), the power loaded on each SC l can be provided as the following equation
where \([z]^{b}_{a}\) is the projection on [a,b] of z.
The lagrangian multipliers λ j and μ can be obtained by solving the dual problem of \(\mathcal {OP}_{2b}\) which is presented as Equation 23.
The dual problem for subproblem \(\mathcal {OP}_{2b}\) can be solved using the sub-gradient method [39] presented as Equations 24 and 25.
where [z]+ is the projection on [0,∞) of z, and α j and β are diminishing step sizes for guaranteeing the convergence of the sub-gradient method [39].
Therefore, the stepwise subcarrier-power allocation (SSPA) algorithm is summarized in Algorithm 2.

6 Simulation results
In this section, simulation results are presented to demonstrate the performance of the proposed network-coded 1S2P cooperation scheme in terms of average achieved transmission rate of SUs and success probability of both PT 1 and PT 2 using the MATLAB R2010b software on a PC equipped with an Intel(R) Core(TM) i3-2130 CPU (3.40 GHz).
6.1 Simulation parameters
The channel gains between each transmitter and receiver is modeled as h=d −α/2 ξ with Rayleigh fading ξ, where d is the normalized distance, and α is the path loss exponent, chosen as 3 [40]. Each point in the simulation curves is the average of 2,000 channel realizations. Moreover, the success probability is calculated by the probability that both the minimum rate requirements of PTs are satisfied. It should be noted that during 2,000 channel realizations, some channel states may be so severely bad that neither minimum rate requirements of PUs can be satisfied and the cooperation agreement cannot be achieved, and thus, the success probability is not always 1.
Some other simulation parameters are listed as follows:
-
1)
Parameters about subcarriers: the subcarrier numbers owned by PT 1 and PT 2 are both equal to 32, i.e., K=M=32; the bandwidth of each subcarrier △f=0.3125MHz; the maximum power constraint on each SC P high=0.5W.
-
2)
Parameters about PUs: unless noted otherwise, the transmission target rates of PU 1 and PU 2 are r 1=30 Mbps and r 2=20 Mbps, respectively; the transmission power of PU 1 and PU 2 equal to 1 W; equal power allocation on SCs is adopted for each PT.
-
3)
Parameters about SUs: the total power for the SS P th=3W; the SD number U equals to 5; the SMG number G equals to 2.
-
4)
Parameters about scene: the distances among cooperation members are listed as follows. For each i,i ′=1,2,i≠i ′, d(PT i,PR i)=3, d(PT i,PR i ′)=1, and d(PT i,SS)=1.2, d(SS,PR i)=2. For each \(u\in \mathcal {K}_{g},g\in \mathcal {G}\), d(SS,SD u) is distributed uniformly over range [1, 2].
6.2 The compared schemes
The proposed network-coded 1S2P cooperation scheme is compared with these three schemes:
-
No-code 2PUs: the cooperation scheme with two primary users assisted by the SS with decode-and-forward protocol but without network code.
-
No-code 1PU: the cooperation scheme with one primary user assisted by the SS with decode-and-forward protocol. Specifically, SS selects the PT →PR pair whose target transmission rate requirement is the most unsatisfied to assist.
-
Direct: non-cooperation scheme. Specifically, the PT 1 →PR1 pair and PT 2 →PR 2 pair transmit directly their data by themselves without the cooperation of the SS.
6.3 Simulation results with different noise power
In this subsection, we compare the average transmission rate of SUs provided by the proposed scheme and the schemes mentioned in the above subsection. Meanwhile, the effects of these schemes on the success transmission probability of PUs under the different channel noise power density N 0 are analyzed.
Figure 4 depicts the average transmission rate of SUs under different noise power density N 0 with different schemes. The curves of Figure 4 accord with the fact that the average transmission rates of SUs for all schemes get smaller as the channel conditions get worse. It is found that the proposed scheme can provide the largest average transmission rate of SUs. When the noise power density N 0 is lower than a certain value Θ, e.g., about 32 dBW/MHz in Figure 4, the ‘No-Code 2PUs’ scheme can supply higher average transmission rate of SUs than ‘No-Code 1PU’ supplies. When the N 0 gets higher than Θ, the average transmission rate of SUs obtained by ‘No-Code 2PUs’ scheme is a litter lower than that obtained by ‘No-Code 1PU’ scheme. It stems from the fact that the ‘No-Code 2PUs’ scheme needs to satisfy the minimum transmission rate requirements of both PUs, and when the channel conditions get worse, it is a little hard to realize for ‘No-Code 2PUs’ scheme. Therefore, we can discover that the proposed network-coded 1S2P cooperation scheme provides the largest profits for SUs.
On the other hand, success transmission probabilities for PUs are displayed under different noise power density N 0 in Figure 5. The success transmission probabilities become smaller with noise power gradually louder for all schemes, and this is mostly the result of channel conditions influence and is within our expectation. We find that the proposed scheme can guarantee the minimum transmission rate requirements of PUs for network-coded 1S2P cooperation with very similar probability as that of the ‘No-Code 1PU’ scheme. Moreover, with channel conditions becoming severely worse, the success transmission probability of the network-coded 1S2P cooperation suffers a little higher degradation than that of the ‘No-Code 1PU’ scheme for guaranteeing two PUs’ minimum transmission rate requirements. Moreover, the ‘No-Code 2PUs’ scheme can guarantee the similar success transmission probability with the proposed scheme when the channel condition is very good, e.g., with the noise power density lower than -40 dBW/MHz in Figure 5. However, when the channels get worse, the success transmission probability of the ‘No-Code 2PUs’ scheme becomes much lower than that of the proposed scheme and even lower than that of the ‘Direct’ scheme. Thus, it can be concluded that the proposed scheme can provide high average transmission rate of SUs with satisfactory success transmission probability.
6.4 Simulation results with different transmission rate requirements
In this subsection, we examine the effects of these schemes on the average transmission rate of SUs and success transmission probability of PUs with the different transmission rate requirements of PUs under the channel noise density N 0 equalling to −30 dBW/MHz. For ease of analysis, both the minimum transmission rates of PUs r 1 and r 2 equal to r p.
From Figure 6, we find that the average transmission rate of SUs versus different target transmission rate R p demonstrates the similar downtrend and intersection of curves shown in Figure 4. It verifies the superiority and the satisfactory performance of the proposed network-coded 1S2P cooperation scheme.
Success probabilities of all schemes for transmissions of PUs under different target transmission rate requirement r p are described in Figure 7. Within a certain target transmission rate range, the proposed scheme gains much higher transmission rate at the expense of lowering a little success transmission probability of PRs. We have to be alert that when the cooperation members PUs make claims for excessive minimum rate requirements, the SU may not afford higher success transmission probability of PUs than that SU assists one PU or even that no SU helps the data forward of PUs. That is because the SU has to guarantee both the transmission rate requirements of PUs, and it also reserves a portion of resources to multicast data for SMGs.
7 Conclusions
In this paper, the 1S2P cooperation based on network coding in OFDM-modulated cognitive multicast networks is investigated. Concentrating on the essential conditions and cooperation context, the network-coded 1S2P cooperation scheme is presented. Meanwhile, the corresponding resource allocation problem is formulated and adopting the heuristic method and dual method, a stepwise subcarrier-power allocation algorithm is proposed with lower computation complexity. The simulation shows that the proposed cooperation scheme guarantees not only the minimum transmission rate requirements of PUs but also provides much higher transmission rate for SUs than that provided by traditional non-NC primary-secondary cooperation schemes. The network-coded 1S2P cooperation provides the inspiration and substance to enhance the spectrum efficiency for 5G systems. In the future research, network-coded multi-secondary-user and multi-primary-user cooperation will be discussed based on the cooperation agreement mentioned in the paper.
References
S Chen, J Zhao, The requirements, challenges, and technologies for 5G of terrestrial mobile telecommunication. IEEE Commun. Mag. 52(5), 36–43 (2014).
J Mitola, GQ Maguire, Cognitive radio: making software radios more personal. IEEE Pers. Commun. 6, 13–18 (1999).
FCC, Spectrum policy task force. ET Docket, 02–135 (2002).
J Mitola III, J Guerci, J Reed, Y-D Yao, Y Chen, TC Clancy, J Dwyer, H Li, H Man, R McGwier, G Yi, Accelerating 5G QoE via public-private spectrum sharing. IEEE Commun. Mag. 52(5), 77–85 (2014).
K Letaief, W Zhang, Cooperative communications for cognitive radio networks. Proc. IEEE. 97(5), 878–893 (2009).
A Nosratinia, TE Hunter, A Hedayat, Cooperative communication in wireless networks. IEEE Commun. Mag. 42(10), 74–80 (2004).
Y Zhou, H Liu, Z Pan, L Tian, J Shi, G Yang, Two-stage cooperative multicast transmission with optimized power consumption and guaranteed coverage. IEEE J. Selected Areas Commun. 32(2), 274–284 (2014).
S Katti, H Rahul, W Hu, D Katabi, M Médard, J Crowcroft, XORs in the air: practical wireless network coding. IEEE/ACM Trans. Netw. 16(3), 497–510 (2008).
X Wang, J Li, Network coding aware cooperative MAC protocol for wireless ad hoc networks. IEEE Trans. Parallel Distributed Syst. 25(1), 167–179 (2013).
PH Tan, CK Ho, S Sun, OFDM modulated cooperative multiple-access channel with network-channel coding. IEEE Trans. Wireless Commun. 11(2), 604–613 (2012).
X Chen, H Chen, W Meng, Cooperative communications for cognitive radio networks-from theory to applications. EEE COmmun. Surveys Tuts. 16(3), 1180–1192 (2014).
O Simeone, J Gambini, Y Bar-Ness, U Spagnolini, in 2007 IEEE International Conference on Communications (ICC). Cooperation and cognitive radio (IEEEGlasgow, 2007), pp. 6511–6519.
Y Zou, Y-D Yao, B Zheng, Diversity-multiplexing tradeoff in selective cooperation for cognitive radio. IEEE Trans. Commun. 60(9), 2467–2481 (2012).
W Jaafar, W Ajib, D Haccoun, in 2012 IEEE International Conference on Communications (ICC): 10–15 June 2012. Opportunistic adaptive relaying in cognitive radio networks (Ottawa, ON, 2012), pp. 1811–1815.
X Jia, M Zhou, X Dang, L Yang, H Zhu, Adaptive power allocation and outage performance of cognitive best relay cooperation systems with multiple primary transceiver pairs and direct path between cognitive source and destination. EURASIP J. Wireless Commun. Netw. 2014(1), 122 (2014).
Q Zhang, J Jia, J Zhang, Cooperative relay to improve diversity in cognitive radio networks. IEEE Commun. Mag. 47(2), 111–117 (2009).
W Lee, D-H Cho, in 2011 Sixth International ICST Conference on Cognitive Radio Oriented Wireless Networks and Communications (CROWNCOM). Cooperation based spectrum management scheme in ad-hoc cognitive radio system (IEEEOsaka, 2011), pp. 36–40.
R Ramamonjison, A Haghnegahdar, V Bhargava, Joint optimization of clustering and cooperative beamforming in green cognitive wireless networks. IEEE Trans. Wireless Commun. 13(2), 982–997 (2014).
T-Y Wu, K-W Lin, P-H Huang, W Liao, in 2013 IEEE 24th International Symposium on Personal Indoor and Mobile Radio Communications (PIMRC). A distributed cooperation strategy in cognitive radio networks (IEEELondon, 2013, pp. 2517–2521.
G Zheng, S Song, K-K Wong, B Ottersten, Cooperative cognitive networks: optimal, distributed and low-complexity algorithms. IEEE Trans. Signal Process. 61(11), 2778–2790 (2013).
F Gabry, N Li, N Schrammar, M Girnyk, L Rasmussen, M Skoglund, On the optimization of the secondary transmitter’s strategy in cognitive radio channels with secrecy. IEEE J. Sel. Area Commun. 32(23), 451–463 (2014).
J Jin, H Xu, B Li, in 2010 Proceedings IEEE INFOCOM: 14–19 March 2010. Multicast scheduling with cooperation and network coding in cognitive radio networksSan Diego, CA, 2010), pp. 1–9.
YJ Chun, NO Hasna, A Ghrayeb, in 2013 IEEE 24th International Symposium on Personal Indoor and Mobile Radio Communications (PIMRC): 8–11 Sept. 2013. Adaptive network coding over cognitive relay networks (London, United Kingdom, 2013), pp. 105–110.
W Lu, J Wang, Opportunistic spectrum sharing based on full-duplex cooperative OFDM relaying. IEEE Commu. Lett. 18(2), 241–244 (2014).
T Jing, S Zhu, H Li, X Xing, X Cheng, Y Huo, R Bie, T Znati, Two-stage cooperative multicast transmission with optimized power consumption and guaranteed coverage. IEEE Trans. Vehicular Technol.PP(99), 1 (2014).
Q Wu, J Zou, Z Wu, in 2014 IEEE International Conference on Communications (ICC). Joint spectrum and power allocation in coded cooperative cognitive radio networks (IEEESydney, 2014), pp. 1596–1601.
J Zou, Q Wu, H Xiong, CW Chen, Joint spectrum and power auction with multiauctioneer and multibidder in coded cooperative cognitive radio networks. IEEE Trans. Wireless Commun. 13(10), 5768–5780 (2014).
S Sharma, Y Shi, J Liu, YT Hou, S Kompella, SF Midkiff, Network coding in cooperative communications: friend or foe?IEEE Trans. Mobile Comput. 11(7), 1073–1085 (2012).
Z Liu, W Xu, S Li, J Lin, in Proceedings of the IEEE Global Telecommunications Conference Workshop (Globecom Workshop2014). Power and spectrum allocation for network coded primary-secondary cooperation in cognitive radio networks (IEEEAustin, 2014), pp. 845–880.
A Omri, MO Hasna, KB Letaief, Inter-relay interference management schemes for wireless multi-user decode-and-forward relay networks. IEEE Trans. Wireless Commun.PP(99), 1 (2014).
O Taghizadeh, R Mathar, in International Conference on Wireless for Space and Extreme Environments (WiSEE): 30–31 Oct. 2014. Cooperative strategies for distributed full-duplex relay networks with limited dynamic range (Noordwijk, 2014), pp. 1–7.
Q Li, W-K Ma, M Lin, J Ge, J Lin, Robust cooperative beamforming and artificial noise design for physical-layer secrecy in AF multi-antenna multi-relay networks. IEEE Trans. Signal Process. 63(1), 206–220 (2015).
X Gao, Adaptive relay techniques for OFDM-based cooperative communication systems. PhD thesis, The University of Western Ontario, Electrical and Computer Engineering Department. (2014).
K Xiong, PY Fan, M Lei, Y Su, Network coding-aware cooperative relaying for downlink cellular relay networks. China Commun. 10(7), 44–56 (2013).
L Fan, X Lei, TQ Duong, M Elkashlan, GK Karagiannidis, Secure multiuser communications in multiple amplify-and-forward relay networks. IEEE Trans. Commun. 62(9), 3299–3310 (2014).
LJ Chen, T Ho, M Chiang, SH Low, JC Doyle, Congestion control for multicast flows with network coding. IEEE Trans. Inf. Theory. 58(9), 5908–5921 (2012).
B Han, M Peng, Z Zhao, W Wang, A multidimensional resource-allocation optimization algorithm for the network-coding-based multiple-access relay channels in OFDM systems. IEEE Trans. Vehicular Technol. 62(8), 4069–4078 (2013).
S Boyd, L Vandenberghe, Convex Optimization (Cambridge university press, Cambridge, 2009).
DP Bertsekas, Nonlinear Programming (Athena Scientific, Nashua, 1999).
B Rankov, A Wittneben, Spectral efficient protocols for half-duplex fading relay channels. IEEE J. Selected Areas Commun. 25(2), 379–389 (2007).
Acknowledgements
This work is supported by National Natural Science Foundation of China (61362008), the 863 Project (2014AA01A701), Fundamental Research Funds for the Central Universities (2014ZD03-01), Special Youth Science Foundation of Jiangxi (20133ACB21007), and ZTE’s Industry-Academy-Research Cooperation Forum Program (A2014172).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, Z., Xu, W., Li, S. et al. Network-coded primary-secondary cooperation in OFDM-based cognitive multicast networks. J Wireless Com Network 2015, 144 (2015). https://doi.org/10.1186/s13638-015-0367-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-015-0367-5


 (SS)
(SS) 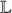 (PR 2)
(PR 2) 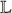 (PR 1)
(PR 1) 



