- Research
- Open access
- Published:
Efficient spectrum scheduling and power management for opportunistic users
EURASIP Journal on Wireless Communications and Networking volume 2016, Article number: 97 (2016)
Abstract
In this paper, we study the centralized spectrum access and power management for several opportunistic users, secondary users (SUs), without hurting the primary users (PUs). The radio resource manager’s objective is to minimize the overall power consumption of the opportunistic system over several orthogonal frequency bands under constraints on the minimum quality of service (QoS) and maximum peak and average interference to the PUs. Given the opposing nature of these constraints, we first study the problem of feasibility, and we provide sufficient conditions and necessary conditions for the existence of a solution. The main challenge lies in the non-convexity of this problem because of the discrete spectrum scheduling: one band can be allocated to at most one SU to avoid interference impairments. To overcome this issue, we use a Lagrangian relaxation technique, and we prove that the discrete solutions of the relaxed problem are the solutions to the initial problem. We propose a projected sub-gradient algorithm to compute the solution, when it exists. Assuming that the channels are drawn randomly from a continuous distribution, this algorithm converges to the optimal solution. We also study a specific symmetric system for which we provide the analytical solution. Our numerical results compare the energy-efficiency of the proposed algorithm with other spectrum allocation solutions and show the optimality of our approach.
1 Introduction
Most frequency bands in the radio spectrum have already been licensed, and it is difficult to find vacant bands for wireless communication systems. At the same time, the most allocated spectrum is under-utilized [1]. Cognitive radio (CR) systems, as explained in [2] and references therein, propose to better utilize the spectrum by allowing an opportunistic access to it. A hierarchy between users is imposed, in which secondary users (SUs) are allowed, by the spectrum manager, to communicate either in the vacant bands left by the licensed users, called primary users (PUs), or the non-vacant bands under the condition that the created interference (at the primary receivers) is kept below some predefined thresholds [3]. The radio resource manager uses channel state information (CSI) to coordinate the access to the wireless radio spectrum. When performed in a centralized way, this management is often referred to as coordinated multi-point (CoMP) radio resource management [4]. In the CR paradigm, CSI is provided by spectrum sensing at different remote locations and/or by backhaul information feedback from the spectrum manager to improve the spectrum usage. Carrier aggregation and multi-carrier communications have been suggested as promising candidates for both the CR and CoMP systems thanks to their flexible usage of the spectrum [5].
In ad-hoc and sensor networks or even in future 5G, a major bottleneck is the power consumption efficiency caused by limited battery-life device systems and operating costs [6, 7]. In this work, we investigate a centralized power minimization problem with quality of service (QoS) requirements for the secondary users imposed by the spectrum manager. In such a centralized setting, the spectrum manager can be more effective when it operates opportunistic users scheduling in addition to the sole power allocation, as mentioned in [8] and [9]. Very few existing works consider both bandwidth scheduling and power allocation jointly in the CR context. In particular, [10] provides a heuristic algorithm for the users scheduling.
In this paper, we consider a joint discrete scheduling and power allocation problem that aims at a minimal power consumption under QoS and interference power constraints in a centralized CR system. Such a problem introduces two major challenges. First, the minimum QoS and maximum interference constraints may not be simultaneously satisfied. Several works in the wireless communications literature [11, 12] have proposed a classical water-filling procedure to solve rate-driven or power-driven resource allocation problems in classical interference or multiple access channels. In our study, the presence of the PUs imposes additional peak and total interference constraints aside the classical minimum QoS constraint for the SU communication. These additional constraints are the main reason why classical numerical approaches are not suitable. In order to tackle the problem of feasibility, we study necessary conditions and sufficient conditions on the CSI for the existence of a feasible allocation point. The second difficulty raised by the problem under investigation is the discrete nature of channel assignments in the scheduling policy. This policy makes the problem a non-convex optimization one. Inspired by the approach in [13], we use a Lagrangian relaxation and a dual approach to obtain a solvable convex optimization problem. We then study the Karush-Kuhn-Tucker (KKT) conditions of the relaxed problem and show that the solutions meeting these conditions are actually the solutions of the initial non-convex problem. To solve the relaxed problem numerically, we propose a projected sub-gradient algorithm [14] when the problem is feasible.
1.1 Related works
Power allocation problems have been the subject of several studies in non-CR systems from a rate maximization point of view and via centralized [15] or decentralized (using non-cooperative games) [16–18] approaches. Also, power allocation problems without spectrum allocation in non-CR networks have been studied from an energy-efficiency point of view in centralized [19, 20] and decentralized systems [21, 22]. In this paper, we consider a centralized radio management, to make the spectrum manager more effective, it operates opportunistic user’s scheduling in addition to the sole power allocation, as mentioned in [8] and [9]. Such joint resource allocation problems have been the subject of several studies in non-cognitive radio settings such as in code division multiple access (CDMA) systems [23] and in downlink and uplink orthogonal frequency division multiplexing (OFDM) systems [24] and [13], respectively. In [23], the scheduling and resource allocation problem for the downlink in a CDMA-based wireless network is considered. The problem is to select a subset of the users for transmission and, for each of these users, to choose the optimal modulation, coding scheme and transmit power allocation policy. In [24], the authors consider the scheduling and resource allocation for the downlink of a cellular OFDM system. An optimal algorithm is proposed assuming that multiple users can time-share each tone and several low complexity heuristics are that enforce integer tone allocations. Among the works on OFDM [13, 24], the closest to our work is [13], in which a dynamic scheduling and power allocation algorithm was proposed to compute the policies of the multiple non-interfering users that maximize the overall QoS. An algorithm is derived (without the interference constraints of the cognitive radio context) using a Lagrangian relaxation technique to overcome the discrete scheduling constraints. However, a rigorous proof of the convergence and optimality of the proposed algorithm is not provided.
In the cognitive radio context, in which additional interference constraints to protect the primary users must be taken into account, the rate maximization problem was studied in [3, 6, 11]. In these works, the authors consider decentralized solutions in MIMO systems via non-cooperative game theory without spectrum scheduling constraints. The major disadvantage of such decentralized approaches is that the Nash equilibrium solution (i.e., the natural solution concept in non-cooperative games) provides an operating point that is often outperformed by a centralized solution. Other works study rate maximization problems under different CSI assumptions. In particular, [25] addresses the scheduling aspect with partial-CSI at the SU which limits the adaptability to the actual channel state. For a time-varying system, the authors of [26] study dynamic cognitive radio settings without explicit interference temperature constraints imposed by the primary users’ presence. Online optimization and no-regret distributed learning algorithms are used in [26] assuming the users do not know the perfect CSI prior to their transmissions. Such a complex approach is not required here, as we consider that CSI is available to the centralized system manager.
Energy efficiency problems in the CR context were studied with QoS and spectrum scheduling constraints in [10], in which the authors minimize the SU’s power consumption. The framework in [10] is the closest among all cited references to our paper. However, there is no proof of optimality of the proposed scheduling, which is based on a heuristic method involving some exhaustive search steps. In our work, we use convex optimization tools to find the optimal joint scheduling and power allocation under interferences and QoS constraints. Our optimal solution is calculated via an iterative sub-gradient algorithm that is proven to converge to the optimal solution.
1.2 Our contributions
The main contributions of this paper are summarized here below:
-
We derive necessary conditions and sufficient conditions for the existence of a solution to the joint spectrum scheduling and power allocation problem in a CR system.
-
We introduce a convex optimization problem based on Lagrangian relaxation of the initial non-convex problem. Then, we prove that the discrete solutions of the relaxed problem are the solutions to the initial problem.
-
The optimal solution of the relaxed problem, when it exists, is computed via a projected sub-gradient algorithm. We prove that, when the problem is feasible, our proposed projected sub-gradient algorithm converges to an optimal solution that satisfies the KKT conditions.
-
We also study the specific case of a symmetric system for which our iterative algorithm is not suitable and we solve it analytically.
-
Numerical results illustrate the energy-efficiency of the proposed allocation strategy compared with other spectrum allocation policies.
The remainder of this paper is organized as follows. The system model is presented in Section 2. In Section 3, we study the joint scheduling and power allocation problem by discussing its feasibility, the Lagrangian relaxation, and its optimality, and then provide a sub-gradient algorithm to solve this problem. Selected numerical results are illustrated in Section 4 to show the efficiency of the proposed solution. Particular cases, for which an analytical solution is found, are studied in Section 5. Finally, Section 6 concludes the paper.
2 System model
We focus on the CR model in Fig. 1 composed of Q≥1 SUs and K≥1 PUs. Each primary/secondary user consists of a primary/secondary transmitter (PT/ST) and a primary/secondary receiver (PR/SR), respectively. The transmission is performed over N orthogonal frequency bands. The transmit power of S T q (of the q th SU) in frequency band \(n \in \mathcal {N} \triangleq \{1, \ldots, N\}\) is denoted by p qn , the power allocation of the q th SU is denoted by \(\underline {p}_{q}=\left (p_{q1},p_{q2},\ldots, p_{qN}\right) \in \mathbb {R}^{N}_{+}\), \(\forall q \in \mathcal {Q} \triangleq \{1, \ldots, Q\}\), and the overall power allocation profile for all SUs is denoted by \(\boldsymbol {p}=\left (\underline {p}_{1},\underline {p}_{2},\ldots, \underline {p}_{Q}\right)\in \mathbb {R}^{N \times Q}_{+}\).
The received signal at S R q in band n can be written as:
where h qn is the power gain of the direct link S T q −S R q ; \(v_{qn}\backsim \mathcal {C N}(0,1)\) is the normalized transmitted signal by SU q (a zero-mean circularly symmetric complex Gaussian variable of unit variance), \(w_{qn}\backsim \mathcal {C N}\left (0,\sigma _{qn}^{2}\right)\) is the noise in band n for S U q of variance \(\sigma _{qn}^{2}\); and \(i^{(k)}_{qn}\backsim \mathcal {C N}\left (0,\left (\tau _{qn}^{(k)}\right)^{2}\right)\) is the interfering signal from PU \(k \in \mathcal {K} \triangleq \{1,\ldots, K\}\) of variance \(\left (\tau _{qn}^{(k)}\right)^{2} \). Since the transmit power of the PUs cannot be impacted by the secondary system, the terms \(i^{(k)}_{qn}\) are just some fixed parameters in our model. Only the knowledge of the SINRs are needed and measured at each SU. All links are assumed to be stationary and independent of the noise.
The Gaussian input, interference and noise assumptions are fairly standard in the signal processing for communications literature [3, 27, 28]. The main scientific reasons behind this are that the Gaussian noise is known to be the worst additive noise distribution in terms of the Shannon achievable rate [29], and that the Gaussian input is optimal in a Gaussian environment [30].
In this context, we define the QoS measure for SU q in band n by the Shannon capacity expression in [31], assuming that the corresponding bandwidth is unitary:
where s qn is the signal-to-interference-plus-noise-ratio (SINR) of the direct link of q th SU (S T q −S R q ), \(s_{qn}=h_{qn}/\left (\sigma _{qn}^{2}+ \sum _{k=1}^{K} \left (\tau _{qn}^{(k)}\right)^{2} \right)\). The spectrum allocation policy for the q th SU is denoted by \(\underline {x}_{q}=(x_{q1},x_{q2},\ldots, x_{qN})\), \(\forall q \in \mathcal {Q}\), and the overall allocation profile for all SUs is denoted by \(\boldsymbol {x}=(\underline {x}_{1},\underline {x}_{2},\ldots, \underline {x}_{Q})\).
This work is solely focused on the case in which at most one SU is allocated in each band n to avoid interference impairments (to the PUs and among SUs). This means that only discrete spectrum allocation policies x qn ∈{0,1} are allowed by the spectrum manager. Assuming orthogonal and unit bandwidth channels, the overall achievable rate of the q th SU transmission is
The assumption that only one SU is allowed in each band is also made for tractability reasons. Indeed, optimizing the system’s achievable sum-rate or some other objective under SU power or rate constraints is a very difficult, intractable and non-convex problem in an interference channel model. The achievable rate of one SU C q is a non-convex function with respect to \(\underline {p}\), because of the interference terms from the other SUs. To overcome this issue, one possibility is to decentralize the decision process and to consider a distributed cognitive radio system, in which each SU chooses its own power allocation policy to optimize its own objective [3, 6, 11]. The underlying non-cooperative game is a convex game as each SU’s rate is convex w.r.t. its own controlled variables \(\underline {p}_{q}\).
However, the major disadvantage of this approach is that the resulting Nash equilibrium solution provides an operating point that performs very poorly compared to a centralized solution. Since we are interested in a centralized cognitive radio system, a second way to overcome this major difficulty (the non convexity of C q ) is to limit the access of the SUs to the spectrum; only one SU is allowed per band.
Although the presence of PUs impacts the rates of the SUs via the SINR terms s qn , their crucial impact is in the additional interference constraints imposed by their presence on the SUs’ transmit powers. Indeed, in our CR system, the SUs are allowed to transmit only if the created interference to the primary receivers is guaranteed to be kept below some predefined thresholds to protect the transmissions of the PUs.
3 Joint scheduling and power allocation problem
The main objective of the paper is to study a centralized resource allocation problem in which the spectrum manager wishes to schedule the SUs in an effort to minimize the overall power consumption (in coherence with the green communications sprint [32, 33]) while meeting minimum QoS constraints at the SUs and without interfering with the PUs above the critical limits. Two main questions arise:
-
Spectrum scheduling: which SU should be scheduled in each band?
-
Power allocation: what is the optimal power allocation policy for each SU in its allocated bands?
In order to tackle these questions, we formulate the problem as follows:
where \(R^{min}_{q}\) represents the target QoS at S U q ; \(g_{qn}^{(k)}\) is the power gain of the interfering link S T q −P R (k); \(\overline {P}^{(k)}_{q}\) is the maximum average interference power that SU q is allowed to inflict on PU k ; and \(P^{peak (k)}_{qn}\) is the maximum peak interference power in band n that SU q is allowed to inflict on PU k .
This optimization problem is difficult for two reasons. First, the target QoS constraints and the maximum interference constraints inflicted on the PUs are opposing ones and, thus, the feasible set may be void depending on the system parameters. Second, to avoid the interference impairments to the PUs and among SUs, we assume that the system owner schedules at most one SU to a given band n and that such a band cannot be further fractioned. This turns the problem into a discrete optimization with respect to the scheduling policy. In the remainder of this section, we tackle both issues and provide an efficient algorithm to compute the optimal solution when it exists.
3.1 Feasible set
The spectrum manager has to schedule all SUs to ensure a non-zero QoS target for each SU. These constraints might require the SUs to transmit at power levels which inflict an interference level that is unacceptable by the primary system. Thus, the first arising question is under what conditions on the system parameters are the QoS and the interference constraints met simultaneously?
We denote the feasible set of (DP 1) by \( \mathcal {S}_{\mathcal {F}}\):
We provide next sufficient and necessary conditions on the system parameters for the existence of at least one solution to (DP 1), i.e., \(\mathcal {S}_{\mathcal {F}} \neq \emptyset \).
We start by assuming, without loss of generality, that \(R_{q}^{min}>0\), for all SU q. Given this assumption and the fact that only one SU is allowed to transmit in a given band, the problem has no solution when N<Q. Thus, a first trivial necessary condition for a solution to exist is that N≥Q. In this case, we derive further necessary conditions and sufficient conditions for the existence of a solution.
Theorem 1.
(Necessary conditions) Assuming that N≥Q and \(R_{q}^{min}>0\), ∀q, if the minimum rate \(R_{\ell }^{min}\) of an arbitrary SU ℓ is greater than its maximum achievable rate \(R_{\ell }^{max}\), then the feasible set \(\mathcal {S}_{\mathcal {F}}\) is void. Here, \( R_{\ell }^{max}\) represents the optimal value of the following optimization problem:
which corresponds to the maximum achievable rate of SU ℓ if it were the only SU in the network.
This result means that, if there is at least one SU ℓ that cannot achieve its minimum requirement \(R^{min}_{\ell }\) even if it were the only SU in the system, the problem (DP 1) is infeasible. In the particular case in which there is only one SU in the system, i.e., Q=1, these necessary conditions are tight as they are also the sufficient conditions guaranteeing the existence of a solution. Although these conditions are not tight when Q>1 (at least one band has to be allocated per SU and, thus, no SU will have access to all bands), they have the merit of being general, fair from the SUs perspective, intuitive, and having a low computational complexity. The proof of this Theorem is detailed in Appendix A1.
Theorem 2.
(Sufficient conditions) Assuming that N≥Q and \(R_{q}^{min}>0\), ∀q, if for each SU q the minimum rate \(R_{q}^{min}\) is lower than the following threshold: \(R_{q }^{CS}= \log _{2} \left (1+ \min \limits _{n} \left \{s_{q n} \min \limits _{k} \left \{\frac {\overline {P}_{q}^{(k)}}{g_{qn}}, \frac {P_{qn}^{peak(k)}}{g_{qn}} \right \} \right \} \right)\), then the feasible set is non-void \( \mathcal {S}_{\mathcal {F}} \neq \emptyset \).
Intuitively, if each S U q has a minimum rate \(R^{min}_{q}\) small enough, i.e., smaller than the rate obtained when using only its worst channel, then the problem (DP 1) is feasible.
Remark 3.1.
When Q=1, N=1, the sufficient conditions of Theorem 2 are identical to the necessary conditions of Theorem 1. However, (similarly to the necessary conditions above) these sufficient conditions are not tight in general. Indeed, when Q=1 and N>1 the necessary conditions in Theorem 1 are the tight sufficient conditions. Nevertheless, in the most general case, it seems very difficult to find better sufficient conditions that are computationally tractable and fair with respect to all SUs. To better understand this, consider first the case in which Q≤N<2Q: there are not enough channels to allocate two channels per SU. Thus, some of the SUs will only be allocated a single channel which may very well be their worst channel. In this case, finding better and fair sufficient conditions seems very unlikely. Now, if γ Q≤N<(γ+1)Q with γ≥2: at least γ≥2 channels may be allocated to each SU. In this case, a better sufficient condition could be found by computing the achievable rate over the worst γ channels for each SU. However, since we cannot know in advance which combination of γ channels results in a worst case achievable rate, one would have to compute all \(C_{N}^{\gamma }\) combinations for each of the Q SUs. The complexity of such an approach is therefore prohibitive.
The proof of this Theorem is detailed in Appendix A2.
Now, if the feasible set \(\mathcal {S_{F}}\) is non-void, finding the solution of (D P 1) is not trivial. Indeed, we notice that the scheduling of SUs is a discrete combinatorial problem x qn ∈{0,1}, ∀n, ∀q. In the following, we will provide an efficient algorithm that computes the optimal solution in a very efficient manner using a Lagrangian relaxation approach [14].
3.2 Lagrangian relaxation
As we have already mentioned, we assume that at most one SU is allowed to transmit in a given band. The constraints on the discrete scheduling policy x make the problem (DP 1) very difficult to solve in this form. In the following, we will use a Lagrangian relaxation technique to overcome this issue.
When the feasible set \(\mathcal {S}_{\mathcal {F}}\) is not void, we propose to solve a continuous problem in which the scheduling parameter is continuous x qn ∈ [ 0,1]. This relaxed problem (CP 2) holds the advantage of being a convex optimization problem, much simpler to solve than (DP 1):
Inspired by [13], the continuous problem (CP 2) is not exactly the Lagrangian relaxation of (DP 1) but that of an equivalent discrete problem. Two differences can be observed in (CP 2). First, the peak interference power constraints \(g_{qn}^{(k)} p_{qn} \leq P^{peak (k)}_{qn}\) are replaced by \( g_{qn}^{(k)} p_{qn} \leq x_{qn} P^{peak (k)}_{qn}\). Second, we replace the Shannon achievable rate of SU q by the function:
where
Remark 3.2.
Our target problem (DP 1) focuses only on discrete spectrum allocation policies x qn ∈{0,1}. Under this assumption, the function in Eq. (7) corresponds exactly to the achievable Shannon rate in (2). However, in the continuous case in which x qn ∈ [ 0,1] expression (7) does not correspond to the Shannon achievable rate. The denominator of the term \(\frac {s_{qn}p_{qn}}{x_{qn}}\) is introduced for technical purposes and plays an important role in proving the optimality of the Lagrangian relaxation approach when solving (DP 1).
The major interest of this approach is that it will allow us to solve the initial non-convex problem using a very efficient algorithm based on convex optimization techniques. Not only is the continuous problem (CP 2) simpler to solve, but also, by using these two modifications, the problem (CP 2) will have discrete solutions in x which will turn out to be the solutions to our initial problem (DP 1), as we will show later on.
In the following, we will give some proprieties of the problem (C P 2) where we denote by (x ∗,p ∗) the pair of scheduling and power allocation that satisfies all the constraints at the optimum:
Proposition 1.
In the continuous problem (CP 2), all the rate constraints are active at the optimal solution, i.e., the rate constraints are satisfied with equality.
This result means that if the feasible set is non-void, the optimal rate at each SU achieves the target QoS R min.
Proposition 2.
In the continuous problem (CP 2), all the scheduling average constraints are all active at the optimal solution : \(\sum _{q} x_{qn}^{*} = 1\), ∀q.
This result means that if the feasible set is non-void, all bands are fully used by the opportunistic users. The proofs of these two propositions are detailed in Appendix B.
3.2.1 Dual formulation
The continuous problem (CP 2) is a convex optimization problem. Indeed, the objective function \(\sum _{q} \sum _{n} p_{qn}\) is affine in the overall power allocation profile \(\boldsymbol {p}=\left (\underline {p}_{1},\underline {p}_{2},\ldots, \underline {p}_{Q}\right)\in \mathbb {R}^{N \times Q}_{+}\) and, regarding the constraints, the interference constraints are both affine in (x,p); the scheduling constraints are affine in x; and the rate constraint is jointly concave in (x,p). From the convex optimization problem definition [34], it follows that (CP 2) is convex and, thus, can be solved via a dual formulation. We associate dual variables \(\boldsymbol {\lambda }= (\lambda _{q})_{q\in \mathcal {Q}}\) with total interference power constraints, \(\boldsymbol {\beta }= (\beta _{q})_{q\in \mathcal {Q}}\) with rate constraints and \(\boldsymbol {\mu }= (\mu)_{n\in \mathcal {N}}\) with scheduling constraints, resulting in the following Lagrangian:
To solve (CP 2) it suffices to solve:
Inspired by [13], in which the authors consider a rate maximization joint scheduling and power allocation problem in OFDM systems without the PU constraints, we propose to solve here a more complex problem (C P 2) via the following steps.
-
Step 1: The optimal power p which minimizes L(λ,β,μ,x,p) given fixed λ, β and μ 1 is a water-filling type of solution:
$$\begin{array}{@{}rcl@{}} \begin{array}{l} p_{qn}^{*}= \displaystyle \frac{x_{qn}}{s_{qn}} \left[ \frac{\beta_{q} s_{qn}}{1+ \sum_{k} \lambda_{q}^{(k)} g_{qn}^{(k)}}-1 \right]_{0}^{\min \limits_{k} \left\{P^{peak(k)}_{qn}\right\}s_{qn}}. \end{array} \end{array} $$((10)) -
Step 2: Substituting p ∗ into L(λ,β,μ,x,p) yields to the following affine function in x:
$$\begin{array}{@{}rcl@{}} \begin{array}{l} \displaystyle \mathrm{G}(\boldsymbol{\lambda},\boldsymbol{\beta},\boldsymbol{\mu}, \mathbf{x})= \displaystyle -\sum_{q}\sum_{n} x_{qn} \left(\varphi_{qn} -\mu_{n} \right) \\ \displaystyle + \sum_{q} \beta_{q} R_{q}^{min} - \sum_{k} \sum_{q} \lambda_{q}^{(k)} \overline{P}_{q}^{(k)} - \sum_{n} \mu_{n}, \end{array} \end{array} $$((11))where φ qn =φ qn (a,b,c,d) is a function of the system parameters defined by:
$$\begin{array}{@{}rcl@{}} \left\{ \begin{array}{ll} 0 & \text{if} \ \frac{a}{c} \geq b \\ -b+\frac{a}{c}+ b \log_{2}\left(\frac{bc}{a}\right) & \text{if} \ \frac{a}{c} \leq b \leq \frac{a(dc+1)}{c} \\ -da+b \log_{2}(1+dc) & \text{if} \ \frac{(a)(dc+1)}{c} < b \end{array} \right. \end{array} $$((12))for \( a=1+\sum _{k} \lambda _{q}^{(k)} g_{qn}^{(k)}\), b=β q , c=s qn and \( d=\min \limits _{k} \left \{P^{peak (k)}_{qn}\right \}\).
-
Step 3: From Eq. (11), we remark that this function is affine in x. Optimizing it over x such that x qn ∈ [ 0,1] yields the dual function:
$$\begin{array}{@{}rcl@{}} \begin{array}{ll} \displaystyle \mathrm{G}(\boldsymbol{\lambda},\boldsymbol{\beta},\boldsymbol{\mu})=& \displaystyle -\sum_{q} \sum_{n} \left[\varphi_{qn} - \mu_{n} \right]^{+} + \sum_{q} \beta_{q} R_{q}^{min} \\ &- \displaystyle \sum_{k} \sum_{q} \lambda_{q}^{(k)} \overline{P}_{q}^{(k)} - \sum_{n} \mu_{n}, \end{array} \end{array} $$((13))where the optimal scheduling allocation x ∗ is:
$$\begin{array}{@{}rcl@{}} x_{qn}^{*}(\boldsymbol{\mu})=\left\{ \begin{array}{llll} &1 & \text{if} & \varphi_{qn}>\mu_{n} \\ &0 & \text{if} & \varphi_{qn}<\mu_{n} \end{array} \right. \end{array} $$((14))and if φ qn =μ n , then the optimal value \(x_{qn}^{*}\) can be anything in the interval [0,1]. In such cases and from Proposition 2, one must only ensure that all scheduling constraints are met: \(\sum _{q} x^{*}_{qn}=1\) for all n.
We can now maximize the dual function G(λ,β,μ) over μ for given λ and β, by setting \(\mu _{n}=\mu _{n}^{*}(\boldsymbol {\lambda },\boldsymbol {\beta })\) similarly to [13] where \(\mu _{n}^{*}\) is obtained as follows:
$$\begin{array}{@{}rcl@{}} \begin{array}{l} \mu_{n}^{*}(\boldsymbol{\lambda},\boldsymbol{\beta})= \max \limits_{q} \varphi_{qn}(\lambda_{q}^{(k)},\beta_{q}). \end{array} \end{array} $$((15))Remark 3.3. From Eqs. ( 14 ) and ( 15 ), it is clear that \(x^{*}_{qn}(\boldsymbol {\mu }) = 0\) if \( q \not \in arg \max \limits _{q \in \mathcal {Q}} \varphi _{qn}\left (\lambda _{q}^{(k)},\beta _{q}\right)\). Intuitively, this means that band n is allocated to a specific SU ℓ if it maximizes a specific channel metric given by \( \varphi _{\ell n}\left (\lambda _{\ell }^{(k)},\beta _{\ell }\right)\). There may be ties when multiple SUs achieve the value \(\mu _{n}^{*}\) in band n. For example, if there exist two SUs r, q such that r≠q and \(\varphi _{qn}=\varphi _{rn}=\mu _{n}^{*}\). These ties happen with zero probability if the independent random channel gains are drawn from continuous distributions. In practice, this implies that such problematic cases almost never occur.
From Eq. (14) we also observe that (CP 2) allows for discrete solutions in x ∗ when it is feasible. Since we are interested in solving the discrete problem (DP 1), we make the choice to select a discrete solution such that
$$\begin{array}{@{}rcl@{}} x_{qn}^{*}(\boldsymbol{\mu}^{*})=\left\{ \begin{array}{llll} &1 & \text{if} & \varphi_{qn} = \mu_{n}^{*} \\ &0 & \text{if} & \varphi_{qn}<\mu_{n}^{*}. \end{array} \right. \end{array} $$((16)) -
Step 4: Substituting μ ∗ into G(λ,β,μ) and noticing that μ ∗,p ∗,x ∗ are all functions of (λ,β) we further have:
$$\begin{array}{@{}rcl@{}} \begin{array}{ll} \displaystyle \mathrm{G}(\boldsymbol{\lambda},\boldsymbol{\beta})= & \displaystyle - \sum_{n} \max_{q} \varphi_{qn}\left(\lambda_{q}^{(k)},\beta_{q}\right) + \sum_{q} \beta_{q} R_{q}^{min} \\ &- \displaystyle \sum_{k} \sum_{q} \lambda_{q}^{(k)} \overline{P}_{q}^{(k)}. \end{array} \end{array} $$((17))The solution to the dual problem (9) can be computed numerically by maximizing G(λ,β) over λ≥0 and β≥0. To this aim, we use a sub-gradient based search [14] to update λ and β.
3.2.2 Projected sub-gradient algorithm
Based on the previous dual formulation, we propose an iterative sub-gradient algorithm to compute the solution of (CP 2) when it exists. The iterations are detailed in Algorithm 1. The sub-gradient approach is usually employed to compute water-filling type of solutions [3, 10, 13]. The proposed algorithm converges to the optimal solution whenever it is feasible.
Other efficient algorithms such as interior point methods, which are based on Newton’s iteration and on second-order derivatives, can be implemented to solve (C P 2). Both types of algorithms have advantages and inconveniences, and their convergence performance depends on the compromise between the number of iterations and the complexity of each iteration. The sub-gradient method has the advantage of being simple as its iterations are of low-complexity and scale as O(Q×(K+N)).
Proposition 3.
If (CP 2) is feasible, then Algorithm 1 always converges and the convergence point is an optimal scheduling and power allocation policy.

The proof of this proposition is based on convex optimization tools and is given in Appendix C. The intuition is that, at the convergence state, the iteration, which is discrete with respect to the spectrum allocation policy by construction, satisfies the KKT conditions which are both necessary and sufficient for optimality in convex optimization problems.
3.3 Optimality of the Lagrange relaxation
Our main objective in the remainder of the paper is to show that Algorithm 1 not only converges to the solution of (CP 2) but to that of the initial discrete problem (DP 1).
Let us define by DP 2 the discrete version of (CP 2). The objective of DP 2 is to minimize the SU overall power consumption subject to the rate constraints, the interference power constraints (identical to the ones in (CP 2)) and the discrete scheduling constraints: x qn ∈{0,1}, ∀n,∀q, \(\sum _{q} x_{qn} \leq 1, \ \forall n\). Because of space limitations, we do not write the expressions of DP 2 explicitly.
Proposition 4.
If (CP 2) is feasible, then all the discrete solutions of (CP 2) (with respect to the optimal scheduling allocation x ∗) are the only optimal solutions of DP 2.
Proof.
The feasible set of DP 2 is included in the feasible set of (CP 2). The only difference between both problems is the scheduling parameter x qn which is discrete in DP 2 and continuous in (CP 2). On the one hand, we can see that if there are any discrete solutions to (CP 2), then these discrete solutions will also be the optimal solutions of DP 2. On the other hand, if the solutions of (CP 2) are continuous (i.e., the scheduling allocations are between 0 and 1), then the SUs’ power allocations policies are constants (as they do not depend on the scheduling allocations), thus, these continuous solutions have the same efficiency comparing to the discrete solutions on the borders (i.e., are equal to 0 or 1).
Next, we compare the discrete problems (DP 1) and DP 2.
Proposition 5.
The optimization problems (DP 1) and DP 2 are equivalent in the sense that their solution sets are identical.
Proof.
If we fix an arbitrary scheduling policy \(\boldsymbol {\widetilde {x}} \in \mathcal {X}\), where the scheduling constraints set is defined as
then, both problems (DP 1) and DP 2 reduce to the same power allocation problem (CP 3) below in which the only variable left is the power allocation policy3 at the SU’s

On the one hand, if the scheduling parameter equals zero, \(\widetilde {x}_{qn}=0\), then the corresponding optimal power is also zero \(\widetilde {p}_{qn}=0\) (because the optimal power is linear in x). On the other hand, if the scheduling parameter equals one, \( \widetilde {x}_{qn}=1\), then the optimal powers \(\widetilde {p}_{qn}\) are given by a water-filling type of solution over the allocated spectrum. Thus, whenever \(\boldsymbol {\widetilde {x}}\) is fixed, both problems (DP 1) and DP 2 reduce to solving the same Q decoupled power allocation problems.
It remains to prove that both DP 2 and (DP 1) have the same set of optimal spectrum allocation policies x ∗. The optimal powers p ∗ will follow by solving (CP 3). Assuming that (DP 1) is feasible, we can easily check that the optimal solutions of (DP 1) meet all the constraints of DP 2 as well. Adding the fact that the feasible set of (DP 1) contains (and is larger) than the feasible set of DP 2, we conclude that the optimal solution sets of the two problems are identical.
Theorem 3.
If (CP 2) is feasible, then all solution of (CP 2) that are discrete w.r.t x ∗ are the optimal solutions of (DP 1).
This Theorem follows from Propositions 4 and 5. In Proposition 5, we have shown that both discrete problems DP 2 and (DP 1) are equivalent. Moreover, from Proposition 4, we have shown that the optimal discrete solutions of DP 2 are the discrete solutions of (CP 2). Thus, we can conclude that all discrete solutions of (CP 2) are the optimal discrete solutions of (DP 1).
Corollary 1.
The feasibility of the relaxed problem (C P 2) implies the feasibility of (D P 1).
This is important because the feasibility of (C P 2) problem, which is a convex problem, is much simpler to study than the feasibility of the discrete problem (D P 1). In other words, to decide whether the initial problem (D P 1) is convex, we have simply to solve the problem of feasibility of (C P 2) which is convex.
In conclusion, our results show that Algorithm 1, initially built to solve (CP 2), selects only the optimal discrete solutions and actually solves DP 2. From Proposition 3, both discrete problems DP 2 and (DP 1) are equivalent; thus, our projected sub-gradient Algorithm 1 solves the initial problem (DP 1) and converges to the optimal scheduling and power allocation policy whenever the problem is feasible.
In the following section, we will present some simulation results which illustrate the performance of our projected sub-gradient algorithm.
4 Numerical results
All observations in this section have been verified via extensive simulations with generic system parameters. We have selected only a few of the most illustrative and interesting results to be presented next.
4.1 Power consumption efficiency
We start by comparing the overall power consumption between our optimal scheduling policy and arbitrarily scheduling techniques such as interleaved and block-wise spectrum scheduling [35]. Once the spectrum scheduling is fixed, computing the power allocation policies follows via water-filling type of sub-gradient methods. We focus only on the cases in which the problem is feasible and in which our Algorithm 1 converges to the optimal solution of (DP 1). Thus, for each of 104 random channel realizations, we choose the minimum target QoS that are equal to the rates in the sufficient conditions of Theorem 2.
Figure 2 illustrates this comparison as function of N∈{Q,2Q,4Q,8Q,16Q} in the scenario: 4 Q=4, K=8, the channel gains are drawn randomly \(g^{(k)}_{qn} \backsim \mathcal {N}(0,4)\), ∀q,∀n,∀k and \({s}_{qn} \backsim \mathcal {N}(0,20)\), ∀q,∀n, \(\overline {P}_{q}^{(k)}=10\) mW, ∀q,∀k, \(P^{peak (k)}_{qn}=20\) mW, ∀q,∀n,∀k.
We remark that the interleaved and block-wise allocations have the same average performance because of the independent and identically distributed (i.i.d) channel gains. Our algorithm outperforms these two fixed-spectrum allocations (interleaved or block-wise allocation), and the performance gap decreases with N.
The sufficient conditions guaranteeing the existence of a solution and the convergence of Algorithm 1 are not tight in general as they rely on the use of Q bands alone and on the assumption that each SU is allowed to transmit in its worst channel. Finding tighter sufficient conditions that are tractable seems a very difficult task. Therefore, we study the performance of our algorithm in the cases in which the sufficient conditions are not met.
4.2 Problem feasibility
Figure 3 illustrates the empirical probability (over 104 random channels realizations) that the problem (DP 1) is not feasible as function of the target QoS R min in the following scenario: N=4, K=8, Q=2, \(R_{q}^{min} = R^{min}, \ \forall q\), \(\overline {P}_{q}^{(k)}=10\) mW, ∀q,∀k, \(\displaystyle \boldsymbol {s}=\left (\begin {array}{llll} 27.8797 & 2.0727 & 0.7779 & 4.3263\\ 7.6688 & 7.6722 & 11.0049 & 1.7281 \end {array}\right)\) 4, \(P^{peak (k)}_{qn}=20\) mW, ∀q,∀n,∀k and the interfering channel gains are drawn randomly such that \(g_{qn}^{(k)} \backsim \mathcal {N}\left (0, {\sigma _{g}^{2}}\right)\), ∀q,∀n,∀k for an arbitrary chosen value \({\sigma _{g}^{2}}=2\).
In order to decide whether the problem is feasible or not, we test if the algorithm converges before the maximum number of iterations is reached. From Proposition 3 and Theorem 3, if the algorithm converges, then the convergence point is an optimal solution of (DP 1). For practical reasons, if the algorithm reaches the maximum number of iterations before convergence, we decide that the problem is not feasible. This approach is based on an empirical search for the maximum number of iterations. In this setting, we fix 105 maximum number of iterations.
In Fig. 3, we remark that there is a threshold, R min≃6.25 bps, below which a solution exists and above which the problem is not feasible. The other two plotted thresholds, CS and CN, illustrate the worst case sufficient conditions and necessary conditions over all random realizations and are computed as follows. We denote by \(R_{q}^{CS (t)}\) the sufficient condition rates of Theorem 2 for the random channel realization t∈{1,…,104}. Similarly, we denote the necessary condition rates by \(R_{q}^{CN (t)}\) of Theorem 1 which also depend on the random realization t. The threshold CS represents the minimum value of the rates \(R_{q}^{CS (t)}\) over all SUs and over all random channel realizations: \(CS = \min \limits _{q,t} \left \{R^{CS(t)}_{q}\right \} = 1.44\) bps and the threshold CN represents the maximum value of the rates \(R_{q}^{max (t)}\) over SUs and over the random channel realizations: \(\max \limits _{q,t}\left \{R^{CN(t)}_{q} \right \}=12.86\) bps.
Although the CS and CN values in Fig. 3 are worst case conditions (over all random channels and all SUs), they still show that our sufficient and necessary conditions are not tight in general, as discussed in Section 3.1. This means that there are a lot of cases in which we do not know a priori whether the problem is feasible or not: all cases in which sufficient conditions are not met but the necessary conditions are met.
4.3 Necessary conditions are not met
We illustrate now the case in which the necessary conditions are not met, i.e., when there exists at least one SU q such that the target rate is above the maximum achievable rate in Theorem 1 : \(R_{q}^{min} \geq R_{q}^{max}\). We consider the following setting 4: N=4, K=8, Q=2, \(\overline {P}_{q}^{(k)}=10\) mW, ∀q,∀k, \(\boldsymbol {s}= \left (\begin {array}{llll} 27.8797 & 2.0727 & 0.7779 & 4.3263\\ 7.6688 & 7.6722 & 11.0049 & 1.7281 \end {array}\right)\), \( \boldsymbol {g}^{(k)}= \left (\begin {array}{llll} 2.4086 & 3.2329 & 1.1983 & 0.4016\\ 1.8904 & 0.1510 & 0.0362 & 0.3318 \end {array}\right)\) 5. We fix the target rates \(R_{1}^{min}=R_{2}^{min}=13\) bps which are higher than the maximum rates that each SU could achieve if they were alone in the system: \(R^{max}_{1}=8.0803\) bps, \(R^{max}_{2}=12.8686\) bps.
Figure 4 illustrates the evolution of the Lagrange multipliers μ n and β q corresponding to the average constraints over the algorithm’s iterations. We remark, that Algorithm 1 does not converge before the maximum number of iterations is reached. In this case, we decide that the problem is not feasible. An alternative would be to further increase the maximum number of iterations, but this process has to be finite and a pragmatic decision has to be made at some point.
4.4 Sufficient conditions are not met although necessary conditions are met
Here, we illustrate the case in which the necessary conditions are met and at least one of the sufficient conditions is not met in the same setting as Fig. 4 except for the target rates which are in between the thresholds of the sufficient conditions and the necessary conditions.
4.4.1 Convergence of Algorithm 1
In Fig. 5, we want to check whether our projected sub-gradient algorithm converges to an optimal solution or not.
In Fig. 5 a, we plot the Lagrange multipliers μ n , β q of the scheduling and target rate constraints when the minimum target rates are \(R^{min}_{1} =R^{min}_{2}=3\) bps. We can see that our algorithm converges in this case and, thus, the problem is feasible and solved via Algorithm 1. Indeed, the Lagrange multipliers converge to the optimal values \(\mu _{n}^{*}\) and \(\beta _{q}^{*}\) that are strictly positive, and the scheduling and rate constraint are satisfied with equality.
In Fig. 5 b, we fix the minimum target rates \(R^{min}_{1}=R^{min}_{2}=8\) bps. In this case, we remark that our algorithm reaches the maximum number of iterations. Because of such high target rates, our algorithm does not converge and, thus, the problem has no solution.
4.5 Water-filling solution
Figure 6 illustrates the optimal scheduling and power allocation policies in the case in which our algorithm converges for the same scenario as in Fig. 5 a.
We remark that the optimal solution is fair in terms of bands per SU; two bands are allocated to each SU. Band 1 and 4 are allocated to SU 1, since SU 1 has higher SNR than SU 2 in these bands. Band 2 and 3 are allocated to SU 2 for the same reason. This power and spectrum allocation policy satisfies all KKT conditions, thus, it is the optimal solution.
In conclusion, when the sufficient conditions are not met although the necessary conditions are met, we do not know a priori if Algorithm 1 converges or not. Nevertheless, we can still exploit our algorithm to decide whether the problem is feasible or not and to compute the optimal solution when it exists. If the algorithm converges before reaching the maximum number of iterations, then we know that the problem is feasible and that the convergence point is an optimal solution to (DP 1). Otherwise, we can increase the maximum number of iterations or decide that the problem is not feasible and has no solution. In such cases, instead of not allowing any SU to transmit, the spectrum manager (instead of not allowing any opportunistic user to transmit) can decrease the minimum SU target rates (lower QoS may be better than no QoS in low data rate applications) or may even decide to schedule only a subset of the SUs and turn the problem into a feasible one [8].
As we have seen before, there exist other cases in which the Algorithm 1 does not calculate the solution. This happens in the indecision cases between several SUs (i.e, to decide whether the SU is allowed to transmit in a given band or not). In the following, we will try to solve some of these specific cases.
5 Particular case: symmetric systems
In this section, we are interested in a specific symmetric system in which Algorithm 1 is not suitable to compute the solution. This happens whenever ties arise between several SUs when deciding on the SU to be allocated a given band: if several SUs have the same maximum value for the decision parameter \(\mu _{n}^{*}\) described in Section 3.2.1 (there exist two SUs q≠r such that \(\varphi _{qn}=\varphi _{rn}=\mu _{n}^{*}\)).
Consider the completely symmetric system in which all SUs experience the same channel gains, the same peak and total interference constraints, and have the same target rates: s qn =s, g qn =g, \(P_{qn}^{peak}=P^{peak}\), \(\overline {P}_{q}=\overline {P}\) and \(R^{min}_{q}=R^{min}\), ∀n, ∀q.
Remark 5.1.
In this case, the optimal power allocation is such that every SU uniformly allocates its power over its allocated bands. For any scheduling policy x, the optimal power allocation is a water-filling type solution [11, 12] derived from the KKT conditions:
and, thus, we have \(p_{qn}^{*}=p_{q}^{*}\), for any band n that is used at the optimal solution.
In the following, the main idea is to simplify the problem (DP 1) in which the unknowns are x and p and reduce it into a problem in which the only unknown is \(N_{q}^{*}\), ∀q where \(N_{q}^{*}\) denotes the number of bands allocated at the optimum to the SU q 6 :
From Proposition 2, since the scheduling constraint is satisfied with equality, the overall number of bands allocated to the SUs, at the solution, equals the total number of bands N.
According to Proposition 1 (rate constraint is met with equality) and Remark 5.1 (uniform power allocation is optimal), we can write the optimal power as:
Using (19), the discrete problem (DP 1) simplifies as follows:
This problem is interesting as it is no longer a joint scheduling and power allocation problem (x,p) and depends only on the number of allocated bands at the optimum \(N_{q}^{*}, \ \forall q\).
For simplicity reasons, we start by assuming that the number of available bands is proportional to the number of SUs. This means that the ratio N/Q is an integer:  .
.
Now, we will prove that the optimal solution to problem (DP N ) is to allocate the spectrum in a fair way to the SUs.
Proposition 6.
The optimal solution of the problem (DP N ), when feasible, is to uniformly allocate the spectrum to the SUs:
The proof of this Proposition is detailed in Appendix D. The closed-form solution of the power allocation policy is given by:
where \(\left \{ x_{qn}^{*} \right \}_{qn}\) is any spectrum allocation policy such that every band is used and each SU is allocated exactly \(\frac {N}{Q}\) bands.
In conclusion, in order to minimize the power consumption of the CR symmetric system, all the spectrum has to be used (see Proposition 1). Since all SUs have the same channel conditions, the spectrum manager does not privilege any particular SU and the spectrum is divided equally among them. There are many ways to allocate the spectrum either by an interleaved or block-wise allocation [35]. These two types of allocations are all equivalent given the symmetry of the system. Then, each SU allocates uniformly its power as in (21) over its allocated bands.
In the following Table 1, we compare the optimal value of the objective function \(\sum _{q} \sum _{n} p_{qn}^{*}\) in different particular cases regarding the scheduling policy to illustrate that the fair spectrum allocation among the different users is optimal. We consider the following scenario, which falls into the hypothesis of Proposition 6: Q=3 SUs, N=9 bands, R min=3 bps, T is chosen randomly such that 1<T<N−2, we choose T=3 and the SINR s=2. Notice that all permutations of \(\left \{\frac {N}{Q}, \frac {N}{Q}-1, \frac {N}{Q}+ 1 \right \}\) are equivalent by symmetry and lead to an identical power consumption; therefore, we provide only one of these permutations in the Table. We remind that the sum of the allocated bands must be equal to N i.e. \(\sum _{q} N_{q}=N\).
We remark that exactly \(\frac {N}{Q}\) bands are allocated to each SU. This numerical result validates our Proposition 6.
Next, we provide a more general solution, in the case in which the number of bands is not proportional to the number of SUs,  . It turns out that the optimal solution to problem (DP
N
) is very similar to the fair spectrum allocation discussed above.
. It turns out that the optimal solution to problem (DP
N
) is very similar to the fair spectrum allocation discussed above.
Proposition 7.
The optimal solution of the problem (DP N ) when feasible is given as follows:
where ⌊y⌋ denotes the integer part of y. The proof of this Proposition is detailed in Appendix D. The optimal power allocation is uniform over all bands that are used by the SUs and is given by (21). The difference with the previous case lies in the number of bands that each SU can use.
In conclusion, when solving the (DP N ) problem in this symmetric system and because of the convex shape of the objective function in a continuous space, two cases arise: (1) either the solution to the relaxed convex continuous problem (i.e., N/Q) is integer and the fair spectrum allocation is optimal \(N_{q}^{*}= \frac {N}{Q}, \ \forall q\); (2) or the solution \(\frac {N}{Q}\) is not an integer and each SU is allocated either \(\lfloor \frac {N}{Q}\rfloor \) or \(\lfloor \frac {N}{Q} \rfloor +1\) bands such that \(\sum _{q} N_{q}^{*}=N\). This means that the solution is not perfectly fair (as the previous case) and a subset of \(\left \{N-\lfloor \frac {N}{Q} \rfloor Q+1, \ldots, Q\right \}\) SUs will be allocated an additional band.
Aside from this particular case (w.r.t. the system parameters), there are other interesting cases but more complicated to solve: (1) the case in which a SUq has the same channel gains and peak interference thresholds over all the frequency bands, but two different SUs do not necessary have the same channel conditions: s qn =s q , g qn =g q , \(P_{qn}^{peak}=P_{q}^{peak}\), ∀n; (2) the case in which in a band n all SUs have the same channel gains and peak interference thresholds: s qn =s n , g qn =g n , \(P_{qn}^{peak}=P_{n}^{peak}\), ∀q. Although, in the first case (1), we can simplify the problem using the optimal power uniform allocation for each SUq, an analytical solution seems difficult or even impossible to find since, as opposed to the perfectly symmetric case, we can no longer conclude from the KKT conditions that the number of allocated bands is the same for all SUs. In the second case, we can no longer use the fact that the optimal power allocation is uniform over the allocated spectrum, so we cannot even simplify the problem as the symmetric case. Since these cases seem difficult and arise with probability zero in practice, we will not detail them here.
6 Conclusions
In this work, we have investigated the usage of full CSI by a cognitive radio manager to jointly schedule spectrum access and power allocation for opportunistic users in a power-efficient CR network. Two main challenges emerge in the underlying optimization problem. A first difficulty lies in the QoS and interference power constraints which may not be met simultaneously. To tackle this issue, we have provided general necessary conditions and sufficient conditions for the existence of an optimal solution.
A second challenge lies in the non-convexity of this problem because of the discrete scheduling policies. This aspect is overcome by exploiting a specific Lagrangian relaxation technique. We have proposed an iterative projected sub-gradient algorithm converging to the optimal joint power and spectrum policy whenever the problem is feasible and the channels are asymmetric. It turns out, that the convergence point is the optimal solution to the initial discrete problem. We have also studied the particular case of a symmetric CR network for which a closed-form solution is found.
Future work may consider further analysis of the cases in which the problem is unfeasible. Instead of not scheduling any SU, the radio-resource manager may decide to remove a subset of SUs chosen (similarly to [8]) to make the optimization problem feasible with a limited outage probability.
7 Endnotes
1We denote
2We denote by [x]+= max(x,0).
3We denote by  the quantity that equals one if \(\widetilde {x}_{qn}=1\) and zero otherwise.
the quantity that equals one if \(\widetilde {x}_{qn}=1\) and zero otherwise.
4We denote by s=[ s qn ] q,n the Q×N dimensional matrix with entries s qn for all SUs and all bands.
5 We denote by \(\boldsymbol {g}^{(k)}= \left [g_{qn}^{(k)}\right ]_{q,n}\) the Q×N dimensional matrix with entries \(g_{qn}^{(k)}\) for all SUs and all bands., ∀k, \(P_{qn}^{peak (k)}=20\) mW, ∀q,∀n,∀k, \(R_{1}^{CS}=1.4421\) bps, \(R_{2}^{CS}=4.7488\) bps.
6We denote by \(Card(\mathcal {X})\) the cardinal value of the set \(\mathcal {X}\).
7We denote by ||X||2 the euclidean norm of X.
8 Appendix A: Feasibility of the joint scheduling and power allocation problem
In the following, we will provide both necessary conditions and sufficient conditions for the existence of at least one solution to (D P 1) problem.
8.1 A1. Proof of Theorem 1, necessary conditions for the existence of a solution
-
We start with a particular case in which Q=1, N≥Q, K≥1. There is only one SU occupying all the spectrum \(i.e., \forall n, x_{1n}^{*}=1\). In this case, we consider the constrained rate maximization problem at the SU level in order to find the maximum achievable rate under interference constraints to PUs. A necessary and sufficient condition (CNS) to have a solution is given by \(R_{1}^{min} \leq R_{1}^{max}\). Otherwise, if the rate of the SU is too restrictive (i.e., the minimum rate requirement is above \(R_{1}^{max}\)), even if this SU owns all the spectrum, there can be no solution meeting all the constraints and the feasible set is void. We can summarize this necessary and sufficient condition as follows:
$$\begin{array}{@{}rcl@{}} \left\{ \begin{array}{l} Q=1, N \geq Q, K \geq 1\\ R_{1}^{min} \leq R_{1}^{max} \end{array} \right. \underset{CNS}{\Leftrightarrow} \mathcal{S}_{\mathcal{F}} \neq \emptyset \end{array} $$ -
Now, we assume that Q≥1, N≥Q, K≥1. If we allocate all the spectrum to only one SU, then it must satisfy its rate requirement otherwise the problem cannot have a solution and the feasible set is void. Thus, each SU must have the demand for its minimum rate lower than the rate that it would have if it was the only SU in the spectrum \(R_{\ell }^{max}\) defined in (5). Assume that it exists an arbitrary SU ℓ, such that it is the only SU in the spectrum i.e., x ℓ n =1, ∀n and if \(R_{\ell }^{min}> R_{\ell }^{max}\) then there is no solution and \(\mathcal {S}_{\mathcal {F}}= \emptyset \). We summarize this necessary condition as follows:
$$\begin{array}{@{}rcl@{}} \left\{ \begin{array}{l} Q \geq 1, N \geq Q, K \geq 1\\ \exists \ \ell : \ R_{\ell}^{min} > R_{\ell}^{max} \end{array} \right. \underset{CN}{\Rightarrow} \mathcal{S}_{\mathcal{F}} = \emptyset \end{array} $$
8.2 A2. Proof of Theorem 2, sufficient conditions for the existence of a solution
Assume that Q≥1, N≥Q, ∀K, we want to find sufficient conditions (CS) on the system parameters that ensure the existence of a pair (x,p) that satisfies all the constraints simultaneously. In order to find these sufficient conditions, we construct \(\widetilde {x}\) and \(\widetilde {p}\) that satisfy the scheduling and power constraints and are defined by:
and
Such construction of \(\widetilde {x}\) is possible because we assumed that N≥Q. Now, we want to find the CS such that the constructed pair \((\widetilde {x}, \widetilde {p})\) (which respects the scheduling and the power constraints) satisfies also the minimum rate constraint. The achievable rate of the SU q under the constructed spectrum and power allocation is
It turns out that this rate is higher than the rate of the worst channel gain \( \min \limits _{n} \{s_{qn} \}\). Thus, the resulted rate in the previous equality becomes:
This inequality follows from the definition of the constructed power in (24). So, the rate constraint is always satisfied if the minimum target rate \(R_{q}^{min}\) is lower than this threshold in (25) and then the feasible set is non-void. To summarize, we have the following sufficient conditions:
Remark that tighter sufficient conditions may be obtained directly by using the rates built in (25). They will depend on the system parameters. However, this construction is likely to be unfair from the SUs perspective and rather arbitrary as it is based on the fact that SU q is allocated precisely the band of index q. Any other permutation out of the Q! possibilities may be also considered to obtain better sufficient conditions for some of SUs and conservative for others.
9 Appendix B: Properties of the relaxed problem
9.1 B1. Proof of Proposition 1
We will show that rate constraint is satisfied with equality at the optimum:
Assume on the contrary (by Reductio ad absurdum) that there exists a SU q such that at the optimum (x ∗,p ∗): \(\displaystyle \sum _{m} x_{qm}^{*} \log _{2} \left (1+ \frac {p_{qm}^{*} s_{qm}}{x_{qm}^{*}}\right) > R_{q}^{min}\). We choose an arbitrary band n and we prove that, in this case, SU q can reduce its overall power consumption while still meeting the constraints which leads to a contradiction. We have
equivalent to
where \( \displaystyle r_{qm}^{*}=x_{qm}^{*} \log _{2} \left (1+ \frac {p_{qm}^{*} s_{qm}}{x_{qm}^{*}}\right).\)
We build a new allocation (x new,p new) as follows: the scheduling allocation policy is the same as the optimum one x new=x ∗ and the power allocation policy is the same as the optimum one \(p_{qm}^{new} = p_{qm}^{*}\) except in the n band in which we decrease power in order to achieve the rate \(R_{q}^{min}\) with equality such that:
where \( p^{new}_{qn}= \frac {1}{s_{qn}} \left (\exp \left (R_{q}^{min} - \sum _{m \neq n} {r}^{*}_{qm}\right)-1\right)\) and we have: \(p^{new}_{qn} < {p}^{*}_{qn}\). Thus, the objective function of power consumption: \(\sum _{n} p^{new}_{qn} < \sum _{n} {p}^{*}_{qn} \). With this new power allocation, the user q satisfies all the constraints and has a strictly lower power consumption than the optimal power p ∗ which is a contradiction. So, we conclude that ∀ q, \(\sum _{n} x_{qn}^{*} \log _{2} \left (1+ \frac {p_{qn}^{*} s_{qn}}{x_{qn}^{*}}\right) = R_{q}^{min}\).
9.2 B2. Proof of Proposition 2
Now, we will show that scheduling constraints are satisfied also with equality at the optimal power and spectrum allocation: ∀ n, \(\sum _{q} x_{qn}^{*}=1.\)
Assume on the contrary (by Reductio ad absurdum) that there exists a band n such that \(\sum _{q} x_{qn}^{*}<1\). We build another allocation (x new,p new) as follows: the allocation of the spectrum is the same as the optimum one x new=x ∗ except for the band n which we decide to allocate to an arbitrary user k as follows:
Therefore, we have that \(x_{kn}^{new} > x_{kn}^{*}\). Since we know, from Proposition 1, that the rate constraint is met with equality at the optimal solution, we build the new power allocation vector p new such that the allocation of the power is the same as the optimum one p new=p ∗ except for the user k for which: \( \sum _{m} {x}^{new}_{km} \log _{2} \left (1+ \frac {{p}^{new}_{km} s_{km}}{{x}^{new}_{km}}\right) = R_{k}^{min}\) which is equivalent to: \(\sum _{m \neq n} {x}^{*}_{km} \log _{2} \left (1+ \frac {{p}^{*}_{km} s_{km}}{{x}^{*}_{km}}\right) + \left (1- \sum _{q} {x}^{*}_{qn}\right) \log _{2} \left (1+ \frac {{p}^{new}_{kn} s_{kn}}{1-\sum _{q} {x}^{*}_{qn}}\right)= R_{k}^{min}.\)
Then, we obtain:
However, the optimal power allocation is given by
Knowing that \(x_{kn}^{*} < 1-\sum _{q} x_{qn}^{*}\) and that the function \(f(X)=\frac {X}{S} \left (\exp \left (\frac {R}{X}\right)-1\right)\) is decreasing, we obtain that \( p_{kn}^{*}>p_{kn}^{new}\). Therefore, user k achieves the rate \(R_{k}^{min}\) with lower consumption than the optimal point (x ∗,p ∗)
Thus, we have a pair (x new,p new) that satisfies all the constraints and gives us a strictly lower power consumption than the optimum which is a contradiction. Then, all average scheduling constraints are satisfied with equality.
In conclusion, if a SU uses an extra bandwidth, it achieves the same rate \(R_{k}^{min}\) with less power consumption. Therefore, at the optimum all bands are entirely used.
10 Appendix C: Convergence proof
In the following, we will prove that if the feasible set of problem (C P 2) is non-void, then our projected sub-gradient Algorithm 1 converges always to an optimal solution.
In order to prove the convergence of our algorithm, we start by proving that our dual function G(λ,β) in Step 4 is concave with respect to (λ,β). Given that the Lagrangian L(λ,β,μ,x,p) in Step 1 is affine in λ,β and μ for any feasible (x, p) and according to [14], the point-wise infimum \(\displaystyle \mathrm {G}(\boldsymbol {\lambda },\boldsymbol {\beta },\boldsymbol {\mu })= \min \limits _{(\mathbf {x}, \mathbf {p})} \mathrm {L}(\boldsymbol {\lambda },\boldsymbol {\beta },\boldsymbol {\mu }, \mathbf {x}, \mathbf {p})\) is then jointly concave w.r.t λ,β and μ. Since the resulting dual function G(λ,β,μ) is jointly concave w.r.t (λ,β) and μ and according to the theorem detailed in [36] (Appendix B.15), we obtain the concavity of the function \(\displaystyle \mathrm {G}(\boldsymbol {\lambda },\boldsymbol {\beta })= \max \limits _{\boldsymbol {\mu }} \mathrm {G}(\boldsymbol {\lambda },\boldsymbol {\beta },\boldsymbol {\mu })\).
Inspired by [14] and since \(\displaystyle \mathrm {G}(\boldsymbol {\lambda },\boldsymbol {\beta })= -\sum _{n} \max _{q} \varphi _{qn}(\lambda _{q}^{(k)},\beta _{q}) + \sum _{q} \beta _{q} R_{q}^{min} - \sum _{k} \sum _{q} \lambda _{q}^{(k)} \overline {P}_{q}^{(k)}\) is jointly concave w.r.t λ and β but not differentiable because of the piecewise function φ qn , in order to maximize G(λ,β), we propose to use a projected sub-gradient method such that
where X (t) is the update of the problem variable \(X=\left ({~}^{\boldsymbol {\lambda }}_{\boldsymbol {\beta }}\right)\) at time t. We project this variable because of the positivity of λ and β and D (t) is any sub-gradient of G at X (t) and τ>0 is a constant step size.
We choose the sub-gradient of the dual function G(λ,β) at λ,β given by the constraints
The proof of this proposition is based on the fact that a sub-gradient of the function G at (λ,β) is any vector D that satisfies the inequality, ∀(λ 1,β 1) and (λ 2,β 2):
Since x and p are bounded such that \(0 \leq g_{qn}^{(k)} p_{qn} \leq P^{peak(k)}_{qn}\) and 0≤x qn ≤1, thus, the norm7 of the sub-gradient is also bounded ||D(λ,β)(t)||2≤D th such that
From [14], we have that our sub-gradient algorithm converges, when t→+∞, to a neighborhood of the optimal solution depending on the step-size:
Regarding such sub-gradient methods, there are a lot of convergence results (such as point-wise convergence) available [37, 38] for different choices of the step-size other than constant: constant step length; square summable but not summable (e.g., τ (t)=a/(b+t), a>0 and b≥0); and non-summable diminishing (e.g., \(\tau ^{(t)} = a/\sqrt {t} \), a>0). The constant step-size and constant step-length choices guarantee that the sub-gradient method converges to a certain neighborhood of the optimal solution set, where the size of that neighborhood depends on the value of the step-size, in our case τ. But, if we want to obtain stronger convergence results, we will have to use variable step-sizes [14, 38].
11 Appendix D: Extreme case where channel gains are uniform for each SU and over each band
We are interested in a particular symmetric case which cannot be solved by our Algorithm 1. In such a case, there are ties regarding the spectrum allocation as we can schedule one band to several SUs with no optimality loss. In this case, we assume that \( s_{qn}=s,\ g_{qn}=g,\ P^{peak}_{qn}= P^{peak},\ \overline {P}_{q}=\overline {P},\ R^{min}_{q}=R^{min}\), ∀n,∀q. In the following, we will prove Propositions 5, 6 and 7.
11.1 Proof of Proposition 6 and Proposition 7
First, we start by solving a simpler problem than (D P N ) by ignoring the interference constraints (C1) and (C2) and taking into account only the scheduling constraint (C3). We begin by studying a relaxed version of this problem in which N q is a positive real:
This problem is convex because its the objective function is jointly convex in (N 1,N 2,…,N Q ) and the constraints are affine in N q . The Lagrangian of this problem is given by:
The KKT optimality conditions for this continuous problem are:
-
\(\displaystyle \frac {\partial \mathrm {L}(\boldsymbol {\alpha }, \boldsymbol {\delta }, \mathbf {N}_{q})}{\partial {N}_{q}^{*}}=0, \ \forall q \)
\(\Rightarrow \displaystyle \exp \left (\frac {R^{min}}{N_{q}^{*}}\right) \left (\frac {1}{s}-\frac {R^{min}}{s N_{q}^{*}}\right) -\frac {1}{s} + \alpha ^{*} - \delta _{q}^{*} =0 \)
-
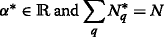
-
\(\forall q,\delta _{q}^{*}=0\) and \(N_{q}^{*}>0\)
From all these KKT conditions, we obtain the system of equations:

From the first equation, we can write:
From Eq. (29) and the fact that the function \(U(M)=\frac {1}{s} -\frac {1}{s} \exp \left (\frac {R^{min}}{M}\right) \left (1-\frac {R^{min}}{M}\\ \right)\) is strictly increasing and bijective, we conclude that at the optimum, we have the same number of allocated bands \(N_{q}^{*}=N_{r}^{*}, \ \ \forall q \neq r\). Considering the constraint \(\sum _{q} N_{q}^{*}=N\) and using the fact that the objective function \(\sum _{q} f(N_{q})\) is convex, we have two cases for the solution of the discrete problem (D P N ) without the constraints (C1) and (C2):
-
If the minimum of the objective function of the convex continuous problem \(\frac {N}{Q}\) is an integer then \(N_{q}^{*}\) is uniform for all the SUs \(N_{q}^{*}= \frac {N}{Q}\), for all SUs.
-
If the minimum of the objective function \(\frac {N}{Q}\) is not an integer
 then a SUq is allocated either \(\lfloor \frac {N}{Q}\rfloor \) or \(\lfloor \frac {N}{Q} \rfloor +1\) bands such that \(\sum _{q} N_{q}^{*}=N\). This means that the solution is not perfectly fair as the previous case and a subset of \(\left \{N\!-\lfloor \frac {N}{Q} \rfloor Q+1, \ldots, Q\right \}\) SUs will be allocated one band more:
$$\begin{array}{@{}rcl@{}} N_{q}^{*}=\left\{ \begin{array}{ll} \lfloor \frac{N}{Q} \rfloor+1 & \text{if} \ q \in \{1, \ldots N-\lfloor \frac{N}{Q} \rfloor Q \}\\ \lfloor\frac{N}{Q}\rfloor & \text{if} \ q \in\{N-\lfloor \frac{N}{Q} \rfloor Q+1, \ldots, Q\} \end{array} \right. \end{array} $$((30))
then a SUq is allocated either \(\lfloor \frac {N}{Q}\rfloor \) or \(\lfloor \frac {N}{Q} \rfloor +1\) bands such that \(\sum _{q} N_{q}^{*}=N\). This means that the solution is not perfectly fair as the previous case and a subset of \(\left \{N\!-\lfloor \frac {N}{Q} \rfloor Q+1, \ldots, Q\right \}\) SUs will be allocated one band more:
$$\begin{array}{@{}rcl@{}} N_{q}^{*}=\left\{ \begin{array}{ll} \lfloor \frac{N}{Q} \rfloor+1 & \text{if} \ q \in \{1, \ldots N-\lfloor \frac{N}{Q} \rfloor Q \}\\ \lfloor\frac{N}{Q}\rfloor & \text{if} \ q \in\{N-\lfloor \frac{N}{Q} \rfloor Q+1, \ldots, Q\} \end{array} \right. \end{array} $$((30))
Now, the objective is to prove that if (D P N ) is feasible, then the optimal solution is either \(N_{q}^{*}= \frac {N}{Q}\), for all SUs if \(\frac {N}{Q}\) is an integer or \(N_{q}^{*}\) in (30) if \(\frac {N}{Q}\) is not an integer. From the feasibility assumption, there exists at least one feasible \( (\widetilde {N}_{1}, \ldots, \widetilde {N}_{Q})\) that satisfies (C1),(C2),(C3), and (C4). From condition (C3), we have that there exists at least one index q such that \(\widetilde {N}_{q} \leq \lfloor N/Q \rfloor \) (otherwise (C3) is not met). So, we have \(N/Q \geq \lfloor N/Q \rfloor \geq \widetilde {N}_{q}. \)
First, from condition (C1) we have \(f(\widetilde {N}_{q})\leq \frac {\overline {P}}{g}\). The fact that f(M)=M/s∗(e x p(R min/M)−1) is strictly decreasing in M implies
Also, we have the trivial inequality ⌊N/Q⌋+1≥⌊N/Q⌋ which leads to
Second, from condition (C2) we have: \(T(\widetilde {N}_{q}) \leq \frac {P^{peak}}{g}, \ \forall q\) where T(M)=1/s∗(e x p(R min/M)−1) is the peak power required to reach R min with uniform allocation on M bands. We know that T(M) is strictly decreasing in M, which implies
and also \(\displaystyle T \left (\lfloor N/Q \rfloor +1 \right) \leq T \left (\lfloor N/Q \rfloor \right) \leq \frac {P^{peak}}{g}.\)
In conclusion, if (D P N ) is feasible, then the optimal solution is either \(N_{q}^{*}= \frac {N}{Q}\) (for all SUs) provided \(\frac {N}{Q}\) is an integer, or \(N_{q}^{*}\) in (30) otherwise.
References
Spectrum Policy Task Force, Report of the spectrum rights and responsibilities working group, tech. rep.,Federal Communications Commission (2002).
JM Peha, Sharing spectrum through spectrum policy reform and cognitive radio. Proc. IEEE. 97(4), 708–719 (2009).
G Scutari, DP Palomar, MIMO cognitive radio: a game theoretical approach. IEEE Trans. Signal Process. 58(2), 761–780 (2010).
D Lee, et al, Coordinated multipoint transmission and reception in LTE-advanced: deployment scenarios and opertaional challenges. IEEE Commun. Mag. 50(2), 148–155 (2012).
KI Pedersen, F Frederiksen, C Rosa, H Nguyen, LGU Garcia, Y Wang, Carrier aggregation for LTE-advanced: functionality and performance aspects. IEEE Commun. Mag. 49(6), 89–95 (2011).
G J-Sh Pang, F Scutari, Ch Facchinei, Wang, Distributed power allocation with rate constraints in gaussian parallel interference channels. IEEE Trans. Inf. Theory. 54(8), 3471–3489 (2008).
R Cavalcante, et al, Toward energy-efficient 5G wireless communications technologies: tools for decoupling the scaling of networks from the growth of operating power. IEEE Signal Proc. Mag. 31(6), 24–34 (2014).
A Alsawah, I Fijalkow, Practical radio link resource allocation for fair QoS-provision on OFDMA downlink with partial channel-state information. EURASIP J. Adv. Signal Process. 2009(1), 1–16 (2008).
D Gesbert, MS Alouini. Selective multi-user diversity, Internaltional Symposium on Signal Processing and Information Technology (Germany, 2003), pp. 162–165.
DT Ngo, T Le-Ngoc, Distributed resource allocation for cognitive radio networks with spectrum-sharing constraints. IEEE Trans. Veh. Technol. 60(7), 3436–3449 (2011).
G Scutari, DP Palomar, S Barbarossa, Asynchronous iterative water- filling for Gaussian frequency-selective interference channels. IEEE Trans. Inf. Theory. 54(7), 2868–2878 (2008).
D Palomar, J Fonollosa, Practical algorithms for a family of waterfilling solutions. IEEE Trans. Signal Process. 53(2), 686–695 (2005).
J Huang, VG Subramanian, R Agrawal, RA Berry, Joint scheduling and resource allocation in uplink OFDM systems for broadband wireless access networks. IEEE JSAC. 27(2), 226–234 (2009).
S Boyd, L Xiao, A Mutapcic, Subgradient Methods, vol. 2004 (Notes for EE392o, Stanford University, Autumn Quarter, 2003).
DD Yu, Cioffi JM, Spc10-2: iterative water-filling for optimal resource allocation in ofdm multiple-access and broadcast channels. IEEE Glob. Telecommun. Conf (2006).
G Scutari, DP Palomar, S Barbarossa, Optimal linear precoding strategies for wideband noncooperative systems based on game theory–part I: Nash equilibria. IEEE Trans. Signal Process. 56(3), 1230–1249 (2008).
G Scutari, DP Palomar, S Barbarossa, Optimal linear precoding strategies for wideband non-cooperative systems based on game theory–part II: algorithms. IEEE Trans. Signal Process. 56(3), 1250–1267 (2008).
EV Belmega, S Lasaulce, M Debbah, Power allocation games for MIMO multiple access channels with coordination. IEEE Trans. Wirel. Commun. 8(6), 3182–3192 (2009).
G Miao, N Himayat, YG Li, Crosslayer optimization for energy efficient wireless communications: a survey. Wirel. Commun. Mob. Comput. 9(4), 529–542 (2009).
Ch Isheden, Z Chong, E Jorswieck, Framework for link-level energy efficiency optimization with informed transmitter. IEEE Trans. Wirel. Commun. 11(8), 2946–2957 (2012).
G Miao, N Himayat, YG Li, Distributed interference-aware energy-efficient power optimization. IEEE IEEE Trans. Wirel. Commun. 10(4), 1323–1333 (2011).
G Bacci, EV Belmega, L Sanguinetti, Distributed energy-efficient power optimization in cellular relay networks with minimum rate constraints. IEEE Int. Conf. Acoust. Speech Signal Process. (ICASSP), 7014–7018 (2014).
VG Subramanian, RA Berry, R Agrawal, Joint scheduling and resource allocation in CDMA systems. IEEE Trans. Inf. Theory. 56(5), 2416–2432 (2010).
J Huang, VG Subramanian, R Agrawal, RA Berry, Downlink scheduling and resource allocation for OFDM systems. IEEE Trans. Wirel. Commun. 8(1), 288–296 (2009).
A Bagayoko, I Fijalkow, P Tortelier, Power control of spectrum-sharing in fading environment with partial channel state information. IEEE Trans. Signal Process. 59(5), 2244–2256 (2011).
P Mertikopoulos, EV Belmega, Transmit without regrets: online optimization in MIMO-OFDM cognitive radio systems. IEEE J. Sel. Areas Commun. 32(11), 1987–1999 (2014).
R Masmoudi, EV Belmega, I Fijalkow, N Sellami, in International Symposium DySPAN. A closed-form solution to the power minimization problem over two orthogonal frequency bands under QoS and cognitive radio interference constraints, pp. 212–222.
R Masmoudi, EV Belmega, I Fijalkow, N Sellami, A unifying view on energy-efficiency metrics in cognitive radio channels. Eur. Signal Process. Conf, 171–175 (2014).
SN Diggavi, TM Cover, The worst additive noise under a covariance constraint. IEEE Trans. Inf. Theory. 47(7), 3072–3081 (2001).
E Telatar, Capacity of multi-antenna Gaussian channels.European Trans. Telecommun. Wiley Online Libr. 10(6), 585–595 (1999).
CE Shannon, Communication in the presence of noise. Proc IRE. 37(1), 10–21 (1949).
E Masera, T Lestable, Econhome project presentation (Mobile World Congress, Barcelona, 2011).
H Congzheng, T Harrold, et al, Green radio: radio techniques to enable energy-efficient wireless networks. IEEE Commun. Mag. 49(6), 46–54 (2011).
S Boyd, L Vandenberghe, Convex Optimization (Cambridge Univ. Press, Cambridge, 2004).
AM Masucci, EV Belmega, I Fijalkow, Optimal blockwise subcarrier allocation policies in single carrier FDMA uplink systems, (2014).
S Foucart, H Rauhut, A mathematical introduction to compressive sensing (Birkhäuser, Boston, 2013).
Nesterov Y, Introductory Lectures on Convex Programming Volume I: Basic course, Lecture notes (1998).
NZ Shor, Minimization methods for non-differentiable functions, vol. 3 (Springer-Science & Business Media, 2012).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Masmoudi, R., Belmega, E.V. & Fijalkow, I. Efficient spectrum scheduling and power management for opportunistic users. J Wireless Com Network 2016, 97 (2016). https://doi.org/10.1186/s13638-016-0594-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-016-0594-4






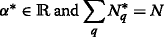
 then a SUq is allocated either
then a SUq is allocated either