- Research
- Open access
- Published:
Stackelberg game-based precoding and power allocation for spectrum auction in fractional frequency reuse cognitive cellular systems
EURASIP Journal on Wireless Communications and Networking volume 2016, Article number: 207 (2016)
Abstract
Spectrum auction has been considered as a promising approach to effectively reallocate spectrum resources in the secondary spectrum market. In our previous work, spectrum auction in a fractional frequency reuse (FFR) cognitive cellular system was studied. However, the bidding and valuation model of secondary users (SUs) are not close to practical applications as they introduced a random value of a fixed scope. In this paper, through an optimal interference price announced by the primary user (PU), a joint precoding and power allocation algorithm via Stackelberg game (OIPPS) is proposed to improve the spectrum auction problem subject to the interference constraint of PU, the transmission power constraint of SUs, and the signal-to-interference-plus-noise ratio (SINR) constraint of each SU in the FFR cognitive cellular system. Simulation results show the effectiveness of the proposed OIPPS algorithm in terms of the convergence of precoding and power allocation vectors and the maximized sum utility of SUs while taking full consideration of the PU’s revenue. Besides, a comparison between the bidding improved spectrum auction scheme and a traditional method is proposed to show the effectiveness of our proposed algorithm.
1 Introduction
With the rapid deployment of cognitive radio (CR) networks, the precious spectrum resource is becoming increasingly crowded. Besides, the requirement for radio spectrum has grown rapidly with the dramatic development of the mobile telecommunication industry in the last decades [1]. So, more efficient resource allocation ways are urgently needed and a key spectrum allocation solution is to allow a secondary user (SU) to simultaneously share a licensed spectrum with the primary link as long as the interference from the secondary transmission does not go beyond the tolerable threshold of the primary link [2]. Meanwhile, it is well known that the existing spectrum allocation policies usually lead to inefficiency in spectrum utilization. Hence, more effective spectrum allocation and utilization schemes are required for next-generation wireless networks. At the same time, spectrum auction has been considered as a promising approach to effectively reallocate spectrum resources. In order to effectively tackle the co-channel interference between SUs and the primary user (PU), fractional frequency reuse (FFR) has been widely applied. On the other hand, as a quite promising interference suppression technique, joint precoding and power allocation has been widely studied for CR networks. It is thus quite natural to combine all these above techniques to achieve higher spectral efficiency.
Auction has been widely applied to spectrum allocation recently and has obtained huge achievement. For example, the authors in [3] indicated that dynamic spectrum auction has been considered as a promising approach to effectively reallocate spectrum resources in the secondary spectrum market. Besides, a combinatorial auction with flexible bidding formats was proposed in [4] for the channel allocation problem in CR networks. Moreover, the current research works and literatures have studied revenue maximization auction [5], truthfulness guaranty auction [6–8], flexible auction [9], and so on. Spectrum auction has been widely discussed in literature [10, 11]. Besides, [12] included a cooperation-based dynamic spectrum leasing mechanism via multi-winner auction for multiple bands. The authors in [13] proposed a scalable collusion-resistant multi-winner spectrum auction, in which the collusive behavior of selfish users was carefully taken into consideration.
FFR, a recent emerged wireless network technology, is an effective and promising approach to tackle interference in cellular systems [14]. The main thoughts of FFR are to divide the cell bandwidth into center and edge, so that cell-edge users do not interfere with each other. Furthermore, it can mitigate the interference to interior users and the available spectrum utilization is more efficient than other traditional frequency reuse methods. The scholars in [15, 16] contributed to design optimal FFR schemes, and they solved the interference coordination problem already. Referring to the FFR scheme, the resources for cell-center and cell-edge users were partitioned. Based on such resource planning, the objective of the resource allocation scheme in [17] is to maximize both cell-edge and cell-center users’ throughput, subject to per base station power constraints. In this paper, we use FFR to manage co-channel interference as well as improve spectrum reusability.
Precoding schemes can be divided into two categories. The first category of hybrid precoding was based on spatially sparse precoding [18–20], which formulated the achievable rate optimization problem as a sparse, approximation problem and solved it by the orthogonal matching pursuit (OMP) algorithm to achieve near-optimal performance. The second category of hybrid precoding was based on codebooks [21–23], which involved an iterative searching procedure among the predefined codebooks to find the optimal hybrid precoding matrix [24]. The author in [25] indicated that matched-filter (MF) data precoding suffers from a large loss in the achievable information rate compared to other linear data precoders such as zero-forcing (ZF) and regularized channel inversion (RCI) precoders as the number of mobile terminals (MTs) increases. Power allocation is used to maximize sum utility derived from a wireless network operation to yield throughput optimal, fair, and energy-efficient communications. Furthermore, precoding and power control are two well-known approaches that can mitigate co-channel interference (CCI) and thus enhance the system capacity. Therefore, joint precoding and power control has been widely studied for CR networks [2]. Aiming to find an efficient way to enhance the secrecy rate with a tractable complexity, the author in [26] proposed a suboptimal joint source and relay linear precoding and power allocation scheme. In [27], the author investigated the linear precoding and power allocation policies to realize the optimal resource allocation for general multiple-input-multiple-output (MIMO) Gaussian channels with arbitrary input distributions, by capitalizing on the relationship between mutual information and minimum mean-square error (MMSE). Moreover, other joint precoding and power control techniques have been widely studied in different communication scenarios recently [28–32]. However, none of them consider the sum utility of SUs and the revenue of PUs together.
Stackelberg game, also known as leader-follower game, is a special case of hierarchical decision-making problems in which a distinguished agent, known as the leader, makes the first move and this action is followed by the actions of the remaining agents (i.e., the followers). In a Stackelberg game-based spectrum auction process, the PU protects itself by pricing the interference of the secondary link so as to maximize its own revenue. Then, the SUs formulate their strategies through precoding and power allocation based on this pricing to maximize their utility function [33]. Besides, when it comes to the resource allocation in CR networks, the Stackelberg game-based model is widely preferred since it is able to reflect the features of hierarchy and ad hoc topology in the network [34]. The author in [35] proposed a two-stage spectrum sharing scheme with combinatorial auction and Stackelberg game in recall-based cognitive radio networks. In fact, choosing a proper pricing mechanism with respect to different utility functions can be an efficient way of determining the equilibrium between the utility of SUs and the revenue of PU.
In our earlier work [36], we have studied a spectrum auction problem under the assumption that the bidding and valuation of SUs take a random number in a certain range. In fact, they are often related to the channel capacity or channel quality (typically SINR). Therefore, we make some corresponding improvements of it to design a more effective spectrum auction algorithm. Besides, given the excellent properties of all the above technologies, in this paper, through an optimal interference price announced by the PU, a joint precoding and power allocation algorithm via Stackelberg game (OIPPS) is proposed to solve the spectrum auction problem subject to the interference constraint of PU, the transmission power constraint of SUs, and the signal-to-interference-plus-noise ratio (SINR) constraint of each SU. The major contributions of this paper are summarized as follows:
-
Through the optimal interference price of the PU, we propose a joint precoding and power allocation algorithm in a FFR cognitive cellular system to balance the revenue of PU and the utility of SUs.
-
We study the secondary network utility maximization problem through Stackelberg game, and the revenue of PU is taken into account simultaneously.
-
We improve the bidding and valuation of spectrum auction to improve the system performance.
The rest of this paper is organized as follows. In Section 2, we describe the system model. In Section 3, the detailed optimization problem is introduced and elaborated. The performance evaluation through numerical simulations is presented in Section 4, and finally, the conclusion is given in Section 5.
2 System model
We reference related researches to consider a two-tier CR network with a single PU and K SUs. The primary network consists of a primary base station (BS) that transmits signals to a single PU. The secondary network has a single femtocell base station, equipped with K antennas, serving K SUs. Besides, the PU and the SUs share the same band and each of them is scheduled to serve one single user at each time interval, as shown in Fig. 1, where H k denotes the channel coefficient from macro BS to user k, H p denotes the channel coefficient from macro BS to PU, g k denotes the channel coefficient from femto BS to user k, and g p denotes the channel coefficient from femto BS to PU. The PU is required to keep the femtocell-to-macrocell interference to an acceptable level. When it comes to multiple PUs, we can expand this typical model into a large cellular network to well represent a real situation. Through the usage of FFR, the complex topology of a network can be divided into several typical parts. So for simplicity, we just analyze one of them, as shown in Fig. 2. Besides, we assume that all the channels involved experience block fading and remain constant during each transmission block.
Furthermore, due to the shortage of spectrum resources, the SUs need to share spectrum resources with the PU and the interference between them is inevitable. Therefore, how to restrain and reduce the interference effectively becomes an urgent problem. In our paper, a FFR cognitive cellular system is considered where the primary base station (PBS) and the PU locate at the center of a cell while SUs are deployed at the center and edge, respectively, as shown in Fig. 2. It can effectively mitigate the interference to interior users created by cell-edge users, and the available spectrum utilization is more efficient than other traditional frequency reuse methods. Furthermore, FFR determines the distribution of the spectrum frequency within a cell (i.e., the center of a cell can use the same spectrum band while specific edge users share the rest of the bands). For example, three nonadjacent edge cells can use the same channel while FFR is equal to 3. Therefore, different locations of the SUs receive different interference conditions and the interference they caused to the PU is also distinct. Generally, a center SU can receive interference from the PU and interference from other center SUs when an edge SU can only receive interference information from co-channel SUs [17].
Considering the interference constraints, SUs compete for the available spectrum so as to satisfy their communication requirements. However, when a SU selfishly chooses a strategy to increase its own utility, it may increase the interference level of the PU and other SUs. Therefore, the strategies chosen by different SUs depend on each other. On the other hand, the PU and SUs all want to maximize their interests during the spectrum allocation process, which can be modeled as a Stackelberg game [34]. Stackelberg game is a strategic game that consists of a leader and several followers competing with each other on certain resources. In this paper, we formulate the PU as the leader and the SUs as the followers. The PU imposes a set of prices on per unit of received interference power from each SU. Then, the SUs update their strategies to maximize their individual utilities based on the assigned interference prices. Furthermore, the quality of service (QoS) and the revenue of PU have the highest priority to be maintained, which is severely affected by the cross-tier interference. A joint precoding and power allocation algorithm on the secondary networks is considered as the most effective solution to adjust the power of SUs. The details are as follows.
3 Problem formulation
In this section, we first present the Stackelberg game model (i.e., giving full consideration of the revenue of PU and the utility of SUs). Then, a joint precoding and power allocation algorithm through an optimal interference price is expounded in detail.
3.1 Revenue of PU
As the PU has sufficient frequency spectrum resources to communicate with each other, the main purpose of them is seeking the maximum revenue under the tolerable interference, rather than improving the quality of communication. However, due to greediness, each SU only focuses on the increase of its own utility without nulling the interference to the PU while sharing spectrum resources with the PU. In order to suppress the interference from SUs, the PU generally employs interference price as an effective tool to optimize the noncooperative game [34]. In fact, the interference price is the bridge of primary and secondary networks. Generally, the interference price (i.e., ω) is distinct for different SUs; we assume that ω k is the asking price to SUk and the maximum interference that the PU can tolerate is I th. Besides, the revenue of PU consists of interference from SUs and the corresponding interference reward (i.e., interference price) [34] and our objective is to maximize the revenue of PU under the tolerable interference, which can be written as
where U p is the revenue of PU, I k is the interference received from user k, it is a function of precoding vector and transmission power vector, with I k = p k |H p f k |2, and ω k , p k , and f k are interference price, transmission power vector, and precoding vector of user k, respectively. H p is a (M × 1) vector representing the channel between the primary base station and PU.
3.2 Sum utility of SUs
Different from the PU, the goal of SUs is to maximize their own utility on the premise of spectrum resource sharing, so they need to get more spectrum bands to improve QoS of their communication regardless of the interference caused to the PU. Considering the principle of communication of the PU and SUs, next, we will analyze the sum utility optimization problem. Before that, we give the correlation definition firstly.
Under the FFR model, as illustrated in Fig. 2, the distribution of SUs in different locations in a cell determines the interference to the PU. That is to say, FFR divides the cell bandwidth into center and edges so that cell-edge users do not interfere with each other, so we discuss it in two different conditions. In fact, a center SU can receive interference from the PU and interference from other center SUs while an edge SU can only accept interference information from co-channel SUs, as illustrated in [17, 37]. Firstly, we assume that SUs locate at the center of the cell. Then, a cell-edge situation is given.
3.2.1 Cell-center SUs
For cell-center SUs, we assume that the number of SUs is K and their communication interference comes from co-channel SUs except itself and co-channel PU as well as the additive complex Gaussian noise. According to the MIMO CR system in Fig. 1 and the FFR condition in Fig. 2, we can get the received SINR of cell-center SUk [2, 17]:
where K is the number of SUs; ω k , p k , and f k are interference price, transmission power vector, and precoding vector of user k, respectively; H k is a (M × 1) vector representing the channel coefficients between the primary base station and SUs, which is assumed to be zero-mean unit-variance circularly symmetric complex Gaussian random variables; \( {\displaystyle {\sum}_{i=1,i\ne k}^K{\left|{H}_k{\mathbf{f}}_i\right|}^2{\mathbf{p}}_i} \) represents the interference from other SUs to user k; |g k |2 p p denotes the interference from the primary node to SUk; and the additive noise is assumed to be complex Gaussian, with zero mean and variance σ 2. It is assumed that the channel coefficients can be simultaneously estimated with the deep sensing paradigm.
The sum utility function of each SU consists of two parts: profit and cost. With the increase of the transmit power of SUs, the SUs will definitely cause more interference to the PU, so the PU will increase interference price to balance this loss. As a result, it has to buy more interference quota from the PU, which increases the cost. In order to prevent the selfish behavior above, the payoff function should consist of revenue and cost, which can be formally stated as follows:
where λ k is the utility gain per unit transmission rate for user k; U C is the sum utility of all center SUs; I k is the interference received from user k, it is a function of precoding vector and transmission power vector, with I k = p k |H p f k |2, which is the difference of utility revenue and cost; and I k is the interference it causes to the PU.
Similarly, our objective is to consider joint optimization of the precoding and power allocation to maximize U C as well as U p when SUs are distributed in the cell center, which can be simplified as
where the first constraint restricting the interference power from SUs to the PU should be less than I th. The second constraint is to guarantee the total transmission power of SUs is bounded by a certain limit p max, and the third constraint ensures the SINR requirement for each SU.
3.2.2 Cell-edge SUs
For cell-edge SUs, FFR can suppress co-channel interference, as illustrated in Fig. 2. We assume that the number of SUs is K. Their communication interference only comes from the additive complex Gaussian noise [17, 37]. So, the received SINR at cell-edge SUk is
The sum throughput of SUs also includes two parts: revenue and cost. Utility is the difference of them, which can be written as
where λ k is the utility gain per unit transmission rate for user k; U E is the sum utility of all edge SUs, which is the difference of utility revenue and cost; and I k is the interference it causes to the PU. Similarly, our objective is to consider joint optimization of the precoding and power allocation to maximize U E as well as U p , which can be simplified as
where the first constraint restricting the interference power from SUs to the PU should be less than I th. The second constraint is to guarantee the total transmission power of SUs is bounded by a certain limit p max, and the third constraint ensures the SINR requirement for each SU.
3.3 Nash equilibrium
In the process of precoding and power allocation, every player is unilaterally optimal and no player can increase its utility alone by changing its own strategy (i.e., a SU selfishly chooses a strategy to increase its own utility, it may increase the interference of other SUs [2]). This is a Stackelberg game, and the achievement of a Nash equilibrium (NE) is a well-known optimality criterion to analyze the outcome of the Stackelberg game. Therefore, the strategies chosen by different SUs depend on each other and an equilibrium between SUs’ utility and the PU’s revenue is achieved at NE point. The specific proof is shown as follows.
For the cell-center SUk, assuming that the precoding vector is fixed, by taking the first and second derivative of the utility function with respect to p k , we have
Similarly, when the transmission power vector is fixed, by taking the first and second derivative of the utility function with respect to |f k |2, we have
As |H k f k |4 ≥ 0, p k 2|H k |4 ≥ 0, so we can get that \( \frac{\partial^2{U}_C}{\partial^2{\mathbf{p}}_k}\le 0 \), \( \frac{\partial^2{U}_C}{\partial^2{\left|{\mathbf{f}}_k\right|}^2}\le 0 \).
Consequently, the utility functions of SUs satisfy all the required conditions and there exists at least one NE of these utility functions.
In the same way, we can get demonstrates when SUs distribute on the edge of the cell. For each SU, assuming that the precoding vector is fixed, by taking the first and second derivative of the utility function with respect to p k, we have
Similarly, when the transmission power vector is fixed, by taking the first and second derivative of the utility function with respect to |f k |2, we have
So, there still exists at least one NE. Therefore, we can say that there always exists a NE.
3.4 Precoding and power allocation algorithm
In this section, we propose an iterative algorithm that repeats the precoding and power allocation steps until a locally optimal pair of precoding and transmission power vectors is achieved. In order to fully analyze our optimal problem within all the location distribution of SUs, we next discuss it in two different conditions (i.e., cell-center and cell-edge SUs), respectively.
3.4.1 Cell-center SUs
For the joint precoding and power allocation problem, we firstly expound the precoding problem and power allocation problem, respectively. Then, a joint algorithm is proposed to get the optimal precoding and transmission power vectors.
-
(1)
Power allocation algorithm
Precoding and power allocation are performed at the cognitive base station to maximize the throughput of the secondary network. First of all, we fix the precoding vectors f to realize the optimization problem through the power vector p. Clearly, this is a concave optimization problem [34] and the optimal solution cannot be reached by individual choice of transmit power p k by each user, since each SINR is affected through the interference terms by the entire transmission power vector.
To find the optimal transmission power vector under the goal of achieving the maximum system utility, we need to get the optimal interference price firstly. So, the revenue of PU described in (1) is our first target to solve. It is observed that problem (1) is a concave function over p k . For a convex optimization problem, the optimal solution must satisfy the Karush-Kuhn-Tucker (KKT) conditions. So, by solving the KKT conditions, the optimal solution for (1) is easy to obtain. For a given interference price ω k , the initial optimal solution for (1) is
$$ {\boldsymbol{p}}_k={\left(\frac{\lambda_k}{\omega_k{\left|{H}_p{\boldsymbol{f}}_k\right|}^2}-\frac{{\displaystyle \sum_{i=1,i\ne k}^K}{\left|{H}_k{\boldsymbol{f}}_i\right|}^2{\boldsymbol{p}}_i+{\left|{g}_k\right|}^2{\boldsymbol{p}}_p+{\sigma}^2}{{\left|{H}_k{\boldsymbol{f}}_k\right|}^2}\right)}^{+} $$(16)
By substituting (16) into (1), the optimization problem of the PU side can be formulated as
$$ \begin{array}{l}{U}_p={\displaystyle \sum_{k=1}^K\left[{\lambda}_k-\frac{\omega_k{\left|{H}_p\right|}^2\left({\displaystyle \sum_{i=1,i\ne k}^K}{\left|{H}_k{\boldsymbol{f}}_i\right|}^2{\boldsymbol{p}}_i+{\left|{g}_k\right|}^2{\boldsymbol{p}}_p+{\sigma}^2\right)}{{\left|{H}_k\right|}^2}\right]}\\ {}\mathrm{s}.\mathrm{t}.\kern0.8em {\displaystyle \sum_{k=1}^K\frac{\lambda_k}{\omega_k}}-{\displaystyle \sum_{k=1}^K\frac{{\left|{H}_p\right|}^2{\displaystyle \sum_{i=1,i\ne k}^K}{\left|{H}_k{\boldsymbol{f}}_i\right|}^2{\boldsymbol{p}}_i+{\left|{g}_k\right|}^2{\boldsymbol{p}}_p+{\sigma}^2}{{\left|{H}_k\right|}^2}}\le {I}_{\mathrm{th}}\end{array} $$(17)Furthermore, by solving the KKT conditions, we can get the optimal interference price ω k * and optimal power vector p k * while guaranteeing the revenue of PU maximum, as follows:
$$ {\omega_k}^{*}=\frac{{\displaystyle \sum_{k=1}^K{\lambda}_k}}{I_{\mathrm{th}}+{\displaystyle \sum_{k=1}^K\frac{{\left|{H}_p\right|}^2}{{\left|{H}_k\right|}^2}\left({\displaystyle \sum_{i=1,i\ne k}^K}{\left|{H}_k{\boldsymbol{f}}_i\right|}^2{\boldsymbol{p}}_i+{\left|{g}_k\right|}^2{\boldsymbol{p}}_p+{\sigma}^2\right)}} $$(18)$$ {{\boldsymbol{p}}_k}^{*}={\left(\frac{\lambda_k}{{\omega_k}^{*}{\left|{H}_p{\boldsymbol{f}}_k\right|}^2}-\frac{{\displaystyle \sum_{i=1,i\ne k}^K}{\left|{H}_k{\boldsymbol{f}}_i\right|}^2{\boldsymbol{p}}_i+{\left|{g}_k\right|}^2{\boldsymbol{p}}_p+{\sigma}^2}{{\left|{H}_k{\boldsymbol{f}}_k\right|}^2}\right)}^{+} $$(19) -
(2)
Precoding design
Next, assume that the transmit power vector p is fixed, so that the maximization of problem (4) is carried out only over the precoding vector f. For each user k, we compute the precoding vector; these are generalized eigenvalue problems as
$$ {{\boldsymbol{f}}_{\mathbf{k}}}^{*}= \arg \kern0.3em \max \frac{x^H{M_k}^Sx}{x^H{M_k}^Ix} $$(20)where M k S = p k |H k |2, \( {M_k}^I=\left({\displaystyle \sum_{i=1,i\ne k}^K}{\left|{H}_k{\boldsymbol{f}}_i\right|}^2{\boldsymbol{p}}_i+{\left|{g}_k\right|}^2{\boldsymbol{p}}_p+{\sigma}^2\right)I \).
-
(3)
Joint precoding and power allocation algorithm
To search the maximum of problem (4) with respect to both precoding and transmission power vectors, through an optimal interference price announced by the PU, a joint precoding and power allocation algorithm via Stackelberg game (OIPPS) is designed to solve the spectrum auction problem. The OIPPS algorithm consists of three parts: First, the power control part runs for a certain iteration to obtain an initial optimization expression p k by using some initial precoding matrix and computes a power vector which may not be optimal because the algorithm stops without necessarily converging. Next, use this optimal transmission power vector to find the optimal interference price ω k *. Then, substitute ω k with ω k * to obtain p k * and f k *. This process of power control and precoding steps are repeated, until convergence is achieved to a locally optimal pair of precoding and transmission power vectors. The OIPPS algorithm is elaborated in Algorithm 1.

3.4.2 Cell-edge SUs
For the cell-edge SUs, they have similar precoding and power allocation process as center SUs. Next, we will introduce it briefly. We firstly expound the precoding problem and power allocation problem, respectively. Then, a joint algorithm is proposed to get the optimal precoding and transmission power vectors.
-
(1)
Power allocation algorithm
For a given interference price ω k , by solving the KKT conditions, the initial optimal solution for (1) is
$$ {\boldsymbol{p}}_k={\left(\frac{\lambda_k}{\omega_k{\left|{H}_p{\boldsymbol{f}}_k\right|}^2}-\frac{\sigma^2}{{\left|{H}_k{\boldsymbol{f}}_k\right|}^2}\right)}^{+} $$(21)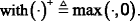
By substituting (16) into (1), the optimization problem of the PU side can be formulated as
$$ \begin{array}{l}{U}_p={\displaystyle \sum_{k=1}^K\left({\lambda}_k-\frac{\omega_k{\left|{H}_p\right|}^2{\sigma}^2}{{\left|{H}_k\right|}^2}\right)}\\ {}\mathrm{s}.\mathrm{t}.\kern0.8em {\displaystyle \sum_{k=1}^K\frac{\lambda_k}{\omega_k}}-{\displaystyle \sum_{k=1}^K\frac{{\left|{H}_p\right|}^2{\sigma}^2}{{\left|{H}_k\right|}^2}}\le {I}_{\mathrm{th}}\end{array} $$(22)Furthermore, by solving the KKT conditions, we can get the optimal interference price ω k * and optimal power vector p k * while guaranteeing the revenue of PU maximum, as follows:
$$ {\omega_k}^{*}=\frac{{\displaystyle \sum_{k=1}^K{\lambda}_k\sqrt{\sigma^2\frac{{\left|{H}_k\right|}^2}{{\left|{H}_p\right|}^2}}}}{I_{\mathrm{th}}+{\displaystyle \sum_{k=1}^K\frac{{\left|{H}_p\right|}^2}{{\left|{H}_k\right|}^2}{\sigma}^2}} $$(23)$$ {{\boldsymbol{p}}_k}^{*}={\left(\frac{\lambda_k}{{\omega_k}^{*}{\left|{H}_p{\boldsymbol{f}}_k\right|}^2}-\frac{\sigma^2}{{\left|{H}_k{\boldsymbol{f}}_k\right|}^2}\right)}^{+} $$(24) -
(2)
Precoding design
Next, assume that the transmit power vector p is fixed, so that the maximization of problem (7) is carried out only over the precoding vector f. For each user k, we compute the precoding vector; these are generalized eigenvalue problems as
$$ {{\boldsymbol{f}}_{\mathbf{k}}}^{*}= \arg \kern0.3em \max \frac{x^H{M_k}^Sx}{x^H{M_k}^Ix} $$(25)where M k S = p k |H k |2, M k I = σ 2 I.
-
(3)
Joint precoding and power allocation algorithm
For cell-edge SUs, our proposed OIPPS algorithm also consists of three parts: First, the power control part runs for a certain iterations to obtain an initial optimization expression p k using some initial precoding matrix and computes a transmission power vector which may not be optimal because the algorithm stops without necessarily converging. Next, use this optimal transmission power vector to find the optimal interference price ω k *. Then, substitute ω k with ω k * to obtain p k * and f k *. This process of power control and precoding steps are repeated, until convergence is achieved to a locally optimal pair of precoding and transmission power vectors. The OIPPS algorithm for edge SUs is elaborated in Algorithm 2.

4 Simulation results
In this section, we provide numerical results to show the convergence properties of the proposed OIPPS algorithm. In order to reflect the superiority of our proposed algorithm, we make comparisons with the algorithm proposed in [2]. Besides, a classical waterfilling algorithm is used to compare with the power allocation method.
4.1 Simulation setup
For simplicity, we suppose that there are a single PU and four SUs, which are distributed in a three-cell model (i.e., two of them are located at the center of the cell and another two distributed on the edge) and the FFR is equal to 3. In the following results, we choose the noise power σ 2 = 3e − 3 W, the PU transmission power p p = 0.1 W, the SU’s maximum transmission power p max = 10 W, the interference threshold I th = 100, λ k = 1, B = 1, and each minimum SINR constraint of SU is γ min = 5 dB. Furthermore, the channel coefficients between the primary base station and SUs are assumed to be zero-mean unit-variance circularly symmetric complex Gaussian random variables and as a common practice of many researchers, the MATLAB tool is used to generate the random channel coefficients. The related simulation setup follows the reference values in [2, 17, 34].
4.2 Performance evaluation
Figure 3 illustrates the total revenue of PU by sharing spectrum resources with all four SUs in our proposed algorithm. We can see that PU’s revenue obtains a stable maximum value when the curve converges after several iterations. That is to say, our proposed OIPPS with optimal price well coordinates the interference and gains between PU and SUs. The Stackelberg game achieves a NE between the revenue of PU and the sum utility of SUs at the ninth iteration.
In Fig. 4, we draw the sum utility tendency comparison between our proposed OIPPS and the fixed price method in [2]. It is obvious that the sum utility of SUs is dramatically improved by adopting OIPPS with optimal price and it converges to a fixed value. Besides, a NE is reached in this game while the sum utility converges. That is because the OIPPS with optimal price successfully contributes to the win-win situation of PU’s revenue maximization and SUs’ utility maximization. Therefore, the Stackelberg game with a flexible price design successfully contributes to the improvement of gains when compared with the fixed price method in [2].
As observed from Fig. 5, we make a sum utility comparison between SUs under classical spectrum auction in our previous work [36] and the bidding improving algorithm by OIPPS auction. We can see that the utility of SUs through the improved auction proposed is higher than the original bidding auction. The reason is that classical auction-based method in [36] introduced a random value in a certain scope as the bidding of SUs and this choice cannot well represent the real auction situation, so the efficiency and sum utility of the auction is low. In order to improve the system performance in our earlier work [36], in this paper, we use the precoding and power allocation method to analyze the SINR of received signals. Furthermore, we add SINR as well as bandwidth into an improved bidding expression and this new scheme can well reflect a real competition mechanism, so greater gains can be obtained than the classical one.
Figure 6 depicts the precoding weights allocated for each secondary link when the initialization of precoding weights is set to be 1 and the power allocation is fixed to the same value. We can see that all transmit precoding vector converges to the optimal levels. In addition, our proposed OIPPS with optimal price has a more stable convergence than the fixed price scheme in [2]. Similar to the sum utility, we can observe that both OIPPS and the fixed price method are effective precoding scheme.
As illustrated in Fig. 7, the description of power allocation situations are given specifically. In order to show the effectiveness of OIPPS, we make a comparison with the classical waterfilling algorithm. We can see that the two power allocation algorithms can effectively realize spectrum allocation under the peak power restriction. Furthermore, through the comparison of power allocation results between OIPPS and the classical waterfilling method, we can see that our proposed OIPPS has a higher power level and faster speed of convergence. The higher the transmission power, the stronger the signal strength at the receiver. Under the same condition, the higher the power level, the better the communication quality of SUs. So, we can conclude that our proposed OIPPS has better performance than the classical waterfilling.
5 Conclusions
In this paper, through an optimal interference price announced by the primary user (PU), we have proposed a joint precoding and power allocation algorithm via Stackelberg game (OIPPS) for a FFR cognitive radio cellular system to improve our earlier spectrum auction work. Based on the optimal interference price, SUs compute their optimal precoding and power vectors in a distributed manner to maximize their utilities under the transmission power constraint of SUs, interference constraint of PUs, and SINR constraint of each SU while giving full consideration of the PU’s revenue. Furthermore, we have improved the previous bidding strategies to achieve a higher spectrum auction efficiency. Simulation results indicate that the proposed precoding and power allocation algorithm via Stackelberg game in the FFR cognitive cellular system can achieve a win-win situation between PU and SUs (i.e., it can not only suppress the interference of PU but also achieve a higher system utility of SUs).
References
AD Domenico, EC Strinati, MG Di Benedetto, A survey on MAC strategies for cognitive radio networks. IEEE Commun. Surveys Tuts 14(no. 1), 21–44 (2012). First Quarter
F. Zhao, B. Li, H. Chen, in Proc. WASA, Joint beamforming and power allocation algorithm for cognitive MIMO systems via game theory, 166-177, Aug 2012
T. Chen, S. Zhong, in Proc. IEEE ICC, On designing truthful spectrum auctions for variable bandwidths, 1434-1438, June 2013
W. Zhou, T. Jing, W. Cheng, in Proc. IEEE ICC, Combinatorial auction based channel allocation in cognitive radio networks, 135-140, Jul 2013
R. Zhu, K.G. Shin, in Proc. IEEE INFOCOM, Differentially private and strategy-proof spectrum auction with approximate revenue maximization, 918-926, May 2015
Z Chen, H Huang, Y Sun, A framework for truthful double multi-channel spectrum auctions. IEEE Trans. Wireless Commun. 12(8), 3838–3850 (2013)
H Huang, Y Sun, X Li, Truthful auction mechanisms with performance guarantee in secondary spectrum markets. IEEE Trans. Mobile Computing 14(6), 1315–1329 (2015)
Z. Chen, L. Huang, L. Li, in Proc. IEEE INFOCOM, Provably secure solution for truthful double spectrum auctions, 1249-1257, Apr 2014
X Feng, P Lin, Q Zhang, Serving dynamic demands in a spectrum trading market with flexible auction. IEEE Trans. Wireless Commun. 14(2), 821–830 (2015)
Y Zhang, C Lee, D Niyato, Auction approaches for resource allocation in wireless systems: a survey. IEEE Commun. Surveys Tuts 15(no. 3), 1020–1041 (2013). Third Quarter
Y Zhang, D Niyato, P Wang, Auction-based resource allocation in cognitive radio systems. IEEE Commun. Mag. 50(11), 108–120 (2012)
H Lim, M Song, G Im, Cooperation-based dynamic spectrum leasing via multi-winner auction of multiple bands. IEEE Trans. Commun. 61(4), 1254–1263 (2013)
Z Xu, W Liang, Collusion-resistant repeated double auctions for relay assignment in cooperative networks. IEEE Trans. Wireless Commun. 13(3), 1196–1207 (2014)
G Huang, J Li, Interference mitigation for femtocell networks via adaptive frequency reuse. IEEE Trans. Veh. Tech. 65(4), 2413–2423 (2016)
H.E. Elfadil, M.A. Ali, M. Abas, in Proc. IEEE WSWAN, Fractional frequency reuse in LTE networks, 1-6 Mar 2015.
Q Li, RQ Hu, Y Xu, Optimal fractional frequency reuse and power control in the heterogeneous wireless networks. IEEE Trans. Wireless Commun. 12(6), 2658–2668 (2013)
W. Zhang, Y. Wang, P. Li, in Proc. IEEE WCNC, Coordinated resource allocation with fractional frequency reuse for downlink OFDMA networks, 1253-1258, Apr 2014
O El Ayach, S Rajagopal, S Abu-Surra, Spatially sparse precoding in millimeter wave MIMO systems. IEEE Trans. Wireless Commun. 13(3), 1499–1513 (2014)
Y Lee, C Wang, Y Huang, A hybrid RF/baseband precoding processor based on parallel-index-selection matrix-inversion-bypass simultaneous orthogonal matching pursuit for millimeter wave MIMO systems. IEEE Trans. Signal Process. 63(2), 305–317 (2015)
C Chen, An iterative hybrid transceiver design algorithm for millimeter wave MIMO systems. IEEE Wireless Commun. Lett. 4(3), 285–288 (2015)
W Roh et al., Millimeter-wave beamforming as an enabling technology for 5G cellular communications: theoretical feasibility and prototype results. IEEE Commun. Mag. 52(2), 106–113 (2014)
T. Kim, J. Park, J. Seol, in Proc. IEEE Global Commun. Conf. (GLOBECOM’13), Tens of Gbps support with mmWave beamforming systems for next generation communications, 3685–3690 Dec. 2013
C. Kim, J. S. Son, T. Kim, in Proc. IEEE WCNC, On the hybrid beamforming with shared array antenna for mmWave MIMO-OFDM systems, 335-340, Apr 2014
X Gao, L Dai, S Han, Energy-efficient hybrid analog and digital precoding for mmWave MIMO systems with large antenna arrays. IEEE J. Sel. Areas Commun 34(no. 4), 998–1009 (2016)
J Zhu, R Schober, VK Bhargava, Linear precoding of data and artificial noise in secure massive MIMO systems. IEEE Trans. Commun. 15(3), 2245–2261 (2016)
H Wang, F Liu, X Xia, Joint source-relay precoding and power allocation for secure amplify-and-forward MIMO relay networks. IEEE Trans. Inf. Forensics Security 9(8), 1240–1250 (2014)
F Perez-Cruz, MRD Rodrigues, S Verdu, MIMO Gaussian channels with arbitrary inputs: optimal precoding and power allocation. IEEE Trans. Inf. Theory 56(3), 1070–1084 (2010)
S. Yu, H. Ma, in Proc. IEEE GLOBECOM, Linear precoding and power allocation optimization with partial CSI under per BS power constraints for cooperative MIMO TDD systems, 3795-3800, Dec 2012
K. Ko, H. Cho, J. Lee, in Proc. IEEE WCNC, Eigenmode BER based MU-MIMO scheduling for rate maximization with linear precoding and power allocation, 142-146, Apr 2012
L. Lu, D. Wang, Y. Liu, in Proc. IEEE WCNC, Joint user association power control and beamforming in HetNets via distributed SOCP, 358-363, Mar 2015
M. Somrobru, N. Sutthisangiam, C. Pirak, in Proc. IEEE ICACT, Interference cancellation using joint beamforming and power control techniques in cooperative networks, 1-6, Feb 2016
M Lin, J Ouyang, W Zhu, Joint beamforming and power control for device-to-device communications underlaying cellular networks. IEEE J. Select. Areas Commun 34(1), 138–150 (2016)
M. Ahmed, M. Peng, I. Ahmad, in Proc. IEEE WCSP, Stackelberg game based optimized power allocation scheme for two-tier femtocell network, 1-6, Oct 2013
X Kang, R Zhang, M Motani, Price-based resource allocation for spectrum-sharing femtocell networks: a Stackelberg same approach. IEEE J. Sel. Areas Commun. 30(3), 538–549 (2012)
C Yi, J Cai, Two-stage spectrum sharing with combinatorial auction and Stackelberg game in recall-based cognitive radio networks. IEEE Trans. Commun. 62(11), 3740–3752 (2014)
F. Zhao, H. Nie, H. Chen, Group buying spectrum auction algorithm for fractional frequency reuse cognitive cellular systems. Ad. Hoc. Netw. published online, doi: 10.1016/j.adhoc.2016.04.009.
Z Xu, G Li, C Yang, Throughput and optimal threshold for FFR schemes in OFDMA cellular networks. IEEE Trans. Wireless Commun. 11(8), 2776–2785 (2012)
Acknowledgements
This research was supported by the National Natural Science Foundation of China (61172055, 61471135), the Guangxi Natural Science Foundation (2013GXNSFGA019004, 2015GXNSFBB139007), the Fund of Key Laboratory of Cognitive Radio and Information Processing, Guilin University of Electronic Technology, Ministry of Education, China, the Guangxi Key Laboratory of Wireless Wideband Communication and Signal Processing (CRKL150104, CRKL160105), and the Innovation Project of GUET Graduate Education (2016YJCX87).
Competing interests
The authors declare that they have no competing interests.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhao, F., Nie, H. & Chen, H. Stackelberg game-based precoding and power allocation for spectrum auction in fractional frequency reuse cognitive cellular systems. J Wireless Com Network 2016, 207 (2016). https://doi.org/10.1186/s13638-016-0712-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-016-0712-3