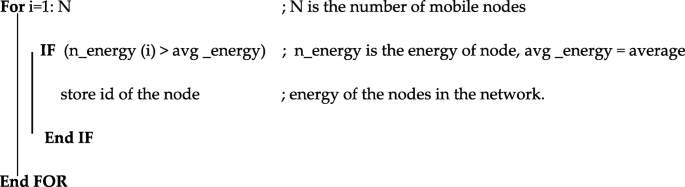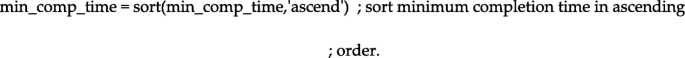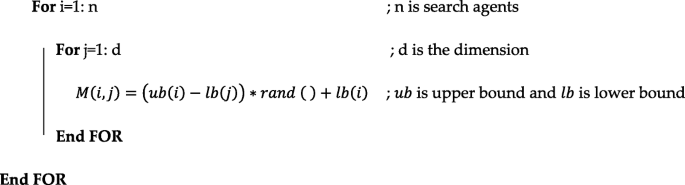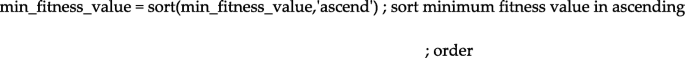- Research
- Open access
- Published:
A novel dynamic source routing (DSR) protocol based on minimum execution time scheduling and moth flame optimization (MET-MFO)
EURASIP Journal on Wireless Communications and Networking volume 2020, Article number: 219 (2020)
Abstract
In general, the conventional routing approaches in mobile ad hoc networks (MANETs) provide a route between the source and the target with a minimum hop count. Dynamic source routing (DSR) as a typical prototype of routing protocols relies on the minimum hop count parameter to provide the path without considering any other factors such as energy consumption and node energy level, which significantly affect the routing algorithm performance. To enhance the performance of the DSR, a novel and efficient routing mechanism based on a hybrid approach using the minimum execution time (MET) scheduling and moth flame optimization (MFO) scheme is proposed. This hybridization version of DSR is called the (MET-MFODSR) algorithm, and it aims to improve the routing mechanism through establishing an optimal route with minimum energy consumption, which increases the network lifetime and reduces route failure issues. The proposed MET-MFODSR protocol is implemented using the MATLAB platform, analyzed and evaluated in different simulation environments. The simulation results demonstrate that the suggested routing algorithm is applicative and practicable, and its performance exceeds the performance of the existing Bee DSR (BEEDSR) and Bee-inspired protocol (BeeIP) algorithms.
1 Introduction
MANETs as an infrastructure-free wireless network can be defined as a non-concentrated multi-hop remote network which consists of a collection of distributed and autonomous mobile nodes that create a temporary network. In this network, each node can move freely and randomly without predicting their movement which indicates that MANETs have a dynamic topology [1,2,3]. The direct communications among nodes or indirect communications via intermediate nodes are achieved without relying on any pre-existing infrastructure (like access points or a base station) [3]. Therefore, in the case of MANETs, there is no centralized administrative role. It is a decentralized architecture, which implies that all nodes cooperate to forward data from the source to the destination [4, 5]. Such features make MANETs to be utilized significantly in a range of different applications such as battlefield communications, health care, and disaster areas [6,7,8]. On the other hand, due to the unstable topology, the absence of centralized administrative, and limited resources [4, 5], MANETs experience critical issues regarding the routing process. Therefore, the routing mechanism in MANETs is one of the challenging research fields that need to be investigated and solved.
The routing mechanism in MANETs is the responsibility of the network layer, which can simply be defined as the process of identifying the route to send data packets between the source and the destination [9,10,11]. Currently, there are many prototype routing protocols used in MANETs that are standardized by the Internet Engineering Task Force (IETF) organization. These protocols can be divided into three classes, which are proactive or table-based, reactive or on-demand, and hybrid routing protocols [8,9,10, 12,13,14,15,16,17,18]. The proactive routing scheme is where each mobile node stores the collected information about the active routes in the form of regularly updated routing tables [3]. Examples of proactive routing schemes were provided in [15, 17, 18]. In terms of the reactive routing mechanism, when any sender node needs to transmit the data packet to the specific sink, at that time only, it starts looking for and determining the path [8, 19, 20]. Types of reactive routing class were presented in [21,22,23]. The hybrid routing method is based on the concept of integrating both proactive and reactive approaches [3, 10, 24]. Examples of this routing approach were introduced in [25,26,27,28].
In such non-concentrated multi-hop remote networks, the mobile nodes are powered with a limited capacity battery, which influences the survivability of the network since the links will be disengaged when these nodes dissipate their battery. Therefore, considering the energy consumption of mobile nodes is important to maintain connectivity and extend the lifetime of the network [29, 30]. Unfortunately, the common problem in the existing prototype classical routing protocols is that they rely on the hop count as the basic factor without paying attention to other factors to establish the route from source to destination, which can subsequently lead to inefficient packet delivery [31]. Other routing factors such as the node energy level and energy consumption should be considered in addition to the hop count. The purpose of adding these routing parameters is to design an efficient routing algorithm that can reduce the energy consumption of mobile nodes and extend network lifetime.
The performance of the routing approach is a significant factor, and it affects the performance of the MANET itself. Therefore, this research article presents a novel and efficient routing algorithm using a DSR protocol based on MET data packet scheduling and MFO (hybridization). This leads to an increase in the packet delivery rate and throughput; further, it decreases the average delay, routing overhead, and energy consumption, which prolongs the network lifetime and reduces route failures. Table 1 presents the important abbreviations used in this manuscript.
1.1 Problem statement
The typical prototype of the DSR protocol standardized by IETF has some disadvantages such as its reliance on the minimum hop count parameter to select the path without considering any other factors that affect the routing algorithm performance like energy consumption, residual energy, and link stabilities. Furthermore, due to the inefficient route discovery mechanism which is based on flooding, DSR provides a low packet delivery ratio in high mobility environments, long delays, high routing overhead information, and very high energy consumption. Therefore, this research work aims to improve the performance of the classical DSR protocol by applying a novel hybrid optimization approach based on combining the MET scheduling method and the MFO algorithm. This hybridization (MET-MFODSR) aims to reduce the average end-to-end delay and at the same time increase the throughput and packet delivery ratio through using MET, whereas the MFO will minimize the average energy expenditure.
1.2 Dynamic source routing (DSR) protocol
It is a straightforward and reactive routing strategy that can be applied in wireless ad hoc networks [32,33,34]. It differs from other protocols as DSR is based on the source routing principle, indicating that the node that owns the data to send must identify and know a multi-hop route to the receiver node [34,35,36]. When any node has data packets to transmit, it immediately starts to search in the cache through the routing table to determine whether a route to the required sink exists or not. If the source finds multiple routes, the route with the minimum hop count will be selected and added as a header of the transmitted data packet [34, 35]. Otherwise, two essential phases based on route discovery and maintenance will be established [32, 34, 37, 38].
In the route discovery stage, a route request (RREQ) packet mainly consists of a unique ID, source address, and the destination address will be employed in this stage [35]. The RREQ will be flooded by the source to all the nodes in the network. Each one of the intermediate participating nodes will receive the RREQ and then check to see whether it knows the destination or not. If not, the node will add its address and rebroadcast until the RREQ arrives at the target node. Then, this target node will send a route reply (RREP) packet back to the source. This packet carries route details obtained from the RREQ, which stored in the source’s cache for the communication requirement [34, 35]. Figure 1 describes the route discovery phase, where N1 represents the source and N7 is the destination. To identify the route, two RREQs with unique different ids (id = 3 and id = 1) will be sent, and two routes will be discovered, which are route 1 [N1, N2, N3, N7] and route 2 [N1, N4, N5, N6, N7]. In this case, route 1 will be selected as it has the minimum hop.
Route discovery using RREQ packets. N1 is the source and N7 is the destination. To obtain the route, two RREQs with unique different ids (id = 3 and id = 1) will be sent and two paths will be discovered, which are route 1 [N1, N2, N3, N7] and route 2 [N1, N4, N5, N6, N7]. Route 1 will be selected as it has the minimum hop
The other mechanism used in DSR is route maintenance, which is applied to find alternative routes to continue the transmission of data packets when the current path experiences failure. In this stage, the source receives a route error (RERR) packet and then deletes the expired route from its cache to start a new search for a new route [32]. Figure 2 depicts the route maintenance mechanism. It shows that when the link between node N3 and destination node N7 is disconnected, the intermediate node N3 sends a RERR message to the source node N1.
1.3 Related work
In MANETs, due to the dynamic topology environment and limited resources such as the battery power of mobile nodes, the routing process can be challenging. Numerous studies have been conducted in this direction to enhance the performance of the routing protocol to provide better performance of MANETs. The most common idea in previous research works is based on the utilization of bio-inspired optimization algorithms to find the optimal path. Chatterjee and Das [29] suggested the implementation of a routing algorithm called enhanced ant colony DSR (E-Ant–DSR), which is based on the combination of the ant colony optimization (ACO) approach and DSR to obtain an efficient path by avoiding link congestion and link break issues. The simulation results indicated that the proposed E-Ant–DSR algorithm had a better performance in terms of performance indexes such as routing overhead, packet delivery ratio, route dis-connectivity, and energy consumption compared with the classical DSR scheme, other ACO methods, and other algorithms based on artificial intelligence. Giagkos et al. [39] proposed a new Bee-inspired protocol (BeeIP) routing algorithm based on swarm intelligence inspired by adaptive bee foraging. This presented algorithm provides an efficient multipath route in MANETs between mobile nodes. The simulation results showed that the recommended BeeIP provided a powerful adaptability level as well as efficiency in terms of the selection of suitable route decisions. Tareq et al. [32] introduced an energy cost Bee DSR (BEE-DSR) algorithm based on integrating the artificial bee colony (ABC) optimization method with the DSR. BEE-DSR is applied to determine the optimal route by considering the level of energy of intermediate nodes and hop count. The simulation results indicated that BEE-DSR provides better performance metrics than DSR and BeeIP protocols. Zhang et al. [34] suggested the combination of a genetic algorithm with a bacteria foraging algorithm (GA-BFO) and applied their extracted advantages to the DSR routing protocol. GA-BFO/DSR has been applied to search the optimal path by considering the energy information of the node. When this algorithm was applied, it improved the routing search efficiency without increasing the routing information of the DSR. Therefore, the average end-to-end delay for data exchange between nodes was decreased. The obtained simulation results showed a significant improvement in overall network efficiency. Pandey et al. [40] suggested applying the MFO approach for clustering and routing purposes to improve the lifetime of the wireless sensor network (WSN). The simulation results indicated that the MFO method provides better performance than the genetic algorithm (GA), particle swarm optimization (PSO), and least distance clustering (LDC) algorithm. In [41], the author used the MFO-based clustering routing algorithm based on threshold-sensitive energy for WSN. The introduced algorithm consists of a set-up stage and steady-state stage, and the MFO is used in the set-up stage to select the optimal cluster head and applied in the steady-state stage for establishing the optimal path. The simulation results indicate that the introduced protocol achieves better performance than existing algorithms regarding network lifetime and energy consumption of the network.
It can be observed from this literature survey that most of the work focused on enhancing the performance of the routing approach based on the application of meta-heuristic optimization algorithms or combining two meta-heuristic optimization algorithms which are very common these days in this research field. However, this research work introduces a novel routing mechanism based on DSR protocol and apply a unique hybridization technique by combining both MET scheduling and MFO method.
2 Methods
This research article introduces a novel and efficient routing algorithm based on the DSR protocol and integrating the MET scheduling and MFO algorithm (hybridization). The aim is to increase the packet delivery ratio, throughput, and reduce end-to-end delay and, furthermore, reduce energy consumption, which prolongs the network lifetime.
2.1 Minimum execution time (MET) scheduling algorithm
In MANETs, data packets flow from source node to destination node through intermediate router nodes. The packet forwarding process needs to be considered carefully to provide a route with the best possible data packet transfer. For this purpose, the data packet scheduling method can play a significant role to accomplish this objective [42]. When any node receives forwarded packets, it starts serving only one of them while the remaining flow packets will be stored in the queue. The scheduling method (scheduler) is deciding which packet (task) will be served between all the remaining packets [43,44,45,46,47]. Therefore, packet scheduling mechanism is vital to ensure quality of service (QoS) provision by increasing the packet delivery rate, throughput, and minimizing end-to-end delay [44, 45].
In the literature of optimizing routing algorithms, the meta-heuristic optimization methods were only considered to provide the optimal path. Unfortunately, these meta-heuristic optimized routing protocols did not consider the packet scheduling method which can participate effectively to ensure QoS provision. In this manuscript, a unique hybrid optimization technique based on data packets scheduling and meta-heuristic optimization method was considered. The applied hybrid optimization mechanism based on the minimum execution time (MET) packet scheduling method and moth flame optimization (MFO) scheme to provide the optimal route. In the MET method, the packets (tasks) are assigned to the mobile nodes in reliance on the finest predictable completion intervals of the process execution without paying attention to the resource accessibility [48, 49]. The execution time represents the required time interval to process the packet on the node without interruption [50]. The estimated minimum execution time is evaluated based on the minimum total sum of the ready time of the packet to execute on the particular route node and estimated time to complete the execution of the packet on the node. Algorithm 1 shows the pseudo-code of the MET process.

The main purpose of the MET algorithm is to process data packets on specific mobile nodes based on the minimal execution period, which increases the packet delivery ratio, throughput, and reduce end to end of the packet transfer.
2.2 Moth flame optimization (MFO) approach
MFO is one of the recently developed meta-heuristic population-based algorithms proposed in 2015 by Seyedali Mirjalili [51]. It is derived from the navigation mechanism of moths, which is known as transverse orientation. This navigation mechanism is based on the fact that moths hover in a straight path by conserving a fixed angle concerning the distant moon as an effective method of traveling long distances in a straight line [51,52,53,54,55]. Although transverse orientation is an effective mechanism for guaranteeing that the moth can fly in a straight line, it is observed that the pattern of a moth flying changes when exposed to artificial sources of light. In the presence of man-made light, moths start to fly in a spiral route around the light source, because it is not far as the moonlight [51, 52]. The mathematical model that describes this behavior is called the moth flame optimizer.
In [51], Mirjalili showed that the MFO algorithm presents more promising and competing results in comparison to other known nature-inspired swarm algorithms such as PSO and evolutionary-based algorithms such as GA. This is because MFO owns two main advantages. Firstly, the MFO method has an extremely high exploration of solution space. Therefore, the local optima problem is eliminated, while various other bio-inspired optimization approaches suffering from this problem. Secondly, the equilibrium between exploration and exploitation which makes MFO more effective. Therefore, the MFO outshines the other well-known algorithms in discovering the optimal solution in real-time challenging problems. Based on these features, MFO can be utilized efficiently in many applications. MFO is processed as follows:
Initialize the random positions of moths, which represent a potential solution in the search solution space. The initialized moths are expressed as in the following matrix:
where n represents the number of moths and d is the dimension of search space (number of variables). The value of fitness for every moth is arranged in an array as follows:
Flames are another significant component of MFO, which can be represented in an analogous matrix to the moths’ matrix as follows:
Here, n indicates the number of moths, and d is the dimension of the search space. Similarly, the value of fitness for each flame can be stored in an array as follows:
where n refers to the number of moths. Here, it should be mentioned that both moths and flames represent solutions; however, the only operative difference between these two solutions is that moths represent the search agents that explore the solution area, while flames refer to the best solution attained until now. Alternatively, flames might be represented in the form of a flag that is visited by moths during the process of searching.
The MFO method utilizes three functions to approximate the global optimum in a certain optimization problem. The functions that are used in MFO are as follows:
where I function initiates a random population of moths with their representative fitness values. The I function is modeled as follows:
P is the main function that represents the moths’ movement in the search area. The P function deals with matrix M as the input and returns an updated copy as the output.
The T function is the termination criterion, which refers to the completion of the search operation. It returns a value of true when the termination criterion is reached and false when it is not reached.
Moths use a transverse orientation mechanism as a navigation tool. Therefore, to represent this behavior mathematically, a random distribution was introduced to generate preliminary solutions and compute the objective function value, as in Eq. (9):
The variable lb(i) is the lower bound and ub(i) is the upper bound.
The updated location for every moth concerning the flame can be defined using Eq. (10):
where Midefines the ith moth, Fjrefers to the jth flame, and S represents the spiral function. The logarithmical spiral function is utilized to update the position of the moths for the flame. This logarithmical spiral function must meet the following requirements:
-
1.
The position of the moth must represent the initial point of the spiral.
-
2.
The endpoint of the spiral should be defined by the flame’s position.
-
3.
The variation of the spiral’s range should not go beyond the search space.
Accordingly, the logarithmic spiral function for updating the moth’s position in MFO can be mathematically modeled as follows:
where Di represents the distance from the ith moth Mi to the jth flame Fj, b is a fixed number that defines the logarithmic spiral shape, and t provides the step size of the moth for the next position in the flame direction, it is defined as a random number between − 1 and 1. Di is computed as the following:
Another issue related to updating the moths’ position to n various positions in the solution space is degradation in the exploitation process to obtain the best solution. Therefore, an adaptive mechanism is used to deal with the number of flames. This mechanism indicates how the number of flames is reduced adaptively during the procedure of iterations. Equation (13) is used in this respect:
where N refers to the number of flames, l represents the present iteration, and T defines the greatest number of iterations.
In this research study, the MFO method is employed to optimize the route for data packet transfer from source to destination with minimal energy expenditure. In the introduced routing algorithm, the metaheuristic MFO method is applied in the decentralized MANET for optimal routing as in the following steps:
-
1.
Initialization: The randomly initialized nodes of MANET on a certain geographical area with a unique ID are treated as the moths in the MFO method. These nodes (moths) are considered potential solutions and stored in a matrix as presented in the Equation (1), and their positions considered as search solution space. This search space is created using Eq. (9) based on some defined parameters which include the dimension of search (d), the lower bound lb(i), and the upper bound ub(i).
-
2.
Fitness function evaluation: The fitness function value is evaluated for each node (moth) based on their position in search space. In the proposed algorithm, the fitness function is formulated as a part of the MFO algorithm to provide optimal data packet routing through intermediate nodes. The optimization variables include the energy consumption of the node (Ex), the distance (Dx) covered by the node (moth) and the total number of nodes (N). The formulated fitness function is given as in Eq. (14):
$$ \mathit{\operatorname{Minimize}}\ fitness\ function=\frac{E_x\times {D}_x}{N} $$(14)
In this iterative processing, the fitness value will be compared with the previous fitness value and stored in ascending order.
-
3.
Location update: After the fitness value evaluation, the location of each month (node) will be updated using the logarithmic spiral formula as given in Eq. (11).
The process of fitness evaluation, arranging, and location update will be repeated until reaching the maximum iteration. Afterward, the coordinates of best forwarding intermediate nodes with the lowest fitness value will be obtained, so that the data packets transferred through them.
2.3 Description of the proposed MET-MFODSR protocol
Based on the aforementioned theories and equations, the design steps of the proposed MET-MFODSR protocol are presented in the following pseudo-code procedures:
-
Input: Number of nodes (N), transmission range (TRx), lower bound (lb), upper bound (up), dimension (d), and logarithmic spiral shape constant (b).
-
Output: Optimal data packet route.
-
1.
Deploy mobile nodes mni with random positions (mni =mn1,mn2,….., mnN) where N = 50 nodes.
-
2.
Each node assumed to have a configured Global Positioning System (GPS) to store X, Y locations, and speed.
-
3.
Initialize random mobility speed for each mobile node.
-
4.
Calculate the average energy of the nodes in the network.
-
5.
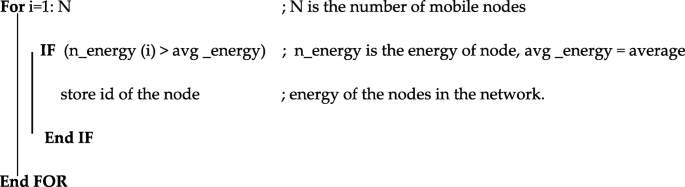
-
6.
Select and identify the source and the destination Ids from those nodes that have a higher energy level than the average energy of the nodes.
-
7.
Form the packets or requests to be sent in the DSR protocol.
-
8.
Start the route initialization phase by broadcasting RREQ packets.
-
9.
Evaluate the distance from the source to the destination using Eq. (15):
$$ D=\sqrt{{\left({x}_d-{x}_s\right)}^2+{\left({y}_d-{y}_s\right)}^2\ } $$(15)
-
1.
where D is the distance in meters, xd is the x-coordinate of the destination, xs is the x-coordinate of the source, yd is the y-coordinate of the destination, and ys is the y-coordinate of the source.
-
10.
Check:

-
11.
Find the route with the minimum hop count and alternative route to the destination node.
-
12.
Start the MET scheduling mechanism

-
13.
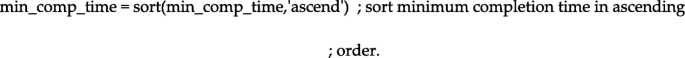
-
14.
Stop the MET process when all the data packets are broadcasted from the route nodes to the destination
-
15.
Start applying the MFO algorithm by creating the search space
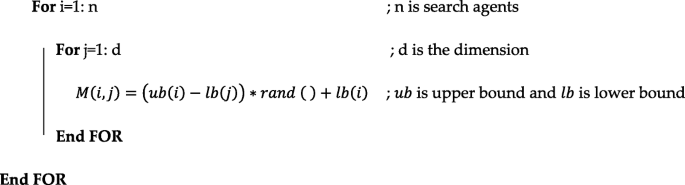
-
16.
WHILE (iteration ≤ max. iteration)
-
17.
Evaluate the fitness value for each node (moth) using the fitness function given in Eq. (14).
-
18.
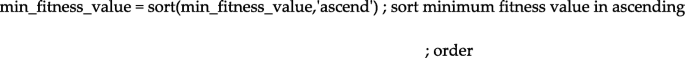
-
19.
Update the locations of each node (moth) using Eq. (11) .
-
20.
Iteration = iteration+1
-
21.
WHILE END
-
22.
Obtain the coordinates of best forwarding intermediate nodes with the lowest fitness value to transfer the data packets through it.
3 Simulation results and discussion
3.1 Simulation settings
In this research paper, the simulation and analysis of the MET-MFODSR algorithm are conducted using the MATLAB program (2019a) version on Windows 10 as the operating system. The performance of the proposed MET-MFODSR protocol was analyzed and compared with the existing BEEDSR algorithm introduced in [32] and the BeeIP algorithm proposed in [39]. In this experimental research, 50 mobile nodes were randomly distributed in a 1670 m × 970 m simulation area. For each node, the transmission range was fixed to 250 m, the level of initial energy for every individual node was adjusted to 100 joules, and the total simulation time was specified as the 50 s. Table 2 summarizes the basis for simulation parameter settings.
The simulation deployment of network topology as obtained in the MATLAB platform is displayed in Fig. 3. The nodes are distributed in random locations and the network topology changes as a result of the mobility feature of the nodes.
3.2 Performance metrics
In this research study, five performance indexes are selected to evaluate the performance of the proposed MET-MFODSR algorithm under two different simulation scenarios (i.e. node velocity and packet size). These five performance metrics that will be defined below include average throughput, average end-to-end delay, packet delivery ratio, routing overhead ratio, and average energy consumption.
-
1.
Average throughput: This index represents the average of the data packets that are successfully received by the destination during the total simulation time. The measurement unit of this index is kilobits per second (kbps) [30, 32, 56]. This index represents the efficiency and effectiveness of the routing method in receiving packets of the data by the sink node. The higher average throughput indicating a more effective and efficient routing protocol. The mathematical formula below is applied to determine this index [34, 57]:
-
2.
Average delay: This indicates the average time taken to successfully broadcast the data in the network from its source to the target node [32, 56, 58]. The delay index is composed of several delay components including buffering delay resulting from the route searching mechanism, queuing delay during the router interface line, delays resulting from the medium access control (MAC) retransmission time, propagation delay, and transmission delay. When this performance index indicates a lower delay in an experimental simulation of the routing approach, it means that better performance is achieved. This parameter of data packets can be evaluated based on the following mathematical representation [30, 32, 58]:
$$ Average\ end- to- end\ delay=\frac{\sum {}_{i=1}{}^{i=n}\left( Ri- Si\right)\ }{n} $$(17)
where Ri defines the time of the received packet, Si represents the time of the transmitted packet, and n is the number of packets.
-
3.
Packet delivery ratio: It shows the rate of data packets that successfully received at the destination with respect to the total number of data packets created at the source [29, 30, 32, 59]. A higher packet delivery ratio provides better reliability and performance of the routing protocol. The following formula is used to compute this parameter [17, 32, 59]:
$$ Packet\ delivery\%=\left(\sum received\ data\ packet/\sum transmitted\ data\ packet s\right)\times 100 $$(18) -
4.
Routing overhead ratio: This factor is defined as the rate between the total number of transmitted routing packets and the overall number of transmitted routing and data packets [30, 32]. The routing overhead ratio informs about the additional bandwidth expenditure through the overhead to deliver the data packets. It is calculated using the following equation [30, 32]:
$$ Routing\ overhead\%=\frac{\kern0.5em Number\ of\kern0.5em routing\ packets}{Number\ of\kern0.5em routing\ packets+ number\ of\kern0.5em data\kern0.5em packets}\kern0.5em \times 100 $$(19) -
5.
Average energy consumption: This performance index represents the rate of total energy depleted by each mobile node concerning the initial amount of energy. The amount of initial energy and the final remaining energy can be calculated when the simulation time has ended. When less energy consumed, the routing method will show better performance. The used formula to calculate this performance index is given as follows [30, 32]:
$$ Average\ energy\ consumption=\frac{\sum energy\ consumed}{\sum initial\ amount\ of\ energy}\times 100 $$(20)
3.3 Results discussion and analysis
In this section, the performance of the proposed MET-MFODSR algorithm will be evaluated and analyzed in comparison with the BEEDSR and BEEIP algorithms. The evaluation is performed in two different scenarios; the first scenario depicts the impact of the packet size variations and the second scenario presents the impact of the node speed variations. Furthermore, the convergence time of the proposed MET-MFODSR method was evaluated and analyzed with a dataset from a Community Resource for Archiving Wireless Data At Dartmouth (CRAWDAD) obtained from the outdoor runs of MANET [60].
3.3.1 Scenario 1: Packet size variations analysis
This scenario presents the effect of packet size variations on the performance indexes for MET-MFODSR, BEEDSR, and BEEIP. The behavior of MET-MFODSR, BEEDSR, and BEEIB have been analyzed by changing the packet size from 128 bytes to 1024 bytes, (i.e., 128, 256, 512, 1024 bytes), considering that there are 50 nodes in total.
Figure 4 shows variations in the average throughput for MET-MFODSR, BEEDSR, and BEEIP. For all three tested algorithms, the average throughput increases as the packet size increases. In MET-MFODSR, it increases from 200.3 to 255.2 kbps, the BEEDSR increases from 72.64 to 133.3 kbps, and the BEEIP increases from 26.09 to 121.9 kbps. The MET-MFODSR provides higher throughput than BEEDSR and BEEIP. This is because the application of the MET scheduling algorithm offers an advantage to the MET-MFODSR approach as it increases the delivery and the execution process of the packets through the neighboring nodes to the destination, which allows more packets to be delivered so that the throughput of the network will increase.
Figure 5 illustrates the changes in the average end-to-end delay with different packet sizes for MET-MFODSR, BEEDSR, and BEEIP. When the packet size increases, the average end-to-end delay will also increase for the three tested algorithms. The MET-MFODSR increases from 3.72 to 6.92 ms, the BEEDSR increases form 27.7 to 60.15 ms, and the BEEIP increases from 31.94 to 70.85 ms. The MET-MFODSR shows a better performance than BEEDSR and BEEIP for the average end-to-end delay factor. The reason behind that is that MET-MFODSR is based on the minimum hop count route and uses the MET scheduling algorithm to reduce the time taken to complete the packet processing on the node which leads to shorter average delays.
Figure 6 shows the impact of modifying the packet size on the packet delivery ratio for the three algorithms. Due to the packet size increment, the packet delivery ratio increases. This is because when the packet size increases, the amount of data delivered will also increase in the network. The results clearly show that the performance of MET-MFODSR exceeds both BEEDSR and BEEIP routing approaches, as MET-MFODSR decreases packet loss by utilizing the MET scheduling method to increase the delivery and execution of the packets through the neighboring nodes to the destination. Furthermore, the network connectivity is high due to the high number of nodes which minimize the probability of packet loss.
Figure 7 illustrates the impact of varying the size of packets on the routing overhead ratio for the MET-MFODSR, BEEDSR, and BEEIP algorithms. If the packet size increases, the routing overhead will also increase for the three compared algorithms. The MET-MFODSR has a lower routing overhead ratio compared to BEEDSR and BEEIP, and this is because in the MET-MFODSR method the data packet delivery rate through the route is much greater due to the MET packet scheduling approach.
Figure 8 depicts the impact of packet size variations on the average energy expenditure for the three approaches. It is observed that due to the packet size increment, the average energy expenditure will also increase for all algorithms. When the load of the packet increases on the network, more energy will be required to transmit and broadcast the packets. The MET-MFODSR has less energy consumption than BEEDSR and BEEIP; the reason behind that is that MET-MFODSR uses the minimum hop count route along with the MFO algorithm to optimize the route for data packet transfer with minimal energy expenditure.
3.3.2 Scenario 2: Node speed variation analysis
In this section, the aforementioned performance metrics of the proposed MET-MFODSR are evaluated and compared to BEEDSR and BEEIP. The speed of the mobile nodes was varied (5 m/s, 10 m/s, 15 m/s, 20 m/s), whereas a fixed number of 50 nodes was used.
Figure 9 demonstrates the impact of node speed variations on the average throughput for MET-MFODSR, BEEDSR, and BEEIP. The results clearly show that the average throughput decreases as the node speed increases. The MET-MFODSR provides higher throughput than BEEDSR and BEEIP. This is because the application of the MET scheduling algorithm offers an advantage to the MET-MFODSR approach as it increases the delivery and the execution process of the packets through the neighboring nodes to the destination, which allows more packets to be delivered, thus increasing the throughput of the network.
Figure 10 illustrates the change in the average delay for the three methods. As the speed of node increases by 0, 5, 10, 15, and 20 m/s, the average delay increases. The random motion of nodes creates an unstable topology of the network, which requires new nodes to be continuously discovered. This will increase the average end-to-end delay. The MET-MFODSR increase from 0.1709 to 14.17 ms, BEEDSR increases from 13.92 to 27.81 ms, and BEEIP increases from 37.11 to 37.98 ms. The MET-MFODSR shows less average delay in comparison with the other two methods. This is because it considers the minimum hop route and uses MET data packet scheduling to minimize the time taken to complete the data packet transmission.
Figure 11 indicates the changes in the packet delivery ratio for MET-MFODSR, BEEDSR, and BEEIP. As the node speed increases, the packet delivery ratio decreases due to unstable dynamic topology. The results clearly show that the MET-MFODSR provides a better performance compared to the BEEDSR and BEEIP approaches. The MET-MFODSR uses MET scheduling to increase the delivery and execution of the packet. This subsequently increases the packet delivery ratio. Besides, the high connectivity of the network due to the high number of mobile nodes reduces the probability of packet loss.
Figure 12 presents the impact of varying the speed of the node on the routing overhead ratio for MET-MFODSR, BEEDSR, and BEEIP. When the speed increases, the routing overhead ratio also increases for all three compared algorithms. The MET-MFODSR increases from 2.875 to 10.6%, the BEEDSR increases from 7.3 to 13.8%, and the BEEIP increases from 12 to 15.6%. The MET-MFODSR has a lower routing overhead ratio compared to the BEEDSR and BEEIP methods. This is because the MET-MFODSR algorithm uses the MET packet scheduling approach which increases the data packet delivery rate through the path compare to routing control packets. Therefore, the minimal routing overhead for MET-MFODSR has resulted.
Figure 13 depicts the effect of node speed variations on the average energy consumption for the proposed MET-MFODSR, BEEDSR, and BEEIP approaches. It can be observed that when the node speed increases, more energy is consumed. When the speed of node motion increases, route disconnectivity commonly occurs, which increases the message transmission for the route setup process, resulting in more consumption of energy. The proposed MET-MFODSR shows less average energy consumption in comparison to BEEDSR and BEEIP, which increases the network lifespan to achieve higher stability in MANETs. This is because the MET-MFODSR algorithm utilizes the MFO method to minimize the energy consumption for data routing in the network.
3.3.3 Convergence time evaluation
Convergence state appears in a dynamic routing environment as a result of frequent changes in the network topology. The frequent changes in the dynamic network topology causing a link failure or disconnectivity, which leads to the intermediate mobile nodes individually run the routing algorithm and recalculating the route and create updated routing tables according to the updated information. Therefore, convergence in the network is the state when all intermediate nodes consensus about the updated topology and optimal path to forward the packets, whereas the convergence time is the time interval required before all intermediate nodes reach the convergence state [61,62,63,64]. The convergence time of the proposed MET-MFODSR algorithm was evaluated with a dataset obtained from the Community Resource for Archiving Wireless Data At Dartmouth CRAWDAD [60]. The sample used dataset was gathered from the outdoor runs of MANET based on generated traffic logs as given in the CRAWDAD dataset [60]. Using this sample dataset, the convergence time of the proposed MET-MFODSR algorithm was evaluated to the node speed variations and the number of nodes as shown in Figs. 14 and 15, respectively.
Figure 14 indicates that as the speed of node increases, the convergence time will also increase and that is because in this case, there is a high chance of topology changing which leads to frequent routes re-establishing.
Figure 15 shows that the convergence time will increase as the number of nodes increases because when the number nodes increase, then the number of hops will increase leading to high congestion and the convergence will also increase. The proposed MET-MFODSR approach is achieving less convergence time which provides high link stability, low path failures, and high network lifetime.
4 Conclusions
This research proposed a novel and efficient version of the DSR approach named MET-MFODSR. The MET-MFODSR routing algorithm is based on the application of a hybrid approach using MET scheduling and MFO scheme. This improved version of DSR called the (MET-MFODSR) algorithm provides an improved routing mechanism by decreasing the energy consumption, which increases the network lifetime and reduces route failures issue. The simulation results for two different simulation environments displayed that the proposed MET-MFODSR approach provides better performance compared to BEEDSR and BEEIP in terms of average throughput, average end-to-end delay, packet delivery ratio, routing overhead ratio, and average energy consumption. Generally, the MET-MFODSR algorithm shows the highest average throughput and packet delivery ratio compared with the other two existing algorithms. Also, the MET-MFODSR shows less average end-to-end delay, routing overhead ratio, and average energy consumption in comparison to BEEDSR and BEEIP algorithms. The proposed MET-MFODSR approach is achieving less convergence time with the CRAWDAD dataset collected from outdoor runs of MANET
In terms of the scope of future work, this proposed routing algorithm can be tested and evaluated under a vehicular ad hoc network (VANET) environment and WSNs. Another suggestion is to apply this hybrid structure of MET scheduling and MFO algorithm with another routing approach to compare it with the proposed MET-MFODSR.
Availability of data and materials
Not applicable.
References
M. Conti, S. Giordano, Mobile ad hoc networking: milestones, challenges, and new research directions. IEEE Commun. Mag. 52(1), 85–96 (2014)
H. Simaremare, A. Abouaissa, R.F. Sari, P. Lorenz, Security and performance enhancement of AODV routing protocol. Int. J. Commun. Syst. 28(14), 2003–2019 (2015). https://doi.org/10.1002/dac.2837
P. Nithiyanandam, J. Sreemathy, Optimized dynamic source routing protocol for MANETs. Cluster Comput. 22(1), 12397–12409 (2019). https://doi.org/10.1007/s10586-017-1638-1
M. Abolhasan, T. Wysocki, E. Dutkiewicz, A review of routing protocols for mobile ad hoc networks. Ad Hoc Netw. 2(1), 1–22 (2004). https://doi.org/10.1016/S1570-8705(03)00043-X
D. Manickavelu, R.U. Vaidyanathan, Particle swarm optimization (PSO)-based node and link lifetime prediction algorithm for route recovery in MANET. EURASIP J. Wirel. Commun. Netw. 107, 1–10 (2014). https://doi.org/10.1186/1687-1499-2014-107
C.E. Perkins, Ad hoc networking, 1st edn. (Addison-Wesley, Boston, 2001)
A. Vasiliou, A.A. Economides, in 2006 International Telecommunications Symposium. MANETs for environmental monitoring (IEEE, Fortaleza, 2006), pp. 813–818
B. Kannhavong, H. Nakayama, Y. Nemoto, N. Kato, A. Jamalipour, A survey of routing attacks in mobile ad hoc networks. IEEE Wirel. Commun. 14(5), 85–91 (2007). https://doi.org/10.1109/MWC.2007.4396947
S. Taneja, A. Kush, A survey of routing protocols in mobile ad hoc networks. Int. J. Innov, Manag.Technol. 1(3), 279–285 (2010)
S.R. Malwe, N. Taneja, G.P. Biswas, Enhancement of DSR and AODV protocols using link availability prediction. Wirel. Pers. Commun. 97(3), 4451–4466 (2017). https://doi.org/10.1007/s11277-017-4733-y
M. Anand, T. Sasikala, M. Anbarasan, Energy efficient channel aware multipath routing protocol for mobile ad-hoc network. Concurrency Computat. Pract. Exper. 31(2), 1–13 (2018). https://doi.org/10.1002/cpe.4940
I. Chlamtac, M. Conti, J.-N. Liu, Mobile ad hoc networking: imperatives and challenges. Ad Hoc Netw. J. 1(1), 13–64 (2003). https://doi.org/10.1016/S1570-8705(03)00013-1
A. Boukerche, B. Turgut, N. Aydin, M.Z. Ahmad, L. Bölöni, D. Turgut, Routing protocols in ad hoc networks: a survey. Comput. Netw. 13(55), 3032–3080 (2011). https://doi.org/10.1016/j.comnet.2011.05.010
E.M. Royer, C.-K. Toh, A review of current routing protocols for ad-hoc mobile wireless networks. IEEE Personal Commun. Mag. 2(6), 46–55 (1999)
R. Shenbagapriya, N. Kumar, in IEEE International Conference on Information Communication and Embedded Systems (ICICES) - Chennai, India. A survey on proactive routing protocols in MANETs (2014), pp. 27–29
H. Yang, Z. Li, Z. Liu, A method of routing optimization using CHNN in MANET. J. Ambient Intell. Humanized Comput. 10(5), 1759–1768 (2019). https://doi.org/10.1007/s12652-017-0614-1
T. Clausen, P. Jacquet, Optimized link state routing protocol (OLSR). RFC 3626, 2003.
T. Clausen, C. Dearlove, P Jacquet, The optimized link state routing protocol version 2. RFC 7181, 2014.
Y. Harold Robinson, S. Balaji, E. Golden Julie, PSOBLAP: particle swarm optimization-based bandwidth and link availability prediction algorithm for multipath routing in mobile ad hoc networks. Wirel. Personal Commun. 106(4), 2261–2289 (2019). https://doi.org/10.1007/s11277-018-5941-9
A. Nasipuri, S.R. Das, in Proceedings Eight International Conference on Computer Communications and Networks. On-demand multipath routing for mobile ad hoc networks (IEEE, Boston, 1999), pp. 64–70
D.B. Johnson, D.A. Maltz, in Mobile Computing. Dynamic source routing in ad hoc wireless networks (Kluwer, Norwood, 1996), pp. 153–181
V.D. Park, J.P. Macker, M.S. Corson, in IEEE Military Communications Conference. Proceedings. MILCOM 98. Applicability of the temporally-ordered routing algorithm for use in mobile tactical networks (IEEE, Boston, 1998), pp. 426–430
C. Perkins, E. Royer, in Proceedings WMCSA'99. Second IEEE Workshop on Mobile Computing Systems and Applications. Ad-hoc on-demand distance vector (AODV) routing (IEEE, New Orleans, 1999), pp. 90–100
N. Harrag, A. Refoufi, A. Harrag, PSO-IZRP: new enhanced zone routing protocol based on PSO independent zone radius estimation. Int. J. Numerical Model. Electron. Netw. Devices Fields 32(1), 1–16 (2019). https://doi.org/10.1002/jnm.2461
P. Samar, M.R. Pearlman, Z.J. Haas, Independent zone routing: an adaptive hybrid routing framework for ad hoc wireless networks. IEEE/ACM Trans. Netw. 12(4), 595–608 (2004)
M. Jao-Ng, I.T. Lu, A peer-to-peer zone-based two-level link state routing for mobile ad hoc networks. IEEE J. Selected Areas Commun. 17(8), 1415–1425 (1999)
H. Cheng, J. Cao, A design framework and taxonomy for hybrid routing protocols in mobile ad hoc networks. IEEE Commun. Surveys Tuts. 10(3), 62–73 (2008)
N. Nikaein, C. Bonnet, N. Nikaein, in International Symposium on Telecommunications, IST. HARP: Hybrid ad hoc routing protocol (Eurecom, Teheran; 2001)
C.E. Perkins, in Proc. Ad Hoc Netw.. Ad hoc networking: an introduction (2001), pp. 20–22
A. Taha, R. Alsaqour, M. Uddin, M. Abdelhaq, T. Saba, Energy efficient multipath routing protocol for mobile ad-hoc network using the fitness function. IEEE Access 5, 10369–10381 (2017)
Z. Guo, S. Sheikh, C. Al-Najjar, H. Kim, B. Malakooti, Mobile ad hoc network proactive routing with delay prediction using neural network. Wirel. Netw. 16(6), 1601–1620 (2010). https://doi.org/10.1007/s11276-009-0217-7
M. Tareq, R. Alsaqour, M. Abdelhaq, M. Uddin, Mobile ad hoc network energy cost algorithm based on artificial bee colony, Wireless Communications and Mobile Computing, 1–14 (2017). https://doi.org/10.1155/2017/4519357
D.J. Rao, K. Sreenu, P. Kalpana, A study on dynamic source routing protocol for wireless ad hoc networks. Int. J. Adv. Res. Comput. Commun. Eng. 1(8), 2319–5940 (2012)
D. G. Zhang, S. Liu, T. Zhang, Y.-Y. Cui, , X.-H. Liu, Novel dynamic source routing protocol (DSR) based on genetic algorithm-bacterial foraging optimization (GA-BFO). Int. J. Commun. Syst., 31(18), 1–20 (2018). doi: https://doi.org/10.1002/dac.3824
S. Chatterjee, S. Das, Ant colony optimization based enhanced dynamic source routing algorithm for mobile ad-hoc network. Inform. Sci. 295, 67–90 (2015). https://doi.org/10.1016/j.ins.2014.09.039
T. Varshney, A. Katiyar, P. Sharma, in International Conference on Issues and Challenges in Intelligent Computing Techniques (ICICT), Ghaziabad. Performance improvement of MANET under DSR protocol using swarm optimization (2014), pp. 58–63. https://doi.org/10.1109/icicict.2014.6781253
S.M. Onyemelukwe, in Master Thesis, Electrical and Computer Engineering, University of Windsor. Evaluation of on-demand routing in mobile ad hoc networks and proposal for a secure routing protocol (2013)
D. Johnson, Y.Hu, D. Maltz, The dynamic source routing protocol (DSR) for mobile ad hoc networks for IPv4. RFC 4728, 2007
A. Giagkos, M.S. Wilson, BeeIP – a swarm intelligence based routing for wireless ad hoc networks. Inform. Sci. 265, 23–35 (2014). https://doi.org/10.1016/j.ins.2013.12.038
A. Pandey, A. Rajan, A. Nandi, in International Conference on Computing, Power and Communication Technologies (GUCON). Lifetime enhancement of wireless sensor networks by using MFO algorithm (IEEE, Greater Noida, 2018), pp. 868–872
N. Mittal, Moth flame optimization based energy efficient stable clustered routing approach for wireless sensor networks. Wirel. Pers. Commun. 104(2), 677–694 (2019). https://doi.org/10.1007/s11277-018-6043-4
A. Sufian, A. Banerjee, P. Dutta, in Industry Interactive Innovations in Science, Engineering and Technology. Survey of various real and non-real-time scheduling algorithms in mobile ad hoc networks (Springer, Singapore, 2018), pp. 121–133
H.D. Kim, J.S. Kim, in Grid and Cooperative Computing. GCC 2003. Lecture Notes in Computer Science, ed. by M. Li, X. H. Sun, Q. Deng, J. Ni. An online scheduling algorithm for grid computing systems, vol 3033 (Springer, Berlin, Heidelberg, 2004), pp. 34–39
D.N. Kanellopoulos, Recent progress on QoS scheduling for mobile ad hoc networks. JOEUC 31(3), 37–66 (2019)
N.I.M. Enzai, S.S. Rais, R. Darus, in Proc. Int. Conf. Comput. Appl. Ind. Electron.. An overview of scheduling algorithms in mobile ad-hoc networks (2010), pp. 120–124
B.C. Sherin, E.A.M. Anita, A survey of scheduling algorithms for wireless ad-hoc networks. Int. J. Adv. Sci. Eng. 4(4), 776–787 (2018). https://doi.org/10.29294/IJASE.4.4.2018.776-787
B.G. Chun, M. Baker, Evaluation of packet scheduling algorithms in mobile ad hoc networks. Mob. Comput. Commun. Rev. 6(3), 36–49 (2002)
M. Hemamalini, M.V. Srinath, Performance analysis of balanced minimum execution time grid task scheduling algorithm. Int. J. Commun. Netw. Syst. 5(1), 96–100 (2016)
S.H.H. Madni, M.S.A. Latiff, M. Abdullahi, S.M. Abdulhamid, M.J. Usman, Performance comparison of heuristic algorithms for task scheduling in IaaS cloud computing environment. PLoS One 12(5), e0176321 (2017). https://doi.org/10.1371/journal.pone.0176321
F. Cottet, J. Delacroix, C. Kaiser, Z. Mammeri, Scheduling in real time systems, 1st edn. (Wiley, Chichester, 2002)
S. Mirjalili, Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 89, 228–249 (2015). https://doi.org/10.1016/j.knosys.2015.07.006
M. Shehab, L. Abualigah, H. Al Hamad, H. Alaboo, M. Alshinwan, A.M. Khasawneh, Moth–flame optimization algorithm: variants and applications. Neural Comput. Applic. (2019). https://doi.org/10.1007/s00521-019-04570-6
Y.A. Shah, H.A. Habib, F. Aadil, M.F. Khan, M. Maqsood, T. Nawaz, CAMONET: moth-flame optimization (MFO) based clustering algorithm for VANETs. IEEE Access 6, 48611–48624 (2018)
S. Kumari, P.K. Mishra, V. Anand, Fault resilient routing based on moth flame optimization scheme for underwater wireless sensor networks. Wirel. Netw. 26(2), 1417–1431 (2020). https://doi.org/10.1007/s11276-019-02209-x
M.Y. Durrani, R. Tariq, F. Aadil, M. Maqsood, Y. Nam, K. Muhammad, Adaptive node clustering technique for smart ocean under water sensor network (SOSNET). Sensors 19(5), 1145 (2019)
X. Hu, J. Wang, C. Wang, Mobility-adaptive routing for stable transmission in mobile ad hoc networks. J. Commun. 6(1), 79–86 (2011)
D. Johnson, D. Maltz, , J. Broch, DSR: the dynamic source routing protocol for multi-hop wireless ad hoc networks, In: C.E. Perkins (Ed.), Ad Hoc Networking, Addison-Wesley, Reading, 2001, pp. 139–172.
R.K. Gujral, J. Grover, S. Rana, in 2012 International Conference on Computing Sciences. Impact of transmission range and mobility on routing protocols over ad hoc networks (IEEE, Phagwara, 2012), pp. 201–206
S. Ali, S.A. Madani, A.U.R. Khan, A.K. Imran, Routing protocols for mobile sensor networks: a comparative study. Int. J. Comput. Syst. Sci. Eng. 29(2), 183–192 (2014)
R.S. Gray, D. Kotz, C. Newport, N. Dubrovsky, A. Fiske, J. Liu, C. Masone, S. McGrath, Y. Yuan, CRAWDAD dataset dartmouth/outdoor (v. 2006-11-06) (2006). https://doi.org/10.15783/C7301Z downloaded from https://crawdad.org/dartmouth/outdoor/20061106
Omnisecu.com, What is convergence of routing tables and what is convergence time, https://www.omnisecu.com/cisco-certified-network-associate-ccna/what-is-convergence-of-routing-tables.php. Accessed 17 Mar 2020.
InfoWorld, Routing toward the future. 19(36), 1997.
S.A. Kumar, S.M. Rajan, Convergence routing analysis in IPv6 networks. IOSR-JECE. 1:18–24 (2016)
V. Tilwari, K. Dimyati, M. Hindia, A. Fattouh, I. Amiri, Mobility, residual energy, and link quality aware multipath routing in MANETs with Q-learning algorithm. Appl. Sci. 9(8), 1582 (2019). https://doi.org/10.3390/app9081582
Acknowledgements
Not applicable.
Funding
The authors received no specific funding for this work.
Author information
Authors and Affiliations
Contributions
Conceptualization, S.A.; methodology, S.A.; software, S.A.; writing—original draft preparation, S.A.; review and editing, B.B; Supervision, B.B. The authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Almazok, S.A., Bilgehan, B. A novel dynamic source routing (DSR) protocol based on minimum execution time scheduling and moth flame optimization (MET-MFO). J Wireless Com Network 2020, 219 (2020). https://doi.org/10.1186/s13638-020-01802-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-020-01802-5