- Research Article
- Open access
- Published:
Novel Heuristics for Cell Radius Determination in WCDMA Systems and Their Application to Strategic Planning Studies
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 314814 (2009)
Abstract
We propose and compare three novel heuristics for the calculation of the optimal cell radius in mobile networks based on Wideband Code Division Multiple Access (WCDMA) technology. The proposed heuristics solve the problem of the load assignment and cellular radius calculation. We have tested our approaches with experiments in multiservices scenarios showing that the proposed heuristics maximize the cell radius, providing the optimum load factor assignment. The main application of these algorithms is strategic planning studies, where an estimation of the number of Nodes B of the mobile operator, at a national level, is required for economic analysis. In this case due to the large number of different scenarios considered (cities, towns, and open areas) other methods than simulation need to be considered. As far as we know, there is no other similar method in the literature and therefore these heuristics may represent a novelty in strategic network planning studies. The proposed heuristics are implemented in a strategic planning software tool and an example of their application for a case in Spain is presented. The proposed heuristics are used for telecommunications regulatory studies in several countries.
1. Introduction
Mobile communications field is, nowadays, one of the most relevant technology research topics. Its fast evolution, from analog (like Advance Mobile Phone System), to digital systems (like Global Systems for Mobile (GSM) Communications or IS-95), and currently to 3G multiservice systems, such as Universal Mobile Telecommunication Systems (UMTSs) and 4G Long Term Evolution (LTE), has required the development of new technics, and produced the convergence of several telecommunication research areas. On the other hand, the high level of acceptance of the mobile technologies by customers (see Figure 1), and their need of new and more complex services, is a catalytic element for doing research to obtain more efficient technics in mobile communications.
The general architecture of a mobile network may be described in the same way as the traditional fixed network; it is formed by an access network and a backbone network. The access network is named Base Station Subsystem (BSSs) in 2G systems like GSM, and UMTS Terrestrial Radio Access Network (UTRAN) in 3G systems like UMTS. The backbone network corresponds to Network Switching Subsystems in GSM and to the Core Network in UMTS. Figure 2 shows an example of these architectures.
One critical problem in mobile network design is the determination of the cell radius [1]. The underestimation of the cell radius leads to an overestimation of the number of Base Stations (BTS) required to provide service in an specific area, and hence excessive deployment investment costs. This is obviously bad news for the business of the network operator. On the other hand, an overestimation of the cell radius results in the installation of fewer BTSs than needed, and then in shadow areas. This means the network operator provides bad Quality of Service (QoS) in terms of coverage, and customers will complain.
Most of second generation systems, like GSM, use Time Division Multiple Access (TDMA) as radio access technology and therefore, they can be defined as hard blocking systems, that is, the number of users in the system is limited by the amount of hardware installed in the Base Station (BTS). Therefore, in GSM systems, the cell radius is mainly determined by the coverage planning (in this paper the term coverage refers to radio propagation coverage). In case that the QoS required (expressed as the blocking probability) is not fulfilled, the network operator must install more electronic equipment to incorporate more traffic channels to the BTS. It is a relatively simple task in TDMA systems.
Most of third generation systems, like UMTS, are based on WCDMA. These are soft blocking systems, where the number of users is not limited by the amount of channels in the BTS, but by the interference generated by their own users, and the users in neighbor cells. The maximum interference allowed in the system can be measured by a parameter named interference margin, which is used in the calculation of the link budget at the coverage planning process, and also to calculate the maximum number of users in the capacity planning process. Note that there is a tight relationship between the capacity and coverage planning processes in this case. Furthermore, the design of 2G systems is mainly oriented to the voice service [2], but 3G systems are designed to handle traffic from different sources, with different bit rates and, obviously, different requirements in terms of Grade and Quality of Service [3]. It is straightforward that this issue increases the planning complexity.
Cell radius calculation in WCDMA systems has been extensively studied before in the literature [4–8]. However, most of these models only consider a single service, which may result in a nonaccurate estimation of the cell radius in multiservice environments. In addition the studies of multiservice environments are usually based on simulation [9, 10], which requires a large set of input parameters. Moreover, user and service simulation models are usually quite complex. As we will see in the body of the paper, the problem of the cell radius determination in WCDMA systems is equivalent to a problem of capacity assignment among different services. Another approach to this complex problem starts from the cell radius, and finds the optimal capacity assignment to the services [11] or to study the maximum throughput.
Currently most operators are deploying their 3G and beyond networks in order to offer high speed data services to their customers. Furthermore in developing countries, or in some rural areas where the 2G deployment is not completely finished, the operators are studying whether implement a proper 3G infrastructure or subcontract it to the dominant operator. Note that a very relevant factor in this decision will be the price that the dominant operator establishes, which may be sometimes conditioned by the National Regulatory Authority (NRA). The determination of the interconnection, roaming or termination price must be based on technoeconomic studies under the so-called Bottom-Up Long Run Incremental Cost model (LRIC) [12, 13] which is recommended by the European Union [14]. The objective of the LRIC is to estimate the costs incurred by an hypothetical operator with the same market power of the operator under study, that tries to implement his network with the best suitable technology. To do this, a complete design of the network has to be done at a national level, that is, to calculate the network equipment for each city, town, rural area, highway, road, and so on. Based on this, the mobile operator will have enough information to make the decision about built or buy, and/or to claim to the NRA with objective data to obtain better price.
It is straightforward that constructing a LRIC model requires the calculation of a large number of different scenarios, where the cell radius of the Nodes B (the 3G Base Stations), has to be estimated. Therefore the heuristic model used for this estimation has to be general enough to be applied to a large set of scenarios with a reduced set of parameters, so simulation is not valid. Furthermore, note that obtaining a good LRIC model for a country involves thousands of B Nodes, so the heuristics applied must be computational efficient. Thus, modern heuristics as evolutionary computation are limited approach in this case. Finally the selected calculation method has to be able to provide a fair estimation of the cell radius.
This paper proposes several novel algorithmic approaches to the cell radius determination problem under the constraints presented previously. Our approach starts from a multiservice scenario and the maximum capacity of the cell, and based on the services parameters we obtain the optimal capacity assignment for each service, and then, as final objective, we obtain the optimal cell radius. We propose the following heuristics. First, an iterative load factor reassignment heuristic is presented, which is able to solve the problem giving encouraging results. An analytical algorithm is also proposed and compared with the iterative heuristic. Finally, a combination of both algorithms is also tested, where the analytical approach is used to generate an initial solution for the iterative approach. We will show the performance of our approaches in several test problems considering WCDMA multiservice scenarios. With the proposed heuristics we fulfil all the requirements defined in the paragraph previously, that is, a fast procedure that is able to provide good estimations of the cell radius using a limited set of input parameters, and hence easy to use in different scenarios.
The rest of the paper is structured as follows. Next section defines the cell radius determination problem in WCDMA networks. In Section 3 we propose the heuristics for solving the problem, and in Section 4 we show the performance of the heuristics proposed by performing some experiments in WCDMA multiservice scenarios. We also present the implementations of our heuristics in a software tool named DIDERO and their applications in different regulatory projects. Section 6 concludes the paper giving some final remarks.
2. Cell Radius Determination in WCDMA Networks
Let us consider a 3G mobile network based on WCDMA technology, where the mobile operator provides a set of  services (voice, data 16 kbps, data 64 kbps, etc.) each one defined by a set of parameters
services (voice, data 16 kbps, data 64 kbps, etc.) each one defined by a set of parameters  (binary rate, user density, quality of service, etc.). The mobile operator needs to have an estimation of the number of B Nodes in each area and thus it is required to calculate the cell radius for each B Node. As it is mentioned in the introduction, cell radius determination in WCDMA is a complicated process because, opposite to TDMA, the number of users and the total throughput is limited by the amount of interference in the radio interface. Of course, this interference not only limits the capacity of the system, but also the coverage by propagation, because the total noise in the system increases as more users are active.
(binary rate, user density, quality of service, etc.). The mobile operator needs to have an estimation of the number of B Nodes in each area and thus it is required to calculate the cell radius for each B Node. As it is mentioned in the introduction, cell radius determination in WCDMA is a complicated process because, opposite to TDMA, the number of users and the total throughput is limited by the amount of interference in the radio interface. Of course, this interference not only limits the capacity of the system, but also the coverage by propagation, because the total noise in the system increases as more users are active.
Propagation coverage studies mainly imply two steps. The first one is to calculate the maximum allowed propagation loss in the cell, defined here as  , and the second is to use an empirical propagation method to calculate the cell radius for this pathloss. Typical methods are the Okumura Hata COST 231 model, [15], or the Walfish and Bertoni [16].
, and the second is to use an empirical propagation method to calculate the cell radius for this pathloss. Typical methods are the Okumura Hata COST 231 model, [15], or the Walfish and Bertoni [16].
The value of  is calculated using a classical link budget equation
is calculated using a classical link budget equation

where  is the transmitter power,
is the transmitter power,  is the sum of all gains in the chain, transmitter antenna, receiver antenna, and soft handover gain,
is the sum of all gains in the chain, transmitter antenna, receiver antenna, and soft handover gain,  is the sum of all the losses in cables, body losses, and in-building losses,
is the sum of all the losses in cables, body losses, and in-building losses,  is the receiver sensitivity which includes the required
is the receiver sensitivity which includes the required  , thermal noise, receiver noise figure, and processing gain, and finally,
, thermal noise, receiver noise figure, and processing gain, and finally,  is the different margins we need to take into account, fast fading margin, log-normal fading margin, and the interference margin,
is the different margins we need to take into account, fast fading margin, log-normal fading margin, and the interference margin,  . This interference margin is a very relevant value, because it measures the maximum interference allowed in the system due to its own users. Therefore this value indirectly limits the maximum number of users in the system. Note that all the parameters in (1) are inputs of the system and therefore
. This interference margin is a very relevant value, because it measures the maximum interference allowed in the system due to its own users. Therefore this value indirectly limits the maximum number of users in the system. Note that all the parameters in (1) are inputs of the system and therefore  can be obtained from this equation.
can be obtained from this equation.
As it was mentioned before the cell radius by propagation is obtained applying the  into an empirical propagation method. In our work we have used the 231-Okumura Hata model because it is broadly considered as the most general one in mobile networks applications [17]
into an empirical propagation method. In our work we have used the 231-Okumura Hata model because it is broadly considered as the most general one in mobile networks applications [17]

where  is the frequency in MHz,
is the frequency in MHz,  is the height of the Node B in meters,
is the height of the Node B in meters,  is the height of the mobile user in meters, and
is the height of the mobile user in meters, and  is the cell radius by propagation in Km. Note that
is the cell radius by propagation in Km. Note that  and
and  are parameters defined in the COST 231 specification. They provide the influence of the height of mobile terminal and the type of city, respectively, and they are defined as follows:
are parameters defined in the COST 231 specification. They provide the influence of the height of mobile terminal and the type of city, respectively, and they are defined as follows:

Note that as the value of  changes for the different services, the propagation coverage study has to be done specifically for each one, and of course for the uplink and the downlink. Therefore the formulation explained previously, and the value
changes for the different services, the propagation coverage study has to be done specifically for each one, and of course for the uplink and the downlink. Therefore the formulation explained previously, and the value  , has to be applied for each service
, has to be applied for each service  and each direction (Uplink (UL) and Downlink (DL)) obtaining a set of two vectors containing, for each service, the cell radius by propagation, (
and each direction (Uplink (UL) and Downlink (DL)) obtaining a set of two vectors containing, for each service, the cell radius by propagation, ( and
and  )
)

Now we focus on capacity studies. As it is done in propagation studies, cell radius must be calculated independently for the uplink and the downlink. The equations that determines the radius in both directions are quite similar. Then for simplicity reasons, this paper focuses in the calculation of the cell radius for the downlink case, since this is the most restrictive direction [18–20].
The interference margin used in (1) determines the maximum load of the cell,  , by means of the following relation, [18, 21]
, by means of the following relation, [18, 21]

This factor indicates the load of the cell. If  there is no user in the system. On the opposite if
there is no user in the system. On the opposite if  , the amount of interference in the system grows to
, the amount of interference in the system grows to  and hence the system goes to an unstable state. Therefore typical values of the
and hence the system goes to an unstable state. Therefore typical values of the  are between 3 and 6 dB, which means a load of 0.5–0.75.
are between 3 and 6 dB, which means a load of 0.5–0.75.
Although in the real operation of the system, there is no capacity reservation between the different services, in the dimensioning process it is required to allocate part of the capacity to each service. Therefore the load factor, that is, the capacity of the cell, must be allocated to the different services, resulting the load factors of the each service 

The number of active connections of each service is calculated by dividing the total load factor of each service type  over the average individual downlink load factor of the connections of the service
over the average individual downlink load factor of the connections of the service

where the downlink load factor is defined by the following equation:

where  is the so-called downlink orthogonality factor,
is the so-called downlink orthogonality factor,  is the binary rate,
is the binary rate,  is the so-called activity factor of the service
is the so-called activity factor of the service  ,
,  is the average intercell interference factor, and
is the average intercell interference factor, and  is the bandwidth of the WCDMA system.
is the bandwidth of the WCDMA system.
The total offered traffic demand,  in Erlangs, is obtained by using the inversion of the Erlang B Loss formula [22]. The inputs for this algorithm are the maximum number of active connections in the cell
in Erlangs, is obtained by using the inversion of the Erlang B Loss formula [22]. The inputs for this algorithm are the maximum number of active connections in the cell  and the Quality of Service (QoS) of the service expressed by the blocking probability
and the Quality of Service (QoS) of the service expressed by the blocking probability 

Note that in (9) the total offered traffic demand,  , is divided by the factor
, is divided by the factor  and the maximum number of active connections,
and the maximum number of active connections,  , of the service
, of the service  is multiplied by it. This is included to considerer the soft blocking feature inherent to the WCDMA system, [23].
is multiplied by it. This is included to considerer the soft blocking feature inherent to the WCDMA system, [23].
Multiservice traffic in UMTS has been extensively studied in the literature [24]. However in the strategic planning mobile operators trend to use simplified models that provides under estimations of the cell capacity to be in the safe side when they estimate the number of Node B's to provide service to the customers in the area under study, [25]. Because of the reasons stated in the previous sentence, in this proposal we use the Erlang B formulation. However it is and independent part that can be substituted by any other traffic model formulation.
The number of users in the cell ( ) is obtained from the division of the total offered traffic demand for service i, (
) is obtained from the division of the total offered traffic demand for service i, ( in Erlangs), by the individual traffic of a single user of this service (obtained from the connection rate
in Erlangs), by the individual traffic of a single user of this service (obtained from the connection rate  and the mean service time
and the mean service time  ):
):

The cell radius for each individual service is calculated as a function of the number of sectors in the BTS,  , the number of users of service i per sector
, the number of users of service i per sector  and the user density
and the user density  as follows (note that a Node B may be divided into several sectors. Each sector corresponds to a cell):
as follows (note that a Node B may be divided into several sectors. Each sector corresponds to a cell):

Note that this process has to be done also for the uplink direction (UL). Therefore, at the end we have obtained another set of two vectors (one for the uplink and one for the downlink), with the cell radius by capacity of each service:

Note that the values of  and
and  largely depend on the distribution of the capacity over the different services by means of the total load factor allocated to each service
largely depend on the distribution of the capacity over the different services by means of the total load factor allocated to each service  and
and  . A bad allocation will lead to large differences in the values of the radius, while an equilibrated one will produce approximately the same value for all the
. A bad allocation will lead to large differences in the values of the radius, while an equilibrated one will produce approximately the same value for all the  services.
services.
Note that at the end of this process we have obtained a set of four vectors,  ,
,  ,
,  , and
, and  . The final cell radius,
. The final cell radius,  will be the minimum value between
will be the minimum value between  and
and  which represents the most restrictive cell radius under propagation and traffic criteria respectively
which represents the most restrictive cell radius under propagation and traffic criteria respectively

As a conclusion of this section we have identified two problems in the cell radius dimensioning, that can be named outer problem and inner problem, as it is shown in Figure 3.
-
(1)
The outer problem is to find the best value for the Interference Margin,
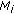 . This will be the value when the cell radius by capacity (traffic),
. This will be the value when the cell radius by capacity (traffic),  , is the same as by propagation,
, is the same as by propagation, 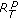 .
. -
(2)
The inner problem that is to find the best capacity allocation, given a value of the
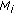 over the complete set of services
over the complete set of services 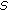 . With this the cell radius by capacity,
. With this the cell radius by capacity,  , is maximized.
, is maximized.
The outer problem is solved just making an iterative process to equilibrate the value of the cell radius between the resulting value calculated by propagation studies and the resulting one calculated by capacity studies. This is done by means of increasing the value of the interference margin,  , when the cell radius by propagation is higher than by capacity or vice versa. The inner problem is much more complicated because it implies the use of the traffic concepts and nonlinear process which underlies to (9)–(12).
, when the cell radius by propagation is higher than by capacity or vice versa. The inner problem is much more complicated because it implies the use of the traffic concepts and nonlinear process which underlies to (9)–(12).
This paper focuses on the design of heuristics for solving the inner problem (from now on we will focus on the donwlink direction, we therefore do not include the DL subindex in the formulation since it is assumed). With the definitions given before, the cell radius determination problem by capacity criterium can be defined as follows:
Find  , such that
, such that

which maximizes  . Note that we focus on the inner problem, where the traffic is the most restrictive factor, therefore,
. Note that we focus on the inner problem, where the traffic is the most restrictive factor, therefore,  in this case.
in this case.
Note that if we allocate optimally the capacity to the services, by means of the  values, the cell radius of all service will have almost the same value, and hence the cell radius by capacity will be maximized. Note that a suboptimal allocation leads to very different values of the cell radius of the different services, and hence to a bad estimation of the final radius. This situation is shown in Figure 4, where the dashed red arrow determines the final cell radius.
values, the cell radius of all service will have almost the same value, and hence the cell radius by capacity will be maximized. Note that a suboptimal allocation leads to very different values of the cell radius of the different services, and hence to a bad estimation of the final radius. This situation is shown in Figure 4, where the dashed red arrow determines the final cell radius.
3. Proposed Heuristics
3.1. Iterative Load Factor Redistribution Heuristic
This first heuristic we propose for the cell radius determination problem starts from an initial load factor assignment, usually provided by estimations of the network planner [7]. From this initial assignment  , we can calculate an initial solution for the cell radius using (7) to (11). If this initial cell radius is not the optimal one, the only service which is using its total capacity is the one with minimum value of
, we can calculate an initial solution for the cell radius using (7) to (11). If this initial cell radius is not the optimal one, the only service which is using its total capacity is the one with minimum value of  associated. The following example shows it in detail.
associated. The following example shows it in detail.
Let us consider a scenario with three services,  voice at 12.2 Kbps,
voice at 12.2 Kbps,  data at 64 Kbps and
data at 64 Kbps and  data at 144 Kbps. Let us also consider that a initial load factor assignment is
data at 144 Kbps. Let us also consider that a initial load factor assignment is  . With this, the values of the cell radius are
. With this, the values of the cell radius are  meters. Note that the limiting value is the cell radius of the first service
meters. Note that the limiting value is the cell radius of the first service  , that is 343 meters. With this value of the cell radius
, that is 343 meters. With this value of the cell radius  , the load factors that the services are really using are
, the load factors that the services are really using are  . So it is obvious that the initial load factor assignment is not correct, because we are not optimizing the cell usage (note that this example is a hard simplification of the complete process).
. So it is obvious that the initial load factor assignment is not correct, because we are not optimizing the cell usage (note that this example is a hard simplification of the complete process).
Note that the rest of the services will use less capacity than they have initially assigned. Let us call this capacity as  . Therefore, there is some remaining capacity,
. Therefore, there is some remaining capacity,  defined as
defined as

This remaining capacity has to be redistributed over the considered services, so that a new cellular radius can be calculated using (11). This will produce new values of  . This iterative process is followed until the difference between two consecutive cell radius is less than a given threshold
. This iterative process is followed until the difference between two consecutive cell radius is less than a given threshold  , usually
, usually  .
.
Several procedures can be applied for the  distribution over the different services. The simplest one is to find the balanced distribution of
distribution over the different services. The simplest one is to find the balanced distribution of  among all services in the system. This method leads, however, to suboptimal solutions, since the service with the most restrictive cell radius in one assignment is kept again as the most restrictive one in the new assignment. A better distribution can be obtained by assigning a larger part of the exceeding load factor,
among all services in the system. This method leads, however, to suboptimal solutions, since the service with the most restrictive cell radius in one assignment is kept again as the most restrictive one in the new assignment. A better distribution can be obtained by assigning a larger part of the exceeding load factor,  , to the service
, to the service  with most restrictive cell radius,
with most restrictive cell radius,  , by means of a prioritizing factor
, by means of a prioritizing factor  (
( ), and a balanced division among the rest of services:
), and a balanced division among the rest of services:

The value of the prioritizing factor,  , depends on the differences of the values of the cell radius of the different services. If the difference
, depends on the differences of the values of the cell radius of the different services. If the difference  -
- is large the value of
is large the value of  will be near to
will be near to  ; otherwise, it will be near to
; otherwise, it will be near to  .
.
The main drawback of this method is the dependency on the initial solution, that is, the dependency on the initial load factor assignment. Note also that the convergence of the algorithms depends on how the remainder capacity (given by  ) is distributed over the different services. A poor distribution procedure may result in a high number of iterations or even may fail to find the solution.
) is distributed over the different services. A poor distribution procedure may result in a high number of iterations or even may fail to find the solution.
3.2. The Reduced Algorithm
The second approach we propose to solve the cell radius determination problem is to find a mathematical model, which calculates an accurate value of the cell radius, under any service scenario and any initial conditions, expressed in terms of the load factor  and the parameters of the services
and the parameters of the services  .
.
The proposed model is named reduced algorithm, since it reduces all the services in the system to a single artificial service to solve the problem. The method starts considering an arbitrary cell radius, typically  . Then, the model calculates the total traffic demand offered to the cell,
. Then, the model calculates the total traffic demand offered to the cell,  , for each service
, for each service  , by means of the user density of each service,
, by means of the user density of each service,  , the individual call rate,
, the individual call rate,  , and the mean call duration,
, and the mean call duration,  .
.
The reduction of the set of services to a unique artificial/equivalent one is performed by a procedure based on a proposal of Lindberger for ATM networks [28]. This proposal is obviously extended to the singularities of the WCDMA cell design. The artificial service is defined in terms of equivalent parameters: binary rate,  , call rate,
, call rate,  , mean call duration,
, mean call duration,  , blocking probability,
, blocking probability,  , activity factor,
, activity factor,  and user density,
and user density,  . Following the Lindberger formulation, the parameters of the artificial service are calculated on the basis of the traffic,
. Following the Lindberger formulation, the parameters of the artificial service are calculated on the basis of the traffic,  , and the binary rate,
, and the binary rate,  , of each service
, of each service  considered in the scenario. The complete set parameters are defined by the following equations:
considered in the scenario. The complete set parameters are defined by the following equations:

Considering this new artificial service, the reduced method calculates a corresponding value of the cell radius,  , assigning the whole load factor,
, assigning the whole load factor,  , to the artificial service. From the obtained
, to the artificial service. From the obtained  , the load factors for each individual service,
, the load factors for each individual service,  , can be calculated inverting the cell radius calculation process shown in Section 2, see [18, 21] which is summarized as follows. From the
, can be calculated inverting the cell radius calculation process shown in Section 2, see [18, 21] which is summarized as follows. From the  , it is possible to calculate the maximum number of users of each service
, it is possible to calculate the maximum number of users of each service  per sector, and hence the total traffic offered to the system. Using the Erlang formula, with the blocking probability,
per sector, and hence the total traffic offered to the system. Using the Erlang formula, with the blocking probability,  , the number of active connections,
, the number of active connections,  , of each service
, of each service  is obtained. Finally the value
is obtained. Finally the value  is calculated by means of the individual load factor of the service,
is calculated by means of the individual load factor of the service,  , times the number of active connections,
, times the number of active connections,  .
.
The total load factors of each service are obtained by simple reduction to the whole load factor,  ,
,

Considering these values of the load factors, a new solution of the cell radius for each individual service is calculated following the process in Section 2, obtaining the solution vector, which minimum value is the cell radius.
3.3. Combined Heuristic
The third heuristic we consider is to find the hybridization of the two algorithms previously described. The reduced algorithm, which does not require an initialization of the load factors, is used for calculating the starting point for the Iterative load factor redistribution heuristic. Thus, it is expected a better performance of the iterative heuristic since it starts from a better initial solution.
4. Computational Experiments and Results
In order to validate the heuristics presented in this paper, we have tested them in several experiments based on scenarios with different service combinations. Specifically, we have defined mixtures of two, three and four services, each one having its own requirements in terms of binary rate, quality of service, user movement speed and user density in the area under study. Furthermore we have modified the traffic figures of the services to consider balanced and unbalanced traffic. Balanced traffic means that the individual throughput of each service is similar to the throughput of the other services.
We have used an interference margin of 6 dB which means a cell load factor of 0.75. We have also configured the radio propagation parameters to make the capacity the most restrictive criteria. This set of radio propagation parameters is shown in Table 1.
The parameters  of the different services
of the different services  are shown in Table 2, with
are shown in Table 2, with  being the binary rate,
being the binary rate,  the user speed in Km/h (services in which users have different speeds can be considered as different services. This is because they have different values of
the user speed in Km/h (services in which users have different speeds can be considered as different services. This is because they have different values of  and therefore different values of individual load factor
and therefore different values of individual load factor  ),
),  the bit energy-to-noise ratio in the downlink,
the bit energy-to-noise ratio in the downlink,  the orthogonality factor and
the orthogonality factor and  the activity factor. The quality of service is defined by the Blocking/Loss probability
the activity factor. The quality of service is defined by the Blocking/Loss probability  . The value of the total downlink load factor,
. The value of the total downlink load factor,  , is 0.75 according to the
, is 0.75 according to the  previously defined. Finally, the value of the average intercell interference factor
previously defined. Finally, the value of the average intercell interference factor  to 0.88 [29].
to 0.88 [29].
As we have mentioned before the complete set of scenarios are divided into balanced and unbalanced traffic scenarios. Tables 3 and 4 provides the traffic figures for the different services in these two general categories. In this case  and
and  are the call attempt rate and the service time in the business hour, respectively, and
are the call attempt rate and the service time in the business hour, respectively, and  is the user density in the considered area. Table 5 shows the combination of the services involved in each experiment. Note that the third column in the table shows if the experiment is based on balanced (B) or unbalanced (U) traffic.
is the user density in the considered area. Table 5 shows the combination of the services involved in each experiment. Note that the third column in the table shows if the experiment is based on balanced (B) or unbalanced (U) traffic.
The results of the different experiments are shown in Table 6 and Figure 5. For the iterative and combined algorithms, Table 6 also shows the number of iterations. The reduced algorithm obtains the optimal value of the cell radius in all experiments, excluding those scenarios in which users are moving at different speeds. This low performance of the reduced algorithm is due to the fact that the differences in the individual load factors of a service with different user speeds are very small. Therefore the algorithm is not able to distinguish between them.
As it was mentioned in Section 2, the optimum value of the cell radius is obtained when there are quite small differences in the cell radius of the different services. We will illustrate this in Experiment  . In this experiment, we have compared the results obtained by the three heuristics proposed against the cell radius calculated with an assignment done using the binary rate and the user density, let us name it free assignment (FA) following the equation
. In this experiment, we have compared the results obtained by the three heuristics proposed against the cell radius calculated with an assignment done using the binary rate and the user density, let us name it free assignment (FA) following the equation

The initial values of the load factors  are
are  for the service
for the service  , voice,
, voice,  for
for  , data 64 Kbps and
, data 64 Kbps and  for
for  , data 144 Kbps. The results for the downlink cell radius per traffic are shown in Table 7.
, data 144 Kbps. The results for the downlink cell radius per traffic are shown in Table 7.
Note that the cell radius of each service is quite similar in the three proposed heuristics but in the FA the cell radius of the  is almost 50% larger than
is almost 50% larger than  .
.
Another interesting point to observe is the final occupancy level of the load factor. In case of an optimal allocation, the sum of the individual load factors, allocated to the services after the cell radius is calculated has to tend to the limit established in the design, in our experiments  . The results are shown in Table 8. Note that the proposed heuristics use more than 99% of the total available capacity, while the FA only uses 62%.
. The results are shown in Table 8. Note that the proposed heuristics use more than 99% of the total available capacity, while the FA only uses 62%.
Finally note that the combined algorithm always obtains the optimal value even in scenarios with different users speeds, and it requires fewer number of iterations than the iterative algorithm. Figure 6 shows a comparison of the number of iterations needed to obtain the optimum cell radius in problem Exp-5. Note that the combined heuristic obtains the optimum cell radius faster than the iterative algorithm, since it starts from the result obtained by the Reduced heuristic.
Finally, regarding the computation time, the three algorithms we propose in this paper for the cell radius determination problem obtain the solution to the problem in less than 1 second. This is a very important point for the inclusion these algorithms in a strategic network planning tool, where a large number of scenarios have to be calculated.
4.1. Validation and Limitations of the Proposed Heuristics
In order to validate our heuristics we have compared the combined algorithm (the one that yields better results in the previous experiments), with the results in [26, 27]. In [26] the authors study the cell radius with three different combination of services as it is shown in Table 9. In [26] the capacity study is not based on a customer basis but considering the total bandwidth offered to the cell. This means that there is no significative impact of service combination in the cell radius. This is not completely accurate, because the service combination and the customer distribution all over the cell have a major relevance in the cell radius. However, the experimental frame given in [26] can be useful for benchmarking purposes. Thus, in order to apply our combine heuristic to the problems in [26] we have used the configuration parameters as the ones given in [26], specifically, the interference margin ( ) has been fixed to 4.31 dB.
) has been fixed to 4.31 dB.
The comparison results are shown in Table 10. Note that in service combination Mix 1 and Mix 2 the combined heuristic outperforms the result obtained in [26]. In the service combination Mix 3 the cell radius calculated by our proposal is slightly lower. The reason for this is that, as we mentioned in the previous paragraph, the authors in [26] only use the total bandwidth required from the cell and do not consider each individual connection. This makes that the influence of the services mixture is quite low in their results. However, note that in the formulation of this paper, we do consider each service individually, and therefore, the influence of service mixture is much important in our heuristic, which reflects better the real behavior of a WCDMA system.
In order to carry out a second comparison, we have used the evolutive algorithm developed in [27]. Evolutionary programming is a population based heuristic, which was first proposed as an approach to artificial intelligence [30]. It has been successfully applied to a large number of numerical optimization problems including telecommunications problems [31]. In this case we have used the same set of experiments as in Section 4, comparing the performance of the evolutionary algorithm (EA) in [27] against the combined algorithm proposed in this paper. The results are shown in Table 11. Note that the differences between the results of the combined algorithm and the evolutionary algorithm are quite small (about 1%) in all experiments but in the Exp-7, where the combined algorithm proposed obtains a result about 5% better. In this case the EA falls into a local solution near the optimum solution.
As final remarks for this section, note that the main limitation of the proposed heuristics in this paper is that they consider trunk reservation for the capacity assignment. This means that the capacity allocated to service  is reserved for this service exclusively, and no other can use it, even when there is some free capacity. In the practical operation of the UMTS system, the capacity is available for all services and only when the system goes to a heavy loaded situation, the capacity reservation will be activated. This also means that, in practice, the cell radius will be slightly larger than the one calculated with the proposed algorithms. However, since the algorithms provide a conservative estimation, they are valid to estimate the maximum network investment.
is reserved for this service exclusively, and no other can use it, even when there is some free capacity. In the practical operation of the UMTS system, the capacity is available for all services and only when the system goes to a heavy loaded situation, the capacity reservation will be activated. This also means that, in practice, the cell radius will be slightly larger than the one calculated with the proposed algorithms. However, since the algorithms provide a conservative estimation, they are valid to estimate the maximum network investment.
5. Implementation, Application, and Real Cases
5.1. Implementation and Application
The proposed algorithms are implemented in a software tool for the strategic design of hybrid 2G and 3G networks. An earlier version software tool named DIDERO, was originally presented in [32].
Using this tool we present a study carried out for Spain. The objective of this study is to compare the differences in the number of Node Bs and in the total network investment cost using different allocations of the load factors to the services. We will use the combined heuristic presented before and three different assignments ( ,
,  ,
,  ) for comparison purposes, based on the binary rate, user density and the traffic, that are the assignments done by a common network planner.
) for comparison purposes, based on the binary rate, user density and the traffic, that are the assignments done by a common network planner.
The  assignment is done considering the binary rate of the service, that is, a service with higher binary rate gets more capacity following the equation
assignment is done considering the binary rate of the service, that is, a service with higher binary rate gets more capacity following the equation

The assignment  takes into account also the user density:
takes into account also the user density:

Finally the third assignment  considers also the individual traffic
considers also the individual traffic

The scenario is composed of the 50 most important counties in Spain, which corresponds to the capitals of the 50 Spanish provinces. We are considering the main cities and the surrounding towns under their administrative influence. The cities, their extension and the number of inhabitants are shown in Table 12.
For this study we have selected the (Exp-3), Experiment  with the same propagation parameters exposed in Section 4. The values of the market share of the operators, the holding time
with the same propagation parameters exposed in Section 4. The values of the market share of the operators, the holding time  and the call attempt rate
and the call attempt rate  for the different services are shown in Table 13.
for the different services are shown in Table 13.
With these premises, the values of the load factors calculated from  ,
,  , and
, and  are shown in Table 14, note that the combined heuristic does not require an initial assignment. The results of the complete Node B deployment for all experiments are shown in Table 15. Note that even for an assignment where several parameters are considered,
are shown in Table 14, note that the combined heuristic does not require an initial assignment. The results of the complete Node B deployment for all experiments are shown in Table 15. Note that even for an assignment where several parameters are considered,  , the resulting number of Node Bs is almost 35% higher than using the combined heuristic proposed.
, the resulting number of Node Bs is almost 35% higher than using the combined heuristic proposed.
The total population of the cities in the considered scenario is 15 258 049. Current Spanish population is 45.12 million (official data of Spanish National Statistic Service), therefore we can extrapolate our results to obtain a fair estimation of the number of Node Bs for the whole country. Considering that the unit investment cost of a Node B rounds 135000 euros (€), and that the investment in the cell deployment is about 60%, [33] of the total network investment in a mobile network we can estimate the total network investment for the four cases presented. These results are shown in Table 16.
The most impact result is the big difference in the total investment in the different cases. Comparing with the second best, that is, with the scenario A3, the difference is about 547 million (€). This is equivalent to the 0.05% of the total Spanish Gross Domestic Product which is 1.12 billion of euros. This result shows the relevance for the network operator of an accurate network planning.
5.2. Real Cases
The combined heuristic presented here has been applied in three regulatory processes with National Regulatory Authorities for the study of the mobile termination charges and comparisons between 2G and 3G network deployments. Specifically it has been applied by a work team with the University of Cantabria and the German consulting firm WIK Consult in the following countries.
6. Conclusions
This paper proposes three different algorithms for the calculation of the cell radius under traffic criteria in multiservices scenarios, named iterative, reduced and combined. We have shown that the three algorithms are able to solve the cell radius determination problem, providing good quality solutions. However, the reduced algorithm is not able to produce optimal solutions when the users are moving at different speeds. The iterative and combined heuristics provides the optimal solution in all the cases studied, but the combined approach converges faster than the iterative heuristic.
The combined heuristic has been implemented in existing strategic planning software tool to calculate the Node B deployment in a whole country. We have presented a work scenario in Spain were our proposed heuristic obtains better solutions in terms of number of Node Bs, which represents a great investment cost saving. This heuristic has been applied in several regulatory processes under the supervision of the corresponding National Regulatory Authority.
References
Ojanperä T, Prasad R: Wideband CDMA for Third Generation Mobile Communications. Artech House, Norwood, Mass, USA; 1988.
Hong D, Rappaport SS: Traffic model and performance analysis for cellular mobile radio telephone systems with prioritized and nonprioritized handoff procedures. IEEE Transactions on Vehicular Technology 1986, 35(3):77-92.
Mendez A, Panduro M, Covarrubias D, Dominguez R, Romero G: Quality of service support for multimedia traffic in mobile networks using a CDMA novel scheduling scheme. Computers and Electrical Engineering 2006, 32(1–3):178-192.
Gilhouse K, Jacobs I, Padovani R, Viterbi A, Weaver L: On the capacity of a cellular CDMA system. IEEE Transactions on Vehicular Technology 1991, 40(2):303-312. 10.1109/25.289411
Viterbi AM, Viterbi AJ: Erlang capacity of a power controlled CDMA system. IEEE Journal on Selected Areas in Communications 1993, 11(6):892-900. 10.1109/49.232298
Sipilä K, Honkasalo Z, Laiho-Steffens J, Wacker A: Estimation of capacity and required transmission power of WCDMA downlink based on a downlink pole equation. Proceedings of the 51st IEEE Vehicular Technology Conference (VTC '00), 2000 2: 1002-1005.
Burley S: Downlink capacity estimation in a WCDMA cellular network. Proceedings of the 12th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '01), 2001 1: A26-A30.
Ahmed BT, Ramón MC, de Haro Ariet L: Capacity and interference statistics of highways W-CDMA cigar-shaped microcells (uplink analysis). IEEE Communications Letters 2002, 6(5):172-174. 10.1109/4234.1001654
Sipilä K, Jasberg M, Laiho-Steffens J, Wacker A: Static simulator for studying WCDMA radio network planning issues. Proceedings of the IEEE Vehicular Technology Conference (VTC '99) 1999, 3: 2436-2440.
Laiho J, Wacker A, Novosad T, Hämäläinen A: Verification of WCDMA radio network planning prediction methods with fully dynamic network simulator. Proceedings of the IEEE Vehicular Technology Conference (VTC '01), 2001 1(54):526-530.
Dou C, Chang Y: Class-based downlink capacity estimation of a WCDMA network in a multiservice context. Computer Communications 2005, 28(12):1443-1455. 10.1016/j.comcom.2005.01.007
Um P, Gille L, Simon L, Rudelle C: A Model for Calculating Interconnection Costs in Telecommunications. PPIAF and The World Bank, Washington, DC, USA; 2004.
Courcoubetis C, Weber R: Pricing Communication Networks. John Wiley & Sons, New York, NY, USA; 2003.
European Commission : European commission recommendation about interconnections. Second part: cost accounting and account division. DOCE L 146 13.5.98, pp. 6–35, April 1998
European Cooperation in the Field of Scientific and Technical Research EURO-COST 231 : Urban transmission loss models for mobile radio in the 900 and 1800 MHz bands. Revision 2, The Hague, 1991
Walfisch J, Bertoni HL: A theoretical model of UHF propagation in urban environments. IEEE Transactions on Antennas and Propagation 1988, 36(12):1788-1796. 10.1109/8.14401
Boucher NJ: The Cellular Radio Handbook. John Wiley & Sons, New York, NY, USA; 2001.
Holma H, Toskala A: WCDMA for UMTS. John Wiley & Sons, New York, NY, USA; 2001.
Garg VK, Yellapantula RV: A tool to calculate Erlang capacity of a BTS supporting 3G UMTS system. Proceedings of the IEEE International Conference on Personal Wireless Communications (ICPWC '00), 2000, Hyderabad, India 173-177.
Shabany M, Navaie K, Sousa ES: A utility-based downlink radio resource allocation for multiservice cellular DS-CDMA networks. EURASIP Journal on Wireless Communications and Networking 2007, 2007:-11.
Laihoo J, Wacker A, Novosad T: Radio Network Planning and Optimisation for UMTS. John Wiley & Sons, New York, NY, USA; 2002.
Jagerman DL: Some properties of the Erlang loss function. Bell System Technical Journal 1974, 53(3):525-551.
Lee J, Miller L: CDMA Systems Engineering Handbook. Artech House, Norwood, Mass, USA; 1998.
Hegde N, Altman E: Capacity of multiservice WCDMA networks with variable GoS. Proceedings of the IEEE Wireless Communications and Networking (WCNC '03), March 2003, New Orleans, La, USA 2: 1402-1407.
Ruzicka Z, Hanus S: Radio network dimensioning in UMTS network planning process. Proceedings of the IEEE 18th International Conference on Applied Electromagnetics and Communications (ICECom '05), 2005
Cordier C, Ortega S: On WCDMA downlink multiservice coverage and capacity. Proceedings of the 54th IEEE Vehicular Technology Conference (VTC '01), 2001 4(54):2754-2758.
Portilla-Figueras A, Salcedo-Sanz S, Oropesa-García A, Bousoño-Calzón C: Cell size determination in WCDMA systems using an evolutionary programming approach. Computers and Operations Research 2008, 35(12):3758-3768. 10.1016/j.cor.2007.02.002
Lindberger K: Dimensioning and design methods for integrated ATM networks. Proceedings of the International Teletraffic Conference (ITC '94), 1944 14: 897-906.
D'avila CK, Yacoub MD: Reuse efficiency for non-uniform traffic distributions in CDMA systems. IEE Electronics Letters 1998, 34(13):1293-1294. 10.1049/el:19980930
Fogel LJ, Owens J, Walsh MJ: Artificial Intelligence through Simulated Evolution. John Wiley & Sons, New York, NY, USA; 1966.
Lim HS, Rao MV, Tan AW, Chuah HT: Multiuser detection for DS-CDMA systems using evolutionary programming. IEEE Communications Letters 2003, 7(3):101-103. 10.1109/LCOMM.2002.808372
Hackbarth K, Portilla JA: DIDERO 3G a strategic network planning tool for 3G mobile networks. International Journal of Information Technology and Decision Making 2003, 2(4):531-555. 10.1142/S0219622003000859
Brinkmann M, Hackbarth K, Ilic D, Neu W, Neumman KH, Portilla-Figueras A: Mobile termination cost model for australia. Final Report http://www.accc.gov.au/
Neu W, Hackbarth K, Portilla-Figueras A: Analysis of Cost Studies presented by Mobile Network Operators. http://www.osiptel.gob.pe/
Acknowledgments
This work has been partially supported by Comunidad de Madrid, Universidad de Alcalá and Ministerio de Educación of Spain, through Projects CCG06-UAH/TIC-0460, CCG08-UAH/AMB-3993 and TEC2006-07010. The authors would like to thank also the support offered by WIK Consult GmbH, in the different projects, both with their expertise and funding.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Portilla-Figueras, A., Salcedo-Sanz, S., Hackbarth, K.D. et al. Novel Heuristics for Cell Radius Determination in WCDMA Systems and Their Application to Strategic Planning Studies. J Wireless Com Network 2009, 314814 (2009). https://doi.org/10.1155/2009/314814
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/314814



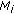 . This will be the value when the cell radius by capacity (traffic),
. This will be the value when the cell radius by capacity (traffic),  , is the same as by propagation,
, is the same as by propagation, 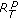 .
.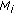 over the complete set of services
over the complete set of services 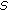 . With this the cell radius by capacity,
. With this the cell radius by capacity,  , is maximized.
, is maximized.

