- Research Article
- Open access
- Published:
An Active Constraint Method for Distributed Routing, and Power Control in Wireless Networks
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 656832 (2010)
Abstract
Efficiently transmitting data in wireless networks requires joint optimization of routing, scheduling, and power control. As opposed to the universal dual decomposition we present a method that solves this optimization problem by fully exploiting our knowledge of active constraints. The method still maintains main requirements such as optimality, distributed implementation, multiple path routing and per-hop error performance. To reduce the complexity of the whole problem, we separate scheduling from routing and power control, including it instead in the constraint set of the joint optimization problem. Apart from the mathematical framework we introduce a routing and power control decomposition algorithm that uses the active constraint method, and we give further details on its distributed application. For verification, we apply the distributed RPCD algorithm to examples of wireless mesh backhaul networks with fixed nodes. Impressive convergence results indicate that the distributed RPCD algorithm calculates the optimum solution in one decomposition step only.
1. Introduction
Nowadays, there is an increased interest in communication via wireless mesh networks such as ad-hoc, sensor, or wireless mesh backhauling networks [1, 2]. In wireless networks the link capacities are variable quantities and can be adjusted by the resource allocation such as scheduling, and power allocation to fully exploit network performance. Hence, for efficient data transmission an integrated routing, time scheduling and power control optimization strategy are required. This strategy has to take different transmission constraints into account, for example, maximum available power level or limited buffer size at nodes. The inherent decentralized nature of wireless mesh networks mandates that distributed algorithms should be developed to implement the joint routing, scheduling, and power control optimization. The first step towards a distributed implementation is to break up this problem into manageable subproblems and solve these subproblems by iterative algorithms. Cruz and Santhanam [3] have addressed the problem of finding an optimal link scheduling and power control policy while minimizing total average power consumption. Their algorithm is designed for single-path routing only, does not consider buffer limitations and has a worst case exponential complexity. In [4], Li and Ephremedis solve at first power control and scheduling jointly. They use the obtained power values to calculate a routing distance that in turn is used by Bellman-Ford routing. However, the proposed separation is performed by not considering the combinational structure of the entire routing, scheduling and power control problem. Although less computationally intensive, the algorithm ends up in a suboptimal solution. It further fully neglects multiple path routing as well as buffer restrictions. Xiao et al. proposed in [5] the dual decomposition as a promising decomposition approach. By dual decomposition the overall problem is split into two subproblems while the master dual problem coordinates them. In this paper we consider joint routing, time-scheduling, and power control for single frequency wireless mesh networks. The wireless transmissions are arranged in time-slots. However, we take into account that simultaneously active transmissions suffer from multiple access interference. Dual decomposition is a universal approach to solve such optimization problems [5, 6], but it does not consider the specific combinational structures of optimization problems. By contrast, we propose a novel method that explicitly exploits the combinational structure of a joint routing, time-scheduling, and power control problem by means of an active constraint method. The formulation of the optimization problem is yet generally valid, so that the method proposed here is applicable to a plurality of wireless networks. The proposed approach meets the following requirements: ( ) less iterations to an optimum solution, (
) less iterations to an optimum solution, ( ) distributed implementation, (
) distributed implementation, ( ) multiple path routing, and (
) multiple path routing, and ( ) per hop error performance. In particular, the approach is as follows. We separate scheduling from routing and power allocation by including it in the constraint set of a S imultaneous R outing and P ower C ontrol (SRPC) problem. For scheduling, several well known approximations such as Greedy-based approaches exist [7, Section
) per hop error performance. In particular, the approach is as follows. We separate scheduling from routing and power allocation by including it in the constraint set of a S imultaneous R outing and P ower C ontrol (SRPC) problem. For scheduling, several well known approximations such as Greedy-based approaches exist [7, Section  ], that we can leverage on. The constraints we use in the SRPC problem are induced by a precalculated colored graph of the network that, in turn, reflects the scheduling decisions of any arbitrary scheduler. Consequently, the main contribution is to introduce a R outing and P ower C ontrol D ecomposition (RPCD) method to solve the simultaneous routing and power control problem while meeting the above-mentioned requirements. The clever bits of the RPCD are manifold. (
], that we can leverage on. The constraints we use in the SRPC problem are induced by a precalculated colored graph of the network that, in turn, reflects the scheduling decisions of any arbitrary scheduler. Consequently, the main contribution is to introduce a R outing and P ower C ontrol D ecomposition (RPCD) method to solve the simultaneous routing and power control problem while meeting the above-mentioned requirements. The clever bits of the RPCD are manifold. ( ) We rewrite the SRPC problem to an equivalent problem by applying the active constraint method. (
) We rewrite the SRPC problem to an equivalent problem by applying the active constraint method. ( ) We decouple the equivalent problem by solving a (convex) network and a (convex) power assignment problem separately. (
) We decouple the equivalent problem by solving a (convex) network and a (convex) power assignment problem separately. ( ) Iterations are performed by switching between the two subproblems for which network and power variables act as interchanging variables. Apart from the mathematical framework we introduce the RPCD algorithm and prove its convergence to a KKT-point of the joint routing and power control problem. We compare the RPCD algorithm with dual decomposition as state-of-art approach with respect to the number of iterations needed to calculate the KKT-point. This verification is performed by applying both algorithms to a wireless cellular mesh backhauling network [1, 2]. The backhauling network describes a "regular" cellular network. This models the situation where, in order to save infrastructure expenses of laying cable or fiber to each node (base station), we try to extend the range of a given source node with wired backhaul connection by using several other nodes. These intermediate nodes have no wired connection and can only communicate with the backhaul via the source node by wireless mesh communications. The simulation set-up correctly models mobile radio channel characteristics such as path-loss and slow fading. The comparison indicates that the RPCD approach requires only one decomposition step to calculate the optimum solution as opposed to dual decomposition. This paper is organized as follows. In Section 2 we describe the network model used for the wireless data network. In Section 3 we formulate the optimization problem and define the standard interference function. The RPCD algorithm for solving the joint routing and power control problem is presented in Section 4. We extend the RPCD algorithm in Section 5 by introducing distributed algorithms for solving the routing and power assignment problem. Finally, in Section 6 we apply the algorithm to a wireless backhaul network and present the simulation results. We conclude the paper in Section 7.
) Iterations are performed by switching between the two subproblems for which network and power variables act as interchanging variables. Apart from the mathematical framework we introduce the RPCD algorithm and prove its convergence to a KKT-point of the joint routing and power control problem. We compare the RPCD algorithm with dual decomposition as state-of-art approach with respect to the number of iterations needed to calculate the KKT-point. This verification is performed by applying both algorithms to a wireless cellular mesh backhauling network [1, 2]. The backhauling network describes a "regular" cellular network. This models the situation where, in order to save infrastructure expenses of laying cable or fiber to each node (base station), we try to extend the range of a given source node with wired backhaul connection by using several other nodes. These intermediate nodes have no wired connection and can only communicate with the backhaul via the source node by wireless mesh communications. The simulation set-up correctly models mobile radio channel characteristics such as path-loss and slow fading. The comparison indicates that the RPCD approach requires only one decomposition step to calculate the optimum solution as opposed to dual decomposition. This paper is organized as follows. In Section 2 we describe the network model used for the wireless data network. In Section 3 we formulate the optimization problem and define the standard interference function. The RPCD algorithm for solving the joint routing and power control problem is presented in Section 4. We extend the RPCD algorithm in Section 5 by introducing distributed algorithms for solving the routing and power assignment problem. Finally, in Section 6 we apply the algorithm to a wireless backhaul network and present the simulation results. We conclude the paper in Section 7.
2. Network Model
The transmission problem we are facing is to transmit messages indexed by  each of size
each of size  in bits via a multiple hop wireless network. Each message has its source node
in bits via a multiple hop wireless network. Each message has its source node  and its destination node
and its destination node  . Let
. Let  be an index set for the set of messages with
be an index set for the set of messages with  . With multiple path routing each message is transmitted via several paths from its source node to its destination node. Thus, nodes can send parts of messages to many receivers and receive parts of messages from many transmitters. We denote the nodes by
. With multiple path routing each message is transmitted via several paths from its source node to its destination node. Thus, nodes can send parts of messages to many receivers and receive parts of messages from many transmitters. We denote the nodes by  with
with  be a finite set of nodes. At any time, each of these nodes
be a finite set of nodes. At any time, each of these nodes  can map any parts of messages
can map any parts of messages  onto a single link
onto a single link  for transmission. The set of all links is denoted by
for transmission. The set of all links is denoted by  . A wireless communication link corresponds to an edge
. A wireless communication link corresponds to an edge  between two nodes
between two nodes  and is described by the ordered pair
and is described by the ordered pair  such that
such that  transmits information directly to
transmits information directly to  . Moreover, we assume that
. Moreover, we assume that  for all
for all  . We have that
. We have that  is a directed graph with node set
is a directed graph with node set  and edge set
and edge set  . For an arbitrary node
. For an arbitrary node  , denote by
, denote by  and
and  the set of outgoing and incoming edges within
the set of outgoing and incoming edges within  at the node
at the node  , respectively. A link represents a wireless resource characterized by a given bandwidth, time duration, space fraction, or by a given code assignment. We assume a time-slotted single frequency network for which the time is divided into equal slots of length
, respectively. A link represents a wireless resource characterized by a given bandwidth, time duration, space fraction, or by a given code assignment. We assume a time-slotted single frequency network for which the time is divided into equal slots of length  while all nodes occupy the same frequency band of bandwidth
while all nodes occupy the same frequency band of bandwidth  . Time slots are indexed by
. Time slots are indexed by  , with
, with  as an index set. We take time scheduling into account by assuming that there is a given coloring of the nodes such that adjacent nodes do not have the same color (half-duplex constraint) [4]. That is, we are given a number
as an index set. We take time scheduling into account by assuming that there is a given coloring of the nodes such that adjacent nodes do not have the same color (half-duplex constraint) [4]. That is, we are given a number  and a function
and a function  such that
such that  for all nodes
for all nodes  with
with  . Here,
. Here,  is at least as large as the chromatic number of
is at least as large as the chromatic number of  . Computing such a coloring can be done by a Greedy approach [7]. To take delay constraints into account we introduce
. Computing such a coloring can be done by a Greedy approach [7]. To take delay constraints into account we introduce  as the maximum number of time slots, a message is allowed to use for transmission from its source to its destination, that is,
as the maximum number of time slots, a message is allowed to use for transmission from its source to its destination, that is,  . The interference model we consider includes multiple access interference caused by simultaneously active transmissions that can not be perfectly separated by, for example, code- or space division multiple access (CDMA/SDMA) techniques. Thus, let
. The interference model we consider includes multiple access interference caused by simultaneously active transmissions that can not be perfectly separated by, for example, code- or space division multiple access (CDMA/SDMA) techniques. Thus, let  be the set of edges interfering edge
be the set of edges interfering edge  at time
at time  . The signal attenuation from node
. The signal attenuation from node  to node
to node  is
is  and it remains unchanged within the duration of a time slot
and it remains unchanged within the duration of a time slot  . We further assume perfect knowledge of
. We further assume perfect knowledge of  at the corresponding senders. Let
at the corresponding senders. Let  be the transmitting node and let
be the transmitting node and let  be the receiving node of edge
be the receiving node of edge  . Hence,
. Hence,  denotes the attenuation a signal suffers that is transmitted from
denotes the attenuation a signal suffers that is transmitted from  but received by node
but received by node  . For link
. For link  such a signal represents multiple-access interference that is caused by link
such a signal represents multiple-access interference that is caused by link  . Furthermore, with
. Furthermore, with  as the (transmit) power to be allocated to link
as the (transmit) power to be allocated to link  at time slot
at time slot  , the received signal power at node
, the received signal power at node  from the transmitter
from the transmitter  is given by
is given by  . We define the signal-to-interference-plus-noise ratio (SINR) of edge
. We define the signal-to-interference-plus-noise ratio (SINR) of edge  at time slot
at time slot  as
as

with  as an additive noise power of edge
as an additive noise power of edge  . If we only assume thermal noise to be the same for all edges, we have
. If we only assume thermal noise to be the same for all edges, we have  with noise spectral density
with noise spectral density  . For the optimization problems to be introduced later we have the following design variables. As network flow variables we have
. For the optimization problems to be introduced later we have the following design variables. As network flow variables we have  as the part of the message
as the part of the message  sent along edge
sent along edge  in time slot
in time slot  (in bits), and
(in bits), and  as the part of the message
as the part of the message  stored in a buffer at node
stored in a buffer at node  directly before the start of time slot
directly before the start of time slot  (in bits). Communication variable
(in bits). Communication variable  is the transmit power allocated to edge
is the transmit power allocated to edge  at time slot
at time slot  to transmit the total traffic on edge
to transmit the total traffic on edge  (in Watt). If we stack the different variables to vectors we obtain
(in Watt). If we stack the different variables to vectors we obtain  ,
,  , and
, and  . We further use the following parameters. Let
. We further use the following parameters. Let  be the size of message
be the size of message  (in bits) and
(in bits) and  be the maximum total buffer size at node
be the maximum total buffer size at node  (in bits). Power constraints are
(in bits). Power constraints are  as the maximum transmission power of a node (in Watt) assumed to be the same for all nodes and
as the maximum transmission power of a node (in Watt) assumed to be the same for all nodes and  as the maximum transmission power per edge (in Watt).
as the maximum transmission power per edge (in Watt).
3. Optimization Problem
3.1. Problem Description
Let us consider an operation of a wireless data network with the objective to minimize a convex cost function  (or to maximize a concave utility function). The design variables
(or to maximize a concave utility function). The design variables  ,
,  , and
, and  are subject to some constraints. For instance, with
are subject to some constraints. For instance, with  we require the power constraints
we require the power constraints



forming the polyhedral set

Since we isolated coloring from the joint routing and power control, we have to take the precalculated colored network graph in the flow constraints into account. Similar to power constraints, we require that flow constraints form a polyhedral set  . For example, if we assume that given source nodes
. For example, if we assume that given source nodes  have to transmit messages of sizes
have to transmit messages of sizes  to destinations
to destinations  in a given time
in a given time  , the polyhedral set
, the polyhedral set  is defined by the equalities and inequalities
is defined by the equalities and inequalities









Equations (7) and (8) avoid buffer overload while (9) and (10) initialize buffer values. To account for delay constraints (11) and (12) ensure that messages reach their destinations completely at  at last. Coloring is ensured by (13) and (14) is a modified Kirchhoff's Law [6]. The SRPC problem under consideration is now as follows
at last. Coloring is ensured by (13) and (14) is a modified Kirchhoff's Law [6]. The SRPC problem under consideration is now as follows

By the last constraints, we assume that at any time  each node
each node  can map all part of messages
can map all part of messages  onto a single link
onto a single link  for transmission [5]. Furthermore, we assume that the amount of information (in bits) we can transmit on a single wireless link
for transmission [5]. Furthermore, we assume that the amount of information (in bits) we can transmit on a single wireless link  at time slot
at time slot  is bounded from above by a maximum mutual information bound
is bounded from above by a maximum mutual information bound  that itself depends on the power setting. The last constraints of (15) are the only constraints coupling network flow variables
that itself depends on the power setting. The last constraints of (15) are the only constraints coupling network flow variables  with communication variables
with communication variables  . Thus, we call them coupling constraints [5], and they represent the most challenging constraints of the SRPC problem. All the other constraints are either constraints for the network flow variables or for the communication variables only. Assuming time-invariant channel conditions within the duration of a single time slot
. Thus, we call them coupling constraints [5], and they represent the most challenging constraints of the SRPC problem. All the other constraints are either constraints for the network flow variables or for the communication variables only. Assuming time-invariant channel conditions within the duration of a single time slot  , function
, function  describes the amount of information of edge
describes the amount of information of edge  and can be expressed with (1) by the well-known Shannon formula
and can be expressed with (1) by the well-known Shannon formula

For each edge  , the factor
, the factor  represents any implementation margin relative to the maximum mutual information given by the Shannon formula [8]. In practice, achieving this mutual information requires adaptive modulation and coding. To accomplish the description of the optimization problem under consideration, we like to list some commonly used examples of cost (utility) functions. Examples are
represents any implementation margin relative to the maximum mutual information given by the Shannon formula [8]. In practice, achieving this mutual information requires adaptive modulation and coding. To accomplish the description of the optimization problem under consideration, we like to list some commonly used examples of cost (utility) functions. Examples are
-
(1)
minimization of total transmitted power
 (17)
(17) -
(2)
maximization of total network throughput
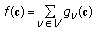 (18)
(18)with
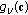 representing any linear combination of flows that egress node
representing any linear combination of flows that egress node  ,
, -
(3)
any linear combination of items (
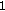 ) and (
) and ( ).
).
A comprehensive overview on commonly used cost functions for wireless data networks is given in [5].
3.2. Standard Interference Function
In the following we give an interpretation of the coupling constraints  of the SRPC problem (15). We define for
of the SRPC problem (15). We define for  and
and 

to be a standard interference function in  [9]. To clarify the meaning of a standard interference function, we restate the definition given in [9]. Here,
[9]. To clarify the meaning of a standard interference function, we restate the definition given in [9]. Here,  and
and  mean componentwise inequality.
mean componentwise inequality.
If we insert (1) into (16) and solve the coupling constraints in (15) for power values, we obtain rewritten coupling constraints as

Definition 1.
For given values  ,
,  is a standard interference function if for all
is a standard interference function if for all  the following properties are satisfied.
the following properties are satisfied.
-
(i)
Positivity:
 .
. -
(ii)
(ii)Monotonicity: if
 then
then 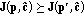 .
. -
(iii)
Scalability: For all
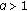 ,
, 
The positivity property ensures positive power values of the joint routing and power control problem (15). If any transmit power level is decreased, the monotonicity guarantees the decrease of the interference on the other links in the network, ensuring the maintenance of the same or even the achievement of a lower interference level for all links. The scalability property implies that if  then
then  for
for  .
.
Interestingly, (20) represents a Quality-of-Service (QoS) constraint, that is, a lower bound on the (implicitly defined) SINR. By reusing the coupling constraints again (15) and solving (16) for SINR we require

SINR is the main indicator for the transmission quality. Hence, given a modulation and coding scheme a specific per-hop error performance implies a respective  . In turn, by varying
. In turn, by varying  we vary the transmission quality.
we vary the transmission quality.
Note that for given values  , we can use a fixed point iteration algorithm to find a unique power vector
, we can use a fixed point iteration algorithm to find a unique power vector  with
with

This power iteration represents a standard power control algorithm as introduced in [9]. The power iteration used herein to solve (15) will be described in detail in Section 5.1. With coupling constraints (20) of problem (15) we can make use of the properties of the standard interference function [9], arriving at the following theorem.
Theorem 1.
Suppose that  , that the objective function
, that the objective function  is monotone in
is monotone in  , and that we want to solve the optimization problem
, and that we want to solve the optimization problem

Suppose there exists a feasible point of this optimization problem, then there exists a feasible point with the same or better objective function value for which all the constraints (20) are active, that is, equality holds in all of them. Especially, for every optimum objective function value there exists an optimum variable setting such that all constraints in (20) are active. If  is strictly monotone in
is strictly monotone in  , then all constraints (20) are active at each optimal solution of this problem.
, then all constraints (20) are active at each optimal solution of this problem.
Proof.
See Appendix A.
Theorem 1 is an extension of the results found in [9]. In contrast to [9] we do not assume that  is just a sum of powers, instead it can be an arbitrary function being monotone in power values. Moreover, the objective as well as the coupling constraints depend on the flow variables
is just a sum of powers, instead it can be an arbitrary function being monotone in power values. Moreover, the objective as well as the coupling constraints depend on the flow variables  and buffers
and buffers  , a case not considered in [9].
, a case not considered in [9].
4. RPCD-Algorithm
In this section we present the RPCD-Algorithm for solving the SRPC problem (15). In contrast to universal approaches, like the dual decomposition method, we fully exploit our knowledge of active constraints of the joint optimization problem.
Based on Theorem 1 we can formulate an equivalent optimization problem but we avoid the extension of the utility function as usually done by applying dual or penalty approaches. We further keep the constraints and we only have to exchange the common network and power variables.
The main idea of the RPCD-Algorithm is to decouple the SRPC problem into two convex subproblems and to find the optimum solution of the SRPC problem by iteratively toggling between the two subproblems (Figure 1).
4.1. RPCD-Principle
Let us consider again problem (15). Due to Theorem 1 we know that all coupling constraints (20) of the SRPC problem are active at least at one optimum solution. By means of this observation, we can rewrite the SRPC problem to an equivalent problem as follows. Activity (equality) means that

We now substitute (24) into the objective of the SRPC problem (15) and obtain an equivalent problem with the rewritten cost function as

In the following we use (25) and decompose the SRPC problem into two convex subproblems.
In particular, by assuming feasible power variables, a routing problem with fixed link capacities is formulated and the optimum flow variables for the routing problem are calculated. Equivalently, we can assume fixed routing variables and formulate a power control problem to calculate optimum power values [10].
The two subproblems are as follows.
4.1.1. Network Flow (Routing) Subproblem
We assume feasible power variables  . With (25) we need to solve the optimization problem
. With (25) we need to solve the optimization problem

where  are the optimization variables.
are the optimization variables.
We have the following lemma.
Lemma 1.
( ) If
) If  is a continuously differentiable and monotone function in
is a continuously differentiable and monotone function in  and in
and in  , then the objective of (26) is a continuously differentiable and monotone function in
, then the objective of (26) is a continuously differentiable and monotone function in  .
.
( ) Let
) Let  (
( ). Suppose that
). Suppose that  is twice continuously differentiable, that
is twice continuously differentiable, that  is a convex and monotone function in
is a convex and monotone function in  for all
for all  and that
and that  is a convex function in
is a convex function in  for all
for all  , for all
, for all  . Assume that at least one of the following holds:
. Assume that at least one of the following holds:
-
(a)
 is strictly convex in
is strictly convex in  for all
for all  ,
, -
(b)
 is strictly convex in
is strictly convex in  for all
for all 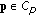 , for all
, for all 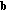 ,
, -
(c)
s
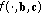 is strictly monotone in
is strictly monotone in 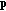 for all
for all  .
.
Then, the objective of (26) is strictly convex in  and the solution to (26) is unique and continuous on
and the solution to (26) is unique and continuous on 
Proof.
See Appendix B
4.1.2. Power Control Subproblem
We assume feasible network variables  . We need to solve the optimization problem
. We need to solve the optimization problem

where  are the optimization variables.
are the optimization variables.
We have the following lemma.
Lemma 2.
Suppose that  is strictly monotone in
is strictly monotone in  and (27) is feasible. Then, we have:
and (27) is feasible. Then, we have:
-
(1)
problem (27) has a unique solution,
-
(2)
the solution for (27) depends continuously on
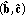 .
.
Proof.
See Appendix C
4.2. RPCD Algorithm
As a consequence of the discussion above, we can replace the SRPC problem (15) by two simple subproblems, coupled to each other via fixed variables (power and network variables). The algorithmic scheme used is exemplified as RPCD algorithm and described in Algorithm 1.
Algorithm 1: RPCD
Input: All parameters for problem (15).
( ) Choose
) Choose  sufficiently large so that problem (26)
sufficiently large so that problem (26)
is feasible;
( ) Choose
) Choose  ,
,  arbitrarily;
arbitrarily;
( )
)  ;
;
( ) while stopping criterion for
) while stopping criterion for not fulfilled
not fulfilled
do
( ) Set
) Set  and solve problem (26).
and solve problem (26).
( ) Denote the result by
) Denote the result by  ,
,  .
.
( ) Set
) Set  and solve problem (27).
and solve problem (27).
Denote the result by  .
.
( )
)  .
.
( ) endw
) endw
Output:
Convergence of the RPCD algorithm is given by the following theorem.
Theorem 2.
Let us consider Lemmas 1 and 2. Under these assumptions and under the assumption that (15) is convex, the RPCD algorithm is well defined and provides a sequence of iterates  such that each subsequence of this sequence converges to an optimal point of (15). Moreover, there exists at least one converging subsequence. Additionally, the sequence
such that each subsequence of this sequence converges to an optimal point of (15). Moreover, there exists at least one converging subsequence. Additionally, the sequence  converges monotonically decreasing.
converges monotonically decreasing.
Proof.
See Appendix D
Note that both subproblems, (26) and (27), are convex and represent standard problems for which many efficient (distributed) algorithms exist. Particularly, we have to solve a flow problem with fixed capacities (fixed power values) [11] while computing optimum power values can be done by means of standard power control algorithms [9].
5. Distributed RPCD
Generally, we can apply centralized as well as distributed implementation for the RPCD algorithm. In this paper we concentrate on distributed algorithm exclusively. For the interested reader, a detailed survey about the centralized and distributed algorithms and their advantages and disadvantages can be found in [12].
Herein, for the distributed approach locally available information is required and we restrict the internode communication between neighbor nodes only.
As we illustrated in the Figure 2, each node executes the distributed RPCD algorithm in advance before a time slot begins. The algorithm allocates the resources optimally, for given network and power variables  and
and  .
.
In the following, as introduced in Section 4.1, we consider again the two subproblems, routing (26) and power control (27), and present distributed algorithms for solving them.
5.1. Distributed Power Control
Let us consider again the power control subproblem (27), which is part of the RPCD algorithm.

Assume given network variables  and that the standard interference function
and that the standard interference function  is feasible, that is, if the power vector
is feasible, that is, if the power vector  satisfies the coupling constraints (20), then we can use the following fixed point iteration to compute the optimum power settings
satisfies the coupling constraints (20), then we can use the following fixed point iteration to compute the optimum power settings

However, in practical systems we have  taking power limitations into account. Given the original interference function
taking power limitations into account. Given the original interference function  and considering the maximum power vector
and considering the maximum power vector  in (3) we define
in (3) we define

It has been proven in [9] that  is a standard interference function fulfilling Definition 1.
is a standard interference function fulfilling Definition 1.
To include the constraint on the output power of a node, we define

and denote by  a projection operator that maps computed power values into the polyhedral set
a projection operator that maps computed power values into the polyhedral set  at each iteration step of the power iteration (29).
at each iteration step of the power iteration (29).
This projection allows us to consider only feasible power values during the course of the iteration.
By coupling the constrained interference function  with this projection on a polyhedral set, we define a new interference function
with this projection on a polyhedral set, we define a new interference function  for given network variables
for given network variables 

It can be easily shown that for all  the interference function
the interference function  satisfies all properties given by Definition 1 and, hence, is also a standard interference function.
satisfies all properties given by Definition 1 and, hence, is also a standard interference function.
For each time step  we can now write the standard constrained power iteration as
we can now write the standard constrained power iteration as

The power iteration (33) we call distributed power control algorithm.
Obviously, (33) is defined in terms of (32), (31), and (19). Due to (19), the information required to update the power values at starting node for a link  is the interference caused by the interfering transmissions measured at the end node for a link
is the interference caused by the interfering transmissions measured at the end node for a link  . Moreover, the projections introduced to consider the power constraints are local only. Hence, (33) represents a distributed power control algorithm [9].
. Moreover, the projections introduced to consider the power constraints are local only. Hence, (33) represents a distributed power control algorithm [9].
We use (33) to find a unique vector  with
with

If  is feasible, then for any initial vector
is feasible, then for any initial vector  , the iteration (33) converges to a unique fixed point
, the iteration (33) converges to a unique fixed point  .
.
Due to Theorems 1 and 2, this unique fixed point of (34) is a solution of the SRPC problem (15). If the SRPC problem is (strictly) convex, the fixed point is the global (unique) solution for the power setting of the joint routing and power control problem.
5.2. Distributed Routing
In the following we present a distributed algorithm for solving the routing subproblem (26) with given power values 

The key to a distributed algorithm is to apply a decomposition method by means of formulating the dual problem of the optimization problem (26). Therefore we exploit the separable structure of the routing problem (26) via the dual decomposition method (see, e.g., [5, 13]). For solving the dual problem, we propose to apply the common approach of using the subgradient method [14].
To form the dual routing problem we rewrite the original routing problem (26) using the Lagrange function [6]. We introduce the Lagrange multipliers for the most involving constraints, which are the coupling constraints of the SRPC problem (15)

and the flow conservation constraints, that is, modified Kirchhoff's Law (14)

This results in the partial Lagrangian of (26) given as

and the Lagrange multipliers are denoted by  and
and  .
.
The Lagrangian dual function is

Given the Lagrange dual function we can formulate the dual problem by [6]

We need to solve the dual problem (40) in order to obtain the best lower bound on  from the Lagrange dual function (39). Since the Lagrangian dual function is convex, the dual problem is a convex optimization problem [5]. Moreover, Slater's condition (see, e.g., [6, 13]) holds and thus, strong duality holds. This means, the optimal value of the original routing problem (26) and the dual optimal value from (39) are equal and we can solve the primal problem (26) by its dual (40).
from the Lagrange dual function (39). Since the Lagrangian dual function is convex, the dual problem is a convex optimization problem [5]. Moreover, Slater's condition (see, e.g., [6, 13]) holds and thus, strong duality holds. This means, the optimal value of the original routing problem (26) and the dual optimal value from (39) are equal and we can solve the primal problem (26) by its dual (40).
The algorithm to solve (39) and (40) is a two stage optimization algorithm. It solves (39) and (40) separately by using the subgradient method [6, 14] and toggling between the two subproblems until a convergence criterion is met.
For the computation of the dual function (39) we use the projected subgradient method [6, 14], which is an algorithm for minimizing a nondifferentiable convex function with the main feature of enabling distributed implementation.
As a first step we have to calculate the subgradients with the respect to the variables  and
and  , for variables
, for variables  and
and  . These subgradients are given by
. These subgradients are given by


where  denotes the node
denotes the node  that represents the starting point for one or more links
that represents the starting point for one or more links  . Analog to
. Analog to  , we denote with
, we denote with  the node
the node  that represents the end point for one or more links
that represents the end point for one or more links  .
.
The subgradient updates on the variables  and
and  are
are

Note that the projection on the nonnegative orthant by  results due to the network constraints
results due to the network constraints  and
and  .
.
Furthermore,  and
and  represent the subgradient step sizes and have to satisfy (shown for
represent the subgradient step sizes and have to satisfy (shown for  )
)

to ensure convergence. By  we denote the iteration step.
we denote the iteration step.
Finally, we have to solve the dual problem. For this, we compute the subgradients of the Lagrangian dual function  due to the dual optimization variables
due to the dual optimization variables  and
and  that are given by
that are given by

Applying subgradient update we obtain for variables  and
and 

Note that the projection on the nonnegative orthant by  results due to the constraints
results due to the constraints  .
.
Furthermore,  and
and  represent the subgradient step sizes, both satisfying the conditions in (44) with
represent the subgradient step sizes, both satisfying the conditions in (44) with  denoting the iteration step.
denoting the iteration step.
As one can see by considering (33), (41), (42), (45), (39), (46), and (41) two types of information are necessary. First, that the information required for the computation to take place at each and every node is the interference caused by the interfering transmissions measured at the receiving node. Second, by (42) Lagrange multipliers from neighbor nodes, for example,  and
and  are required.
are required.
The distributed routing algorithm tries to achieve an optimum coordination between the network variables  and
and  on the one hand and the dual variables
on the one hand and the dual variables  and
and  on the other hand. For the considered wireless network, this means that the distributed routing algorithm tries to achieve an optimum coordination between node buffers and capacities allocated to the links, subject to the network constraints as defined in (26).
on the other hand. For the considered wireless network, this means that the distributed routing algorithm tries to achieve an optimum coordination between node buffers and capacities allocated to the links, subject to the network constraints as defined in (26).
6. Simulation Results
In this section, we present some numerical results of the distributed RPCD algorithm as applied to a wireless mesh backhaul network. Furthermore, we compare the results with the dual decomposition method introduced by Xiao et al. in [5]. The network under consideration is a typical cellular network with hexagonal cell structure. The cells are arranged around a center cell by rings and a node is located in the center of a hexagon as depicted in Figure 3.
This models the situation where, to save infrastructure expenses like laying cable or fiber to each node in a network, we try to extend the range of given source node (center node) by intermediate nodes being wireless connected. The source node has wired backhaul connection only, while all other nodes have no wired backhaul connection and can only communicate with the wireless mesh backhaul via the source node. We require that wireless links can only be formed between nodes in adjacent rings. This means, ( ) a node can not transmit to any node that is more than one ring away, and (
) a node can not transmit to any node that is more than one ring away, and ( ) intraring communication is not allowed so that nodes belonging to the same ring have no wireless link established. Figure 4 shows the resulting directed graph of the wireless mesh backhaul network for the case where the first ring composes three, the second ring five, and the third ring the destination node only.
) intraring communication is not allowed so that nodes belonging to the same ring have no wireless link established. Figure 4 shows the resulting directed graph of the wireless mesh backhaul network for the case where the first ring composes three, the second ring five, and the third ring the destination node only.
Each intermediate node can transmit to and receive along multiple links from nodes, neither multicast nor broadcast is considered. The network is a single frequency network. For the sake of simplicity, we assume that the scheduler does not take in-band signaling users into account, rather we might interpret in-band users as additive noise. We further require in the simulations that simultaneously active links do not interfere. Hence, the SRPC problem under consideration is convex, therefore, the optimum solution is global. This means, we assume orthogonal transmission between links, possibly performed by Space Division Multiple Access (SDMA) schemes such as sending/receiving beamforming [15, 16]. Due to the setup of the wireless backhaul links, the nodes we consider are cellular base stations with high processing capability. Without loss of generality, the objective function we assume is to minimize total transmitted power with  .
.
The scenario shown in Figure 4 is denoted as [ , 3, 5, 1] scenario. So, we have 10 nodes forming a wireless mesh backhauling network with 23 edges. The simulation parameter set up is as follows. The wireless network has to transmit data of
, 3, 5, 1] scenario. So, we have 10 nodes forming a wireless mesh backhauling network with 23 edges. The simulation parameter set up is as follows. The wireless network has to transmit data of  = 10 Mbit size from the source node to the destination, but due to the delay constraint the transmission has to be completed within a maximum number of
= 10 Mbit size from the source node to the destination, but due to the delay constraint the transmission has to be completed within a maximum number of  time slots, that is,
time slots, that is,  . The bandwidth per link is
. The bandwidth per link is  = 5 MHz, the length of an time-slot is
= 5 MHz, the length of an time-slot is  ms and the radius per hexagonal cell is
ms and the radius per hexagonal cell is  m. We assume an exponential path-loss model with factor 3, but no shadow-fading. The thermal spectral noise density is
m. We assume an exponential path-loss model with factor 3, but no shadow-fading. The thermal spectral noise density is  dBm/Hz. The buffer size per node is restricted to
dBm/Hz. The buffer size per node is restricted to  Mbit. To account for power constraints we upper bound the power per node by
Mbit. To account for power constraints we upper bound the power per node by  Watt, whereas for each specific link we assume no explicit power restriction. Regarding the distributed RPCD algorithm, we use a stopping criterion based on the variables
Watt, whereas for each specific link we assume no explicit power restriction. Regarding the distributed RPCD algorithm, we use a stopping criterion based on the variables  to check for convergence. We proceed with the iteration as long as the maximum norm of two consecutive iteration steps is greater than
to check for convergence. We proceed with the iteration as long as the maximum norm of two consecutive iteration steps is greater than  . To show convergence, we apply the algorithm for a huge number of different starting points as well as for several networks, that is, [
. To show convergence, we apply the algorithm for a huge number of different starting points as well as for several networks, that is, [ , 3, 1], [
, 3, 1], [ , 3, 5, 1], [
, 3, 5, 1], [ , 3, 5, 7, 1].
, 3, 5, 7, 1].
We observe the following result.
For a given feasible starting point
 the distributed RPCD algorithm converges to an optimum solution within one step only.
the distributed RPCD algorithm converges to an optimum solution within one step only.
Since the algorithm converges globally the zero vector is always a feasible starting point.
The optimum solution is cross checked twice. First, we verify the solution by applying the NPSOL solver of TOMLAB that reflects centralized implementation. Secondly, we compare our results with another distributed algorithm, the dual decomposition approach [5]. Figure 5 shows the dual function versus iteration  . Clearly, the dual function slowly converges to the unique optimum solution (as proposed in [5], we applied the subgradient method to update the dual variables ).
. Clearly, the dual function slowly converges to the unique optimum solution (as proposed in [5], we applied the subgradient method to update the dual variables ).
Hence, it is obvious that the proposed method significantly outperforms the dual decomposition approach in terms of required iterations steps towards the optimum solution. Moreover, the distributed RPCD approach requires an inter-node communication where nodes share the power and network variables only. The dual decomposition, however, requires an extra communication of the dual variables [17]. Finally, Figure 6 shows the average rate allocation of the data values per edge, where averaging is performed over the time slots the links are active. The amount of transmitted bits is given in [Mbit] while the power values are given in [Watt]. For illustration purposes, the thickness of the links reflects the amount of data transmitted, while dotted links are never active during the entire transmission. As expected, we observe that due to the geometry of the network traffic is mainly concentrated in inner links and the algorithm use one single route from the source to the destination, although multiple path routing could be performed.
Further, we decrease the bandwidth for every link in the network and use  MHz. In Figure 7 we can observe that the algorithm can not transmit the total amount of the data over one single route anymore and multiple path routing has to be performed. The transmission of the data expands over more routes in the wireless mesh backhaul network. Nevertheless the data traffic is generally concentrated in the inner links, which can be explained with the geometry of the network.
MHz. In Figure 7 we can observe that the algorithm can not transmit the total amount of the data over one single route anymore and multiple path routing has to be performed. The transmission of the data expands over more routes in the wireless mesh backhaul network. Nevertheless the data traffic is generally concentrated in the inner links, which can be explained with the geometry of the network.
7. Conclusion
In this paper we have considered the joint routing, time scheduling and power control problem for single frequency, time-slotted wireless mesh networks. We presented an approach for optimally solving this crosslayer optimization problem while meeting the requirements, such as distributed implementation, multiple path routing, and per-hop error performance. The main contribution is the distributed Routing and Power Control Decomposition (RPCD) Algorithm, which is based on the idea of decoupling the SRPC problem into two subproblems, power control and routing, and including scheduling in the constraint set of the SRPC problem. Moreover, we presented distributed algorithms for solving both, the power control and the routing subproblem. For illustration purpose we applied the distributed RPCD algorithm to a wireless mesh backhaul network. The observed convergence results are impressive: only one decomposition step is needed to achieve the optimal solution.
Appendices
A. Proof of Theorem 1
Proof.
Choosing feasible variables  (
( ) for the problem above, we immediately see that the interference function defined by (29) is a standard interference function. Therefore, the power iteration (29) started from, say,
) for the problem above, we immediately see that the interference function defined by (29) is a standard interference function. Therefore, the power iteration (29) started from, say,  converges to a point
converges to a point  with (22). Clearly, for this point the constraints (20) are active. Moreover, in [9] it was shown that
with (22). Clearly, for this point the constraints (20) are active. Moreover, in [9] it was shown that  has the smallest objective function value for all possible choices of the variables
has the smallest objective function value for all possible choices of the variables  (
( ) with prespecified and fixed variables
) with prespecified and fixed variables  (
( ). Therefore, the constraints (20) have to be active in all solutions of the optimization problem above.
). Therefore, the constraints (20) have to be active in all solutions of the optimization problem above.
B. Proof of Lemma 1
Proof.
( ) This can be seen by differentiating the objective under consideration with respect to
) This can be seen by differentiating the objective under consideration with respect to  .
.
( ) The Hessian of the objective under consideration with respect to
) The Hessian of the objective under consideration with respect to  can be written as
can be written as

where  is a diagonal matrix with entries
is a diagonal matrix with entries

The objective is strict convex in  if and only if this Hessian is positive definite. Now, the first summand above is clearly positive semidefinite, since
if and only if this Hessian is positive definite. Now, the first summand above is clearly positive semidefinite, since  is convex in
is convex in  . Likewise, the third summand is positive semidefinite, since
. Likewise, the third summand is positive semidefinite, since  is convex in
is convex in  . Finally, the diagonal matrix
. Finally, the diagonal matrix  has nonnegative entries on the main diagonal, since
has nonnegative entries on the main diagonal, since  is strictly convex in
is strictly convex in  and
and  is monotone in
is monotone in  . Accordingly, the Hessian above is positive definite as long as one of the summands is positive definite. Assumption (a) leads to the positive definiteness of the first summand, assumption (b) leads to the positive definiteness of the last summand, while assumption (c) leads to the positive definiteness of
. Accordingly, the Hessian above is positive definite as long as one of the summands is positive definite. Assumption (a) leads to the positive definiteness of the first summand, assumption (b) leads to the positive definiteness of the last summand, while assumption (c) leads to the positive definiteness of  .
.
From this, the strict convexity under the given assumptions readily follows.
Clearly, the variables  (
( ,
,  ,
,  ) are unique in an optimum of the problem under consideration. Using (9), (10), and (14) and induction over
) are unique in an optimum of the problem under consideration. Using (9), (10), and (14) and induction over  , one easily concludes that optimal variables
, one easily concludes that optimal variables  (
( ) are unique, too.
) are unique, too.
The continuity is a classic result from parametric optimization, see, for example, [18], and follows from the strict convexity of the objective in  and from the fact that the set of feasible points is a polyhedron.
and from the fact that the set of feasible points is a polyhedron.
Remark 1.
The following remarks hold with respect to Lemma 1.
(1)The second result of Lemma 1 can be weakened a bit. In case  is not strictly convex in, say,
is not strictly convex in, say,  , it suffices to assume that the diagonal entries of the matrix
, it suffices to assume that the diagonal entries of the matrix  are sufficiently large. That amounts to saying that either
are sufficiently large. That amounts to saying that either  is sufficiently large or that
is sufficiently large or that  is sufficiently large, that is, there is certain amount of monotonicity build into the objective function (
is sufficiently large, that is, there is certain amount of monotonicity build into the objective function ( ,
,  ,
,  ).
).
(2)The convexity assumptions of Lemma 1 do not amount in assuming that  is convex, as the example
is convex, as the example  shows.
shows.
C. Proof of Lemma 2
Proof.
( ) See Theorem 1 and [9].
) See Theorem 1 and [9].
( ) This follows by noting that the solution to the problem at hand is uniquely characterized by the fixed-point equation
) This follows by noting that the solution to the problem at hand is uniquely characterized by the fixed-point equation  , the latter being a linear system in
, the latter being a linear system in  . The corresponding solution depends continuously on
. The corresponding solution depends continuously on  .
.
Remark 2.
In Lemma 2, strict monotonicity cannot be replaced by monotonicity. However, uniqueness of the results of Lemma 2 hold again if only the (unique)  -solution of the optimization problem under consideration is considered.
-solution of the optimization problem under consideration is considered.
D. Proof of Theorem 2
Proof.
The well-definedness rests on the two lemmas above, which also tell us that the maps  and
and  , mapping parameters to solutions of optimization problems, that are considered in the algorithm are point-to-point. Moreover, both maps are continuous. We call an arbitrary mapping
, mapping parameters to solutions of optimization problems, that are considered in the algorithm are point-to-point. Moreover, both maps are continuous. We call an arbitrary mapping  closed if
closed if  =
=  and
and  =
=  imply
imply  =
=  . Clearly, continuous mappings are closed, and therefore the two mappings mentioned above are closed. (See also [19, page 123],. Actually, closedness is a property usually associated with point-to-set mappings, but we only consider point-to-point mappings here. For point-to-point mappings, continuity is sufficient for closedness, and these two notions are equivalent if the set of arguments is compact.) The rest of the theorem follows the convergence proof of the coordinate descent method [19, Section
. Clearly, continuous mappings are closed, and therefore the two mappings mentioned above are closed. (See also [19, page 123],. Actually, closedness is a property usually associated with point-to-set mappings, but we only consider point-to-point mappings here. For point-to-point mappings, continuity is sufficient for closedness, and these two notions are equivalent if the set of arguments is compact.) The rest of the theorem follows the convergence proof of the coordinate descent method [19, Section  ], replacing the set
], replacing the set  =
=  with the set of feasible points for which there does not exist a feasible direction of descent: since
with the set of feasible points for which there does not exist a feasible direction of descent: since  is compact, the coupling constraint implies that
is compact, the coupling constraint implies that  is compact, too, and therefore the whole set of feasible points is compact. Accordingly, the composition of maps
is compact, too, and therefore the whole set of feasible points is compact. Accordingly, the composition of maps

that is,

is closed, see [19, page 124]. That the sequence  is monotonically decreasing (and therefore convergent) follows by construction of the sequence. We can now define the compact set
is monotonically decreasing (and therefore convergent) follows by construction of the sequence. We can now define the compact set

that is, the set of feasible points from which the algorithm does not improve objective function values any more. In the convex case this is a set of KKT-points which is the same as the set of the optimal points. It is easy to see that every converging subsequence of  converges to a point in
converges to a point in  , more precisely to a fixed point of
, more precisely to a fixed point of  (see also [20]), which is thereby a point for which no feasible direction of descent exists.
(see also [20]), which is thereby a point for which no feasible direction of descent exists.
Remark 3.
The following remarks hold with respect to Theorem 2.
-
(1)
The convexity assumptions within the theorem have mainly be imposed to guarantee that the map
 is well-defined (i.e., the solution to the corresponding optimization problem is unique). If we simply assume this well-definedness (or enforce it by, say, computing the least-squares optimal solution), we can drop the corresponding assumptions on
is well-defined (i.e., the solution to the corresponding optimization problem is unique). If we simply assume this well-definedness (or enforce it by, say, computing the least-squares optimal solution), we can drop the corresponding assumptions on 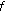 instead.
instead. -
(2)
(2)In principle, strict monotonicity of
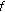 in
in  is required to obtain that
is required to obtain that  is continuous. However, what usually happens is that in step 5 the power iteration is used, which results in the computation of the unique
is continuous. However, what usually happens is that in step 5 the power iteration is used, which results in the computation of the unique  -solution to
-solution to  . In case the power iteration is replaced by another algorithm, uniqueness of the corresponding solution has to be guaranteed in a different way.
. In case the power iteration is replaced by another algorithm, uniqueness of the corresponding solution has to be guaranteed in a different way.
References
Viswanathan H, Mukherjee S: Throughput-range tradeoff of wireless mesh backhaul networks. IEEE Journal on Selected Areas in Communications 2006, 24(3):593-602.
The IEEE 802.16 Working Group on Broadband Wireless Access Standards http://www.wirelessman.org/
Cruz RL, Santhanam AV: Optimal routing, link scheduling and power control in multi-hop wireless networks. Proceedings of the 22nd Annual Joint Conference on the IEEE Computer and Communications Societies (INFOCOM '03), March-April 2003, San Francisco, Calif, USA 1: 702-711.
Li Y, Ephremides A: Joint scheduling, power control, and routing algorithm for ad-hoc wireless networks. Proceedings of the 38th Annual Hawaii International Conference on System Sciences, January 2005, Big Island, Hawaii, USA 322.
Xiao L, Johansson M, Boyd SP: Simultaneous routing and resource allocation via dual decomposition. IEEE Transactions on Communications 2004, 52(7):1136-1144. 10.1109/TCOMM.2004.831346
Boyd S, Vandenberghe L: Convex Optimization. Cambridge University Press, Cambridge, UK; 2004.
Maurer SB, Ralston A: Discrete Algorithmic Mathematics. Addison-Wesley, Reading, Mass, USA; 1991.
Eyuboglu MV, Forney GD Jr.: Trellis precoding: combined coding, precoding and shaping for intersymbol interference channels. IEEE Transactions on Information Theory 1992, 38(2, part I):301-314. 10.1109/18.119688
Yates RD: Framework for uplink power control in cellular radio systems. IEEE Journal on Selected Areas in Communications 1995, 13(7):1341-1347. 10.1109/49.414651
Dekorsy A, Fliege J, Sollner M: Optimal distributed routing and power control decomposition for wireless networks. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '07), November 2007, Washington, DC, USA 4920-4924.
Bertsekas DP, Gallager RG: Data Networks. Prentice-Hall, Englewood Cliffs, NJ, USA; 1992.
Bertsekas DP: Parallel and Distributed Computation. Prentice-Hall, Englewood Cliffs, NJ, USA; 1989.
Bertsekas DP: Nonlinear Programming. Athena Scientific, Nashua, NH, USA; 1999.
Ferizi A: Distributed routing and power control algorithms in fixed wireless networks, Diploma Thesis. University Erlangen-Nuremberg, Erlangen, Germany; 2007.
Paulraj A, Nabar R, Gore D: Introduction to Space-Time Wireless Communications. Cambridge University Press, Cambridge, UK; 2003.
Czylwik A, Dekorsy A, Chalise B: Smart antenna solutions for UMTS. In Smart Antennas–State of the Art, EURASIP Book Series on Signal Processing and Communications. Volume 3. Hindawi Publishing Corporation, Cairo, Egypt; 2005:729-758.
Chiang M: Balancing transport and physical layers in wireless multihop networks: jointly optimal congestion control and power control. IEEE Journal on Selected Areas in Communications 2005, 23(1):104-116.
Bonnans JF, Shapiro A: Perturbation Analysis of Optimization Problems, Springer Series in Operations Research. Springer, New York, NY, USA; 2000.
Luenberger DG: Introduction to Linear and Nonlinear Programming. Addison-Wesley, Reading, Mass, USA; 1973.
Zangwill WI: Nonlinear Programming: A Unified Approach. Prentice-Hall, Englewood Cliffs, NJ, USA; 1969.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ferizi, A., Dekorsy, A., Fliege, J. et al. An Active Constraint Method for Distributed Routing, and Power Control in Wireless Networks. J Wireless Com Network 2009, 656832 (2010). https://doi.org/10.1155/2009/656832
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/656832

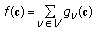
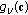 representing any linear combination of flows that egress node
representing any linear combination of flows that egress node  ,
,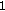 ) and (
) and ( ).
). .
. then
then 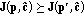 .
.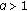 ,
, 

 is strictly convex in
is strictly convex in  for all
for all  ,
, is strictly convex in
is strictly convex in  for all
for all 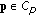 , for all
, for all 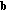 ,
,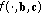 is strictly monotone in
is strictly monotone in 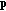 for all
for all  .
.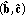 .
.


 3 5 1].
3 5 1].

 3 5 1] network.
3 5 1] network.

 : Average rate allocation, Bandwidth
: Average rate allocation, Bandwidth
 MHz.
MHz.

 : Average rate allocation, Bandwidth
: Average rate allocation, Bandwidth
 MHz.
MHz.
 is well-defined (i.e., the solution to the corresponding optimization problem is unique). If we simply assume this well-definedness (or enforce it by, say, computing the least-squares optimal solution), we can drop the corresponding assumptions on
is well-defined (i.e., the solution to the corresponding optimization problem is unique). If we simply assume this well-definedness (or enforce it by, say, computing the least-squares optimal solution), we can drop the corresponding assumptions on 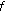 instead.
instead.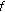 in
in  is required to obtain that
is required to obtain that  is continuous. However, what usually happens is that in step 5 the power iteration is used, which results in the computation of the unique
is continuous. However, what usually happens is that in step 5 the power iteration is used, which results in the computation of the unique  -solution to
-solution to  . In case the power iteration is replaced by another algorithm, uniqueness of the corresponding solution has to be guaranteed in a different way.
. In case the power iteration is replaced by another algorithm, uniqueness of the corresponding solution has to be guaranteed in a different way.