- Research Article
- Open access
- Published:
OFDMA Cellular Networks with Opportunistic Two-Hop Relays
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 702659 (2009)
Abstract
We investigate the benefits of two-hop opportunistic relay in time division duplex (TDD) OFDMA cellular network configurations. The paper starts with a short analytical model for the two-hop opportunistic relay. The model expresses the probability of finding a suitable relay node in the presence of lognormal fading and it allows the computation of the expected number of out-of-coverage nodes, as well as the end-to-end spectrum efficiency increase due to opportunistic relaying. The paper then presents results for Monte Carlo simulations of opportunistic relay in some realistic scenarios. Specifically, the simulations consider two scenarios. The first scenario uses the propagation model and a wide-area 19-cell configuration specified in 802.16 OFDMA cellular standard evaluation methodologies. In the second scenario, a Manhattan-like 19-cell topology is used. Our simulations show 11% to 33% in throughput increase when the opportunistic relay technology is used. Our results evaluate the benefits of the opportunistic relay in both scenarios in terms of coverage extension and throughput increase.
1. Introduction
The use of relays to extend or improve throughput and coverage is a well-covered subject in literature. First introduced by the European Telecommunication Standards Institute (ETSI) in 1996 [1, 2], the concept of Opportunity-Driven Multiple Access (ODMA) is defined as a UMTS communications relaying protocol standard. ODMA has been adopted by the 3rd Generation Partnership Project (3GPP) to improve the efficiency of UMTS networks using the TDD mode. In ODMA each mobile phone can act as a repeater so the call reaches its destination via a number of hops. Unfortunately, the concept was never implemented in a product. The concept of relaying was recently further developed in the IEEE 802.16j standard [3, 4].
A number of papers are devoted to the performance of relay systems. In [5], the authors use a 3D Markov model to evaluate the impact of ODMA radio resource management for packet transmissions in the UMTS Terrestrial Radio Access Network (UTRAN). In paper [6], the authors analyze the capacity of ODMA in relation to the coverage of a cell. It is shown that after the coverage limit of a non-ODMA UTRAN Time Division Duplex (TDD) system has been reached, ODMA will provide enhanced coverage. The coverage extension of WiMax (802.16) cellular networks is addressed in [7], and the UL performance of an IEEE 802.16j system is investigated in [8]. In this paper, the authors use two-hop relaying for forwarding information from out-of-coverage mobile subscribers to the base station (BS). Using simulations, they show that the two-hop relay will increase the cell radius at the expense of cell throughput. In [9], the authors use a Monte Carlo simulation to investigate the throughput increase in a TDD CDMA cellular multi-hop configuration. Both uniform and nonuniform traffics are investigated. Using simulations, the authors show that the throughput gain becomes insignificant for more than 3 hops.
In our paper, we analyze the concept of two-hop opportunistic relay as a means of attaining throughput increase in 802.16 OFDMA networks. This type of relaying is termed "opportunistic" because it takes place only when the end-to-end throughput is increased by relaying relative to the single hop connection. The concept of opportunistic relay is different from the fixed relay approach proposed in 802.16j. By opportunistic relaying, we mean communication between a base station (BS) and a mobile station (MS) via another MS that serves as a relay. In the opportunistic relaying approach, two MSs can directly communicate via an inband mobile-to-mobile (M2M) connection. The opportunistic relaying concept is related to the hybrid networks presented in [10–14]. In these papers, the authors define the hybrid networks as cellular networks augmented with ad hoc M2M connectivty. The cited papers though do not investigate the system capacity of the hybrid solutions. In [15], the authors offer an asymptotic analysis of the capacity of hybrid networks under a fixed interference range and k-nearest-cell routing strategy in the absence of lognormal fading.
Although our paper considers a network similar to those in [7, 16], we have several novel contributions in our paper. A new analytical model is proposed for opportunistic relay, with the coverage increase analyzed in terms of out-of-coverage subscribers and not in terms of cell radius increase. The spectrum efficiency increase is studied in more realistic environments specified in the IEEE 802.16m evaluation methodology. In addition, the end-to-end link throughput increase is also investigated.
The paper is organized as follows. In Section 2, we propose a new analytic model for two-hop opportunistic relays. Section 3 is based on the proposed analytical model that gives some insights into two-hop relaying in cellular networks. In Section 4, we present our simulation results. Section 5 describes some real system implementation issues. Finally, we draw conclusions in Section 6. This paper extends our previous effort presented in [17].
2. Analytic Aspects of Opportunistic Relaying
Simply speaking, opportunistic relaying stands for relaying when there is a benefit and a relay is available. An opportunistic relay is a two-hop topology consisting of a base station (BS), a mobile station relay (RS) that performs the relay, and a mobile station that becomes relayed (MS). In the proposed approach, all MSs are capable of relaying data to and from other MSs. Therefore, each MS can potentially become an RS.
To analyze the benefits of two-hop opportunistic relays, we consider an OFDMA 802.16 cellular network. The uplink and the downlink are assumed to work independently as specified in 802.16 standards. An RS uses time division duplexing to forward data to and from BS. The mobile-to-mobile connection between RS and MS takes place in a separate subframe called the ad hoc zone. This subframe is proposed as an addition to the standard 802.16 frame which consists of downlink and uplink subframes.
We start by developing a simple analytical model for the two-hop opportunistic relay. In this paper, we use the term direct link to indicate the link between a base station and a mobile relay station or to indicate the link between BS and a mobile subscriber; we use the term mobile-to-mobile link to indicate the link between a relay station and a mobile station. In our theoretical model, an opportunistic relay is activated in the absence of external interference if the following three conditions are simultaneously satisfied.
(i)Direct link received power at the MS is less than an arbitrary value  , that is,
, that is,  . This value corresponds to the the minimum received power for cellular coverage and is equivalent to a spectrum efficiency
. This value corresponds to the the minimum received power for cellular coverage and is equivalent to a spectrum efficiency  , that is,
, that is,  (obtained via Shannon law). The Spectrum Efficiency (SE) is defined as the throughput per subcarrier in bits/s/Hz units or equivalently as bits/symbol/subcarrier units.
(obtained via Shannon law). The Spectrum Efficiency (SE) is defined as the throughput per subcarrier in bits/s/Hz units or equivalently as bits/symbol/subcarrier units.
(ii)Direct link received power at the RS is  watts above the cellular coverage limit
watts above the cellular coverage limit  , that is,
, that is,  watts, which corresponds to
watts, which corresponds to  bits/s/Hz. In other words, the direct link spectrum efficiency at RS is at least
bits/s/Hz. In other words, the direct link spectrum efficiency at RS is at least  bits/s/Hz greater than the direct link SE at MS.
bits/s/Hz greater than the direct link SE at MS.
-
(iii)
Mobile-to-mobile (M2M) link received power at MS is
 watts, which corresponds to spectrum efficiency
watts, which corresponds to spectrum efficiency 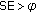 bits/s/Hz.
bits/s/Hz.
The received power at the receiver is the result of the difference between the transmitted power and the sum of the propagation pathloss and the lognormal fading. In other words,

where  represents the received power at distance
represents the received power at distance  from transmitter;
from transmitter;  and
and  represent the transmit power and, respectively, the power loss for the reference distance
represent the transmit power and, respectively, the power loss for the reference distance  (usually one meter). The coefficient
(usually one meter). The coefficient  represents the pathloss exponent and
represents the pathloss exponent and  denotes the lognormal fading that has a normal distribution with zero mean and standard deviation
denotes the lognormal fading that has a normal distribution with zero mean and standard deviation  . In fact, a more accurate model of the lognormal fading is a Gaussian random 2D field with a given decorrelation distance
. In fact, a more accurate model of the lognormal fading is a Gaussian random 2D field with a given decorrelation distance  . In other words, the correlation between the fading values at any two arbitrary points depends only on their relative distance
. In other words, the correlation between the fading values at any two arbitrary points depends only on their relative distance  . We use for the correlation coefficient the model
. We use for the correlation coefficient the model  , which was first proposed in [18].
, which was first proposed in [18].
Observe that in the absence of interference, the received power  expressed in dB is a normal random variable due to lognormal fading. The corresponding random variables
expressed in dB is a normal random variable due to lognormal fading. The corresponding random variables  and
and  are correlated and their correlation is distance dependent. The M2M received power
are correlated and their correlation is distance dependent. The M2M received power  is not correlated with the other two random variables, but is actually distance-based self-correlated. The joint normal distribution of these three random variables can be written as follows:
is not correlated with the other two random variables, but is actually distance-based self-correlated. The joint normal distribution of these three random variables can be written as follows:

where  represents the covariance matrix and
represents the covariance matrix and  represents the vector of the average received powers (in dB) from the BS at the MS, from the BS at the RS, and, respectively, from the RS at the relayed MS as follows:
represents the vector of the average received powers (in dB) from the BS at the MS, from the BS at the RS, and, respectively, from the RS at the relayed MS as follows:

The covariance matrix

where  represents the distance between MS and RS,
represents the distance between MS and RS,  represents lognormal decorrelation distance for the direct link (usually 50-meters),
represents lognormal decorrelation distance for the direct link (usually 50-meters),  represents the standard deviation of the lognormal fading of the direct link (5–8 dB), and
represents the standard deviation of the lognormal fading of the direct link (5–8 dB), and  represents the standard deviation of the lognormal fading of the M2M link (8–10 dB). In our model, there is no correlation between direct link lognormal fading and the M2M lognormal fading.
represents the standard deviation of the lognormal fading of the M2M link (8–10 dB). In our model, there is no correlation between direct link lognormal fading and the M2M lognormal fading.
Using the above notations, the probability of MS located at distance  from BS to relay through a station RS located at distance
from BS to relay through a station RS located at distance  from BS and
from BS and  from MS, given that MS is in low coverage, (
from MS, given that MS is in low coverage, ( ) becomes
) becomes

where  .
.
If the users' distribution is modeled by a spatial Poisson process, the probability of existence of  users in area
users in area  is
is  , where
, where  represents the user density in unit area. If
represents the user density in unit area. If  defines an area element in polar coordinates given by
defines an area element in polar coordinates given by  , the probability of
, the probability of  users (MS) existence in the element area is
users (MS) existence in the element area is  . Each of these users has a probability of being a relay equal to
. Each of these users has a probability of being a relay equal to  . Therefore, if there are
. Therefore, if there are  users in the unit area element, the expected number of relays is
users in the unit area element, the expected number of relays is  . The expected number of relays in the area element is given by
. The expected number of relays in the area element is given by

The expected number of all potential relays surrounding MS located at an arbitrary distance  from the BS is expressed as
from the BS is expressed as

This number must be equal or greater than one in order for an opportunistic relay to take place.
The analytic approach allows the definition of a number of metrics of interest for the opportunistic relay scenario. The number of out-of-coverage MS (in the absence of opportunistic relay) in the cell radius is given by the number of mobiles in a cell radius having the received signal strength lower than the minimum threshold value  :
:

The number of relayed out-of-coverage MS is given by:

where the function I is defined as

The relative spectrum efficiency increase is defined as

The condition for a positive SE increase gives the limits of direct link SE  .
.
3. Opportunistic Relay Insights
To gain insight into the opportunistic relay behavior, we start with a simple analysis of the preceding analytical results by neglecting the lognormal fading and assuming that spectrum efficiency is given by the well-known Shannon capacity expression.

where  represents the frequency bandwidth,
represents the frequency bandwidth,  is the Boltzman constant, and
is the Boltzman constant, and  is the absolute temperature. Furthermore, we consider that the MS expected coverage radius
is the absolute temperature. Furthermore, we consider that the MS expected coverage radius  is fixed. This value is derived from the minimum control rate required between MS and its relay as a function of the separation distance. When MS is opportunistically relayed to increase its throughput, it selects from its coverage area the MS with the best direct link SNR and then verifies the conditions for the throughput increase (provided in Section 2) are satisfied. If the expected throughput increase is satisfactory, the MS uses the opportunistic relay. Otherwise it uses the direct link to the base.
is fixed. This value is derived from the minimum control rate required between MS and its relay as a function of the separation distance. When MS is opportunistically relayed to increase its throughput, it selects from its coverage area the MS with the best direct link SNR and then verifies the conditions for the throughput increase (provided in Section 2) are satisfied. If the expected throughput increase is satisfactory, the MS uses the opportunistic relay. Otherwise it uses the direct link to the base.
Figure 2 shows the rate as a function of distance from BS in the absence of lognormal fading. The exponential curve from Figure 2 is derived from (12). Figure 3 shows the spectrum efficiency (SE) for the direct link (SE from BS) and for the end-to-end opportunistic relay case (SE relayed). The RS-MS M2M link has minimum required SE = 5 bits/symbol/carrier. The relay (RS) is selected in a limited radius ( ) around the MS. The figure shows the end-to-end SE for
) around the MS. The figure shows the end-to-end SE for  ,
,  and
and  m. In this figure the lognormal fading is not considered.
m. In this figure the lognormal fading is not considered.
From Figure 3, notice that only stations far from BS benefit from opportunistic relaying. For MS, it is advantageous to use the direct link when it is close to the BS and to use the opportunistic relay when it is close to the cell border. The second observation is that a shorter M2M radius  corresponds to a lower increase in the end-to-end spectrum efficiency. The shorter the M2M radius, the farther the MS must be from the BS to benefit from an opportunistic relay.
corresponds to a lower increase in the end-to-end spectrum efficiency. The shorter the M2M radius, the farther the MS must be from the BS to benefit from an opportunistic relay.
In Figure 3, we observe for instance, that MS with coverage range of 300 m will start relaying when they are farther than 1100 m from BS, while those MS with M2M radius of 200 m start relaying when they are farther than 1250 m from BS. Also, MS with a lower M2M coverage will have less overall throughput gain.
Opportunistic relaying becomes more attractive in the presence of lognormal fading. In Figure 4, the lognormal fading spreads the spectrum efficiency values above and below the average direct link pathloss curve (i.e., SE from BS (average)). Therefore, there are more chances for stations with poor coverage to find an attractive relay in their vicinity. As a function of distance, the pathloss (in dB) between BS and MS (or RS) has a normal distribution. Therefore there is a 31% probability that in one location MS has a direct link SNR one  dB higher than the average SNR for that location, where the 31% probability corresponds to one
dB higher than the average SNR for that location, where the 31% probability corresponds to one  deviation from the average in a normal distribution. On the other hand, at the same location, in the presence of lognormal fading there is a 31% chance that MS receives one
deviation from the average in a normal distribution. On the other hand, at the same location, in the presence of lognormal fading there is a 31% chance that MS receives one  dB lower SNR than the average SNR for that distance.
dB lower SNR than the average SNR for that distance.
Figure 4 shows the SE curves for the direct link in the presence of lognormal fading. The figure shows the SE for the average pathloss (SE from BS average) and the SE of one  deviations of the pathloss below and above the average (SE from BS 31% high, SE from BS 31% low). In addition, the same figure shows the end-to-end SE curve when the relay (RS) experiences a lognormal fading less than one
deviations of the pathloss below and above the average (SE from BS 31% high, SE from BS 31% low). In addition, the same figure shows the end-to-end SE curve when the relay (RS) experiences a lognormal fading less than one  deviation lower than average and the distance RS-MS is not limited (SE with RS pathloss limited). A second end-to-end SE curve represents the end-to-end SE when the relay (RS) is selected from all the potential relays in a radius
deviation lower than average and the distance RS-MS is not limited (SE with RS pathloss limited). A second end-to-end SE curve represents the end-to-end SE when the relay (RS) is selected from all the potential relays in a radius  of MS (SE radius limited
of MS (SE radius limited  m), that is the relays's pathloss is not limited by the one
m), that is the relays's pathloss is not limited by the one  deviation constraint as in the previous curve. Users with average or lower direct link spectrum efficiency benefit more from relaying while mobile subscribers with a higher SE can become relays for other MS. In the presence of lognormal fading relaying becomes efficient at closer distance from BS (around 650 m in this figure). When there is no constraint of the M2M radius (
deviation constraint as in the previous curve. Users with average or lower direct link spectrum efficiency benefit more from relaying while mobile subscribers with a higher SE can become relays for other MS. In the presence of lognormal fading relaying becomes efficient at closer distance from BS (around 650 m in this figure). When there is no constraint of the M2M radius ( ), the pool of the potential relays is increased and a better relay can be selected. In this case even the MS with a good direct link starts relaying. However, in real life the M2M relaying radius is reduced by the propagation conditions between the RS and MS. Both the RS and the MS are relatively low height (1.5 m) and therefore the propagation range is shorter.
), the pool of the potential relays is increased and a better relay can be selected. In this case even the MS with a good direct link starts relaying. However, in real life the M2M relaying radius is reduced by the propagation conditions between the RS and MS. Both the RS and the MS are relatively low height (1.5 m) and therefore the propagation range is shorter.
One also observes that those users farther from the BS have a larger benefit from the opportunistic relaying and have a relative higher increase in the spectrum efficiency. For instance, in the presence of the lognormal fading at a distance of 1600 m from the BS, the users with average spectrum efficiency could double their SE, while low SE users at the same distance could triple their SE when relaying.
4. Simulation Results
The concept of opportunistic relay was implemented in Monte Carlo simulations using a Matlab based system simulator. The system configuration and parameters were chosen to be representative of typical system deployments, although the cell sizes vary by operator and by environment. Most parameters were recommended by the IEEE 802.11m Evaluation Methodology Document (EMD) [19].
The simulator models a system configured with 1000 m cell radius in a 19-cell topology (Figure 5). Each cell has three sectors and a 70 degree antenna beamwidth serves each sector.  MIMO is assumed for both the BS and MS. Base station antenna height is 32-meters, and MS height is 1.5-meters. The carrier frequency is 2.5 GHz. The total bandwidth is 10 MHz divided into 48 subchannels. The MS transmit power is 23 dBm and is spread over a subset of all 48 subchannels, while the BS transmits at 33 dBm over all subchannels. The simulations use a composite of an exponential path-loss [19] and log-normal fading model. Lognormal fading for direct link had a standard deviation of 8 dB and decorrelation distance of 50-meters and it was expressed as the weighted sum of a common component to all cell sites and an independent component for each cell site. The Rayleigh fading is implemented via the SNR curves used to calculate SE.
MIMO is assumed for both the BS and MS. Base station antenna height is 32-meters, and MS height is 1.5-meters. The carrier frequency is 2.5 GHz. The total bandwidth is 10 MHz divided into 48 subchannels. The MS transmit power is 23 dBm and is spread over a subset of all 48 subchannels, while the BS transmits at 33 dBm over all subchannels. The simulations use a composite of an exponential path-loss [19] and log-normal fading model. Lognormal fading for direct link had a standard deviation of 8 dB and decorrelation distance of 50-meters and it was expressed as the weighted sum of a common component to all cell sites and an independent component for each cell site. The Rayleigh fading is implemented via the SNR curves used to calculate SE.
The simulations used two system environments for the pathloss and user distribution. The first environment uses a statistical model of a metropolitan system deployment that is representative of typical BS to MS direct link. The model associated with this type of environment gives a good first order approximation of the system performance, but requires artificial constraints or unrealistic expression of the propagation between MS and RS. The second environment attempts to enhance the propagation characteristics of an urban area where some of the RS-MS (opportunistic) link connections experience severe pathloss found around street corners and through one or more building walls. In addition, the second environment allows the use of the idle (inactive) users, while in the first environment the relaying is done by active users; that is users that are already established a call.
The pathloss from BS to MS is defined in the 802.16m Evaluation Methodology Document (EMD) [19] as the baseline test model for urban/suburban pathloss as follows:

In addition, the pathloss for the M2M link is an exponential pathloss with a randomly selected pathloss exponent from the set 2.4, 3.1, and 4.2. These exponents correspond to line of sight propagation below the tree canopy, above the tree canopy and respectively non-line of sight propagation. The lognormal (shadow) fading for the M2M link has standard deviation of 6 dB and it was implemented as the sum of two lognormal components each corresponding to the lognormal fading around each end of the M2M link. Figure 6 presents a snapshot of the MS-MS pathloss versus distance in the presence of lognormal fading.
The M2M pathloss exponents were estimated from RF propagation measurements in a suburban environment; the transmitter and the receiver antennas were at 1.5-meters height and they were placed on perpendicular streets at various distances from the street's intersection.
In each drop, a number of active users were uniformly placed in the simulation space. Each active user evaluates its direct link spectral efficiency, versus the relayed spectral efficiency and selects another active user as a relay if it potentially improves its end-to-end spectral efficiency. A threshold of  dB corresponding to bits/symbol/subcarrier was used to distinguish between in coverage and out of coverage nodes. In order to better capture the out of cell interference, the results were collected only in the central cluster of 7 cells.
dB corresponding to bits/symbol/subcarrier was used to distinguish between in coverage and out of coverage nodes. In order to better capture the out of cell interference, the results were collected only in the central cluster of 7 cells.
The benefits of the opportunistic relays in terms of the number of out of coverage (OOC) users and respectively the cell average throughput increase are presented in Table 1. The throughput increase is a function of the increase in spectral efficiency for a relayed connection versus a direct link connection of the MS with the BS. Figure 7 shows the cumulative distribution (CDF) of the spectrum efficiency distribution for the opportunistic relay use versus the non-relayed scenario.
The second system simulation environment was selected to represent a Manhattan like topology. The Manhattan style environment consists of a 100 m street grid with buildings occupying the space between streets. The Winner pathloss model from the 802.16m EMD [19] was used for outdoor to indoor building penetration from BS to MS as follows:

where  and
and  .
.  is also defined in the 16 m EMD as the baseline test model for urban/suburban pathloss as described previously. In addition, a M2M pathloss model was used for MS-MS connections based on field measurements for Line-of-sight (LOS), around a street corner, and into buildings. Pathloss exponents are used in an exponential pathloss model between the MSs corresponding to these environments. When the environment contains streets and buildings, the specific exponents used for this environment were 2.4 LOS, 3.1 around corner
is also defined in the 16 m EMD as the baseline test model for urban/suburban pathloss as described previously. In addition, a M2M pathloss model was used for MS-MS connections based on field measurements for Line-of-sight (LOS), around a street corner, and into buildings. Pathloss exponents are used in an exponential pathloss model between the MSs corresponding to these environments. When the environment contains streets and buildings, the specific exponents used for this environment were 2.4 LOS, 3.1 around corner  100 m,
100 m,  around corner, 4.2 through one exterior wall, and 5.1 through multiple exterior walls.
around corner, 4.2 through one exterior wall, and 5.1 through multiple exterior walls.
Two system configurations were modeled with this Manhattan environment to contrast two typical system deployments. The first configuration consists of cells with a 750-meter radius and a BS transmits power of 46 dBm in a 19-cell topology as specified in 802.16m EMD. The second configuration increases the cell size to 1000-meter radius while lowering the BS transmit power to 33 dBm.
To evaluate the potential for opportunistic relay, we assume that the total user density is made up of idle and active users. This means that both active and idle MS are permitted to relay. Initially, for these simulations we chose a total user density (active + idle) of 160 users/km2 where 5% of users are assumed to be active in a call (i.e., 8 users/km2). Later, we increase the percent of active users.
As with the first environment, results are tabulated from the center cluster of 7 cells from the 19-cell configuration of this Manhattan environment. In this simulation environment, all MS that are out-of-coverage are excluded from the results. Out-of-coverage uplink occurs when MS cannot reach BS at QPSK rate with 4 repetitions. Out-of-coverage direct link occurs when BS cannot reach MS at QPSK rate with 2 repetitions.
The benefit of opportunistic relay for the 750-meter cell radius configuration is contrasted with the benefits of opportunistic relay for the 1000-meter cell radius configuration in Table 2. In Table 2, the results for the average system throughput gain are presented, as well as the relay-only throughput gain when examining only the benefit to the relayed users. The average throughput gain represents the spectral efficiency of all users in the system assuming that all users in the system are in the best connection configuration (i.e., relaying when it is beneficial) versus all users in the system are in direct link (none of them relayed). The relay-only gain is computed the same way except that only the users that end up being relayed are considered in the gain analysis.
Additional results for the 750-meter cell configuration are shown in Figures 8 and 9. Figure 8 illustrates the distance between MS and its relay (RS) for all relay occurrences. Figure 9 illustrates the distance between every MS that is relayed and its BS that ultimately serves that MS. Figure 8 shows that the distance between the relayed MS and the relay RS is relatively small compared to the distance between the relayed MS and the BS, which is presented in Figure 9. Furthermore, Figure 9 shows that not all relayed MS are at the fringe of the cell. We noticed in our simulations that the cell radius does not impact the distance between the relayed MS and the relay MS, however, an increase in cell radius from 750 m to 1000 m causes the mean distance from relayed MS to BS to shift proportionally to the increase in cell radius.
Assuming a fixed user density of 160 users/sq. km, the impact of increasing the percent of active users is shown in Table 3.
Unlike the results shown in Table 1 from the first statistically modeled simulation environment, we see in Table 3 that while the average throughput increases significantly with relays through idle users, the percent of active users has little impact on the average throughput gain. This is because the number of idle users dominates the user density to provide an opportunistic relay. Consequently, the throughput gains remain constant. We also see that a little less than 50% of the active users are relayed, but only 2–4% of the idle user base is actively performing a relay.
5. Real System Implementation Issues
The results presented in Section 4 were obtained from a system simulator designed to model IEEE 802.16m system deployments. A couple different approaches are possible to enable Opportunistic Relay connections with the physical layer frame structure of IEEE 802.16m. The 802.16m frame structure is divided in time into 8 subframes. The use of these subframes may vary, but one example use divides the subframes evenly between downlink (DL) and uplink (UL) communications. Each subframe consists of 6 symbol times. In a 10 MHz channel bandwidth, the individual subcarriers are divided into 48 subchannels. The 48 subchannels represent the resources that can be allocated to individual users. Multiple subchannels can be allocated per user depending on the number of bits to communicate and the channel conditions of the allocated subchannels.
One approach to enable Opportunistic Relay is to reserve an UL subframe for communications between MS in all opportunistic relay configurations. This UL subframe is designated as an ad hoc zone (AHZ). The presence of the AHZ is determined by traffic requirements for MS relay as well as the overall resource demands for non-relay connections (which have a higher priority for resource allocations). When the traffic demands for opportunistic relay communications are low, the AHZ may not be present in every frame. When the system demand is very high, the AHZ may not be present in any frame. The AHZ is depicted in Figure 10.
The use of an AHZ provides several advantages, but also has some disadvantages. OFDM data symbols in an AHZ can be allocated as logical channels. Logical channels enable a variety of traffic and control uses. For example, a control channel could be implemented to advantageously enable an opportunistic relay communication between an out-of-coverage MS with an in-coverage MS. The AHZ also allows the mitigation of various forms of interference when the AHZ is defined within one of the UL subframes since this would insure that all mobile-to-mobile communications occur at the same time independent other UL and DL transmissions within the system. However, the AHZ does occupy one fourth of all UL resources. When the number of opportunistic relay connections is small, there will be unused UL resources within the AHZ that reduce overall system capacity since the resources cannot be assigned to any other user. Hence, this is the reason for reducing the presence of the AHZ under light and heavy system demands. Finally, the AHZ competes for UL subframe resources with infrastructure relay (i.e., 802.16j) which also occupies a full UL subframe.
Regarding signaling overhead, our proposal utilizes a dedicated Ad Hoc Relay Zone within a single subframe, and this ad hoc zone has two logical channels dedicated for signaling between nodes that perform a relay, nodes that are relayed, or nodes that are involved in a direct link connection. The Ad Hoc Relay Zone is dynamically allocated to match traffic demands for relay and direct link connections. Our analysis shows that the signaling control overhead is 0.65% under optimum conditions and 2.6% under impaired channel conditions. This overhead can be reduced to 0% under heavy system loading where the ad hoc zone is not required.
For these system simulations, the use of an AHZ was assumed. However, an alternate approach to enable Opportunistic Relay allows subchannel resources to be allocated for MS to MS communications within any of the uplink subframes. The advantage of this approach is that no UL resources are wasted when the demand for opportunistic relay is sparse. This reduces the overall complexity of managing system resources. However, the disadvantage of this approach is the inability to enable opportunistic relay to out-of-coverage MS, in other words the opportunistic relay would only be used to improve throughput for MS in poor coverage. An additional disadvantage is the increased likelihood of near/far interference from UL transmissions of non-opportunistic relay connections. This is because the PMP (point-to-multi-point) connections are sharing the same subframe as the mobile-to-mobile connections of the opportunistic relay connections. A future study will contrast the performance of the AHZ approach with the no-AHZ approach.
6. Conclusions
In the present paper, we investigate the benefits of two-hop opportunistic relays in OFDMA cellular networks. The paper presents a simple statistical model for two-hop relay in cellular networks. The proposed model allows the estimation of probability of relaying for throughput increase and coverage extension. The benefits of the opportunistic relays, in terms of coverage increase and end-to-end spectrum efficiency increase, are further studied via realistic Monte Carlo simulations. Our simulations show 11% to 33% in throughput increase when the opportunistic relay technology is used. Higher gains are observed in city-like environments. In addition, the simulations exhibited a significant reduction in the number of out-of-coverage nodes. Both the analytical model and the computer simulations show that the benefits of cooperative relays are increasing with the increase in user density. We hope that our results provide a better understanding of the opportunistic relay technology in cellular networks and will contribute to the acceptance of this technology in the cellular standards.
References
3rd generation partnership project; technical specification group radio access network; opportunity driven multiple access(3g tr 25.924 version 1.0.0) December 1999, http://www.3gpp.org/
Aggélou GN, Tafazolli R: On the relaying capability of next-generation GSM cellular networks. IEEE Personal Communications 2001, 8(1):40-47. 10.1109/98.904898
IEEE standard for local and metropolitan area networks part 16: air interface for fixed broadband wireless access systems 2004, http://www.wirelessman.org
Draft standard for local and metropolitan area networks—part 16: air interface for fixed and mobile broadband wireless access systems-multihop relay specification 2004, http://www.wirelessman.org
Lin P, Lai W-R, Gan C-H: Modeling opportunity driven multiple access in UMTS. IEEE Transactions on Wireless Communications 2004, 3(5):1669-1677. 10.1109/TWC.2004.833446
Rouse T, McLaughlin S, Haas H: Coverage-capacity analysis of opportunity driven multiple access (ODMA) in UTRA TDD. Proceedings of 2nd International Conference on 3G Mobile Communication Technologies (3G '01), 2001 252-256.
Muller C, Klein A, Wegner F: Coverage extensionof wimax using multihop in low user density environment. Proceedings of the 11th International OFDM Workshop, Hamburg, Germany, August 2006
Visotsky E, Bae J, Peterson R, Berryl R, Honig M: Net 22-3: on the uplink capacity of an 802.16j system. Proceedings of IEEE Wireless Communications and Networking Conference (WCNC '08), April 2008 2657-2662.
Cho J, Haas ZJ: Throughput enhancement by multi-hop relaying in cellular radio networks with non-uniform traffic distribution. Proceedings of the 58th IEEE Vehicular Technology Conference (VTC '03), October 2003, Jeju, South Korea 3065-3069.
Lin Y-D, Hsu Y-C: Multihop cellular: a new architecture for wireless communications. Proceedings of the 19th Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '00), March 2000, Tel Aviv, Israel 3: 1273-1282.
Gruber I, Bandouch G, Li H: Ad hoc routing for cellular coverage extension. Proceedings of the 57th IEEE Vehicular Technology Conference (VTC '03), April 2003, Jeju, South Korea 57: 1816-1820.
Wu H, Qiao C, De S, Tonguz O: Integrated cellular and ad hoc relaying systems: iCAR. IEEE Journal on Selected Areas in Communications 2001, 19(10):2105-2115. 10.1109/49.957326
Luo H, Meng X, Ramjee R, Sinha P, Li L: The design and evaluation of unified cellular and ad hoc networks. IEEE Transactions on Mobile Computing 2007, 6(9):1060-1074.
Wu J, Jaseemuddin M, Esmailpour A: Integrating UMTS and mobile ad hoc networks. Proceedings of the IEEE International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob '06), June 2006 196-204.
Liu B, Liu Z, Towsley D: On the capacity of hybrid wireless networks. Proceedings of the 22nd Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '03), April 2003, San Francisco, Calif, USA 2: 1543-1552.
Law LK, Krishnatnurthy SV, Faloutsos M: Capacity of hybrid cellular-ad hoc data networks. Proceedings of the 27th Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '08), 2008, Phoenix, Ariz, USA 1606-1614.
Calcev G, Bonta J: Opportunistic two-hop relays for OFDMA cellular networks. Proceedings of the IEEE Globecom Workshops (GLOBECOM '08), December 2008 1-6.
Gudmundson M: Correlation model for shadow fading in mobile radio systems. Electronics Letters 1991, 27(23):2145-2146. 10.1049/el:19911328
Project 802.16m evaluation methology document IEEE Unapproved Draft Std P802.16m, March 2008, http://www.wirelessman.org/
Aknowledgment
The authors wish to thank to the anonymous reviewers for their suggestions and comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Calcev, G., Bonta, J. OFDMA Cellular Networks with Opportunistic Two-Hop Relays. J Wireless Com Network 2009, 702659 (2009). https://doi.org/10.1155/2009/702659
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/702659
 watts, which corresponds to spectrum efficiency
watts, which corresponds to spectrum efficiency 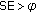 bits/s/Hz.
bits/s/Hz.








