- Research Article
- Open access
- Published:
Block Interleaved Frequency Division Multiple Access for Power Efficiency, Robustness, Flexibility, and Scalability
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 720973 (2009)
Abstract
The multiple access solution in an IMT-Advanced mobile radio system has to meet challenging requirements such as high throughput, low delays, high flexibility, good robustness, low computational complexity, and a high power efficiency, especially in the uplink. In this paper, a novel multiple access scheme for uplinks denoted as B-IFDMA is presented. We show that this scheme is able to provide equal or better error rate performance than the Single-Carrier Frequency Division Multiple Access (SCFDMA) schemes IFDMA and LFDMA, when considering realistic channel estimation performance at the receiver and no reliable channel state information at the transmitter. We also show that B-IFDMA provides better amplifier efficiency than OFDMA and can provide better end-to-end energy efficiency than IFDMA and LFDMA. Moreover, the scheme shows a promisingly high robustness to frequency-offsets and Doppler spread. Thus, this scheme can be regarded as a promising solution for the uplink of future mobile radio systems.
1. Introduction
Future mobile communication systems need to efficiently support fully packet-based services with largely different requirements on data rates, ranging from a few kbps to hundreds of Mbps, and largely varying Quality of Service (QoS) requirements. The systems need to flexibly support deployment in various propagation scenarios ranging from isolated hot spots to wide area cellular, including support for high speed trains. In addition, they need to support deployment in various spectrum allocation scenarios with system bandwidths up to 100 MHz at a carrier frequency of several GHz, cf. [1–5]. These system requirements imply that the multiple access solution in an IMT-Advanced mobile radio system has many challenges to meet.
It has been shown feasible to implement a fully synchronous network, [6, 7]. Thus, resources can be allocated based on a chunk concept, where a chunk is a time-frequency resource unit. With multiple antennas, spatial reuse of chunks is enabled and denoted as chunk layers [2, 4, 5, 8, 9]. The chunk concept is adopted in 3GPP Long Term Evolution (LTE), where a chunk is denoted as Resource Block. The chunk size is chosen in such a way that it experiences essentially flat fading in its time-frequency extent, also in largely frequency selective channels and for users at vehicular speeds.
With channel quality information (CQI) available at the transmitter it is possible to adapt to the small-scale fading of the chunk resources, so-called frequency-adaptive (FA) transmission [9]. Adaptive Orthogonal Frequency Division Multiple Access (OFDMA) with a chunk-based Time Division Multiple Access (TDMA) component is such an FA multiple access scheme [9]. Adaptive TDMA/OFDMA can provide a large increase in the system capacity, also in presence of channel prediction errors due to gains in multiuser scheduling and chunk-wise link adaptation [10, 11]. This is very important for high cell load situations. FA transmission is best suited for scenarios with favorable channel conditions such as high Signal to Interference and Noise Ratios (SINR), and reasonably low speeds [10]. FA is especially suited for transmission of rather large data volumes and high instantaneous data rates for low service latency. However, the FA scheme must be accompanied by a robust diversity based transmission mode, since FA transmission without reliable CQI can deteriorate.
The diversity-based scheme, here denoted as nonfrequency-adaptive (NFA) transmission, should efficiently support users in all other usage scenarios, such as low SINR, high user equipment (UE) velocities, small and delay critical packet transfers, broadcasting that cannot benefit from a retransmission scheme, as well as for multicast transmission to multiple users with widely varying channels. In these scenarios a diversity based scheme has the potential to be more robust, more spectrally efficient and also more energy efficient.
Various relaying concepts are also considered in future wireless systems, [2–5]. However, multihop relaying increases the end-to-end delay in the Radio Access Network (RAN). Thus, an important requirement of the multiple access solution is to support a very low delay. This requirement also enables FA transmission at vehicular speeds even with a several GHz carrier frequency. It furthermore enables the use of retransmissions also for delay constrained services such as voice. However, such a low delay requirement implies a very short frame duration with very limited time diversity. Thus, the diversity for the NFA transmission scheme must come from the frequency domain and/or the spatial domain.
Below we summarize important requirements that we have identified for the NFA multiple access scheme.
-
(i)
Robustness to small-scale fading without time diversity.
-
(ii)
Tuneable degree of frequency-diversity.
-
(iii)
Need to support high energy efficiency in the transmitters and the receivers.
-
(iv)
Robustness to carrier frequency offsets and large Doppler spread.
-
(v)
Support for widely varying packet sizes.
-
(vi)
Enable efficient resource allocation.
-
(vii)
Be of use for in-band control signals.
-
(viii)
Enable efficient coexistence with adaptive TDMA/OFDMA.
-
(ix)
Facilitate low complexity transmitter in UE.
To define a scheme that optimally fulfills all of these requirements at the same time is challenging, and a tradeoff is needed. In addition, the tradeoff would look different in different deployment and usage scenarios. Thus a flexible scheme is desirable that can be adjusted towards a good tradeoff in each scenario.
In this paper, we present a novel multiple access scheme denoted as Block-Interleaved Frequency Division Multiple Access (B-IFDMA), which is intended to fulfill the above requirements and also to provide a good tradeoff between them for NFA transmission in uplinks. We have briefly introduced the scheme in [12]. B-IFDMA is based on OFDMA. In B-IFDMA equidistantly frequency-separated blocks, each consisting of a few subcarriers, are allocated to each user. A Discrete Fourier Transform (DFT) precoding step is performed on each Orthogonal Frequency-Division Multiplexing (OFDM) symbol before transmission. In addition, a short TDMA component is introduced within the chunks. B-IFDMA is a generalization of DFT precoded OFDMA with interleaved subcarrier allocation, as described in [13], also denoted as Interleaved Frequency Division Multiple Access (IFDMA) in the original paper [14] or Single-Carrier Frequency Division Multiple Access (SC-FDMA) with distributed mapping [15, 16]. (Some authors distinguish between DFT precoded OFDMA and the original IFDMA scheme as the frequency domain generation and the time domain generation approaches, and regard them as different schemes with different performance by assuming that spectrum shaping is made in the corresponding domain. Here we regard the two schemes as equivalent.) B-IFDMA is also a generalization of Localized Frequency Division Multiple Access (LFDMA) [17], also denoted as Localized DFTS-OFDM or SC-FDMA with localized mapping, [15, 16]. In this paper we use the acronym IFDMA for SC-FDMA with distributed mapping and LFDMA for SC-FDMA with localized mapping. In contrast to IFDMA, B-IFDMA can assign adjacent subcarriers in the blocks, and in contrast to LFDMA multiple noncontiguous subcarriers can be assigned, see illustration in Figure 1.
Illustration of B-IFDMA using  subcarriers and
subcarriers and  OFDM symbols per subcarrier block within a time-frequency resource denoted as chunk. SC-FDMA with localized mapping (LFDMA) and SC-FDMA with distributed mapping (IFDMA) are shown for comparison. In B-IFDMA, high rate users are allocated more blocks within the chunks in either the time or the frequency direction. (A similar illustration is included in [12].)
OFDM symbols per subcarrier block within a time-frequency resource denoted as chunk. SC-FDMA with localized mapping (LFDMA) and SC-FDMA with distributed mapping (IFDMA) are shown for comparison. In B-IFDMA, high rate users are allocated more blocks within the chunks in either the time or the frequency direction. (A similar illustration is included in [12].)
The IFDMA scheme has been considered in the uplink of the LTE standard, but LFDMA was adopted [15, 16] in LTE Release  . In LTE, with rather flat fading Resource Blocks (RBs), link adaptation and multiuser diversity gains can be obtained whenever reliable CQI is available. Some frequency-diversity collected over multiple slots can be obtained when needed through frequency-hopping, but at the cost of higher delay and delay jitter. To maintain a low RAN delay in a multihop relaying scenario, frequency hopping is less attractive.
. In LTE, with rather flat fading Resource Blocks (RBs), link adaptation and multiuser diversity gains can be obtained whenever reliable CQI is available. Some frequency-diversity collected over multiple slots can be obtained when needed through frequency-hopping, but at the cost of higher delay and delay jitter. To maintain a low RAN delay in a multihop relaying scenario, frequency hopping is less attractive.
Our evaluations in this paper of the B-IFDMA scheme towards the identified requirements for NFA transmission are focused on the error rate performance, energy efficiency and robustness of the scheme compared to OFDMA, IFDMA and LFDMA. We investigate the properties of the scheme under close to real conditions such as realistic pulse shaping and realistic power amplifiers, correlated Multiple Input Multiple Output (MIMO) mobile radio channels, realistic channel estimation performance under constraints set by a low pilot overhead loss and a realistic frame structure. Such a system is hard to analyze theoretically, but for application in IMT Advanced systems such a property analysis is of interest. Thus, the performance investigations in this paper are performed with simulations.
The investigations show that in an IMT-Advanced scenario, B-IFDMA provides equal or better error rate performance than the Single-Carrier Frequency Division Multiple Access (SC-FDMA) schemes IFDMA and LFDMA, when considering realistic channel estimation performance at the receiver and no reliable channel state information at the transmitter. We also show that B-IFDMA provides better amplifier efficiency than OFDMA and can provide better end-to-end energy efficiency than IFDMA and LFDMA. Moreover, the scheme shows a promisingly high robustness to frequency-offsets (CFOs) and Doppler spread (DS). Thus, this scheme can be regarded as a promising solution for the uplink of future mobile radio systems. (The B-IFDMA scheme has been adopted for the NFA uplink in the WINNER system concept [2, 4, 5]. A scheme similar to B-IFDMA denoted as Block Equidistant Frequency Division Multiple Access (B-EFDMA) has also been proposed for NFA downlinks [4, 5, 18]. The difference to B-IFDMA is that the DFT precoding step is not included, since the benefit of DFT precoding is lost in the multiple signal multiplexing in the downlink. The other benefits are similar as for B-IFDMA, including the possibility to time localize the transmission in the base station (BS) in low load situations, in order to save energy in both the BS and the UE. The B-EFDMA scheme has been adopted for the WINNER NFA downlink.)
This paper is organized as follows: we start in Section 2 with a detailed definition of B-IFDMA. Then, in Section 3 we investigate the error rate performance of B-IFDMA with perfect and nonperfect channel estimation at the receiver. These investigations show the capability of B-IFDMA to collect large diversity gains under realistic assumptions on channel estimation performance, also for rather low data rates, without using time-diversity. We proceed in Section 4 with the energy efficiency of B-IFDMA with respect to High Power Amplifier (HPA) performance and end-to-end energy efficiency. These investigations motivate the use of a DFT precoding step, and the integration of the TDMA component within the B-IFDMA scheme. These results also motivate the regular subcarrier allocation in B-IFDMA. In Section 5 we investigate the robustness of B-IFDMA to carrier frequency offsets and to Doppler spreads. These results show that B-IFDMA offers the possibility to combine robustness and provision of frequency diversity. In Section 6 we summarize our investigation results, and we comment on the suitability of B-IFDMA to meet our identified list of requirements above on the NFA uplink scheme. In Section 7 we conclude the paper.
2. System Model
As an introduction to B-IFDMA, the resource allocation for B-IFDMA is illustrated in Figure 1 along with IFDMA and LFDMA for comparison, assuming the Frequency Division Duplex (FDD) chunk size in [19]. The scheme is defined in detail in the subsequent sections.
2.1. Signal Definition
In this section, a transmitter signal model for B-IFDMA is given, following the block diagram in Figure 2. In the following, all signals are represented by their discrete time equivalents in the complex baseband. Upper case bold letters denote matrices and lower case bold letters denote column vectors. Further on,  denotes the pseudo-inverse and
denotes the pseudo-inverse and  the Hermitian of a matrix and
the Hermitian of a matrix and  the transpose of a vector or a matrix, respectively. Finally,
the transpose of a vector or a matrix, respectively. Finally,  denotes the element of a matrix in the
denotes the element of a matrix in the  th row and
th row and  th column.
th column.
B-IFDMA transceiver, transmitter (top) and receiver (bottom). In case the same amount of resources are allocated per user, for each user  out of
out of  uplink user terminals,
uplink user terminals,  out of
out of  subcarriers are allocated by the subcarrier mapping matrix
subcarriers are allocated by the subcarrier mapping matrix  . The allocated subcarriers consist of
. The allocated subcarriers consist of  blocks, each containing
blocks, each containing  adjacent subcarriers.
adjacent subcarriers.
An uplink transmission system with  users with user index
users with user index  ,
,  is considered. Let
is considered. Let  ,
,  , denote a sequence of data symbols of user
, denote a sequence of data symbols of user  at symbol rate
at symbol rate  taken from the alphabet of an arbitrary bit mapping scheme applied after channel encoding and bit interleaving.
taken from the alphabet of an arbitrary bit mapping scheme applied after channel encoding and bit interleaving.
At first, the data symbols  are grouped into data symbol vectors
are grouped into data symbol vectors

with  elements
elements  ,
,  ,
,  . For sake of simplicity, throughout this section it is assumed that the number
. For sake of simplicity, throughout this section it is assumed that the number  is the same for all users. However, note that for B-IFDMA also different numbers
is the same for all users. However, note that for B-IFDMA also different numbers  can be assigned to the users, cf. [20]. Each data symbol vector
can be assigned to the users, cf. [20]. Each data symbol vector  is precoded by a DFT represented by a
is precoded by a DFT represented by a  matrix
matrix  with elements
with elements

After DFT precoding, the  elements of the vector
elements of the vector  are mapped to a set of
are mapped to a set of  out of
out of  subcarriers available in the system. The mapping is performed in a block-interleaved manner. Let
subcarriers available in the system. The mapping is performed in a block-interleaved manner. Let  denote the number of subcarriers in each subcarrier block,
denote the number of subcarriers in each subcarrier block,  denote the numbers of subcarrier blocks and let
denote the numbers of subcarrier blocks and let  . The block-interleaved mapping can be described by an
. The block-interleaved mapping can be described by an  matrix
matrix  with elements
with elements

where  ,
,  , and
, and  . After subcarrier mapping, OFDM modulation is applied. The OFDM modulation is performed by an
. After subcarrier mapping, OFDM modulation is applied. The OFDM modulation is performed by an  -point Inverse DFT (IDFT) represented by matrix
-point Inverse DFT (IDFT) represented by matrix  with elements
with elements

The  th B-IFDMA-modulated data vector
th B-IFDMA-modulated data vector

of user  with elements
with elements  ,
,  , at sampling rate
, at sampling rate  is, thus, given by
is, thus, given by

From (6), it follows that B-IFDMA can be considered as OFDMA with block-interleaved subcarrier allocation and DFT precoding of the data symbols before OFDMA modulation. For the special case  , that is, for one subcarrier per block in the allocated OFDM symbols, B-IFDMA is equivalent to IFDMA [14, 21]. For the special case
, that is, for one subcarrier per block in the allocated OFDM symbols, B-IFDMA is equivalent to IFDMA [14, 21]. For the special case  , that is, for one block of subcarriers, B-IFDMA is equivalent to LFDMA [17]. Thus, B-IFDMA can be understood as a generalization of these schemes. In the appendix we show that a B-IFDMA signal can be efficiently generated in the time domain, that is, without the DFT operation.
, that is, for one block of subcarriers, B-IFDMA is equivalent to LFDMA [17]. Thus, B-IFDMA can be understood as a generalization of these schemes. In the appendix we show that a B-IFDMA signal can be efficiently generated in the time domain, that is, without the DFT operation.
2.2. Receiver Structure
In the following a B-IFDMA receiver is described for an uplink scenario, following the block diagram in Figure 2. Let

denote the  vector representation of a multipath channel of user
vector representation of a multipath channel of user  . Let further
. Let further  ,
,  , denote the
, denote the  nonzero channel coefficients at sampling rate
nonzero channel coefficients at sampling rate  with
with  . Before transmission over the channel
. Before transmission over the channel  , a Cyclic Prefix (CP), with length at least
, a Cyclic Prefix (CP), with length at least  , is inserted in between consecutive modulated data vectors
, is inserted in between consecutive modulated data vectors  . At the receiver, the CP is removed before demodulation. For the time interval
. At the receiver, the CP is removed before demodulation. For the time interval  required for transmission of vector
required for transmission of vector  and the CP, the channel is assumed to be time invariant. Moreover, perfect time and frequency synchronization is assumed. Thus, with
and the CP, the channel is assumed to be time invariant. Moreover, perfect time and frequency synchronization is assumed. Thus, with  denoting the circulant channel matrix with vector
denoting the circulant channel matrix with vector  in its first column [22], the
in its first column [22], the  th received signal vector
th received signal vector  after removal of the CP is given by
after removal of the CP is given by

where

denotes an Additional White Gaussian Noise (AWGN) vector with samples  ,
,  at sampling rate
at sampling rate  .
.
At the receiver, after removal of the CP, an  -point DFT is applied to the received signal
-point DFT is applied to the received signal  . Subsequently, the signal is user specifically demapped. After demapping, for each user
. Subsequently, the signal is user specifically demapped. After demapping, for each user  the impact of the channel is compensated by an equalizer and the DFT precoding is compensated by a
the impact of the channel is compensated by an equalizer and the DFT precoding is compensated by a  -point IDFT. In the following, a Frequency Domain Equalizer (FDE) [23, 24] represented by a
-point IDFT. In the following, a Frequency Domain Equalizer (FDE) [23, 24] represented by a  diagonal matrix
diagonal matrix  is considered. Thus, at the receiver, estimates
is considered. Thus, at the receiver, estimates  of the data symbol vectors
of the data symbol vectors  for user
for user  are given by
are given by

3. Error Rate Performance
In this section we investigate the error rate performance of B-IFDMA with various block sizes. The aim of these investigations is to show the capability of B-IFDMA to collect large diversity gains under realistic assumptions on channel estimation performance, also for rather low data rates, without using time-diversity. We start in Section 3.1 by investigating the diversity gains under the assumption of perfect channel estimation at the receiver. Then, in Section 3.2 we quantify the channel estimation performance for various B-IFDMA block sizes. With these performance results at hand, we proceed in Section 3.3 by discussing the tradeoff between these performance measures for different B-IFDMA block sizes, and we illustrate with quantitative examples.
3.1. Diversity Gains
As discussed in Section 1 robustness to small-scale fading based on frequency diversity and/or spatial diversity is needed to satisfy delay critical services, especially in bad channel conditions. Time diversity based schemes are less attractive in order to keep a short delay over the air interface. In this section, we investigate the uplink performance of B-IFDMA with Quadrature Phase Shift Keying (QPSK) modulated and Forward Error Correction (FEC) encoded transmission over a frequency-selective fading wide area mobile radio channel. We show results for single antenna transmission (SISO), two transmit antennas at the UE using Alamouti Space-Frequency Coding [25, 26] with one receive antenna (MISO, Alamouti) and for two transmit antennas at the UE using Alamouti Space-Frequency Coding with two receive antennas at the base station (BS) applying Maximum Ratio Combining (MIMO, Alamouti and MRC). Each OFDM symbol is formed as described in Section 2 and a joint FEC encoding and interleaving is performed over the used OFDM symbols in the chunk. All simulation assumptions are listed in Table 1.
The coherence time  and the coherence bandwidth
and the coherence bandwidth  of the mobile radio channel play an important role. In the literature various different definitions for coherence time and coherence bandwidth are used, but in Table 1 they are calculated as follows. Let
of the mobile radio channel play an important role. In the literature various different definitions for coherence time and coherence bandwidth are used, but in Table 1 they are calculated as follows. Let  ,
,  and
and  denote the speed of light, the carrier frequency and the velocity of a mobile station, respectively. Let further
denote the speed of light, the carrier frequency and the velocity of a mobile station, respectively. Let further  denote the maximum Doppler frequency for this mobile station. The coherence time
denote the maximum Doppler frequency for this mobile station. The coherence time  can be defined as
can be defined as

where  is the well-known Doppler bandwidth.
is the well-known Doppler bandwidth.
The coherence bandwidth  can be defined as
can be defined as

where  denotes the time difference between the first and the last received propagation path of the mobile radio channel, usually denoted as the delay spread of the channel.
denotes the time difference between the first and the last received propagation path of the mobile radio channel, usually denoted as the delay spread of the channel.
The Bit Error Rate (BER) performance of B-IFDMA for different numbers  of subcarriers per block is given in Figures 3, 4, and 5. Perfect channel estimation is assumed and the pilot symbol overhead required for channel estimation is not considered. In these figures the
of subcarriers per block is given in Figures 3, 4, and 5. Perfect channel estimation is assumed and the pilot symbol overhead required for channel estimation is not considered. In these figures the  dB antenna gain in the
dB antenna gain in the  times
times  MIMO cases is removed to simplify the comparison of the diversity gains in the different scenarios.
MIMO cases is removed to simplify the comparison of the diversity gains in the different scenarios.
When the distance of the subcarrier blocks is large compared to the coherence bandwidth, they receive almost independent fading, and thus the frequency diversity is improved. For large numbers  of subcarriers per user, the distance between the subcarrier blocks is reduced and, thus, the frequency diversity gains are decreased. Regarding the simulation results for MISO and MIMO transmission it can be concluded that even for B-IFDMA exploiting spatial diversity, the differences in frequency diversity are still considerable.
of subcarriers per user, the distance between the subcarrier blocks is reduced and, thus, the frequency diversity gains are decreased. Regarding the simulation results for MISO and MIMO transmission it can be concluded that even for B-IFDMA exploiting spatial diversity, the differences in frequency diversity are still considerable.
From Figures 3, 4, and 5 it can also be concluded that for a given data rate, that is, for a given number  of subcarriers assigned to a user, the performance of B-IFDMA increases with decreasing number
of subcarriers assigned to a user, the performance of B-IFDMA increases with decreasing number  of subcarriers per block. The reason for that is that for a given number
of subcarriers per block. The reason for that is that for a given number  with decreasing number
with decreasing number  , the number of subcarrier blocks
, the number of subcarrier blocks  increases. However, as discussed in Section 4.2 and illustrated in Figure 1, for a given average data rate per frame the number of blocks can be maintained by introducing a TDMA component with increased number of used subcarriers and a correspondingly smaller duty cycle within the chunk. In Figure 6 we can see that the diversity gain depends mainly on the number of blocks
increases. However, as discussed in Section 4.2 and illustrated in Figure 1, for a given average data rate per frame the number of blocks can be maintained by introducing a TDMA component with increased number of used subcarriers and a correspondingly smaller duty cycle within the chunk. In Figure 6 we can see that the diversity gain depends mainly on the number of blocks  . Hence the same robustness towards small-scale fading can be maintained also with time-localized transmission to take advantage of the gain in transceiver power efficiency as discussed later in Section 4.2.
. Hence the same robustness towards small-scale fading can be maintained also with time-localized transmission to take advantage of the gain in transceiver power efficiency as discussed later in Section 4.2.
3.2. Channel Estimation
In Section 3.1 we showed the simulated diversity gains for B-IFDMA with various parameterizations under the assumption of perfect channel estimation. However, in general the less correlation among the subcarriers the better diversity but also the less correlation to be used in the channel estimation scheme over the subcarrier blocks. In addition, with pilot-aided channel estimation it is important to keep the pilot overhead low. Thus, with a given pilot overhead, there is an inherent tradeoff to be made between attainable diversity gains and loss due to nonideal channel estimation performance. In this section, we first define in Section 3.2.1 what we mean by pilot overhead, and then in Section 3.2.2 we show the attainable performance of memory-based and memory-less pilot-aided channel estimation schemes for various B-IFDMA block sizes.
3.2.1. Pilot Overhead
In pilot-aided channel estimation [29–31], the complex gain of the OFDM subcarriers is estimated at the receiver based on known time-frequency pilot symbols (also denoted as reference symbols) placed within each block. The channel equalization and payload data detection/decoding is then based on inferred complex channel gains at the payload symbol locations.
With pilot aided channel estimation, there is a pilot overhead loss in both signal-to-noise ratio (SNR) degradation due to the energy put on the pilots and in spectral efficiency due to the channel symbols occupied by the pilot symbols. Below we assume that the pilot symbols are inserted as subcarrier channel symbols with the same energy as the data carrying channel symbols (i.e., no pilot boosting). In this case the SNR loss and the spectral efficiency loss are the same. Assuming that there are  pilots per block and the block size equals
pilots per block and the block size equals  subcarriers times
subcarriers times  OFDM symbols, the pilot overhead loss becomes
OFDM symbols, the pilot overhead loss becomes  and the SNR degradation
and the SNR degradation  dB.
dB.
Below in Section 3.2.2 we discuss the suitable pilot schemes and corresponding channel estimation performance under the assumption of a constant pilot overhead loss of  for the different block sizes, that is,
for the different block sizes, that is,  loss in spectral efficiency and
loss in spectral efficiency and  dB in SNR degradation.
dB in SNR degradation.
3.2.2. Block Size Effect on Channel Estimation
Because of the variation of the complex gain with frequency (due to the multipath propagation) and with time (due to mobility), the channel at payload positions will in general differ from that at the pilot positions. The coherence time and coherence bandwidth as defined in (11) and (12), respectively give an estimate of the order of the needed sampling interval in time and frequency for the mobile radio channel according to the sampling theorem [32]. However, the channel has to be estimated based on received noisy pilot symbols, and in a packet oriented system the channel resources needed per packet transmission are not very large. Hence, due to the limited number of noisy pilots available for channel estimation, an oversampling factor is typically needed, that is, a more dense pilot pattern means better estimation performance.
For the considered diversity-based transmission schemes, a problem is then encountered in uplinks: large blocks will have many embedded pilots and thus good possibilities for interpolation, which is more robust than extrapolation. But if the pilot overhead is to be held fixed, small blocks will contain only one or a few pilot symbols. This effect may partly or completely cancel the effect of frequency diversity.
Good channel estimation performance is achieved by mainly three different strategies.
-
(i)
Use pilots from adjacent blocks, to enable interpolation over frequency. This strategy is possible and recommended in downlinks, but it cannot be used in uplinks, where adjacent blocks are either unused or used by other UEs. Blocks used by the UE itself are in general placed significant distances apart in frequency, with low inter-block channel correlation. They are therefore of limited use for channel estimation.
-
(ii)
Use pilots from previous blocks. This can be done in general in downlinks. In uplinks, it becomes possible only if the UE uses the same blocks over multiple frames (persistent scheduling). In the investigation below, we illustrate the potential maximum estimation performance obtainable by using optimal Kalman smoothing that uses an unlimited amount of past payload symbols.
-
(iii)
Use also data symbols for channel estimation, by iterative channel estimation. The pilot based channel estimate is then used as a first step. Decoded soft bits are then used in a second step to improve the channel estimates. Iterative channel estimation has been found to be beneficial for the IMT Advanced scenarios and pilot schemes, see [7, 33]. It improves upon pilot-based estimates by 1-2 dB in realistic cases. The almost constant offset makes it possible to roughly estimate the accuracy of iterative schemes if the accuracy of the initializing pilot-based estimate is known. We therefore focus here on pilot-based noniterative schemes.
The channel estimation performance is investigated below for two schemes:
-
(i)
Block Least Squares Estimation (Block-LSE): least squares estimation based on present but not past pilot data, also often called 2D-Wiener filtering [29, 30];
-
(ii)
Kalman smoothing [34, 35], using present and past pilots from every second time-slot backwards in time. Blocks from odd numbered past time-slots are not used. In half-duplex FDD uplinks they would be used by other UEs. In Time Division Duplex (TDD) systems, they would be used for downlink transmissions. The time-slots (half frames) are assumed to have duration
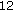 OFDM symbols as in [4, 5, 36].
OFDM symbols as in [4, 5, 36].
The block sizes used in the investigations and the related pilot positions are illustrated by Figure 7. The choice of these block sizes is related to the frame structure in the FDD mode of [4, 5]. In order to maintain a low radio access delay and to support also high speed trains, one slot (half frame) consists of only  OFDM symbols, [4, 5].
OFDM symbols, [4, 5].
The pilot patterns used for the investigated block allocations that use combinations of a basic block of 4 subcarriers by-3-OFDM-symbols, with one pilot and 11 payload symbols (i. e., pilot overhead  ): B-IFDMA
): B-IFDMA  (
( ,
,  ),
),  (
( ,
,  ),
),  (
( ,
,  ),
),  (
( ,
,  ), IFDMA (
), IFDMA ( ,
,  ), and LFDMA (
), and LFDMA ( ,
,  ). Time axis is horizontal and frequency axis is vertical in this figure. The pilot positions within blocks have been determined by global optimization of the channel estimation performance of the Block-LSE (Wiener) method, and they differ from those specified for uplinks in [4, 5].
). Time axis is horizontal and frequency axis is vertical in this figure. The pilot positions within blocks have been determined by global optimization of the channel estimation performance of the Block-LSE (Wiener) method, and they differ from those specified for uplinks in [4, 5].
Here we consider uplinks, so neither method uses pilot information from subcarriers outside of the blocks. The results for the two estimation methods for the various block sizes are shown in Figure 8, for UE velocity 50 km/h at 3.7 GHz carrier frequency as well as all other parameters as in Table 1. Please refer to [37] for further details on the channel estimation methods and for additional results for other UE velocities and block sizes.
Performance degradation in dB due to imperfect channel estimation versus ideal SNR. The vertical axis shows the difference between actual perceived signal-to-estimation-error-plus noise ratio (SENR, in dB) and ideal SNR (in dB). The horizontal axis shows the ideal SNR, that is, assuming perfect channel state information. For example, the value  on the vertical axis means that a bit-error-rate curve generated in an idealized setting where perfect channel estimation is assumed should be displaced
on the vertical axis means that a bit-error-rate curve generated in an idealized setting where perfect channel estimation is assumed should be displaced  dB to the right to correctly represent performance when the influence of channel estimation is taken into consideration. Solid curves represent (optimal) smoothed Kalman filter performance. Dashed curves represent Wiener filter performance, where no previous measurements are used by the estimator.
dB to the right to correctly represent performance when the influence of channel estimation is taken into consideration. Solid curves represent (optimal) smoothed Kalman filter performance. Dashed curves represent Wiener filter performance, where no previous measurements are used by the estimator.
In [7] it has been shown that the effect of channel estimation errors on various decoder and detection algorithms in OFDM receivers can be well modelled by treating the estimation error as an additional white noise contribution at the receiver, with a variance given by the estimation error variance. Therefore, in Figure 8 we show the channel estimation results in terms of SNR offset due to channel estimation errors at the receiver. This performance measure makes the results directly comparable to the SNR gains and losses due to different choices of number of subcarriers  per block in Figures 3, 4, and 5, as discussed further in Section 3.3.
per block in Figures 3, 4, and 5, as discussed further in Section 3.3.
It is evident that significant performance gains can be obtained by using Kalman smoothing which takes blocks in previous time-slots into account. Note that in the investigated case assuming half-duplex FDD, every second of the past timeslots cannot be used. The performance gain increases for slower UE velocities as shown in [37]. Full duplex FDD UEs would also benefit from the more dense slot and thus more dense pilot structure in time.
3.3. Performance Tradeoffs
By analyzing the results in Sections 3.1 and 3.2, we can quantify the tradeoff between frequency diversity gains and channel estimation performance for different B-IFDMA subcarrier block sizes. To this end, we adopt the parameters of the FDD wide area mode in the IMT Advanced capable system concept in [4, 5].
In Figure 9, we show such an example of combined diversity and channel estimation performance for the SISO case with Block-LSE channel estimation and  subcarriers assigned per user. As seen, despite the better channel estimation with LFDMA, at this rather low number of
subcarriers assigned per user. As seen, despite the better channel estimation with LFDMA, at this rather low number of  ; IFDMA and B-IFDMA are substantially better than LFDMA. The reason is the low frequency diversity obtained with the adjacent subcarriers in LFDMA. With increasing
; IFDMA and B-IFDMA are substantially better than LFDMA. The reason is the low frequency diversity obtained with the adjacent subcarriers in LFDMA. With increasing  , B-IFDMA approaches IFDMA, and B-IFDMA becomes better than IFDMA when the diversity gains saturates in IFDMA. The reason for this is the better channel estimation performance for B-IFDMA, cf. Figure 8. In particular, making the same comparison as in Figure 9 but with
, B-IFDMA approaches IFDMA, and B-IFDMA becomes better than IFDMA when the diversity gains saturates in IFDMA. The reason for this is the better channel estimation performance for B-IFDMA, cf. Figure 8. In particular, making the same comparison as in Figure 9 but with  subcarriers, B-IFDMA is better than IFDMA for both
subcarriers, B-IFDMA is better than IFDMA for both  and
and  . At BER
. At BER  , B-IFDMA with
, B-IFDMA with  is
is  dB better and B-IFDMA with
dB better and B-IFDMA with  is
is  dB better than IFDMA. Note also that due to the block length
dB better than IFDMA. Note also that due to the block length  used in B-IFDMA, this performance is achieved with an average data rate over the chunk that is half compared to IFDMA and LFDMA, which is useful for transmission of small packets.
used in B-IFDMA, this performance is achieved with an average data rate over the chunk that is half compared to IFDMA and LFDMA, which is useful for transmission of small packets.
Coded SISO performance for B-IFDMA, IFDMA and LFDMA with nonperfect channel estimation, and  subcarriers assigned per user. The Block-LSE channel estimation performance results from Figure 8 are used. B-IFDMA uses block of sizes (
subcarriers assigned per user. The Block-LSE channel estimation performance results from Figure 8 are used. B-IFDMA uses block of sizes ( ,
,  ) or (
) or ( ,
,  ).
).
Below we exemplify the diversity versus channel estimation tradeoff for B-IFDMA, assuming different block lengths  for both Block-LSE and Kalman channel estimation. Since the pilot overhead is the same for all considered schemes, this loss is not included.
for both Block-LSE and Kalman channel estimation. Since the pilot overhead is the same for all considered schemes, this loss is not included.
Example 1.
Referring to Table 2, under the assumption that  subcarriers are assigned to a user, we can see in Figure 3 that at BER
subcarriers are assigned to a user, we can see in Figure 3 that at BER  in the SISO case when going from
in the SISO case when going from  to
to  subcarriers per block, that is, changing from number of subcarrier blocks
subcarriers per block, that is, changing from number of subcarrier blocks  to
to  , there is a diversity gain of
, there is a diversity gain of  dB, that is, a reduction in required SNR from around
dB, that is, a reduction in required SNR from around  to
to  dB. This gain should be compared to the loss in channel estimation performance in Figure 8 due to the fewer number of subcarriers per block. With block length
dB. This gain should be compared to the loss in channel estimation performance in Figure 8 due to the fewer number of subcarriers per block. With block length  , the channel estimation loss at the intermediate SNR
, the channel estimation loss at the intermediate SNR  dB is
dB is  1.2 dB for
1.2 dB for  and
and  1.7 dB for
1.7 dB for  subcarriers per block with Kalman filtering. That is, there is an overall gain of
subcarriers per block with Kalman filtering. That is, there is an overall gain of  dB including channel estimation for using
dB including channel estimation for using  subcarriers compared to
subcarriers compared to  . With Block-LSE, the corresponding overall gain is
. With Block-LSE, the corresponding overall gain is  dB. With the longer blocks having
dB. With the longer blocks having  (double mean data rate over the slot for a given number of blocks
(double mean data rate over the slot for a given number of blocks  ) the corresponding gains when going from
) the corresponding gains when going from  to
to  are
are  dB (Kalman) and
dB (Kalman) and  dB (Block-LSE).
dB (Block-LSE).
Example 2.
In Table 2, we also show the corresponding case with  subcarriers per user based on the results in Figures 4 and 8. Here the two cases with
subcarriers per user based on the results in Figures 4 and 8. Here the two cases with  and
and  subcarriers per block perform very similar, that is, the diversity gain with
subcarriers per block perform very similar, that is, the diversity gain with  blocks compared to
blocks compared to  blocks is almost completely lost due to the worse channel estimation performance.
blocks is almost completely lost due to the worse channel estimation performance.
Similar tradeoff comparisons can be made for the MISO with Alamouti case and the MIMO with Alamouti and MRC case based on the diversity results in Figure 6 and the channel estimation performance results in Figure 8, since the results on channel estimation performance in Figure 8 are directly applicable to uplinks with multiple UE antennas. Pilots are then placed at different time-frequency positions for different antennas, and these positions are not used by payload data at the other antennas to limit interference. Therefore, the pilot overhead increases, but the channel estimation accuracy stays unchanged. Due to the additional spatial diversity gains, fewer blocks  are typically needed, down to
are typically needed, down to  to
to  .
.
4. Energy Efficiency
In this section we aim to quantify the end-to-end energy efficiency of B-IFDMA. The aim of these investigations is to motivate the use of a DFT precoding step, and the advantage of the TDMA component within the B-IFDMA scheme. To this end, we start in Section 4.1 by characterizing the envelope properties of B-IFDMA in terms of popular envelope variation metrics. These metrics are commonly used in the literature to characterize the signal envelope variations and to give an indication of the efficiency of a generic High Power Amplifier (HPA). These results also motivate the regular subcarrier allocation in B-IFDMA. In order to give a quantitative measure of the energy efficiency with a representative HPA, we continue in Section 4.2 by showing the HPA efficiency with different B-IFDMA parameterizations and different HPA operation modes for a real HPA. These investigations enable us to quantify the energy efficiency gains of DFT precoded schemes compared to OFDMA. In addition, they allow us to characterize the gains with time-localized transmission, and to quantify the end-to-end energy efficiency with various B-IFDMA parameterizations.
4.1. Envelope Properties
It is well known that for increasing envelope fluctuations of the transmit signal, the cost of a typical commercial HPA in the UE increases and the power efficiency decreases. Thus, especially in the uplink, the provision of low envelope fluctuations is important for the transmitted signal. In this section we investigate the envelope properties of B-IFDMA, and we predict the efficiency of the HPA based on an amplifier model. For that purpose, a signal model including oversampling, pulse shaping and windowing is assumed, all according to [38]. The oversampling factor is  and the pulse shaping filter is chosen such that an OFDM-like rectangular spectrum of the B-IFDMA signal is provided. Furthermore, a Raised-Cosine window with a roll-off region that is 5% of the symbol duration is applied.
and the pulse shaping filter is chosen such that an OFDM-like rectangular spectrum of the B-IFDMA signal is provided. Furthermore, a Raised-Cosine window with a roll-off region that is 5% of the symbol duration is applied.
In Figure 10, the envelope of the B-IFDMA transmit signal is investigated in terms of the well-known Peak-to-Average Power Ratio (PAPR) [39] for  subcarriers in the system and
subcarriers in the system and  subcarriers assigned to a user using QPSK modulation. As references, the PAPR of two signals are given that differ from the B-IFDMA in the following properties. The first signal does not use DFT precoding and the second signal uses a random allocation of the subcarrier blocks instead of a regular one. From Figure 10 it can be clearly seen that both DFT precoding and regular allocation of the subcarrier blocks is required in order to provide a low PAPR. B-IFDMA provides a mean PAPR that is 1.2–1.5 dB lower than the mean PAPR of the corresponding scheme without DFT precoding. Compared to a scheme with random allocation of the subcarrier blocks with DFT precoding, the PAPR gain of B-IFDMA is greater than 3 dB for a number
subcarriers assigned to a user using QPSK modulation. As references, the PAPR of two signals are given that differ from the B-IFDMA in the following properties. The first signal does not use DFT precoding and the second signal uses a random allocation of the subcarrier blocks instead of a regular one. From Figure 10 it can be clearly seen that both DFT precoding and regular allocation of the subcarrier blocks is required in order to provide a low PAPR. B-IFDMA provides a mean PAPR that is 1.2–1.5 dB lower than the mean PAPR of the corresponding scheme without DFT precoding. Compared to a scheme with random allocation of the subcarrier blocks with DFT precoding, the PAPR gain of B-IFDMA is greater than 3 dB for a number  subcarrier blocks, that is, for the special case of IFDMA. The gain decreases to
subcarrier blocks, that is, for the special case of IFDMA. The gain decreases to  0.7 dB for
0.7 dB for  subcarrier blocks. For
subcarrier blocks. For  , the regular and the random allocation of the subcarrier blocks are equivalent except for the distance of the subcarrier blocks and, thus, the mean PAPR is similar.
, the regular and the random allocation of the subcarrier blocks are equivalent except for the distance of the subcarrier blocks and, thus, the mean PAPR is similar.
Figure 11 analyzes the envelope of the B-IFDMA transmit signal based on different metrics. In addition to the PAPR, the well-known Raw Cubic Metric (RCM) as defined in [40, equation (15)], which is related to the 3GPP Cubic Metric (CM) in [41], is regarded. The motivation for the CM and RCM are the fact that the primary cause of distortion is the third order nonlinearity of the amplifier gain characteristic. Moreover, the HPA power efficiency is predicted. For that purpose, a nonlinear amplifier is assumed that produces increased out-of-band radiation due to nonlinear distortions dependent on the envelope of the input signal. The power efficiency of the given HPA depends on the power back-off (BO) that is required to meet a given spectral mask for the transmit signal. Thus, for investigation of the impact of the envelope fluctuations on the power efficiency, also the required BO is analyzed. In the following, for the HPA, the well-known Rapp model [39] with Rapp-parameter  is used which represents the model of a power amplifier with high nonlinearities. The spectrum requirement mask is representative for IMT Advanced systems, and is given in [38].
is used which represents the model of a power amplifier with high nonlinearities. The spectrum requirement mask is representative for IMT Advanced systems, and is given in [38].
The results for the different metrics are summarized in Figure 11. Again,  subcarriers is assumed in the system, with
subcarriers is assumed in the system, with  subcarriers per user and QPSK modulation. A scheme without DFT precoding is regarded as a reference. It can be concluded that, regardless of the number
subcarriers per user and QPSK modulation. A scheme without DFT precoding is regarded as a reference. It can be concluded that, regardless of the number  of subcarrier blocks, for B-IFDMA, the envelope fluctuations are significantly lower compared to the scheme without DFT precoding. The mean PAPR and the RCM have a minimum for
of subcarrier blocks, for B-IFDMA, the envelope fluctuations are significantly lower compared to the scheme without DFT precoding. The mean PAPR and the RCM have a minimum for  and
and  , that is, for LFDMA and for IFDMA, where B-IFDMA can be interpreted as a single-carrier scheme and have a maximum for
, that is, for LFDMA and for IFDMA, where B-IFDMA can be interpreted as a single-carrier scheme and have a maximum for  . However, even at the maximum, the envelope fluctuations of B-IFDMA are considerably lower than for a corresponding scheme without DFT precoding. In difference to the mean PAPR and the RCM, the required BO increases with decreasing number
. However, even at the maximum, the envelope fluctuations of B-IFDMA are considerably lower than for a corresponding scheme without DFT precoding. In difference to the mean PAPR and the RCM, the required BO increases with decreasing number  of subcarrier blocks. The reason for that is that in addition to the envelope of the signal also the shape of the spectrum changes and the side-lobes are increased. However, for the special case of
of subcarrier blocks. The reason for that is that in addition to the envelope of the signal also the shape of the spectrum changes and the side-lobes are increased. However, for the special case of  , that is, for LFDMA, the side-lobes are significantly reduced. Thus, in this case, the spectral mask is less relevant, and results for
, that is, for LFDMA, the side-lobes are significantly reduced. Thus, in this case, the spectral mask is less relevant, and results for  are omitted.
are omitted.
From Figure 11 it can be concluded that the effects shown in Figure 10 can be considered to be almost independent of the metric that is used. Thus, B-IFDMA can be considered to provide a higher power efficiency and lower envelope fluctuations compared to schemes without DFT precoding and without regular subcarrier allocation, respectively.
4.2. Gain with Time Localized Transmission
In Section 4.1, we characterized the envelope properties of B-IFDMA according to different metrics. In this section we make an analysis of the energy efficiency of B-IFDMA with a real amplifier. The aim of this investigation is to correlate the HPA energy efficiency with the prediction by the metrics in Section 4.1. The aim is also to show and quantify the gain by optimizing the operation point of the power amplifier, in order to motivate the benefit of the TDMA component within the B-IFDMA scheme.
4.2.1. HPA Efficiency
The efficiency of an HPA is best described by the overall efficiency, defined as

where  is the power at the input of the HPA, and
is the power at the input of the HPA, and  is the resulting output power.
is the resulting output power.  is the power at the DC input of the amplifier, computed as the product between the DC voltage and the DC current,
is the power at the DC input of the amplifier, computed as the product between the DC voltage and the DC current,  . For a given
. For a given  , the efficiency is a function mainly of the desired output power; the general trend is that the efficiency is higher for high output powers. However, by varying the drive voltage
, the efficiency is a function mainly of the desired output power; the general trend is that the efficiency is higher for high output powers. However, by varying the drive voltage  , the efficiency curve of the amplifier can be changed. In Figure 12, we illustrate the overall efficiency as a function of output power for different drive voltages
, the efficiency curve of the amplifier can be changed. In Figure 12, we illustrate the overall efficiency as a function of output power for different drive voltages  , when the input signal is an unmodulated carrier signal, using the HPA in [42].
, when the input signal is an unmodulated carrier signal, using the HPA in [42].
Illustration of overall efficiency as a function of output power for different amplifier drive voltages
 using the HPA in [
42
], where
using the HPA in [
42
], where
 V is the highest possible drive voltage.
V is the highest possible drive voltage.
Figure 12 shows that the efficiency of the amplifier is highest when its output power is close to the maximum attainable output power, that is, when it is driven close to saturation. However, due to the signal dynamics and other system considerations such as power control, it is in general not possible to drive the amplifier in its most efficient mode at all times. In situations when we need a lower average output power, we can see that by lowering the (constant) drive voltage we can get an improved efficiency, but the overall efficiency is still lower than when its output power is close to the maximum attainable output power. (The optimal way of driving the amplifier would be to jointly vary the drive and Radio Frequency (RF) power for maximum efficiency [42], but this is not generally regarded as practical to implement today.)
We have evaluated the overall efficiency of several different amplifiers, when driven at different constant  and with different modulated signals. The constant
and with different modulated signals. The constant  drive voltage has been chosen for maximum overall efficiency, and the following modulated input signals have been used: OFDM, IFDMA, LFDMA and B-IFDMA with different numbers of blocks (
drive voltage has been chosen for maximum overall efficiency, and the following modulated input signals have been used: OFDM, IFDMA, LFDMA and B-IFDMA with different numbers of blocks ( ) and pulse shaped as in Section 4.1.
) and pulse shaped as in Section 4.1.
To compute the overall efficiency of the HPA, we use the measured characteristics of the HPA in terms of required  for a given
for a given  and desired
and desired  of each signal sample, and then we perform a weighted averaging over the consumed and transmitted powers using the desired output power histograms for the modulated signal. Thus, ideal predistortion of the signals is assumed, and the operation point is chosen such that maximum
of each signal sample, and then we perform a weighted averaging over the consumed and transmitted powers using the desired output power histograms for the modulated signal. Thus, ideal predistortion of the signals is assumed, and the operation point is chosen such that maximum  of the samples are above the saturation point, which is generally regarded as an acceptable level of signal distortion. The results are shown in Table 3. As can be seen, we have the following.
of the samples are above the saturation point, which is generally regarded as an acceptable level of signal distortion. The results are shown in Table 3. As can be seen, we have the following.
-
(i)
Due to the different amplitude distributions of these signals, they lead to different power efficiencies.
-
(ii)
In accordance with the envelope metric results in Section 4.1, and compared to the TDMA-OFDM system, the various DFT-precoding based schemes perform better both with respect to the overall efficiency and with respect to the maximum output power (not shown in Table 3). This can potentially be used for increasing the cell size and/or larger data rates at a given path loss, provided regulations on maximum transmit power are not violated. The better HPA efficiency also implies less heat dissipation in the UE, which simplifies the design and can cut other supporting component costs.
-
(iii)
The difference in efficiency of the various DFT precoded schemes is very small, including the B-IFDMA scheme. In particular, these differences are smaller than predicted by the envelope metric results in Section 4.1.
 chosen for maximum overall efficiency for different input signals, all using QPSK symbol constellations and a system with N = 1024 subcarriers.
chosen for maximum overall efficiency for different input signals, all using QPSK symbol constellations and a system with N = 1024 subcarriers.The results in Table 3 were obtained using the class E Laterally Diffused Metal Oxide Semiconductor (LDMOS) amplifier in [42]. However, to verify the qualitative conclusions we have also repeated the experiments with a class D LDMOS and a class E Gallium Nitride (GaN) amplifier. We have also studied other designs in the literature, for example, [43], and other classes of operation, such as class A, AB, or B. The overall conclusion is that the qualitative results are the same as above regardless of the amplifier.
4.2.2. Efficient HPA Operation
From the results in Table 3 we see that there is a gain to be made if the power amplifier as often as possible can operate close to its optimal operation point. However, in order to limit the Multiple Access Interference (MAI) from different users in a multicarrier based uplink due to imperfections in transmitter hardware, synchronization and Doppler spread, it is important to have some kind of power control to limit the difference in received power spectral density from different users. Thus, if all users were allocated the same number of subcarriers, with a constraint on maximum received power spectral density, there would be situations when the HPA has to operate at a low and suboptimal transmit power level. In these scenarios HPA efficiency would benefit from an increase in the number of allocated subcarriers in a given OFDM symbol, because then the UE could transmit during a shorter time, that is, on a lower number of OFDM symbols, for a given average data rate. One possibility to do this would be to decrease the subcarrier separation in an IFDMA scheme, but that would imply a larger channel estimation overhead due to the low correlation among the subcarriers as shown in Section 3.2. With a short frame duration, aiming at low delays, this overhead would be prohibitive. In addition, it would limit the possibility for coexistence with adaptive TDMA/OFDMA as discussed in [9].
In order to quantify the HPA efficiency with and without time localized transmission, we assume that the choices are to either (a) transmit at full power  of the time, and turn off the transmitter for
of the time, and turn off the transmitter for  of the time, or (b) to transmit at
of the time, or (b) to transmit at  of full power all the time. Thus, in scenario (b) the amplifier is backed-off
of full power all the time. Thus, in scenario (b) the amplifier is backed-off  dB compared to scenario (a). In a BS, the amplifier is usually optimized for a high output power, while in the UEs the amplifier works at a low power level most of the time, for example, 21–46 dBm for BSs and 21–24 dBm for UEs depending on the deployment scenario ranging from local area to wide area, [19].
dB compared to scenario (a). In a BS, the amplifier is usually optimized for a high output power, while in the UEs the amplifier works at a low power level most of the time, for example, 21–46 dBm for BSs and 21–24 dBm for UEs depending on the deployment scenario ranging from local area to wide area, [19].
As seen in Table 3 maximum overall efficiency is obtained when operating the HPA close to the maximum output power level. Thus scenario (a) leads to higher efficiency in all cases. For example, assume the same number of well separated blocks  . If the options are to use IFDMA in the full duration of a chunk with
. If the options are to use IFDMA in the full duration of a chunk with  subcarriers at a constant output power level of
subcarriers at a constant output power level of  dBm, we get an overall HPA efficiency of
dBm, we get an overall HPA efficiency of  (Table 3 row
(Table 3 row  , column
, column  ), whereas if we use B-IFDMA with
), whereas if we use B-IFDMA with  subcarriers and
subcarriers and  subcarriers per block (i.e.,
subcarriers per block (i.e.,  blocks) one quarter of the frame duration and an instantaneous output power level of
blocks) one quarter of the frame duration and an instantaneous output power level of  dBm, we get an overall HPA efficiency of
dBm, we get an overall HPA efficiency of  (Table 3 row
(Table 3 row  , column
, column  ). The corresponding difference is smaller when the average transmit power is closer to the maximum efficiency. For example, at
). The corresponding difference is smaller when the average transmit power is closer to the maximum efficiency. For example, at  dBm average transmit power the corresponding overall efficiencies are
dBm average transmit power the corresponding overall efficiencies are  (Table 3 row
(Table 3 row  , column
, column  ) for IFDMA and
) for IFDMA and  (Table 3 row
(Table 3 row  , column
, column  ) for B-IFDMA. Thus, there is a large benefit to introduce a TDMA component in the B-IFDMA scheme in order to allow a shorter transmit duration than a full frame with a larger instantaneous data rate, except in case the required overall data rate is already close to the maximum supported. With time-localized transmission and reception, we also introduce the additional possibility of micro-sleep mode within scheduled frames. The feasibility and potential of micro-sleep mode is discussed in [12].
) for B-IFDMA. Thus, there is a large benefit to introduce a TDMA component in the B-IFDMA scheme in order to allow a shorter transmit duration than a full frame with a larger instantaneous data rate, except in case the required overall data rate is already close to the maximum supported. With time-localized transmission and reception, we also introduce the additional possibility of micro-sleep mode within scheduled frames. The feasibility and potential of micro-sleep mode is discussed in [12].
4.3. End-to-End Energy Efficiency
By combining the results in Sections 4.1 and 4.2 with the results in Section 3, we can quantify the end-to-end energy efficiency for different B-IFDMA parameterizations. Below we illustrate this tradeoff, by building on the examples in Section 3.3, assuming a target BER of  .
.
Example 3 (revisited).
Similar to the mean PAPR results for  subcarriers in Figure 10, the mean PAPR for B-IFDMA with
subcarriers in Figure 10, the mean PAPR for B-IFDMA with  subcarriers is very similar for
subcarriers is very similar for  (
( ) and
) and  (
( ). In addition, not shown in this paper, the mean PAPR values of B-IFDMA have been found to correlate well with the overall HPA efficiency values. Thus, with SISO using
). In addition, not shown in this paper, the mean PAPR values of B-IFDMA have been found to correlate well with the overall HPA efficiency values. Thus, with SISO using  subcarriers, the scheme with
subcarriers, the scheme with  blocks with
blocks with  subcarriers each seems to provide the best tradeoff also considering end-to-end energy efficiency.
subcarriers each seems to provide the best tradeoff also considering end-to-end energy efficiency.
Example 4 (revisited).
The HPA efficiency for  predicted by the mean PAPR as shown in Figure 10 is very similar also for
predicted by the mean PAPR as shown in Figure 10 is very similar also for  blocks compared to
blocks compared to  . Thus, also with respect to end-to-end energy efficiency the two cases with
. Thus, also with respect to end-to-end energy efficiency the two cases with  and
and  subcarriers per block seem to perform very similar. If instead the HPA efficiency is predicted by the required power backoff to satisfy a spectrum mask, the results for required BO in Figure 11 apply. In this case, the end-to-end energy efficiency seems to be around
subcarriers per block seem to perform very similar. If instead the HPA efficiency is predicted by the required power backoff to satisfy a spectrum mask, the results for required BO in Figure 11 apply. In this case, the end-to-end energy efficiency seems to be around  dB better with
dB better with  , that is, for
, that is, for  subcarriers per block.
subcarriers per block.
In the next example, we now make a comparison between B-IFDMA and IFDMA with the same data rate, also taking the end-to-end energy efficiency into account.
Example 5.
Let us compare the two options to use IFDMA in SISO at the same data rate, for example, B-IFDMA using  ,
,  and
and  having
having  subcarriers for the user with B-IFDMA using
subcarriers for the user with B-IFDMA using  ,
,  and
and  having
having  subcarriers. The data rate is the same since in both cases
subcarriers. The data rate is the same since in both cases  symbols are transmitted per slot. To generate the same RF energy, IFDMA would operate with
symbols are transmitted per slot. To generate the same RF energy, IFDMA would operate with  dB less transmit power during
dB less transmit power during  times longer duty cycle. Thus, this scenario is especially relevant for the case when the required uplink data rate is below the maximum achievable for the UE at the given channel conditions. Consider the diversity gains in Figure 6, the channel estimation performance in Figure 8 and the HPA efficiency for this case in Table 3. Using the corresponding HPA efficiency values as discussed in Section 4.2.2, the end-to-end energy efficiency comparison is shown in Table 4 for target BER
times longer duty cycle. Thus, this scenario is especially relevant for the case when the required uplink data rate is below the maximum achievable for the UE at the given channel conditions. Consider the diversity gains in Figure 6, the channel estimation performance in Figure 8 and the HPA efficiency for this case in Table 3. Using the corresponding HPA efficiency values as discussed in Section 4.2.2, the end-to-end energy efficiency comparison is shown in Table 4 for target BER  . As seen in Table 4, there is an overall gain for B-IFDMA with
. As seen in Table 4, there is an overall gain for B-IFDMA with  over the IFDMA case. The gain is more than
over the IFDMA case. The gain is more than  dB at low output power levels, but there is a substantial gain also at operation closer to the maximum output power level. This gain is achieved without considering additional potential sleep mode gains enabled by the short blocks, as mentioned in Section 4.2.2.
dB at low output power levels, but there is a substantial gain also at operation closer to the maximum output power level. This gain is achieved without considering additional potential sleep mode gains enabled by the short blocks, as mentioned in Section 4.2.2.
 and Q = 128 subcarriers per user at two different HPA output power levels versus B-IFDMA using block size M = 1,
and Q = 128 subcarriers per user at two different HPA output power levels versus B-IFDMA using block size M = 1,  and Q = 32 subcarriers per user at
and Q = 32 subcarriers per user at  6 dBm lower HPA output power level. IFDMA uses 4 times longer blocks. L = 32 in both cases and there are N = 1024 subcarriers in the system.
6 dBm lower HPA output power level. IFDMA uses 4 times longer blocks. L = 32 in both cases and there are N = 1024 subcarriers in the system.5. Robustness
In this section, the robustness of B-IFDMA to carrier frequency offsets (CFOs) and to Doppler spreads (DSs) is analyzed for the uplink dependent on the signal parameters. The aim of this investigation is to show that the block based subcarrier allocation in B-IFDMA enables the possibility to combine robustness and provision of frequency diversity.
In mobile radio applications, CFOs are typically caused by oscillator imperfections due to low cost hardware components or Doppler shifts due to the mobility of the users. The CFOs result in a shift of the spectra of the different users' signals. Hence, the orthogonality of the subcarriers is destroyed and inter-carrier interference (ICI) occurs.
In general, two types of ICI can be distinguished. Regarding a particular user's signal, on the one hand, due to the shift of the spectrum, interference between the subcarriers of this user occurs. In the following this is denoted as self-interference (SI). On the other hand, in addition interference between the subcarriers of different users occurs. This case is in the following denoted as multiple access interference (MAI).
The DS is caused by the fact that in a mobile radio channel typically the same signal is received from different propagation paths where each path suffers from a different Doppler shift. The superposition of differently shifted replicas of the same signal at the receiver leads to a spread of the subcarriers of the different users' signals. Consequently, also for DSs the orthogonality of the subcarriers is destroyed and ICI occurs. Similar to the effects of CFOs, also for DSs two types of ICI, namely SI and MAI can be distinguished.
For uplink transmission, the CFOs and the DS for the received signals of different users are different. Thus, if CFOs and DS are known at the receiver, compensation of SI is possible, whereas compensation of MAI can only be obtained by application of joint detection techniques that require a high computational effort.
For the analysis of the robustness of B-IFDMA to CFOs, let

denote the relative CFO of user  normalizing the CFO
normalizing the CFO  of user
of user  to the subcarrier bandwidth
to the subcarrier bandwidth  . The relative CFO
. The relative CFO  is modeled as a random variable that is uniformly distributed in
is modeled as a random variable that is uniformly distributed in  with
with  denoting the maximum relative CFO of user
denoting the maximum relative CFO of user  that occurs. The CFOs
that occurs. The CFOs  are assumed to be known at the receiver. Thus, SI can be perfectly compensated by reversing the CFO
are assumed to be known at the receiver. Thus, SI can be perfectly compensated by reversing the CFO  . For the compensation of the MAI, joint detection techniques are required. For this investigation, it is assumed that, due to the high complexity, the compensation of MAI at the receiver is not feasible. In order to analyze the robustness to CFOs independently of the diversity effects, a B-IFDMA transmission over an AWGN channel is regarded.
. For the compensation of the MAI, joint detection techniques are required. For this investigation, it is assumed that, due to the high complexity, the compensation of MAI at the receiver is not feasible. In order to analyze the robustness to CFOs independently of the diversity effects, a B-IFDMA transmission over an AWGN channel is regarded.
For the analysis of the robustness of B-IFDMA to DSs, let

denote the relative DS of user  normalizing the DS
normalizing the DS  of user
of user  to the subcarrier bandwidth
to the subcarrier bandwidth  . Similar to the modelling of the CFOs, also the DS
. Similar to the modelling of the CFOs, also the DS  is modelled as a random variable. Assuming that for the different propagation paths the angle of arrival is uniformly distributed in
is modelled as a random variable. Assuming that for the different propagation paths the angle of arrival is uniformly distributed in  , the relative Doppler shift is Jakes distributed in
, the relative Doppler shift is Jakes distributed in  , where
, where  denotes the maximum Doppler shift normalized to the subcarrier bandwidth
denotes the maximum Doppler shift normalized to the subcarrier bandwidth  . At the receiver, SI is combatted by application of a linear Minimum Mean Square Error (MMSE) receiver, cf. [44]. For the compensation of the MAI, again, joint detection techniques are required and it is assumed that, due to the high complexity, the compensation of MAI at the receiver is not feasible. In order to separate the effect of the Doppler spread from frequency selective fading effects that are also caused by multipath propagation, a Doppler spread channel according to [44] is regarded, that is, the different propagation paths are assumed to arrive at the receiver at the same time. The channel is distorted by AWGN and the received signals from the different propagation paths suffer from mutually independent relative Doppler shifts.
. At the receiver, SI is combatted by application of a linear Minimum Mean Square Error (MMSE) receiver, cf. [44]. For the compensation of the MAI, again, joint detection techniques are required and it is assumed that, due to the high complexity, the compensation of MAI at the receiver is not feasible. In order to separate the effect of the Doppler spread from frequency selective fading effects that are also caused by multipath propagation, a Doppler spread channel according to [44] is regarded, that is, the different propagation paths are assumed to arrive at the receiver at the same time. The channel is distorted by AWGN and the received signals from the different propagation paths suffer from mutually independent relative Doppler shifts.
Figure 13 depicts the performance results without coding for the robustness investigations to CFOs assuming  subcarriers in the system,
subcarriers in the system,  subcarriers per user,
subcarriers per user,  users and
users and  for all users. From Figure 13 it can be concluded that, for B-IFDMA, the robustness to CFOs increases with an increasing number
for all users. From Figure 13 it can be concluded that, for B-IFDMA, the robustness to CFOs increases with an increasing number  of subcarriers per block. The reason for that is that the strongest inter-carrier interference is caused by neighboring subcarriers. Thus, increasing the number of neighboring subcarriers belonging to the same user increases the robustness to MAI at the expense of additional SI that, however, can be compensated. Note, that already for low numbers
of subcarriers per block. The reason for that is that the strongest inter-carrier interference is caused by neighboring subcarriers. Thus, increasing the number of neighboring subcarriers belonging to the same user increases the robustness to MAI at the expense of additional SI that, however, can be compensated. Note, that already for low numbers  of subcarriers per block the robustness of B-IFDMA to CFOs is significantly improved.
of subcarriers per block the robustness of B-IFDMA to CFOs is significantly improved.
Figure 14 depicts the performance results for the robustness investigations to DS assuming the same parameters as in Figure 13 and  for all users. The value for
for all users. The value for  represents the maximum relative Doppler shift for a system with
represents the maximum relative Doppler shift for a system with  kHz and a carrier frequency of 5 GHz with a user velocity of 315 km/h and, thus, represents a high mobility scenario, for example, for high speed trains.
kHz and a carrier frequency of 5 GHz with a user velocity of 315 km/h and, thus, represents a high mobility scenario, for example, for high speed trains.
From the results in Figure 14 it can be concluded that also the robustness of B-IFDMA to DS increases with an increasing number  of subcarriers per block. The reason is the same as for the improved robustness to CFOs. Again, already for small numbers
of subcarriers per block. The reason is the same as for the improved robustness to CFOs. Again, already for small numbers  a significant robustness gain is provided. The increased robustness to CFOs and DSs of B-IFDMA with
a significant robustness gain is provided. The increased robustness to CFOs and DSs of B-IFDMA with  makes B-IFDMA suitable for high speed users and systems with limited frequency synchronization.
makes B-IFDMA suitable for high speed users and systems with limited frequency synchronization.
6. Discussion of Results
In this section we summarize and comment on the investigations made in Sections 3, 4, and 5. In Section 1, we identified the following important requirements for the diversity based multiple access scheme, which should complement the FA multiple access scheme in an IMT Advanced capable system. Below we comment on the suitability of B-IFDMA to meet these requirements.
-
(i)
Robustness to small-scale fading without time diversity. The results in Section 3 showed that B-IFDMA can be defined based on a rather few number of subcarriers per block also with realistic channel estimation performance. Thus, also at rather low data rates, that is, rather few subcarriers assigned to a user per slot, a large frequency diversity can be obtained.
-
(ii)
Tuneable degree of frequency-diversity. As shown in Sections 3.3 and 4.3 rather small blocks, also with a sub-slot duration, can provide a good error rate performance. Thus, for a given data rate additional blocks can be allocated either well-separated in frequency to provide additional frequency-diversity, or adjacent in time or frequency (i.e., in same chunk cf. Figure 1), if enough diversity is already obtained from the frequency and/or spatial domain.
-
(iii)
Need to support high energy efficiency in the transmitters and the receivers. We showed in Section 4 that B-IFDMA including pulse shaping can provide similar HPA efficiency as IFDMA and LFDMA, which is substantially better than for TDMA-OFDM without DFT precoding. In addition, whenever the UE is not power limited, in Section 4.3 a substantial overall gain of more than
 dB is shown with time localized transmission in a fraction of the time slot, also when including realistic channel estimation performance and disregarding potential sleep mode gains. (These results are valid also for a downlink scenario using the B-EFDMA scheme.)
dB is shown with time localized transmission in a fraction of the time slot, also when including realistic channel estimation performance and disregarding potential sleep mode gains. (These results are valid also for a downlink scenario using the B-EFDMA scheme.) -
(iv)
Robustness to carrier frequency offsets and large Doppler spread. This property was evaluated in Section 5 and the conclusion is that already for small numbers of subcarriers per block a significant robustness gain against carrier CFOs as well as against Doppler spreads is provided compared to IFDMA. This property could provide a significant gain in certain scenarios, like for deployment in frequency bands using a several GHz carrier frequency. Another scenario is to support high-speed trains, and/or to deploy a system with rather narrow subcarrier bandwidth.
-
(v)
Support for widely varying packet sizes. Due to the good error rate performance of B-IFMDA with few number of subcarriers, transmission of rather small blocks perform well by using the TDMA component. Large packets can use the full chunk duration. The benefit of configuration flexibility motivates the introduction of a small basic block consisting of, for example,
 (subcarriers
(subcarriers  OFDM symbols) in B-IFDMA as a building block to enable adaptive block allocation in different deployment and usage scenarios, as illustrated in Figure 1, see [5, 45] for further discussion.
OFDM symbols) in B-IFDMA as a building block to enable adaptive block allocation in different deployment and usage scenarios, as illustrated in Figure 1, see [5, 45] for further discussion. -
(vi)
Enable efficient resource allocation. As discussed in [45] just a few different block allocations should be sufficient in a cell. The regular block allocation is beneficial for low addressing overhead, and it was shown in Section 4.1 to also be beneficial for lowering the envelope variations.
-
(vii)
Be of use for in-band control signals. This is possible due to the efficient support for small packets as discussed above. In addition, the short TDMA component in B-IFDMA is useful to support precise timing of control messages for FA transmission, cf. [9].
-
(viii)
Enable efficient coexistence with adaptive TDMA/OFDMA. Since B-IFDMA also is based on OFDM with the same parameters, these two schemes are compatible. With well-separated regular block allocations in frequency, adaptive TDMA/OFDMA resources can be interlaced as shown, for example, in [9, Figure 2].
-
(ix)
Facilitate low complexity transmitter in UEs. The good envelope properties of B-IFDMA enables the use of a less complex HPA and predistortion unit. In the appendix we show that a B-IFDMA signal can be efficiently generated in the time domain, that is, without the DFT operation.
7. Conclusions
In this paper we have shown that B-IFDMA, which is a generalization of the SC-FDMA concept, is a power efficient, flexible and scalable multiple access scheme that can serve as a robust complement to future adaptive IMT Advanced capable wireless systems. Based on the included investigations, we have shown that B-IFDMA is able to provide equal or better error rate performance than IFDMA and LFDMA, when considering realistic channel estimation performance at the receiver and no reliable channel state information at the transmitter, also for rather low data rates, and without using time diversity.
We also showed that B-IFDMA provides better amplifier efficiency than OFDMA and can provide better end-to-end energy efficiency than IFDMA and LFDMA. These investigations motivated the use of the DFT precoding step, and the integration of the TDMA component within the B-IFDMA scheme. These results also motivated the use of a regular subcarrier allocation in B-IFDMA.
Then, we showed that B-IFDMA offers the possibility to combine robustness against carrier frequency offsets and Doppler spread with provision of frequency diversity. This property could provide a significant gain in certain scenarios, like for deployment in frequency bands using a several GHz carrier frequency. Another scenario is to support high-speed trains, and/or to deploy a system with rather narrow subcarrier bandwidth.
Finally, we argued for that B-IFDMA has the capability to fulfill and provide a good tradeoff between the requirements envisioned for the robust transmission mode in the uplink of future IMT Advanced capable wireless systems.
Appendix
Time Domain Representation
In this appendix, the samples of the B-IFDMA time domain signal are analyzed. For sake of simplicity, throughout this appendix, the index  is omitted. Combining the precoding, the user specific block-interleaved subcarrier mapping and the OFDM modulation, the elements
is omitted. Combining the precoding, the user specific block-interleaved subcarrier mapping and the OFDM modulation, the elements  ,
,  , of the modulated data vector
, of the modulated data vector  in (6) can be written as
in (6) can be written as

with

for  . The derivation can be found in [46]. Equation (A.1) is illustrated in Figure 15.
. The derivation can be found in [46]. Equation (A.1) is illustrated in Figure 15.
The sequence  in (A.1) can be interpreted as a compression of the sequence of data symbols
in (A.1) can be interpreted as a compression of the sequence of data symbols  ,
,  , in time by factor
, in time by factor  , a subsequent
, a subsequent  -fold repetition and, finally, a cyclic shift of the
-fold repetition and, finally, a cyclic shift of the  elements of the resulting sequence by
elements of the resulting sequence by  , as illustrated in [46, Figure 3]. Thus, B-IFDMA can be considered as a superposition of
, as illustrated in [46, Figure 3]. Thus, B-IFDMA can be considered as a superposition of  single carrier signals weighted by different complex numbers
single carrier signals weighted by different complex numbers  .
.
The expression  in (A.2) represents a user specific frequency shift by
in (A.2) represents a user specific frequency shift by  . For
. For  the expression
the expression  reduces to
reduces to

and (A.1) simplifies to compression and repetition of the data symbols, subsequent user specific frequency shift and a normalization to  . This is equivalent to the generation of an IFDMA signal [14] which is a single carrier signal, that is, a serially modulated carrier. Note that also for the special case
. This is equivalent to the generation of an IFDMA signal [14] which is a single carrier signal, that is, a serially modulated carrier. Note that also for the special case  , an expression is obtained that is equivalent to a single carrier signal because for this case the expression from (A.1) is equivalent to the time domain samples of an LFDMA signal that are described in [47].
, an expression is obtained that is equivalent to a single carrier signal because for this case the expression from (A.1) is equivalent to the time domain samples of an LFDMA signal that are described in [47].
Since the coefficients by (A.2) are independent from the data symbols, they can be calculated offline. Thus, (A.1) also represents an alternative implementation for B-IFDMA modulation that does not require  and
and  to be powers of 2 as it would be the case for an implementation of B-IFDMA modulation according to (6), if the Fast Fourier Transform (FFT) algorithm is used.
to be powers of 2 as it would be the case for an implementation of B-IFDMA modulation according to (6), if the Fast Fourier Transform (FFT) algorithm is used.
Similar to the modulation, also the B-IFDMA demodulation can be reformulated as follows. The elements  ,
,  of the demodulated B-IFDMA signal
of the demodulated B-IFDMA signal

can be expressed as

with

The derivation of the demodulator can be found in [46] with an illustration in [46, Figure 4]. It can be regarded as a generalization of the demodulation for IFDMA described in [14].
References
International Telecommunication Union Radiocommunication Sector ITU-R : Recommendation ITU-R M1645, framework and overall objectives of the future development of IMT-2000 and systems beyond IMT-2000. 2003
Wijing C, Doppler K, Kalliojärvi K, et al.: WINNER II system concept: advanced radio technologies for future wireless systems. Proceedings of the ICT-Mobile Summit Conference, June 2008
Parkvall S, Dahlman E, Furuskär A, et al.: LTE-advanced evolving LTE towards IMT-advanced. Proceedings of the 68th IEEE Vehicular Technology Conference (VTC '08), September 2008, Calgary, Canada 1-5.
Auer G, Döttling M, Doppler K, et al.: D6.13.14 WINNER II system concept description. WINNER; January 2008.
Döttling M, Mohr W, Osseiran A: Radio Technologies and Concepts for IMT-Advanced. John Wiley & Sons, New York, NY, USA; 2009.
Tyrrell A, Auer G: Imposing a reference timing onto firefly synchronization in wireless networks. Proceedings of the 65th IEEE Vehicular Technology Conference (VTC '07), April 2007, Dublin, Ireland 222-226.
Falconer D, Ng B, Lam C-T, et al.: D2.3.3 WINNER II link level procedures for the WINNER system. WINNER; November 2007.
Döttling M, Sternad M, Klang G, von Häfen J, Olsson M: Integration of spatial processing in the WINNER B3G air interface design. Proceedings of the 63rd IEEE Vehicular Technology Conference (VTC '06), May 2006, Melbourne, Australia 1: 246-250.
Sternad M, Svensson T, Ottosson T, Ahlén A, Svensson A, Brunstrom A: Towards systems beyond 3G based on adaptive OFDMA transmission. Proceedings of the IEEE 2007, 95(12):2432-2455.
Sternad M, Falahati S, Svensson T, Aronsson D: Adaptive TDMA/OFDMA for wide-area coverage and vehicular velocities. Proceedings of the IST Mobile and Vehicular Communication Summit, June 2005, Dresden, Germany
Safjan K, Oszmianski J, Döttling M, Bohdanowicz A: Frequency-domain link adaptation for wideband OFDMA systems. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC '08), April 2008, Las Vegas, Nev, USA 1703-1708.
Svensson T, Franky T, Falconer D, et al.: B-IFDMA—a power efficient multiple access scheme for non-frequency- adaptive transmission. Proceedings of the 16th IST Mobile and Wireless Communications Summit, July 2007, Budapest, Hungary
Galda D, Rohling H, Costa E, Haas H, Schulz E: A low complexity transmitter structure for OFDM-FDMA uplink systems. Proceedings of the IEEE Vehicular Technology Conference (VTC '02), May 2002, Birmingham, UK 4: 1737-1741.
Sorger U, De Broeck I, Schnell M: IFDMA—a new spreadspectrum multiple-access scheme. In Multi-Carrier Spread-Spectrum. Kluwer Academic Publishers, Amsterdam, The Netherlands; 1997:111-118.
Dahlman E, Parkvall S, Sköld J, Beming P: 3G Evolution: HSPA and LTE for Mobile Broadband. Academic Press, New York, NY, USA; 2007.
The 3rd Generation Partnership Project (3GPP) : Physical layer aspects for evolved Universal Terrestrial Radio Access (UTRA). In Technical Specification Group Radio Access Network TR 25.814 v7.1.0,. 3GPP, Sophia Antipolis Cedex, France; 2006.
Myung HG, Lim J, Goodman DJ: Single carrier FDMA for uplink wireless transmission. IEEE Vehicular Technology Magazine 2006, 1(3):30-38.
Plass S, Svensson T, Dammann A: Block-equidistant resource mapping in OFDM, MC-CDMA and SS-MC-MA. Proceedings of the 12th International OFDM Workshop, August 2007, Hamburg, Germany
Döttling M, et al.: D6.13.7 WINNER II test scenarios and calibration cases issue 2. WINNER; December 2006.
Frank T, Klein A, Costa E, Schulz E: Interleaved orthogonal frequency division multiple access with variable data rates. Proceedings of the International OFDM Workshop, August-September 2005, Hamburg, Germany 179-183.
Frank T, Klein A, Costa E: IFDMA: a scheme combining the advantages of OFDMA and CDMA. IEEE Wireless Communications 2007, 14(3):9-17.
Wang Z, Giannakis GB: Wireless multicarrier communications. IEEE Signal Processing Magazine 2000, 17(3):29-48. 10.1109/79.841722
Sari H, Karam G, Jeanclaude I: Frequency domain equalization of mobile radio terrestrial broadcast channels. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM '94), November-December 1994, San Francisco, Calif, USA 1-5.
Falconer D, Ariyavisitakul S, Benyamin-Seeyar A, Eidson B: Frequency domain equalization for single-carrier broadband wireless systems. IEEE Communications Magazine 2002, 40: 58-66.
Alamouti SM: A simple transmit diversity technique for wireless communications. IEEE Journal on Selected Areas in Communications 1998, 16(8):1451-1458. 10.1109/49.730453
Boelcskei H, Paulraj AJ: Space-frequency coded broadband OFDM systems. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC '00), September 2000, Chicago, Ill, USA 1: 1-6.
Bahl LR, Cocke J, Jelinek F, Raviv J: Optimal decoding of linear codes for minimizing symbol error rate. IEEE Transactions on Information Theory 1974, 20(2):284-287.
Kyösti P, Meinilä J, Hentila L, et al.: D1.1.2 WINNER II channel models—part I channel models. WINNER; September 2007.
Auer G: Analysis of pilot-symbol aided channel estimation for OFDM systems with multiple transmit antennas. Proceedings of the IEEE International Conference on Communications (ICC '04), June 2004, Paris, France 6: 3221-3225.
Hoeher P, Kaiser S, Robertson P: Two-dimensional pilot-symbol aided channel estimation by Wiener filtering. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '97), April 1997, Munich, Germany 3: 1845-1848.
Edfors O, Sandell M, van de Beek J-J, Wilson S, Börjesson P: OFDM channel estimation by singular value decomposition. IEEE Transactions on Communications 1998, 46(7):931-939. 10.1109/26.701321
Fazel K, Kaiser S: Multi-Carrier Spread Spectrum Systems. 1st edition. John Wiley & Sons, New York, NY, USA; 2003.
Lam CT, Falconer D, Danilo-Lemoine F: Channel estimation for sub-chunk-based DFT-precoded OFDM systems. Proceedings of the 18th Meeting on Wireless World Research Forum (WWRF '07), June 2007, Helsinki, Finland
Kailath T, Sayed AH, Hassibi B: Linear Estimation. Prentice-Hall, Upper Saddle River, NJ, USA; 2000.
Aronsson D: Channel estimation and prediction from a Bayesian perspective, Licentiate thesis. Department of Signals and Systems, Uppsala University, Uppsala, Sweden; 2007.
Wijting C, Doppler K, Kalliojärvi K, et al.: Key technologies for IMT-advanced mobile communication systems. IEEE Wireless Communications Magazine 2009.
Aronsson D, Svensson T, Sternad M: Performance evaluation of memory-less and Kalman-based channel estimation for OFDMA. Proceedings of the IEEE Vehicular Technology Conference (VTC '09), April 2009, Barcelona, Spain
Frank T, Klein A, Haustein T: A survey on the envleope fluctuations of DFT precoded OFDMA. Proceedings of the International Conference on Communications (ICC '08), May 2008, Beijing, China
van Nee R, Prasad R: OFDM for Wireless Multimedia Communications. 1st edition. Artech House, Boston, Mass, USA; 2000.
Skrzypczak A, Siohan P, Javaudin J-P: Power spectral density and cubic metric for the OFDM/OQAM modulation. Proceedings of the 6th IEEE International Symposium on Signal Processing and Information Technology (ISSPIT '06), August 2006, Vancouver, Canada 846-850.
The 3rd Generation Partnership Project (3GPP) : Comparison of PAR and cubic metric for powerderating. In Technical Documents TDoc R4-040367, TSG RAN WG4 31, 3GPP, Sophia Antipolis Cedex, France; 2004.
Nemati HM, Fager C, Gustavsson U, et al.: Characterization of switched-mode LDMOS and GaN power amplifiers for optimal use in polar transmitter architectures. Proceedings of the IEEE International Microwave Symposium, June 2008, Atlanta, Ga, USA
Wang F, Kimball D, Popp J, et al.: Wideband envelope elimination and restoration power amplifier with high efficiency wideband envelope amplifier for WLAN 802.11g applications. Proceedings of the Microwave Symposium Digest, June 2005, La Jolla, Calif, USA 645-648.
Eggen TH, Baggeroer AB, Preisig JC: Communication over doppler spread channels-part I: channel and receiver presentation. IEEE Journal of Oceanic Engineering 2000, 25(1):62-71. 10.1109/48.820737
Sternad M, Svensson T, Döttling M: Resource allocation and control signaling in the WINNER flexible MAC concept. Proceedings of the IEEE Vehicular Technology Conference (VTC '08), September 2008, Calgary, Canada
Frank T, Klein A, Costa E: An efficient implementation for block-IFDMA. Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '07), September 2007, Athens, Greece
Myung HG, Lim J, Goodman DJ: Peak-to-average power ratio of single carrier FDMA signals with pulse shaping. Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '06), September 2006, Helsinki, Finland
Acknowledgments
This work has partly been performed in the framework of the IST project IST-4-027756 WINNER II, which was partly funded by the European Union. The authors would like to acknowledge the contributions of their colleagues in WINNER II, although the views expressed are those of the authors and do not necessarily represent the project.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Svensson, T., Frank, T., Eriksson, T. et al. Block Interleaved Frequency Division Multiple Access for Power Efficiency, Robustness, Flexibility, and Scalability. J Wireless Com Network 2009, 720973 (2009). https://doi.org/10.1155/2009/720973
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/720973



 subcarriers per user with normalized antenna gain.
subcarriers per user with normalized antenna gain.
 subcarriers per user with normalized antenna gain.
subcarriers per user with normalized antenna gain.
 subcarriers per user with normalized antenna gain.
subcarriers per user with normalized antenna gain.
 blocks per user and with normalized antenna gain.
blocks per user and with normalized antenna gain.
 OFDM symbols as in [
OFDM symbols as in [



 as a function of number of blocks
as a function of number of blocks
 compared to the corresponding schemes without DFT precoding and schemes with random allocation of the subcarrier blocks.
compared to the corresponding schemes without DFT precoding and schemes with random allocation of the subcarrier blocks.

 (with DFT) compared to signals without DFT precoding for different numbers
(with DFT) compared to signals without DFT precoding for different numbers
 of subcarriers per block using different metrics.
of subcarriers per block using different metrics.


 maximum relative CFO for different numbers
maximum relative CFO for different numbers
 of subcarriers per block, assuming
of subcarriers per block, assuming
 subcarriers and
subcarriers and
 subcarriers per user.
subcarriers per user.

 relative carrier frequency offset per path for different numbers
relative carrier frequency offset per path for different numbers
 of subcarriers per block, assuming
of subcarriers per block, assuming
 subcarriers and
subcarriers and
 subcarriers per user.
subcarriers per user.
 dB is shown with time localized transmission in a fraction of the time slot, also when including realistic channel estimation performance and disregarding potential sleep mode gains. (These results are valid also for a downlink scenario using the B-EFDMA scheme.)
dB is shown with time localized transmission in a fraction of the time slot, also when including realistic channel estimation performance and disregarding potential sleep mode gains. (These results are valid also for a downlink scenario using the B-EFDMA scheme.) (subcarriers
(subcarriers  OFDM symbols) in B-IFDMA as a building block to enable adaptive block allocation in different deployment and usage scenarios, as illustrated in Figure
OFDM symbols) in B-IFDMA as a building block to enable adaptive block allocation in different deployment and usage scenarios, as illustrated in Figure 