- Research Article
- Open access
- Published:
Power Allocation and Admission Control in Multiuser Relay Networks via Convex Programming: Centralized and Distributed Schemes
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 901965 (2009)
Abstract
The power allocation problem for multiuser wireless networks is considered under the assumption of amplify-and-forward cooperative diversity. Specifically, optimal centralized and distributed power allocation strategies with and without minimum rate requirements are proposed. We make the following contributions. First, power allocation strategies are developed to maximize either (i) the minimum rate among all users or (ii) the weighted-sum of rates. These two strategies achieve different throughput and fairness tradeoffs which can be chosen by network operators depending on their offering services. Second, the distributed implementation of the weighted-sum of rates maximization-based power allocation is proposed. Third, we consider the case when the requesting users have minimum rate requirements, which may not be all satisfied due to the limited-power relays. Consequently, admission control is needed to select the number of users for further optimal power allocation. As such a joint optimal admission control and power allocation problem is combinatorially hard, a heuristic-based suboptimal algorithm with significantly reduced complexity and remarkably good performance is developed. Numerical results demonstrate the effectiveness of the proposed approaches and reveal interesting throughput-fairness tradeoff in resource allocation.
1. Introduction
Recently, a new form of diversity, namely, cooperative diversity, has been introduced to enhance the performance of wireless networks [1, 2]. It has been noticed that besides smart cooperative diversity protocol engineering, efficient radio resource management also has profound impacts on performance of wireless networks in general and relay networks in particular [3]. Consequently, there are numerous works on radio resource (such as time, power, and bandwidth) allocation to improve performance of relay networks (e.g., see [4–8] and references therein). However, a single user scenario is typically considered in these existing works which neglects and simplifies many important network-wide aspects of cooperative diversity.
In this paper, we consider a more general and practical network model, in which multiple sources and destination pairs share radio resources from a set of relays. Note that a preliminary version of a portion of this work has been appeared in [9]. Although various relay models have been studied, the simple two-hop relay model has attracted extensive research attention [2–6, 10]. It is also assumed in this work. In particular, each relay is delegated to assist one or more users, especially when the number of relays is (much) smaller than the number of users. A typical example of such scenarios is the deployment of few relays in a cellular network for both uplink and downlink transmissions. In such scenarios, it is clear that the aforementioned resource allocation schemes for single-user relay network cannot be directly applied. Resource allocation in a multiuser system should provide a certain degree of fairness for different users. Depending on underlying wireless applications, one fairness criterion is more suitable than the others. Studying the tradeoff between fairness and network performance (e.g., network throughput) for multiuser relay networks is an interesting but challenging problem, and thus, deserves more investigation.
This paper considers resource allocation problems for multiuser relay networks under two different scenarios. Particularly, we first consider applications in which users do not have minimum rate requirements. This scenario is applicable for wireless networks which offer best-effort services. Under the assumption that the channel state information (CSI) of wireless links is available, we derive optimal power allocation schemes to maximize either (i) the minimum rate of all users (max-min fairness); or (ii) the weighted-sum of rates (weighted-sum fairness). We show that the corresponding optimization problems are convex; therefore, their optimal power allocation solutions can be efficiently obtained using standard convex programming algorithms. Numerical results show that the max-min fairness provides a significant performance improvement for the worst user(s) at the cost of a loss in network throughout, while the weighted-sum fairness provides larger network throughput. In addition, by changing the weights of different users, we can differentiate users' throughput performance which would be useful in provisioning wireless networks with nonhomogeneous services. In general, these formulations provide different tradeoffs between the network throughput and fairness which can be chosen by network operators depending on their offering services.
Centralized implementation of power allocation schemes requires a central controller to collect CSI of all wireless links in order to find an optimal solution and distribute the solution to the corresponding wireless nodes. This would incur large communications overhead and render the power allocation problem difficult for online implementation. To resolve this problem, we propose distributed implementation for the power allocation which requires each user to collect CSI only from its immediate neighbors. Such distributed algorithm requires corresponding pricing information to be transferred from relays to destination nodes and requested power levels to be transferred in the reversed direction. An iterative algorithm, which implements this strategy, should converge to an optimal solution which must be the same as that obtained by centralized implementation. The proposed distributed algorithm can be used in infrastructureless wireless networks such as sensor and ad hoc networks.
In addition, we also consider applications in which users have minimum rate requirements to maintain their QoS guarantees. Such applications include networks which must provide QoS and/or real-time services such as voice and video. Due to limitation of power resource, minimum rate requirements for all users may not be satisfied simultaneously. This motivates the investigation of admission control where users are not automatically admitted into the network. Such the joint technique for another application to multiuser downlink beamforming and admission control has been first developed in [11]. In particular, we propose an algorithm to solve the joint admission control and power allocation problem. Such algorithm first aims at maximizing the number of users that can be admitted while meeting their minimum rate requirements. Then, optimal power allocation is performed for the admitted users. We show that this 2-stage optimization problem can be equivalently reformulated as a single-stage problem which assists us in developing a heuristic-based approach to efficiently solve the underlying joint admission control and power allocation problem. Through numerical analysis, we observe that the power required by the heuristic algorithm is only slightly larger than that required by the optimal solution using exhaustive search. However, the complexity in terms of running time of the former is much lower than that of the latter. Since such heuristic-based approach uses convex optimization, the joint admission control and power allocation problem can be solved efficiently even for large networks.
Note that although this paper considers similar problems as in [12, 13], it is significantly different from [12, 13], especially in the system implementation and modeling. In terms of mathematical methods, the approach used in this paper is based on general convex optimization while that in [12, 13] was based on geometric programming. Specifically, it was assumed in [12, 13] that each user is relayed by one relay. This current research considers a more general scenario where one user is assisted by several relays and focuses on efficient power allocation to the relays. Moreover, while this work assumes that one source transmit power is independent of the others, sources were assumed to share their power resource in [12, 13]. Another new contribution in this paper is the development of a distributed power allocation algorithm. In addition, although the admission control concept is similar in both previous and current works, a new heuristic algorithm is derived by relaxing the binary variables, and user is dropped if it has largest gap between its achievable rate and target rate. In [13], no such binary relaxation was required and user was dropped because it required the most power.
The rest of this paper is organized as follows. In Section 2, a multiuser wireless relay model with multiple relays is presented. Two power allocation problems are discussed in Section 3, and their centralized implementation is developed. Section 4 presents a distributed algorithm to implement the power allocation scheme presented in Section 3. The optimal joint admission control and power allocation problem and its solution are presented in Section 5. Numerical results are given in Section 6, followed by the conclusion in Section 7.
2. System Model and Assumptions
Consider a multiuser relay network where  source nodes
source nodes  transmit data to their corresponding destination nodes
transmit data to their corresponding destination nodes  . There are
. There are  relay nodes
relay nodes  which are employed to assist transmissions from source to destination nodes. The set of relays assisting the transmission of
which are employed to assist transmissions from source to destination nodes. The set of relays assisting the transmission of  is denoted by
is denoted by  . The set of sources using the
. The set of sources using the  relay is denoted by
relay is denoted by  , that is,
, that is,  . In other words, one particular relay can forward data for several users. Amply-and-forward (AF) cooperative diversity is assumed.
. In other words, one particular relay can forward data for several users. Amply-and-forward (AF) cooperative diversity is assumed.
Orthogonal transmissions are used for simultaneous transmissions among different users by using different channels, (e.g., different frequency bands) and time division multiplexing is employed by AF cooperative diversity for each user. One possible implementation for our considered network model is as follows. The available bandwidth is equally divided into as many bands as the number of users. Each user is allocated one frequency band and communication between each source and destination pair via relay nodes is carried out in a time multiplexing manner [2], that is, each source  transmits data to its chosen relays in the set
transmits data to its chosen relays in the set  in the first stage and each relay amplifies and forwards its received signal to
in the first stage and each relay amplifies and forwards its received signal to  in the second stage. Note that our approaches can still be used for other possible implementations as long as the assumption of orthogonal transmissions is satisfied.
in the second stage. Note that our approaches can still be used for other possible implementations as long as the assumption of orthogonal transmissions is satisfied.
The system model under investigation is illustrated in Figure 1. Note that this model is quite general, and it covers a large number of applications in different network settings. For example, this model can be applied to cellular wireless networks which use relays for uplink with one destination base station (BS) or downlink with one source BS and many destinations. The model can also be directly applied to multihop wireless networks such as sensor/ad hoc or wireless mesh networks. Moreover, in our model, each source can be assisted by one, several, or all available relays. Therefore, it captures most relay models considered in literature.
Let  denote the power transmitted by
denote the power transmitted by  . The power transmitted by the relay
. The power transmitted by the relay  for assisting the source
for assisting the source  is denoted by
is denoted by  . For simplicity, we present the signal model for link
. For simplicity, we present the signal model for link  -
- only. In the first time interval, source
only. In the first time interval, source  broadcasts the signal
broadcasts the signal  with unit energy to the relays
with unit energy to the relays  . The received signal at relay
. The received signal at relay  can be written as
can be written as

where  denotes the channel gain for link
denotes the channel gain for link  is the additive circularly symmetric white Gaussian noise (AWGN) at the relay
is the additive circularly symmetric white Gaussian noise (AWGN) at the relay  with variance
with variance  . The channel gain includes the effects of path loss, shadowing, and fading. In the second time interval, relay
. The channel gain includes the effects of path loss, shadowing, and fading. In the second time interval, relay  amplifies its received signal and retransmits it to the destination node
amplifies its received signal and retransmits it to the destination node  . After some manipulations, the received signal at the destination node
. After some manipulations, the received signal at the destination node  can be written as
can be written as

where  is the channel gain for link
is the channel gain for link  is the AWGN at the destination node
is the AWGN at the destination node  with variance
with variance  is the modified AWGN noise at
is the modified AWGN noise at  with equivalent variance
with equivalent variance  . Assuming that maximum-ratio-combining is employed at the destination node
. Assuming that maximum-ratio-combining is employed at the destination node  , the Signal-to-Noise Ratio (SNR) of the combined signal at the destination node
, the Signal-to-Noise Ratio (SNR) of the combined signal at the destination node  can be written as [2]
can be written as [2]

where

Note that we consider the case when the source-to-relay link is (much) better than the source-to-destination link, which is a typical outcome of a good relay selection by each source node. This is a practical assumption since source nodes are likely to use the closely located relays. The following lemma is in order.
Lemma 1.
The rate function of user  defined as
defined as  (b/s/Hz) is a concave increasing function of
(b/s/Hz) is a concave increasing function of  .
.
Proof.
We start by rewriting  as
as

It can be seen that  is a concave increasing function of
is a concave increasing function of  . Furthermore, since the
. Furthermore, since the  function is concave increasing, and using the composition rule [14], it can be concluded that
function is concave increasing, and using the composition rule [14], it can be concluded that  is concave increasing as well, that is, by increasing the power allocated at the relays to user
is concave increasing as well, that is, by increasing the power allocated at the relays to user  , its rate
, its rate  is increased. In addition, the maximum achievable rate
is increased. In addition, the maximum achievable rate  is equal to
is equal to  . However, since
. However, since  is concave increasing, the incremental increase of rate w.r.t.
is concave increasing, the incremental increase of rate w.r.t.  is smaller for larger
is smaller for larger  .
.
The convexity and monotonicity properties of  are extremely useful. While the former helps to exploit convex programming, the latter provides some insights into optimization problems under consideration as will be shown shortly.
are extremely useful. While the former helps to exploit convex programming, the latter provides some insights into optimization problems under consideration as will be shown shortly.
3. Power Allocation: Problem Formulations
In general, resource allocation in wireless networks should take into account the fairness among users. It is known that an attempt to maximize the sum rate of all users can significantly degrade the performance of the worst user(s). To balance fairness and throughput performance for all users, we consider two different optimization criteria for developing power allocation algorithms. The first criterion aims at maximizing minimum rate among all users. In essence, this criterion tries to make rates of all users as equal as possible. For the second criterion, users are given different weights, and power allocation is performed to maximize the weighted-sum of rates for all users. In this case, large weights can be allocated to users in unfavorable condition in order to prevent severe degradation of their performance. Moreover, this objective also captures the scenarios in which one needs to perform QoS differentiation for users. Then, the users of higher service priority can be allocated larger weights. For both aforementioned optimization criteria, we add constraints on the total maximum power that each relay can use to assist the corresponding users.
3.1. Max-Min Rate Fairness-Based Power Allocation
The power allocation problem under max-min rate fairness can be mathematically formulated as


where  is the maximum power available in relay
is the maximum power available in relay  . The left-hand side of (6b) is the total power that relay
. The left-hand side of (6b) is the total power that relay  allocates to its assisted users which is constrained to be less than its maximum power budget. Instead of constraining the transmit power for a particular relay as in (6b), we can equivalently limit the sum of power transmitted by its relayed source nodes, or limit its received sum of power. This constraint is required to avoid overloading relays in the network.
allocates to its assisted users which is constrained to be less than its maximum power budget. Instead of constraining the transmit power for a particular relay as in (6b), we can equivalently limit the sum of power transmitted by its relayed source nodes, or limit its received sum of power. This constraint is required to avoid overloading relays in the network.
Numerical results show that although this power allocation criterion results in a loss in network throughput, it helps to improve performance of the worst users. Therefore, this criterion is applicable for networks in which all users are (almost) equally important. This could be the case, for example, when all wireless users pay the same subscription fees, and thus, demand similar level of QoS. It can be seen that the set of linear inequality constraints with positive variables in the optimization problem (6a) and (6b) is compact and nonempty. Hence, the optimization problem (6a) and (6b) is always feasible. Moreover, since the objective function  is an increasing function of the allocated powers, the inequality constraints (6b) should be met with equality at optimality. Introducing a new variable
is an increasing function of the allocated powers, the inequality constraints (6b) should be met with equality at optimality. Introducing a new variable  , the optimization problem (6a) and (6b) can be equivalently rewritten in a standard form as
, the optimization problem (6a) and (6b) can be equivalently rewritten in a standard form as



The objective function (7a) is linear, and thus, convex. The constraints (7b) are convex due to Lemma 1, while the constraints (7c) are linear, and thus, also convex. Therefore, the optimization problem (7a)–(7c) is convex. Moreover, at least one of the constraints (7b) must be met with equality at optimality. Otherwise,  can be increased, or equivalently,
can be increased, or equivalently,  can be decreased, and thus, contradicting the optimality assumption. The convexity of the formulated power allocation problem is very useful to obtain its optimal solution by using any standard convex optimization algorithm such as interior-point algorithms [14]. In the special case when all users share the same set of relays, we have the following result.
can be decreased, and thus, contradicting the optimality assumption. The convexity of the formulated power allocation problem is very useful to obtain its optimal solution by using any standard convex optimization algorithm such as interior-point algorithms [14]. In the special case when all users share the same set of relays, we have the following result.
Proposition 1.
Consider a special case when all users have the same set of relays (e.g., users are assisted by all relays). Then the rates of all users are equal at optimality.
Proof.
Suppose that there is at least one user achieving the rate strictly larger than the minimum rate at optimality. Without loss of generality, let  be the set of users achieving minimum rate and suppose that user
be the set of users achieving minimum rate and suppose that user  has rate larger than that of any user
has rate larger than that of any user  at optimality. Note that there exists at least one relay
at optimality. Note that there exists at least one relay  which has nonzero allocated power
which has nonzero allocated power  at optimality. If we take an arbitrarily small amount of power
at optimality. If we take an arbitrarily small amount of power  from
from  and allocate an amount of power equal to
and allocate an amount of power equal to  to each user
to each user  where
where  denotes the cardinality of set
denotes the cardinality of set  , then the resulting rate of user
, then the resulting rate of user  is still larger than the minimum rate of all users while we can improve the minimum rates for all users in
is still larger than the minimum rate of all users while we can improve the minimum rates for all users in  . This is a contradiction to the optimality condition. Hence, the proposition is proved.
. This is a contradiction to the optimality condition. Hence, the proposition is proved.
3.2. Weighted-Sum of Rates Fairness-Based Power Allocation
As discussed above, the max-min rate fairness-based power allocation tends to improve performance of the worst user at the cost of total network throughput degradation. The weighted-sum of rates maximization can potentially achieve certain fairness for different users by allocating large weights to users in unfavorable channel conditions while maintaining good network performance in general. Let  denote the allocated weight for user
denote the allocated weight for user  , then the weighted-sum of rates based power allocation problem can be mathematically posed as
, then the weighted-sum of rates based power allocation problem can be mathematically posed as


In general, users of higher priority are given larger weights. Specifically, all users can be grouped into different classes and users in the same class are assigned same weight. It can be seen that the constraints (8b) must be met with equality at optimality. Otherwise, the allocated powers can be increased to improve the objective value, that contradicts the optimality assumption. In addition, it can be verified that the optimization problem (8a) and (8b) is convex; therefore, its optimal solution can be obtained by any standard convex optimization algorithm.
We conclude this section by noting that power allocation schemes based on other possible fairness criteria can also be considered. For instance, the proportional fairness criterion can be adopted. In terms of system-wide performance metric such as the network throughput, this criterion can ensure more fairness than the weighted-sum of rates, while achieving better performance than the max-min fairness in term of the network throughput [15]. It can be shown that the objective function to be maximized for the proportional fairness-based power allocation scheme is  . Consequently, this objective function can be reformulated as a convex function using the
. Consequently, this objective function can be reformulated as a convex function using the  function. Due to space limitation, investigation of this scheme is not presented in this paper.
function. Due to space limitation, investigation of this scheme is not presented in this paper.
4. Distributed Implementation for Power Allocation
To relax the need for centralized channel estimation and to implement online power allocation for multiuser relay networks, we propose a distributed algorithm for solving the problem (8a) and (8b). The distributed algorithm is developed based on the dual decomposition approach in convex optimization (see, e.g., [16, 17] and references therein). An application of this optimization technique for distributed routing can be also found in [18].
4.1. Dual Decomposition Approach
The main idea behind the dual decomposition approach is to decompose the original problem into independent subproblems that are coordinated by a higher-level master dual problem. Toward this end, we first write the Lagrangian function by relaxing the total power constraint for all relays as follows:

where  are the Lagrange multipliers corresponding to the
are the Lagrange multipliers corresponding to the  linear constraints on the maximum powers available in relay nodes. Using the fact that
linear constraints on the maximum powers available in relay nodes. Using the fact that

the Lagrangian in (9) can be rewritten as

Then, the corresponding dual function of the Lagrangian can be written as

Since the original optimization is convex and strong duality holds, the solution of the underlying optimization problem can be obtained by solving the corresponding dual problem


The dual function in (12) can be found by solving the following  separate subproblems, which correspond to
separate subproblems, which correspond to  different users,
different users,


where  corresponds to the
corresponds to the  th component of the Lagrangian. Let
th component of the Lagrangian. Let  be the optimal value of
be the optimal value of  found by solving (14a) and (14b), then, the dual problem in (13a) and (13b) can be rewritten as
found by solving (14a) and (14b), then, the dual problem in (13a) and (13b) can be rewritten as


The distributed power allocation algorithm is developed by iteratively and sequentially solving the problems (14a) and (14b) and (15a) and (15b). This algorithm is known as a primal-dual algorithm in optimization theory [14]. The Lagrange multiplier  represents the pricing coefficient for each unit power at relay
represents the pricing coefficient for each unit power at relay  . Therefore,
. Therefore,  can be seen as the price which user
can be seen as the price which user  must pay for using power
must pay for using power  at each relay
at each relay  . Then, the optimization problem (14a) and (14b) as a whole can be seen as an attempt of user
. Then, the optimization problem (14a) and (14b) as a whole can be seen as an attempt of user  to maximize its rate minus the total price that it has to pay given the price coefficients at relays. Moreover, the weight
to maximize its rate minus the total price that it has to pay given the price coefficients at relays. Moreover, the weight  can be seen as a "gain" coefficient for each unit rate for user
can be seen as a "gain" coefficient for each unit rate for user  .
.
4.2. Implementation
The master dual problem is solved in a distributed fashion with assistance of all relay. Specifically, each relay  first broadcasts its initial "price" value, that is, Lagrange multipliers
first broadcasts its initial "price" value, that is, Lagrange multipliers  . These price values are used by the receivers to compute the optimal power levels that the relays should allocate to that particular user. The optimal power values are then sent back to the relays, so as to yield the next value of the Lagrange multipliers
. These price values are used by the receivers to compute the optimal power levels that the relays should allocate to that particular user. The optimal power values are then sent back to the relays, so as to yield the next value of the Lagrange multipliers  . This procedure is repeated until the solution converges to the optimal one.
. This procedure is repeated until the solution converges to the optimal one.
Since the dual function  is differentiable, the master dual problem (13a) and (13b) can be solved by using the gradient method. The dual decomposition presented in (14a) and (14b) allows each user
is differentiable, the master dual problem (13a) and (13b) can be solved by using the gradient method. The dual decomposition presented in (14a) and (14b) allows each user  to find optimal allocated power
to find optimal allocated power  for given
for given  as
as

which is unique due to the strict concavity.
Using the fact that  is differentiable, the following iterative gradient method can be used to update the dual variables
is differentiable, the following iterative gradient method can be used to update the dual variables 

where  is the iteration index,
is the iteration index,  is the sufficiently small positive step size, and
is the sufficiently small positive step size, and  denotes the projection onto the feasible set of nonnegative numbers. The dual variables
denotes the projection onto the feasible set of nonnegative numbers. The dual variables  will converge to the dual optimal
will converge to the dual optimal  as
as  , and the primal variable
, and the primal variable  will also converge to the primal optimal variable
will also converge to the primal optimal variable  . Updating
. Updating  based on (17) can be interpreted as the relay
based on (17) can be interpreted as the relay  updates its price depending on the requested levels from its users. The price is increased when the total requested power resource from users is larger than its maximum limit. Otherwise, the price is decreased. This so-called "price-based" allocation is very popular in wired networks to control congestion, that is, rate control for Internet [19]. We summarize the distributed power allocation algorithm as follows.
updates its price depending on the requested levels from its users. The price is increased when the total requested power resource from users is larger than its maximum limit. Otherwise, the price is decreased. This so-called "price-based" allocation is very popular in wired networks to control congestion, that is, rate control for Internet [19]. We summarize the distributed power allocation algorithm as follows.
Distributed Power Allocation Algorithm
-
(i)
Parameters: The receiver of each user estimates/collects its weighted coefficient
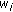 and channel gains of its transmitter-relay and relay-receiver links.
and channel gains of its transmitter-relay and relay-receiver links. -
(ii)
Initialization: Set
 and initialize
and initialize 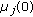 for each relay
for each relay 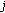 equal to some nonnegative value and broadcast this value.
equal to some nonnegative value and broadcast this value. -
(iii)
Step 1. The receiver of user
 solves its problem (16) and then sends the solution
solves its problem (16) and then sends the solution 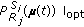 to its relays.
to its relays. -
(iv)
Step 2. Each relay
 receives the requested power levels and updates its prices with the gradient iteration (17) using the information received from the receivers of its assisted users. Then, it broadcasts the new value
receives the requested power levels and updates its prices with the gradient iteration (17) using the information received from the receivers of its assisted users. Then, it broadcasts the new value  .
. -
(v)
Step 3. Set
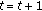 and go to Step 1 until satisfying the stopping criterion.
and go to Step 1 until satisfying the stopping criterion.The convergence proof of the general primal-dual algorithm can be found in [16, 17]. This algorithm requires message exchange only between relays and their assisted receivers. These message exchanges are performed using single-hop communications. Therefore, the total overhead would be the overhead involved in one message exchange operation multiplied by the number of iterations. Moreover, after optimal solution is first reached, the algorithm needs very few iterations to reach its new optimal solution which can be changed due to small changes in channel gains and users's partnership (i.e., a set of relays which help each user may slightly change due to users' mobility). In contrast, a centralized algorithm would require the full knowledge of all channel gains, relay power limits, and users' partnership information at a central controller before calculating an optimal solution which is then forwarded to each user for implementation. These information exchanges need to be performed over multihop transmissions, and it has to be done frequently due to frequent changes in wireless channel and system parameters. Considering these factors, our proposed distributed algorithm is clearly significantly better than the centralized algorithm in terms of the data overhead. The stopping criterion for the proposed algorithm is that the difference of congestion prices and/or allocated relay power in two consecutive iteration must be smaller than a predetermined value (e.g.,
 ).
).
5. Joint Admission Control and Power Allocation
As noticed before, if users have minimum rate requirements, an admission control mechanism should be employed to determine which users to be admitted into the network due to limited power resources at relays. Then, radio resources are allocated to admitted users in order to ensure that each admitted user achieves the required QoS performance. This scenario is important for real-time/multimedia applications.
5.1. Power Minimization-Based Allocation for Relay Networks
Consider a resource allocation problem which aims at minimizing the total relay power. In addition, each user has a minimum rate requirement. For the above described wireless systems with multiple users and multiple relays, the problem of minimizing the transmit power given the constraints on minimum rates for users can be mathematically posed as



where  denotes the minimum rate requirement for user
denotes the minimum rate requirement for user  . There are instances in which the optimization problem (18a)–(18c) becomes infeasible. A practical implication of the infeasibility is that it is impossible to serve all
. There are instances in which the optimization problem (18a)–(18c) becomes infeasible. A practical implication of the infeasibility is that it is impossible to serve all  users at their desired QoS requirements. In QoS-supported systems, some users can be dropped or the rate targets can be relaxed as a consequence. We investigate the former scenario and try to maximize the number of users that can be admitted at their minimum rate requirements.
users at their desired QoS requirements. In QoS-supported systems, some users can be dropped or the rate targets can be relaxed as a consequence. We investigate the former scenario and try to maximize the number of users that can be admitted at their minimum rate requirements.
5.2. Joint Admission Control and Power Allocation
The joint admission control and power allocation problem can be mathematically posed as a two-stage optimization problem [11]. All possible sets of admitted users  with possibly maximal cardinality (can be only one or several sets) are found in the first admission control stage, while the optimal set of admitted users
with possibly maximal cardinality (can be only one or several sets) are found in the first admission control stage, while the optimal set of admitted users  is the one among the sets
is the one among the sets  which requires minimum transmit power in the second power allocation stage. Once the candidate sets of admitted users are determined, the power allocation problem can be shown to be a convex programming problem. However, the admission control problem is combinatorially hard, which introduces high complexity for practical implementation. Therefore, a low-complexity solution approach for the joint admission control and power allocation problem is highly desirable.
which requires minimum transmit power in the second power allocation stage. Once the candidate sets of admitted users are determined, the power allocation problem can be shown to be a convex programming problem. However, the admission control problem is combinatorially hard, which introduces high complexity for practical implementation. Therefore, a low-complexity solution approach for the joint admission control and power allocation problem is highly desirable.
5.3. Reformulation of Joint Admission Control and Power Allocation Problem
The admission control problem can be mathematically written as



where  denotes the indicator function for user
denotes the indicator function for user  , that is,
, that is,  corresponds to the situation when user
corresponds to the situation when user  is not admitted, while
is not admitted, while  means that user
means that user  is admitted. Note that the constraint (19b) is automatically satisfied for the users who are not admitted. The indicator variables help to represent the admission control problem in a more compact form. However, the combinatorial nature of the admission control problem still remains due to the binary variables
is admitted. Note that the constraint (19b) is automatically satisfied for the users who are not admitted. The indicator variables help to represent the admission control problem in a more compact form. However, the combinatorial nature of the admission control problem still remains due to the binary variables  .
.
Following the conversion steps similar to those used in [11, 13], the joint admission control and power allocation problem can be converted to the following one-stage optimization problem:


where  is some constant which is chosen such that
is some constant which is chosen such that 
The problem (20a) and (20b) is a compact mathematical formulation of the joint optimal admission control and power allocation problem. Moreover, it is always feasible since in the worst case no users are admitted, that is,  .
.
Although the original optimization problem (20a) and (20b) is NP-hard, its relaxation for which  are allowed to be continuous can be shown to be a convex programming problem by using Lemma 1. In the following subsection, we propose a reduced-complexity heuristic algorithm to perform joint admission control and power allocation. Albeit theoretically suboptimal, the heuristic algorithm performance very close to the optimal solution for most testing instances summarized in the next section.
are allowed to be continuous can be shown to be a convex programming problem by using Lemma 1. In the following subsection, we propose a reduced-complexity heuristic algorithm to perform joint admission control and power allocation. Albeit theoretically suboptimal, the heuristic algorithm performance very close to the optimal solution for most testing instances summarized in the next section.
5.4. Proposed Algorithm
The following heuristic algorithm, which has some similarities to the one in [11], can be used to solve (20a) and (20b).
Joint Admission Control and Power Allocation Algorithm
-
(i)
Step 1. Set
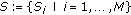 .
. -
(ii)
Step 2. Solve convex problem (20a) and (20b) for the sources in
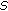 with
with 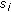 being relaxed to be continuous in the interval
being relaxed to be continuous in the interval  . Denote the resulting power allocation values as
. Denote the resulting power allocation values as 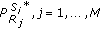 .
. -
(iii)
Step 3. For each
 , check whether
, check whether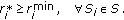 (21)
(21)If this is the case, then stop and
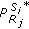 are power allocation values. Otherwise, remove the user
are power allocation values. Otherwise, remove the user  with largest gap to its target
with largest gap to its target 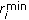 , that is,
, that is,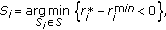 (22)
(22)from the set
 and go to Step 2.
and go to Step 2.
It can be seen that after each iteration, either the set of admitted users and the corresponding power allocation levels are determined or one user is removed from the list of most possibly admitted users. Since there are  initial users, the complexity is bounded above by that of solving
initial users, the complexity is bounded above by that of solving  convex optimization problems with different dimensions, where the dimension of the problem depends on the iteration. It is worth mentioning that the proposed reduced-complexity algorithm always returns one solution.
convex optimization problems with different dimensions, where the dimension of the problem depends on the iteration. It is worth mentioning that the proposed reduced-complexity algorithm always returns one solution.
6. Numerical Results
Consider a wireless relay network as shown in Figure 1 with ten users and three relays distributed in a two-dimensional region of a size  . The relays are fixed at coordinates
. The relays are fixed at coordinates  , and
, and  . The source and destination nodes are deployed randomly in the area inside the box areas
. The source and destination nodes are deployed randomly in the area inside the box areas  and
and  , respectively. In our simulation, each user is assisted by two relays. The noise power is taken to be equal to
, respectively. In our simulation, each user is assisted by two relays. The noise power is taken to be equal to  . All users and relays are assumed to have the same minimum rate
. All users and relays are assumed to have the same minimum rate  and maximum transmit power
and maximum transmit power  . The unit for the power is Watt (W) in our simulation. To evaluate the efficiency of the proposed algorithm for the joint admission control and power allocation, the performance of the optimal algorithm by searching all possible user combinations is used as a benchmark. We also adopt a convenient and informative way proposed in [11] to represent the results. The CVX software package [20] is used for solving convex programs in our simulations.
. The unit for the power is Watt (W) in our simulation. To evaluate the efficiency of the proposed algorithm for the joint admission control and power allocation, the performance of the optimal algorithm by searching all possible user combinations is used as a benchmark. We also adopt a convenient and informative way proposed in [11] to represent the results. The CVX software package [20] is used for solving convex programs in our simulations.
6.1. Numerical Results for Power Allocation Problem
In this subsection, the locations of the source and destination nodes are fixed and the source nodes transmit power  are chosen to be 1. The channel gain for each transmission link is affected by the path loss and Rayleigh fading. The pass loss component is
are chosen to be 1. The channel gain for each transmission link is affected by the path loss and Rayleigh fading. The pass loss component is  where
where  is the Euclidean distance between two transmission ends, while the variance of the Rayleigh fading equals to 1 in our simulations. Instantaneous channel fading gains are assumed to be known and not varied during the time required to compute the solutions, that is, it is assumed that the algorithms can provide their solutions faster than the time variation of the channel fading. The results are averaged over 800 channel instances.
is the Euclidean distance between two transmission ends, while the variance of the Rayleigh fading equals to 1 in our simulations. Instantaneous channel fading gains are assumed to be known and not varied during the time required to compute the solutions, that is, it is assumed that the algorithms can provide their solutions faster than the time variation of the channel fading. The results are averaged over 800 channel instances.
Figure 2 shows the data rate of the worst user(s) versus relay maximum transmit power  for the proposed allocation schemes: max-min rate fairness and weighted-sum of rates fairness with equal weight coefficients. The equal power allocation (EPA) scheme in which each relay distributes power equally among all relayed sources is included as reference. It can be observed that the worst user obtains the best rate under the max-min fairness scheme and the worst rate under the weighted-sum fairness scheme with equal weight coefficients. Over the wide range of maximum relay power, the best rate offered by the max-min fairness scheme has much smaller variation (about 0.12 b/s/Hz) than the worst rate achieved by the weighted-sum of rates scheme (with variation of about 0.35 b/s/Hz). In other words, as expected, the weighted-sum of rates maximization based power allocation scheme can introduce unfairness in terms of the achievable rate of the worst user, especially when relays have low-power limits. Moreover, it can be seen that with large power available at the relays, that is, larger
for the proposed allocation schemes: max-min rate fairness and weighted-sum of rates fairness with equal weight coefficients. The equal power allocation (EPA) scheme in which each relay distributes power equally among all relayed sources is included as reference. It can be observed that the worst user obtains the best rate under the max-min fairness scheme and the worst rate under the weighted-sum fairness scheme with equal weight coefficients. Over the wide range of maximum relay power, the best rate offered by the max-min fairness scheme has much smaller variation (about 0.12 b/s/Hz) than the worst rate achieved by the weighted-sum of rates scheme (with variation of about 0.35 b/s/Hz). In other words, as expected, the weighted-sum of rates maximization based power allocation scheme can introduce unfairness in terms of the achievable rate of the worst user, especially when relays have low-power limits. Moreover, it can be seen that with large power available at the relays, that is, larger  , all three schemes provide better performance for the worst users, and thus, for all users.
, all three schemes provide better performance for the worst users, and thus, for all users.
In our second example, we show that by proper weight setting, the weighted-sum of rates maximization based power allocation scheme provides the flexibility required to support users with differentiated service requirements. Particularly, we suppose that users 1 and 2 have higher priority than other users, and set the corresponding weights as  in the optimization problem (8a) and (8b). Figure 3 displays the resulting rate of the high-priority users. We observe that users 1 and 2 have indistinguishable performance, so only one curve for each scheme is plotted. The results obtained by EPA and by weighted-sum of rates maximization with equal weight coefficients are also plotted in the same figure for reference. Over the wide range of the relay power limits, the weighted-sum of rates maximization scheme outperforms the EPA. The performance of the EPA is quite close to that of the weighted-sum of rates maximization with equal weight coefficients. On the other hand, the weighted-sum of rates maximization with unequal weight coefficients provides noticeable rate enhancement to the high-priority users as compared to other users, especially when the relays have severe power limitation, for example, a rate gain of about 0.2 b/s/Hz when
in the optimization problem (8a) and (8b). Figure 3 displays the resulting rate of the high-priority users. We observe that users 1 and 2 have indistinguishable performance, so only one curve for each scheme is plotted. The results obtained by EPA and by weighted-sum of rates maximization with equal weight coefficients are also plotted in the same figure for reference. Over the wide range of the relay power limits, the weighted-sum of rates maximization scheme outperforms the EPA. The performance of the EPA is quite close to that of the weighted-sum of rates maximization with equal weight coefficients. On the other hand, the weighted-sum of rates maximization with unequal weight coefficients provides noticeable rate enhancement to the high-priority users as compared to other users, especially when the relays have severe power limitation, for example, a rate gain of about 0.2 b/s/Hz when  . Both Figures 2 and 3 indicate that the performance difference between different algorithms becomes smaller for larger relay power limits. In other words, this reveals an interesting property that when the relays have more (or unlimited) available power, different (relay) power allocation strategies have much less impact on the user rate performance, which is limited by the source transmit power in this case.
. Both Figures 2 and 3 indicate that the performance difference between different algorithms becomes smaller for larger relay power limits. In other words, this reveals an interesting property that when the relays have more (or unlimited) available power, different (relay) power allocation strategies have much less impact on the user rate performance, which is limited by the source transmit power in this case.
Figure 4 shows the network throughput for the aforementioned power allocation schemes. It can be seen that there is a significant loss in the network throughput for the max-min rate fairness-based power allocation scheme, since the objective is to improve the performance of the worst users. This confirms that achieving the max-min fairness among users results in a performance loss for the whole system. It can be also seen that the weighted-sum of rates fairness-based scheme results in maximum throughput. Moreover, the rate gain of the weighted-sum of rates scheme over the EPA scheme is about 1.8 b/s/Hz over the range of the relay power limits. This gain comes at the cost of higher complexity in system implementation to optimize the power levels. The weighted-sum of rates based scheme with unequal weights achieves slightly worse performance as compared to its counterpart with equal weights while providing better performance for the high priority users, that is, users 1 and 2 in Figure 3.
In the next example, we study the fairness behavior by showing the fairness index which is calculated as  [21] for different power allocation schemes. Specifically, we plot the fairness index versus
[21] for different power allocation schemes. Specifically, we plot the fairness index versus  in Figure 5. The fairness index is closer to 1 when the power allocation, or equivalently rate allocation, becomes fairer. Clearly, the max-min fairness scheme achieves the best fairness for all the users, and the weight-sum of rates fairness scheme is least fair. It is implied from Figures 2, 3, 4, and 5 that our proposed approaches equip network operators with different design options each of which presents a different tradeoff between throughput and fairness for the users.
in Figure 5. The fairness index is closer to 1 when the power allocation, or equivalently rate allocation, becomes fairer. Clearly, the max-min fairness scheme achieves the best fairness for all the users, and the weight-sum of rates fairness scheme is least fair. It is implied from Figures 2, 3, 4, and 5 that our proposed approaches equip network operators with different design options each of which presents a different tradeoff between throughput and fairness for the users.
Figures 6 and 7 show the evolution of different parameters of the proposed distributed algorithm for a specific channel realization. Particularly, Figure 6 shows the evolution of the price values  and the power at each relay. Figure 7 displays the rates for all ten users and the sum rate of all users. The update parameter
and the power at each relay. Figure 7 displays the rates for all ten users and the sum rate of all users. The update parameter  is set to 0.001. With such choice of parameter, we can see that after about 50 updates, the algorithm converges to the optimal solution obtained by solving the optimization problem centrally.
is set to 0.001. With such choice of parameter, we can see that after about 50 updates, the algorithm converges to the optimal solution obtained by solving the optimization problem centrally.
6.2. Results for Joint Admission Control-Power Allocation
In this subsection, QoS requirements for users will be presented in minimum rate and/or the corresponding minimum SNR (there is one-to-one mapping between these two quantities). Figure 8 displays the power required at the relays for all users to achieve a minimum  when
when  . To obtain this figure, we solve the optimization problem (18a)–(18c) without the constraint (18c) and plot the optimal values of the objective function (18a), the minimum, and the maximum powers. It can be seen that to satisfy users with higher SNR requirements, that is, better QoS, more power is required. Moreover, Figure 8 shows that when admission control is needed in limited power systems. For example, when the total power available at the relays is constrained to be less than some value, let us say 30, we cannot meet the SNR target
. To obtain this figure, we solve the optimization problem (18a)–(18c) without the constraint (18c) and plot the optimal values of the objective function (18a), the minimum, and the maximum powers. It can be seen that to satisfy users with higher SNR requirements, that is, better QoS, more power is required. Moreover, Figure 8 shows that when admission control is needed in limited power systems. For example, when the total power available at the relays is constrained to be less than some value, let us say 30, we cannot meet the SNR target  dB for all users. In such a case, admission control is necessary to drop some users.
dB for all users. In such a case, admission control is necessary to drop some users.
In this simulation example, we investigate the performance of the proposed joint admission control and power allocation algorithm with  and different minimum SNR/rate requirements as shown in Tables 1 and 2 for
and different minimum SNR/rate requirements as shown in Tables 1 and 2 for  . It is assumed that the channel gain is due to the path loss only and the locations of the source and destination nodes are fixed. Different values of
. It is assumed that the channel gain is due to the path loss only and the locations of the source and destination nodes are fixed. Different values of  have been used. For reference, we also consider the optimal admission control and power allocation scheme using exhaustive search over all feasible user subsets. A feasible user subset contains the maximum possible number of users and is selected as the optimum user subset if it requires the smallest transmit power. The simulation parameters and the performance results for the optimal admission control and power allocation scheme, and the proposed heuristic scheme are recorded in the columns "optimum allocation" and "proposed algorithm", respectively. Note that the running time is measured in seconds. It can be seen that the proposed algorithm determines exactly the optimal number of admitted users in all cases except when
have been used. For reference, we also consider the optimal admission control and power allocation scheme using exhaustive search over all feasible user subsets. A feasible user subset contains the maximum possible number of users and is selected as the optimum user subset if it requires the smallest transmit power. The simulation parameters and the performance results for the optimal admission control and power allocation scheme, and the proposed heuristic scheme are recorded in the columns "optimum allocation" and "proposed algorithm", respectively. Note that the running time is measured in seconds. It can be seen that the proposed algorithm determines exactly the optimal number of admitted users in all cases except when  . The transmit power required by our proposed algorithm is just marginally larger than that required by the optimal admission control and power allocation based on exhaustive search. However, the running time for the proposed algorithm is dramatically smaller than that required by the optimal one. This makes the proposed approach attractive for practical implementation. As expected, when
. The transmit power required by our proposed algorithm is just marginally larger than that required by the optimal admission control and power allocation based on exhaustive search. However, the running time for the proposed algorithm is dramatically smaller than that required by the optimal one. This makes the proposed approach attractive for practical implementation. As expected, when  increases, a smaller number of users is admitted with a fixed amount of power. For example, when
increases, a smaller number of users is admitted with a fixed amount of power. For example, when  , nine users and four users are admitted with SNR
, nine users and four users are admitted with SNR  dB and 14 dB, respectively. Similarly, when the relays have more available power, a larger number of users are likely to be admitted for a given
dB and 14 dB, respectively. Similarly, when the relays have more available power, a larger number of users are likely to be admitted for a given  threshold. For instance, when
threshold. For instance, when  dB, eight and six users are admitted with
dB, eight and six users are admitted with  and 10, respectively.
and 10, respectively.
 (running time in seconds).
(running time in seconds). .
.In the last example, we provide a comparative investigation on the performance of our proposed algorithm and the optimal algorithm. Due to a long running time required to obtain intensive results for the optimal algorithm based on the exhaustive search, only 20 different sets of data for each  are tested. Each set of data has different locations for source and destination nodes which are generated randomly. All other parameters remain the same, for example,
are tested. Each set of data has different locations for source and destination nodes which are generated randomly. All other parameters remain the same, for example,  , and the SNR thresholds
, and the SNR thresholds  . The results are shown in Table 3 in terms of the following comparison metrics: (INFO 1) is the number of simulation runs in which the proposed algorithm provides different number of admitted users as compared to the optimum allocation using exhaustive search; (INFO 2) is the number of simulation runs in which the algorithms provide the same number of admitted users as the optimum algorithm; (INFO 3) is the number of cases in which both algorithms provide the same set of admitted users; (INFO 4) and (INFO 5) show, respectively, the average increase percentage in the required power and the average improvement ratio in running time offered by the proposed algorithm as compared to the optimum allocation using exhaustive search. We can see that the proposed algorithm performs remarkably well with dramatically smaller running time as compared to the optimal algorithm, while the performance loss in the required power is acceptable.
. The results are shown in Table 3 in terms of the following comparison metrics: (INFO 1) is the number of simulation runs in which the proposed algorithm provides different number of admitted users as compared to the optimum allocation using exhaustive search; (INFO 2) is the number of simulation runs in which the algorithms provide the same number of admitted users as the optimum algorithm; (INFO 3) is the number of cases in which both algorithms provide the same set of admitted users; (INFO 4) and (INFO 5) show, respectively, the average increase percentage in the required power and the average improvement ratio in running time offered by the proposed algorithm as compared to the optimum allocation using exhaustive search. We can see that the proposed algorithm performs remarkably well with dramatically smaller running time as compared to the optimal algorithm, while the performance loss in the required power is acceptable.
 (20 runs).
(20 runs).7. Conclusion
In this paper, two power allocation schemes have been proposed for wireless multiuser relay networks based on amplify-and-forward cooperative diversity to maximize either the minimum rate among all users or the weighted-sum of rates. The proposed approaches make use of a computationally efficient convex programing. The distributed algorithm for the weighted-sum of rates maximization based power allocation has been also developed by using the dual decomposition approach. Numerical results demonstrate the effectiveness of the proposed methods and reveal interesting tradeoff between throughput and fairness for different power allocation schemes. Moreover, the joint admission control and power control algorithm for the scenario in which users have minimum rate requirements which aims at minimizing total relay power has been developed. Because the underlying problem is nonconvex and combinatorially hard, the suboptimal algorithm which achieves excellent admission control performance while requiring moderate computational cost is proposed. However, whether distributed joint admission control and power allocation is possible remains an interesting open research problem.
References
Knopp R, Humblet PA: Information capacity and power control in single-cell multiuser communications. Proceedings of the IEEE International Conference on Communications (ICC '95), June 1995, Seattle, Wash, USA 1: 331-335.
Laneman JN, Tse DNC, Wornell GW: Cooperative diversity in wireless networks: efficient protocols and outage behavior. IEEE Transactions on Information Theory 2004, 50(12):3062-3080. 10.1109/TIT.2004.838089
Le L, Hossain E: Multihop cellular networks: potential gains, research challenges, and a resource allocation framework. IEEE Communications Magazine 2007, 45(9):66-73.
Li Y, Vucetic B, Zhou Z, Dohler M: Distributed adaptive power allocation for wireless relay networks. IEEE Transactions on Wireless Communications 2007, 6(3):948-958.
Maric I, Yates RD: Bandwidth and power allocation for cooperative strategies in Gaussian relay networks. Proceedings of the 38th Asilomar Conference on Signals, Systems and Computers, November 2004, Pacific Grove, Calif, USA 2: 1907-1911.
Tang J, Zhang X: Cross-layer resource allocation over wireless relay networks for quality of service provisioning. IEEE Journal on Selected Areas in Communications 2007, 25(4):645-655.
Michalopoulos DS, Karagiannidis GK: PHY-layer fairness in amplify and forward cooperative diversity systems. IEEE Transactions on Wireless Communications 2008, 7(3):1073-1083.
Luo J, Blum RS, Cimini LJ, Greenstein LJ, Haimovich AM: Decode-and-forward cooperative diversity with power allocation in wireless networks. IEEE Transactions on Wireless Communications 2007, 6(3):793-799.
Phan KT, Le LB, Vorobyov SA, Le-Ngoc T: Centralized and distributed power allocation in multi-user wireless relay networks. Proceedings of the 43rd IEEE International Conference on Communications (ICC '09), June 2009, Dresden, Germany
Nechiporenko T, Phan KT, Tellambura C, H. Nguyen H: On the capacity of rayleigh fading cooperative systems under adaptive transmission. IEEE Transactions on Wireless Communications 2009, 8(4):1626-1631.
Matskani E, Sidiropoulos ND, Luo Z-Q, Tassiulas L: Convex approximation techniques for joint multiuser downlink beamforming and admission control. IEEE Transactions on Wireless Communications 2008, 7(7):2682-2693.
Phan KT, Le-Ngoc T, Vorobyov SA, Tellambura C: Power allocation in wireless relay networks: a geometric programming-based approach. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM '08), November-December 2008, New Orleans, La, USA 1-5.
Phan KT, Le-Ngoc T, Vorobyov SA, Tellambura C: Power allocation in wireless multi-user relay networks. IEEE Transactions on Wireless Communications 2009, 8(5):2535-2545.
Boyd S, Vandenberghe L: Convex Optimization. 1st edition. Cambridge University Press, Cambridge, UK; 2004.
Kelly FP, Maulloo AK, Tan DKH: Rate control for communication networks: shadow prices, proportional fairness and stability. Journal of the Operational Research Society 1998, 49(3):237-252.
Bertsekas DP: Nonlinear Programming. 2nd edition. Athena Scientific, Belmont, Mass, USA; 1999.
Palomar DP, Chiang M: A tutorial on decomposition methods for network utility maximization. IEEE Journal on Selected Areas in Communications 2006, 24(8):1439-1451.
Xiao L, Johansson M, Boyd SP: Simultaneous routing and resource allocation via dual decomposition. IEEE Transactions on Communications 2004, 52(7):1136-1144. 10.1109/TCOMM.2004.831346
Low SH, Lapsley DE: Optimization flow control. I. Basic algorithm and convergence. IEEE/ACM Transactions on Networking 1999, 7(6):861-874. 10.1109/90.811451
Grant M, Boyd S: CVX: Matlab software for disciplined convex programming. February 2008, http://stanford.edu/~boyd/cvx
Jain R, Durresi A, Babic G: Throughput fairness index: an explanation. Document no. ATM Forum/99-0045, February 1999
Acknowledgments
The first author is grateful to D. S. Michalopoulos from the Aristotle University of Thessaloniki, Greece for discussions on the subject. This work was supported by the Natural Sciences and Engineering Research Council (NSERC) of Canada, and the Alberta Ingenuity Foundation, AB, Canada.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Phan, K., Le, L., Vorobyov, S. et al. Power Allocation and Admission Control in Multiuser Relay Networks via Convex Programming: Centralized and Distributed Schemes. J Wireless Com Network 2009, 901965 (2009). https://doi.org/10.1155/2009/901965
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/901965

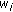 and channel gains of its transmitter-relay and relay-receiver links.
and channel gains of its transmitter-relay and relay-receiver links. and initialize
and initialize 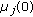 for each relay
for each relay 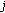 equal to some nonnegative value and broadcast this value.
equal to some nonnegative value and broadcast this value. solves its problem (16) and then sends the solution
solves its problem (16) and then sends the solution 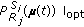 to its relays.
to its relays. receives the requested power levels and updates its prices with the gradient iteration (17) using the information received from the receivers of its assisted users. Then, it broadcasts the new value
receives the requested power levels and updates its prices with the gradient iteration (17) using the information received from the receivers of its assisted users. Then, it broadcasts the new value  .
.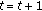 and go to Step 1 until satisfying the stopping criterion.
and go to Step 1 until satisfying the stopping criterion. ).
).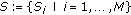 .
.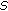 with
with 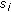 being relaxed to be continuous in the interval
being relaxed to be continuous in the interval  . Denote the resulting power allocation values as
. Denote the resulting power allocation values as 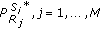 .
. , check whether
, check whether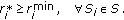
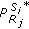 are power allocation values. Otherwise, remove the user
are power allocation values. Otherwise, remove the user  with largest gap to its target
with largest gap to its target 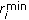 , that is,
, that is,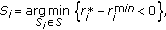
 and go to Step 2.
and go to Step 2.
 .
.
 .
.
 .
.
 .
.

