- Research Article
- Open access
- Published:
Super-Orthogonal Block Codes with Multichannel Equalisation and OFDM in Frequency Selective Fading
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 153846 (2010)
Abstract
Super-orthogonal block codes in space-time domain (i.e., Super-orthogonal space-time trellis codes (SOSTTCs)) were initially designed for frequency nonselective (FNS) channels but in frequency selective (FS) channels these super-orthogonal block codes suffer performance degradation due to signal interference. To combat the effects of signal interference caused by the frequency selectivity of the fading channel, the authors employ two methods in this paper, namely, multichannel equalization (ME) and orthogonal frequency division multiplexing (OFDM). In spite of the increase complexity of the SOSTTC-ME optimum receiver design scheme, the SOSTTC-ME scheme maintains the same diversity advantage as compared to the SOSTTC scheme in FNS channel. In OFDM environments, the authors consider two forms of the super-orthogonal block codes, namely, super-orthogonal space-time trellis-coded OFDM and super-orthogonal space-frequency trellis-coded OFDM. The simulation results reveal that super-orthogonal space-frequency trellis-coded OFDM outperforms super-orthogonal space-time trellis-coded OFDM under various channel delay spreads.
1. Introduction
The use of channel codes in combination with multiple transmit antennas achieves diversity, but the drawback is loss in bandwidth efficiency. Diversity can be achieved without any sacrifice in bandwidth efficiency, if the channel codes are specifically designed for multiple transmit antennas. Space-time coding is a bandwidth and power efficient method of communication over fading channels. It combines, in its design, channel coding, modulation, transmit diversity, and receive diversity. Space-time codes provide better performance compared to an uncoded system. Some basic space-time coding techniques include layered space-time codes [1], space-time trellis codes (STTCs) [2, 3], space-time block codes (STBCs) [4, 5], and super-orthogonal space-time trellis codes (SOSTTCs) [6, 7]. SOSTTCs are a new class of space-time codes that combine set partitioning and a super set of orthogonalblock codes in a systematic way, in order to provide full diversity and improved coding gain when compared with earlier space-time trellis constructions [2–5]. SOSTTCs, in a frequency nonselective (FNS) fading channel, do not only provide a scheme that has an improvement in coding gain when compared with earlier constructions, but they also solve the problem of systematic design for any rate and number of states. The super-orthogonal block code transmission matrix used in the design of SOSTTCs is given in [6] as

For an  -Phase Shift Keying (PSK) modulation with constellation signal represented by
-Phase Shift Keying (PSK) modulation with constellation signal represented by  , one can pick
, one can pick  , where
, where
 . In this case, the resulting transmitted signals of (1) are also members of the
. In this case, the resulting transmitted signals of (1) are also members of the  -PSK constellation alphabet and thus no expansion of the constellation signals is required. Since the transmitted signals are from a PSK constellation, the peak-to-average power ratio of the transmitted signals is equal to one. The choice of
-PSK constellation alphabet and thus no expansion of the constellation signals is required. Since the transmitted signals are from a PSK constellation, the peak-to-average power ratio of the transmitted signals is equal to one. The choice of  that can be used in (1) for both Binary Phase Shift Keying (BPSK) and Quaternary Phase Shift Keying (QPSK) is given as
that can be used in (1) for both Binary Phase Shift Keying (BPSK) and Quaternary Phase Shift Keying (QPSK) is given as  ,
,  and
and  ,
,  ,
,  ,
,  respectively.
respectively.
It should be noted that when  , (1) becomes the code presented in [4] (i.e., Alamouti code). The construction of SOSTTCs is based on the expansion of a super-orthogonal block code transmission matrix using a unique method of set partitioning [8]. In [6], the set partitioning method applied to SOSTTCs is explained. These set partitioning methods maximize coding gain without sacrificing data rates.
, (1) becomes the code presented in [4] (i.e., Alamouti code). The construction of SOSTTCs is based on the expansion of a super-orthogonal block code transmission matrix using a unique method of set partitioning [8]. In [6], the set partitioning method applied to SOSTTCs is explained. These set partitioning methods maximize coding gain without sacrificing data rates.
However, the performance of super-orthogonal block code in space-time domain is based on two fundamental assumptions with regard to the fading channel, which are given as follows:
-
(i)
frequency nonselective channel, that is, the channel does not have multipath interference;
-
(ii)
the fading coefficients from each transmit antenna to any receive antenna are independently identically distributed (i.i.d.) random variables—this assumption is valid if the antennas are located far apart from each other (at least
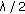 separation between antennas).
separation between antennas).
The first assumption may not be guaranteed in outdoor settings where delay spreads are significantly large (i.e., occurrence of multipath) due to the frequency selectivity of the fading channel. Multipath interference can severely degrade the performance of space-time codes. Space-time codes typically suffer from an irreducible error-floor, both in terms of the frame error-rate and in terms of the bit-error rate [9]. The two main approaches that can be used to enhance the performance of space-time codes in frequency selective fading channels are the following:
-
(i)
orthogonal frequency division multiplexing, that is, multipath-induced intersymbol interference is reduced by converting the FS fading channel into parallel flat fading subchannels,
-
(ii)
employing maximum likelihood sequence estimation with multichannel equalization.
In [10], a multichannel equalizer with maximum likelihood sequence estimation was proposed to mitigate the effect of intersymbol interference for STTC in a multipath environment. Optimum receiver design was proposed for the STTC in the multipath environment. The number of states of the optimum receiver for the STTC in a multipath fading channel with L rays was given in [10] as  , where S is the original state number of the STTC. Alternatively, OFDM can also be used to mitigate the effects of intersymbol interference for space-time codes in multipath fading channels [11, 12]. In [12], the performance of space time trellis-coded OFDM was discussed and compared with Reed Solomon coded OFDM. The scheme in [12] is capable of providing reliable transmission at relatively low SNRs for a variety of power delay profiles, making it a robust solution. In [11], space-time trellis-coded OFDM systems, with no interleavers, over quasistatic FS fading channels were also considered. The performance of the code was analyzed under various channel conditions in terms of the coding gain. The work in [11] points out that the minimum determinant of the space-time-coded OFDM system increases with the maximum tap delay of the channel, thereby increasing coding gain.
, where S is the original state number of the STTC. Alternatively, OFDM can also be used to mitigate the effects of intersymbol interference for space-time codes in multipath fading channels [11, 12]. In [12], the performance of space time trellis-coded OFDM was discussed and compared with Reed Solomon coded OFDM. The scheme in [12] is capable of providing reliable transmission at relatively low SNRs for a variety of power delay profiles, making it a robust solution. In [11], space-time trellis-coded OFDM systems, with no interleavers, over quasistatic FS fading channels were also considered. The performance of the code was analyzed under various channel conditions in terms of the coding gain. The work in [11] points out that the minimum determinant of the space-time-coded OFDM system increases with the maximum tap delay of the channel, thereby increasing coding gain.
The main contributions of this paper are as follows.
-
(i)
Multichannel equaliser was applied to the super-orthogonal block code in space-time domain and an optimum receiver design was proposed for the code.
-
(ii)
Coding in OFDM environment of the super-orthogonal block code in space-frequency domain was proposed.
-
(iii)
The performance comparison of using both ME and OFDM to mitigate the effects of signal interference for super-orthogonal block code in a multipath environment was presented.
The paper is organised as follows. Section 2 presents the system model for super-orthogonal block code in space-time domain designed for frequency nonselective fading channels. Section 3 presents the two main approaches (i.e., ME and OFDM) to mitigate the effects of intersymbol interference for super-orthogonal block codes in FS fading channels. Simulation results are presented in Section 4 and finally conclusions are drawn in Section 5.
2. System Model
A communication system equipped with  antennas at the transmitter and
antennas at the transmitter and  antennas at the receiver is considered. The transmitter employs a concatenated coding scheme where a Multiple-Trellis-Coded Modulation (M-TCM) encoder with multiplicity of
antennas at the receiver is considered. The transmitter employs a concatenated coding scheme where a Multiple-Trellis-Coded Modulation (M-TCM) encoder with multiplicity of  is used as an outer code and an
is used as an outer code and an  super-orthogonal block code is used as the inner code. The transmitter encodes
super-orthogonal block code is used as the inner code. The transmitter encodes  information bits into
information bits into  symbols (i.e.,
symbols (i.e.,  in matrix dimension) corresponding to the edge in the trellis of the space-time code with
in matrix dimension) corresponding to the edge in the trellis of the space-time code with  states, where
states, where  is the memory of the space-time encoder. The encoded symbols are divided into
is the memory of the space-time encoder. The encoded symbols are divided into  streams, where each stream is linearly modulated and simultaneously transmitted via each antenna using the super-orthogonal block transmission matrix in (1). The rate of this space-time code is defined as
streams, where each stream is linearly modulated and simultaneously transmitted via each antenna using the super-orthogonal block transmission matrix in (1). The rate of this space-time code is defined as  bits /symbol. For example, let us consider a transmitter that encodes 4 information bits into 4 symbols, that is,
bits /symbol. For example, let us consider a transmitter that encodes 4 information bits into 4 symbols, that is,  and
and  . This makes
. This makes  bits/symbol which is the rate for a QPSK constellation. This shows that the transmission scheme employed is a full rate system. The transmission trellises for the two-state and four-state super-orthogonal block code in space-time domain (i.e., SOSTTC) scheme are given in Figure 1, which consist of eight parallel transitions per branch
bits/symbol which is the rate for a QPSK constellation. This shows that the transmission scheme employed is a full rate system. The transmission trellises for the two-state and four-state super-orthogonal block code in space-time domain (i.e., SOSTTC) scheme are given in Figure 1, which consist of eight parallel transitions per branch  and
and  are transmission matrices of the form given in (1) ) where
are transmission matrices of the form given in (1) ) where

3. Super-Orthogonal Block-Coded Schemes in FS Fading Channels
3.1. Multichannel Equalization with SOSTTC
To combat the distortive channel effects caused by frequency selectivity of fading channel in a multiple-input multiple-output (MIMO) scheme, a multichannel equalization is needed. The purpose of the equalisation is to reduce the distortive channel effects as much as possible by maximising the probability of correct decision being made at the receiver. Figure 2 shows the block diagram of a super-orthogonal block coding scheme with multichannel equalisation.
Various equalisation techniques for MIMO schemes that is STBC have been proposed [13, 14]. The solution for multipath interference of STBC as stated in [13] assumes that the space-time coding is done over two large blocks of data symbols instead of just two symbols as in the original proposed scheme (i.e., [4]). At the receiver of the scheme proposed in [13] there is an increase in complexity due to the doubled front-end convolution of the overall system. In [14], a generalisation was proposed for the space time block code structure in [13]. The paper derived a receiver that consists of a frequency domain space time detector followed by a predictive decision feedback equaliser. In this paper, by assuming that the multipath interference of the super-orthogonal block code scheme in FS fading channels is over every two-symbol block as proposed in Asokan and Arslan [15] for [4], the authors design a new equalised trellis for the super-orthogonal block code in space-time domain at the receiver.
Based on the above assumptions and that the  , the received samples over the t th coded super-orthogonal block transmission can be arranged in matrix form as
, the received samples over the t th coded super-orthogonal block transmission can be arranged in matrix form as

where L is the number of channel taps and the channel response  stands for the
stands for the  channel tap at time
channel tap at time  from
from  transmit to the
transmit to the  receive antenna. From (3), one can write
receive antenna. From (3), one can write  as
as

The noise terms  in (3) are independent identically distributed complex zero mean Gaussian samples, each with variance of
in (3) are independent identically distributed complex zero mean Gaussian samples, each with variance of  per dimension. It is assumed that the channel coefficients are Rayleigh distributed.
per dimension. It is assumed that the channel coefficients are Rayleigh distributed.
At the receiver, a resultant trellis (i.e., equalised trellis) that will take the multipath interference into account is needed for maximum likelihood decoding. As an example of the resultant trellis for the super-orthogonal block codes, the authors consider a scheme with only two rays in each subchannel and the multipath interference that spans two consecutive symbols. The numbers of states in the receiver structures for the two-state and four-state QPSK super-orthogonal block coding system increase to four and eight, respectively. The number of transition paths increases to 64 parallel paths. The resultant code trellis for the receiver structure is given in Figure 3.
The trellises in Figure 3 represent the multichannel equalised decoding trellis for the two-state and the four-state super-orthogonal block coding system in an FS fading channel with multipath interference that spans a two-symbol block. The transition per state contains 64 parallel paths of signal sets. In the trellises  represent the delayed version of two-symbol blocks,
represent the delayed version of two-symbol blocks,  affected by the second tap and
affected by the second tap and  represent the two-symbol block affected by the first tap (our analysis assumes
represent the two-symbol block affected by the first tap (our analysis assumes  ). By deduction the number of states in the received trellis, when the multipath interference spans two-symbol blocks with
). By deduction the number of states in the received trellis, when the multipath interference spans two-symbol blocks with  rays, is given by
rays, is given by  , where
, where  is the original number of states of the super-orthogonal block code in space-time domain.
is the original number of states of the super-orthogonal block code in space-time domain.
3.2. Super-Orthogonal Block Codes for OFDM
The OFDM technique transforms an FS fading channel into parallel flat fading sub-channels and eliminates the signal interference caused by multipaths. OFDM can be implemented using inverse fast Fourier transform/fast Fourier transform-based multicarrier modulation and demodulation. The block diagram of a super-orthogonal block transmission in an OFDM environment is shown in Figure 4.
In this paper the authors consider two transmit diversity techniques that are possible for coded-OFDM schemes. These are the following
-
(i)
Space-Time-Coded OFDM Schemes. These schemes are capable of realizing both spatial and Temporal diversity gains in MIMO fading channels [12].
-
(ii)
Space-Frequency-Coded OFDM schemes. These schemes are capable of realizing both spatial and Frequency diversity gain in multipath MIMO fading channels.
The time domain channel impulse representation between the i th transmit antenna and the j th receive antenna can be modeled as an L-tapped delay line. The channel response at time  with delay
with delay  can be expressed as
can be expressed as

where  is the Kronecker delta function, L denotes the number of nonzero taps,
is the Kronecker delta function, L denotes the number of nonzero taps,  is the complex amplitude of the
is the complex amplitude of the  non-zero tap with delay of
non-zero tap with delay of  ,
,  is an integer, and
is an integer, and  is the tone spacing of the OFDM system. In (5)
is the tone spacing of the OFDM system. In (5)  ) is modeled by the wide-sense stationary narrowband complex Gaussian processes with power
) is modeled by the wide-sense stationary narrowband complex Gaussian processes with power  , which is normalized as
, which is normalized as .
.
For an OFDM system with proper cyclic prefix, the channel frequency response is expressed as

where  consist of the channel vectors and
consist of the channel vectors and  is the FFT coefficients. The time index
is the FFT coefficients. The time index  will be ignored in the rest of our analysis since the analysis is done for one OFDM frame.
will be ignored in the rest of our analysis since the analysis is done for one OFDM frame.
Using the super-orthogonal block code transmission matrix given in (1) and assuming that the channel frequency response is constant for  consecutive symbol intervals, the scheme becomes an SOSTTC-OFDM scheme [16] (the received expression is given in (7)). Also we propose a case where the super-orthogonal block code takes advantage of the spatial and frequency diversity possible in the coded OFDM scheme by assuming that the channel frequency response is identical across the
consecutive symbol intervals, the scheme becomes an SOSTTC-OFDM scheme [16] (the received expression is given in (7)). Also we propose a case where the super-orthogonal block code takes advantage of the spatial and frequency diversity possible in the coded OFDM scheme by assuming that the channel frequency response is identical across the  adjacent subcarrier; the scheme becomes super-orthogonal space-frequency trellis-coded-OFDM (SOSFTC-OFDM) scheme (i.e., (8)). The received signal at the j th received antenna for an SOSTTC-OFDM scheme
adjacent subcarrier; the scheme becomes super-orthogonal space-frequency trellis-coded-OFDM (SOSFTC-OFDM) scheme (i.e., (8)). The received signal at the j th received antenna for an SOSTTC-OFDM scheme  and on the n th subcarrier is given as follows:
and on the n th subcarrier is given as follows:

while the received signal at the j th received antenna for the SOSFTC-OFDM scheme  and on the
and on the  subcarrier is given as
subcarrier is given as

where  consist of channel frequency response vectors
consist of channel frequency response vectors  from the i th transmit antenna to the j th receive antenna for the n th subcarrier and
from the i th transmit antenna to the j th receive antenna for the n th subcarrier and  consists of the noise component
consists of the noise component  at the receive antenna j and subcarrier n. The noise components are independently identical complex Gaussian random variables with zero-mean and variance
at the receive antenna j and subcarrier n. The noise components are independently identical complex Gaussian random variables with zero-mean and variance  per dimension. The super-orthogonal block codes for the two transmit antennas in (8) are written:
per dimension. The super-orthogonal block codes for the two transmit antennas in (8) are written:

The super-orthogonal block codes in space-time domain under FNS fading channel are designed by maximising the pairwise error probability (PEP), which is done by maximising the minimum rank of the codeword sequence matrix (equivalent to the diversity order) and the minimum determinant codeword sequence matrix (equivalent to the coding gain). Also to enumerate the design criteria of the SOSFTC-OFDM scheme, the authors consider the PEP of the scheme. To evaluate the PEP of an SOSFTC-OFDM scheme, that is, the probability of choosing the codeword is  , where
, where  , when in fact the codeword
, when in fact the codeword  , where
, where  was transmitted, the maximum likelihood metric corresponding to the correct and the incorrect path will be used. The metric corresponding to the correct path and the incorrect path is given in (10):
was transmitted, the maximum likelihood metric corresponding to the correct and the incorrect path will be used. The metric corresponding to the correct path and the incorrect path is given in (10):

The realisation of the PEP over the entire frame length and for a given channel frequency response is given in (11):

Simplifying (10) and substituting it in (11) gives (12):

where  ,
,  is the block codeword matrix that characterise the SOSFTC-OFDM system, and
is the block codeword matrix that characterise the SOSFTC-OFDM system, and  stands for the norm of the matrix element. The expression of
stands for the norm of the matrix element. The expression of  is given in (13):
is given in (13):

The conditional PEP given in (12) can be expressed in terms of the Gaussian  function [17] as
function [17] as

The function  is a diagonal matrix of the form shown in (15),
is a diagonal matrix of the form shown in (15),  represents the conjugate transpose of the matrix element, and
represents the conjugate transpose of the matrix element, and  stands for the symbol SNR:
stands for the symbol SNR:

The diagonal element of (15) and further expansion of  are given in (16) and (17):
are given in (16) and (17):


The conditional PEP in (14) can now be written as (18) using the expanded form of the  matrix (i.e., (17)) and the expression of
matrix (i.e., (17)) and the expression of  given in (16):
given in (16):

The  function is defined by
function is defined by

and by using the inequality 


 ,
,  , the PEP given in (18) can be upper bounded as
, the PEP given in (18) can be upper bounded as

The PEP given in (20) can be averaged over all possible channel realisation as

The above expression (21) can be simplified further using the results in [18]. For a complex circularly distributed Gaussian random row vector  with mean
with mean  and covariance matrix
and covariance matrix  , and a Hermitian matrix
, and a Hermitian matrix  , we have
, we have

where  is an identity matrix. Applying (22) in solving (21), (23) is obtained. Knowing that
is an identity matrix. Applying (22) in solving (21), (23) is obtained. Knowing that  ,
,  (It should be noted that since
(It should be noted that since  is a diagonal matrix,
is a diagonal matrix,  is a Hermitian matrix, i.e.,
is a Hermitian matrix, i.e.,  has Rayleigh distribution), and
has Rayleigh distribution), and 

At high SNR  , the identity matrix at the denominator of (23) may be ignored and PEP upper bound averaged over all possible channel realisations is derived as follows:
, the identity matrix at the denominator of (23) may be ignored and PEP upper bound averaged over all possible channel realisations is derived as follows:

where  is the rank of matrix
is the rank of matrix  and
and  are the set of nonzero eigenvalues of matrix
are the set of nonzero eigenvalues of matrix  . From (24), the design criteria for an SOSFTC-OFDM scheme under the assumption of asymptotically high SNRs should be based on the rank and eigenvalue criterion. The rank criterion optimises the diversity of the SOSFTC-OFDM scheme while the eigenvalue criterion optimises the coding gain of the SOSFTC-OFDM scheme. The rank criterion is to maximise the minimum rank of
. From (24), the design criteria for an SOSFTC-OFDM scheme under the assumption of asymptotically high SNRs should be based on the rank and eigenvalue criterion. The rank criterion optimises the diversity of the SOSFTC-OFDM scheme while the eigenvalue criterion optimises the coding gain of the SOSFTC-OFDM scheme. The rank criterion is to maximise the minimum rank of  for any codeword
for any codeword  and
and  , and the eigenvalue criterion is to maximise the minimum product of the nonzero eigenvalues of
, and the eigenvalue criterion is to maximise the minimum product of the nonzero eigenvalues of  . As a comparison of both SOSTTC-OFDM and SOSFTC-OFDM systems we use a 16-state trellis (given in Figure 5) designed in [16] that maximises the space-frequency diversity and coding gain and minimises the number of parallel path for the SOSTTC-OFDM scheme. The QPSK symbols
. As a comparison of both SOSTTC-OFDM and SOSFTC-OFDM systems we use a 16-state trellis (given in Figure 5) designed in [16] that maximises the space-frequency diversity and coding gain and minimises the number of parallel path for the SOSTTC-OFDM scheme. The QPSK symbols  0, 1, 2, and 3 correspond to the QPSK signal constellations and the value of the rotation angle is denoted by 0 and
0, 1, 2, and 3 correspond to the QPSK signal constellations and the value of the rotation angle is denoted by 0 and  .
.
4. Performance Results
Simulation results are shown to demonstrate the frame error rate (FER) performance of super-orthogonal block-coded schemes in both OFDM and multichannel equalisation environments. The wireless channels with two transmit antennas and one receive antenna are assumed to be quasistatic frequency selective Rayleigh fading channels with an average power of unity. The total power of the transmitted coded symbol was normalized to unity and the authors assumed an equal-power, two-path channel impulse response (CIR). The maximum Doppler frequency was 200 Hz. The entire multipath channel undergoes independent Rayleigh fading and the receiver is assumed to have perfect knowledge of the channel state information. The super-orthogonal block coding schemes with OFDM (i.e., SOSTTC-OFDM and SOSFTC-OFDM) are assumed to have a bandwidth of 1 MHz and 128 OFDM subcarriers (i.e., for SOSTTC-OFDM, the frame length equals 512 bits while for SOSFTC-OFDM, the frame length equals 256 bits), and with multichannel equalisation, the system is assumed to have 512 bits per frame (QPSK modulation assumed for all simulations). Cyclix prefixes that are equal to or greater than the delay spread of the channel are used for the OFDM-based schemes, to eliminate intersymbol interference.
Figures 6 and 7 show FER of two-state and four-state super-orthogonal block coding schemes in both FS and FNS fading channels when both OFDM and ME are employed for the FS fading channel scenario. From Figures 6 and 7 we can see that the two-state and four-state super-orthogonal block coding schemes with ME in FS channels achieve the same diversity order (i.e., slope of the error rate curve) compared with the scheme in the FNS fading scenario, although the scheme suffers some coding gain loss. The simulation results in Figures 6 and 7 also show that, in an FS channel, both the two-state and four-state SOSFTC-OFDM schemes outperform the two-state and four-state SOSTTC-OFDM schemes. However, the SOSTTC system in an FNS channel outperforms them all. The performance degradation in Figures 6 and 7 for the SOSTTC with ME in an FS fading channel can be attributed to the increase in parallel path transitions per state of the scheme. If one assumes that all the 64 transitions per branch in the decoding trellis (i.e., Figure 3) are equally likely to be decoded, the probability of correctly decoding a transmitter codeword per state is equal to  while the probability of decoding a transmitted codeword in the scheme under the FNS fading assumption is
while the probability of decoding a transmitted codeword in the scheme under the FNS fading assumption is  . Hence the probability of decoding the transmitted codewords correctly is greater in the FNS fading case compared to the FS fading case. Although there is an increase in the number of decoder trellis states for super-orthogonal block coding scheme with ME in FS channels, compared with SOSTTC in an FNS channel, the overall probability of decoding correctly is still lower. This accounts for the performance loss obtained in terms of the coding advantage (i.e., shift in the error curve upward). The same argument goes for the four-state scenario in Figure 7. It should be noted that neither the two-state nor the four-state SOSTTC-OFDM schemes in FS channels are optimum, as the presence of parallel transitions degrades the code performance in the FS fading environment. This is due to the fact that they do not exploit the diversity order possible in such scenarios which is why the two-state SOSTTC in a FNS channel outperforms both of them. In Figures 8 and 9, the FER performance of, respectively, the sixteen-state super-orthogonal block coding OFDM schemes (i.e., SOSTTC-OFDM and SOSFTC-OFDM systems) sixteen-state STTC-OFDM and STBC OFDM schemes (i.e. SFBC and STBC OFDM systems) for
. Hence the probability of decoding the transmitted codewords correctly is greater in the FNS fading case compared to the FS fading case. Although there is an increase in the number of decoder trellis states for super-orthogonal block coding scheme with ME in FS channels, compared with SOSTTC in an FNS channel, the overall probability of decoding correctly is still lower. This accounts for the performance loss obtained in terms of the coding advantage (i.e., shift in the error curve upward). The same argument goes for the four-state scenario in Figure 7. It should be noted that neither the two-state nor the four-state SOSTTC-OFDM schemes in FS channels are optimum, as the presence of parallel transitions degrades the code performance in the FS fading environment. This is due to the fact that they do not exploit the diversity order possible in such scenarios which is why the two-state SOSTTC in a FNS channel outperforms both of them. In Figures 8 and 9, the FER performance of, respectively, the sixteen-state super-orthogonal block coding OFDM schemes (i.e., SOSTTC-OFDM and SOSFTC-OFDM systems) sixteen-state STTC-OFDM and STBC OFDM schemes (i.e. SFBC and STBC OFDM systems) for  s and
s and  s delay spreads between the two paths is shown. In both graphs the super-orthogonal space-frequency trellis-coded OFDM outperforms super-orthogonal space-time trellis coded OFDM under the two-channel delay spread scenario. It should be noted from Figure 10 that, for coded SOSFTC-OFDM schemes, a higher delay spread results in better performance.
s delay spreads between the two paths is shown. In both graphs the super-orthogonal space-frequency trellis-coded OFDM outperforms super-orthogonal space-time trellis coded OFDM under the two-channel delay spread scenario. It should be noted from Figure 10 that, for coded SOSFTC-OFDM schemes, a higher delay spread results in better performance.
5. Conclusion
The paper shows the performance of super-orthogonal block coding schemes in fading channels, that is, FS and FNS fading channels. The receiver structure of an SOSTTC in an FS channel is given so that multichannel equalisation is used to mitigate the effects of multipath interference. New decoding trellises for two-state and four-state coding schemes are designed. The formula for the number of states of the SOSTTC in FS channels with ME equalisation was deduced as a function of the number of divergent paths per state, the multipath rays, and the original number of states of the super-orthogonal block coding scheme. The simulation results proved that although the code was designed for flat fading channels, it provides at least the same diversity advantage when applied to FS Rayleigh fading channels.
To demonstrate the performance of the super-orthogonal block coding schemes in OFDM environment (i.e, SOSTTC-OFDM, SOSFTC-OFDM) and the STTC-OFDM, trellises are used that have no parallel paths between transitions. FER performance shows that the SOSFTC-OFDM scheme outperforms the SOSTTC-OFDM scheme, the STBC-OFDM scheme, and the STTC-OFDM scheme for both  s and
s and  s delay spread scenarios. The results also show that an increase in coding gain is obtained when there is an increase in the delay spread of the channel.
s delay spread scenarios. The results also show that an increase in coding gain is obtained when there is an increase in the delay spread of the channel.
References
Foschini GJ: Layered space-time architecture for wireless communication in a fading environment when using multi-element antennas. Bell Labs Technical Journal 1996, 1(2):41-59.
Tarokh V, Seshadri N, Calderbank AR: Space-time codes for high data rate wireless communication: performance criterion and code construction. IEEE Transactions on Information Theory 1998, 44(2):744-765. 10.1109/18.661517
Bäro S, Bauch G, Hansmann A: Improved codes for space-time trellis-coded modulation. IEEE Communications Letters 2000, 4(1):20-22. 10.1109/4234.823537
Alamouti SM: Space-time block coding: a simple transmit diversity technique for wireless communications. IEEE Journal on Selected Areas in Communications 1998, 16(8):1451-1458. 10.1109/49.730453
Tarokh V, Jafarkhani H, Calderbank AR: Space-time block codes from orthogonal designs. IEEE Transactions on Information Theory 1999, 45(5):1456-1467. 10.1109/18.771146
Jafarkhani H, Seshadri N: Super-orthogonal space-time trellis codes. IEEE Transactions on Information Theory 2003, 49(4):937-950. 10.1109/TIT.2003.809607
Bale M, Laska B, Dunwell D, Chan F, Jafarkhani H: Computer design of super-orthogonal space-time trellis codes. IEEE Transactions on Wireless Communications 2007, 6(2):463-467.
Ungerboeck G: Channel coding with multilevel/phase signals. IEEE Transactions on Information Theory 1982, 28(1):55-67. 10.1109/TIT.1982.1056454
Gong Y, Letaief KB: Performance evaluation and analysis of space-time coding in unequalized multipath fading links. IEEE Transactions on Communications 2000, 48(11):1778-1782. 10.1109/26.886466
Luo P, Guan Y: Optimum receiver for space-time trellis code in multipath fading channel. Proceedings of the International Zurich Seminar on Broadband Communication, February 2002 43-1-43-5.
Hong Y, Dong ZY: Performance analysis of space-time trellis coded OFDM system. International Journal of Applied Mathematics and Computer Science 2006, 2(2):59-65.
Agrawal D: Space-time coded OFDM for high data-rate wireless communication over wideband channels. Proceedings of the 48th IEEE Vehicular Technology Conference (VTC '98), May 1998, Ontario, Canada 3: 2232-2236.
Mudulodu S, Paulraj A: A transmit diversity scheme for frequency selective fading channels. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM '00), June 2000, San Francisco, Calif, USA 2: 1089-1093.
Amis K, Le Roux D: Predictive decision feedback equalization for space time block codes with orthogonality in frequency domain. Proceedings of the 16th International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '05), September 2005, Berlin, Germany 2: 1140-1144.
Asokan R, Arslan H: Detection of STBC signal in frequency selective fading channels. Proceedings of the World Wireless Congress, May 2003, San Francisco, Calif, USA
Aksoy K, Aygölü Ü: Super-orthogonal space-time-frequency trellis coded OFDM. IET Communications 2007, 1(3):317-324. 10.1049/iet-com:20060094
Simon MK, Jafarkhani H: Performance evaluation of super-orthogonal space-time trellis codes using a moment generating function-based approach. IEEE Transactions on Signal Processing 2003, 51(11):2739-2751. 10.1109/TSP.2003.818227
Turin G: The characteristic function of Hermetian quadratic forms in complex normal random variables. Biometrika 1960, 199-201.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sokoya, O., Maharaj, B.T. Super-Orthogonal Block Codes with Multichannel Equalisation and OFDM in Frequency Selective Fading. J Wireless Com Network 2010, 153846 (2010). https://doi.org/10.1155/2010/153846
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/153846
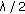 separation between antennas).
separation between antennas).

 ,
, 


 ,
,  ,
,  and delay spread of
and delay spread of 





