- Research Article
- Open access
- Published:
Resource Allocation in MU-OFDM Cognitive Radio Systems with Partial Channel State Information
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 189157 (2010)
Abstract
In wireless communications, the assumption that the transmitter has perfect channel state information (CSI) is often unreasonable, due to feedback delays, estimation errors, and quantization errors. In order to accurately assess system performance, a more careful analysis with imperfect CSI is needed. In this paper, the impact of partial CSI due to feedback delays in a multiuser Orthogonal Frequency Division Multiplexing (MU-OFDM) cognitive radio (CR) system is investigated. The effect of partial CSI on the bit error rate (BER) is analyzed. A relationship between the transmit power and the number of bits loaded on a subcarrier is derived which takes into account the target BER requirement. With this relationship, existing resource allocation schemes which are based on perfect CSI being available can be applied when only partial CSI is available. Simulation results are provided to illustrate how the system performance degrades with increasingly poor CSI.
1. Introduction
In performance analyses of wireless communication systems, it is often assumed that perfect channel state information (CSI) is available at the transmitter. This assumption is often not valid due to channel estimation errors and/or feedback delays. To ensure that the system can satisfy target quality of service (QoS) requirements, a careful analysis which takes into account imperfect CSI is required [1].
Cognitive radio (CR) is a relatively new concept for improving the overall utilization of spectrum bands by allowing unlicensed secondary users (also referred to as CR users or CRUs) to access those frequency bands which are not currently being used by licensed primary users (PUs) in a given geographical area. In order to avoid causing unacceptable levels of interference to PUs, CRUs need to sense the radio environment and rapidly adapt their transmission parameter values [2–6].
Orthogonal frequency division multiplexing (OFDM) is a modulation scheme which is attractive for use in a CR system due to its flexibility in allocating resources among CRUs. The problem of optimal allocation of subcarriers, bits, and transmit powers among users in a multiuser-(MU-) OFDM system is a complex combinatorial optimization problem. In order to reduce the computational complexity, the problem is solved in two steps by many suboptimal algorithms [7–10]:  determine the allocation of subcarriers to users and
determine the allocation of subcarriers to users and  determine the allocation of bits and transmit powers to subcarriers. Resource allocation algorithms for MU-OFDM systems have been studied in [11–14]. These algorithms are designed for non-CR MU-OFDM systems in which there are no PUs.
determine the allocation of bits and transmit powers to subcarriers. Resource allocation algorithms for MU-OFDM systems have been studied in [11–14]. These algorithms are designed for non-CR MU-OFDM systems in which there are no PUs.
In an MU-OFDM CR system, mutual interference between PUs and CRUs needs to be considered. The problem of optimal allocation of subcarriers, bits, and transmit powers among users in an MU-OFDM CR system is more complex. It is commonly assumed that perfect CSI is available at the transmitter [15, 16]. As noted earlier, this assumption is often not reasonable. In this paper, we investigate the problem of resource allocation in an MU-OFDM CR system when only partial CSI is available at the CR base station (CRBS). We assume that CSI is acquired perfectly at the CRUs and fed back to the CRBS with a delay of  seconds. The channel experiences frequency-selective fading. The objective is to maximize the total bit rate while satisfying BER, transmit power, and mutual interference constraints.
seconds. The channel experiences frequency-selective fading. The objective is to maximize the total bit rate while satisfying BER, transmit power, and mutual interference constraints.
The rest of the paper is organized as follows. The system model is described in Section 2. Based on the system model, a constrained multiuser resource allocation problem is formulated in Section 3. A suboptimal algorithm for solving the problem is discussed in Section 4. Simulation results are presented in Section 5 and the main findings are summarized in Section 6.
2. System Model
We consider the problem of allocating resources on the downlink of an MU-OFDM CR system with one base station (BS) serving one PU and  CRUs. The basic system model is the same as that described in [15] and is summarized here for the convenience of the reader.
CRUs. The basic system model is the same as that described in [15] and is summarized here for the convenience of the reader.
The PU channel is  Hz wide and the bandwidth of each OFDM subchannel is
Hz wide and the bandwidth of each OFDM subchannel is  Hz. On either side of the PU channel, there are
Hz. On either side of the PU channel, there are  OFDM subchannels. The BS has only partial CSI and allocates subcarriers, transmit powers, and bits to the CRUs once every OFDM symbol period. The channel gain of each subcarrier is assumed to be constant during an OFDM symbol duration.
OFDM subchannels. The BS has only partial CSI and allocates subcarriers, transmit powers, and bits to the CRUs once every OFDM symbol period. The channel gain of each subcarrier is assumed to be constant during an OFDM symbol duration.
Suppose that  is the transmit power allocated on subcarrier
is the transmit power allocated on subcarrier  and
and  is the channel gain of subcarrier
is the channel gain of subcarrier  from the BS to the PU. The resulting interference power spilling into the PU channel is given by
from the BS to the PU. The resulting interference power spilling into the PU channel is given by

where

represents the interference factor for subcarrier  ,
,  is the spectral distance between the center frequency of subcarrier
is the spectral distance between the center frequency of subcarrier  and that of the PU channel, and
and that of the PU channel, and  denotes the normalized baseband power spectral density (PSD) of each subcarrier.
denotes the normalized baseband power spectral density (PSD) of each subcarrier.
Let  be the channel gain of subcarrier
be the channel gain of subcarrier  from the BS to CRU
from the BS to CRU  , and let
, and let  be the baseband PSD of the PU signal. The interference power to CRU
be the baseband PSD of the PU signal. The interference power to CRU  on subcarrier
on subcarrier  is given by
is given by

Let  denote the transmit power allocated to CRU
denote the transmit power allocated to CRU  on subcarrier
on subcarrier  . For QAM modulation, an approximation for the BER on subcarrier
. For QAM modulation, an approximation for the BER on subcarrier  of CRU
of CRU  is [13]
is [13]

where  is the one-sided noise PSD and
is the one-sided noise PSD and  is given by (3). Rearranging (4), the maximum number of bits per OFDM symbol period that can be transmitted on this subcarrier is given by
is given by (3). Rearranging (4), the maximum number of bits per OFDM symbol period that can be transmitted on this subcarrier is given by

where  and
and  denotes the floor function.
denotes the floor function.
Equation (4) shows the relationship between the transmit power and the number of bits loaded on the subcarrier for a given BER requirement when perfect CSI is available at the transmitter. We now establish an analogous relationship when only partial CSI is available.
The imperfect CSI that is available to the BS is modeled as follows. We assume that perfect CSI is available at the receiver. The channel gain, hnk, for subcarrier n and CRU k is the outcome of an independent complex Gaussian random variable, that is,  [17], corresponding to Rayleigh fading. For clarity, we will denote random variables and their outcomes by uppercase and lowercase letters, respectively.
[17], corresponding to Rayleigh fading. For clarity, we will denote random variables and their outcomes by uppercase and lowercase letters, respectively.
For notational simplicity, we will use  to denote an arbitrary channel gain. The BS receives the CSI after a feedback delay
to denote an arbitrary channel gain. The BS receives the CSI after a feedback delay  , where
, where  is the OFDM symbol duration. We assume that the noise on the feedback link is negligible. Suppose that
is the OFDM symbol duration. We assume that the noise on the feedback link is negligible. Suppose that  is the channel gain information that is received at the BS, then
is the channel gain information that is received at the BS, then  . From [18], the correlation between
. From [18], the correlation between  and
and  is given by
is given by

where the correlation coefficient,  , is given by
, is given by

In (6) and (7),  denotes the zeroth-order Bessel function of the first kind,
denotes the zeroth-order Bessel function of the first kind,  is the Doppler frequency,
is the Doppler frequency,  is the expectation operator, and
is the expectation operator, and  denotes the complex conjugate of
denotes the complex conjugate of  .
.
The minimum mean square error (MMSE) estimator of  based on
based on  is given by [19]
is given by [19]

From (6), the actual channel gain can be written as [20] follows:

where  with
with  .
.
3. Formulation of the Multiuser Resource Allocation Problem
Based on the partial CSI available at the BS, we wish to maximize the total CRU transmission rate while maintaining a target BER performance on each subcarrier and satisfying PU interference and total BS CRU transmit power constraints. Let  denote the average BER on subcarrier
denote the average BER on subcarrier  , and let
, and let  represent the prescribed target BER. The optimization problem can be expressed as follows:
represent the prescribed target BER. The optimization problem can be expressed as follows:

subject to







where  is the total power budget for all CRUs,
is the total power budget for all CRUs,  is the maximum interference power that can be tolerated by the PU, and
is the maximum interference power that can be tolerated by the PU, and  is a subcarrier assignment indicator, that is,
is a subcarrier assignment indicator, that is,  if and only if subcarrier
if and only if subcarrier  is allocated to CRU
is allocated to CRU  . The term
. The term  represents the nominal bit rate weight (NBRW) for CRU
represents the nominal bit rate weight (NBRW) for CRU  , and
, and

denotes the total bit rate achieved by CRU  . Constraint (11) ensures that the average BER for each subcarrier is below the given BER target. Constraint (12) states that the total power allocated to all CRUs cannot exceed
. Constraint (11) ensures that the average BER for each subcarrier is below the given BER target. Constraint (12) states that the total power allocated to all CRUs cannot exceed  , while constraint (14) ensures that the interference power to the PU is maintained below an acceptable level
, while constraint (14) ensures that the interference power to the PU is maintained below an acceptable level  . Constraint (15) results from the assumption that each subcarrier can be assigned to at most one CRU. Constraint (17) ensures that the bit rate achieved by a CRU satisfies a proportional fairness condition.
. Constraint (15) results from the assumption that each subcarrier can be assigned to at most one CRU. Constraint (17) ensures that the bit rate achieved by a CRU satisfies a proportional fairness condition.
Based on (9), we calculate the average of the right-hand side (RHS) of (4), treating  as an outcome of an independent complex Gaussian variable. For an arbitrary vector
as an outcome of an independent complex Gaussian variable. For an arbitrary vector  , we have [21] the following:
, we have [21] the following:

where  denotes the identity matrix. Applying (19) to (4), we obtain
denotes the identity matrix. Applying (19) to (4), we obtain

where  ,
,  , and
, and  denotes the channel gain that is fedback to the BS.
denotes the channel gain that is fedback to the BS.
From (20), an explicit relationship between minimum transmit power and number of transmitted bits cannot be easily derived. However, since  in (20) is a monotonically decreasing function of
in (20) is a monotonically decreasing function of  , we obtain the minimum power requirement while satisfying the constraint in (11) by setting
, we obtain the minimum power requirement while satisfying the constraint in (11) by setting  .
.
We now derive a simpler, albeit approximate, relationship between the required transmit power,  , and the number of loaded bits.
, and the number of loaded bits.
When setting  ,
,  ,
,  , and
, and  , the RHS of (20) has the form
, the RHS of (20) has the form

with  . The function
. The function  is Rician distributed with Rician factor
is Rician distributed with Rician factor  [20]. A Rician distribution with
[20]. A Rician distribution with  can be approximated by a Nakagami-
can be approximated by a Nakagami- distribution [22] as follows:
distribution [22] as follows:

with  , where
, where  . Therefore, we approximate the RHS of (20) by
. Therefore, we approximate the RHS of (20) by

Then, from (23), we obtain

where  . From (24), we obtain
. From (24), we obtain

where  .
.
4. Resource Allocation with Partial Csi
Note that the joint subcarrier, bit, and power allocation problem in (10)–(17) belongs to the mixed integer nonlinear programming (MINP) class [23]. For brevity, we use the term "bit allocation" to denote both bit and power allocation. Since the optimization problem in (10)–(17) is generally computationally complex, we first use a suboptimal algorithm, which is based on a greedy approach, to solve the subcarrier allocation problem in Section 4.1. After subcarriers are allocated to CRUs, we apply a memetic algorithm (MA) to solve the bit allocation problem in Section 4.2.
4.1. Subcarrier Allocation
From (17), it can be seen that the subcarrier allocation depends not only on the channel gains, but also on the number of bits allocated to each subcarrier. Moreover, allocation of subcarriers close to the PU band should be avoided in order to reduce the interference power to the PU to a tolerable level. Therefore, we use a threshold scheme to select subcarriers for CRUs.
Suppose that  subcarriers are available for allocating to CRUs. We assume equal transmit power for each subcarrier. Let
subcarriers are available for allocating to CRUs. We assume equal transmit power for each subcarrier. Let


If a subcarrier is assigned to CRU  , the maximum number of bits which can be loaded on the subcarrier is given by
, the maximum number of bits which can be loaded on the subcarrier is given by

Using (26)–(28), we can determine the number of subcarriers assigned to each CRU as follows. Let  be the number of subcarriers allocated to CRU
be the number of subcarriers allocated to CRU  . Assuming that the same number of bits is loaded on every subcarrier assigned to a given CRU, the objective in (10) is equivalent to finding a set of
. Assuming that the same number of bits is loaded on every subcarrier assigned to a given CRU, the objective in (10) is equivalent to finding a set of  subcarriers to maximize
subcarriers to maximize

subject to



where  is the total transmit power allocated to all subcarriers and
is the total transmit power allocated to all subcarriers and  is the total interference power experienced by the PU due to CRU signals. The subcarrier allocation problem in (29)–(32) can be solved using the SA algorithm proposed in [24]. Note that we need to make use of (24) in the SA algorithm if only partial CSI is available. A pseudocode listing for the SA algorithm is shown in Pseudocode 1. The algorithm has a relatively low computational complexity
is the total interference power experienced by the PU due to CRU signals. The subcarrier allocation problem in (29)–(32) can be solved using the SA algorithm proposed in [24]. Note that we need to make use of (24) in the SA algorithm if only partial CSI is available. A pseudocode listing for the SA algorithm is shown in Pseudocode 1. The algorithm has a relatively low computational complexity  . After subcarriers are allocated to CRUs, we then determine the number,
. After subcarriers are allocated to CRUs, we then determine the number,  , of bits allocated to subcarrier
, of bits allocated to subcarrier  .
.
4.2. Bit Allocation
Memetic algorithm (MAs) are evolutionary algorithms which have been shown to be more efficient than standard genetic algorithms (GAs) for many combinatorial optimization problems [25–27]. Using (24), the bit allocation problem can be solved using the MA algorithm proposed in [24]. It should be noted that the chosen genetic operators and local search methods greatly influence the performance of MAs. The selection of these parameters for the given optimization problem is based on the results in [24]. A pseudocode listing of the proposed memetic algorithm is shown in Pseudocode 2.
Let  be the chromosome of member
be the chromosome of member  in a population, expressed as
in a population, expressed as

where  denotes the population size. A brief description of the MA algorithm in [24] is now provided.
denotes the population size. A brief description of the MA algorithm in [24] is now provided.
-
(1)
The
 function selects a set,
function selects a set,  , of chromosomes from
, of chromosomes from  in a roulette wheel fashion, that is, selection with replacement.
in a roulette wheel fashion, that is, selection with replacement. -
(2)
Crossover: suppose that
 . Let
. Let 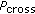 denote the crossover probability, and let
denote the crossover probability, and let  ,
,  denote the outcome of an independent random variable which is uniformly distributed in
denote the outcome of an independent random variable which is uniformly distributed in 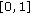 , then
, then  is selected as a candidate for crossover if and only if
is selected as a candidate for crossover if and only if 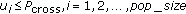 . Suppose that we have
. Suppose that we have 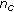 such candidates, we then form
such candidates, we then form 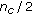 disjoint pairs of candidates (parents).
disjoint pairs of candidates (parents).For each pair of parents
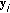 and
and 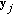 ,
,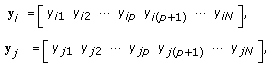 (34)
(34)we first generate a random integer
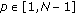 , then we obtain the (possibly identical) chromosomes of two children as follows:
, then we obtain the (possibly identical) chromosomes of two children as follows: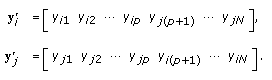 (35)
(35) -
(3)
Mutation: let
 denote the mutation probability. For each chromosome in
denote the mutation probability. For each chromosome in  , we generate
, we generate  , where
, where 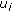 denotes the outcome of an independent random variable which is uniformly distributed in
denotes the outcome of an independent random variable which is uniformly distributed in  . Then for each component
. Then for each component  for which
for which 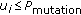 , we substitute the value with a randomly chosen admissible value.
, we substitute the value with a randomly chosen admissible value. -
(4)
Selection of surviving chromosomes: we select the
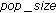 chromosomes of parents and offsprings with the best fitness values as input for the next generation.
chromosomes of parents and offsprings with the best fitness values as input for the next generation.
5. Results
In this section, performance results for the proposed algorithm described in Section 4 are presented. In the simulation, the parameters of the MA algorithm were chosen as follows: population size,  ; number of generations = 20; crossover probability,
; number of generations = 20; crossover probability,  ; mutation probability,
; mutation probability,  .
.
We consider a system with one PU and  CRUs. The total available bandwidth for CRUs is 5 MHz and supports 16 subcarriers with
CRUs. The total available bandwidth for CRUs is 5 MHz and supports 16 subcarriers with  MHz. We assume that
MHz. We assume that  and an OFDM symbol duration,
and an OFDM symbol duration,  of
of  s. In order to understand the impact of the fair bit rate constraint in (17) on the total bit rate, three cases of user bit rate requirements with
s. In order to understand the impact of the fair bit rate constraint in (17) on the total bit rate, three cases of user bit rate requirements with  were considered. In addition, three cases of partial CSI with
were considered. In addition, three cases of partial CSI with  were studied. It is assumed that the subcarrier gains
were studied. It is assumed that the subcarrier gains  and
and  , for
, for  are outcomes of independent identically distributed (i.i.d.) Rayleigh-distributed random variables (rvs) with mean square value
are outcomes of independent identically distributed (i.i.d.) Rayleigh-distributed random variables (rvs) with mean square value  . The additive white Gaussian noise (AWGN) PSD,
. The additive white Gaussian noise (AWGN) PSD,  , was set to
, was set to  W/Hz. The PSD,
W/Hz. The PSD,  , of the PU signal was assumed to be that of an elliptically filtered white noise process. The total CRU bit rate,
, of the PU signal was assumed to be that of an elliptically filtered white noise process. The total CRU bit rate,  , results were obtained by averaging over 10,000 channel realizations. The
, results were obtained by averaging over 10,000 channel realizations. The  confidence intervals for the simulated
confidence intervals for the simulated  results are within
results are within  of the average values shown.
of the average values shown.
Figure 1 shows the average total bit rate,  , as a function of the total CRU transmit power,
, as a function of the total CRU transmit power,  , for
, for  , and 1 with
, and 1 with  ,
,  W, and a PU transmit power,
W, and a PU transmit power,  , of 5 W. As expected, the average total bit rate increases with the maximum transmit power budget
, of 5 W. As expected, the average total bit rate increases with the maximum transmit power budget  . It can be seen that the average total bit rate,
. It can be seen that the average total bit rate,  , varies greatly with
, varies greatly with  . For example, at
. For example, at  W,
W,  increases by a factor of 2 as
increases by a factor of 2 as  increases from 0.7 to 0.9. This illustrates the big impact that inaccurate CSI may have on system performance. The
increases from 0.7 to 0.9. This illustrates the big impact that inaccurate CSI may have on system performance. The  curves level off as
curves level off as  increases due to the fixed value of the maximum interference power that can be tolerated by the PU.
increases due to the fixed value of the maximum interference power that can be tolerated by the PU.
Corresponding results for  and
and  are plotted in Figures 2 and 3, respectively. The average total bit rate,
are plotted in Figures 2 and 3, respectively. The average total bit rate,  , decreases as the NBRW distribution becomes less uniform; the reduction tends to increase with
, decreases as the NBRW distribution becomes less uniform; the reduction tends to increase with  .
.
Figure 4 shows  as a function of
as a function of  for three different cases of
for three different cases of  with
with  ,
,  W, and
W, and  W. As to be expected,
W. As to be expected,  increases with
increases with  . It can be seen that
. It can be seen that  for
for  is larger than for
is larger than for  , and
, and  for
for  is larger than for
is larger than for  . When the bit rate requirements for CRUs become less uniform,
. When the bit rate requirements for CRUs become less uniform,  decreases due to a decrease in the benefits of user diversity. With
decreases due to a decrease in the benefits of user diversity. With  W,
W,  increases by about
increases by about  when
when  changes from
changes from  to
to  . Results for
. Results for  are shown in Figure 5 and are qualitatively similar to those in Figure 4.
are shown in Figure 5 and are qualitatively similar to those in Figure 4.
The average total bit rate,  , is plotted as a function of the maximum PU tolerable interference power,
, is plotted as a function of the maximum PU tolerable interference power,  , with
, with  W and
W and  W, for
W, for  and 0.7 in Figures 6 and 7, respectively. As expected,
and 0.7 in Figures 6 and 7, respectively. As expected,  increases with
increases with  and decreases as the CRU bit rate requirements become less uniform. The
and decreases as the CRU bit rate requirements become less uniform. The  curves level off as
curves level off as  increases due to the fixed value of the total CRU transmit power,
increases due to the fixed value of the total CRU transmit power,  .
.
6. Conclusion
The assumption of perfect CSI being available at the transmitter is often unreasonable in a wireless communication system. In this paper, we studied an MU-OFDM CR system in which the available partial CSI is due to a delay in the feedback channel. The effect of partial CSI on the BER was investigated; a relationship between transmit power, number of bits loaded, and BER was derived. This relationship was used to study the performance of a resource allocation scheme when only partial CSI is available. It is found that the performance varies greatly with the quality of the partial CSI.
Pseudocode 1: Pseudocode for subcarrier allocation algorithm.
Algorithm: SA
for to number of subcarriers do
to number of subcarriers do
find  which maximizes
which maximizes
 ;
;
Using (25), calculate the number of bits loaded on
Subcarrier
 as
as  with
with  ;
;
initialize  to 0;
to 0;
if then
then
subcarrier  is available; increment
is available; increment  by 1;
by 1;
else
subcarrier  is not available;
is not available;
end if
end for
For each  , initialize the number,
, initialize the number,  , of
, of
subcarriers allocated to CRU  to 0
to 0
calculate  using (28);
using (28);
for to
to  do
do
find the value,  , of
, of  which minimizes
which minimizes
 ;
;
allocate subcarrier  to CRU
to CRU  ;
;
increment  by one.
by one.
end for
Pseudocode 2: Pseudocode for the memetic algorithm.
Algorithm: MA
initialize Population  ;
; 

 ;
;
for to Number_of_Generatio do
to Number_of_Generatio do
 ;
;
 ;
;
 ;
;
add  to
to  ;
;
 ;
;
 ;
;
add  to
to  ;
;
 ;
;
end for
return .
. 

References
Ye S, Blum RS, Cimini LJ Jr.: Adaptive OFDM systems with imperfect channel state information. IEEE Transactions on Wireless Communications 2006, 5(11):3255-3265.
Mitola J III, Maguire GQ Jr.: Cognitive radio: making software radios more personal. IEEE Personal Communications 1999, 6(4):13-18. 10.1109/98.788210
Mitola J: Cognitive Radio Architecture: The Engineering Foundations of Radio XML. Wiley-Interscience, New York, NY, USA; 2006.
Haykin S: Cognitive radio: brain-empowered wireless communications. IEEE Journal on Selected Areas in Communications 2005, 23(2):201-220.
Weiss T, Hillenbrand J, Krohn A, Jondral FK: Mutual interference in OFDM-based spectrum pooling systems. Proceedings of the 59th IEEE Vehicular Technology Conference (VTC '04), May 2004 4: 1873-1877.
Weiss TA, Jondral FK: Spectrum pooling: an innovative strategy for the enhancement of spectrum efficiency. IEEE Communications Magazine 2004, 42(3):S8-S14.
Fischer RFH, Huber JB: A new loading algorithm for discrete multitone transmission. Proceedings of the IEEE Global Telecommunications Conference, November 1996 1: 724-728.
Sonalkar RV, Shively RR: An efficient bit-loading algorithm for DMT applications. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM '98), November 1998 5: 2683-2688.
Wong C, Tsui C, Cheng R, Letaief K: A real-time sub-carrier allocation scheme for multiple access downlink OFDM transmission. Proceedings of the 50th IEEE Vehicular Technology Conference (VTC '99), 1999 2: 1124-1128.
Chen Y-F, Chen J-W, Li C-P: A real-time joint subcarrier, bit, and power allocation scheme for multiuser OFDM-based systems. Proceedings of the 59th IEEE Vehicular Technology Conference (VTC '04), May 2004 3: 1826-1830.
Shen Z, Andrews JG, Evans BL: Optimal power allocation in multiuser OFDM systems. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM '03), December 2003 1: 337-341.
Wong CY, Cheng RS, Letaief KB, Murch RD: Multiuser OFDM with adaptive subcarrier, bit, and power allocation. IEEE Journal on Selected Areas in Communications 1999, 17(10):1747-1758. 10.1109/49.793310
Jang J, Lee KB: Transmit power adaptation for multiuser OFDM systems. IEEE Journal on Selected Areas in Communications 2003, 21(2):171-178. 10.1109/JSAC.2002.807348
Ng DWK, Schober R: Cross-layer scheduling for OFDMA amplify-and-forward relay networks. Proceedings of the 70th IEEE Vehicular Technology Conference (VTC '09), 2009 1-5.
Qin T, Leung C: Fair adaptive resource allocation for multiuser OFDM cognitive radio systems. Proceedings of the 2nd International Conference on Communications and Networking in China (ChinaCom '07), August 2007, Shanghai, China 115-119.
Zhang Y, Leung C: Cross-layer resource allocation for mixed services in multiuser OFDM-based cognitive radio systems. IEEE Transactions on Vehicular Technology 2009, 58(8):4605-4619.
Xia P, Zhou S, Giannakis GB: Adaptive MIMO-OFDM based on partial channel state information. IEEE Transactions on Signal Processing 2004, 52(1):202-213. 10.1109/TSP.2003.819986
Jakes W: Microwave Mobile Communications. Wiley-IEEE Press, New York, NY, USA; 1994.
Kay S: Fundamentals of Statistical Signal Processing: Estimation Theory. Prentice-Hall, Upper Saddle River, NJ, USA; 1993.
Zhou S, Giannakis GB: Optimal transmitter eigen-beamforming and space-time block coding based on channel mean feedback. IEEE Transactions on Signal Processing 2002, 50(10):2599-2613. 10.1109/TSP.2002.803355
Taricco G, Biglieri E: Exact pairwise error probability of space-time codes. IEEE Transactions on Information Theory 2002, 48(2):510-513. 10.1109/18.979326
Simon MK, Alouini M-S: A unified approach to the performance analysis of digital communication over generalized fading channels. Proceedings of the IEEE 1998, 86(9):1860-1877. 10.1109/5.705532
Bertsekas D, Homer M, Logan D, Patek S: Nonlinear Programming. Athena Scientific; 1995.
Huang D, Shen Z, Miao C, Leung C: Fitness landscape analysis for resource allocation in multiuser OFDM based cognitive radio systems. ACM SIGMOBILE Mobile Computing and Communications Review 2009, 13(2):26-36. 10.1145/1621076.1621080
Merz P, Freisleben B: Memetic algorithms for the traveling salesman problem. Complex Systems 2001, 13(4):297-345.
Merz P, Katayama K: Memetic algorithms for the unconstrained binary quadratic programming problem. BioSystems 2004, 78(1–3):99-118.
Merz P: On the performance of memetic algorithms in combinatorial optimization. Proceedings of the 2nd GECCO Workshop on Memetic Algorithms (WOMA '01), 2001, San Francisco, Calif, USA 168-173.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Huang, D., Shen, Z., Miao, C. et al. Resource Allocation in MU-OFDM Cognitive Radio Systems with Partial Channel State Information. J Wireless Com Network 2010, 189157 (2010). https://doi.org/10.1155/2010/189157
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/189157
 function selects a set,
function selects a set,  , of chromosomes from
, of chromosomes from  in a roulette wheel fashion, that is, selection with replacement.
in a roulette wheel fashion, that is, selection with replacement. . Let
. Let 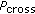 denote the crossover probability, and let
denote the crossover probability, and let  ,
,  denote the outcome of an independent random variable which is uniformly distributed in
denote the outcome of an independent random variable which is uniformly distributed in 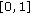 , then
, then  is selected as a candidate for crossover if and only if
is selected as a candidate for crossover if and only if 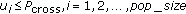 . Suppose that we have
. Suppose that we have 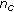 such candidates, we then form
such candidates, we then form 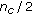 disjoint pairs of candidates (parents).
disjoint pairs of candidates (parents).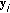 and
and 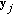 ,
,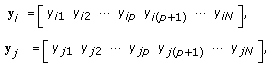
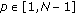 , then we obtain the (possibly identical) chromosomes of two children as follows:
, then we obtain the (possibly identical) chromosomes of two children as follows: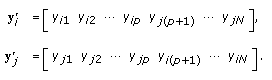
 denote the mutation probability. For each chromosome in
denote the mutation probability. For each chromosome in  , we generate
, we generate  , where
, where 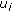 denotes the outcome of an independent random variable which is uniformly distributed in
denotes the outcome of an independent random variable which is uniformly distributed in  . Then for each component
. Then for each component  for which
for which 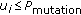 , we substitute the value with a randomly chosen admissible value.
, we substitute the value with a randomly chosen admissible value.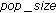 chromosomes of parents and offsprings with the best fitness values as input for the next generation.
chromosomes of parents and offsprings with the best fitness values as input for the next generation.
 , versus total CRU transmit power,
, versus total CRU transmit power,
 , with
, with
 W,
W,
 W, and
W, and
 .
.

 , versus total CRU transmit power,
, versus total CRU transmit power,
 , with
, with
 W,
W,
 W, and
W, and
 .
.

 , versus total CRU transmit power,
, versus total CRU transmit power,
 , with
, with
 W,
W,
 W, and
W, and
 .
.

 , versus total CRU transmit power,
, versus total CRU transmit power,
 , with
, with
 W,
W,
 W, and
W, and
 .
.

 , versus total CRU transmit power,
, versus total CRU transmit power,
 , with
, with
 W,
W,
 W, and
W, and
 .
.

 , versus maximum PU tolerable interference power,
, versus maximum PU tolerable interference power,
 , with
, with
 W,
W,
 W, and
W, and
 .
.

 , versus maximum PU tolerable interference power,
, versus maximum PU tolerable interference power,
 , with
, with
 W,
W,
 W, and
W, and
 .
.