- Research Article
- Open access
- Published:
Secure Network Coding against Wiretapping and Byzantine Attacks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 216524 (2010)
Abstract
In wireless networks, an attacker can tune a receiver and tap the communication between two nodes. Whether or not some meaningful information is obtained by tapping a wireless connection depends on the transmission scheme. In this paper, we design some secure network coding by combining information-theoretic approaches with cryptographic approaches. It ensures that the wiretapper cannot get any meaningful information no matter how many channels are wiretapped. In addition, if each source packet is augmented with a hash symbol which is computed from a simple nonlinear polynomial function of the data symbols, then the probability of detecting the modification is very high.
1. Introduction
Network coding is a packet-level coding technique that generalizes the classical routing paradigm [1]. Based on linear superposition of incoming packets at intermediate nodes, linear network coding achieves multicast capacity in single-source wired networks [2]. Recently, wireless network coding has gained much attention as one skill to enhance the overall throughput in a wireless multihop network that supports multiple communication flows [1–4]. Like in wired networks, the basic idea is also that a relay node can combine several incoming packets. The wireless communication medium has inherent particularities, such as the broadcast nature, high error rates, and unpredictable signal strength, which create some opportunities for attackers. Thus, secure network coding [5–8] is a hot topic in wireless networks.
In [9], Cai and Yeung proposed a model which incorporates network coding and information security. This is the first time that network coding was used for secure transmission. Later, Jain [5] widened the sufficient condition in [9] and generalized these results to wireless networks. In general, secure network coding is designed against two kinds of attacks: wiretapping and Byzantine modification. And we call them type I and type II secure network coding, respectively.
Type I Secure Network Coding
The wiretapping attack means that some adversary can wiretap some communication signals with the purposes of curiosity or recovering the messages. In traditional transmission, packets are generally encrypted against wiretapping. However, Cai and Yeung [9] found that without cryptographic approaches one can securely transmit the message by using network coding. With the similar model for wireless networks, Jain [5] explored widening the sufficient condition in [9] so that it becomes necessary, too. Under the transmission rate of one unit, the sender can send a message to the receiver without leaking any information to a wiretapper. In [10], Feldman et al. showed that if a small amount of overall capacity is given up, then a random code achieves security by using a much smaller base field than that in [9]. Furthermore, they pointed out that a large field size may sometimes be required to achieve security without giving up any capacity. In [11], Bhattad and Narayanan generalized the model in [9] and gave a new information theoretic model for security which accommodates a lot more practical requirements on security.
In general, this previous secure network coding by information-theoretic approaches has to restrict the eavesdropping set or give up some capacities. To address this problem, in this paper, we present a new secure network coding scheme by combining information-theoretic and cryptographic approaches. In our scheme, we do not restrict the eavesdropping set, that is, the wiretapper can eavesdrop any communication signals. Moreover, we do not give up any capacity. Based on these superiorities, our scheme is more suitable for wireless multicast compared with the previous schemes [5, 9, 10].
Type II Secure Network Coding
Byzantine attack means that attackers may modify the coded packets. For this case, since some important packets that are modified by an adversary will mislead the receivers and maybe cause the receivers to make wrong decisions, the modification detection of packets transmitted is also very important compared with the modification correction. How to detect the modification is a hot topic in network coding theory. With cryptographic approaches, Charles et al. [6] proposed a signature scheme for network coding based on Weil pairing on elliptic curves. Later, in [7, 8] the authors proposed some signature schemes by the linearity property of the packets in a coded system for network coding. In these schemes, one detects the modifications at intermediate nodes, so they are computationally expensive. With information-theoretic approaches, Ho et al. [12] showed a scheme in which Byzantine modification detections are done at sink nodes. In this scheme, he used random network coding by incorporating a polynomial hash value in each packet. By this way, the computing complexity is much less.
In this paper, to optimize the capacity loss and computation complexity, we propose a new scheme with Byzantine modification detection. Our scheme only needs one hash symbol which is much less than previous results in [12] and can achieve higher detection probability. Moreover, its computation complexity is lower than that in [12]. Furthermore, by combining cryptographic and information-theoretic approaches, we present secure network coding against wiretapping and Byzantine attacks.
The rest of this paper is organized as follows. In Section 2, we mainly give some necessary notations and definitions. In Section 3, we show some secure network coding against wiretapping or detecting Byzantine modification. One example is given at the end of this section. Some conclusions are presented in Section 4.
2. Primaries
In this section, some necessary notations and definitions such as network model, descriptions of a linear network code and all-or-nothing transform are presented. We denote matrices and linear spaces with bold uppercase letters and vectors with bold lowercase letters. All vectors are column unless some additional illustrations.
2.1. Network Model
Network coding has been leveraged as a generic technique in several types of wireless networks, such as vehicular ad hoc networks [13], wireless sensor networks [14], and Mesh networks [15],. In this paper, our focus is on secure network coding for acyclic wired networks and acyclic wireless networks which include parts of vehicular ad hoc networks, wireless sensor networks and Mesh networks. In detail, by the broadcast nature of the wireless interface each node is possiblly connected to several other nodes, where one node  connects to node
connects to node  means that
means that  is in the coverage of
is in the coverage of  s signal. By this way, we can obtain a directed graph
s signal. By this way, we can obtain a directed graph  . Our attentions are mainly focused on the acyclic wired networks and acyclic wireless networks, both of which can be represented by a directed acyclic network
. Our attentions are mainly focused on the acyclic wired networks and acyclic wireless networks, both of which can be represented by a directed acyclic network  , where
, where  is the set of nodes and
is the set of nodes and  is the set of edges. The source node is denoted by
is the set of edges. The source node is denoted by  , and edges are denoted by round brackets
, and edges are denoted by round brackets  , in which
, in which  and
and  . Let In
. Let In (Out
(Out ) be the set of edges that end (start) at a vertex
) be the set of edges that end (start) at a vertex  .
.
2.2. Descriptions of a Linear Network Code
Now we give two kinds of descriptions of a linear network code.
Definition 1 (see [16] (Local Description of a Linear Network Code)).
An  -dimensional linear network code on an acyclic network over a base field
-dimensional linear network code on an acyclic network over a base field  consists of a scalar
consists of a scalar  , called the local encoding coefficient, for every adjacent pair of channels
, called the local encoding coefficient, for every adjacent pair of channels  in the network. The matrix
in the network. The matrix

is called the local encoding kernel at node  .
.
Definition 2 (see [16] (Global Description of a Linear Network Code)).
An  -dimensional linear network code on an acyclic network over a base field
-dimensional linear network code on an acyclic network over a base field  consists of a scalar
consists of a scalar  for every adjacent pair of channels
for every adjacent pair of channels  in the network as well as a column
in the network as well as a column  -vector
-vector  for every channel
for every channel  such that
such that
-
(1)
 for
for 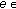 Out
Out ;
; -
(2)
the vectors for the
 imaginary channels
imaginary channels 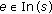 form a standard basis of
form a standard basis of 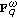 .
.
The vector  is called the global encoding kernel for channel
is called the global encoding kernel for channel  .
.
For convenience of decode, during the transmission process, global encoding kernels are combined in the head of packets.
2.3. All-Or-Nothing Transform
In [17], Rivest presented a model of encryption for block ciphers, which is called all-or-nothing transform (AONT in short). AONT is defined for information-theoretic security [18]. In detail, let  be a finite field and
be a finite field and  be an
be an  -dimensional space over
-dimensional space over  . Suppose that
. Suppose that  .
.  is named as an
is named as an  -AONT if
-AONT if  satisfies the following properties:
satisfies the following properties:
-
(1)
 is a bijection;
is a bijection; -
(2)
If any
 of the
of the  output values
output values  is fixed, then the value of any input value
is fixed, then the value of any input value  is completely undetermined.
is completely undetermined.
From this definition, for some input vectors  (a basis of the space
(a basis of the space  ) and the corresponding output vectors
) and the corresponding output vectors  , we have the following result.
, we have the following result.
Theorem 1.
For any  -
-
 , if any
, if any  of
of  output vectors
output vectors  is fixed, then each input vector
is fixed, then each input vector  is completely undetermined.
is completely undetermined.
Proof.
Let  and
and  , where
, where  denotes the transpose of vector
denotes the transpose of vector  . For any
. For any  , from the definition of AONT if any
, from the definition of AONT if any  of the
of the  output
output  is fixed, then the value of any input
is fixed, then the value of any input  is completely undetermined. Therefore, when any
is completely undetermined. Therefore, when any  of
of  output vectors
output vectors  is fixed, any input vector
is fixed, any input vector  is completely undetermined.
is completely undetermined.
If an  -AONT
-AONT  is also
is also  -linear,
-linear,  is called a linear all-or-nothing transform. In fact, the linear AONT is very useful for constructing secure linear network coding because of its low computation complexity and convenience for decoding. In [18], Stinson proved that for prime power
is called a linear all-or-nothing transform. In fact, the linear AONT is very useful for constructing secure linear network coding because of its low computation complexity and convenience for decoding. In [18], Stinson proved that for prime power  and positive integer
and positive integer  there exists a linear
there exists a linear  -ANOT. Moreover, he constructed the following linear AONT which can be implemented very efficiently. Let
-ANOT. Moreover, he constructed the following linear AONT which can be implemented very efficiently. Let  , where
, where  is prime and
is prime and  is a positive integer.
is a positive integer.  such that
such that  . Then the linear function
. Then the linear function  defined by
defined by  is a linear
is a linear  -ANOT, where
-ANOT, where

We call  an
an  -ANOT matrix. This transform (and the inverse transform) can be implemented very efficiently. Given
-ANOT matrix. This transform (and the inverse transform) can be implemented very efficiently. Given  , we can compute
, we can compute  as follows:
as follows:

Conversely, given  , we can compute
, we can compute  as follows:
as follows:

where  .
.
3. Main Schemes
In this section, we present some schemes that achieve different securities. Suppose that  is the source rate. Each packet is represented by one vector in some linear space based on
is the source rate. Each packet is represented by one vector in some linear space based on  . The output packets of an AONT is called pseudopackets. In our schemes, AONT, the hash function and cryptosystem are public. The only shared secret is the key of the encryption when we use symmetric cryptsystem.
. The output packets of an AONT is called pseudopackets. In our schemes, AONT, the hash function and cryptosystem are public. The only shared secret is the key of the encryption when we use symmetric cryptsystem.
3.1. Against Wiretapping Attack
In wireless networks, because of the broadcast nature of the wireless interface, we canot determine which edges can be eavesdropped. So we canot obtain the same secure communication on the wireless networks if we made use of the scheme in [9] against wiretapping attacks. For example, consider the wireless network shown in Figure 1(a). From the presentation of the wireless network model in Section 2.1, we can get its equivalent graph model shown in Figure 1(b).
(a) Source  wants to send two messages to sink nodes
wants to send two messages to sink nodes  and
and  .
. and
and  are within the coverage of source
are within the coverage of source  ,
,  is within the coverage of
is within the coverage of  and
and  , and terminals
, and terminals  and
and  are within the coverage of
are within the coverage of  . The region bounded by the dash lines denotes the signal coverage of the broadcast node. (b) The equivalent graph model of (a).
. The region bounded by the dash lines denotes the signal coverage of the broadcast node. (b) The equivalent graph model of (a).
As for this wireless network, the scheme in [9] is not efficient and secure enough against wiretapping attack. In detail, the scheme in [9] for the network in Figure 1(b) is shown in Figure 2(a). The collection of sets of wiretap edges is  ,
, ,
, ,
, . For secure transmission, Cai et al. added some randomly chosen key vector
. For secure transmission, Cai et al. added some randomly chosen key vector  to the packet vector
to the packet vector  at source node
at source node  . If the wiretapper only eavesdrops one channel in
. If the wiretapper only eavesdrops one channel in  , he will get nothing about packet
, he will get nothing about packet  . However, the source only transmits one packet to the sink nodes in one transmission process. It means that one gets a secure transmission by giving up some capacity. In fact, if we choose an appropriate local encoding kernel for source node we can obtain the similarly secure transmission without capacity loss. In Figure 2(b), let a
. However, the source only transmits one packet to the sink nodes in one transmission process. It means that one gets a secure transmission by giving up some capacity. In fact, if we choose an appropriate local encoding kernel for source node we can obtain the similarly secure transmission without capacity loss. In Figure 2(b), let a  -AONT matrix
-AONT matrix  defined in (2) be the local encoding kernel of the source node
defined in (2) be the local encoding kernel of the source node  , and
, and  . The network codes of the intermediate nodes in Figures 2(a) and 2(b) are the same. If the wiretapper only wiretaps one channel, he can not get any meaningful information about
. The network codes of the intermediate nodes in Figures 2(a) and 2(b) are the same. If the wiretapper only wiretaps one channel, he can not get any meaningful information about  or
or  even if he knows
even if he knows  . Therefore, we can get secure transmission without giving up any capacity.
. Therefore, we can get secure transmission without giving up any capacity.
In reality, however, as for this wireless network, it is possible that the wiretapper can eavesdrop all the network linkages because of the broadcast nature of the wireless interface. Then the previous two schemes are not secure enough in practical applications. So some cryptographic approaches are required to address this problem. In fact, by combining ANOT with symmetrical cryptography, without constrictions of wiretapping sets, we can construct secure network coding in the sense of cryptographic security. That means the wiretapper cannot obtain any massage if he has not the secret key. Our secure network coding is presented as follows.
Scheme 1.
Let  be
be  packets, where
packets, where  . An
. An  -AONT matrix
-AONT matrix  is the local encoding kernel of source node
is the local encoding kernel of source node  .
.
Step 1.
Let  . The source node encrypts
. The source node encrypts  using AES cryptsystem (the source can also choose other high speed asymmetric cryptsystem. And the only secret for this scheme is the private key owned by the sender and receiver.) and sends out
using AES cryptsystem (the source can also choose other high speed asymmetric cryptsystem. And the only secret for this scheme is the private key owned by the sender and receiver.) and sends out  , where
, where  .
.
Step 2.
Based on Jaggi's construction of network coding [19] for wired networks and Rajawat's [20] for wireless networks, we can construct the codes for the intermediate nodes in wired networks and wireless networks, respectively.
Step 3.
Each sink node first decodes the received packets and gets  then decrypts
then decrypts  and obtains
and obtains  . By the inverse of
. By the inverse of  , they get the original packets
, they get the original packets  .
.
Time Complexity Analysis
Since the orders of matrix  and its inverse are both
and its inverse are both  , the time complexity of multiplying
, the time complexity of multiplying  or
or  is at most
is at most  . In addition, there are two operations, encryption and decryption. So the more time complexity of this construction than those of Jaggi's and Rajawat's is
. In addition, there are two operations, encryption and decryption. So the more time complexity of this construction than those of Jaggi's and Rajawat's is  and the time for encryption and decryption.
and the time for encryption and decryption.
Security Analysis
Since the network coding in this paper is linear, all of the network coding operations in the network are linear. The packets in the network are linear combinations of  . On one hand, if the rank of the linear packets that an adversary eavesdrops is less than
. On one hand, if the rank of the linear packets that an adversary eavesdrops is less than  , he can only get some (not all) of the packets
, he can only get some (not all) of the packets  . By the definition of AONT, he can not obtain any original packet
. By the definition of AONT, he can not obtain any original packet  . On the other hand, even if the rank of eavesdropped packets is equal to
. On the other hand, even if the rank of eavesdropped packets is equal to  , the wiretapper can not get the pseudopacket
, the wiretapper can not get the pseudopacket  without the private key. So he can not obtain any original packet either by Theorem 1.
without the private key. So he can not obtain any original packet either by Theorem 1.
In this model, we do not need to encrypt all the transmitted packets (In [18], all pseudopackets are encrypted, because this requires an adversary to decrypt all the blocks of ciphertext to determine any block of plaintext by the definition of AONT. Then the attack will be slowed down without any change in the size of the secrete key. Therefore, AONT is used to afford a certain amount of additional security for a block cipher encryption.). Only one is enough by combing with AONT. By Theorem 1, each original packet is relative to all the pseudopackets. When we encrypt one of the pseudopackets, the wiretapper canot get all of the pseudopackets without the private key. So he canot obtain any original packet. For example in Figure 2(b), we only need to encrypt  or
or  , then the wiretapper can not get any meaningful information about
, then the wiretapper can not get any meaningful information about  and
and  . The security here combines the information-theoretic security with cryptographic security. However, by the wooden barrel theory the whole security of this scheme is reduced to cryptographic security.
. The security here combines the information-theoretic security with cryptographic security. However, by the wooden barrel theory the whole security of this scheme is reduced to cryptographic security.
Now, we show the advantages of AONT as the local encoding kernel of the source node. Firstly, from the information-theoretic point: we not only increase the achievable throughput, but also get secure transmission. Secondly, from the cryptographic point: we only need to encrypt one packet out from the source node instead of encrypting all the packets which will be sent to sink nodes. Moreover, we can save lots of time consumption, explained from Table 1, where  denotes the source rate, the length of each packet is 2 bytes and "clk" is the abbreviated clock.
denotes the source rate, the length of each packet is 2 bytes and "clk" is the abbreviated clock.
3.2. Byzantine Modification Detection
Since some important packets that are modified by an adversary will mislead the receivers and may cause the receivers to make wrong decisions, the modification detection of packets transmitted is also very important compared with the modification correction in both wireless and wired networks. In this subsection, we present a scheme to detect the Byzantine modification combining AONT with a simple polynomial hash function.
By the definition of AONT, we find that if one of the pseudopackets from source node is damaged, then it is likely that every packet will be damaged. This is the error-propagation property of AONT. So we can append a suitable block of redundancy to the packet before applying an AONT. And this redundancy can be used to verify the integrity of the packets and also can be removed after decode.
Suppose source  multicast
multicast  vector packets
vector packets  to the sink nodes. For convenience, each packet in the network is represented by a column vector
to the sink nodes. For convenience, each packet in the network is represented by a column vector  of
of  (
( ) symbols over a finite field
) symbols over a finite field  , where the first
, where the first  entries are data symbols and the last one is a redundant hash symbol. The hash symbol in each augmented packet is given by a hash function
entries are data symbols and the last one is a redundant hash symbol. The hash symbol in each augmented packet is given by a hash function  of the data symbols. Of course, we can choose any nonlinear hash function. In fact, we find that the security can be ensured by a simple nonlinear function. In detail, we take the following simple nonlinear function as the secure hash function in this scheme.
of the data symbols. Of course, we can choose any nonlinear hash function. In fact, we find that the security can be ensured by a simple nonlinear function. In detail, we take the following simple nonlinear function as the secure hash function in this scheme.
Let  be the function mapping
be the function mapping  to
to

Denote  . Denote the augmented packets by
. Denote the augmented packets by

where  denotes the concatenation of two vectors
denotes the concatenation of two vectors  and
and  , and
, and  is the hash symbol satisfying
is the hash symbol satisfying

Now we give a brief description of our scheme as follows.
Scheme 2.
Initialization: For each original packets  , the source
, the source  calculates the hash values
calculates the hash values  , and obtains the augmented packets
, and obtains the augmented packets  , by concatenating the hash value
, by concatenating the hash value  to each original packet
to each original packet  .
.
Step 1.
The source  takes the AONT matrix
takes the AONT matrix  as its local encoding kernel and computes
as its local encoding kernel and computes  . Then sends out
. Then sends out  .
.
Step 2.
Based on the Jaggi's construction of network coding for wired networks and Rajawat's for wireless networks, we can construct the codes for the intermediate nodes.
Step 3.
Each sink node first decodes the received packets and gets  . (Since in this scheme, we donot consider the wiretapping but the integrity of the packets, it does not need to encrypt any pseudopackets from the source. We note that
. (Since in this scheme, we donot consider the wiretapping but the integrity of the packets, it does not need to encrypt any pseudopackets from the source. We note that  is the local encoding kernel of the source
is the local encoding kernel of the source  , and thus we can decode directly and get the packets
, and thus we can decode directly and get the packets  .) Then it verifies whether
.) Then it verifies whether  . If
. If  for all
for all  , then there does not exist modification on the transmission and
, then there does not exist modification on the transmission and  . Finally, they remove the hash values and obtain the original packets
. Finally, they remove the hash values and obtain the original packets  .
.
Time Complexity Analysis
This scheme is similar to Scheme 1. The differences are additional calculations for hash symbols in Step 1 and verifications for hash symbols in Step 3. The time complexity of these two operations is  . So the time complexity of Steps 1 and 3 is polynomial on the length
. So the time complexity of Steps 1 and 3 is polynomial on the length  of the packet vector and equal to
of the packet vector and equal to  . So the total time complexity of this secure network coding construction is only
. So the total time complexity of this secure network coding construction is only  more than that of Jaggi's for wired networks and Rajawat's for wireless networks.
more than that of Jaggi's for wired networks and Rajawat's for wireless networks.
Security Analysis
Based on the model above, an adversary successfully modifies the packet that he can construct the logical hash symbol after modifying the data symbols (actually here he modifies the pseudopackets). From the following theorem we will find that an adversary can construct a logical hash symbol after modifying the data symbols with a very low probability.
Theorem 2.
In Scheme 2, the probability of not detecting an error is at most  , where
, where  is the source rate.
is the source rate.
To prove this theorem, we first prove the following two lemmas.
Lemma 3.
Given the vector  and scalar value
and scalar value  , the probability of randomly choosing a vector
, the probability of randomly choosing a vector  such that the inner product
such that the inner product  is
is  .
.
Proof.
The number of points on the hyperplane  is
is  . And the cardinality of the field
. And the cardinality of the field  is
is  . So the probability of choosing a vector
. So the probability of choosing a vector  such that
such that  is
is  .
.
Lemma 4.
The probability of randomly choosing a vector  such that
such that

is at most  , where the vectors
, where the vectors  and scalar values
and scalar values  are fixed and independent.
are fixed and independent.
Proof.
By Lemma 3, we randomly choose a vector  such that
such that  with probability
with probability  . Then the probability that choosing an appropriate vector
. Then the probability that choosing an appropriate vector  such that
such that  satisfies (8) is at most
satisfies (8) is at most  .
.
Now we prove Theorem 2.
Let  be the
be the  packet vectors transmitted, each of which consists of
packet vectors transmitted, each of which consists of  symbols from a finite field
symbols from a finite field  and is a column vector. The first
and is a column vector. The first  entries are data symbols and the rest one is the redundant hash symbol. It can be represented as
entries are data symbols and the rest one is the redundant hash symbol. It can be represented as

where  denotes the data. The hash symbol
denotes the data. The hash symbol  .
.
The matrix  is the local encoding kernel of source node, and let
is the local encoding kernel of source node, and let


So the hash symbols satisfy

where  denotes the hash symbol of
denotes the hash symbol of  . Therefore,
. Therefore,  because
because  from (3). Notice that the hash function is not a linear function, that is,
from (3). Notice that the hash function is not a linear function, that is,  . When the adversary modifies some pseudopacket
. When the adversary modifies some pseudopacket  , he has to modify the hash symbol
, he has to modify the hash symbol  such that the sink nodes can not detect the modification. The proof can be completed by two steps.
such that the sink nodes can not detect the modification. The proof can be completed by two steps.
Step 1.
We suppose that only the first pseudopacket  is modified and the new pseudopacket is denoted by
is modified and the new pseudopacket is denoted by  . Let
. Let  and
and  .
.  is known to the adversary.
is known to the adversary.
The adversary wants to know  . By the representation of
. By the representation of  in (4), we have
in (4), we have

So even only one of  is modified, all the packets
is modified, all the packets  will be changed. From (13), we have
will be changed. From (13), we have

Firstly, suppose that  and
and  . Then, by the definition of hash function in (5),
. Then, by the definition of hash function in (5),

In (15),  are unknown to the adversary except for
are unknown to the adversary except for  and
and  . Moreover,
. Moreover,  is unknown to the adversary, but fixed. By Lemma 4, the probability of constructing an appropriate
is unknown to the adversary, but fixed. By Lemma 4, the probability of constructing an appropriate  satisfying (15) is at most
satisfying (15) is at most  .
.
Secondly, suppose that  and
and  are modified. Let
are modified. Let  and
and  . Then,
. Then,

From (16), the probability of randomly choosing the right  and
and  for constructing logical hash symbols is also at most
for constructing logical hash symbols is also at most  by Lemma 4.
by Lemma 4.
Thirdly, when the adversary modifies more data symbols of  , by the similar method, we can prove that the probability of constructing the logical hash symbols is at most
, by the similar method, we can prove that the probability of constructing the logical hash symbols is at most  .
.
Step 2.
When the adversary modifies more pseudopackets  at one time, from the similar method above, the probability of constructing the logical hash symbols is no more than
at one time, from the similar method above, the probability of constructing the logical hash symbols is no more than  .
.
From the proof of Theorem 2, we have the following two corollaries.
Corollary 1.
The probability of not detecting an error is not related to both the number of modified packets  and the symbols of one pseudopacket, but the cardinality of
and the symbols of one pseudopacket, but the cardinality of  and the source rate.
and the source rate.
Corollary 2.
If the redundant hash symbol in the packet is a constant or a linear function of the data symbols, then the scheme can not defend the Byzantine modification.
Proof.
First, when the hash symbol is a constant. The adversary only modifies the data symbols and keeps the hash symbols unchanged. Then the receivers can not detect the modification.
Second, when the hash symbol is a linear function of the data symbols, we have

By (15), 
 are known by attackers. So, by the relationship between
are known by attackers. So, by the relationship between  and
and  ,
,  are easily calculated and this scheme canot defend Byzantine modification.
are easily calculated and this scheme canot defend Byzantine modification.
3.3. Against Wiretapping and Byzantine Attacks
Further, by combining with Scheme 1, we can improve Scheme 2 to against wiretapping attack. Before sending out  , the source encrypts the last packet
, the source encrypts the last packet  and denotes the encrypted packet by
and denotes the encrypted packet by  . The aim is to prevent wiretapper from recovering any original packets.
. The aim is to prevent wiretapper from recovering any original packets.
Scheme 3 provides not only security but also authenticity.
Scheme 3.
Initialization: For each packet  , the source calculates the hash values
, the source calculates the hash values  , and obtains the augmented packets
, and obtains the augmented packets  , by concatenating the hash value
, by concatenating the hash value  to each original packets
to each original packets  .
.
Step 1.
The source takes  as its local encoding kernel. Computes
as its local encoding kernel. Computes  and encrypts
and encrypts  using AES cryptsystem (Here we use symmetry cryptsystem. Because if we use asymmetry cryptsystem, by the public key the adversary may successfully modify all the pseudopackets at the same time when he controls
using AES cryptsystem (Here we use symmetry cryptsystem. Because if we use asymmetry cryptsystem, by the public key the adversary may successfully modify all the pseudopackets at the same time when he controls  edge disjoint paths.) to get
edge disjoint paths.) to get  . Then sends out
. Then sends out  .
.
Step 2.
Based on the Jaggi's construction of network coding for wired networks and Rajawat's for wireless network, we can construct the codes for the intermediate nodes.
Step 3.
Each sink node first decodes the received packets and gets  , then gets
, then gets  by decrypting
by decrypting  . Verify whether
. Verify whether  ,
,  . If
. If  for all
for all  , there does not exist modification on the transmission. They get the original packets
, there does not exist modification on the transmission. They get the original packets  by
by  .
.
These three schemes are based on Jaggi's construction for wired networks and Rajawat's construction for wireless networks. Actually, we can also use Ho's random network coding [21]. In Scheme 2, the only change is to randomly choose the local encoding kernels from a large finite field. Except for the change in Scheme 2, in Schemes 1 and 3 the packets from the source will be appended with an  -dimensional identity vector, the global encoding kernel, before being sent out. However, random network coding for wireless networks requires a large alphabet size to render networks robust to link failures.
-dimensional identity vector, the global encoding kernel, before being sent out. However, random network coding for wireless networks requires a large alphabet size to render networks robust to link failures.
Example 5.
We construct a secure network code on the wireless network in Figure 1(a) to detect Byzantine modifications. Suppose the base field is  . Let
. Let  . Then
. Then  So the AONT matrix
So the AONT matrix  , which is used to encode the two original packets at the source node
, which is used to encode the two original packets at the source node  , is
, is

Suppose the packets  and
and  will be sent to the sink nodes
will be sent to the sink nodes  and
and  . The two encoded packets (pseudopackets) from the source are
. The two encoded packets (pseudopackets) from the source are

Then the pseudopackets transmitted on the edges are shown in Figure 3. When an adversary wiretaps any one of  , he can not get any meaningful information about packet
, he can not get any meaningful information about packet  or
or  . If we encrypt the packet
. If we encrypt the packet  , then the adversary can get nothing even when he wiretaps all the channels.
, then the adversary can get nothing even when he wiretaps all the channels.
Let  . The last symbol is the hash symbol and calculated using the hash function in (4). The two augmented pseudopackets are
. The last symbol is the hash symbol and calculated using the hash function in (4). The two augmented pseudopackets are

Suppose that an adversary modifies the data packet  and let
and let  Then, the receiver can decode the packet vectors and get
Then, the receiver can decode the packet vectors and get  . It is easy to verify that
. It is easy to verify that  and
and  . So the receivers can find that the packets are modified.
. So the receivers can find that the packets are modified.
4. Conclusion
For secure transmission, if only the information-theoretic approach is used, some bandwidth has to be given up or a high computation complexity is necessary. As to cryptographic approach, all the packets have to be encrypted against wiretapping. Even if the data is hashed and appended with its hash value, one may not detect the modifications when the adversary modifies the data and its hash value simultaneously. To address these problems, we combine the information-theoretic approach with cryptographic approach to design secure network coding. On one hand, we do not give up any network capacity to achieve the same security as that of Cai and Yeung. More importantly, our Scheme 1 does not require any restrictions on the wiretapping sets compared with that of Cai and Yeung. It means that our secure network coding is suitable for both wired networks and wireless networks. On the other hand, we decrease the resource consumptions of encryption and decryption. Furthermore, based on some simple hash function, our Scheme 2 is designed to detect the Byzantine modification. It can achieve a high detection probability with only one hash symbol and low computation complexity. In the end, combining the two schemes above we propose Scheme 3 which provides not only security but also authenticity.
References
Ahlswede R, Cai N, Li SYR, Yeung RW: Network information flow. IEEE Transactions on Information Theory 2000, 46(4):1204-1216. 10.1109/18.850663
Li SYR, Yeung RW, Cai N: Linear network coding. IEEE Transactions on Information Theory 2003, 49(2):371-381.
Chou PA, Wu Y: Network coding for the internet and wireless networks. IEEE Signal Processing Magazine 2007, 24(5):77-85.
Deb S, Effros M, Ho T, et al.: Network coding for wireless applications: a brief tutorial. Proceedings of the International Workshop on Wireless Ad-hoc Networks (IWWAN '05), May 2005, London, UK
Jain K: Security based on network topology against the wiretapping attack. IEEE Wireless Communications 2004, 11(1):68-71. 10.1109/MWC.2004.1269720
Charles D, Jain K, Lauter K: Signatures for network coding. Proceedings of the 40th Annual Conference on Information Sciences and Systems (CISS '06), January 2006, Princeton, NJ, USA 857-863.
Zhao F, Kalker T, Médard M, Han KJ: Signatures for content distribution with network coding. Proceedings of the IEEE International Symposium on Information Theory (ISIT '07), June 2007 556-560.
Boneh D, Freeman D, Katz J, Waters B: Signing a linear subspace: signature schemes for network coding. Proceedings of the Public Key Cryptography (PKC '09), 2009, Lecture Notes in Computer Science 5443: 68-87.
Cai N, Yeung RW: Secure network coding. Proceedings of the IEEE International Symposium on Information Theory (ISIT '02), June 2002
Feldman J, Malkin T, Servedio RA, Stein C: On the capacity of secure network coding. Proceedings of the 42nd Annual Allerton Conference on Communication, Control, and Computing, October 2004
Bhattad K, Narayanan KR: Weakly secure network coding. Proceedings of the 1st Workshop on Network Coding, Theory, and Applications (NETCOD '05), 2005
Ho T, Leong B, Koetter R, Médard M, Effros M, Karger DR: Byzantine modification detection in multicast networks with random network coding. IEEE Transactions on Information Theory 2008, 54(6):2798-2803.
Lee S-H, Lee U, Lee K-W, Gerla M: Content distribution in VANETs using network coding: the effect of disk I/O and processing O/H. Proceedings of the 5th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON '08), July 2008, San Francisco, Calif, USA 117-125.
Guo Z, Xie P, Cui J-H, Wang B: On applying network coding to underwater sensor networks. In Proceedings of the 1st ACM International Workshop on Underwater Networks (WUWNet '06), 2006, New York, NY, USA. ACM Press; 109-112.
Al Hamra A, Barakat C, Turletti T: Network coding for wireless mesh networks: a case study. Proceedings of the International Symposium on a World of Wireless, Mobile and Multimedia Networks (WoWMoM '06), 2006
Yeung RW: Information Theory and Network Coding. Springer, New York, NY, USA; 2008.
Rivest RL: All-or-nothing encryption and the packege transform. Proceedings of the Fast Software Encryption (FSE '97), 1997, Lecture Notes in Computer Science 1267: 210-218.
Stinson DR: Something about all or nothing (transforms). Designs, Codes, and Cryptography 2001, 22(2):133-138. 10.1023/A:1008304703074
Jaggi S, Sanders P, Chou PA, et al.: Polynomial time algorithms for multicast network code construction. IEEE Transactions on Information Theory 2005, 51(6):1973-1982. 10.1109/TIT.2005.847712
Rajawat K, Giannakis GB: Non-random wireless network coding. Proceedings of the 6th IEEE Annual Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks Workshops, (SECON '09), June 2009, Rome, Italy 1-6.
Ho T, Médard M, Köetter R, et al.: A random linear network coding approach to mul ticast. IEEE Transactions on Information Theory 2006, 52(10):4413-4430.
Acknowledgments
The authors would like to thank editor and all the anonymous reviewers for their helpful advices. This paper was supported by the National Natural Science Foundation of China and the Research Grants Council of Hong Kong Joint Research Scheme (no. 60731160626), the National Natural Science Foundation of China (no. 60821001), the Specialized the Foundation for the Author of National Excellent Doctoral Dissertation of PR China (FANEDD) (Grant no. 200951), the 111 Project (no. B08004).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Guo, Q., Luo, M., Li, L. et al. Secure Network Coding against Wiretapping and Byzantine Attacks. J Wireless Com Network 2010, 216524 (2010). https://doi.org/10.1155/2010/216524
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/216524
 for
for 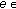 Out
Out ;
; imaginary channels
imaginary channels 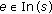 form a standard basis of
form a standard basis of 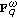 .
. is a bijection;
is a bijection; of the
of the  output values
output values  is fixed, then the value of any input value
is fixed, then the value of any input value  is completely undetermined.
is completely undetermined.

 sends
sends  to sink nodes
to sink nodes  and
and  . For security Cai et al. add an independent random packet
. For security Cai et al. add an independent random packet  to
to  . (b) At source node
. (b) At source node  we transform the packets
we transform the packets  into
into  by a linear ANOT
by a linear ANOT  then send the pseudopackets
then send the pseudopackets  and
and  to sink nodes.
to sink nodes.
 transforms the packets
transforms the packets  and
and  by
by  , and sends the outputs
, and sends the outputs  and
and  to sink nodes
to sink nodes  and
and  .
.