- Research Article
- Open access
- Published:
A Fluid Model for Performance Analysis in Cellular Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 435189 (2010)
Abstract
We propose a new framework to study the performance of cellular networks using a fluid model and we derive from this model analytical formulas for interference, outage probability, and spatial outage probability. The key idea of the fluid model is to consider the discrete base station (BS) entities as a continuum of transmitters that are spatially distributed in the network. This model allows us to obtain simple analytical expressions to reveal main characteristics of the network. In this paper, we focus on the downlink other-cell interference factor (OCIF), which is defined for a given user as the ratio of its outer cell received power to its inner cell received power. A closed-form formula of the OCIF is provided in this paper. From this formula, we are able to obtain the global outage probability as well as the spatial outage probability, which depends on the location of a mobile station (MS) initiating a new call. Our analytical results are compared to Monte Carlo simulations performed in a traditional hexagonal network. Furthermore, we demonstrate an application of the outage probability related to cell breathing and densification of cellular networks.
1. Introduction
Estimation of cellular networks capacity is one of the key points before deployment and mainly depends on the characterization of interference. As downlink is often the limited link w.r.t. capacity, we focus on this direction throughout this paper, although the proposed framework can easily be extended to the uplink. An important system parameter for this characterization is the other-cell interference factor (OCIF). It represents the "weight" of the network on a given cell.
OCIF is traditionally defined as the ratio of other-cell interference to inner-cell interference. In this paper, we rather consider an OCIF, which is defined as the ratio of total other-cell received power to the total inner-cell received power. Although very close, this new definition is interesting for three reasons. Firstly, total-received power is the metric mobile stations (MS) are really able to measure on the field. Secondly, the power ratio is now a characteristic of the network and does not depend on the considered MS or service. At last, the definition of OCIF is still valid if we consider cellular systems without inner-cell interference; in this case, the denominator of the ratio is reduced to the useful power. The precise knowledge of the OCIF allows the derivation of performance parameters, such as outage probabilities, capacity, as well as the definition of Call Admission Control mechanisms, in CDMA (Code Division Multiple Access) and OFDMA (Orthogonal Frequency Division Multiple Access) systems.
Pioneering works on the subject [1] mainly focused on the uplink. Working on this link, [2] derived the distribution function of a ratio of path-losses, which is essential for evaluating the external interference. For this purpose, authors approximated the hexagonal cell with a disk of same area. Based on this result, Liu and Everitt proposed in [3] an iterative algorithm for the computation of the OCIF for the uplink.
On the downlink, [4, 5] aimed at computing an averaged OCIF over the cell by numerical integration in hexagonal networks. In [6], Gilhousen et al. provided Monte Carlo simulations and obtained a histogram of the OCIF. In [7], other-cell interference was given as a function of the distance to the base station (BS) using Monte-Carlo simulations. Chan and Hanly [8] precisely approximated the distribution of the other-cell interference. They, however, provided formulas that are difficult to handle in practice. Baccelli et al. [9] studied spatial blocking probabilities in random networks. Focusing on random networks, power ratios were nevertheless not their main concern and authors relied on approximated formulas, which are not validated by simulations.
In contrast to previous works in the field, the modeling key of our approach is to consider the discrete BS entities of a cellular network as a continuum. Recently, the authors of [10] described a network in terms of macroscopic quantities such as node density. The same idea was used in [11] for ad hoc networks. They however assumed a very high density of nodes in both papers and infinite networks. We show hereafter that our model is accurate even when the density of BS is very low and the network size is limited (see Section 3.2).
Central idea of this paper has been originally proposed in conference papers [12–15], which provide a simple closed-form formula for the OCIF on the downlink as a function of the distance to the BS, the path-loss exponent, the distance between two BS, and the network size. We validate here the formulas by Monte Carlo simulations and show that it is possible to get a simple outage probability approximation by integrating the OCIF over a circular cell. In addition, as this ratio is obtained as a function of the distance to the BS, it is possible to derive a spatial outage probability, which depends on the location of a newly initiated call. Outage probability formula allows us to analyze the phenomenon of cell breathing, which results in coverage holes when the traffic load increases. An answer to this issue is to increase the BS density (i.e., network densification). Thanks to the proposed formulas, we are able to quantify this increase.
We first introduce the interference model and the notations (Section 2), then present the fluid model and its validation (Section 3). In the fourth section, we derive outage probabilities. In the last section, we apply the theoretical results to the characterization of cell breathing and to network densification.
2. Interference Model and Notations
We consider a cellular network and focus on the downlink. BS have omnidirectional antennas, so that a BS covers a single cell. Let us consider a mobile station  and its serving base station
and its serving base station  .
.
The propagation path gain  designates the inverse of the path-loss
designates the inverse of the path-loss  between base station
between base station  and mobile
and mobile  ; that is,
; that is,  .
.
The following power quantities are considered:
-
(i)
 is the transmitted power from serving base station
is the transmitted power from serving base station 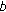 to mobile
to mobile  (for user's traffic);
(for user's traffic); -
(ii)
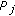 is the total transmitted power by a generic base station
is the total transmitted power by a generic base station 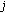 ;
; -
(iii)
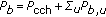 is the total power transmitted by station
is the total power transmitted by station  ,
,  represents the amount of power used to support broadcast and common control channels;
represents the amount of power used to support broadcast and common control channels; -
(iv)
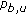 is the power received at mobile
is the power received at mobile  from station
from station  ; we can write
; we can write 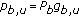 ;
; -
(v)
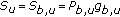 is the useful power received at mobile
is the useful power received at mobile  from serving station
from serving station 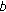 (for traffic data). Since we do not consider soft-handover (SHO), serving station is well defined and the subscript
(for traffic data). Since we do not consider soft-handover (SHO), serving station is well defined and the subscript 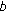 can be omitted for the sake of readability.
can be omitted for the sake of readability.
The total amount of power experienced by a mobile station  in a cellular system consists of three terms: useful signal power (
in a cellular system consists of three terms: useful signal power ( ), interference and noise power (
), interference and noise power ( ). It is common to split the system power into two terms:
). It is common to split the system power into two terms:  , where
, where  is the internal (or own-cell) received power and
is the internal (or own-cell) received power and  is the external (or other-cell) interference. Note that we made the choice of including the useful signal
is the external (or other-cell) interference. Note that we made the choice of including the useful signal  in
in  , and, as a consequence, it should not be confused with the commonly considered own-cell interference.
, and, as a consequence, it should not be confused with the commonly considered own-cell interference.
With the above notations, we define the OCIF in  , as the ratio of total power received from other BS to the total power received from the serving BS
, as the ratio of total power received from other BS to the total power received from the serving BS  as
as

The quantities  ,
,  , and
, and  are location dependent and can thus be defined in any location
are location dependent and can thus be defined in any location  as long as the serving BS is known.
as long as the serving BS is known.
In this paper, we use the signal to interference plus noise ratio (SINR) as the criteria of radio quality:  is the SINR target for the service requested by MS
is the SINR target for the service requested by MS  . This figure is a priori different from the SINR
. This figure is a priori different from the SINR  evaluated at mobile station
evaluated at mobile station  . However, we assume perfect power control, so that
. However, we assume perfect power control, so that  for all users.
for all users.
2.1. CDMA Network
On the downlink of CDMA networks, orthogonality between physical channels may be approached by Hadamard multiplexing if the delay spread is much smaller than the chip duration  . As a consequence, a coefficient
. As a consequence, a coefficient  may be introduced to account for the lack of perfect orthogonality in the own cell.
may be introduced to account for the lack of perfect orthogonality in the own cell.
With the introduced notations, the SINR experimented by  can thus be derived (see, e.g., [16])
can thus be derived (see, e.g., [16])

From this relation, we can express  as
as

As we defined the OCIF as  , we have
, we have

In case of a homogeneous network,  for all
for all  and
and

The transmitted power for MS  can now be written as
can now be written as

From this relation, the output power of BS  can be computed as follows:
can be computed as follows:

and so, according to (6),

In HSDPA (High Speed Downlink Packet Access), (2) and (8) are valid for each TTI (Transmission Time Interval). Parameter  should be now interpreted as an experienced SINR and not any more as a target. Sums are done on the number of scheduled users per TTI. If a single user is scheduled per TTI (which is a common case), sums reduce to a single term. Even in this case, parameter
should be now interpreted as an experienced SINR and not any more as a target. Sums are done on the number of scheduled users per TTI. If a single user is scheduled per TTI (which is a common case), sums reduce to a single term. Even in this case, parameter  has to be considered since common control channels and traffic channels are not perfectly orthogonal due to multipath.
has to be considered since common control channels and traffic channels are not perfectly orthogonal due to multipath.
Even if previous equations use the formalism of CDMA networks, it is worth noting that they are still valid for other multiplexing schemes. For cellular technologies without internal interference (TDMA, Time Division Multiple Access, and OFDMA),  reduces to
reduces to  and
and  is the cochannel interference in (2). The definition of
is the cochannel interference in (2). The definition of  is unchanged provided that sums in (4) and (5) are done over the set of cochannel interfering BS (to account for frequency reuses different from reuse one).
is unchanged provided that sums in (4) and (5) are done over the set of cochannel interfering BS (to account for frequency reuses different from reuse one).
2.2. OFDMA Network
In OFDMA, (2) can be applied to a single carrier.  is now the base station output power per subcarrier. In OFDMA, data is multiplexed over a great number of subcarriers. There is no internal interference, so we can consider that
is now the base station output power per subcarrier. In OFDMA, data is multiplexed over a great number of subcarriers. There is no internal interference, so we can consider that  . Since
. Since  , we can write
, we can write

so we have

Moreover, when  , which is typically verified for cell radii less than about
, which is typically verified for cell radii less than about  Km, we can neglect this term and write
Km, we can neglect this term and write

For each subcarrier of an OFDMA system (e.g., WiMax, LTE), the parameter  represents the inverse of the SIR (Signal-to-Interference Ratio).
represents the inverse of the SIR (Signal-to-Interference Ratio).
Consequently,  appears to be an important parameter characterizing cellular networks. This is the reason why we focus on this factor in the next section and, with the purpose of proposing a closed form formula of
appears to be an important parameter characterizing cellular networks. This is the reason why we focus on this factor in the next section and, with the purpose of proposing a closed form formula of  , we develop a physical model of the network.
, we develop a physical model of the network.
3. Fluid Model
In this section, we first present the model, derive the closed-form formula for  , and validate it through Monte-Carlo simulations for a homogeneous hexagonal network.
, and validate it through Monte-Carlo simulations for a homogeneous hexagonal network.
3.1. OCIF Formula
The key modelling step of the model we propose consists in replacing a given fixed finite number of interfering BS by an equivalent continuum of transmitters, which are spatially distributed in the network. This means that the transmitting interference power is now considered as a continuum field all over the network. In this context, the network is characterized by a MS density  and a cochannel base station density
and a cochannel base station density  [12]. We assume that MS and BS are uniformly distributed in the network, so that
[12]. We assume that MS and BS are uniformly distributed in the network, so that  and
and  are constant. As the network is homogeneous, all base stations have the same output power
are constant. As the network is homogeneous, all base stations have the same output power  .
.
We focus on a given cell and consider a round shaped network around this central cell with radius  . In Figure 1, the central disk represents the cell of interest, that is, the area covered by its BS. The continuum of interfering BS is located between the dashed circle and the outer circle. By analogy with the discrete regular network, where the half distance between two BS is
. In Figure 1, the central disk represents the cell of interest, that is, the area covered by its BS. The continuum of interfering BS is located between the dashed circle and the outer circle. By analogy with the discrete regular network, where the half distance between two BS is  , we consider that the minimum distance to interferers is
, we consider that the minimum distance to interferers is  .
.
For the assumed omnidirectional BS network, we use a propagation model, where the path gain,  , only depends on the distance
, only depends on the distance  between the BS
between the BS  and the MS
and the MS  . The power,
. The power,  , received by a mobile at distance
, received by a mobile at distance  can thus be written
can thus be written  , where
, where  is a constant and
is a constant and  is the path-loss exponent.
is the path-loss exponent.
Let us consider a mobile  at a distance
at a distance  from its serving BS
from its serving BS  . Each elementary surface
. Each elementary surface  at a distance
at a distance  from
from  contains
contains  base stations which contribute to
base stations which contribute to  . Their contribution to the external interference is
. Their contribution to the external interference is  . We approximate the integration surface by a ring with centre
. We approximate the integration surface by a ring with centre  , inner radius
, inner radius  , and outer radius
, and outer radius  (see Figure 2)
(see Figure 2)

Moreover, MS  receives internal power from
receives internal power from  , which is at distance
, which is at distance  :
:  . So, the OCIF
. So, the OCIF  can be expressed by
can be expressed by

Note that  does not depend on the BS output power. This is due to the assumption of a homogeneous network (all base stations have the same transmit power). In our model,
does not depend on the BS output power. This is due to the assumption of a homogeneous network (all base stations have the same transmit power). In our model,  only depends on the distance
only depends on the distance  to the BS. Thus, if the network is large; that is,
to the BS. Thus, if the network is large; that is,  is large compared to
is large compared to  ,
,  can be further approximated by
can be further approximated by

This closed-form formula will allow us to quickly compute performance parameters of a cellular network. However, before going ahead, we need to validate the different approximations we made in this model.
3.2. Validation of the Fluid Model
In this section, we validate the fluid model presented in the last section. In this perspective, we will compare the figures obtained with (13) to those obtained numerically by simulations. Our simulator assumes a homogeneous hexagonal network made of several rings surrounding a central cell. Figure 3 shows an example of such a network with the main parameters involved in the study:  , the half distance between BS,
, the half distance between BS,  , the maximum distance in the hexagon to the BS, and
, the maximum distance in the hexagon to the BS, and  , the range of the network.
, the range of the network.
The fluid model and the traditional hexagonal model are both simplifications of the reality. None is a priori better than the other but the latter is widely used, especially for dimensioning purposes. That is the reason why a comparison is useful.
The validation is done by Monte Carlo simulations:
-
(i)
at each snapshot, a location is randomly chosen for MS
 in the cell of interest
in the cell of interest 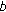 with uniform spatial distribution;
with uniform spatial distribution; -
(ii)
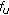 is computed using (5) with
is computed using (5) with  , where
, where 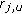 is the distance between the BS
is the distance between the BS  and the MS
and the MS  . The serving BS
. The serving BS 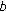 is the closest BS to MS
is the closest BS to MS  ;
; -
(iii)
the value of
 and the distance to the central BS
and the distance to the central BS  are recorded;
are recorded; -
(iv)
at the end of the simulation, all values of
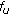 corresponding to a given distance are averaged and we plot the average value in Figure 4.
corresponding to a given distance are averaged and we plot the average value in Figure 4.
Figure 4 shows the simulated OCIF as a function of the distance to the base station. Simulation parameters are the following:  Km;
Km;  between
between  and
and  ;
;  ;
;  is chosen, such that the number of rings of interfering BS is 15; and the number of snapshots is 1000. Equation (13) is also plotted for comparison. In all cases, the fluid model matches very well the simulations on a hexagonal network for various figures of the path-loss exponent. Note that at the border of the cell (between
is chosen, such that the number of rings of interfering BS is 15; and the number of snapshots is 1000. Equation (13) is also plotted for comparison. In all cases, the fluid model matches very well the simulations on a hexagonal network for various figures of the path-loss exponent. Note that at the border of the cell (between  and
and  Km), the model is a little bit less accurate because hexagon corners are not well captured by the fluid model.
Km), the model is a little bit less accurate because hexagon corners are not well captured by the fluid model.
Note that the considered network size can be finite and chosen to characterize each specific local network environment. Figure 5 shows the influence of the network size. This model allows thus to develop analyses, adapted to each zone, taking into account each specific considered zone parameters.
We moreover note that our model can be used even for great distances between the base stations. We validate in Figure 6 the model considering two cell radii: a small one,  m and a large one,
m and a large one,  Km. The latter curve allows us to conclude that our approach is accurate even for a very low base station density. It also shows that we can use the model for systems with frequency reuse different from one since in this case distances between cochannel BS are greater.
Km. The latter curve allows us to conclude that our approach is accurate even for a very low base station density. It also shows that we can use the model for systems with frequency reuse different from one since in this case distances between cochannel BS are greater.
Figure 7 shows the dispersion of  at each distance for
at each distance for  . For example, at
. For example, at  Km,
Km,  is between
is between  and
and  for an average value of
for an average value of  . This dispersion around the average value is due to the fact that in a hexagonal network,
. This dispersion around the average value is due to the fact that in a hexagonal network,  is not isotropic.
is not isotropic.
3.3. OCIF Formula for Hexagonal Networks
Two frameworks for the study of cellular networks are considered in this paper: the traditional hexagonal model and the fluid model. While the former is widely used, the latter is very simple and allows the derivation of an analytical formula for  . The last section has shown that both models lead to comparable results for the OCIF as a function of the distance to the BS. If we want to go further in the comparison of both models, in particular with the computation of outage probabilities, we need however to be more accurate.
. The last section has shown that both models lead to comparable results for the OCIF as a function of the distance to the BS. If we want to go further in the comparison of both models, in particular with the computation of outage probabilities, we need however to be more accurate.
Such calculations require indeed the use of the  function (see Section 4.3 and (23) and (24)), which is very sensitive to its arguments (mean and standard deviation). This point is rarely raised in literature: analysis and Monte Carlo simulations can lead to quite different outage probabilities even if analytical average and variance of the underlying Gaussian distribution are very close to simulated figures.
function (see Section 4.3 and (23) and (24)), which is very sensitive to its arguments (mean and standard deviation). This point is rarely raised in literature: analysis and Monte Carlo simulations can lead to quite different outage probabilities even if analytical average and variance of the underlying Gaussian distribution are very close to simulated figures.
In this perspective, we provide an alternative formula for  that better matches the simulated figures in a hexagonal network. Note that this result is not needed if network designers use the new framework proposed in this paper.
that better matches the simulated figures in a hexagonal network. Note that this result is not needed if network designers use the new framework proposed in this paper.
We first note that  can be rewritten in the following way:
can be rewritten in the following way:

where  and
and  . As a consequence,
. As a consequence,  only depends on the relative distance to the serving BS,
only depends on the relative distance to the serving BS,  , and on the path-loss exponent,
, and on the path-loss exponent,  . For hexagonal networks, it is thus natural to find a correction of
. For hexagonal networks, it is thus natural to find a correction of  that only depends on
that only depends on  . An accurate fitting of analytical and simulated curves shows that
. An accurate fitting of analytical and simulated curves shows that  should simply be multiplied by an affine function of
should simply be multiplied by an affine function of  to match with Monte Carlo simulations in a hexagonal network. Equation (14) can then be rewritten as follows:
to match with Monte Carlo simulations in a hexagonal network. Equation (14) can then be rewritten as follows:

where  is a corrective term obtained by least-square fitting. For example,
is a corrective term obtained by least-square fitting. For example,  (the correction is tiny) and
(the correction is tiny) and  (the correction is significative).
(the correction is significative).
4. Outage Probabilities
In this section, we compute the global outage probability and the spatial outage probability with the Gaussian approximation. Closed-form formulas for the mean and standard deviation of  over a cell are provided.
over a cell are provided.
Quality of service in cellular networks can be characterized by two main parameters: the blocking probability and the outage probability. The former is evaluated at the steady state of a dynamical system considering call arrivals and departures. It is related to a call admission control (CAC) that accepts or rejects new calls. The outage probability is evaluated in a semistatic system [9], where the number of MS is fixed and their locations are random. This approach is often used (see, e.g., [17]) to model mobility in a simple way: MS jump from one location to another independently. For a given number of MS per cell, outage probability is thus the proportion of configurations, where the needed BS output power exceeds the maximum output power:  .
.
4.1. Global Outage Probability
For a given number of MS per cell,  , outage probability,
, outage probability,  , is the proportion of configurations, for which the needed BS output power exceeds the maximum output power:
, is the proportion of configurations, for which the needed BS output power exceeds the maximum output power:  . If noise is neglected and if we assume a single service network (
. If noise is neglected and if we assume a single service network ( for all
for all  ), we deduce from (8)
), we deduce from (8)

where  and
and  .
.
4.2. Spatial Outage Probability
For a given number  of MS per cell, a spatial outage probability can also be defined. In this case, it is assumed that
of MS per cell, a spatial outage probability can also be defined. In this case, it is assumed that  MS have already been accepted by the system, that is, the output power needed to serve them does not exceed the maximum allowed power. The spatial outage probability at location
MS have already been accepted by the system, that is, the output power needed to serve them does not exceed the maximum allowed power. The spatial outage probability at location  is the probability that maximum power is exceeded if a new MS is accepted in
is the probability that maximum power is exceeded if a new MS is accepted in  .
.
As for  , we make the approximation that the spatial outage,
, we make the approximation that the spatial outage,  , only depends on the distance to the BS and thus, can be written
, only depends on the distance to the BS and thus, can be written

4.3. Gaussian Approximation
In order to compute these probabilities, we rely on the Central Limit theorem and use a Gaussian approximation. As a consequence, we need to compute the spatial mean and standard deviation of  . The area of a cell is
. The area of a cell is  with
with  . So, we integrate
. So, we integrate  on a disk of radius
on a disk of radius  . As MS are uniformly distributed over the equivalent disk, the probability density function (pdf) of
. As MS are uniformly distributed over the equivalent disk, the probability density function (pdf) of  is:
is:  Let
Let  and
and  be respectively the mean and standard deviation of
be respectively the mean and standard deviation of  , when
, when  is uniformly distributed over the disk of radius
is uniformly distributed over the disk of radius 

where  is the hypergeometric function, whose integral form is given by
is the hypergeometric function, whose integral form is given by

and  is the gamma function.
is the gamma function.
Note that for  , we have the simple closed formula
, we have the simple closed formula

where  . In the same way, the variance of
. In the same way, the variance of  is given by
is given by

As a conclusion of this section, the outage probability can be approximated by

where  . And the spatial outage probability can be approximated by:
. And the spatial outage probability can be approximated by:

where  is given by (14). This equation allows us to precisely compute the influence of an entering mobile station whatever its position in a cell and is thus the starting point for an efficient call admission control algorithm.
is given by (14). This equation allows us to precisely compute the influence of an entering mobile station whatever its position in a cell and is thus the starting point for an efficient call admission control algorithm.
For cellular systems without internal interference, the definition of  is unchanged and (23) and (24) are still valid provided that
is unchanged and (23) and (24) are still valid provided that  .
.
Note that for an accurate fitting of the analytical formulas, which are presented in this section, to the Monte Carlo simulations performed in a hexagonal network,  should be multiplied by
should be multiplied by  ,
,  by
by  and (14) replaced by (16).
and (14) replaced by (16).
The question arises of the validity of the Gaussian approximation. The number of users per WCDMA (Wideband CDMA) cell is indeed usually not greater than some tens. Figure 8 compares the pdf of a gaussian variable with mean  and standard deviation
and standard deviation  with the pdf of
with the pdf of  for different values for
for different values for  . The latter pdf has been obtained by Monte Carlo simulations done on a single cell, assuming fluid model formula for
. The latter pdf has been obtained by Monte Carlo simulations done on a single cell, assuming fluid model formula for  . We observe that gaussian approximation matches better and better when the number of mobiles increases. Even for very few mobiles in the cell (
. We observe that gaussian approximation matches better and better when the number of mobiles increases. Even for very few mobiles in the cell ( ), the approximation is acceptable. So we can use it to calculate the outage probability
), the approximation is acceptable. So we can use it to calculate the outage probability
4.4. Simulation Methodology
Monte Carlo simulations have been performed in order to validate the analytical approach. A fixed number  of MS are uniformly drawn on a given cell. All interferers are assumed to have the same transmitted power (homogeneous network). OCIF is computed according to (5). Power transmitted by the cell is then compared to
of MS are uniformly drawn on a given cell. All interferers are assumed to have the same transmitted power (homogeneous network). OCIF is computed according to (5). Power transmitted by the cell is then compared to  for the calculation of the global outage probability.
for the calculation of the global outage probability.
For the spatial outage probability calculation, only snapshots without outage are considered. A new MS is added in the cell. The new transmitted power is again compared to  and the result is recorded with the distance of the new MS.
and the result is recorded with the distance of the new MS.
4.5. Results
Figures 9, 10, and 11 show some results we are able to obtain instantaneously using the simple formulas derived in this paper for voice service ( dB). Analytical formulas are compared to Monte Carlo simulations in a hexagonal cellular network (
dB). Analytical formulas are compared to Monte Carlo simulations in a hexagonal cellular network ( ). Therefore, (16) is used. Figure 9 shows the global outage probabilities as a function of the number of MS per cell for various values of the path-loss exponent
). Therefore, (16) is used. Figure 9 shows the global outage probabilities as a function of the number of MS per cell for various values of the path-loss exponent  . It allows us to easily find the capacity of the network for any target outage. For example, a maximal outage probability of
. It allows us to easily find the capacity of the network for any target outage. For example, a maximal outage probability of  leads to a capacity of about
leads to a capacity of about  users when
users when  . Figure 10 shows, as an example, the capacity with
. Figure 10 shows, as an example, the capacity with  outage as a function of
outage as a function of  .
.
Figure 11 shows the spatial outage probability as a function of the distance to the BS for  and for various numbers of MS per cell. Given that there are already
and for various numbers of MS per cell. Given that there are already  , these curves give the probability that a new user, initiating a new call at a given distance, implies an outage. As an example, a new user in a cell with already
, these curves give the probability that a new user, initiating a new call at a given distance, implies an outage. As an example, a new user in a cell with already  ongoing calls, will cause outage with probability
ongoing calls, will cause outage with probability  at
at  m from the BS and with probability
m from the BS and with probability  at
at  m from the BS.
m from the BS.
Traditional admission control schemes are based on the number of active MS in the cell. With the result of this paper, an operator would be able to admit or reject new connections also according to the location of the entering MS.
5. Application to Network Densification
In this section, we show the application of previous results to network densification. During the dimensioning process, the cell radius is determined by taking into account a maximum value of outage probability. This value characterizes the quality of service in terms of coverage the network operator wants to achieve. The number of BS to cover a given zone is directly derived from the cell radius.
Considering a maximum value of the outage probability, we first characterize cell breathing; that is, the fact that cell coverage decreases when the cell load increases. We then analyze BS densification as an answer to cell breathing.
5.1. Cell Breathing Characterization
Let consider a maximum value of outage probability  . From (23), we can write:
. From (23), we can write:

Denoting  , that equation can be expressed as
, that equation can be expressed as

As  is the mobile density, we can write
is the mobile density, we can write  , where
, where  is the maximum number of mobiles served by a BS for maximum outage probability
is the maximum number of mobiles served by a BS for maximum outage probability  , and
, and  is the area covered by the BS. Let
is the area covered by the BS. Let  be the cell area. When mobile density increases,
be the cell area. When mobile density increases,  decreases, so that
decreases, so that  .
.
We now obtain the following equation

This equation has two solutions. The maximum mobile density can be expressed as

In this equation, mean and standard deviation of  , and
, and  , are computed over the covered area
, are computed over the covered area  with surface
with surface 

Equation (28) shows the link between the mobile density and the covered area and is now used to characterize cell breathing.
Numerical values in Figure 12 shows the results we obtain thanks to (28) assuming voice service ( dB),
dB),  in a CDMA network.
in a CDMA network.
The solid curve shows the mobile density as a function of the coverage area of base stations. On this curve, the BS density is supposed to be constant,  Km and thus
Km and thus  Km2. The coverage area
Km2. The coverage area  however shrinks when the traffic (characterized here by the density of mobiles
however shrinks when the traffic (characterized here by the density of mobiles  ) increases. For example, going from point
) increases. For example, going from point  with
with  mobiles/Km2 to point
mobiles/Km2 to point  with
with  mobiles/Km2 reduces the covered area from
mobiles/Km2 reduces the covered area from  Km2 to approximately
Km2 to approximately  Km2. As a consequence, the cell is not completely covered, and due to cell breathing, coverage holes appear.
Km2. As a consequence, the cell is not completely covered, and due to cell breathing, coverage holes appear.
5.2. Base Station Densification
A way of solving the issue of cell breathing is to densify the network. The dotted line in Figure 12 plots the mobile density as a function of the covered area assuming full coverage of the cell. Along this curve,  and when
and when  is decreasing, the BS density is increasing. We are thus able to find, for a given mobile density, the BS density that will ensure continuous coverage in the network. For example, for
is decreasing, the BS density is increasing. We are thus able to find, for a given mobile density, the BS density that will ensure continuous coverage in the network. For example, for  mobiles/Km2, the cell area should be approximately
mobiles/Km2, the cell area should be approximately  Km2 in order to avoid coverage holes.
Km2 in order to avoid coverage holes.
The sequence  -
- -
- shows an example of scenario, where BS densification is needed. In point
shows an example of scenario, where BS densification is needed. In point  , the network has been dimensioned for
, the network has been dimensioned for  mobiles/Km2. If the cellular operator is successful and so more subscribers are accessing the network, mobile density increases along the solid line of Figure 12. At point
mobiles/Km2. If the cellular operator is successful and so more subscribers are accessing the network, mobile density increases along the solid line of Figure 12. At point  , coverage holes appear and the operator decides to densify the network. While adding new BS, he has to jump to point
, coverage holes appear and the operator decides to densify the network. While adding new BS, he has to jump to point  in order to ensure continuous coverage. At point
in order to ensure continuous coverage. At point  , he needs approximately
, he needs approximately  BS per Km2 (
BS per Km2 ( Km2), while at point 3, he needs about
Km2), while at point 3, he needs about  BS per Km2 (
BS per Km2 ( Km2), which corresponds to a
Km2), which corresponds to a  increase.
increase.
6. Conclusion
In this paper, we have proposed and validated by Monte Carlo simulations a fluid model for the estimation of outage and spatial outage probabilities in cellular networks. This approach considers BS as a continuum of transmitters and provides a simple formula for the other-cell power ratio (OCIF) as a function of the distance to the BS, the path-loss exponent, the distance between BS and the network size. Simulations show that the obtained closed-form formula is a very good approximation, even for the traditional hexagonal network. The simplicity of the result allows a spatial integration of the OCIF leading to closed-form formula for the global outage probability and for the spatial outage probability. At last, this approach allows us to quantify cell breathing and network densification.
References
Viterbi AM, Viterbi AJ: Erlang capacity of a power controlled CDMA system. IEEE Journal on Selected Areas in Communications 1993, 11(6):892-900. 10.1109/49.232298
Evans JS, Everitt D: Effective bandwidth-based admission control for multiservice CDMA cellular networks. IEEE Transactions on Vehicular Technology 1999, 48(1):36-46. 10.1109/25.740058
Liu T, Everitt D: Analytical approximation of other-cell interference in the uplink of CDMA cellular systems. Proceedings of the IEEE Vehicular Technology Conference (VTC '06), May 2006 2: 693-697.
Viterbi AJ, Viterbi AM, Zehavi E: Other-cell interference in cellular power-controlled CDMA. IEEE Transactions on Communications 1994, 42(2):1501-1504. 10.1109/TCOMM.1994.582830
Viterbi AJ: CDMA—Principles of Spread Spectrum Communication. Addison-Wesley, Reading, Mass, USA; 1995.
Gilhousen KS, Jacobs IM, Padovani R, Viterbi AJ, Weaver LA Jr., Wheatley CE III: On the capacity of a cellular CDMA system. IEEE Transactions on Vehicular Technology 1991, 40(2):303-312. 10.1109/25.289411
Elayoubi S-E, Chahed T: Admission control in the downlink of WCDMA/UMTS. In Proceedings of the 1st International Workshop of the EURO-NGI Network of Excellence, 2005, Lecture Notes in Computer Science. Springer; 136-151.
Chan CC, Hanly SV: Calculating the outage probability in a CDMA network with spatial poisson traffic. IEEE Transactions on Vehicular Technology 2001, 50(1):183-204. 10.1109/25.917918
Baccelli F, Błaszczyszyn B, Karray MK: Blocking rates in large CDMA networks via a spatial Erlang formula. Proceedings of the 24th Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '05), March 2005, Miami, Fla, USA 58-67.
Toumpis S, Tassiulas L: Packetostatics: deployment of massively dense sensor networks as an electrostatics problem. Proceedings of the 24th Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '05), March 2005, Miami, Fla, USA 2290-2301.
Jacquet P: Geometry of information propagation in massively dense ad hoc networks. In Proceedings of the 5th ACM International Symposium on Mobile Ad Hoc Networking and Computing (MoBiHoc '04), May 2004. ACM; 157-162.
Kelif J-M: Admission control on fluid CDMA networks. Proceedings of the 3rd International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks (WiOpt '06), April 2006, Trentino, Italy
Kelif J-M, Alman E: Downlink fluid model of CDMA networks. Proceedings of the 2005 IEEE 61st Vehicular Technology Conference (VTC '05), June 2005 2264-2268.
Kelif J-M, Coupechoux M, Godlewski P: Spatial outage probability for cellular networks. Proceedings of the 50th Annual IEEE Global Telecommunications Conference (GLOBECOM '07), November 2007 4445-4450.
Kelif J-M, Coupechoux M, Godlewski P: Fluid model of the outage probability in sectored wireless networks. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC '08), April 2008 2933-2938.
Lagrange X: Principes et évolutions de l'UMTS. Hermes; 2005.
Bonald T, Proutière A: Conservative estimates of blocking and outage probabilities in CDMA networks. Performance Evaluation 2005, 62(1–4):50-67.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kelif, JM., Coupechoux, M. & Godlewski, P. A Fluid Model for Performance Analysis in Cellular Networks. J Wireless Com Network 2010, 435189 (2010). https://doi.org/10.1155/2010/435189
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/435189
 is the transmitted power from serving base station
is the transmitted power from serving base station 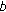 to mobile
to mobile  (for user's traffic);
(for user's traffic);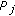 is the total transmitted power by a generic base station
is the total transmitted power by a generic base station 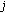 ;
;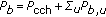 is the total power transmitted by station
is the total power transmitted by station  ,
,  represents the amount of power used to support broadcast and common control channels;
represents the amount of power used to support broadcast and common control channels;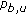 is the power received at mobile
is the power received at mobile  from station
from station  ; we can write
; we can write 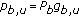 ;
;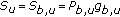 is the useful power received at mobile
is the useful power received at mobile  from serving station
from serving station 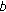 (for traffic data). Since we do not consider soft-handover (SHO), serving station is well defined and the subscript
(for traffic data). Since we do not consider soft-handover (SHO), serving station is well defined and the subscript 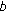 can be omitted for the sake of readability.
can be omitted for the sake of readability.
 and the interfering network is made of a continuum of base stations.
and the interfering network is made of a continuum of base stations.


 in the cell of interest
in the cell of interest 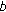 with uniform spatial distribution;
with uniform spatial distribution;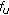 is computed using (5) with
is computed using (5) with  , where
, where 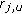 is the distance between the BS
is the distance between the BS  and the MS
and the MS  . The serving BS
. The serving BS 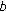 is the closest BS to MS
is the closest BS to MS  ;
; and the distance to the central BS
and the distance to the central BS  are recorded;
are recorded;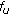 corresponding to a given distance are averaged and we plot the average value in Figure
corresponding to a given distance are averaged and we plot the average value in Figure 
 ,
,  ,
,  , and
, and  .
.
 ).
).
 m and
m and  Km (
Km ( ).
).
 snapshots) on a hexagonal network with
snapshots) on a hexagonal network with  .
.
 (solid line) and its Gaussian approximation (dotted line).
(solid line) and its Gaussian approximation (dotted line).

 ,
,  , and
, and  , simulation and analysis.
, simulation and analysis.
 outage as a function of the path-loss exponent
outage as a function of the path-loss exponent  , simulations (solid lines) and analysis (dotted lines) are compared.
, simulations (solid lines) and analysis (dotted lines) are compared.
 .
.