- Research Article
- Open access
- Published:
Performance of Some Metaheuristic Algorithms for Multiuser Detection in TTCM-Assisted Rank-Deficient SDMA-OFDM System
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 473435 (2010)
Abstract
We propose two novel and computationally efficient metaheuristic algorithms based on Artificial Bee Colony (ABC) and Particle Swarm Optimization (PSO) principles for Multiuser Detection (MUD) in Turbo Trellis Coded modulation- (TTCM-) based Space Division Multiple Access (SDMA) Orthogonal Frequency Division Multiplexing (OFDM) system. Unlike gradient descent methods, both ABC and PSO methods ensure minimization of the objective function without the solution being trapped into local optima. These techniques are capable of achieving excellent performance in the so-called overloaded system, where the number of transmit antennas is higher than the number of receiver antennas, in which the known classic MUDs fail. The performance of the proposed algorithm is compared with each other and also against Genetic Algorithm- (GA-) based MUD. Simulation results establish better performance, computational efficiency, and convergence characteristics for ABC and PSO methods. It is seen that the proposed detectors achieve similar performance to that of well-known optimum Maximum Likelihood Detector (MLD) at a significantly lower computational complexity and outperform the traditional MMSE MUD.
1. Introduction
Multiinput-Multioutput Orthogonal Frequency Division Multiplexing (MIMO-OFDM) [1] is considered as candidates for future 4G broadband wireless services. Among various topics related to MIMO-OFDM technologies, Space Division Multiple Access (SDMA) [2] based OFDM communication invoking Multiuser Detection (MUD) techniques has recently attracted intensive research interests. In SDMA MIMO systems the  different users transmitted signals are separated at the base-station (BS) using their unique, user-specific spatial signature, which is constituted by the
different users transmitted signals are separated at the base-station (BS) using their unique, user-specific spatial signature, which is constituted by the  -element vector of their channel transfer function between the user's single transmit antenna and the
-element vector of their channel transfer function between the user's single transmit antenna and the  different receiver antenna elements at the BS, upon assuming flat fading channel conditions in each of the OFDM subcarriers. A variety of MUDs [3, 4] have been proposed for separating different users at the BS on a per-subcarrier basis. The most popular among them is constituted by the Minimum Mean Squared Error (MMSE) MUD and was found to give poor performance. ML detection gives the best performance having dramatically increased computational complexity. By incorporating Forward Error Correction (FEC) schemes such as Turbo Trellis Coded Modulationb (TTCM) [5], the achievable performance can be further improved.
different receiver antenna elements at the BS, upon assuming flat fading channel conditions in each of the OFDM subcarriers. A variety of MUDs [3, 4] have been proposed for separating different users at the BS on a per-subcarrier basis. The most popular among them is constituted by the Minimum Mean Squared Error (MMSE) MUD and was found to give poor performance. ML detection gives the best performance having dramatically increased computational complexity. By incorporating Forward Error Correction (FEC) schemes such as Turbo Trellis Coded Modulationb (TTCM) [5], the achievable performance can be further improved.
In the existing literature, although there are a number of papers dealing with optimization-based approaches for MIMO-MUD, metaheuristic approaches still remain largely unexplored. Metaheuristics are general high-level procedures that coordinate simple heuristics and rules to find good (often optimal) approximate solutions to computationally difficult combinatorial optimization problems [6]. In the context of SDMA multiuser MIMO OFDM systems, none of the known classic multi user detectors allow the number of transmitters ( ) to be higher than the number of receivers, which is often referred to as an overloaded scenario, owing to the constraint imposed by the rank of the MIMO channel matrix. Against this background, in this paper we propose two computationally efficient metaheuristic algorithms based on ABC [7–11] and PSO [12–15] for multiuser detection in SDMA-OFDM systems, which provide an effective solution to the multiuser MIMO detection problem in the above-mentioned high-throughput rank-deficient scenario. Both ABC and PSO are efficient stochastic optimization tools with the capability of avoiding local minima, a feature not present in gradient search-based nonlinear optimization methods. The methods proposed approach the optimum performance of the ML detector. Finally, the computational complexity of the proposed schemes is significantly lower than that of the optimum ML system, especially in high-throughput scenarios.
) to be higher than the number of receivers, which is often referred to as an overloaded scenario, owing to the constraint imposed by the rank of the MIMO channel matrix. Against this background, in this paper we propose two computationally efficient metaheuristic algorithms based on ABC [7–11] and PSO [12–15] for multiuser detection in SDMA-OFDM systems, which provide an effective solution to the multiuser MIMO detection problem in the above-mentioned high-throughput rank-deficient scenario. Both ABC and PSO are efficient stochastic optimization tools with the capability of avoiding local minima, a feature not present in gradient search-based nonlinear optimization methods. The methods proposed approach the optimum performance of the ML detector. Finally, the computational complexity of the proposed schemes is significantly lower than that of the optimum ML system, especially in high-throughput scenarios.
Our major contributions in this paper are (i) the development of two relatively accurate, computationally efficient metaheuristic algorithm suitable for multi user detection in SDMA-OFDM system; (ii) a thorough analysis of the performance of the proposed algorithms under both fully loaded and overloaded scenario; (iii) computational complexity comparison of the proposed algorithms with existing MUDs such as ML and MMSE. From the analysis it is found that the ABC- and PSO-based methods outperform the existing MMSE- and GA-based MUDs. The structure of this paper is as follows. Section 2 provides a description of the related works. The SDMA MIMO system model is described in Section 3, while the proposed MUDs based on ABC and PSO are explained in Section 4. Our simulation results are provided in Section 5, while the associated complexity issues are discussed in Section 6. Our final conclusions are summarized in Section 7.
2. Related Work
Multi User Detection in SDMA-OFDM has drawn significant research interest in recent years. Among the various MUDs, Least Square (LS) and MMSE exhibit the lowest complexity, but they suffer from performance loss. The nonlinear MUDs such as SIC and PIC [16] are prone to error propagation. ML detector was found to give best performance at the cost of dramatically increased computational complexity. The performance of numerous known classic MUD techniques such as Vertical Bell Labs Layered Space-Time architecture (V-BLAST) [17] and the QR Decomposition combined with the M-algorithm (QRD-M) [18] will fail in the overloaded scenario where the number of users exceeds the number of receivers. Damen et al. [19] proposed a powerful sphere decoding (SD) algorithm which was suitable for overloaded MIMO MUD. The derivatives of SD such as Optimized Hierarchy Reduced Search Algorithm (OHRSA) [20] were proposed which are capable of achieving ML performance at a lower complexity. Other MUD techniques based on minimum bit error rate (MBER) are also proposed. GA-based MUD has been proposed by Juntti et al. [21] and Wang et al. [22] where the analysis was based on the Additive White Gaussian Noise (AWGN) channel. Its employment in Rayleigh fading channels was considered by Yen and Hanzo in [23]. In 2004, Jiang and Hanzo proposed GA-assisted TTCM-S DMA-OFDM [24].
Inspired by the work of Hanzo we propose ABC and PSO-based stochastic optimization algorithms and show that they have better computational efficiency, convergence characteristics, and BER performance than MMSE and GA algorithm for the multi user detection problem in SDMA-OFDM system.
3. System Model
Figure 1 shows the MIMO OFDM system model in which there are  mobile users each having single transmit antenna and the Base station receiver has
mobile users each having single transmit antenna and the Base station receiver has  receiving antennas. The OFDM signal at the transmitter is obtained by Inverse Fast Fourier Transform (IFFT), and Fast Fourier Transform (FFT) is done to detect the signal at the receiver. The
receiving antennas. The OFDM signal at the transmitter is obtained by Inverse Fast Fourier Transform (IFFT), and Fast Fourier Transform (FFT) is done to detect the signal at the receiver. The  th subcarrier of
th subcarrier of  th OFDM symbol of
th OFDM symbol of  th receive antenna is given by
th receive antenna is given by

where  is the transmitted data symbol,
is the transmitted data symbol,  is the additive white Gaussian noise at the
is the additive white Gaussian noise at the  th receive antenna.
th receive antenna.  is the frequency domain channel coefficient between
is the frequency domain channel coefficient between  th transmitting antenna and
th transmitting antenna and  th receiving antenna. We can write (1) in matrix form as
th receiving antenna. We can write (1) in matrix form as

where  is
is  dimensional received signal,
dimensional received signal,  is
is  dimensional channel matrix,
dimensional channel matrix,  is
is  dimensional transmitted signal, and
dimensional transmitted signal, and  is a
is a  dimensional noise vector. Transmitted symbols of each user are estimated by using MMSE-based MUD. It is done by linearly combining the signal from each received antenna with the weight matrix
dimensional noise vector. Transmitted symbols of each user are estimated by using MMSE-based MUD. It is done by linearly combining the signal from each received antenna with the weight matrix  resulting in
resulting in

MMSE-based weight matrix  is given by
is given by

where  is the noise variance.
is the noise variance.
3.1. Optimization Metric
An important step to implement ABC and PSO methods is to define a fitness function; this is the link between the optimization algorithm and the real-world problem. Fitness function is unique for each optimization problem The decision metric for finding most likely transmitted  user symbol vector
user symbol vector  in ML MUD is given by
in ML MUD is given by

It requires  evaluations of decision metric, where
evaluations of decision metric, where  denotes the number of bits per symbol. The set of
denotes the number of bits per symbol. The set of  number of trial vectors can be formulated as
number of trial vectors can be formulated as

where  denotes the set containing
denotes the set containing  number of constellation points of the modulation scheme used. The ML-based decision metric can be used in ABC and PSO MUDs for detecting estimated transmitted symbols. Here the decision metric required for the
number of constellation points of the modulation scheme used. The ML-based decision metric can be used in ABC and PSO MUDs for detecting estimated transmitted symbols. Here the decision metric required for the  th receiver antenna is given by
th receiver antenna is given by

where  is the received symbol at a specific OFDM subcarrier and
is the received symbol at a specific OFDM subcarrier and  is the
is the  th row of channel transfer function matrix
th row of channel transfer function matrix  . The estimated symbol vectors of
. The estimated symbol vectors of  users is given by
users is given by

The combined objective function for  number of receiver antennas is given by
number of receiver antennas is given by

The MMSE MUD when combined with ABC/PSO forms a more powerful concatenated MMSE-ABC/PSO MUD. It achieves a similar performance as that of ML MUD with low computational complexity and at high user loads. The schematic of concatenated MMSE-ABC/PSO MUD aided multiuser MIMO-OFDM system is shown in Figure 1. The incoming data bits are encoded using a TTCM coder. The OFDM symbols are constructed after interleaving and modulation mapping, followed by their transmission over the SDMA MIMO channel. At the BS, FFT-based OFDM demodulation is done at each receiver antenna. The demodulated outputs are then applied to MUD block to separate out different users signal, and it is then given to TTCM decoders.
4. Metaheuristic Algorithms for SDMA-OFDM Multi User Detection
4.1. Overview of Artificial Bee Colony Algorithm
In 2005, Karaboga [7] proposed ABC algorithm, and Basturk and Karaboga [8–11] compared the performance of ABC with some other popular population-based metaheuristic algorithms. In this algorithm, foraging behaviour of a honey bee swarm is considered. Employed, onlookers, and scouts are the three classifications of foraging bees. Employed bees are those who currently exploit the food source. They take loads of nectar from the food source to the hive and pass the information about food source to onlooker bees. Onlooker bees wait in the hive for getting information about food sources from the employed bees, and scouts are those which currently search for new food sources in the vicinity of the hive. Employed bees dance in a common area in the hive called dance area. The duration of a dance by employed bee is proportional to the nectar content of the food source. Onlooker bees watch various dances and choose a food source based on the probability proportional to the quality of that food source. The good food sources are attracted by more onlooker bees. Scout or onlooker bees become employed when they find a food source. Employed bees, which abandon a food source after exploiting it fully, become scouts or onlookers. Scout bees perform the job of exploration, whereas employed and onlooker bees perform the job of exploitation.
In ABC algorithm, the solution of the problem under consideration is represented by the food source, and the quality of the solution is represented by the nectar amount of the food source. Employed bees come in the first half, and onlookers come in the second half of the colony. There is only one employed bee for every food source. The employed bee becomes a Scout when it abandons a food source and returns to employed when it finds a new food source. It is an iterative algorithm. All employed bees are associated with randomly generated food sources at the starting time of algorithm. During each iteration, every employed bee finds a neighboring source and evaluates its nectar amount. If the nectar amount of neighbor is better than that of current food source then that employed bee moves to this new food source, otherwise it remains in old food source. After finishing this process, the employed bees share the nectar information of the food sources with the onlookers. The onlookers select a food source based on the probability proportional to the nectar amount of that food source. The probability  of selecting a food source
of selecting a food source  is given by
is given by

where  is the nectar amount (fitness) of the food source (solution)
is the nectar amount (fitness) of the food source (solution)  and
and  is the total number of food sources. Good food sources will get more onlookers. Onlookers then find neighborhood of their chosen food source and compute its fitness. The best food source among the neighbors of food source
is the total number of food sources. Good food sources will get more onlookers. Onlookers then find neighborhood of their chosen food source and compute its fitness. The best food source among the neighbors of food source  and food source
and food source  itself will be the new location of the food source
itself will be the new location of the food source  . If the solution of a particular food source does not improve for a predetermined number of iterations then employed bee abandons that food source, and it becomes a scout and search for a new food source randomly. This assigns a random food source to this scout, and it becomes employed. After finding the new location of each food source, next iteration of ABC algorithm begins. These steps are repeated until a stopping criterion is met.
. If the solution of a particular food source does not improve for a predetermined number of iterations then employed bee abandons that food source, and it becomes a scout and search for a new food source randomly. This assigns a random food source to this scout, and it becomes employed. After finding the new location of each food source, next iteration of ABC algorithm begins. These steps are repeated until a stopping criterion is met.
The neighbor food source position of a particular food source is found out by changing the value of one randomly chosen solution parameter and keeping other parameters unchanged. This is carried out by adding the value of the chosen parameter with the product of a uniform random number in  and the difference in values of this parameter and some other randomly chosen food source. Suppose that each solution consists of
and the difference in values of this parameter and some other randomly chosen food source. Suppose that each solution consists of  parameters, and let
parameters, and let  be a solution with parameter values
be a solution with parameter values  . For determining a solution
. For determining a solution  in the neighborhood of
in the neighborhood of  , a solution parameter
, a solution parameter  and another solution
and another solution  are selected randomly. All parameters except the value of selected parameter
are selected randomly. All parameters except the value of selected parameter  of
of  are same as
are same as  , that is,
, that is,  . The
. The  th parameter of
th parameter of  is determined as
is determined as

where  is a uniform random variable in
is a uniform random variable in  .
.
4.2. The ABC Algorithm for the MIMO-OFDM MUD Problem (Figure 2)
The main steps of our ABC algorithm for the MIMO-OFDM MUD problem are described below.
Step 1.
Initialization. Initial population containing  number of food sources is created. First food source is created from the output of the MMSE MUD. The
number of food sources is created. First food source is created from the output of the MMSE MUD. The  th food source is expressed as
th food source is expressed as  , and we have
, and we have  , where
, where  denotes the set containing
denotes the set containing  number of constellation points of the modulation scheme used and
number of constellation points of the modulation scheme used and  denotes the number of bits per symbol. If
denotes the number of bits per symbol. If  , then
, then  is the best solution.
is the best solution.  . After initialization, the food sources are subjected to repeated cycles,
. After initialization, the food sources are subjected to repeated cycles,  (maximum cycle number), of the search processes of the employed bees, the onlooker bees, and scout bees.
(maximum cycle number), of the search processes of the employed bees, the onlooker bees, and scout bees.
Step 2.
Search by Employed Bee. Each employed bee locates a new symbol near their current symbol. An employed bee at  locates a new symbol
locates a new symbol  .
. 
 , where
, where  is a uniform random variable in
is a uniform random variable in  .
.
 is the
is the  th bit of
th bit of  th symbol in the population. If
th symbol in the population. If  then
then  (
( represents the value of objective function). All the symbols are then updated.
represents the value of objective function). All the symbols are then updated.
Step 3.
Selection by Onlookers. Each onlooker bee in the hive selects a symbol. Good symbols get more onlooker bees.
Step 4.
Search by Onlookers. All symbols selected by onlookers are updated. Each onlooker bee at  locates a neighboring symbol. Best symbol
locates a neighboring symbol. Best symbol  located by the onlooker of
located by the onlooker of  is found out. If
is found out. If  then
then  .
.
Step 5.
Search by Scouts. If there is no improvement in the symbol at a location in predetermined (LIMIT) number of times employed bee becomes scout. Then that symbol is replaced by random symbol found by scout.
Step 6.
Evaluate the Best Solution. If  then
then  is the best solution. All symbols selected by onlookers are updated. If
is the best solution. All symbols selected by onlookers are updated. If  then
then  .
.
Step 7.
Termination. If number of iteration = MCN then terminate ABC else go to Step 2. Then optimum solution  will be considered as the detected
will be considered as the detected  -user transmitted symbol vector corresponding to the specific OFDM subcarrier considered.
-user transmitted symbol vector corresponding to the specific OFDM subcarrier considered.
4.3. Overview of Particle Swarm Optimization
PSO is a population-based stochastic optimization technique developed by Kennedy and Eberhart [13] in 1995, which simulates the social behavior of bird flocking. It is easy to implement and is computationally efficient because its memory and CPU requirements are low. The PSO technique employs a set of feasible solutions called a swarm of particles that are populated in the search space with random initial locations. The values of the objective function corresponding to the particle locations are evaluated. The particles are then moved in the search space obeying rules inspired by bird flocking behavior. Each particle is moved towards a randomly weighted average of the best position that the particle have come across so far (pbest) and the best position encountered by the entire particle population (gbest). Let  be the
be the  -dimensional vector representing the position of the
-dimensional vector representing the position of the  th particle in the swarm,
th particle in the swarm,  the position vector of the best particle in the swarm (i.e., the particle with the smallest objective function value),
the position vector of the best particle in the swarm (i.e., the particle with the smallest objective function value),  the position vector of the
the position vector of the  th particles personal best, and
th particles personal best, and  the velocity of the
the velocity of the  th particle. The particles evolve according to the following equations:
th particle. The particles evolve according to the following equations:

where  ;
;  is the size of the swarm population. In (12),
is the size of the swarm population. In (12),  is the inertial weight, which determines the confidence of a particle in its own movement unaffected by
is the inertial weight, which determines the confidence of a particle in its own movement unaffected by  and
and  ;
;  determines how much a particle is influenced by the memory of its best solution, whereas
determines how much a particle is influenced by the memory of its best solution, whereas  is an indication of the impact of rest of the swarm on the particle.
is an indication of the impact of rest of the swarm on the particle.  and
and  are termed cognitive and social scaling parameters, respectively.
are termed cognitive and social scaling parameters, respectively.  and
and  are uniform random numbers in the interval
are uniform random numbers in the interval  .
.
The parameters  ,
,  , and
, and  have a critical role in the convergence characteristics of PSO. The coefficient
have a critical role in the convergence characteristics of PSO. The coefficient  should be neither too small, which results in an early convergence, nor too large, which on the contrary slows down the convergence process. A value of
should be neither too small, which results in an early convergence, nor too large, which on the contrary slows down the convergence process. A value of  and
and  was recommended for faster convergence by Eberhart and Shi [14, 15] after experimental tests.
was recommended for faster convergence by Eberhart and Shi [14, 15] after experimental tests.
4.4. The PSO Algorithm for the MIMO-OFDM MUD Problem
The major challenge in designing Binary PSO- (BPSO-) based MIMO-OFDM detector was selection of BPSO parameters that fit the symbol detection optimization problem. The basic fitness function used by the optimization algorithm to converge to the near optimal solution is (9). Selection of initial guess is essential for these algorithms to perform. Therefore, our detector takes the output of MMSE as its initial solution guess. This guess enables the algorithm to reach more refined solution iteratively by ensuring fast convergence.
The proposed detection algorithm is detailed below.
-
(1)
Take the output of MMSE as initial particles (initial solution bit string) instead of selecting randomly from the solution space.
-
(2)
The algorithm parameters are initialized.
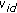 is initialized to zero;
is initialized to zero; 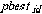 and
and 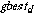 are initialized to maximum Euclidean distance depending upon the QAM size.
are initialized to maximum Euclidean distance depending upon the QAM size. -
(3)
Evaluate the fitness of each particle (bit)
 (13)
(13)Minimum Euclidean distance for each symbol represents the fitness of solution. Effect on the Euclidean distance due to search space bits is measured. Find the global best performance
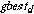 in the population that represents the least Euclidean distance found so far. Record the personal best
in the population that represents the least Euclidean distance found so far. Record the personal best  for each bit along its previous values.
for each bit along its previous values. -
(4)
For each search space bit at
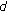 th side of the bit string of particle
th side of the bit string of particle 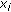 , compute bits velocity using following PSO velocity update equation:
, compute bits velocity using following PSO velocity update equation: 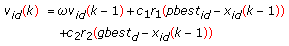 (14)
(14) -
with
 .
. -
(5)
The particle position is updated depending on the following binary decision rule:
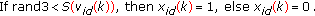 (15)
(15) -
(6)
Go to Step 3 until the maximum number of iterations is reached. The number of iterations is system and requirement dependent (usually kept less than 25 to avoid large complexity). Solution gets refined iteratively.
Here  is the number of iterations, and
is the number of iterations, and  is sigmoid transformation function:
is sigmoid transformation function:

The parameter  is the particles predisposition to make 1 or 0; it determines the probability threshold to make this choice. The individual is more likely to choose 1 for higher
is the particles predisposition to make 1 or 0; it determines the probability threshold to make this choice. The individual is more likely to choose 1 for higher  , whereas its lower values will result in the choice of 0. Such a threshold needs to stay in the range of
, whereas its lower values will result in the choice of 0. Such a threshold needs to stay in the range of  . The sigmoid logistic transformation function maps the value of
. The sigmoid logistic transformation function maps the value of  to a range of
to a range of  . The terms
. The terms  and
and  are positive acceleration constants used to scale the contribution of cognitive and social components such that
are positive acceleration constants used to scale the contribution of cognitive and social components such that  . These are used to stochastically vary the relative pull of pbest and gbest.
. These are used to stochastically vary the relative pull of pbest and gbest.  sets a limit to further exploration after the particles have converged. Its values are problem dependent, usually set in the range of
sets a limit to further exploration after the particles have converged. Its values are problem dependent, usually set in the range of  .
.
4.5. Channel Model
For computer simulation, the MIMO channel model used in this work is the IEEE 802.11n channel model (IEEE P802.11 TGn channel models, 2004), [25, 26] which specifies a set of channel models applicable to MIMO WLAN systems. The channel models comprise a set of 6 profiles, labeled A to F, which cover the scenarios of dispersive multipath fading, residential, residential/small office, typical office, large office, and large space (indoors and outdoors). Each channel model has a certain number of taps (one for model A, and 9 to 18 for models B–F). Each model further comprises a number of clusters, which correspond to overlapping subsets of the tap delays. The RMS delay spread for the models varies from 15 to 150 ns, and the number of clusters varies from 2 to 6. In this cluster-based channel model the impulse response is given by

where the first summation corresponds to the clusters and the second corresponds to rays within the clusters. The complex attenuation factor for the  th path is
th path is  , which is Rayleigh distributed. The time of arrival of the
, which is Rayleigh distributed. The time of arrival of the  th cluster is
th cluster is  , and
, and  is the time of arrival of the
is the time of arrival of the  th path. The TGn channel model F in NLOS condition is considered here.
th path. The TGn channel model F in NLOS condition is considered here.
5. Simulation Results
The OFDM modem used in our simulations employed 128 subcarriers. The half-rate TTCM code employed two Recursive Systematic Convolutional (RSC) component codes having a constraint-length of  , and the standard 124-bit turbo code interleaver was also used. The octally represented RSC generator polynomial of (7 5) was used. The Minimum Mean Square Error (MMSE) algorithm was used for creating the ABCs initial population. Simulations were carried out on a PC with 2.99 GHz dual core AMD opteron processor and 2.5 GB RAM using Matlab 7.2.0.232(R2006a).
, and the standard 124-bit turbo code interleaver was also used. The octally represented RSC generator polynomial of (7 5) was used. The Minimum Mean Square Error (MMSE) algorithm was used for creating the ABCs initial population. Simulations were carried out on a PC with 2.99 GHz dual core AMD opteron processor and 2.5 GB RAM using Matlab 7.2.0.232(R2006a).
In this section, we characterize the achievable performance of the proposed TCM-assisted concatenated MMSE-ABC/PSO multiuser detected SDMA-OFDM system. The various parameters used in the ABC and PSO MUDs are summarized in Table 1. The channel is assumed to be OFDM symbol-invariant, in which the taps of the impulse response are assumed to be constant for the duration of one OFDM symbol, but they are faded at the beginning of each OFDM symbol. The simulation results were obtained using a 4QAM scheme. The Bit Error Rate (BER) performance of the TTCM-assisted MMSE-ABC/PSO-SDMA-OFDM system employing a 4QAM scheme is given in Figure 3, where six users are supported with the aid of six receiver antenna elements. The performance of the TCM-aided MMSE-detected SDMA-OFDM system, the TCM-assisted optimum ML-detected system, is also provided for reference. It is observed from Figure 3 that the BER performance of the TTCM-assisted MMSE-SDMA-OFDM system was significantly improved with the aid of the ABC and PSO having a sufficiently large food source (population) size  or a larger number of iterations
or a larger number of iterations  . This improvement was achieved, since a larger food source may contain a higher variety of
. This improvement was achieved, since a larger food source may contain a higher variety of  symbol individuals. Similarly, a larger number of iterations imply that, again, a more diverse set of individuals may be evaluated, thus extending the ABC and PSOs search space, which may be expected to increase the chance of finding a lower-BER solution. The proposed TTCM-assisted MMSE-ABC-SDMA-OFDM technique, results in 1.5 dB degraded performance at 10−4 BER in comparison with ML. However, in comparison to MMSE, it shows 4 dB better performance, and with GA it shows 1 dB better performance. Also the proposed MMSE-PSO-SDMA technique results in 2 dB degraded performance at 10−4 BER in comparison with ML. It shows 3 dB better performance in comparison to MMSE. In comparison with MMSE-GA-SDMA-OFDM technique it shows 0.5 dB better performance.
symbol individuals. Similarly, a larger number of iterations imply that, again, a more diverse set of individuals may be evaluated, thus extending the ABC and PSOs search space, which may be expected to increase the chance of finding a lower-BER solution. The proposed TTCM-assisted MMSE-ABC-SDMA-OFDM technique, results in 1.5 dB degraded performance at 10−4 BER in comparison with ML. However, in comparison to MMSE, it shows 4 dB better performance, and with GA it shows 1 dB better performance. Also the proposed MMSE-PSO-SDMA technique results in 2 dB degraded performance at 10−4 BER in comparison with ML. It shows 3 dB better performance in comparison to MMSE. In comparison with MMSE-GA-SDMA-OFDM technique it shows 0.5 dB better performance.
In Figure 4 we provide the BER performance recorded in the overloaded scenario, where  transmit antennas and
transmit antennas and  receiver antennas were employed. In overloaded scenarios, the weight matrix calculated by the MMSE algorithm becomes a singular matrix, which will lead to a theoretically unresolvable detection problem. By contrast, the system aided by the ABC/PSO was capable of attaining an undistinguishable performance from that of the optimum ML detected arrangement in the overloaded scenario of Figure 4. Again a 1 dB and 0.5 dB
receiver antennas were employed. In overloaded scenarios, the weight matrix calculated by the MMSE algorithm becomes a singular matrix, which will lead to a theoretically unresolvable detection problem. By contrast, the system aided by the ABC/PSO was capable of attaining an undistinguishable performance from that of the optimum ML detected arrangement in the overloaded scenario of Figure 4. Again a 1 dB and 0.5 dB  gain were obtained, when comparing ABC-MUD and PSO-MUD, respectively, with GA-MUD at
gain were obtained, when comparing ABC-MUD and PSO-MUD, respectively, with GA-MUD at  BER.
BER.
Figures 5 and 6 show the simulation results for MIMO OFDM systems with different QAM constellations, that is, 16-QAM and 64-QAM. High-order constellations assure more transmitted bits per symbol. In the case of high-order constellations, the points must be closer together and are thus more susceptible to noise and other corruption, which results in a higher BER, and so high-order QAM can deliver more less reliable data than lower-order QAM. From Figures 5 and 6, it is clear that the proposed schemes outperform the existing GA-based suboptimal method.
As an investigation on the ABCs convergence characteristics, in Figure 7 the performance of the  rank deficient TTCM-aided MMSE-ABC-SDMA-OFDM system is illustrated, at a fixed
rank deficient TTCM-aided MMSE-ABC-SDMA-OFDM system is illustrated, at a fixed  value of 2 dB. More specifically, in Figure 7 the population size
value of 2 dB. More specifically, in Figure 7 the population size  was varied with the number of iterations fixed at
was varied with the number of iterations fixed at  , while in Figure 8 the effect of a different number of iterations
, while in Figure 8 the effect of a different number of iterations  was evaluated at a fixed population size of
was evaluated at a fixed population size of  . Explicitly, as
. Explicitly, as  or
or  increases, a consistently reduced BER is observed, which approaches the optimum ML performance. The convergence of the proposed algorithm in different conditions is illustrated in Figure 9. From Figure 9 it can be concluded that as the population size increases, the algorithm produces better results. However, after a sufficient value for colony size, any increment in the value does not improve the performance of the ABC algorithm significantly.
increases, a consistently reduced BER is observed, which approaches the optimum ML performance. The convergence of the proposed algorithm in different conditions is illustrated in Figure 9. From Figure 9 it can be concluded that as the population size increases, the algorithm produces better results. However, after a sufficient value for colony size, any increment in the value does not improve the performance of the ABC algorithm significantly.
5.1. Comparison of Algorithms Based on Control Parameters
The efficiency of a metaheuristic algorithm is greatly dependent on its tuning parameters. In the case of ABC the percentage of onlooker bees was 50% of the colony, the employed bees were 50% of the colony, and the number of scout bees was selected to be at most one for each cycle. In ABC, the number of onlooker bees is taken equal to the number of employed bees so that ABC has less control parameters. There are three control parameters used in the ABC: the number of food sources which is equal to the number of employed or onlooker bees (SN), the value of limit, and the maximum cycle number (MCN). TS uses three control parameters such as population size, number of iterations, and tabu memory size. The TS-based MUD algorithm generally requires more memory resources than ABC and GA, since it has to maintain the tabu list during the search process. Compared to ABC and TS, there are a more number of tuning parameters in the case of GA which makes GA more complex. The control parameters of GA include population size, number of generations, crossover type, crossover rate, mutation type, and mutation rate. It is evident that the ABC- and TS-based methods outperform the GA-based method in terms of BER performance and convergence characteristics for given terminating criteria. Moreover, the GA method requires the involvement of the operations like crossover and mutation that complicate the solution and slow down the convergence of the solution and also add to the computation cost. Typical values of control parameters used in our MIMO-MUD problem are given in Table 1.
6. Complexity Analysis
We will quantify the complexity imposed in terms of the number of metric computations required by the process as follows. ML MUD requires  number of metric computations for finding the optimum solution, namely, the most likely transmitted
number of metric computations for finding the optimum solution, namely, the most likely transmitted  -user vector, where
-user vector, where  denotes the number of bits per symbol. In the case of our proposed ABC and PSO MUDs, maximum of (
denotes the number of bits per symbol. In the case of our proposed ABC and PSO MUDs, maximum of ( ) metric evaluations are required, since
) metric evaluations are required, since  number of
number of  -symbol vectors are evaluated during each of the
-symbol vectors are evaluated during each of the number of iterations. In Figure 10, we compare both the ML- and the ABC/PSO-aided schemes in terms of their complexity, that is, the number of metric computations. As shown in Figure 10, the ML-aided system imposes an exponentially increasing complexity on the order of
number of iterations. In Figure 10, we compare both the ML- and the ABC/PSO-aided schemes in terms of their complexity, that is, the number of metric computations. As shown in Figure 10, the ML-aided system imposes an exponentially increasing complexity on the order of  , when the number of users increases, while the complexity of the ABC- and PSO-aided systems required for maintaining a near-optimum performance increases only slowly. CPU time required for various MUD algorithms is illustrated in Table 2. We can see that the proposed algorithms (ABC and PSO) converge to a better solution in minimum time.
, when the number of users increases, while the complexity of the ABC- and PSO-aided systems required for maintaining a near-optimum performance increases only slowly. CPU time required for various MUD algorithms is illustrated in Table 2. We can see that the proposed algorithms (ABC and PSO) converge to a better solution in minimum time.
In order to characterize the advantage of the ABC-MUD scheme in terms of the performance-versus-complexity tradeoff, in Table 3 we summarize the computational complexity imposed by the different MUDs assuming an  value of 3 dB, where the associated complexity was quantified in terms of the number of complex additions and multiplications imposed by the different MUDs on a per-user basis. As observed in Table 3, the complexity of the ML MUD is significantly higher than that of the MMSE MUD or the ABC MUD, especially in highly rank-deficient scenarios. By contrast, the ABC MUD reduced the BER by up to five orders of magnitude in comparison to the MMSE MUD at a moderate complexity.
value of 3 dB, where the associated complexity was quantified in terms of the number of complex additions and multiplications imposed by the different MUDs on a per-user basis. As observed in Table 3, the complexity of the ML MUD is significantly higher than that of the MMSE MUD or the ABC MUD, especially in highly rank-deficient scenarios. By contrast, the ABC MUD reduced the BER by up to five orders of magnitude in comparison to the MMSE MUD at a moderate complexity.
7. Conclusion
In this paper, we have proposed two algorithms to solve multi user detection problem in SDMA-OFDM system using ABC and PSO methods. ABC and PSO having the advantages of simple mathematical model, lesser implementation complexity, resistance to being trapped in local minima, and convergence to reasonable solution in lesser iterations makes them suitable candidates for real-time wireless communications systems. The performance analysis of these algorithms shows a significant improvement in the BER performance and in convergence characteristics compared to the GA-based algorithm, a metaheuristic method already available in the literature. These algorithms show promising results when compared to the optimal ML and traditional MMSE detectors. ABC- and PSO-optimized MIMO symbol detection mechanisms approach near-optimal performance with significant reduction in computational complexity, especially for complex systems with multiple transmitting antennas, where conventional ML detector is computationally expensive and impractical to deploy. For example, a complexity reduction in excess of a factor of 100 can be achieved by the proposed systems for  , as evidenced by Figure 10. Although MMSE detector offers a reduced complexity, its BER performance is inferior to the proposed detectors. Furthermore, the proposed techniques are capable of achieving an excellent performance even in the so-called overloaded systems, where the number of transmit antennas is higher than the number of receiver antennas.
, as evidenced by Figure 10. Although MMSE detector offers a reduced complexity, its BER performance is inferior to the proposed detectors. Furthermore, the proposed techniques are capable of achieving an excellent performance even in the so-called overloaded systems, where the number of transmit antennas is higher than the number of receiver antennas.
References
Hanzo L, Munster M, Choi B, Keller T: OFDM and MC-CDMA for Broadband Multiuser Communications, WLANs and Broadcasting. IEEE Press-John Wiley & Sons, New York, NY, USA; 2003.
Hanzo L, Keller T: An OFDM and MC-CDMA Primer. IEEE Press/Wiley, Piscataway, NJ, USA; 2006.
Verdu S: Multiuser Detection. Cambridge University Press, Cambridge, UK; 1998.
Hassell CZW, Thompson JS, Mulgrew B, Grant PM: A comparison of detection algorithms including BLAST for wireless communication using multiple antennas. Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '00), September 2000, London, UK 1: 698-703.
Hanzo L, Liew T, Yeap B: Turbo Coding, Turbo Equalisation and Space-Time Coding for Transmission Over Fading Channels. IEEE Press-John Wiley & Sons, New York, NY, USA; 2002.
Martins SL, Ribeiro CC: Metaheuristics and applications to optimization problems in telecommunications. In Handbook of Optimization in Telecommunications. Edited by: Resende MGC, Pardalos PM. Springer Science/Business Media, New York, NY, USA; 2006:103-128.
Karaboga D: An idea based on honey bee swarm for numerical optimization. Computer Engineering Department, Erciyes University, Kayseri, Turkey; 2005.
Basturk B, Karaboga D: An artificial bee colony (ABC) algorithm for numeric function optimization. Proceedings of the IEEE Swarm Intelligence Symposium, May 2006, Indianapolis, Ind, USA
Karaboga D, Basturk B: A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm. Journal of Global Optimization 2007, 39(3):459-471. 10.1007/s10898-007-9149-x
Karaboga D, Basturk B: Artificial Bee Colony (ABC) optimization algorithm for solving constrained optimization problems. In Foundations of Fuzzy Logic and Soft Computing, Lecture Notes in Computer Science. Volume 4529. Springer, Berlin, Germany; 2007:789-798. 10.1007/978-3-540-72950-1_77
Karaboga D, Basturk B: On the performance of artificial bee colony (ABC) algorithm. Applied Soft Computing Journal 2008, 8(1):687-697. 10.1016/j.asoc.2007.05.007
Kennedy J, Eberhart RC: Discrete binary version of the particle swarm algorithm. Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC '97), October 1997 4104-4108.
Kennedy J, Eberhart R: Particle swarm optimization. Proceedings of the IEEE International Conference on Neural Networks, December 1995 1942-1948.
Eberhart RC, Shi Y: Particle swarm optimization: developments, applications and resources. Proceedings of the IEEE Congress on Evolutionary Computation (CEC '01), May 2001 1: 81-86.
Eberhart RC, Shi Y: Tracking and optimizing dynamic systems with particle swarms. Proceedings of the IEEE Congress on Evolutionary Computation (CEC '01), May 2001 94-100.
Sellathurai M, Haykin S: A simplified diagonal BLAST architecture with iterative parallel-interference cancelation receivers. Proceedings of IEEE International Conference on Communications (ICC '01), June 2001, Helsinki, Finland 10: 3067-3071.
Wolniansky PW, Foschini GJ, Golden GD, Valenzuela RA: V-BLAST: an architecture for realizing very high data rates over the rich-scattering wireless channel. Proceedings of the International Symposium on Signals, Systems and Electronics (ISSSE '98), September-October 1998, Pisa, Italy 295-300.
Kim KJ, Yue J, Iltis RA, Gibson JD: A QRD-M/Kalman filter-based detection and channel estimation algorithm for MIMO-OFDM systems. IEEE Transactions on Wireless Communications 2005, 4(2):710-721.
Damen MO, Abed-Meraim K, Belfiore JC: Generalized sphere decoder for asymmetrical space-time communication architecture. Electronics Letters 2000, 36(2):166-167. 10.1049/el:20000168
Akhtman J, Hanzo L: An optimized-hierarchy-aided maximum likelihood detector for MIMO-OFDM. Proceedings of the IEEE 63rd Vehicular Technology Conference (VTC '06), May 2006, Melbourne, Australia 3: 1526-1530.
Juntti MJ, Schlosser T, Lilleberg JO: Genetic algorithms for multiuser detection in synchronous CDMA. Proceedings of the IEEE International Symposium on Information Theory (ISIT '97), July 1997, Ulm, Germany 492.
Wang XF, Lu WS, Antoniou A: A genetic-algorithm-based multiuser detector for multiple-access communications. Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS '98), June 1998, Monterey, Calif, USA 4: 534-537.
Yen K, Hanzo L: Antenna-diversity-assisted genetic-algorithm-based multiuser detection schemes for synchronous CDMA systems. IEEE Transactions on Communications 2003, 51(3):366-370. 10.1109/TCOMM.2003.809755
Jiang M, Hanzo L: Genetically enhanced TTCM assisted MMSE multi-user detection for SDMA-OFDM. Proceedings of the 60th IEEE Vehicular Technology Conference (VTC '04), September 2004, Los Angeles, Calif, USA 3: 1954-1958.
Saleh AAM, Valenzuela RA: A statistical model for indoor multipath propagation. IEEE Journal on Selected Areas in Communications 1987, 5(2):128-137.
Tse D, Vishwanath P: Fundamentals of Wireless Communications. Cambridge University Press, Cambridge, UK; 2005.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Haris, P.A., Gopinathan, E. & Ali, C.K. Performance of Some Metaheuristic Algorithms for Multiuser Detection in TTCM-Assisted Rank-Deficient SDMA-OFDM System. J Wireless Com Network 2010, 473435 (2010). https://doi.org/10.1155/2010/473435
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/473435


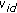 is initialized to zero;
is initialized to zero; 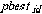 and
and 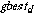 are initialized to maximum Euclidean distance depending upon the QAM size.
are initialized to maximum Euclidean distance depending upon the QAM size.
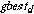 in the population that represents the least Euclidean distance found so far. Record the personal best
in the population that represents the least Euclidean distance found so far. Record the personal best  for each bit along its previous values.
for each bit along its previous values.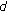 th side of the bit string of particle
th side of the bit string of particle 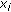 , compute bits velocity using following PSO velocity update equation:
, compute bits velocity using following PSO velocity update equation: 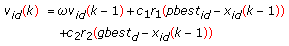
 .
.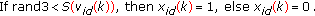

 performance comparison of
performance comparison of  system.
system.
 versus
versus  performance comparison of
performance comparison of  system for 4-QAM demodulator.
system for 4-QAM demodulator.
 performance comparison of
performance comparison of  system for 16-QAM demodulator.
system for 16-QAM demodulator.
 performance comparison of
performance comparison of  system for 64-QAM demodulator.
system for 64-QAM demodulator.
 ) performance with the number of iterations fixed at
) performance with the number of iterations fixed at  for
for  system.
system.
 for
for  system.
system.
 for
for  system.
system.