- Research Article
- Open access
- Published:
An Information-Theoretic Approach for Energy-Efficient Collaborative Tracking in Wireless Sensor Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 641632 (2010)
Abstract
The problem of collaborative tracking of mobile nodes in wireless sensor networks is addressed. By using a novel metric derived from the energy model in LEACH (W.B. Heinzelman, A.P. Chandrakasan and H. Balakrishnan, Energy-Efficient Communication Protocol for Wireless Microsensor Networks, in: Proceedings of the 33rd Hawaii International Conference on System Sciences (HICSS '00), 2000) and aiming at an efficient resource solution, the approach adopts a strategy of combining target tracking with node selection procedures in order to select informative sensors to minimize the energy consumption of the tracking task. We layout a cluster-based architecture to address the limitations in computational power, battery capacity and communication capacities of the sensor devices. The computation of the posterior Cramer-Rao bound (PCRB) based on received signal strength measurements has been considered. To track mobile nodes two particle filters are used: the bootstrap particle filter and the unscented particle filter, both in the centralized and in the distributed manner. Their performances are compared with the theoretical lower bound PCRB. To save energy, a node selection procedure based on greedy algorithms is proposed. The node selection problem is formulated as a cross-layer optimization problem and it is solved using greedy algorithms.
1. Introduction
Wireless sensor networks (WSNs), which normally consist of hundreds or thousands of sensor nodes each capable of sensing, processing, and transmitting environmental information, are deployed to monitor certain physical phenomena or to detect and track certain targets in an area of interests [1]. The issue of tracking moving targets in WSNs has received significant attention in recent years [2–4]. As any other algorithm designed for sensor networks, a tracking algorithm should be: (1) self-organizing, i.e. it should not depend on global infrastructure; (2) energy efficient, i.e. it should require little computation and, especially, communication; (3) robust, i.e. it should not depend on noise and movement of the target; (4) accurate, i.e. it should work with accuracy and precision in various environments, and should not depend on sensor-to-sensor connectivity in the network; (5) reliable, i.e. it should be tolerant to node failures.
Tracking a target in sensor networks is mainly challenging regardless of the energy consumption due to resource-constrained features of such a network. The minimization of energy consumption for a sensor network with target activities is complicated since target estimation involves collaborative sensing and communication between different nodes. The problem of selecting the best nodes for tracking a target in a distributed wireless sensor network was investigated since [5].
The main idea is for a network to determine participants in a sensor collaboration by dynamically optimizing the utility function of data for a given cost of communication and computation.
Previous research [6–9] has focused on information-theoretic node selection approaches, that is, on heuristics to select an informative sensor such that the fusion of the selected sensor observation with the prior target location distribution would yield on average the greatest reduction in the entropy of the target location distribution. In [6], the sensor node which will result in the smallest expected posterior uncertainty of the target state is chosen as the next node to contribute to the movement decision. Specially, minimizing the expected posterior uncertainty is equivalent to maximizing the mutual information between the sensor node output and the target state [6]. In [7], an entropy-based sensor selection heuristic is proposed for target localization in which a sensor node is chosen at each step and the observation of that node is incorporeted into the target location distribution using sequential Bayesian filering. Instead, the main idea underlying our approach is that the heuristics select an informative sensor such that the fusion of the selected sensor observation with the prior target location distribution would yield to minimize the overall energy consumption in a cluster while maximizing the mutual information between the sensor node observation and the target state in order to improve the quality of the tracking data. We show that properly selected nodes to collect measurements in a cluster head, we can save energy to maximize the sensor network lifetime, and we will compare our node selection algorithm with that of Kaplan [8, 9].
1.1. Main Contribution
The main contributions are as follows.
-
(i)
By using the energy model in [10], we propose a novel energy-based metric to evaluate the energy consumption of node selection algorithms in a cluster of sensor nodes.
-
(ii)
We formulate the node selection problem as a cross-layer optimization problem and determine the optimal solution by greedy algorithm.
-
(iii)
We compare the proposed node selection algorithms with the existing literature.
-
(iv)
We implement distributed tracking algorithms using particle filter method and we compare them with the existing literature.
Preliminary results of this work were published in the author references [11]. The remainder of this paper is organized as follows: in Section 1.2 we describe the existing work. Section 2 provides the preliminary information by describing the model of the overall system, by introducing the energy-based metrics. Section 3 provides a concise review of some basic concepts and statistical model of the nonlinear dynamical system. Section 4 describes the tracking algorithms and formulates the distributed tracking problem introducing a node selection rule. In Section 5 we describe the optimization problem and provide solutions. Section 6 discusses the performances of proposed algorithms, while in Section 7, we draw the main conclusions.
1.2. Related Work
Many criteria influence the design of energy-efficient tracking approaches, and a wide range of schemes have been proposed. This Section is devoted to provide an overview of existing energy-efficient techniques for tracking a target in a wireless sensor network.
Generally, the hierarchical structures include tree-based, cluster-based, and prediction-based structures. The tree-based approaches [12–15] use a hierarchy tree to represent the sensors and record information about presence of the objects being detected by the sensors. Kung and Vlah [12] propose STUN (Scalable Tracking Using Networked Sensors), a scalable tracking architecture that employs hierarchical structure to allow the system to handle a large number of tracked objects. Additionally to the tree, Lin and Tseng [13] consider an in-network moving object tracking in a sensor network, consisting of two operations: location update and query. The drawback is the building of the tree as the target moves. Zhang and Cao [14, 15] propose DCTC (Dynamic Convoy Tree-Based Collaboration). They introduce a message-pruning tree structure called convoy tree, which is dynamically configured to add and prune some nodes as the target moves and the tracking problem is formalized as a multiple objective optimization problem. The solution to the problem is a convoy tree sequence with high tree coverage and low energy consumption. Building such a convoy tree sequence requires global network information, and reconfiguration and maintenance of a convoy tree incurs considerable computational and communication overhead. As a result, the tree-based approaches are usually centralized and applied in the deployment phase of sensor networks.
Wang et al. [16] and Chen et al. [17] propose cluster-based tracking schemes. They envision a hierarchical sensor network that is composed of (a) a static backbone of sparsely placed position-aware sensors which will assume the role of a cluster head (CH) upon triggered by certain signal events and (b) moderately to densely populated low-end sensors whose function is to provide sensor information to CHs upon request. In these schemes, sensors are grouped into clusters either statically or dynamically (upon detection of the target in the vicinity), and a cluster head collects information from its cluster members and determines the target location using either the trilateration technique [16] or the Voronoi diagram-based approach [17]. Both localization approaches aim to determine the exact location of the target at the expense of considerable computational overhead because of the potentially high number of nodes in the cluster.
From the topology perspective, the tracking approaches could use a global or local knowledge about the location of every node in the network. As opposed to the tree-based schemes [12–15] that use a global information, the cluster-based schemes [16, 17] rely on local topology knowledge to limit the scope of target's location updates.
As to the signal processing, the tracking approaches can be classified as centralized or distributed. Usually the tree-based schemes are centralized approaches, while the cluster-based schemes are distributed schemes in which the cluster head is the leader node in the processing. The works in [13, 18] are centralized approaches, while those in [3, 4, 14, 16, 19] are distributed approaches.
As defined in [20] the sensor management is the process of dynamically retasking sensors in response to an evolving environment. The goal of sensor management is to choose actions for individual sensors dynamically so as to maximize overall network utility. In a tracking task the sensor management addresses the problem of choosing informative sensors needed to obtain information about the target state and therefore maximize the network lifetime. Based on the collaboration, the existing approach of target tracking can be classified in information-driven and information-based. Zhao et al. [19] propose IDSQ (Information Driven Sensor Querying), in which the selection of the best node is based on a Mahalanobis distance that leads to a heuristic method favoring the sensors whose Euclidean distance to the target is small. In [7–9] the node selection problem has been addressed using an information-based approach. The main idea behind this approach is to optimize a utility function, representing the location accuracy, using entropy-based metrics.
As will be discussed in detail in the next sections, the main idea underlined our proposed information-theoretic approach is to optimize an utility function representing the overall energy in a cluster, using energy-based metrics, jointly to the mutual information between the sensor node observation and the target state.
2. System Model
We make the following assumptions about the sensor network. First, the network is composed of a single gateway (sink) node and multiple sources. Next, the network is modeled as a combination of  a static backbone of sensor nodes aware of their position which assume the role of a cluster head and
a static backbone of sensor nodes aware of their position which assume the role of a cluster head and  randomly distributed low-end sensors which sense a moving target and report data to CHs upon request. Finally, we assume that the network is composed of dynamic clusters, depending on the predicted target trajectory (see Figure 1). Indeed, to facilitate collaborative data processing in target tracking sensor networks, usually the sensors are aggregated in clusters, led by a CH.
randomly distributed low-end sensors which sense a moving target and report data to CHs upon request. Finally, we assume that the network is composed of dynamic clusters, depending on the predicted target trajectory (see Figure 1). Indeed, to facilitate collaborative data processing in target tracking sensor networks, usually the sensors are aggregated in clusters, led by a CH.
The details of the clustering algorithm are out of the aim of this paper. In the following we will limit ourselves to consider only the intra-cluster communication issues. We only highlight that to waste less power the cluster-head should be selected with a shorter distance to the target. The active sensor of the cluster, which will assume the role of cluster head, will predict the trajectory of a target by means of a particle filter based on the history of the target location and some observations which come from some active sensors in the cluster. These sensors in the cluster are chosen to minimize the overall energy consumption.
2.1. Energy Model
The main concept underlying the proposed energy efficient tracking algorithm is that the CH should select the active neighbors with the goal of reducing the total energy needed to transmit its data through its radio. In this subsection we introduce two metrics based on energy consumption for a tracking task.
2.1.1. Energy-Based Metric
To describe the energy consumption of a tracking algorithm for power-constrained sensor network, we use the energy model for wireless sensor networks introduced by Heinzelman et al. [10]. The energy consumption per bit at the physical layer is

where  is a distance independent term that takes into account overheads of transmitter electronics (PLLs, VCOs, bias currents, etc.) and digital processing;
is a distance independent term that takes into account overheads of transmitter electronics (PLLs, VCOs, bias currents, etc.) and digital processing;  is a distance independent term that takes into account overheads of receiver electronics; finally
is a distance independent term that takes into account overheads of receiver electronics; finally  accounts for the radiated power necessary to transmit one bit over a distance
accounts for the radiated power necessary to transmit one bit over a distance  between source and destination, where
between source and destination, where  is the exponent of the path loss (
is the exponent of the path loss ( ).
).
According to [21] we assume that  . Hence, given
. Hence, given  bits of data, the overall energy consumption to transmit the packet of
bits of data, the overall energy consumption to transmit the packet of  bit between two nodes at a distance
bit between two nodes at a distance  with a given received SNR can be expressed as
with a given received SNR can be expressed as

where  [Joule/bit] is the energy needed by the transceiver circuitry to transmit or receive one bit and
[Joule/bit] is the energy needed by the transceiver circuitry to transmit or receive one bit and  [Joule
[Joule is a constant which represents the energy needed to transmit one bit over a distance
is a constant which represents the energy needed to transmit one bit over a distance  to achieve an acceptable SNR at the destination.
to achieve an acceptable SNR at the destination.
This model assumes that the energy consumption is dominated by the radio communication rather than the computation. We refer to (2) as the energy-based metric.
2.1.2. Residual Energy-Based Metric
According to [22, 23] we propose another metric combining energy and remaining energy at nodes. Hence, if we refer to a link ( ,
, ) with distance
) with distance  , the overall energy consumption to transmit a
, the overall energy consumption to transmit a  -bit packet between the node
-bit packet between the node  and node
and node  at a distance
at a distance  with a given received SNR can be expressed as
with a given received SNR can be expressed as

where the first addend  is the remaining energy at node
is the remaining energy at node  and the second addend is the transmission energy required for the node
and the second addend is the transmission energy required for the node  to transmit
to transmit  bits to its neighboring node
bits to its neighboring node  . We refer to (3) as the residual energy-based metric.
. We refer to (3) as the residual energy-based metric.
2.2. Network Model
In our analysis, we consider a network composed of randomly deployed sensor nodes which sense a moving target and forward the information into a position-aware sensor which acts as a data gathering node. The network is divided into  clusters each having
clusters each having  nodes. Each sensor is equipped by a low data rate radio interface. The position-aware sensors are equipped by two radio transmitters, that is, a low data rate transmitter to communicate with the sensors, and a high rate wireless interface for CH-CH communication.
nodes. Each sensor is equipped by a low data rate radio interface. The position-aware sensors are equipped by two radio transmitters, that is, a low data rate transmitter to communicate with the sensors, and a high rate wireless interface for CH-CH communication.
In our analysis, we assume to know the position of the CH (static node) and to estimate the distance of each neighbor with respect the CH. Many types of sensors provide measurements that are function of the relative distance between the sensor and the sensed object (e.g., acoustic sensors, sonar, etc.). We consider a common example, newly in [4], where sensors measure the power of a radio signal emitted by the object.
Therefore, we assume the log-normal shadowing model for the channel and we suppose that the power of a received signal decreases exponentially with the propagation distance:

where  is the received power at a receiver at distance
is the received power at a receiver at distance  from a transmitter,
from a transmitter,  is the transmitted power at a reference distance
is the transmitted power at a reference distance  ,
,  is the path loss exponent
is the path loss exponent  , and
, and  is the shadow fading component, with
is the shadow fading component, with  Gaussian distribution
Gaussian distribution  .
.
Hence, the distance from the  th sensor of the cluster to the CH can be estimated as
th sensor of the cluster to the CH can be estimated as  , where
, where  is the received signal strength in the sensor, and
is the received signal strength in the sensor, and  is the (unknown) strength of the signal from the sensor.
is the (unknown) strength of the signal from the sensor.
3. Basic Concepts and Theoretical Bound
We begin our analysis with a concise review of some basic concepts and the models of a nonlinear dynamical system.
We consider the state estimation of a nonlinear dynamical system:

where,  is the discrete time index;
is the discrete time index;  is the state vector;
is the state vector; is the observation vector;
is the observation vector;  is the zero-mean white Gaussian process noise with nonsingular covariance matrix
is the zero-mean white Gaussian process noise with nonsingular covariance matrix  ;
;  is the zero-mean white Gaussian measurement noise independent of
is the zero-mean white Gaussian measurement noise independent of  with nonsingular covariance matrix
with nonsingular covariance matrix  ;
; and
and  are the (in general) nonlinear functions.
are the (in general) nonlinear functions.
The functions  and
and  may depend on time
may depend on time  . Further we assume that the initial state
. Further we assume that the initial state  has a known probability density function
has a known probability density function  . Let
. Let  and
and  be operators of the first- and second-order partial derivatives, respectively,
be operators of the first- and second-order partial derivatives, respectively,

Using this notation, the Fisher Information Matrix (FIM) given by [24] for this problem can be written as

where  represents the joint probability density of
represents the joint probability density of  In the following sections
In the following sections  is denoted by
is denoted by  for brevity. The following proposition [25] gives an efficient method for computing
for brevity. The following proposition [25] gives an efficient method for computing  recursively.
recursively.
Proposition 1.
The sequence  of Fisher information submatrices for estimating state vectors
of Fisher information submatrices for estimating state vectors  obeys the recursion:
obeys the recursion:

where

3.1. Time-Invariant Model
We assume that the functions  and
and  are time invariant (independent of
are time invariant (independent of  ). Using this assumption and according to [25], the matrices
). Using this assumption and according to [25], the matrices  do not depend on
do not depend on  and additionally for
and additionally for 

 , the matrix
, the matrix  converges to a matrix
converges to a matrix  , which is given as a solution to the following equation:
, which is given as a solution to the following equation:

Note that (10) is a discrete-time algebraic Riccati equation. A common form of the Riccati equation is obtained if the recursion (8) is equivalently written as

which can be easily proved by simple algebraic manipulations. Then, put  =
=  =
=  .
.
3.2. Model for State Estimation of a Nonlinear Dynamical System
The problem of estimating the state vector of a nonlinear dynamical system (i.e., single target tracking) can be formulated as follows. The state and the observations of the target of interest are assumed to follow the following model:

where  ,
,  ,
,  , and
, and  were introduced in Section 3. The matrices
were introduced in Section 3. The matrices  ,
,  , and
, and  are independent of the state vector whereas
are independent of the state vector whereas  is a function dependent of the state vector
is a function dependent of the state vector  . From the assumption that the noises
. From the assumption that the noises  and
and  are Gaussian with zero mean and invertible covariances matrices
are Gaussian with zero mean and invertible covariances matrices  and
and  respectively, and that the elements of the noise vectors
respectively, and that the elements of the noise vectors  and
and  are independent and identically distributed (IID) it follows that the conditional densities can be written as
are independent and identically distributed (IID) it follows that the conditional densities can be written as

In the derivation above, we assume that the system model is time-invariant, implying that  and
and  . Consequently, from (13), we have
. Consequently, from (13), we have

where  and
and  are constants, and
are constants, and

4. Tracking Algorithms
The aim of this section is to describe the proposed cross-layer predictive tracking algorithm and to discuss that it can consistently reduce the energy consumption on sensors with respect to existent one-level location algorithms. As stated above, in this paper we use sequential Monte Carlo (SMC) approaches, also known as particle filtering [26, 27], for tracking a moving target while Kaplan [8, 9] estimates the target location using a Kalman filter based on the current measurement at a sensor and the past history at other sensors. The particle filter provides simulation-based solutions to estimate the posterior distribution of nonlinear discrete time dynamic models. The main idea of particle filtering is to represent the required posterior distribution density by a set of random samples with associated weights and to compute estimates based on these samples and weights, updating them recursively in time using the sequential importance sampling (SIS) algorithm. As the number of samples becomes very large, the SIS filter approaches the optimal Bayesian estimate. A common problem with the SIS particle filter is the degeneracy phenomenon, since after a few iterations all the particles, with exception of one of them, will have negligible weight. Because of this phenomenon, resampling techniques are used to eliminate particles that have small weights and to concentrate on particles with large weights. The particle filter using sequential importance resampling (SIR) techniques is known as bootstrap filter or SIR particle filter (PF). Therefore, in the following we use the SIR filter to achieve the tracking task. Moreover, we compare the performance of bootstrap filter with the unscented particle filter. Indeed, unfortunately even when resampling schemes are used, degeneracy may still be a problem. Using the prior distribution as importance distribution could lead to the degeneracy problem of the particles because the most recent observations are ignored. Samples may eventually collapse to a single point if, during the resampling stage, samples with high importance weights are duplicated an extremely large number of times. There have been numerous proposals to rectify the degeneracy problem improving the performance of the SIR particle filter [28]. Notable techniques include local linearization using the extended Kalman filter (EKF) [29, 30] or the unscented Kalman filter (UKF) to estimate the importance distribution [31]. A particle filter which uses UKF to generate the importance distribution is referred as unscented particle filter (UPF) or sigma-point particle filter [31].
In this paper, we analyze the energy efficiency of particle filtering looking at collaborative and distributed schema for tracking a moving target.
4.1. Node Selection
We formulate the problem of distributed tracking as a sequential Monte Carlo estimation problem. Assume that the state of a target we wish to estimate is  . Each new sensor measurement
. Each new sensor measurement  is combined with the current estimate
is combined with the current estimate  , hereafter called belief state, to form a new belief state of the target
, hereafter called belief state, to form a new belief state of the target  . The problem of selecting a sensor in order to provide greatest improvement to the estimation at the lowest cost becomes an optimization problem. We let
. The problem of selecting a sensor in order to provide greatest improvement to the estimation at the lowest cost becomes an optimization problem. We let  be all measurements that have already been used at time
be all measurements that have already been used at time  in the inference of the current belief state and refer the sensor which holds the belief state as the leader node. The objective function for this optimization problem can be defined as a mixture of both information gain and cost. In the remainder of the section we consider the information gain, while the computation of the energy consumption cost is discussed in the next section.
in the inference of the current belief state and refer the sensor which holds the belief state as the leader node. The objective function for this optimization problem can be defined as a mixture of both information gain and cost. In the remainder of the section we consider the information gain, while the computation of the energy consumption cost is discussed in the next section.
The information gain to select the sensor  can be defined as
can be defined as  , where
, where  is the new measurement from sensor
is the new measurement from sensor  at time
at time  . The utility function can be defined as the uncertainty of the target state reduced by the additional measurements
. The utility function can be defined as the uncertainty of the target state reduced by the additional measurements  [6], that is,
[6], that is,  . Furthermore, the utility function can be defined with the mutual information
. Furthermore, the utility function can be defined with the mutual information  , which means the information of
, which means the information of  conveyed by the new measurements
conveyed by the new measurements  [18].
[18].
The utility function based on the entropy is difficult to compute in practice since we need to have the measurement before deciding how useful it is. Instead of the true a posteriori distribution, a more practical alternative is to compute the entropy based on the expected posterior distribution. In the ideal case when a real new measurement  is available, the new belief or posterior is evaluated using sequential Bayesian filtering
is available, the new belief or posterior is evaluated using sequential Bayesian filtering  Without having the data
Without having the data  , we need to compute the expected posterior distribution
, we need to compute the expected posterior distribution  We can estimate the measurement
We can estimate the measurement  from the predicted belief and compute the expected likelihood function
from the predicted belief and compute the expected likelihood function  Then, the expected posterior belief can be defined as follows:
Then, the expected posterior belief can be defined as follows:

The entropy of expected posterior distribution can be compute based on the discrete belief state  [32], where
[32], where  is the importance sampling weight in the resampling step of the particle filters and
is the importance sampling weight in the resampling step of the particle filters and  represents the number of weights namely the number of particles. According to (16), the expected posterior belief for sensor
represents the number of weights namely the number of particles. According to (16), the expected posterior belief for sensor  can be represented by the discrete belief state
can be represented by the discrete belief state  with the weights
with the weights  given by
given by

The entropy of the discrete belief state  can be computed by
can be computed by

This expected posterior entropy can be used as a criteria to select the best among the sensor candidates to maximize the information gain. The objective function expected to improve the estimation of the target is given by

where  indicates the set, with cardinality
indicates the set, with cardinality  , of active nodes in the cluster that receive from the CH a signal exceeding a predetermined RSS threshold.
, of active nodes in the cluster that receive from the CH a signal exceeding a predetermined RSS threshold.
5. Energy Efficient Tracking
Let us consider the following location discovery protocol for a given snapshot. With reference to Figure 2, the target  periodically sends discovery signal, with period
periodically sends discovery signal, with period  , to all the sensors of the network. We indicate with
, to all the sensors of the network. We indicate with  the set of active neighbor nodes that maximize the utility function as in (19). The subset
the set of active neighbor nodes that maximize the utility function as in (19). The subset  of desired anchor nodes needed for the localization algorithm will be chosen so as to minimize the energy consumption of the location discovery protocol. Then, each node
of desired anchor nodes needed for the localization algorithm will be chosen so as to minimize the energy consumption of the location discovery protocol. Then, each node  transmits the sensing information (the distance of the node
transmits the sensing information (the distance of the node  from the target) to the CH which processes the data and updates the current target location.
from the target) to the CH which processes the data and updates the current target location.
According to metric (2), the energy cost in the communication with one sensor  is given by
is given by

where  represents the bit rate (bit/s) between the CH and the neighbor
represents the bit rate (bit/s) between the CH and the neighbor  ,
,  (s) is the period between two consecutive discovery signal of the target,
(s) is the period between two consecutive discovery signal of the target,  and
and  are, respectively, the distance of the node i from the CH and the target, and
are, respectively, the distance of the node i from the CH and the target, and  is the number of desired neighbors of the CH. Finally, in (20)
is the number of desired neighbors of the CH. Finally, in (20)  represents the energy needed at the neighbors to receive one bit. In the energy cost we have omitted the energy consumption in the path between the target and the CH due to the calibration phase of the clustering and we have considered only the communication between each node of the cluster and its cluster head.
represents the energy needed at the neighbors to receive one bit. In the energy cost we have omitted the energy consumption in the path between the target and the CH due to the calibration phase of the clustering and we have considered only the communication between each node of the cluster and its cluster head.
On the other hand, according to the metric (3) and the location discovery protocol herein discussed, the energy cost in the communication with the sensor  , based on (20), is given by
, based on (20), is given by

The total utility function, for all nodes in the set  , is given by
, is given by

As stated above, our objective is to select the optimal subset  which maximizes the total utility function in (22), subject to a constraint of the cardinality
which maximizes the total utility function in (22), subject to a constraint of the cardinality  of said subset. This gives formally the following objective function and associated constraint:
of said subset. This gives formally the following objective function and associated constraint:

A unique solution to this problem exists, since the objective function is strictly concave and the feasible set is convex. The solution of this optimization problem is illustrated in the following subsections.
5.1. The Solution in the Static Scenario
To find the optimal solution for such problem it is theoretically possible to enumerate the solutions and evaluate each with respect to the stated objective. However, from a practical perspective, it is infeasible to follow such a strategy because the number of combinations grows exponentially with the size of problem.
Indeed, if we formulate our combinatorial optimization problem as an integer linear programming problem, the computational complexity consists of enumerating all the  -node subsets,
-node subsets,  , and adding the computational complexity of the assignment problem,
, and adding the computational complexity of the assignment problem,  . In such cases, heuristic methods are usually employed to find good, but not necessarily guaranteed optimal solutions. More than one technique is applicable, that is, integer linear programming, graph theory, genetic algorithms, and greedy heuristics; see [33] for further details. Here we adopt the meta-heuristic greedy randomized adaptive search procedures (GRASP) [34], in which each iteration consists of two phases, a construction phase, in which a feasible solution is produced, and a local search phase, in which a local optimum in the neighborhood of the constructed solution is sought. The best overall solution is kept as the result.
. In such cases, heuristic methods are usually employed to find good, but not necessarily guaranteed optimal solutions. More than one technique is applicable, that is, integer linear programming, graph theory, genetic algorithms, and greedy heuristics; see [33] for further details. Here we adopt the meta-heuristic greedy randomized adaptive search procedures (GRASP) [34], in which each iteration consists of two phases, a construction phase, in which a feasible solution is produced, and a local search phase, in which a local optimum in the neighborhood of the constructed solution is sought. The best overall solution is kept as the result.
The implementation of the optimal Greedy node selection procedure is described in Algorithm 1. It provides the set of desired nodes  , new set of candidate nodes in the cluster
, new set of candidate nodes in the cluster  , total energy of the desired set
, total energy of the desired set  , last node selected in the current snapshot node, energy of this node
, last node selected in the current snapshot node, energy of this node  , and time
, and time  .
.
Algorithm 1: Greedy random node selection.
Synopsis: [ ] = Greedy(
] = Greedy( ).
).
Given: Set of nodes in the cluster  number of desired
number of desired
nodes 
Output: Set of desired nodes  new set of candidate
new set of candidate
nodes in the cluster  total energy of the desired set
total energy of the desired set
 last node selected in the current snapshot node,
last node selected in the current snapshot node,
energy of this node  time
time 
Initialize the candidate set:


Initialize the objective function:

Randomly select a candidate node 


while  do
do
for each  do
do
if  then
then


end if
end for





end while

5.2. The Solution in the Dynamic Scenario
In previous sections, we have considered the static version of the problem, namely, a snapshot model. In this section we extend the Greedy node selection procedure over multiple snapshots, so that we can select active nodes for the next measurement intervals. In a dynamic scenario, due to the target mobility, the distance  in (20) varies with the time and hence the total utility function (22) is a function of time
in (20) varies with the time and hence the total utility function (22) is a function of time  .
.
In the dynamic version of the optimization problem we use the Dynamic Programming [35], that is based on the idea of breaking down the problem into stages at which the decisions take place and finding a recurrence relation that takes us backward from one stage to the previous stage. For this purpose, a branch-and-bound method is developed, in which the branch refers to the partitioning process into stages, that are repeatedly decomposed until a solution is found or infeasibility is proved, and the bound refers to lower bounds that are used to construct a proof of optimality without exhaustive search. We introduce an energy bound as in the following definition.
Definition 1.
The energy bound is the maximum energy referred to the energy costs associated to the nodes selected in the previous their snapshot.
Algorithm 2 shows pseudocode of an efficient implementation of our branch-and-bound approach. It provides the set of desired nodes  , the new set of candidate nodes in the cluster
, the new set of candidate nodes in the cluster  and the total energy of the desired set
and the total energy of the desired set  . Note that the total utility function of the desired set can be obtained from the following equation:
. Note that the total utility function of the desired set can be obtained from the following equation:

assuming that the nodes of the cluster have an even remaining energy, that is,

Finally, in Algorithm 3 has been reported the overall tracking algorithm which combines the node's selection procedures with the particle filtering algorithm.
Algorithm 2: Branch and bound algorithm.
Synopsis:  = BranchBound(
= BranchBound( ).
).
Given: Number of desired nodes  , candidate nodes
, candidate nodes
set of the cluster  , energy bound
, energy bound  , node related
, node related
to the energy bound  .
.
Output: Set of desired nodes  , new set of candidate
, new set of candidate
nodes in the cluster  , total energy of the desired set
, total energy of the desired set

Initialize the candidate set:

Initialize the objective function:

while  do
do
for each  do
do
if  then
then
break
else


end if
end for



end while

Algorithm 3: Tracking algorithm.
Synopsis:  DynamicSelection(
DynamicSelection( ,
, ).
).
Output: Set of desired nodes  , new set of candidate
, new set of candidate
nodes in the cluster  ,total energy of the desired
,total energy of the desired
set  .
.
 The initial leader node does the following step:
The initial leader node does the following step:
(a) draw initial samples  of the target
of the target
from the prior information; (b) update the belief state
 by the sensor fusion algorithm
by the sensor fusion algorithm
based on the new measurement  at the leader node
at the leader node
in the set  ; (c) compute the expected posterior
; (c) compute the expected posterior
belief state  for each neighboor node
for each neighboor node 
with the weights  computed by (17); (d) compute
computed by (17); (d) compute
the entropy of the expected posterior belief state
 for each neighboor node
for each neighboor node  by(18)
by(18)
and determine the next best sensor, say (b) in the set
 .
.
( )
)  Greedy(
Greedy( ,
, )
)
( ) Loop until time runs out:
) Loop until time runs out:
( ) Prediction step and Update step of particle
) Prediction step and Update step of particle
filtering to estimate the target's trajectory.
( ) Update the candidate set
) Update the candidate set  during the dynamic of
during the dynamic of
the target.
( )
) BranchBound(
BranchBound(
6. Performance Evaluation
In this section, we investigate the performance of the overall target tracking system looking first at the node selection algorithm and then at the tracking algorithm and energy consumption.
6.1. Optimal Node Selection
In the following we compare our greedy node selection algorithm with the Kaplan algorithm in [8, 9]. The only difference between [8] and [9] is that in [8] the global topology knowledge is assumed, in which every active node reaches the entire network, while in [9] the only knowledge of the relative position to the target and the active nodes from the previous snapshot is required. Table 1 shows the computational complexity of the proposed node selection algorithm and the Kaplan algorithm for each iteration. Hence, the computational complexity for all iterations is given by the following.
-
(i)
Greedy computational complexity:
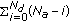 =
= 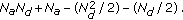
-
(ii)
Kaplan computational complexity:
 =
= 
Indeed, in the above analysis we have omitted the computational complexity of the initialization step of the Simplex algorithm, in which two nodes are chosen by exhaustive search. Definitely, due to computational complexity and because the simplex does not always find the global minimum, our approach outperforms the Kaplan algorithm.
As stated in Section 4.1, the node selection procedure is combined with the maximization of the utility function. Hence in our analysis the computational complexity of the problem in (19) needs to be considered, namely, O( ) where
) where  is the number of weights. Finally, the computational complexity for all iterations is given by
is the number of weights. Finally, the computational complexity for all iterations is given by  .
.
In Table 2 the results of a runtime measurement are illustrated, conducted on a system with AMD Opteron XP Processor 250, approximately 2400 MHz frequency, and 4,00 GB RAM. Table 2 provides the execution time of the node's selection algorithm versus the number of desired nodes using  equal to 10 and
equal to 10 and  equal to 100.
equal to 100.
6.2. Estimation Bound for Range-Based Tracking
In this paper we assume as dynamic model of the target the constant velocity model [36]. Hence, denoting by  the state vector (coordinates along
the state vector (coordinates along  ,
,  axes and the velocities) of a target, the state-space model is given by
axes and the velocities) of a target, the state-space model is given by

where  denotes the motion noise and
denotes the motion noise and  the length of the measurement interval.
the length of the measurement interval.
Additionally, as observation model of the measurements, we use the log-normal shadowing model [37]. Hence, let  be the fixed position of sensor
be the fixed position of sensor  and let
and let  be the distance between the sensor
be the distance between the sensor  and the target; in a logarithmic scale the target-originated measurements are modeled by
and the target; in a logarithmic scale the target-originated measurements are modeled by

where the measurement noise  accounts for the shadowing effects and other uncertainties. The noise
accounts for the shadowing effects and other uncertainties. The noise  is assumed to be a zero-mean Gaussian with covariances values
is assumed to be a zero-mean Gaussian with covariances values  , and the sensor noises are assumed uncorrelated;
, and the sensor noises are assumed uncorrelated;  is the transmission power, and
is the transmission power, and  is the path loss exponent.
is the path loss exponent.
Consequently, a straightforward calculation of (15) gives

From (11), the recursion of information matrix can be written as

where

Substituting (30) in (29) the recursion of information matrix is given by

The initial information matrix required for the recursion is calculated from the prior probability density function  . We assume that the initial target state is a Gaussian random variable and
. We assume that the initial target state is a Gaussian random variable and  . Then, if the state is Gaussian with covariance
. Then, if the state is Gaussian with covariance  ,
,  can be recursively computed from the initial condition
can be recursively computed from the initial condition  .
.
6.3. Tracking Accuracy
We implemented the node's selection algorithms and the particle filters in a Matlab simulator. We present simulation results for the scenarios illustrated in Table 3. Figure 3 shows the target trajectories for two different velocities, equal to 0.1 and 0.3 m/s, used in the experiment.
In Figures 4 and 5, we have shown the PCRBs for the position, meaning that the (1,1) and (3,3) elements of  are considered. Furthermore, we compare the PCRB with the root mean square errors of PF and UPF for different numbers
are considered. Furthermore, we compare the PCRB with the root mean square errors of PF and UPF for different numbers  of active nodes. It should be noted that the empirical error curves for the PF and the UPF closely match the theoretical PCRB for the problem considered. This means that the PF and the UPF appear to be efficient sequential estimators of the target state vector. The simulation results provide that the PCRB decreases as the number of active nodes increases. Note that in Figure 4(d), contrarily to the PCRB, the root mean square error of the two filters shows a divergence from the expected decreasing behavior. We believe it is due to the degeneracy phenomenon of particle filters; however, an additional investigation is needed.
of active nodes. It should be noted that the empirical error curves for the PF and the UPF closely match the theoretical PCRB for the problem considered. This means that the PF and the UPF appear to be efficient sequential estimators of the target state vector. The simulation results provide that the PCRB decreases as the number of active nodes increases. Note that in Figure 4(d), contrarily to the PCRB, the root mean square error of the two filters shows a divergence from the expected decreasing behavior. We believe it is due to the degeneracy phenomenon of particle filters; however, an additional investigation is needed.
Figure 6 shows the root-mean-squared error (RMSE) on the position of the target of different filters versus the number of desired nodes using 100 runs. The bootstrap particle filter and the unscented particle filter have been implemented in both centralized and distributed manner using the node selection rules. The performance of the distributed PF (DPF) and distributed UPF (DUPF) is compared with the performance of the distributed sigma-point information filter (DSPIF) from [4]. Confidence intervals are not shown for the sake of clarity.
In Scenario1, nodes are randomly deployed on an area of  and the target speed is 0.1 m/s (see Figure 3(a)). In Figure 6(a) a process variance
and the target speed is 0.1 m/s (see Figure 3(a)). In Figure 6(a) a process variance  equal to 1.0 has been used for the trajectory 3(a). Clearly, the centralized filter PF outperforms the distributed filter DPF in tracking quality because in the distributed algorithms nodes only have local knowledge. Also the RMSE of DUPF is always larger than that for UPF. On the other hand, as we will show, the energy consumption is higher for the centralized approach. Finally, DPF and DUPF outperform DSPIF.
equal to 1.0 has been used for the trajectory 3(a). Clearly, the centralized filter PF outperforms the distributed filter DPF in tracking quality because in the distributed algorithms nodes only have local knowledge. Also the RMSE of DUPF is always larger than that for UPF. On the other hand, as we will show, the energy consumption is higher for the centralized approach. Finally, DPF and DUPF outperform DSPIF.
In Scenario2, nodes are randomly deployed on an area of  and the target speed is 0.3 m/s (see Figure 3(b)). Figure 6(b) illustrates the root-mean-squared error (RMSE) on the position of the target, depending on the number of active nodes in the network. Figure 6(b) shows the RMSE for a process variance
and the target speed is 0.3 m/s (see Figure 3(b)). Figure 6(b) illustrates the root-mean-squared error (RMSE) on the position of the target, depending on the number of active nodes in the network. Figure 6(b) shows the RMSE for a process variance  equal to 1.8. Again the unscented particle filter with 100 particles gives best results than the bootstrap particle filter using 100 particles as it is clear in Figure 6(b). Simulation results indicate a decrease in tracking performance with increase of noise and fast target movement. Note that, in Figure 6(b), the values of the error when the number of desired nodes is equal two are omitted because in this case the filter diverges. Other simulation results that we have not reported, with target velocity equal to 0.5 and 1.0 m/s, show that to estimate the track when the velocity increases a high number of anchor nodes are needed. For each value of
equal to 1.8. Again the unscented particle filter with 100 particles gives best results than the bootstrap particle filter using 100 particles as it is clear in Figure 6(b). Simulation results indicate a decrease in tracking performance with increase of noise and fast target movement. Note that, in Figure 6(b), the values of the error when the number of desired nodes is equal two are omitted because in this case the filter diverges. Other simulation results that we have not reported, with target velocity equal to 0.5 and 1.0 m/s, show that to estimate the track when the velocity increases a high number of anchor nodes are needed. For each value of  , 10000 different random configurations were generated, where, for each configuration, we assume a maximum range between node and target equal to 30 meters, and a maximum range between node and cluster head equal to 10 meters. The DPF and DUPF computational complexity is given by
, 10000 different random configurations were generated, where, for each configuration, we assume a maximum range between node and target equal to 30 meters, and a maximum range between node and cluster head equal to 10 meters. The DPF and DUPF computational complexity is given by  , while the Kaplan computational complexity is given by
, while the Kaplan computational complexity is given by  as the Kalman filter has been used. Particularly, the time to process the bootstrap particle filter with 100 and 500 particles is equal to 1,605 seconds and 8,052 seconds, respectively, with three active nodes, while the time to process the unscented particle filter with 100 particles is equal to 3,281 seconds. In conclusion, the UPF is less computational efficient than the PF but performs a more accurate estimation of the target's position compared to the UPF.
as the Kalman filter has been used. Particularly, the time to process the bootstrap particle filter with 100 and 500 particles is equal to 1,605 seconds and 8,052 seconds, respectively, with three active nodes, while the time to process the unscented particle filter with 100 particles is equal to 3,281 seconds. In conclusion, the UPF is less computational efficient than the PF but performs a more accurate estimation of the target's position compared to the UPF.
6.4. Energy Consumption
Figure 7 shows the energy consumption of node selection algorithms. In Figure 7(a), we compare the energy consumption of the proposed greedy algorithm and Kaplan algorithm as the number of selected nodes increases, using the the residual energy-based metrics defined in (3). Simulation results indicate an increase of the energy consumption with growing number of nodes. We highlight that the rise of the greedy algorithm energy consumption is superlinear using the energy-based metric introduced by Heinzelman in [10] while the rise is linear using our proposed residual energy-based metric. Definitively can be concluded that the greedy selection algorithm outperforms the Kaplan selection algorithm to select the sensors that would give the most prolonged life to the network. In Figure 7(b), RMSE versus energy consumption of PF, DPF, UPF, and DUPF algorithms using greedy selection has been shown.
In conclusion, the energy consumption increases with the number of active nodes; on the other hand the tracking error decreases as the the number of active nodes increases. A tradeoff between the performance and the number of nodes is needed to save energy.
7. Conclusion
The focus of the article was the energy-efficient and collaborative target tracking in wireless sensor networks. The tracking problem was formulated as a cross-layer optimization with the aim of maximizing the total utility function in the cluster. The node selection procedures were integrated into a particle filter and tested on simulated data. The optimal greedy-based algorithm was extended at the real scenario to consider the energy consumption over more measurement intervals. A lower bound was also introduced. The experiments indicate that the proposed approach outperforms the existing algorithms in literature. Extensive simulations showed that the target tracking system yields good accuracy for lower velocity of the target. The tracking performances get worse as the noise and the target velocity increase. The bootstrap particle filter and the unscented particle filter for the centralized and distributed scheme and the distributed sigma-point information filter [4] have been implemented and the accuracies have been compared. Furthermore, we have presented a closed-form derivation of PCRB as a performance criterion, eliciting the influence of the number of active nodes, the channel parameters and the model parameters. The formula has been derived and the tracking protocol has been evaluated for linear dynamic's models and for a nonlinear Gaussian observation's model. Finally, in this study we assumed an intra-cluster communication and limited ourselves to consider a single cluster in which an even energy consumption by the sensor nodes has been assumed. Future work is investigating the implementation of algorithms to report tracking samples to multiple cluster heads.
References
Akyildiz IF, Su W, Sankarasubramaniam Y, Cayirci E: Wireless sensor networks: a survey. Computer Networks 2002, 38: 393-422. 10.1016/S1389-1286(01)00302-4
Ihler AT, Fisher JW III, Moses RL, Willsky AS: Nonparametric belief propagation for self-localization of sensor networks. IEEE Journal on Selected Areas in Communications 2005, 23(4):809-819.
Lee J, Cho K, Lee S, Kwon T, Choi Y: Distributed and energy-efficient target localization and tracking in wireless sensor netwoks. Computer Communications 2006, 29: 2494-2505. 10.1016/j.comcom.2006.02.004
Vercauteren T, Wang X: Decentralized sigma-point information filters for target tracking in collaborative sensor networks. IEEE Transactions on Signal Processing 2005, 53(8):2997-3009.
Estrin D, Govindan R, Heidemann J, Kumar S: Next century challenges: Scalable coordination in sensor networks. Proceedings of 5th ACM/IEE International Conference on Mobile Computing and Networking (MobiCom '99), August 1999, Seattle, Washington 263-270.
Ertin E, Fisher JW, Potter LC: Maximum mutual information principle for dynamic sensor query problems. Proceedings of the International Workshop on Information Processing in Sensor Networks (IPSN '03), April 2003, Palo Alto, Calif, USA 405-416.
Wang H, Pottie G, Yao K, Estrin D: Entropy-based sensor selection heuristic for target localization. Proceeding of the 3rd International Symposium on Information Processing in Sensor Networks (IPSN '04), April 2004, Berkeley, Calif, USA 36-45.
Kaplan LM: Global node selection for localization in a distributed sensor network. IEEE Transactions on Aerospace and Electronic Systems 2006, 42(1):113-135. 10.1109/TAES.2006.1603409
Kaplan LM: Local node selection for localization in a distributed sensor network. IEEE Transactions on Aerospace and Electronic Systems 2006, 42(1):136-146. 10.1109/TAES.2006.1603410
Heinzelman WB, Chandrakasan AP, Balakrishnan H: Energy-Efficient Communication Protocol forWireless Microsensor Networks. Proceedings of 33rd Hawaii International Conference on System Sciences (HICSS '00), January 2000, Maui, Hawaii
Arienzo L, Longo M: Energy-efficient tracking strategy for wireless sensor networks. Proceeding of the 5th IEEE International Conference on Mobile Ad-Hoc and Sensor Systems (MASS '08), September 2008, Atlanta, Ga, USA 595-602.
Kung HT, Vlah D: Efficient location tracking using sensor networks. Proceedings of the IEEE Wireless Communications & Networking Conference (WCNC '03), March 2003
Lin C-Y, Tseng Y-C: Structures for in-network moving object tracking in wireless sensor networks. Proceeding of the 1st International Conference on Broadband Networks (BroadNets '04), October 2004 718-727.
Zhang W, Cao G: DCTC: dynamic convoy tree-based collaboration for target tracking in sensor networks. IEEE Transactions on Wireless Communications 2004, 3(5):1689-1701. 10.1109/TWC.2004.833443
Zhang W, Cao G: Optimizing tree reconfiguration for mobile target tracking in sensor networks. Proceedings of the 23rd Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '04), 2004 4: 2434-2445.
Wang Q, Chen W-P, Zheng R, Lee K, Sha L: Acoustic target tracking using tiny wireless sensor devices. Proceedings of the International Workshop on Information Processing in Sensor Networks (IPSN '03), 2003 642-657.
Chen W-P, Hou JC, Sha L: Dynamic clustering for acoustic target tracking in wireless sensor networks. IEEE Transactions on Mobile Computing 2004, 3(3):258-271. 10.1109/TMC.2004.22
Liu J, Reich J, Zhao F: Collaborative in-network processing for target tracking. EURASIP Journal on Applied Signal Processing 2003, 2003(4):378-391. 10.1155/S111086570321204X
Zhao F, Shin J, Reich J: Information-driven dynamic sensor collaboration for tracking applications. IEEE Signal Processing Magazine 2002, 19(2):61-72. 10.1109/79.985685
Kreucher CM, Hero AO, Kastella KD, Morelande MR: An Information-based approach to sensor management in large dynamic networks. Proceeding of IEEE 2007, 95: 978-999.
Heinzelman WB, Chandrakasan AP, Balakrishnan H: An application-specific protocol architecture for wireless microsensor networks. IEEE Transactions on Wireless Communications 2002, 1(4):660-670. 10.1109/TWC.2002.804190
Chang JH, Tassiulas L: Energy conserving routing in wireless ad-hoc networks. Proceedings of the 19th Annual Conference on Computer Communications (INFOCOM '00), March 2000, Tel Aviv, Israel 1: 22-31.
Stojmenovic I, Lin X: Power-aware localized routing in wireless networks. IEEE Transactions on Parallel and Distributed Systems 2001, 12(11):1122-1133. 10.1109/71.969123
Van Trees H: Detection, Estimation, and Modulation Theory, Part I. John Wiley & Sons, New York, NY, USA; 1968.
Tichavsky P, Muravchik CH, Nehorai A: Posterior cramér-rao bounds for discrete-time nonlinear filtering. IEEE Transactions on Signal Processing 1998, 46(5):1386-1396. 10.1109/78.668800
Doucet A, De Freitas N, Gordon N: Sequential Monte Carlo Methods in Practice. Springer, London, UK; 2001.
Gordon NJ, Salmond DJ, Smith AFM: Novel approach to nonlinear/non-Gaussian Bayesian state estimation. IEE Proceedings-F 1993, 140(2):107-113.
Arulampalam MS, Maskell S, Gordon N, Clapp T: A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Transactions on Signal Processing 2002, 50(2):174-188. 10.1109/78.978374
Bar-Shalom Y, Li XR, Kirubarajan T: Estimation with Applications to Tracking and Navigation. John Wiley & Sons, New York, NY, USA; 2001.
Jazwinski AH: Stochastic Processes and Filtering Theory. Academic Press, New York, NY, USA; 1970.
Van der Merwe R, Doucet A, De Freitas N, Wan E: The unscented particle filter. Advances in Neural Information Processing Systems 2000, 548-590.
Guo D, Wang X: Dynamic sensor collaboration via sequential Monte Carlo. IEEE Journal on Selected Areas in Communications 2004, 22(6):1037-1047. 10.1109/JSAC.2004.830897
Papadimitriou CH, Steiglitz K: Combinatorial Optimization: Algorithms and Complexity. Prentice-Hall, Englewood Cliffs, NJ, USA; 1982.
Feo TA, Resende MGC: Greedy randomized adaptive search procedures. Journal of Global Optimization 1995, 6(2):109-133. 10.1007/BF01096763
Koontz WLG, Narendra PM, Fukunaga K: A branch and bound clustering algorithm. IEEE Transactions on Computers 1975, 24(9):908-915.
Arienzo L: Energy-efficient target tracking through wireless sensor networks. Cross-layer design and optimization, Ph.D. thesis. School of Electrical and Information Engineering, University of Salerno, Salerno, Italy; March 2008.
Rappaport TS: Wireless Communications: Principles and Practice. 2nd edition. Prentice Hall, Englewood Cliffs, NJ, USA; 2001.
Acknowledgement
The author would like to thank Professor Ian Akyildiz for the helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Arienzo, L. An Information-Theoretic Approach for Energy-Efficient Collaborative Tracking in Wireless Sensor Networks. J Wireless Com Network 2010, 641632 (2010). https://doi.org/10.1155/2010/641632
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/641632


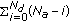 =
= 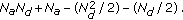
 =
= 




 and
and  (b) target velocity = 0.3 m/s,
(b) target velocity = 0.3 m/s,  and
and 
