- Research Article
- Open access
- Published:
Multiagent  -Learning for Aloha-Like Spectrum Access in Cognitive Radio Systems
-Learning for Aloha-Like Spectrum Access in Cognitive Radio Systems
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 876216 (2010)
Abstract
An Aloha-like spectrum access scheme without negotiation is considered for multiuser and multichannel cognitive radio systems. To avoid collisions incurred by the lack of coordination, each secondary user learns how to select channels according to its experience. Multiagent reinforcement leaning (MARL) is applied for the secondary users to learn good strategies of channel selection. Specifically, the framework of  -learning is extended from single user case to multiagent case by considering other secondary users as a part of the environment. The dynamics of the
-learning is extended from single user case to multiagent case by considering other secondary users as a part of the environment. The dynamics of the  -learning are illustrated using a Metrick-Polak plot, which shows the traces of
-learning are illustrated using a Metrick-Polak plot, which shows the traces of  -values in the two-user case. For both complete and partial observation cases, rigorous proofs of the convergence of multiagent
-values in the two-user case. For both complete and partial observation cases, rigorous proofs of the convergence of multiagent  -learning without communications, under certain conditions, are provided using the Robins-Monro algorithm and contraction mapping, respectively. The learning performance (speed and gain in utility) is evaluated by numerical simulations.
-learning without communications, under certain conditions, are provided using the Robins-Monro algorithm and contraction mapping, respectively. The learning performance (speed and gain in utility) is evaluated by numerical simulations.
1. Introduction
In recent years, cognitive radio has attracted intensive studies in the community of wireless communications. It allows users without license (called secondary users) to access licensed frequency bands when licensed users (called primary users) are not present. Therefore, the cognitive radio technique can substantially alleviate the problem of underutilization of frequency spectrum [1, 2].
The following two problems are key to cognitive radio systems.
-
(i)
Resource mining, that is, how to detect the available resource (the frequency bands that are not being used by primary users); usually it is done by spectrum sensing.
-
(ii)
Resource allocation, that is, how to allocate the available resource to different secondary users.
Substantial work has been done for the resource mining problem. Many signal processing techniques have been applied to sense the frequency spectrum [3], for example, cyclostationary feature [4], quickest change detection [5], and collaborative spectrum sensing [6]. Meanwhile, a significant amount of research has been conducted for the resource allocation in cognitive radio systems [7, 8]. Typically, it is assumed that secondary users exchange information about available spectrum resources and then negotiate on the resource allocation according to their own requirements of traffic (since the same resource cannot be shared by different secondary users if orthogonal transmission is assumed). These studies typically apply theories in economics, for example, game theory, bargaining theory, or microeconomics.
However, in many applications of cognitive radio, such a negotiation-based resource allocation may incur significant overhead. In traditional wireless communication systems, the available resource is almost fixed (even if we consider the fluctuation of channel quality incurred by fading, the change of available resource is usually very slow and thus can be considered stationary). Therefore, the negotiation need not be carried out frequently, and the negotiation result can be applied for a long period of data communication, thus incurring only tolerable overhead. However, in many cognitive radio systems, the resource may change very rapidly since the activity of primary users may be highly dynamic. Therefore, the available resource needs to be updated very frequently, and the data communication period between two spectrum sensing periods should be fairly short since minimum violation to primary users should be guaranteed. In such a situation, the negotiation of resource allocation may be highly inefficient since a substantial portion of time needs to be used for the negotiation. To alleviate such an inefficiency, high-speed transceivers need to be used to minimize the time consumed on negotiation. Particularly, the turn-around time that is, the time needed to switch from receiving (transmitting) to transmitting (receiving) should be very small, which is a substantial challenge to hardware design.
Motivated by the above discussion and observation, in this paper, we study the problem of spectrum access without negotiation in multiuser and multichannel cognitive radio systems. The spectrum access without negotiation is achieved by applying the framework of reinforcement learning. In such a scheme, each secondary user senses channels and then chooses an idle frequency channel to transmit data, as if no other secondary user exists. If two secondary users choose the same channel for data transmission, they will collide with each other and the corresponding data packets cannot be decoded. Such a procedure is illustrated in Figure 1, where three secondary users access an access point via four channels. Note that such a scheme is similar to Aloha [9] where no explicit collision avoidance is applied. We can also apply techniques similar to  -persistent Carrier Sensing Multiple Access (CSMA) that is, each secondary user transmits with probability
-persistent Carrier Sensing Multiple Access (CSMA) that is, each secondary user transmits with probability  when it finds an available channel. However, it is beyond the scope of this paper. In the Aloha-like approach, since there is no mutual communication among these secondary users, collision is unavoidable. However, the secondary users can try to learn collision avoidance, as well as channel qualities (we assume that the secondary users have no a priori information about the channel qualities), according to their experience. In such a context, the learning procedure includes not only the available frequency spectrum but also the behavior of other secondary users.
when it finds an available channel. However, it is beyond the scope of this paper. In the Aloha-like approach, since there is no mutual communication among these secondary users, collision is unavoidable. However, the secondary users can try to learn collision avoidance, as well as channel qualities (we assume that the secondary users have no a priori information about the channel qualities), according to their experience. In such a context, the learning procedure includes not only the available frequency spectrum but also the behavior of other secondary users.
To accomplish the learning of Aloha-like spectrum access, multiagent reinforcement learning (MARL) [10] is applied in this paper. One challenge of MARL in our context is that the secondary users do not know the payoffs (thus do not know the strategies) of other secondary users in each stage; thus the environment of each secondary user, including other secondary users, is nonstationary and may not assure the convergence of learning. Due to the assumption that there is no mutual communication between different secondary users, many traditional MARL techniques like fictitious play [11, 12] and Nash-Q learning [13] cannot be used since they need information exchange among players (e.g., exchanging their action information). To alleviate the lack of mutual communication, we extend the principle of single-agent  -learning, that is, evaluating the values of different state-action pairs in an incremental way, to the multiagent situation without information exchange. By applying the theory of stochastic approximation [14], which has been used in many studies on wireless networks [15, 16], we will prove the main result of this paper, that is, the learning converges to a stationary point regardless of the initial strategies (Propositions 1 and 2).
-learning, that is, evaluating the values of different state-action pairs in an incremental way, to the multiagent situation without information exchange. By applying the theory of stochastic approximation [14], which has been used in many studies on wireless networks [15, 16], we will prove the main result of this paper, that is, the learning converges to a stationary point regardless of the initial strategies (Propositions 1 and 2).
Some studies on reinforcement learning in cognitive radio networks have been done [17–19]. In [17] and [19], the studies are focused on the resource competition in a spectrum auction system, where the channel allocation is determined by the spectrum regulator, which is different from this paper in which no regulator exists. Reference [18] discusses correlated equilibrium and achieves it by no-regret learning; that is, minimizing the gap between the current reward and optimal reward. In this approach, mutual communication is needed among the secondary users. However, in our study, no intersecondary-user communication is assumed.
Note that the study in this paper has subtle similarities to the evolutionary game theory [20], which has been successfully applied in the cooperative spectrum sensing in cognitive radio systems [21]. Both our study and the evolutionary game focus on the dynamics of strategy changes of users. However, there is a key difference between the two studies. The evolutionary game theory assumes pure strategies for the players (e.g., cooperate or free-ride in cooperative spectrum sensing [21]) and studies the proportions of players using different pure strategies. The key equation in the evolutionary game theory, called replicator equation, describes the dynamics of the corresponding proportions. In contrast to the evolutionary game, the players in our study use mixed strategies and the basic (16) describes the dynamics of the  -values for different channels. Although the convergence is proved by studying ordinary different equations in both studies, the proof is significantly different since the equations have totally different expressions.
-values for different channels. Although the convergence is proved by studying ordinary different equations in both studies, the proof is significantly different since the equations have totally different expressions.
The remainder of this paper is organized as follows. In Section 2, the system model is introduced. Basic elements of the game and the proposed multiagent  -learning for fully observable case (i.e., each secondary user can sense all channels) are introduced in Section 3. The corresponding convergence of
-learning for fully observable case (i.e., each secondary user can sense all channels) are introduced in Section 3. The corresponding convergence of  -learning is proved in Section 4. The
-learning is proved in Section 4. The  -learning for partially observable case (i.e., each secondary user can sense a subset of the channels) is discussed in Section 5. Numerical results are provided in Section 6, while conclusions are drawn in Section 7.
-learning for partially observable case (i.e., each secondary user can sense a subset of the channels) is discussed in Section 5. Numerical results are provided in Section 6, while conclusions are drawn in Section 7.
2. System Model
We consider  active secondary users accessing
active secondary users accessing  licensed frequency channels. (When there are more than
licensed frequency channels. (When there are more than  channels, there is less competition; thus making the problem easier. We do not consider the case when the number of channels is less than the number of secondary users since a typical cognitive radio system can provide sufficient channels. Meanwhile, the proposed algorithm can also be applied to all possible cases of
channels, there is less competition; thus making the problem easier. We do not consider the case when the number of channels is less than the number of secondary users since a typical cognitive radio system can provide sufficient channels. Meanwhile, the proposed algorithm can also be applied to all possible cases of  ) We index the secondary users, as well as the channels, by integers 1, 2,
) We index the secondary users, as well as the channels, by integers 1, 2, ,
,  . For simplicity, we denote by
. For simplicity, we denote by  the set of users (channels) different from user (channel)
the set of users (channels) different from user (channel)  .
.
The following assumptions are made throughout this paper.
-
(i)
The secondary users are sufficiently close to each other such that they share the same activity of primary users. There is no communication among these secondary users, thus excluding the possibility of negotiation.
-
(ii)
We assume that the activity of primary users over each channel is a Markov chain (A more reasonable model for the activity of primary users is the semi-Markov chain. The corresponding analysis is more tedious but similar to that in this paper. Therefore, for simplicity of analysis, we consider only Markov chain in this paper)with states
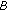 (busy: the channel is occupied by primary users and cannot be used by secondary users) and
(busy: the channel is occupied by primary users and cannot be used by secondary users) and 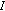 (idle: there is no primary user over this channel). We denote by
(idle: there is no primary user over this channel). We denote by 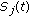 the state of channel
the state of channel 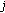 in the sensing period of the
in the sensing period of the 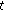 th spectrum access period. For channel
th spectrum access period. For channel  , the transition probability from state
, the transition probability from state 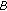 to state
to state 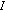 (resp., from state
(resp., from state 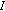 to state
to state 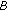 ) is denoted by
) is denoted by 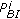 (resp.,
(resp., 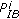 ). We assume that the
). We assume that the 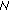 Markov chains for the
Markov chains for the  channels are mutually independent. We also assume perfect spectrum sensing and do not consider possible errors of spectrum sensing.
channels are mutually independent. We also assume perfect spectrum sensing and do not consider possible errors of spectrum sensing. -
(iii)
We assume that the channel state transition probabilities, as well as the channel rewards, are unknown with the secondary users at the beginning. They are fixed throughout the game, unless otherwise noted. Therefore, the secondary users need to learn the channel properties.
-
(iv)
The timing structure of spectrum sensing and data transmission is illustrated in Figure 2, where data is transmitted after the spectrum sensing period. We assume that each secondary user is able to sense only one channel during the spectrum sensing period and transmit over only one channel during the data transmission period.
In Sections 3 and 4, we consider the case in which all secondary users have full knowledge of channel states in the previous spectrum access period (complete observation). Note that this does not contradict the assumption that a secondary user can sense only one channel during the spectrum sensing period since the secondary user can continue to sense other channels during the data transmission period (suppose that the signal from primary users can be well distinguished from that from secondary users, e.g., using different cyclostationary features [22]). If we consider the set of channel states in the previous spectrum access period as the system state, denoted by  at spectrum access period
at spectrum access period  , then the previous assumption implies a completely observable system state, which substantially simplifies the analysis. In Section 5, we will also study the case in which secondary users cannot continue to sense during the data transmission period (partial observation); thus each secondary user has only partial observations about the system state.
, then the previous assumption implies a completely observable system state, which substantially simplifies the analysis. In Section 5, we will also study the case in which secondary users cannot continue to sense during the data transmission period (partial observation); thus each secondary user has only partial observations about the system state.
3. Game and 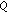 -Learning
-Learning
In this section, we introduce the game associated to the learning procedure and the application of  -learning to the Aloha-like spectrum access problem. Note that in this section and Section 3, we assume that each secondary user knows all channel states in the previous time slot, that is, the completely observable case.
-learning to the Aloha-like spectrum access problem. Note that in this section and Section 3, we assume that each secondary user knows all channel states in the previous time slot, that is, the completely observable case.
3.1. Game of Aloha-Like Spectrum Access
The Aloha-like spectrum access problem is essentially an  game. When secondary user
game. When secondary user  transmits over an idle channel
transmits over an idle channel  , it receives reward
, it receives reward  (e.g., channel capacity or successful transmission probability), if no other secondary user transmits over this channel, and reward 0, if one or more other secondary users are transmitting over this channel, since collision will happen. We assume that the reward
(e.g., channel capacity or successful transmission probability), if no other secondary user transmits over this channel, and reward 0, if one or more other secondary users are transmitting over this channel, since collision will happen. We assume that the reward  does not change with time. When channels change slowly, the learning algorithm proposed in this paper can also be applied to track the change of channels. When channels change very fast, it is impossible for secondary users to learn. Since there is no explicit information exchange among secondary users, the collision avoidance is completely based on the received reward. The payoff matrices for the case of
does not change with time. When channels change slowly, the learning algorithm proposed in this paper can also be applied to track the change of channels. When channels change very fast, it is impossible for secondary users to learn. Since there is no explicit information exchange among secondary users, the collision avoidance is completely based on the received reward. The payoff matrices for the case of  are given in Figure 3. Note that the actions, denoted by
are given in Figure 3. Note that the actions, denoted by  for user
for user  at time
at time  , in the game are the selections of channels. Obviously, the diagonal elements in the payoff matrices are all zero since collision yields zero reward.
, in the game are the selections of channels. Obviously, the diagonal elements in the payoff matrices are all zero since collision yields zero reward.
It is well known that Nash equilibrium means the strategies such that unilaterally changing strategy incurs the degradation of its own performance. Mathematically, a Nash equilibrium means a set of strategies  , where
, where  is the strategy of player
is the strategy of player  , which satisfy
, which satisfy

where  means the reward of player
means the reward of player  and
and  means the strategies of all players except player
means the strategies of all players except player  .
.
It is easy to verify that there are multiple Nash equilibrium points in the game. Obviously, orthogonal transmission strategies, that is,  ,
,  , are pure equilibria. The reason is the following. If a secondary user changes its strategy and transmits over other channels with nonzero probability, those transmission will collide with other secondary users (recall that, for the Nash equilibrium, all other secondary users do not change their strategies) and incurs performance degradation. The orthogonal channel assignment can be achieved in the following approach: let all secondary users sense the channel randomly at the very beginning; once a secondary user finds an idle channel, it will access this channel forever; after a random number of rounds, all secondary users will find different channels, thus achieving the orthogonal transmission. We call this scheme the simple orthogonal channel assignment since it is simple and fast. However, in this scheme, the different rewards of different channels are ignored. As will be seen in the numerical simulation results, the proposed learning procedure can significant outperform the simple orthogonal channel assignment.
, are pure equilibria. The reason is the following. If a secondary user changes its strategy and transmits over other channels with nonzero probability, those transmission will collide with other secondary users (recall that, for the Nash equilibrium, all other secondary users do not change their strategies) and incurs performance degradation. The orthogonal channel assignment can be achieved in the following approach: let all secondary users sense the channel randomly at the very beginning; once a secondary user finds an idle channel, it will access this channel forever; after a random number of rounds, all secondary users will find different channels, thus achieving the orthogonal transmission. We call this scheme the simple orthogonal channel assignment since it is simple and fast. However, in this scheme, the different rewards of different channels are ignored. As will be seen in the numerical simulation results, the proposed learning procedure can significant outperform the simple orthogonal channel assignment.
3.2. 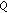 -Value
-Value
We define the  -function as the expected reward in one time slot (since the channel states are completely known to the secondary users and are not controlled by the secondary users, each secondary user needs to consider only the expected reward in one time slot, that is, a myopic strategy) of each action under different states; that is, for secondary user
-function as the expected reward in one time slot (since the channel states are completely known to the secondary users and are not controlled by the secondary users, each secondary user needs to consider only the expected reward in one time slot, that is, a myopic strategy) of each action under different states; that is, for secondary user  and system state
and system state  , the
, the  -value of choosing channel
-value of choosing channel  is given by
is given by

where  is the reward obtained by secondary user
is the reward obtained by secondary user  , which is dependent on the action, as well as the system state, and the expectation is over the randomness of other users' actions, as well as the primary users' occupancies.
, which is dependent on the action, as well as the system state, and the expectation is over the randomness of other users' actions, as well as the primary users' occupancies.
3.3. Exploration
In contrast to fictitious play [11], which is deterministic, the action in  -learning is random. We assign nonzero probabilities for all channels such that all channels will be explored. Such an exploration guarantees that good channels will not be missed during the learning procedure. We consider Boltzmann distribution [23] for random exploration, that is,
-learning is random. We assign nonzero probabilities for all channels such that all channels will be explored. Such an exploration guarantees that good channels will not be missed during the learning procedure. We consider Boltzmann distribution [23] for random exploration, that is,

where  is called temperature, which controls the randomness of exploration. Obviously, the smaller
is called temperature, which controls the randomness of exploration. Obviously, the smaller  is (the colder), the more focused the actions are. When
is (the colder), the more focused the actions are. When  , each user chooses only the channel having the largest
, each user chooses only the channel having the largest  -value.
-value.
When secondary user  selects channel
selects channel  and the system state is
and the system state is  , the expected reward is given by
, the expected reward is given by

since secondary user  (
( ) chooses channel
) chooses channel  with probability
with probability  (collision happens and secondary user
(collision happens and secondary user  receives no reward) and channel
receives no reward) and channel  is idle with probability
is idle with probability  ; then the product in (4) is the probability that no other secondary user accesses channel
; then the product in (4) is the probability that no other secondary user accesses channel  .
.
3.4. Updating 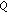 -Values
-Values
In the procedure of  -learning, the
-learning, the  -functions are updated after each spectrum access using the following rule:
-functions are updated after each spectrum access using the following rule:

where  is a step factor (when channel
is a step factor (when channel  is not selected by user
is not selected by user  , we set
, we set  ),
),  is the reward of secondary user
is the reward of secondary user  and
and  is the characteristic function of the event that channel
is the characteristic function of the event that channel  is selected by secondary user
is selected by secondary user  at the
at the  th spectrum access. Note that this is the standard
th spectrum access. Note that this is the standard  -learning without considering the future states. An intuitive explanation for (5) is that, once channel
-learning without considering the future states. An intuitive explanation for (5) is that, once channel  is accessed, the corresponding
is accessed, the corresponding  -value is updated by combining the old value and the new reward; if channel
-value is updated by combining the old value and the new reward; if channel  is not chosen, we keep the old value by setting
is not chosen, we keep the old value by setting  . Our study is focused on the dynamics of (5). To assure convergence, we assume that
. Our study is focused on the dynamics of (5). To assure convergence, we assume that

as well as

Note that, in a typical stochastic game setting and  -learning, the updating rule in (5) should consider the reward of the future and add a discounted term of the future reward to the right hand side of (5). However, in this paper, the optimal strategy is myopic since we assume that the system state is known, and thus the secondary users' actions do not affect the system state. For the case of partial observation (i.e., each secondary user knows only the state of a single channel), the action does change each secondary user's state (typically the belief of system state), and the future reward should be included in the right hand side of (5), which will be discussed in Section 5.
-learning, the updating rule in (5) should consider the reward of the future and add a discounted term of the future reward to the right hand side of (5). However, in this paper, the optimal strategy is myopic since we assume that the system state is known, and thus the secondary users' actions do not affect the system state. For the case of partial observation (i.e., each secondary user knows only the state of a single channel), the action does change each secondary user's state (typically the belief of system state), and the future reward should be included in the right hand side of (5), which will be discussed in Section 5.
3.5. Stationary Point
The  -values for different users are mutually coupled and all
-values for different users are mutually coupled and all  -values change if one
-values change if one  -value is changed since the strategy of the corresponding user is changed, thus changing the expected rewards of other users. We define
-value is changed since the strategy of the corresponding user is changed, thus changing the expected rewards of other users. We define  -values satisfying the following equations as a stationary point
-values satisfying the following equations as a stationary point

Note that the stationarity is only in the statistical sense since the  -values can fluctuate around the stationary point due to the randomness of exploration. Obviously, as
-values can fluctuate around the stationary point due to the randomness of exploration. Obviously, as  , the stationary point converges to a Nash equilibrium point. However, we are still not sure about the existence of such a stationary point. The following lemma assures the existence of stationary point. The proof is given in Appendix .
, the stationary point converges to a Nash equilibrium point. However, we are still not sure about the existence of such a stationary point. The following lemma assures the existence of stationary point. The proof is given in Appendix .
Lemma 1.
For sufficiently small  , there exists at least one stationary point satisfying (8).
, there exists at least one stationary point satisfying (8).
4. Convergence of 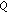 -learning without Information Exchange
-learning without Information Exchange
In this section, we study the convergence of the proposed  -learning algorithm. First, we provide an intuitive explanation for the convergence in
-learning algorithm. First, we provide an intuitive explanation for the convergence in  case. Then, we apply the tools of stochastic approximation and ordinary differential equation (ODE) to prove the convergence rigorously.
case. Then, we apply the tools of stochastic approximation and ordinary differential equation (ODE) to prove the convergence rigorously.
4.1. Intuition on Convergence
As will be shown in Proposition 1, the updating rule of  -values in (5) will converge to a stationary equilibrium point close to Nash equilibrium. Before the rigorous proof, we provide an intuitive explanation for the convergence using the geometric argument proposed in [24].
-values in (5) will converge to a stationary equilibrium point close to Nash equilibrium. Before the rigorous proof, we provide an intuitive explanation for the convergence using the geometric argument proposed in [24].
The intuitive explanation is provided in Figure 4 for the case of  (we call it Metrick-Polak plot since it was originally proposed by A. Metrick and B. Polak in [24]). For simplicity, we ignore the indices of state and assume that both channels are idle. The axes are
(we call it Metrick-Polak plot since it was originally proposed by A. Metrick and B. Polak in [24]). For simplicity, we ignore the indices of state and assume that both channels are idle. The axes are  and
and  , respectively. As labeled in the figure, the plane is divided into four regions separated by two lines
, respectively. As labeled in the figure, the plane is divided into four regions separated by two lines  and
and  , in which the dynamics of
, in which the dynamics of  -learning are different. We discuss these four regions separately.
-learning are different. We discuss these four regions separately.
-
(i)
Region I: in this region,
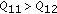 ; therefore, secondary user 1 prefers visiting channel 1; meanwhile, secondary user 2 prefers accessing channel 2 since
; therefore, secondary user 1 prefers visiting channel 1; meanwhile, secondary user 2 prefers accessing channel 2 since  ; then, with large probability, the strategies will converge to a stationary point in which secondary users 1 and 2 access channels 1 and 2, respectively.
; then, with large probability, the strategies will converge to a stationary point in which secondary users 1 and 2 access channels 1 and 2, respectively. -
(ii)
Region II: in this region, both secondary users prefer accessing channel 1, thus causing many collisions. Therefore, both
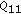 and
and 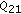 will be reduced until entering either region I or region III.
will be reduced until entering either region I or region III. -
(iii)
Region III: similar to region I.
-
(iv)
Region IV: similar to region II.
Then, we observe that the points in Regions II and IV are unstable and will move into Region I or III with large probability. In Regions I and III, the strategy will move close to the stationary point with large probability. Therefore, regardless where the initial point is, the updating rule in (5) will converge to a stationary point with large probability.
4.2. Stochastic Approximation-Based Convergence
In this section, we prove the convergence of the  -learning of the proposed Aloha-like spectrum access with Boltzman distributed exploration. First, we find the equivalence between the updating rule (5) and Robbins-Monro iteration [25] for solving an equation with unknown expression (a brief introduction is provided in Appendix ). Then, we apply a conclusion in stochastic approximation [14] to relate the dynamics of the updating rule to an ODE and prove the convergence of the ODE.
-learning of the proposed Aloha-like spectrum access with Boltzman distributed exploration. First, we find the equivalence between the updating rule (5) and Robbins-Monro iteration [25] for solving an equation with unknown expression (a brief introduction is provided in Appendix ). Then, we apply a conclusion in stochastic approximation [14] to relate the dynamics of the updating rule to an ODE and prove the convergence of the ODE.
4.2.1. Robbins-Monro Iteration
At a stationary point, the expected values of  -functions satisfy the equations in (8). For system state
-functions satisfy the equations in (8). For system state  , define
, define

Then, (8) can be rewritten as

where

and (function mod means the remainder of dividing integer
means the remainder of dividing integer  with integer
with integer  )
)

with convention  . Obviously,
. Obviously,  is the probability that channel
is the probability that channel  can be used by secondary user
can be used by secondary user  without collision with other secondary users, when the current system state is
without collision with other secondary users, when the current system state is  .
.
Then, the updating rule in (5) is equivalent to solving (8) (the expression of the equation is unknown since the rewards, channel transition probabilities, as well as the strategies of other users, are all unknown) using Robbins-Monro algorithm [14], that is,

where  is the vector of all step factors,
is the vector of all step factors,  is the vector of rewards obtained at spectrum access period
is the vector of rewards obtained at spectrum access period  and
and  is a random observation on function
is a random observation on function  contaminated by noise, that is,
contaminated by noise, that is,

where  ,
,  is noise and (recall that
is noise and (recall that  means the reward of secondary user
means the reward of secondary user  at time
at time  )
)

Obviously,  since the expectation of the difference between the reward and the expected reward is equal to 0. Therefore, the observation
since the expectation of the difference between the reward and the expected reward is equal to 0. Therefore, the observation  is a Martingale difference.
is a Martingale difference.
4.2.2. ODE and Convergence
The procedure of Robbins-Monro algorithm (i.e., the updating of  -value) is the stochastic approximation of the solution of the equation. It is well known that the convergence of such a procedure can be characterized by an ODE. Since the noise
-value) is the stochastic approximation of the solution of the equation. It is well known that the convergence of such a procedure can be characterized by an ODE. Since the noise  in (14) is a Martingale difference, it is easy to verify the conditions in Theorem 1 in Appendix and obtain the following lemma (the proof is given in Appendix ).
in (14) is a Martingale difference, it is easy to verify the conditions in Theorem 1 in Appendix and obtain the following lemma (the proof is given in Appendix ).
Lemma 2.
With probability 1, the sequence  ,
,  , converges to some limit set of the ODE
, converges to some limit set of the ODE

What remains to do is to analyze the convergence property of the ODE (16). We obtain the following lemma by applying Lyapunov function. The proof is given in Appendix .
Lemma 3.
If a stationary point determined by (10) exists, the solution of ODE (16) converges to the stationary point for sufficiently large  .
.
Combining Lemmas 1, 2, and 3, we obtain the main result in this paper.
Proposition 1.
Suppose that a stationary point determined by (10) exists. For any system state  and sufficiently large
and sufficiently large  , the
, the  -learning converges to a stationary point with probability 1.
-learning converges to a stationary point with probability 1.
Note that a sufficiently small  guarantees the existence of stationary point and a sufficiently large
guarantees the existence of stationary point and a sufficiently large  assures the convergence of the learning procedure. However, they do not conflict since they are not necessary conditions. As we found in our simulations, we can always choose a suitable
assures the convergence of the learning procedure. However, they do not conflict since they are not necessary conditions. As we found in our simulations, we can always choose a suitable  to guarantee the existence of the stationary point and the convergence.
to guarantee the existence of the stationary point and the convergence.
5.  -Learning with Partial Observations
-Learning with Partial Observations
In this section, we remove the assumption that all secondary users know all channel states in the previous spectrum access period and assume that each secondary user knows the state of only the channel sensed in the previous spectrum access period; thus making the system state partially observable. The difficulties of analyzing such a scenario are given below:
-
(i)
The system state is partially observable.
-
(ii)
The game is imperfectly monitored, that is, each player does not know other players' actions.
-
(iii)
The game has incomplete information, that is, each player does not know the strategies of other players, as well as their beliefs on the system state.
Note that the latter two difficulties are common for both the complete and partial observation cases. However, the imperfect monitoring and incomplete information add much more difficulty in the partial observation case. In this section, we formulate the  -learning algorithm and then prove the convergence under certain conditions.
-learning algorithm and then prove the convergence under certain conditions.
5.1. State Definition
It is well known that, in partially observable Markov decision process (POMDP) problems, the belief on the system state, that is,  (
( is the observation history before period
is the observation history before period  ), can play the role of system state. Due to the special structure of the game, we can define the state of secondary user
), can play the role of system state. Due to the special structure of the game, we can define the state of secondary user  at period
at period  as
as

where  ,
,  , means the number of consecutive periods during which channel
, means the number of consecutive periods during which channel  has not been sensed before period
has not been sensed before period  (e.g., if the last time that channel
(e.g., if the last time that channel  was sensed by secondary user
was sensed by secondary user  is time slot
is time slot  ,
,  .) and
.) and  is the state of channel
is the state of channel  in the last time when it is sensed before period
in the last time when it is sensed before period  .
.
5.2. Learning in the POMDP Game
For the purpose of learning, we define the objective function for user  as the discounted sum of rewards in each spectrum access period with discount factor
as the discounted sum of rewards in each spectrum access period with discount factor  , that is,
, that is,

Then, to maximize the objectively function, the corresponding  -learning strategy is given by [23]
-learning strategy is given by [23]

where  is uniquely determined by
is uniquely determined by  and
and  , and
, and  is the step factor dependent on the time, channel, user, and belief state. Note that
is the step factor dependent on the time, channel, user, and belief state. Note that  is the system state in the next time slot, which is random. Intuitively, the new
is the system state in the next time slot, which is random. Intuitively, the new  -value is updated by combining the old value and the new estimation, which is the sum of the new reward and discounted old
-value is updated by combining the old value and the new estimation, which is the sum of the new reward and discounted old  -value.
-value.
Similarly to the complete information situation, we have the following proposition which states the convergence of the learning procedure with partial information and large  . The proof is given in Appendix . Note that numerical simulation shows that small
. The proof is given in Appendix . Note that numerical simulation shows that small  also results in convergence. However, we are still unable to prove it rigorously.
also results in convergence. However, we are still unable to prove it rigorously.
Proposition 2.
When  is sufficiently large, the learning procedure in (19) converges.
is sufficiently large, the learning procedure in (19) converges.
6. Numerical Results
In this section, we use numerical simulations to demonstrate the theoretical results obtained in previous sections. For the fully observable case, we use the following step factor:

where  is the initial learning factor. A similar step factor
is the initial learning factor. A similar step factor  is used for the partially observable case. In Sections 6.1, 6.2, and 6.3, we consider the fully observable case and, in Section 6.4, we consider the partially observable case. Note that, in all simulations, we initialize the
is used for the partially observable case. In Sections 6.1, 6.2, and 6.3, we consider the fully observable case and, in Section 6.4, we consider the partially observable case. Note that, in all simulations, we initialize the  -values by choosing uniformly random variables in the interval
-values by choosing uniformly random variables in the interval  .
.
6.1. Dynamics
Figures 5 and 6 show the dynamics of  versus
versus  (recall that
(recall that  and
and  ) of several typical trajectories for the state of both channels being idle when
) of several typical trajectories for the state of both channels being idle when  . We assume that
. We assume that  for all
for all  and
and  . Note that
. Note that  in Figure 5 and
in Figure 5 and  in Figure 6. We observe that the trajectories move from unstable regions (II and IV in Figure 4) to stable regions (I and III in Figure 4). We also observe that the trajectories for smaller temperature
in Figure 6. We observe that the trajectories move from unstable regions (II and IV in Figure 4) to stable regions (I and III in Figure 4). We also observe that the trajectories for smaller temperature  is smoother since less explorations are carried out.
is smoother since less explorations are carried out.
Figure 7 shows the evolution of the probability of choosing channel 1 when  ,
,  and both channels are idle. We observe that both secondary users prefer channel 1 at the beginning and soon secondary user 1 intends to choose channel 2, thus avoiding collisions.
and both channels are idle. We observe that both secondary users prefer channel 1 at the beginning and soon secondary user 1 intends to choose channel 2, thus avoiding collisions.
6.2. CDF of Rewards
In this subsection, we consider the performance of reward averaged over all system states. When  , we set
, we set  and
and  for the three channels, respectively. When
for the three channels, respectively. When  , we use the first two channels in the case of
, we use the first two channels in the case of  . The rewards of different channels for different secondary users are randomly generated with a uniform distribution between
. The rewards of different channels for different secondary users are randomly generated with a uniform distribution between  . The CDF curves of performance gain, defined as the difference of average rewards after and before the learning procedure, are plotted in Figure 8 for both
. The CDF curves of performance gain, defined as the difference of average rewards after and before the learning procedure, are plotted in Figure 8 for both  and
and  . Note that the CDF curves are obtained from 100 realizations of learning procedure. From a CDF curve, we can read the distribution of the performance gains. For example, for the curve
. Note that the CDF curves are obtained from 100 realizations of learning procedure. From a CDF curve, we can read the distribution of the performance gains. For example, for the curve  , performance gain 0.4 in the horizontal axis corresponds to 0.6 in the vertical axis; this means that around 60% of the secondary users obtain performance gain less than 0.4. We observe that when
, performance gain 0.4 in the horizontal axis corresponds to 0.6 in the vertical axis; this means that around 60% of the secondary users obtain performance gain less than 0.4. We observe that when  , most performance gains are positive. However, when
, most performance gains are positive. However, when  , a small portion of the performance gains are negative, that is, the performance is decreased after the learning procedure. Such a performance reduction is reasonable since Nash equilibrium may not be Pareto optimal. We also plotted the average performance gains versus different
, a small portion of the performance gains are negative, that is, the performance is decreased after the learning procedure. Such a performance reduction is reasonable since Nash equilibrium may not be Pareto optimal. We also plotted the average performance gains versus different  and
and  in Figure 9. We observe that larger
in Figure 9. We observe that larger  results in worse performance gain. When
results in worse performance gain. When  is small, smaller
is small, smaller  yields better performance, but decreases faster than larger
yields better performance, but decreases faster than larger  when
when  increases. The performance gain over the simple orthogonal channel assignment scheme is given in Figure 10. We observe that the learning procedure generates a much better performance than the simple orthogonal channel assignment.
increases. The performance gain over the simple orthogonal channel assignment scheme is given in Figure 10. We observe that the learning procedure generates a much better performance than the simple orthogonal channel assignment.
6.3. Learning Speed
We define the stopping time of learning as the time that the relative fluctuation of average reward, which is obtained from 2000 spectrum access periods using the current  -values, has been below 5 percent for successive 5 time slots. That is, compute the relative fluctuation at time slot
-values, has been below 5 percent for successive 5 time slots. That is, compute the relative fluctuation at time slot  using
using

where  is the vector containing all
is the vector containing all  -values and the norm is 2-norm. Then, when
-values and the norm is 2-norm. Then, when  is smaller than 0.05 for 5 consecutive times, we claim that the learning is completed. Then, the learning delay is the time spent before the stopping time. Obviously, the smaller the learning delay is, the faster the learning is. Figures 11 and 12 show the delays of learning, which characterizes the learning speed, for different learning factor
is smaller than 0.05 for 5 consecutive times, we claim that the learning is completed. Then, the learning delay is the time spent before the stopping time. Obviously, the smaller the learning delay is, the faster the learning is. Figures 11 and 12 show the delays of learning, which characterizes the learning speed, for different learning factor  and different temperature
and different temperature  , respectively, when
, respectively, when  . The original
. The original  values are randomly selected. When the probabilities of choosing channel 1 are larger than 0.95 for one secondary user and smaller than 0.05 for the other secondary user, we claim that the learning procedure is completed. We observe that larger learning factor
values are randomly selected. When the probabilities of choosing channel 1 are larger than 0.95 for one secondary user and smaller than 0.05 for the other secondary user, we claim that the learning procedure is completed. We observe that larger learning factor  results in smaller delay while smaller
results in smaller delay while smaller  yields faster learning procedure.
yields faster learning procedure.
The speed of learning is compared for  ,
,  and
and  in Figure 13 (both
in Figure 13 (both  and
and  are fixed). We observe that, for more than 90% of the realizations, the learning can be completed within 20 spectrum access periods. However, the learning procedure may last for a long period of time for some situations. We can notice that the learning speeds are similar for cases
are fixed). We observe that, for more than 90% of the realizations, the learning can be completed within 20 spectrum access periods. However, the learning procedure may last for a long period of time for some situations. We can notice that the learning speeds are similar for cases  and
and  . We also observe that, when
. We also observe that, when  is much larger (
is much larger ( ), the increase of delay is not significant.
), the increase of delay is not significant.
6.4. Time-Varying Channel Rewards
In previous simulations, the rewards of successfully accessing channels,  are assumed to be constant. In practical systems, they may change with time since wireless channels are usually dynamic. In Figure 14, we show the CDF of performance gains (the configuration is the same as that in Figure 8) when channel changes slowly. We used a simple model for channel reward, which is given by
are assumed to be constant. In practical systems, they may change with time since wireless channels are usually dynamic. In Figure 14, we show the CDF of performance gains (the configuration is the same as that in Figure 8) when channel changes slowly. We used a simple model for channel reward, which is given by

where  is a random variable uniformly distributed between 0 and 1. From Figure 14, we observe that the learning algorithm still improves the performance significantly.
is a random variable uniformly distributed between 0 and 1. From Figure 14, we observe that the learning algorithm still improves the performance significantly.
6.5. Partial Observation Case
Figure 15 shows the performance gain of learning in the case of partial observations. We adopt the  -learning mechanism introduced in Section 5. Note that there are infinitely many belief states since a channel could be unsensed for an infinite period of time. For computational simplicity, we set all
-learning mechanism introduced in Section 5. Note that there are infinitely many belief states since a channel could be unsensed for an infinite period of time. For computational simplicity, we set all  to
to  (recall that
(recall that  is the period of time that channel
is the period of time that channel  has not been sensed by user
has not been sensed by user  before time
before time  ). From Figure 15, we observe that the performance is actually degraded for around 40% (
). From Figure 15, we observe that the performance is actually degraded for around 40% ( ) or 50% (
) or 50% ( ) cases. However, the amplitude of performance degradation is averagely less than the amplitude of performance gain. We also observe that the performance gain is decreased when
) cases. However, the amplitude of performance degradation is averagely less than the amplitude of performance gain. We also observe that the performance gain is decreased when  is increased from 2 to 3.
is increased from 2 to 3.
The learning delay for the partial observation case is shown in Figure 16, where the simulation setup is similar to that of Figure 13. Again, we observe that the learning speeds of  and
and  are similar to each other.
are similar to each other.
7. Conclusions
We have discussed a learning procedure for Aloha-like spectrum access without negotiation in cognitive radio systems. During the learning, each secondary user considers the channel and other secondary users as its environment, updates its  -values, and takes the best action. An intuitive explanation for the convergence of learning is provided using Metrick-Polak plot. By applying the theory of stochastic approximation and ODE, we have shown the convergence of learning under certain conditions. We also extended the case of full observations to the case of partial observations. Numerical results show that secondary users can learn to avoid collision quickly. The performance after the learning is significantly better than that before the learning and that using a simple scheme to achieve a Nash equilibrium. Note that our study is one extreme of the resource allocation problem since no negotiation is considered, while the other extreme is full negotiation to achieve optimal performance. Our future work will be the intermediate case; that is, limited negotiation for resource allocation.
-values, and takes the best action. An intuitive explanation for the convergence of learning is provided using Metrick-Polak plot. By applying the theory of stochastic approximation and ODE, we have shown the convergence of learning under certain conditions. We also extended the case of full observations to the case of partial observations. Numerical results show that secondary users can learn to avoid collision quickly. The performance after the learning is significantly better than that before the learning and that using a simple scheme to achieve a Nash equilibrium. Note that our study is one extreme of the resource allocation problem since no negotiation is considered, while the other extreme is full negotiation to achieve optimal performance. Our future work will be the intermediate case; that is, limited negotiation for resource allocation.
References
Mitola J III: Cognitive radio for flexible mobile multimedia communications. Mobile Networks and Applications 2001, 6(5):435-441. 10.1023/A:1011426600077
Mitola J III: Cognitive Radio, Licentiate Proposal. KTH, Stockholm, Sweden; 1998.
Zhao Q, Sadler BM: A survey of dynamic spectrum access. IEEE Signal Processing Magazine 2007, 24(3):79-89.
Kim K, Akbar IA, Bae KK, Um J-S, Spooner CM, Reed JH: Cyclostationary approaches to signal detection and classification in cognitive radio. Proceedings of the 2nd IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, April 2007 212-215.
Li H, Li C, Dai H: Quickest spectrum sensing in cognitive radio. Proceedings of the 42nd Annual Conference on Information Sciences and Systems (CISS '08), March 2008, Princeton, NJ, USA 203-208.
Ghasemi A, Sousa ES: Collaborative spectrum sensing for opportunistic access in fading environments. Proceedings of the 1st IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN '05), November 2005 131-136.
Kloeck C, Jaekel H, Jondral F: Multi-agent radio resource allocation. Mobile Networks and Applications 2006, 11(6):813-824. 10.1007/s11036-006-0051-4
Niyato D, Hossain E, Han Z: Dynamics of multiple-seller and multiple-buyer spectrum trading in cognitive radio networks: a game-theoretic modeling approach. IEEE Transactions on Mobile Computing 2009, 8(8):1009-1022.
Kuo FF: The ALOHA system. In Computer Networks. Prentice-Hall, Englewood Cliffs, NJ, USA; 1973:501-518.
Buşoniu L, Babuška R, De Schutter B: A comprehensive survey of multiagent reinforcement learning. IEEE Transactions on Systems, Man and Cybernetics Part C 2008, 38(2):156-172.
Fudenberg D, Levine DK: The Theory of Learning in Games. The MIT Press, Cambridge, Mass, USA; 1998.
Robinson J: An iterative method of solving a game. The Annals of Mathematics 1969, 54(2):296-301.
Hu J, Wellman MP: Multiagent reinforcement learning: theoretical framework and an algorithm. Proceedings of the 15th International Conference on Machine Learning (ICML '98), July 1998 242-250.
Kushner HJ, Yin GG: Stochastic Approximation and Recursive Algorithms and Applications. Springer, New York, NY, USA; 2003.
Liu J, Yi Y, Proutiere A, Chiang M, Poor HV: Towards utility-optimal random access without message passing. Wireless Communications and Mobile Computing 2010, 10(1):115-128. 10.1002/wcm.897
Yi Y, de Veciana G, Shakkottai S: MAC scheduling with low overheads by learning neighborhood contention patterns. submitted to IEEE/ACM Transactions on Networking
Fu F, van der Schaar M: Learning to compete for resources in wireless stochastic games. IEEE Transactions on Vehicular Technology 2009, 58(4):1904-1919.
Han Z, Pandana C, Liu KJK: Distributive opportunistic spectrum access for cognitive radio using correlated equilibrium and no-regret learning. Proceedings of IEEE Wireless Communications and Networking Conference (WCNC '07), March 2007 11-15.
van der Schaar M, Fu F: Spectrum access games and strategic learning in cognitive radio networks for delay-critical applications. Proceedings of the IEEE 2009, 97(4):720-739.
Hofbauer J, Sigmund K: Evolutionary Games and Population Dynamics. Cambridge University Press, Cambridge, UK; 1998.
Wang B, Liu KJR, Clancy TC: Evolutionary game framework for behavior dynamics in cooperative spectrum sensing. Proceedings of IEEE Conference on Global Communications (Globecom '08), November-December 2008, New Orleans, La, USA 3123-3127.
Sutton PD, Nolan KE, Doyle LE: Cyclostationary signatures in practical cognitive radio applications. IEEE Journal on Selected Areas in Communications 2008, 26(1):13-24.
Sutton RS, Barto AG: Reinforcement Learning: A Introduction. The MIT Press, Cambridge, Mass, USA; 1998.
Metrick A, Polak B: Fictitious play in 2 × 2 games: a geometric proof of convergence. Economic Theory 1994, 4(6):923-933. 10.1007/BF01213819
Robbins H, Monro S: A stochastic approximation method. The Annals of Mathematical Statistics 1951, 2: 400-407.
Tsitsiklis JN: Asynchronous stochastic approximation and Q -learning. Machine Learning 1994, 16(3):185-202.
Acknowledgment
This work was supported by the National Science Foundation under grant CCF-0830451.
Author information
Authors and Affiliations
Corresponding author
Appendices
A. Stochastic Approximation
For being self-contained, we briefly introduce the theory of stochastic approximation and cite the conclusion used for proving Lemma 2.
Essentially, stochastic approximation is used to solve an equation with unknown expression and noisy observations. Consider equation


where  is the unknown variable and the expression of function
is the unknown variable and the expression of function  is unknown. Denote by
is unknown. Denote by  the solution to this equation (we assume that there is only one solution to the equation). Suppose that
the solution to this equation (we assume that there is only one solution to the equation). Suppose that  for
for  and
and  for
for  . We have a series of noisy observations of
. We have a series of noisy observations of  , denoted by
, denoted by  . Then, we can approximate the solution iteratively in the following way (called Robbins-Monro algorithm).
. Then, we can approximate the solution iteratively in the following way (called Robbins-Monro algorithm).


where  is the step for the
is the step for the  th iteration.
th iteration.
The convergence of (A.2) is deeply related to a "mean" ODE, which is given by


The following Theorem (part of Theorem  in [14]) discloses the relationship between the convergence in (A.2) and the mean ODE in (A.3).
in [14]) discloses the relationship between the convergence in (A.2) and the mean ODE in (A.3).
Theorem 1.
If the following assumptions are satisfied,  converges to a limit set
converges to a limit set  in which all points satisfy
in which all points satisfy  with probability 1:
with probability 1:
-
(A)
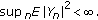
-
(B)
Noise is a martingale difference, that is,
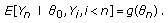 (A.4)
(A.4) -
(C)
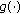 is continuous.
is continuous. -
(D)
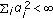 .
. -
(E)
There exists a continuously differentiable function
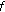 such that
such that 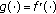 and
and 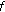 is a constant on the limit set
is a constant on the limit set 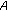 .
.
B. Proof of Lemma 1
Proof.
For simplicity, we fix one system state  since the
since the  -learning procedures for different state
-learning procedures for different state  are mutually independent when the system state is fully observable and the action of each secondary user does not affect the system state. Consider a Nash equilibrium point, at which there is no collision. Without loss of generality, we assume that secondary users
are mutually independent when the system state is fully observable and the action of each secondary user does not affect the system state. Consider a Nash equilibrium point, at which there is no collision. Without loss of generality, we assume that secondary users  use channels
use channels  , respectively.
, respectively.
Now, we choose a set of  such that
such that


Then, we can always choose a sufficiently small  such that
such that




since the right hand sides of (B.2) and (B.3) converge to  and 0, respectively, as
and 0, respectively, as  .
.
Then, we carry out the following iterations, that is, the  -values of the
-values of the  th iteration is given by,
th iteration is given by,  ,
,


Next, we show that,  ,
,  increases while
increases while  (
( ) decreases during the iterations by carrying out inductions on
) decreases during the iterations by carrying out inductions on  . For the first iteration,
. For the first iteration,  is increased while
is increased while  (
( ) is decreased due to the conditions (B.2) and (B.3). Suppose that, in the
) is decreased due to the conditions (B.2) and (B.3). Suppose that, in the  th iteration, the conclusion holds. Then, in the
th iteration, the conclusion holds. Then, in the  th iteration,
th iteration,  is increased due to the expression of the right hand side of (B.4) and the assumptions
is increased due to the expression of the right hand side of (B.4) and the assumptions  and
and  (
( ). For the same reason,
). For the same reason,  is decreased in the
is decreased in the  th iteration. This concludes the induction.
th iteration. This concludes the induction.
Now, we have shown that  is a monotonically increasing sequence while
is a monotonically increasing sequence while  (
( ) is a monotonically decreasing sequence. Since all sequences are bounded (
) is a monotonically decreasing sequence. Since all sequences are bounded ( and
and  (
( )), all sequences converge to their limits, which is the stationary point. This concludes the proof.
)), all sequences converge to their limits, which is the stationary point. This concludes the proof.
C. Proof of Lemma 2
Proof.
We verify the conditions in Theorem 1 one by one.
-
(i)
Condition (A): This is obvious since
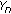 is upper bounded by
is upper bounded by 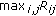 (recall that
(recall that  is the difference between the instantaneous reward and the
is the difference between the instantaneous reward and the 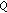 -value).
-value). -
(ii)
Condition (B): The martingale difference noise has been proved right after (14).
-
(iii)
Condition (C): The function
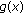 is given by
is given by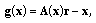 (C.1)
(C.1)where
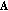 is defined in (12). We only need to verify the continuity of
is defined in (12). We only need to verify the continuity of 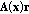 . Obviously, each element in
. Obviously, each element in 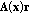 is differentiable with respect to
is differentiable with respect to  . Therefore,
. Therefore, 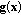 is not only continuous but also differentiable.
is not only continuous but also differentiable. -
(iv)
Condition (D): It is guaranteed by (7).
-
(v)
Condition (E): The function
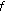 can be defined as the integral of
can be defined as the integral of 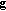 . It is continuously differentiable since
. It is continuously differentiable since  is continuous. It is a constant on the limit set since there is only one point at the limit set.
is continuous. It is a constant on the limit set since there is only one point at the limit set.
D. Proof of Lemma 3
Proof.
We apply Lyapunov's method to analyze the convergence of the ODE in (16). We define the Lyapunov function as


where  is the expected reward of secondary user
is the expected reward of secondary user  at period
at period  .
.
Then, we examine the derivative of the Lyapunov function with respect to time  , that is,
, that is,


where  .
.
We have


where we applied the ODE (16).
Then, we focus on the computation of  .
.
For secondary user  and channel
and channel  , we have
, we have


where the first equation is due to the definition of  and the second equation is due to the rule of the derivative of products.
and the second equation is due to the rule of the derivative of products.
We consider the derivative in (D.4), that is,


where the last equation is obtained from ODE (16).
Substituting (D.5) into (D.4), we obtain


Combining (D.2) and (D.6), we have


where the coefficient  is given by
is given by


if  and
and  , and
, and


if  and
and  . When
. When  ,
,  .
.
It is easy to verify




Therefore, when  is sufficiently large, we have
is sufficiently large, we have


Then, we have


Therefore, when  is sufficiently large, the derivative of the Lyapunov function is strictly negative, which implies that the ODE (16) converges to a stationary point. This concludes the proof.
is sufficiently large, the derivative of the Lyapunov function is strictly negative, which implies that the ODE (16) converges to a stationary point. This concludes the proof.
Remark 1.
We can actually obtain a stronger conclusion from the last part of the proof, that is, the convergence can be assured if


E. Proof of Proposition 2
Proof.
We define a mapping from all  -values to another set of
-values to another set of  -values, which is given by
-values, which is given by


where  is determined by
is determined by  and
and  and
and  is the average reward when secondary user
is the average reward when secondary user  chooses channel
chooses channel  . Note that
. Note that  is a function of all
is a function of all  -values.
-values.
What we need to prove is that  is a contraction mapping. Once this is proved, the remainder part is exactly the same as the proof of the convergence of
is a contraction mapping. Once this is proved, the remainder part is exactly the same as the proof of the convergence of  -learning in [26]. Therefore, we focus on the analysis on the mapping
-learning in [26]. Therefore, we focus on the analysis on the mapping  .
.
We consider two sets of  -values, denoted by
-values, denoted by  and
and  , respectively. Considering the difference after the mapping
, respectively. Considering the difference after the mapping  between the two sets of
between the two sets of  -values, we have
-values, we have


where  means the average reward when the
means the average reward when the  -values are
-values are  . Then, we have
. Then, we have


We discuss the two terms in (E.3) separately. For the first term, we have


where  is the set of states of secondary users except user
is the set of states of secondary users except user  and
and  is the probability of the set of states
is the probability of the set of states  conditioned on the state of secondary user
conditioned on the state of secondary user  ,
,  .
.
When  is sufficiently large, we have
is sufficiently large, we have


where  is a polynomial of order
is a polynomial of order  .
.
Then, it is easy to verify that (E.4) can be rewritten as


where  and
and  are both polynomials of smaller order than
are both polynomials of smaller order than  . Note that the coefficients of both polynomials are independent of the
. Note that the coefficients of both polynomials are independent of the  -values.
-values.
Then, we have


Then, we can always take a sufficiently large  such that
such that


Now, we turn to the second term in (E.3). Without loss of generality, we assume  . We have
. We have


where, in the first inequality, we define  as
as


Due to symmetry, we have


Combining (E.8) and (E.11), we have


which implies


Therefore,  is a contraction mapping under the norm
is a contraction mapping under the norm  . This concludes the proof.
. This concludes the proof.
Remark 2.
Note that, in contrast to the stochastic approximation approach for the proof of the convergence in the complete observation case, we used a different approach to prove the convergence of the learning with partial observations since it is difficult to apply the stochastic approximation in the partial observation case. Although the stochastic approximation approach is slightly more complicated, we can find a finite value for  in (D.14) to assure the convergence. For the contraction mapping approach, we are still unable to find such a finite value for
in (D.14) to assure the convergence. For the contraction mapping approach, we are still unable to find such a finite value for  .
.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, H. Multiagent  -Learning for Aloha-Like Spectrum Access in Cognitive Radio Systems.
J Wireless Com Network 2010, 876216 (2010). https://doi.org/10.1155/2010/876216
-Learning for Aloha-Like Spectrum Access in Cognitive Radio Systems.
J Wireless Com Network 2010, 876216 (2010). https://doi.org/10.1155/2010/876216
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/876216

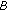 (busy: the channel is occupied by primary users and cannot be used by secondary users) and
(busy: the channel is occupied by primary users and cannot be used by secondary users) and 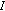 (idle: there is no primary user over this channel). We denote by
(idle: there is no primary user over this channel). We denote by 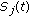 the state of channel
the state of channel 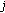 in the sensing period of the
in the sensing period of the 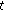 th spectrum access period. For channel
th spectrum access period. For channel  , the transition probability from state
, the transition probability from state 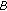 to state
to state 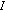 (resp., from state
(resp., from state 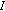 to state
to state 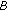 ) is denoted by
) is denoted by 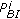 (resp.,
(resp., 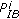 ). We assume that the
). We assume that the 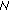 Markov chains for the
Markov chains for the  channels are mutually independent. We also assume perfect spectrum sensing and do not consider possible errors of spectrum sensing.
channels are mutually independent. We also assume perfect spectrum sensing and do not consider possible errors of spectrum sensing.
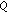 -Learning
-Learning
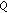 -Value
-Value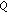 -Values
-Values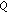 -learning without Information Exchange
-learning without Information Exchange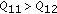 ; therefore, secondary user 1 prefers visiting channel 1; meanwhile, secondary user 2 prefers accessing channel 2 since
; therefore, secondary user 1 prefers visiting channel 1; meanwhile, secondary user 2 prefers accessing channel 2 since  ; then, with large probability, the strategies will converge to a stationary point in which secondary users 1 and 2 access channels 1 and 2, respectively.
; then, with large probability, the strategies will converge to a stationary point in which secondary users 1 and 2 access channels 1 and 2, respectively.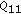 and
and 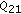 will be reduced until entering either region I or region III.
will be reduced until entering either region I or region III.

 -learning.
-learning. -Learning with Partial Observations
-Learning with Partial Observations
 -learning when
-learning when  ,
,  , and system state is fully observable.
, and system state is fully observable.
 -learning when
-learning when  ,
,  , and system state is fully observable.
, and system state is fully observable.
 and system state is fully observable.
and system state is fully observable.

 values when system state is fully observable.
values when system state is fully observable.

 values versus different
values versus different  and
and  when system state is fully observable.
when system state is fully observable.

 when
when
 and system state is fully observable.
and system state is fully observable.

 when
when
 and system state is fully observable.
and system state is fully observable.



 values in partial observation case.
values in partial observation case.

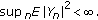
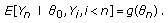
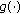 is continuous.
is continuous.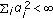 .
.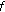 such that
such that 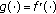 and
and 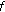 is a constant on the limit set
is a constant on the limit set 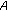 .
.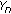 is upper bounded by
is upper bounded by 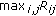 (recall that
(recall that  is the difference between the instantaneous reward and the
is the difference between the instantaneous reward and the 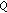 -value).
-value).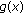 is given by
is given by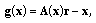
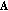 is defined in (12). We only need to verify the continuity of
is defined in (12). We only need to verify the continuity of 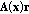 . Obviously, each element in
. Obviously, each element in 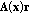 is differentiable with respect to
is differentiable with respect to  . Therefore,
. Therefore, 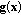 is not only continuous but also differentiable.
is not only continuous but also differentiable.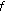 can be defined as the integral of
can be defined as the integral of 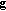 . It is continuously differentiable since
. It is continuously differentiable since  is continuous. It is a constant on the limit set since there is only one point at the limit set.
is continuous. It is a constant on the limit set since there is only one point at the limit set.