- Research Article
- Open access
- Published:
Carrier Frequency Offset Estimation for Multiuser MIMO OFDM Uplink Using CAZAC Sequences: Performance and Sequence Optimization
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 570680 (2011)
Abstract
This paper studies carrier frequency offset (CFO) estimation in the uplink of multi-user multiple-input multiple-output (MIMO) orthogonal frequency division multiplexing (OFDM) systems. Conventional maximum likelihood estimator requires computational complexity that increases exponentially with the number of users. To reduce the complexity, we propose a sub-optimal estimation algorithm using constant amplitude zero autocorrelation (CAZAC) training sequences. The complexity of the proposed algorithm increases only linearly with the number of users. In this algorithm, the different CFOs from different users destroy the orthogonality among training sequences and introduce multiple access interference (MAI), which causes an irreducible error floor in the CFO estimation. To reduce the effect of the MAI, we find the CAZAC sequence that maximizes the signal to interference ratio (SIR). The optimal training sequence is dependent on the CFOs of all users, which are unknown. To solve this problem, we propose a new cost function which closely approximates the SIR-based cost function for small CFO values and is independent of the actual CFOs. Computer simulations show that the error floor in the CFO estimation can be significantly reduced by using the optimal sequences found with the new cost function compared to a randomly chosen CAZAC sequence.
1. Introduction
Compared to single-input single-output (SISO) systems, multiple-input multiple-output (MIMO) systems increase the capacity of rich scattering wireless fading channels enormously through employing multiple antennas at the transmitter and the receiver [1, 2]. Orthogonal Frequency Division Multiplexing (OFDM) is a widely used technology for wireless communication in frequency selective fading channels due to its high spectral efficiency and its ability to "divide" a frequency selective fading channel into multiple flat fading subchannels (subcarriers). Hence, MIMO-OFDM is an ideal combination for applying MIMO technology in frequency fading channels and has been included in various wireless standards such as IEEE 802.11n [3] and IEEE 802.16e [4]. An extension of the MIMO-OFDM system is the multiuser MIMO-OFDM system as illustrated in Figure 1. In such a system, multiple users, each with one or multiple antennas, transmit simultaneously using the same frequency band. The receiver is a base-station equipped with multiple antennas. It uses spatial processing techniques to separate the signals of different users. If we view the signals from different users as signals from different transmit antennas of a virtual transmitter, then the whole system can be viewed as a MIMO system. This system is also known as the virtual MIMO system [5].
Carrier frequency offset (CFO) is caused by the Doppler effect of the channel and the difference between the transmitter and receiver local oscillator (LO) frequencies. In OFDM systems, CFO destroys the orthogonality between subcarriers and causes intercarrier interference (ICI). To ensure good performance of OFDM systems, the CFO must be accurately estimated and compensated. For SISO-OFDM systems, periodic training sequences are used in [6, 7] to estimate the CFO. It is shown that these CFO estimators reach the Cramer-Rao bound (CRB) with low-computational complexity. A similar idea was extended to collocated MIMO-OFDM systems [8–10], where all the transmit antennas are driven by a centralized LO and so are all the receive antennas. In this case, the CFO is still a single parameter. For multiuser MIMO-OFDM systems, each user has its own LO, while the multiple antennas at the base-station (receiver) are driven by a centralized LO. Therefore, in the uplink, the receiver needs to estimate multiple CFO values for all the users. In [11, 12], methods were proposed to estimate multiple CFO values for MIMO systems in flat fading channels. In [13], a semiblind method was proposed to jointly estimate the CFO and channel for the uplink of multiuser MIMO-OFDM systems in frequency selective fading channels. An asymptotic Cramer-Rao bound for joint CFO and channel estimation in the uplink of MIMO-Orthogonal Frequency Division Multiple Access (OFDMA) system was derived in [14] and training strategies that minimize the asymptotic CRB were studied. In [15], a reduced-complexity CFO and channel estimator was proposed for the uplink of MIMO-OFDMA systems using an approximation of the ML cost function and a Newton search algorithm. It was also shown that the reduced-complexity method is asymptotically efficient. The joint CFO and channel estimation for multiuser MIMO-OFDM systems was studied in [16]. Training sequences that minimize the asymptotic CRB were also designed in [16].
It is known in the literature that the computational complexity for obtaining the ML CFO estimates in the uplink of multiuser MIMO-OFDM system grows exponentially with the number of users [15, 16]. A low-complexity algorithm was proposed in [16] for CFO estimation in the uplink of multiuser MIMO OFDM systems based on importance sampling. However, the complexity required to generate sufficient samples for importance sampling may still be high for practical implementations. In this paper, we study algorithms that can further reduce the computational complexity of the CFO estimation. Following a similar approach as in [17], we first derive the maximum likelihood (ML) estimator for the multiple CFO values in frequency selective fading channels. Obtaining the ML estimates requires a search over all possible CFO values and the computational complexity is prohibitive for practical implementations. To reduce the complexity, we propose a sub-optimal algorithm using constant amplitude zero autocorrelation (CAZAC) training sequences, which have zero autocorrelation for any nonzero circular shifts. Using the proposed algorithm, the CFO estimates can be obtained using simple correlation operations and the complexity of this algorithm grows only linearly with the number of users. However, the multiple CFO values destroy the orthogonality between the training sequences of different users. This introduces multiple access interference (MAI) and causes an irreducible error floor in the mean square error (MSE) of the CFO estimates. We derive an expression for the signal to interference ratio (SIR) in the presence of multiple CFO values. To reduce the MAI, we find the training sequence that maximizes the SIR. The optimal training sequence turns out to be dependent on the actual CFO values from different users. This is obviously not practical as it is not possible to know the CFO values and hence select the optimal training sequence in advance. To remove this dependency, we propose a new cost function, which is the Taylor's series approximation of the original cost function. The new cost function is independent of the actual CFO values and is an accurate approximation of the original SIR-based cost function for small CFO values. Using the new cost function, we obtain the optimal training sequences for the following three classes of CAZAC sequences:
-
(i)
Frank and Zadoff Sequences [18],
-
(ii)
Chu Sequences [19],
-
(iii)
Polyphase Sequence by Sueshiro and Hatori (S&H Sequences) [20].
Both Frank and Zadoff sequences and S&H sequences exist for sequence length of  , where
, where  is the length of the sequence and
is the length of the sequence and  is a positive integer, while Chu sequences exist for any integer length. For both Frank and Zadoff and Chu sequences, there are a finite number of sequences for each sequence length. Therefore, the optimal sequence can be obtained using a search among these sequences. However, for S&H sequences, there are infinitely many possible sequences. As the optimization problem for S&H sequences cannot be solved analytically, we resort to a numerical method to obtain a near-optimal solution. To this end, we use the adaptive simulated annealing (ASA) technique [21]. For small sequence lengths, for example,
is a positive integer, while Chu sequences exist for any integer length. For both Frank and Zadoff and Chu sequences, there are a finite number of sequences for each sequence length. Therefore, the optimal sequence can be obtained using a search among these sequences. However, for S&H sequences, there are infinitely many possible sequences. As the optimization problem for S&H sequences cannot be solved analytically, we resort to a numerical method to obtain a near-optimal solution. To this end, we use the adaptive simulated annealing (ASA) technique [21]. For small sequence lengths, for example,  and
and  , we are able to use exhaustive search to verify that the solution obtained using ASA is globally optimal. (Because CFO values are continuous variables, theoretically, it is not possible to obtain the exact optimum using exhaustive computer search, which works in discrete variables. If we keep the step size in the search small enough, we can be sure that the obtained "optimum" is very close to the actual optimum and can be practically assumed to the actual optimum. In this way, we are able to verify the solution obtained by the ASA is "practically" optimal.) Computer simulations were conducted to evaluate the performance of the CFO estimation using CAZAC sequences. We first compare the performance using CAZAC sequences with the performance using two other sequences with good correlation properties, namely, the IEEE 802.11n short training field (STF) [3] and the
, we are able to use exhaustive search to verify that the solution obtained using ASA is globally optimal. (Because CFO values are continuous variables, theoretically, it is not possible to obtain the exact optimum using exhaustive computer search, which works in discrete variables. If we keep the step size in the search small enough, we can be sure that the obtained "optimum" is very close to the actual optimum and can be practically assumed to the actual optimum. In this way, we are able to verify the solution obtained by the ASA is "practically" optimal.) Computer simulations were conducted to evaluate the performance of the CFO estimation using CAZAC sequences. We first compare the performance using CAZAC sequences with the performance using two other sequences with good correlation properties, namely, the IEEE 802.11n short training field (STF) [3] and the  sequences [22]. The results show that the error floor using the CAZAC sequences is more than 10 times smaller compared to the other two sequences. Comparing the three classes of CAZAC sequences, we find that the performance of the Chu sequences is better than the Frank and Zadoff sequences due to the larger degree of freedom in the sequence construction. The S&H sequences have the largest number of degree of freedom in the construction of the CAZAC sequences. However, the simulation results show that they have only very marginal performance gain compared to the Chu sequences. This makes Chu sequences a good choice for practical implementation due to its simple construction and flexibility in sequence lengths. By using the identified optimal sequences, the error floor in the CFO estimation is significantly lower compared to using a randomly selected CAZAC sequence.
sequences [22]. The results show that the error floor using the CAZAC sequences is more than 10 times smaller compared to the other two sequences. Comparing the three classes of CAZAC sequences, we find that the performance of the Chu sequences is better than the Frank and Zadoff sequences due to the larger degree of freedom in the sequence construction. The S&H sequences have the largest number of degree of freedom in the construction of the CAZAC sequences. However, the simulation results show that they have only very marginal performance gain compared to the Chu sequences. This makes Chu sequences a good choice for practical implementation due to its simple construction and flexibility in sequence lengths. By using the identified optimal sequences, the error floor in the CFO estimation is significantly lower compared to using a randomly selected CAZAC sequence.
The rest of the paper is organized as follows. In Section 2, we present the system model and derive the ML estimator for the multiple CFO values. The sub-optimal CFO estimation algorithm using CAZAC sequences is proposed in Section 3. The training sequence optimization problem is formulated in Section 4 and methods are given to obtain the optimal training sequence. In Section 5, we present the computer simulation results and Section 6 concludes the paper.
2. System Model
In this paper, we study a multiuser MIMO-OFDM system with  users. For simplicity of illustration and analysis, we assume that each user has a single transmit antenna. The base-station has
users. For simplicity of illustration and analysis, we assume that each user has a single transmit antenna. The base-station has  receive antennas, where
receive antennas, where  . The received signal at the
. The received signal at the  th receive antenna can be written as
th receive antenna can be written as

where  is the CFO of the
is the CFO of the  th user,
th user,  is the time index, and
is the time index, and  is the number of multipath components in the channel. The
is the number of multipath components in the channel. The  th tab of the channel impulse response between the
th tab of the channel impulse response between the  th user and the
th user and the  th receive antenna is denoted as
th receive antenna is denoted as  ,
,  denotes the transmitted signal from the
denotes the transmitted signal from the  th user and
th user and  is the additive white Gaussian noise at the
is the additive white Gaussian noise at the  th receive antenna. Here we assume the initial phase for each user is absorbed in the channel impulse response. From (1), we can see that we have
th receive antenna. Here we assume the initial phase for each user is absorbed in the channel impulse response. From (1), we can see that we have  different CFO values (
different CFO values ( 's) to estimate. We consider a training sequence of length
's) to estimate. We consider a training sequence of length  and cyclic prefix (CP) of length
and cyclic prefix (CP) of length  . The received signal after removal of CP can be written in an equivalent matrix form
. The received signal after removal of CP can be written in an equivalent matrix form

where  and superscript
and superscript  denotes vector transpose. The CFO matrix of user
denotes vector transpose. The CFO matrix of user  is denoted
is denoted  and is a diagonal matrix with diagonal elements equal to
and is a diagonal matrix with diagonal elements equal to  . We use
. We use  to denote the transmitted signal matrix for the
to denote the transmitted signal matrix for the  th user, which is an
th user, which is an  circulant matrix with the first column defined by
circulant matrix with the first column defined by  . Here we assume
. Here we assume  so the channel vector between the
so the channel vector between the  th user and the
th user and the  th receive antenna
th receive antenna  is an
is an  vector by appending the
vector by appending the  channel impulse response
channel impulse response  vector with
vector with  zeros.
zeros.
Using this system model, the received signals from all  receive antennas can be written as
receive antennas can be written as

where

For clearness of presentation, we use subscripts under the square bracket to denote the size of the corresponding matrix. The vector  is the CFO vector containing the CFO values from all users, and the channels of all users are stacked into the channel matrix
is the CFO vector containing the CFO values from all users, and the channels of all users are stacked into the channel matrix  given as
given as

with  being the channel matrix for the
being the channel matrix for the  th user. The noise matrix is given by
th user. The noise matrix is given by  .
.
Because the noise is Gaussian and uncorrelated, the likelihood function for the channel  and CFO values
and CFO values  can be written as
can be written as

where  and
and  are trial values for
are trial values for  and
and  and
and  is the variance of the AWGN noise. Following a similar approach as in [17], we find that for a fixed CFO vector
is the variance of the AWGN noise. Following a similar approach as in [17], we find that for a fixed CFO vector  , the ML estimate of the channel matrix is given by
, the ML estimate of the channel matrix is given by

where superscript  denotes matrix Hermitian. Substituting (7) into (6) and after some algebraic manipulations, we obtain that the ML estimate of the CFO vector
denotes matrix Hermitian. Substituting (7) into (6) and after some algebraic manipulations, we obtain that the ML estimate of the CFO vector  is given by
is given by

with

and  denotes the trace of a matrix. To obtain the ML estimate of the CFO vector
denotes the trace of a matrix. To obtain the ML estimate of the CFO vector  , a search needs to be performed over the possible ranges of CFO values of all the users. The complexity of this search grows exponentially with the number of users and hence the search is not practical.
, a search needs to be performed over the possible ranges of CFO values of all the users. The complexity of this search grows exponentially with the number of users and hence the search is not practical.
3. CAZAC Sequences for Multiple CFOs Estimation
To reduce the complexity of the CFO estimation for multiuser MIMO-OFDM systems, in this section, we propose a sub-optimal algorithm using CAZAC sequences as training sequences. CAZAC sequences are special sequences with constant amplitude elements and zero autocorrelation for any nonzero circular shifts. This means for a length- CAZAC sequence, we have
CAZAC sequence, we have  and the auto-correlation
and the auto-correlation

for all values of  . Here we use
. Here we use  to denote circular subtraction. Let
to denote circular subtraction. Let  be a circulant matrix with the first column equal to
be a circulant matrix with the first column equal to  . The autocorrelation property of CAZAC sequences can be written in equivalent matrix form as
. The autocorrelation property of CAZAC sequences can be written in equivalent matrix form as

where  is the identity matrix of size
is the identity matrix of size  . This means that
. This means that  is both a unitary (up to a normalization factor of
is both a unitary (up to a normalization factor of  ) and a circulant matrix.
) and a circulant matrix.
In [23], we showed that for collocated MIMO-OFDM systems, using CAZAC sequences as training sequences reduces overhead for channel estimation while achieving Cramer Rao Bound (CRB) performance in the CFO estimation. Here, we extend the idea to the estimation of multiple CFO values in the uplink of multiuser MIMO-OFDM systems. Let the training sequence of the first user be  . The training sequence of the
. The training sequence of the  th user is the cyclic shifted version of the first user, that is,
th user is the cyclic shifted version of the first user, that is,  , where
, where  denotes the shift value. It is straightforward to show that the training sequences between different users have the following properties.
denotes the shift value. It is straightforward to show that the training sequences between different users have the following properties.
-
(i)
The autocorrelation of the training sequence for the
 th user satisfies
th user satisfies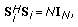 (12)
(12)for
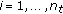 .
. -
(ii)
The cross correlation between training sequences of the
 th and
th and  th users satisfies
th users satisfies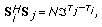 (13)
(13)where
 denotes a matrix which results from cyclically shifting the one elements of the identify matrix to the right by
denotes a matrix which results from cyclically shifting the one elements of the identify matrix to the right by 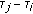 positions.
positions.
For SISO-OFDM systems, an efficient CFO estimation technique is to use periodic training sequences [6, 7]. In this paper, we extend the idea to multiuser MIMO-OFDM systems. In this case, each user transmit two periods of the same training sequences and the received signal over two periods can be written as (We assume here timing synchronization is perfect. We also assume a cyclic prefix with length  is appended to the training sequence during transmission and removed at the receiver.)
is appended to the training sequence during transmission and removed at the receiver.)

Without loss of generality, we show how to estimate the CFO of the first user and the same procedure is applied to all the other users to estimate the other CFO values. Since same procedure is applied to all the users, the complexity of this CFO estimation method increases linearly with the number of users.
We first consider a special case when there are no CFOs for all the other uses except user one, that is,  for
for  . In this case, we cross correlate the training sequence of the first user with the received signal as shown below
. In this case, we cross correlate the training sequence of the first user with the received signal as shown below

Because  is a matrix resulting from cyclic shifting the identity matrix to the right by
is a matrix resulting from cyclic shifting the identity matrix to the right by  elements,
elements,  produces a matrix resulting by cyclic shifting the rows of
produces a matrix resulting by cyclic shifting the rows of  by
by  elements downwards.
elements downwards.
We make sure that the cyclic shift between the  th and
th and  th users is not smaller than the length of the channel impulse response, that is,
th users is not smaller than the length of the channel impulse response, that is,  . Since the channel has only
. Since the channel has only  multipath components, only the first
multipath components, only the first  rows in the
rows in the  matrix
matrix  are nonzero. Therefore,
are nonzero. Therefore,  has all zero elements in the first
has all zero elements in the first  rows when
rows when  for
for  and
and  (notice that to ensure these conditions hold, we need to have the training sequence length
(notice that to ensure these conditions hold, we need to have the training sequence length  ). Hence, the first
). Hence, the first  rows of
rows of  will be free of the interference from all the other users. Let us define
will be free of the interference from all the other users. Let us define  as the first
as the first  rows of the
rows of the  identity matrix; we have
identity matrix; we have

The multiplication of  is to select the first
is to select the first  rows from the matrix
rows from the matrix  . Because the CFOs of all the other users are 0, the shift orthogonality between their training sequences and user 1's training sequence is maintained. In this case,
. Because the CFOs of all the other users are 0, the shift orthogonality between their training sequences and user 1's training sequence is maintained. In this case,  is free of interferences from the other users. Following the similar approach as in [23], we can show that the ML estimate of user 1's CFO given
is free of interferences from the other users. Following the similar approach as in [23], we can show that the ML estimate of user 1's CFO given  can be obtained as
can be obtained as

where  denotes the angle of a complex number. The computational complexity of this estimator is low.
denotes the angle of a complex number. The computational complexity of this estimator is low.
When the other users' CFO values are not zero,  is given by
is given by

From (18), we can see that the orthogonality between the training sequences from different users is destroyed by the non-zero CFO values  . As a result, there is an extra Multiple Access Interference (MAI) term
. As a result, there is an extra Multiple Access Interference (MAI) term  in the correlation output
in the correlation output  . This interference is independent of the noise and therefore it will cause an irreducible error floor in MSE of the CFO estimator in (17). The covariance matrix of the MAI can be expressed as
. This interference is independent of the noise and therefore it will cause an irreducible error floor in MSE of the CFO estimator in (17). The covariance matrix of the MAI can be expressed as

We assume the channels between different transmit and receive antennas are uncorrelated in space and different paths in the multipath channel are also uncorrelated. We define  as the power delay profile (PDP) of the channel between the
as the power delay profile (PDP) of the channel between the  th user and the
th user and the  th receive antenna and we have
th receive antenna and we have

Defining  , we can rewrite the covariance matrix of the interference as
, we can rewrite the covariance matrix of the interference as

where

We can see that the interference power is a function of the training sequence  , the channel delay power profile
, the channel delay power profile  , and the CFO matrices
, and the CFO matrices  .
.
4. Training Sequence Optimization
In the previous section, we showed that the multiple CFO values destroy the orthogonality among the training sequences of different users and introduces MAI. In this section, we study how to find the training sequence such that the signal to interference ratio (SIR) is maximized.
4.1. Cost Function Based on SIR
From the signal model in (18), we can define the SIR of the first user as

From the denominator of (23), we can see that the total interference power depends on the CFO values  of all the other users. As a result, the optimal training sequence that maximizes the SIR is also dependent on
of all the other users. As a result, the optimal training sequence that maximizes the SIR is also dependent on  for
for  . In this case, even if we can find the optimal training sequences for different values of
. In this case, even if we can find the optimal training sequences for different values of  , we still do not know which one to choose during the actual transmission as the values
, we still do not know which one to choose during the actual transmission as the values  are not available before transmission. This makes (23) an unpractical cost function.
are not available before transmission. This makes (23) an unpractical cost function.
Let us look at user 1 again. In the absence of the CFO, the signal from user 1 is contained in the first  rows of the received signal
rows of the received signal  . When the CFO is present, such orthogonality is destroyed and some information from user 1 will be "spilled" to the other rows of
. When the CFO is present, such orthogonality is destroyed and some information from user 1 will be "spilled" to the other rows of  , thus causing interference to the other users. For user 1, therefore, to keep the interference to the other users small, such "spilled" signal power should be minimized. On the other hand, the useful signal we used to estimate the CFO of user 1 is contained in the first
, thus causing interference to the other users. For user 1, therefore, to keep the interference to the other users small, such "spilled" signal power should be minimized. On the other hand, the useful signal we used to estimate the CFO of user 1 is contained in the first  rows of
rows of  and such signal power should be maximized. Therefore, considering user 1 alone, we can define the signal to "spilled" interference (to other users) ratio for user 1 as
and such signal power should be maximized. Therefore, considering user 1 alone, we can define the signal to "spilled" interference (to other users) ratio for user 1 as

where  is the complement of
is the complement of  , that is,
, that is,  is the last
is the last  rows of the
rows of the  identity matrix.
identity matrix.
The denominator in (24) can be expressed as

Substituting this into (24), we have

Now we can define the training sequence optimization problem as

where  denotes
denotes  .
.
From (27), we can see that the optimal training sequence depends on the power delay profile  and the actual CFO value
and the actual CFO value  . The channel delay profile is an environment-dependent statistical property that does not change very frequently. Therefore, in practice, we can store a few training sequences for different typical power delay profiles at the transmitter and select the one that matches the actual channel delay profile. On the other hand, it is impossible to know the actual CFO
. The channel delay profile is an environment-dependent statistical property that does not change very frequently. Therefore, in practice, we can store a few training sequences for different typical power delay profiles at the transmitter and select the one that matches the actual channel delay profile. On the other hand, it is impossible to know the actual CFO  in advance to select the optimal training sequence. In the following, we will propose a new cost function based on SIR approximation which can remove the dependency on the actual CFO
in advance to select the optimal training sequence. In the following, we will propose a new cost function based on SIR approximation which can remove the dependency on the actual CFO  in the optimization.
in the optimization.
4.2. CFO Independent Cost Function
Let us assume that the CFO value  is small. In this case, we can approximate the exponential function in the original cost function by its first-order Taylor series expansion, that is,
is small. In this case, we can approximate the exponential function in the original cost function by its first-order Taylor series expansion, that is,  . Therefore, we have
. Therefore, we have

where  is a diagonal matrix given by
is a diagonal matrix given by  . Using this approximation, we get
. Using this approximation, we get

Here we omitted the subscript 1 for the clearness of the presentation. Therefore, the optimization problem can be approximated as

Notice that the first term  in the summation is independent of
in the summation is independent of  and hence can be dropped. It can be shown that the diagonal elements of the second term
and hence can be dropped. It can be shown that the diagonal elements of the second term  are constant and independent of
are constant and independent of  . Therefore,
. Therefore,  is also independent of
is also independent of  and hence can be dropped from the cost function. The same applies to the third term
and hence can be dropped from the cost function. The same applies to the third term  , which is the conjugate of the second term. Therefore, the final form of the optimization using Taylor's series approximation can be written as
, which is the conjugate of the second term. Therefore, the final form of the optimization using Taylor's series approximation can be written as

The advantage of (31) is that the optimization problem is independent of the actual CFO value  as long as the value of
as long as the value of  is small enough to ensure the accuracy of the Taylor's series approximation in (28).
is small enough to ensure the accuracy of the Taylor's series approximation in (28).
Now we look at how we can obtain the optimal CAZAC training sequences for the cost function (31). In particular, we look at three classes of CAZAC sequences, namely, the Frank-Zadoff sequences [18], the Chu sequences [19], and the S&H sequences [20]. The Frank-Zadoff sequences exist for sequence length  where
where  is any positive integer. For
is any positive integer. For  , all elements of the Frank-Zadoff sequences are BPSK symbols while for
, all elements of the Frank-Zadoff sequences are BPSK symbols while for  , all elements are BPSK and QPSK symbols. Therefore, the advantage of the Frank-Zadoff sequences is that they are simple for practical implementation. The disadvantage is that there are limited numbers of sequences available for each sequence length as shown in Table 1. The advantage of Chu sequences is that the length of the sequence can be an arbitrary integer
, all elements are BPSK and QPSK symbols. Therefore, the advantage of the Frank-Zadoff sequences is that they are simple for practical implementation. The disadvantage is that there are limited numbers of sequences available for each sequence length as shown in Table 1. The advantage of Chu sequences is that the length of the sequence can be an arbitrary integer  . Compared to Frank-Zadoff sequences, there are more sequences available for the same sequence length as shown in Table 1. For both Frank-Zadoff and Chu sequences, there are a finite number of possible sequences for each
. Compared to Frank-Zadoff sequences, there are more sequences available for the same sequence length as shown in Table 1. For both Frank-Zadoff and Chu sequences, there are a finite number of possible sequences for each  . The optimal sequence can be found by using a computer search using the cost function (31). The S&H sequences only exist for sequence length
. The optimal sequence can be found by using a computer search using the cost function (31). The S&H sequences only exist for sequence length  . The sequences are constructed using a size
. The sequences are constructed using a size  phase vector
phase vector  . Therefore, the optimization of training sequence
. Therefore, the optimization of training sequence  is equivalent to the optimization on the phase vector
is equivalent to the optimization on the phase vector  given by
given by

Notice that this is an unconstrained optimization problem and each element of the phase vector can take any values in the interval  . From the construction of the S&H sequence [20], it can be easily shown that
. From the construction of the S&H sequence [20], it can be easily shown that  , where
, where  . Hence, from (32), we can get
. Hence, from (32), we can get  . By letting
. By letting  , the original optimization problem over the
, the original optimization problem over the  -dimension phase vector
-dimension phase vector  can be simplified to the optimization over a
can be simplified to the optimization over a  -dimension phase vector
-dimension phase vector  where
where  .
.
There are an infinite number of possible S&H sequences for each sequence length; it is impossible to use exhaustive computer search to obtain the optimal sequence. We resort to numerical methods and use the adaptive simulated annealing (ASA) method [21] to find a near-optimal sequence. To test the near-optimality of the sequence obtained using the ASA, for smaller sequence lengths of  and
and  , we use exhaustive computer search to obtain the globally optimal S&H sequence. The obtained sequence through computer search is consistent with the sequence obtained using ASA and this proves the effectiveness of the ASA in approaching the globally optimal sequence.
, we use exhaustive computer search to obtain the globally optimal S&H sequence. The obtained sequence through computer search is consistent with the sequence obtained using ASA and this proves the effectiveness of the ASA in approaching the globally optimal sequence.
5. Simulation Results
In this section, we use computer simulations to study the performance of the CFO estimation using CAZAC sequences and demonstrate the performance gain achieved by using the optimal training sequences. In the simulations, we assume a multiuser MIMO-OFDM systems with two users. (In multiuser MIMO-OFDM systems, the number of receive antennas has to be no less than the number of transmit antennas from all users. Due to the practical limitations, it is not possible to implement too many base-station antennas. Therefore, to accommodate more users, the multiuser MIMO-OFDM systems can be used in conjunction with other multiple access schemes such as TDMA and FDMA.) Each user has one transmit antenna and the base-station has two receive antennas. We simulate an OFDM system with 128 subcarriers. The CFO is normalized with respect to the subcarrier spacing. Unless otherwise stated, the actual CFO values for the two users are modeled as random variables uniformly distributed between [−0.5, 0.5]. The mean square error (MSE) of the CFO estimation is defined as

where  and
and  represent the estimated and true CFO's, respectively,
represent the estimated and true CFO's, respectively,  is the number of subcarriers, and
is the number of subcarriers, and  denotes the total number of Monte Carlo trials.
denotes the total number of Monte Carlo trials.
First we compare the performance of CFO estimation using CAZAC sequences with the following two sequences which also have good autocorrelation properties:
In the simulations, we use the 802.11n STF for 40 MHz operations which has a length of 32. For the  sequence, we use a sequence length of 31. To provide a fair comparison, we compare the performance using the 802.11n STF with a length-32 Chu (CAZAC) sequence generated by [19]
sequence, we use a sequence length of 31. To provide a fair comparison, we compare the performance using the 802.11n STF with a length-32 Chu (CAZAC) sequence generated by [19]

and we compare the performance with the  sequence using a length-31 Chu sequence generated by [19]
sequence using a length-31 Chu sequence generated by [19]

The performance of CFO estimation using the 802.11n STF and  Chu sequence is shown in Figure 2. Here we use 16-tab multipath channels and the circular shift between the training sequences of the two users
Chu sequence is shown in Figure 2. Here we use 16-tab multipath channels and the circular shift between the training sequences of the two users  . To gauge the performance of the CFO estimation, we also included the single-user CRB in the comparison. The single-user CRB is obtained by assuming no MAI and can be shown to be [24]
. To gauge the performance of the CFO estimation, we also included the single-user CRB in the comparison. The single-user CRB is obtained by assuming no MAI and can be shown to be [24]

where  is the SNR per receive antenna and
is the SNR per receive antenna and  is the number of subcarriers. From the results, we can see that the CFO estimation using the 802.11n STF has a very high error floor above MSE of
is the number of subcarriers. From the results, we can see that the CFO estimation using the 802.11n STF has a very high error floor above MSE of  . The performance using CAZAC sequences is much better. In low to medium SNR regions, the performance is very close to the single-user CRB. An error floor starts to appear at SNR of about 25 dB. The error floor is around 100 times smaller compared to the error floor using the 802.11n STF.
. The performance using CAZAC sequences is much better. In low to medium SNR regions, the performance is very close to the single-user CRB. An error floor starts to appear at SNR of about 25 dB. The error floor is around 100 times smaller compared to the error floor using the 802.11n STF.
The performance of the CFO estimation using the 
 sequence and Chu sequence is shown in Figure 3. Here to satisfy the condition of
sequence and Chu sequence is shown in Figure 3. Here to satisfy the condition of  , we use 15-tab multipath fading channels and the circular shift between user 1 and 2's training sequence is also set to 15. Again using CAZAC sequences leads to a much better performance. We can see that in low to medium SNR regions, their performance is very close to the single-user CRB. The error floor using CAZAC sequences is more than 10 times smaller than that using the
, we use 15-tab multipath fading channels and the circular shift between user 1 and 2's training sequence is also set to 15. Again using CAZAC sequences leads to a much better performance. We can see that in low to medium SNR regions, their performance is very close to the single-user CRB. The error floor using CAZAC sequences is more than 10 times smaller than that using the  sequence.
sequence.
The performance of CFO estimation using different CAZAC sequences is compared in Figure 4. Here we fix the sequence length to 36 and the multipath channel has  tabs with uniform power delay profile. Comparing the performances of optimal Chu sequence and the optimal Frank-Zadoff sequence, we can see that the error floor of the Chu sequence is smaller. This is because there are more possible Chu sequences compared to Frank-Zadoff sequences and hence more degrees of freedom in the optimization. However, comparing the performance of optimal Chu sequence with that of the optimal S&H sequence, we can see that the additional degrees of freedom in the S&H sequence do not lead to significant performance gain. Compared to the performance using a randomly selected CAZAC sequence, we can see that the error floor using an optimized sequence is significantly smaller. Simulations were also performed in multipath channels with exponential power delay profile and root mean square delay spread equal to 2 sampling intervals. The other simulation parameters are the same as in the uniform power delay profile simulations. Simulation results in Figure 5 show again that the error floor in CFO estimation can be significantly reduced when using the optimized training sequence.
tabs with uniform power delay profile. Comparing the performances of optimal Chu sequence and the optimal Frank-Zadoff sequence, we can see that the error floor of the Chu sequence is smaller. This is because there are more possible Chu sequences compared to Frank-Zadoff sequences and hence more degrees of freedom in the optimization. However, comparing the performance of optimal Chu sequence with that of the optimal S&H sequence, we can see that the additional degrees of freedom in the S&H sequence do not lead to significant performance gain. Compared to the performance using a randomly selected CAZAC sequence, we can see that the error floor using an optimized sequence is significantly smaller. Simulations were also performed in multipath channels with exponential power delay profile and root mean square delay spread equal to 2 sampling intervals. The other simulation parameters are the same as in the uniform power delay profile simulations. Simulation results in Figure 5 show again that the error floor in CFO estimation can be significantly reduced when using the optimized training sequence.
From both Figures 4 and 5, we can see that the gain of using S&H sequences compared to Chu sequences is really small. Therefore, in practical implementation, it is better to use the Chu sequence because it is simple to generate and it is available for all sequence lengths. Another advantage of the Chu sequence is that the optimal Chu sequence obtained using cost function (31) is the same for the uniform power delay profile and some exponential power delay profiles we tested. Hence, a common optimal Chu sequence can be used for both channel PDP's. This is not the case for the S&H sequences.
Figure 6 shows the performance of CFO estimation for different lengths of optimal Chu sequences. Here we fix the channel length to  . From the previous sections, to accommodate two users, the minimum sequence length is
. From the previous sections, to accommodate two users, the minimum sequence length is  . Therefore, we need Chu sequences of length at least 36. We compare the performance of the optimal length-36 sequence with that of optimal length-49 and length-64 sequences. For the length-49 sequence, the cyclic shift between training sequence of two users is 24, while for length-64 sequence, the cyclic shift is 32. From the comparison, we can see that there are two advantages using a longer sequence. Firstly, in the low to medium SNR regions, there is SNR gain in the CFO estimation due to the longer sequences length. Secondly, in the high SNR regions, the error floor using longer sequences is much smaller. This can be explained using Figure 7. In Figure 7, we plotted the signal power for user 1 and user 2 after the correlation operation in (15) for sequence length of 36 and 64. In the absence of the CFO, user 1's signal should be contained in the first 18 samples (
. Therefore, we need Chu sequences of length at least 36. We compare the performance of the optimal length-36 sequence with that of optimal length-49 and length-64 sequences. For the length-49 sequence, the cyclic shift between training sequence of two users is 24, while for length-64 sequence, the cyclic shift is 32. From the comparison, we can see that there are two advantages using a longer sequence. Firstly, in the low to medium SNR regions, there is SNR gain in the CFO estimation due to the longer sequences length. Secondly, in the high SNR regions, the error floor using longer sequences is much smaller. This can be explained using Figure 7. In Figure 7, we plotted the signal power for user 1 and user 2 after the correlation operation in (15) for sequence length of 36 and 64. In the absence of the CFO, user 1's signal should be contained in the first 18 samples ( ). However, due to CFO, some signal components are leaked into the other samples and become interference to user 2. For the case of
). However, due to CFO, some signal components are leaked into the other samples and become interference to user 2. For the case of  and
and  , all the leaked signals from user 1 become interference to user 2 and vice versa. If we use a longer training sequence, there is some "guard time" between the useful signals of the two users as shown in Figure 7 for the
, all the leaked signals from user 1 become interference to user 2 and vice versa. If we use a longer training sequence, there is some "guard time" between the useful signals of the two users as shown in Figure 7 for the  case. As we only take the useful
case. As we only take the useful  samples for CFO estimation (16), only part of the leaked signal becomes interference. Hence, the overall SIR is improved. The cost of using longer sequences is the additional training overhead that is required. Therefore, based on the requirement on the precision of CFO estimation, the system design should choose the best sequence length that achieves the best compromise between performance and overhead.
samples for CFO estimation (16), only part of the leaked signal becomes interference. Hence, the overall SIR is improved. The cost of using longer sequences is the additional training overhead that is required. Therefore, based on the requirement on the precision of CFO estimation, the system design should choose the best sequence length that achieves the best compromise between performance and overhead.
6. Conclusions
In this paper, we studied the CFO estimation algorithm in the uplink of the multiuser MIMO-OFDM systems. We proposed a low-complexity sub-optimal CFO estimation methods using CAZAC sequences. The complexity of the proposed algorithm grows only linearly with the number of users. We showed that in this algorithm, multiple CFO values from multiple users cause MAI in the CFO estimation. To reduce such detrimental effect, we formulated an optimization problem based on the maximization of the SIR. However, the optimization problem is dependent on the actual CFO values which are not known in advance. To remove such dependency, we proposed a new cost function which closely approximate the SIR for small CFO values. Using the new cost function, we can obtain optimal training sequences for a different class of CAZAC sequences. Computer simulations show that the performance of the CFO estimation using CAZAC sequence is very close to the single-user CRB for low to medium SNR values. For high SNR, there is an error floor due to the MAI. By using the obtained optimal CAZAC sequence, such error floor can be significantly reduced compared to using a randomly chosen CAZAC sequence.
References
Foschini GJ: Layered space-time architecture for wireless communication in a fading environment when using multi-element antennas. Bell Labs Technical Journal 1996, 1(2):41-59.
Telatar E: Capacity of multi-antenna Gaussian channels. European Transactions on Telecommunications 1999, 10(6):585-595. 10.1002/ett.4460100604
IEEE P802.11n/D1.10 Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) specifications: Enhancements for HigherThroughput IEEE Std., February 2007
IEEE 802.16e: Air Interface for Fixed and Mobile Broadband Wireless Access Systems Amendment 2: Physical and Medium AccessControl Layers for Combined Fixed and Mobile Operation in Licensed Bands IEEE Std., 2006
Dohler M, Lefranc E, Aghvami H: Virtual antenna arrays for future wireless mobile communication systems. Proceedings of the International Conference on Telecommunications (ICT '02), June 2002, Beijing, China 501-505.
Moose PH: Technique for orthogonal frequency division multiplexing frequency offset correction. IEEE Transactions on Communications 1994, 42(10):2908-2914. 10.1109/26.328961
Schmidl TM, Cox DC: Robust frequency and timing synchronization for OFDM. IEEE Transactions on Communications 1997, 45(12):1613-1621. 10.1109/26.650240
Mody AN, Stüber GL: Synchronization for MIMO OFDM systems. Proceedings of the IEEE Global Telecommunicatins Conference (GLOBECOM '01), November 2001 1: 509-513.
Stuber GL, Barry JR, Mclaughlin SW, Li YE, Ingram MA, Pratt TG: Broadband MIMO-OFDM wireless communications. Proceedings of the IEEE 2004, 92(2):271-293. 10.1109/JPROC.2003.821912
Van Zelst A, Schenk TC: Implementation of a MIMO OFDM-based wireless LAN system. IEEE Transactions on Signal Processing 2004, 52(2):483-494. 10.1109/TSP.2003.820989
Besson O, Stoica P: On parameter estimation of MIMO flat-fading channels with frequency offsets. IEEE Transactions on Signal Processing 2003, 51(3):602-613. 10.1109/TSP.2002.808102
Yao Y, Ng TS: Correlation-based frequency offset estimation in MIMO system. Proceedings of the 58th IEEE Vehicular Technology Conference (VTC '03), October 2003 1: 438-442.
Zeng Y, Leyman RA, Ng TS: Joint semiblind frequency offset and channel estimation for multiuser MIMO-OFDM uplink. IEEE Transactions on Communications 2007, 55(12):2270-2278.
Sezginer S, Bianchi P, Hachem W: Asymptotic Cramér-Rao bounds and training design for uplink MIMO-OFDMA systems with frequency offsets. IEEE Transactions on Signal Processing 2007, 55(7):3606-3622.
Sezginer S, Bianchi P: Asymptotically efficient reduced complexity frequency offset and channel estimators for uplink MIMO-OFDMA systems. IEEE Transactions on Signal Processing 2008, 56(3):964-979.
Chen J, Wu YC, Ma S, Ng TS: Joint CFO and channel estimation for multiuser MIMO-OFDM systems with optimal training sequences. IEEE Transactions on Signal Processing 2008, 56(8):4008-4019.
Morelli M, Mengali U: Carrier-frequency estimation for transmissions over selective channels. IEEE Transactions on Communications 2000, 48(9):1580-1589. 10.1109/26.870025
Frank R, Zadoff S, Heimiller R: Phase shift pulse codes with good periodic correlation properties (corresp.). IRE Transactionson Information Theory 1962, 8(6):381-382. 10.1109/TIT.1962.1057786
Chu DC: Polyphase codes with good periodic correlation properties. IEEE Transactions on Information Theory 1972, 18(4):531-532. 10.1109/TIT.1972.1054840
Sueshiro N, Hatori M: Modulatable orthogonal seqeuences and their application to SSMA systems. IEEE Transactions on Information Theory 1988, 34(1):93-100. 10.1109/18.2605
Ingber L: Adaptive simulated annealing (ASA). Global optimization C-code, Caltech Alumni Association, Pasadena, Calif, USA, 1993, http://www.ingber.com
Solomon S, Gong G: Signal Design for Good Correlation: For Wireless Communication, Cryptography, and Radar. Cambridge Univeristy Press, Cambridge, UK; 2005.
Yan W, Attallaht S, Bergmans JWM: Efficient training sequence for joint carrier frequency offset and channel estimation for MIMO-OFDM systems. Proceedings of the IEEE International Conference on Communications (ICC '07), June 2007 2604-2609.
Schenk TCW, Van Zelst A: Frequency synchronization for MIMO OFDM wireless LAN systems. Proceedings of the IEEE 58th Vehicular Technology Conference (VTC '03), October 2003 2: 781-785.
Acknowledgment
The work presented in this paper was supported (in part) by the Dutch Technology Foundation STW under the project PREMISS. Parts of this work were presented at IEEE Wireless Communication and Networking conference (WCNC) April 2009.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wu, Y., Bergmans, J.W.M. & Attallah, S. Carrier Frequency Offset Estimation for Multiuser MIMO OFDM Uplink Using CAZAC Sequences: Performance and Sequence Optimization. J Wireless Com Network 2011, 570680 (2011). https://doi.org/10.1155/2011/570680
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/570680

 th user satisfies
th user satisfies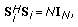
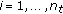 .
. th and
th and  th users satisfies
th users satisfies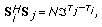
 denotes a matrix which results from cyclically shifting the one elements of the identify matrix to the right by
denotes a matrix which results from cyclically shifting the one elements of the identify matrix to the right by 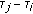 positions.
positions. sequences [
sequences [
 Chu sequences and IEEE 802. 11n STF for uniform power delay profile.
Chu sequences and IEEE 802. 11n STF for uniform power delay profile.
 Chu sequences and
Chu sequences and
 sequence for uniform power delay profile.
sequence for uniform power delay profile.

 CAZAC sequences for
CAZAC sequences for
 channel for uniform power delay profile.
channel for uniform power delay profile.

 CAZAC sequences for
CAZAC sequences for
 channel for exponential power delay profile.
channel for exponential power delay profile.

 channel for uniform power delay profile.
channel for uniform power delay profile.
