- Research Article
- Open access
- Published:
Secure Clustering and Symmetric Key Establishment in Heterogeneous Wireless Sensor Networks
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 893592 (2011)
Abstract
Information security in infrastructureless wireless sensor networks (WSNs) is one of the most important research challenges. In these networks, sensor nodes are typically sprinkled liberally in the field in order to monitor, gather, disseminate, and provide the sensed data to the command node. Various studies have focused on key establishment schemes in homogeneous WSNs. However, recent research has shown that achieving survivability in WSNs requires a hierarchy and heterogeneous infrastructure. In this paper, to address security issues in the heterogeneous WSNs, we propose a secure clustering scheme along with a deterministic pairwise key management scheme based on public key cryptography. The proposed security mechanism guarantees that any two sensor nodes located in the same cluster and routing path can directly establish a pairwise key without disclosing any information to other nodes. Through security performance evaluation, it is shown that the proposed scheme guarantees node-to-node authentication, high resiliency against node capture, and minimum memory space requirement.
1. Introduction
The extensive rise of using wireless sensor networks (WSNs) in diverse applications such as hostile, unattended, and inaccessible environments mandates the users to be more assured about the security compared to the survivability. The inherent nature of wireless sensor nodes, such as being subject to resource constraints (power, processing, and communication), easily captured, and possibly tampered with, causes other security schemes developed for infrastructure-based wireless networks to be infeasible for WSNs [1, 2]. An example of these sensor nodes is the reduced function devices (RFDs) defined in the IEEE 802.15.4-2006 standard [3].
As long as security schemes provide confidentiality, authentication, and integrity, which are critical for such applications, a secure and survivable infrastructure is always desired. Network survivability has been defined as the ability of the network to fulfill its mission in the presence of attacks and/or failures in a timely manner [4]. As a standard criteria to enhance scalability and survivability in the WSNs, clustering sensor nodes into some groups is considered in the literature, see, for example, [5–9]. Due to the energy constraint nature of wireless sensor nodes and their limited transmission range, establishing multihop routing toward the gateway is more efficient than having direct transmission [7]. Moreover, data transmission consumes the most energy in comparison with data computation. Consequently, sending signals in an optimal power level is very crucial. From the security point of view, through compromising a sensor node by an adversary in a multi-hop path, the information on the node is exposed, and an attacker might be able to control the operation of the captured node. Therefore, for the purpose of securing communication links in WSNs, every message should be encrypted and authenticated by any two individual sensor nodes [10].
The secure clustering and key establishments are challenging problem in the WSNs. Therefore, an efficient key management scheme should be designed in order to distribute the cryptographic keys amongst the sensor nodes. It is noted that using a single traditional symmetric key is not secure; because sensor nodes are not tamper proof and upon being captured by an adversary, all information will be exposed to the adversaries [11]. Recently, incorporating pairwise keys for secure communication amongst sensor nodes in the heterogeneous WSNs has been considered in [12, 13].
In this paper, we investigate secure clustering of wireless sensor nodes with evaluating their survivability concurrently. To date, numerous key establishment schemes have been proposed for homogeneous WSNs incorporating symmetric keys, that is, what is mentioned in [1, 11, 14–17]. In these schemes, the secure connectivity is based on the probability of sharing some symmetric keys and key materials among sensor nodes. Note that these schemes not only suffer from high computation cost, communication overhead, and large memory requirements, but also there is no guarantee for secure key establishment among all sensor nodes. Moreover, due to the resource constraint nature of sensor nodes, employing asymmetric and public key cryptography in WSNs using these schemes is slow, complex, and infeasible [18].
Recently, Malan et al., [19], demonstrated that a light-weight type of public key cryptography called elliptic curve cryptography (ECC) is computationally feasible for resource-constrained sensor nodes in WSNs. In [20], a public key cryptography scheme called TinyECC is presented. This scheme is based on software implementation of ECC on TinyOS for sensor nodes. To have an acceptable security level, it has been demonstrated that ECC requires considerably less resources compared with RSA [21] depending on the key size. In [22], it has been shown that even RSA can be feasible for sensor nodes under certain conditions, such as employing a dedicated hardware accelerator for cryptographic computations. Furthermore, recent works such as those in [23, 24] have presented the use of ECC public key cryptography for WSNs.
In clustered WSNs, there is a hierarchy among the nodes regarding their capabilities. Gateways are more powerful and have greater resources while sensor nodes are limited in resources. In these networks, gateways form a virtual infrastructure and sensor nodes connect to the gateways in a direct or multi-hop routes [25]. The gateways are assumed to be tamper proof and can be used to distribute cryptographic keys to the sensor nodes. Recent research (see, e.g., [11, 12, 26–29]) has assumed that the adversary is present after node deployment and key establishment phases. Consequently, the adversary is unable to compromise the links without actually capturing a sensor node. However, in situations such as enemy battle fields, borderline monitoring, and autonomous networks with high-security requirements, it is not practical to assume that the adversary does not exist in the field during deployment and the exchanged information may be recorded/altered by the adversary. Therefore, a security mechanism should be proposed to solve this problem.
In this paper, we capitalize on the strength of public key cryptography to establish secure communication in clustered WSNs. Since gateways in clustered WSNs are assumed to be powerful and tamper proof, they can operate as a key distribution center (KDC) within each cluster. We present a deterministic pairwise key establishment scheme for the clustered WSNs using public key cryptography. In comparison with the previous works available in the literature, the proposed scheme has the following contributions.
-
(i)
We propose a new secure clustering scheme for the heterogeneous WSNs incorporating ECC. The key management scheme is performed in the early phase of clustering and bootstrapping with the assumption that the adversary exists in the environment.
-
(ii)
Instead of preloading large number of keys into each sensor node, we embed the public key of the gateways into each sensor node before deployments. Therefore, any broadcast from the gateways can be authenticated easily by the legitimate sensor nodes using elliptic curve digital signature algorithm (ECDSA) [30].
-
(iii)
The memory complexity and the overall communication overhead of the presented scheme are analyzed in terms of the number of neighbor nodes available for each sensor node. Consequently, the number of symmetric keys required to be stored in each sensor node is obtained efficiently. It is shown that the memory requirements of the proposed scheme are less than its counterparts.
-
(iv)
We investigate the node/link compromise probability regarding the number of hops. Note that when a node is captured by the adversary, the pairwise nature of the proposed scheme exposes no information from other communication links.
In the proposed scheme, all messages broadcasted from the gateways should be authenticated. Therefore, the messages from illegitimate users or compromised sensor nodes can be easily rejected by the other nodes.
The organization of this paper is as follows. In Section 2, we review the related work. The preliminaries and network model are stated in Section 3. The proposed secure clustering scheme is presented in Section 4. Section 5 shows an analysis on node degree in the proposed network model for clustered WSNs. The performance analysis and simulation results are reported in Section 6. Finally, we conclude the paper in Section 7.
2. Related Work
In this section, we review the related works that have been previously proposed for key management in WSNs. To be more specific and to improve the comparison, we focus on the hierarchical/heterogeneous networks rather than distributed and homogeneous WSNs.
The idea of using a pairwise key scheme to secure communication links in WSNs is proposed by Chan et al., [14]. In this scheme, each node stores pairwise keys between other nodes in the entire network. This scheme allows node-to-node authentication; however, upon node capture all the keys in the WSN are revealed. Furthermore, the scheme is not scalable for large networks. In [26], a low-energy key management protocol for clustered WSNs is presented, where all sensor nodes of the cluster are randomly assigned to each gateway within the clusters before deployment.
Recently, a probabilistic unbalanced and distributed scheme is presented for heterogeneous WSNs in [31]. Their scheme leverages the existence of a small percentage of powerful (more capable) sensor nodes beyond the low-power sensor nodes. The powerful nodes are equipped with additional keys and act as gateways within the network. These nodes are assumed to be tamper proof if they are captured by an adversary. It has been shown that their scheme, which is based on the work proposed entirely in [11], not only provides an equal level of security but also reduces the effects of both single and multiple node capture attacks.
A uniform framework for random key management in the distributed peer-to-peer WSNs with heterogeneous sensor nodes is proposed in [12]. Indeed, similar to [31], the deployment of some heterogeneous sensor nodes (called high-class nodes) amongst the low-class sensor nodes has been studied. In this heterogeneous WSN, the connectivity between a low-class node and a high-class node is more important than the connectivity between two low-class sensor nodes. In [31], a hybrid security mechanism is proposed that can work with or without the presence of KDC. Here, all the sensor nodes are preloaded with a random set of keys drawn from a pool before deployment. Whenever KDC is available, each gateway shares a public and private key combination with KDC. The authors evaluate connectivity, reliability, and resiliency of their scheme, but the memory requirement may not be scalable in certain situations.
In [18], the concept of incorporating deployment knowledge for key establishments in heterogeneous WSNs is presented. This scheme relies on prior deployment knowledge and location information. It should be noted that in some applications such information is not available.
An efficient public key-based heterogeneous sensor network key distribution scheme is proposed in [32]. This scheme provides facilities for in-network processing, which helps optimize usage of sensor resources incorporating a certificate generation using the private key of the base station. The authors of [2] proposed a key predistribution scheme for heterogeneous WSNs based on symmetric key techniques. Note that they do not provide a prefect tradeoff between resiliency against node capture and memory storage requirements.
In [33], an identity and pairing-based secure key management scheme for heterogeneous sensor networks is presented. In this scheme, sensor nodes do not need to store any key of the other nodes, rather it computes secret sharing key using pairing and identity properties. In [34], a multiuser broadcast authentication is presented that emphasizes the use of public key cryptography in heterogeneous WSNs. The scheme is of interest but is applicable for special kind of WSNs with many user nodes.
3. Preliminaries
In this section, we describe the notations and network model used for the clustered WSNs.
3.1. Notations and Definitions
Let  and
and  denote the senor node
denote the senor node  ,
,  and the gateway
and the gateway  ,
,  , in the network, respectively. We assume that each sensor node and gateway are identified by a unique ID number
, in the network, respectively. We assume that each sensor node and gateway are identified by a unique ID number  and
and  , respectively, where
, respectively, where  and
and  are the largest ID numbers. We use
are the largest ID numbers. We use  to represent the number of edges connected securely to a sensor node
to represent the number of edges connected securely to a sensor node  . The transmission ranges of all sensor nodes and all the gateways are noted by
. The transmission ranges of all sensor nodes and all the gateways are noted by  and
and  , respectively, where
, respectively, where  . Therefore, a sensor node and a gateway can communicate with each other if they are within the distance
. Therefore, a sensor node and a gateway can communicate with each other if they are within the distance  of each other.
of each other.
Definition 1.
A set of sensor nodes  is a covering set of area
is a covering set of area  if and only if for each point, say
if and only if for each point, say  , there is
, there is  that
that  covers
covers  . The senor node
. The senor node  covers point
covers point  if it falls into the transmission range of the node
if it falls into the transmission range of the node  , that is,
, that is,  [8].
[8].
The largest radius of a cluster was covered by a gateway  , defined by
, defined by  , and approximated by multiplying the range of each sensor node,
, and approximated by multiplying the range of each sensor node,  , with the number of hops to the gateway,
, with the number of hops to the gateway,  , that is,
, that is,  .
.
Definition 2.
Minimum spanning tree [35]: given a connected weighted graph  , a minimum spanning tree covers all the vertices
, a minimum spanning tree covers all the vertices (contains
(contains  edges) of
edges) of  that has minimal total edge weight.
that has minimal total edge weight.
Definition 3.
Shortest path tree [35]: a shortest path tree of a connected weighted graph  is a spanning tree of
is a spanning tree of  , consisting of a root node
, consisting of a root node  , that the distance between
, that the distance between  and all other vertices in
and all other vertices in  is minimal.
is minimal.
The goal of a minimum spanning tree is minimum weight, while the goal of a shortest path tree is to preserve distances from the root [35].
Definition 4.
Digital signature [30]: a digital signature algorithm is a mathematical scheme and a cryptographic tool for demonstrating nonrepudiation, authenticating the integrity and origin of a signed message. A private key is used by the signer to generate the digital signature for the message, and the public key is used by anyone to verify the signature. Note that ECDSA and RSA are popular digital signature algorithms.
All other notations used in this paper with their definition are summarized in Table 1.
3.2. Network Model
In this section, an explanation regarding secure operation of the clustered WSNs is presented. Then, an elaboration on how to establish security in the initial phase of bootstrapping and clustering of these networks is given. In this model, it is assumed that the number of gateways is relatively small in comparison with the number of sensor nodes, that is,  , and the gateways are aware of their location information and can communicate with each other and the base station (BS) securely. An illustration of a typical clustered WSNs is shown in Figure 1. To meet the coverage requirements, we assume that all sensor nodes are distributed uniformly and randomly in the monitoring area
, and the gateways are aware of their location information and can communicate with each other and the base station (BS) securely. An illustration of a typical clustered WSNs is shown in Figure 1. To meet the coverage requirements, we assume that all sensor nodes are distributed uniformly and randomly in the monitoring area  . Note that sensor nodes have no knowledge about their geographic location information.
. Note that sensor nodes have no knowledge about their geographic location information.
In this model, two phases of operations, namely preloading and deployment, are proposed. In what follows, these phases are explained.
3.2.1. Prior Deployment and Preloading Phase
Before sensor nodes are randomly deployed in an environment, a server is used to generate and preload required keys based on ECC into sensor nodes and gateways. As illustrated in Figure 2(a), a sensor node, say  , is preloaded with its own public key, that is,
, is preloaded with its own public key, that is,  , private key, that is,
, private key, that is,  , and the public key of all existing gateways in the network, that is,
, and the public key of all existing gateways in the network, that is,  . Consequently, the gateway
. Consequently, the gateway  is preloaded with the public key of all gateways (including its own)
is preloaded with the public key of all gateways (including its own)  , its private key
, its private key  , and the public keys of all sensor nodes
, and the public keys of all sensor nodes  in the network. These keys are embedded in the sensor nodes and the gateways.
in the network. These keys are embedded in the sensor nodes and the gateways.
3.2.2. Deployment Phase
In clustered WSNs, sensor nodes are deployed randomly and uniformly in a manner similar to distributed WSNs as explained entirely in [11, 36]. The gateways are deployed within the field, such that each sensor node can hear from at least one gateway. This is achieved by varying the transmission range of gateways,  , in the network during the initial communication setup. We assume that the gateways know the location of the BS and communicate with the BS directly or in a multi-hop manner securely.
, in the network during the initial communication setup. We assume that the gateways know the location of the BS and communicate with the BS directly or in a multi-hop manner securely.
4. Proposed Secure Clustering
Sensor nodes in clustered WSNs should be securely partitioned into clusters. Therefore, we assume that if the adversaries exist in the field, they are unable to comprehend the exchanged information. In Figure 1, a simple network with two gateways ( and
and  ) and 16 sensor nodes (
) and 16 sensor nodes ( to
to  ) is illustrated. The gateway
) is illustrated. The gateway  in each cluster should securely discover all the sensor nodes which belong to it. Additionally, sensor nodes should be aware of their assigned gateway/cluster.
in each cluster should securely discover all the sensor nodes which belong to it. Additionally, sensor nodes should be aware of their assigned gateway/cluster.
As depicted in Figure 2(b), each gateway  broadcasts the message
broadcasts the message  to all sensor nodes with a random delay, that is,
to all sensor nodes with a random delay, that is,

Here,  denotes the broadcast message and as presented in (1)
denotes the broadcast message and as presented in (1)  calculates
calculates  as follows. First, a one-way hash function
as follows. First, a one-way hash function  is executed over the
is executed over the  , where "
, where " " denotes the concatenation operator. Second, an elliptic curve digital signature [30] is calculated over the hash results using the private key of the gateway
" denotes the concatenation operator. Second, an elliptic curve digital signature [30] is calculated over the hash results using the private key of the gateway  , that is,
, that is,  . The final message should be accompanied by the public key of the gateway
. The final message should be accompanied by the public key of the gateway  , that is,
, that is,  , message
, message  , and
, and  . This broadcast will be repeated several times to ensure that the maximum number of sensor nodes receives it.
. This broadcast will be repeated several times to ensure that the maximum number of sensor nodes receives it.
For the purpose of message authentication, upon receiving the broadcast message, the sensor node  makes a list for all the received messages from the gateways as
makes a list for all the received messages from the gateways as  , where
, where  ,
,  , is the number of gateways from which a sensor node received a broadcast message. Priority of the generated list is based on signal-to-noise ratio (SNR) of the received message, that is,
, is the number of gateways from which a sensor node received a broadcast message. Priority of the generated list is based on signal-to-noise ratio (SNR) of the received message, that is,  , where the
, where the  is the received signal power from the gateway
is the received signal power from the gateway  for
for  . Afterwards, each sensor node
. Afterwards, each sensor node  will verify the message integrity using ECDSA with public key of the gateways and compares the received public key with its pre-loaded one. Note that verifying the authenticity of the public key of a gateway is finding out whether the attached public key of the gateway is the same as the one embedded in the memory of a sensor node. If the received public key does not match the pre-loaded one, sensor node
will verify the message integrity using ECDSA with public key of the gateways and compares the received public key with its pre-loaded one. Note that verifying the authenticity of the public key of a gateway is finding out whether the attached public key of the gateway is the same as the one embedded in the memory of a sensor node. If the received public key does not match the pre-loaded one, sensor node  will reject the broadcast message. This prevents sensor nodes from performing expensive verification on the fake signatures broadcasted from the adversaries [37].
will reject the broadcast message. This prevents sensor nodes from performing expensive verification on the fake signatures broadcasted from the adversaries [37].
Furthermore, each sensor node  can determine the distance
can determine the distance  from the desired gateway
from the desired gateway  incorporating received signal strength indicator (RSSI) [38]. The minimum distance from the gateway
incorporating received signal strength indicator (RSSI) [38]. The minimum distance from the gateway  is called one-hop distance as
is called one-hop distance as  , in which sensor nodes in this distance can communicate with the gateway directly. Using a global positioning system (GPS) for location finding [36] and time distance calculation [15] requires extra hardware costs and tight time synchronization, respectively. Furthermore, it has been shown in [38] that employing RSSI is more reliable in determining connectivity compared to the location information, as the location information is not available in various applications.
, in which sensor nodes in this distance can communicate with the gateway directly. Using a global positioning system (GPS) for location finding [36] and time distance calculation [15] requires extra hardware costs and tight time synchronization, respectively. Furthermore, it has been shown in [38] that employing RSSI is more reliable in determining connectivity compared to the location information, as the location information is not available in various applications.
The Breadth-First search algorithm [39] is used by the gateway in each cluster to find which sensor nodes select the gateway  as their cluster head. Note that a similar algorithm is used in [6]. The gateway
as their cluster head. Note that a similar algorithm is used in [6]. The gateway  broadcasts a message requesting sensor nodes to notify the gateway if they are within the communication distance
broadcasts a message requesting sensor nodes to notify the gateway if they are within the communication distance  from the gateway. In this case, each sensor node
from the gateway. In this case, each sensor node  encrypts its ID concatenated with its public key using the public key of the desired gateway. This message is transmitted by a sensor node at maximum power to acknowledge the desired gateway in the top of its list
encrypts its ID concatenated with its public key using the public key of the desired gateway. This message is transmitted by a sensor node at maximum power to acknowledge the desired gateway in the top of its list  as follows:
as follows:

where  denotes the encryption function using the public key of gateway
denotes the encryption function using the public key of gateway  . Then, the gateway
. Then, the gateway  decrypts this message by using its private key as follows:
decrypts this message by using its private key as follows:

In this case, the gateway  compares the received public key from the sensor nodes with the ones that are embedded in its memory prior to deployment. This helps to prevent an adversary from throwing illegitimate nodes into a cluster and mounting a denial-of-service (DoS) attack.
compares the received public key from the sensor nodes with the ones that are embedded in its memory prior to deployment. This helps to prevent an adversary from throwing illegitimate nodes into a cluster and mounting a denial-of-service (DoS) attack.
As a large number of sensor nodes will respond to a gateway, avoiding contention is difficult. Since contention causes collisions, this affects the survivability of the network. Therefore, a suitable medium access control (MAC) protocol is required to be installed in each sensor node. It is noted that assuming sensor nodes to be time synchronized is infeasible because of the large number of nodes. To overcome this problem, the contention-based and self-stabilizing MAC protocol presented in [40] is incorporated here. Eventually, each gateway will compile a list of all the sensor nodes in its cluster along with their IDs and public keys.
At this point, the public keys of sensor nodes and gateways are authenticated. Now, each gateway  will ask its one-hop sensor nodes
will ask its one-hop sensor nodes  (e.g.,
(e.g.,  ,
,  , and
, and  of cluster 2 in Figure 1) within the cluster to broadcast a message to ask its one-hop neighbors in the cluster to report to
of cluster 2 in Figure 1) within the cluster to broadcast a message to ask its one-hop neighbors in the cluster to report to  . In this case, sensor node
. In this case, sensor node  acts as the parent node to the nodes in its one-hop neighborhood. Similarly, the other neighbors ask their one-hop neighbors to report themselves. Therefore, every node within the cluster will connect to the gateway in a single or multi-hop route, that is,
acts as the parent node to the nodes in its one-hop neighborhood. Similarly, the other neighbors ask their one-hop neighbors to report themselves. Therefore, every node within the cluster will connect to the gateway in a single or multi-hop route, that is,  ,
,  ,
,  ,
,  ,
,  , where
, where  is the number of hops from a node
is the number of hops from a node  to the gateway
to the gateway  . All these sensor nodes send their information to the
. All these sensor nodes send their information to the  node, and
node, and  notifies the gateways about these sensor nodes.
notifies the gateways about these sensor nodes.
Every sensor node which has selected  as the gateway and is within the preferred cluster will be discovered by the gateway
as the gateway and is within the preferred cluster will be discovered by the gateway  . Note that a unique path exists from each node to the gateway as each node has just one parent. For routing the information to the gateway in each cluster, an appropriate routing algorithm is required. It defines the path that the packets can be forwarded to the gateway. Therefore, a minimum cost path algorithm can be used to find the optimal spanning tree rooted at the given node.
. Note that a unique path exists from each node to the gateway as each node has just one parent. For routing the information to the gateway in each cluster, an appropriate routing algorithm is required. It defines the path that the packets can be forwarded to the gateway. Therefore, a minimum cost path algorithm can be used to find the optimal spanning tree rooted at the given node.
Theorem 5.
The nodes that immediately follow the root node  in the minimum cost tree constitute the minimum neighborhood of node
in the minimum cost tree constitute the minimum neighborhood of node  . The minimum cost routes between the node
. The minimum cost routes between the node  and the gateway
and the gateway  are all contained in the minimum neighborhoods of the nodes [25].
are all contained in the minimum neighborhoods of the nodes [25].
4.1. Secure and Survivable Routing
In this subsection, we present the routing algorithm for the sensor nodes to forward data toward the gateway in each cluster. If data from neighborhoods are highly correlated, then the minimum spanning tree (MST) is beneficial in terms of survivability and network lifetime [41]. However, in the case of low correlation amongst sensor nodes, shortest path tree (SPT) should be incorporated to achieve survivability and better network lifetime [41]. Additionally, shorter paths are more secure than the longer paths (as we explain more in Section 6.1). Note that using the shortest path limits the number of paths which can be used to relay data toward the gateway. In [42], a shortest cost path routing algorithm for maximizing network lifetime based on link costs is presented. The costs reflect both the communication energy consumption rates and the residual energy level.
Here, the use of link estimation and parent selection (LEPS) scheme was employed as proposed in [43] as a routing algorithm. In this method, each node monitors all traffic received within the one-hop range, including route updates from the neighbor nodes. Using the least cost path, it manages the nearest available neighbor node and decides the next hop. To find a least cost path, one needs to calculate the costs of all edges between each sensor node then obtain a set of least cost paths. To accomplish this, we use the cost function as formulated in [5].
-
(i)
 : the function of remaining energy of the sensor node
: the function of remaining energy of the sensor node  , for all
, for all 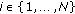 .
. -
(ii)
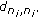 : the distance between sensor nodes
: the distance between sensor nodes 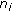 and
and 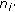 .
. -
(iii)
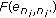 : the error function between sensor node
: the error function between sensor node  and
and 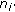 .
.
Then, the cost function for a link between sensor node  and
and  can be estimated as
can be estimated as

where α is free space loss exponent and typically  . The error function is related to the maximum data buffered in sensor node
. The error function is related to the maximum data buffered in sensor node  and the distance between sensor nodes
and the distance between sensor nodes  and
and  . Then one can write it as
. Then one can write it as

where  is a constant coefficient. To find the least cost path from a sensor node
is a constant coefficient. To find the least cost path from a sensor node  to the gateway
to the gateway  , the number of hops should be considered as well [5].
, the number of hops should be considered as well [5].
4.2. Symmetric Key Establishment
After secure clustering, broadcast authentication, and determining the desired routing algorithm among sensor nodes and gateways, sensor nodes should establish secure communication between each other to reach the gateway securely in a multi-hop path. Since gateways are aware of the one-hop neighbors of the sensor nodes and have enough information to control sensor nodes, they send pairwise keys to each sensor node and its potential one-hop neighbors. To achieve this, gateway  will send the pairwise key to the sensor node
will send the pairwise key to the sensor node  which is common between its neighbors
which is common between its neighbors  regarding the least-cost path routing algorithm.
regarding the least-cost path routing algorithm.
First, the symmetric key generated for the sensor node  and
and  , that is,
, that is,  , should be encrypted using the public key of the sensor node
, should be encrypted using the public key of the sensor node  , that is,
, that is,  , for
, for  . Then, each gateway
. Then, each gateway  unicasts this message to the sensor node
unicasts this message to the sensor node  . Each sensor node decrypts this message using its own private key
. Each sensor node decrypts this message using its own private key  and obtains the symmetric key
and obtains the symmetric key  . Since this message should be encrypted by the public key (based on ECC) of every individual sensor node, then disclosing symmetric key is not possible to the adversary. As an example, in Figure 1, the sensor node
. Since this message should be encrypted by the public key (based on ECC) of every individual sensor node, then disclosing symmetric key is not possible to the adversary. As an example, in Figure 1, the sensor node  will receive the symmetric keys for nodes
will receive the symmetric keys for nodes  ,
,  , and
, and  as
as  ,
,  , and
, and  , respectively.
, respectively.
In the proposed scheme, we do not consider unicast authentication for performance reasons. However, the following explains unicast authentication mechanism for the proposed symmetric key establishment method.
Unicast Authentication
The question is how sensor node  ensures that the encrypted symmetric key, that is,
ensures that the encrypted symmetric key, that is,  , is originated from gateway
, is originated from gateway  and not from the adversary?
and not from the adversary?
To address this issue, ECDSA authentication can be incorporated as follows. To ensure that the message, that is,  , is unicasted from the gateway
, is unicasted from the gateway  , the elliptic curve digital signature can be calculated by the gateway on the message. Therefore, sensor node
, the elliptic curve digital signature can be calculated by the gateway on the message. Therefore, sensor node  can verify the signature using the public key of gateway
can verify the signature using the public key of gateway  , and this assures that the message is coming from a legitimate gateway, and not from an adversary. This scheme requires
, and this assures that the message is coming from a legitimate gateway, and not from an adversary. This scheme requires  times signature generation by the gateways, and all the sensor nodes should verify and decrypt the unicasted message. Note that this increases the computation cost as the verification of a signature is an expensive operation. However, a one-time digital signature generation can reduce some of the overheads.
times signature generation by the gateways, and all the sensor nodes should verify and decrypt the unicasted message. Note that this increases the computation cost as the verification of a signature is an expensive operation. However, a one-time digital signature generation can reduce some of the overheads.
Another scheme is to allow each sensor node and its corresponding gateway to obtain a shared symmetric key during the first broadcast authentication (secure clustering) incorporating elliptic curve Diffie-Hellman (ECDH) method. Then, using symmetric key, the unicast authentication can be performed by generating a message authentication code (MAC). Therefore, any unicast from the gateway can be authenticated by the sensor nodes.
Authentication methods imply overheads in computation and communication times. Therefore, a trade-off must be achieved between the required level of security in the authentication and the time costs, otherwise the arising overheads could be against the survivability of the network.
Message Freshness
Beyond guaranteeing confidentiality and authentication, it is important to ensure that data is recent, fresh, and no adversary replayed old messages. A sensor node  can achieve this through a nonce (which is a unpredictable random number). In the proposed scheme, before unicasting the symmetric keys by the gateways, sensor node
can achieve this through a nonce (which is a unpredictable random number). In the proposed scheme, before unicasting the symmetric keys by the gateways, sensor node  can send a key request message to the gateway
can send a key request message to the gateway  accompanying with a random nonce, i.e.,
accompanying with a random nonce, i.e.,  and encrypted by
and encrypted by  . Therefore, when a gateway wants to unicast the symmetric key (encrypted by
. Therefore, when a gateway wants to unicast the symmetric key (encrypted by  ) to node
) to node  , gateway
, gateway  includes its random nonce, that is,
includes its random nonce, that is,  and
and  to the unicast message. After this exchange, node
to the unicast message. After this exchange, node  ensures that the message is recently initiated and is not a replay of old messages.
ensures that the message is recently initiated and is not a replay of old messages.
4.3. Survivable-Secure Connectivity
To better present the connectivity in each cluster of the proposed infrastructure for a WSN, we define a graph  to model the connectivity between a set of sensor nodes. Each sensor node is represented by a vertex in
to model the connectivity between a set of sensor nodes. Each sensor node is represented by a vertex in  ,
,  , where
, where  represents the number of sensor nodes within each cluster (In Section 5.1, we study the average number of sensor nodes inside a cluster.). For any two nodes
represents the number of sensor nodes within each cluster (In Section 5.1, we study the average number of sensor nodes inside a cluster.). For any two nodes  and
and  in
in  , the edge
, the edge  exists if and only if the nodes are within communication range of each other. The node degree is defined as the number of edges connected to the node. For example, in Figure 1,
exists if and only if the nodes are within communication range of each other. The node degree is defined as the number of edges connected to the node. For example, in Figure 1,  . Now, let us assume that node
. Now, let us assume that node  wishes to send information to the node
wishes to send information to the node  , and let
, and let  be the received power at
be the received power at  . In this case, gateway
. In this case, gateway  compares the SNR with the environment noise threshold, and if it is more than the noise threshold, then
compares the SNR with the environment noise threshold, and if it is more than the noise threshold, then  can send a message to the
can send a message to the  . In this situation, these nodes have achieved survivable connectivity and the edge
. In this situation, these nodes have achieved survivable connectivity and the edge  exists. To obtain the
exists. To obtain the  in each cluster, the following steps should be completed.
in each cluster, the following steps should be completed.
-
(1)
The gateway broadcasts a start message.
-
(2)
Each sensor node
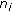 transmits a message with its
transmits a message with its 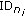 .
. -
(3)
All the sensor nodes record the received signal strength.
-
(4)
The gateways request each sensor node to report (the recorded information) to the gateway.
To achieve secure connectivity, in addition to the above conditions for survivable connectivity, sensor nodes should have previously established a symmetric/secret common key  for each edge in
for each edge in  . In this case, the proposed graph is securely connected. Finally, the gateway
. In this case, the proposed graph is securely connected. Finally, the gateway  will be aware of the degree of each sensor node within its cluster. Note that
will be aware of the degree of each sensor node within its cluster. Note that  determines the amount of symmetric keys which should be loaded from the gateway
determines the amount of symmetric keys which should be loaded from the gateway  to each sensor node.
to each sensor node.
5. Node Degree Analysis in the Proposed Scheme
The proposed scheme for establishing security for clustered WSNs is based on using PKC. The required symmetric key for each sensor node depends on the node degree and routing algorithm. In the proposed scheme, each sensor node has one secure path to the gateway across multiple hops. Therefore, the degree of connectivity of each sensor node may be different. Our routing algorithm is based on minimum neighborhood path, but some sensor nodes may have a higher neighborhood degree. Therefore, it is interesting to see how many neighbors a sensor can have related to the proposed scheme.
The question iswhat is the number of nodes in a certain area in the environment of
in the environment of ? Since sensor nodes have a random and uniform deployment, one can assume a Poisson distribution [11]. Therefore, the probability mass function can be defined for the random deployment as
? Since sensor nodes have a random and uniform deployment, one can assume a Poisson distribution [11]. Therefore, the probability mass function can be defined for the random deployment as

From the Poisson process and node density as  , one can write
, one can write

Then, the average number of nodes in the radius of  and area of
and area of  can be obtained by
can be obtained by

To determine the probability of having average number of sensor nodes in neighborhood of a sensor node, one can write

As the  regards the Sterling's formulas, one can simplify that
regards the Sterling's formulas, one can simplify that

It is interesting to note that the density of sensor nodes after the clustering will be the same because the deployment of sensor nodes is randomly uniform.
To calculate the probability that each sensor node has at least  neighbors, the minimum node degree can be written as follows:
neighbors, the minimum node degree can be written as follows:

As an example, assume that  nodes are to be deployed randomly in an area of
nodes are to be deployed randomly in an area of  m2 and the transmission range of each sensor node
m2 and the transmission range of each sensor node  m. From (8), the average number of neighbor nodes is found as
m. From (8), the average number of neighbor nodes is found as  , and the probability of having this as neighbor degree is about 7.2% (10). Note that the number of neighbor nodes defines the
, and the probability of having this as neighbor degree is about 7.2% (10). Note that the number of neighbor nodes defines the  and the number of symmetric keys that should be stored dynamically in each sensor node consequently.
and the number of symmetric keys that should be stored dynamically in each sensor node consequently.
As shown in Figure 1, the one-hop neighbors for gateways  and
and  are
are  and
and  , respectively. To establish secure communication between nodes in routing path, the gateway
, respectively. To establish secure communication between nodes in routing path, the gateway  sends secret keys to the sensor node within its cluster by encrypting them with the public key of the given node. For example, one-hop neighbors of sensor node
sends secret keys to the sensor node within its cluster by encrypting them with the public key of the given node. For example, one-hop neighbors of sensor node  are
are  , then it receive these
, then it receive these  symmetric keys encrypted with
symmetric keys encrypted with  . All the sensor nodes in the network will get the secret key shared with their neighborhood nodes similarly.
. All the sensor nodes in the network will get the secret key shared with their neighborhood nodes similarly.
5.1. Average Number of Sensor Nodes and Number of Hops Inside a Cluster
Since we assumed the sensor nodes to be uniformly deployed in the field, we propose the following approximation for the average number of nodes per cluster and cluster size. Let  be the number of the sensor nodes inside a cluster with radius
be the number of the sensor nodes inside a cluster with radius  . It is clear that,
. It is clear that,  follows the Poisson distribution similar to the node degree analysis introduced before (7). Then,
follows the Poisson distribution similar to the node degree analysis introduced before (7). Then,  can be calculated as
can be calculated as

where  is the average number of sensor nodes inside the cluster. Employing
is the average number of sensor nodes inside the cluster. Employing  ,
,

where  is the maximum number of hops between a node and the gateway as shown in Figure 3. From (8), then
is the maximum number of hops between a node and the gateway as shown in Figure 3. From (8), then

and the number of hops can be approximated as

It should be noted that in a real scenario with a fixed range of gateway,  , increasing the range of each sensor node,
, increasing the range of each sensor node,  , should be accompanied by decreasing the number of hops for energy saving purposes and node lifetime. Therefore, the average number of sensor nodes inside a cluster remains unchanged. As illustrated in Table 2, we vary the range of sensor nodes from 25 m up to 100 m and obtain the relevant maximum number of hops.
, should be accompanied by decreasing the number of hops for energy saving purposes and node lifetime. Therefore, the average number of sensor nodes inside a cluster remains unchanged. As illustrated in Table 2, we vary the range of sensor nodes from 25 m up to 100 m and obtain the relevant maximum number of hops.
 .
.6. Performance Analysis
Here, we analyze the memory storage, communication overhead, and resiliency for the proposed scheme.
6.1. Link Compromise Probability
The previously proposed schemes based on probabilistic key pre-distribution, and there is a known trade-off between the secure connectivity, memory storage, and resiliency against node capture. Here, we adopted the definition of resiliency as proposed entirely in [14].
Definition 6.
Let us assume that  nodes are randomly captured within a cluster. Then, the probability that the link between two fixed noncompromised nodes is not affected is defined as resiliency. The inverse of resiliency also called the fraction of the network that can be compromised.
nodes are randomly captured within a cluster. Then, the probability that the link between two fixed noncompromised nodes is not affected is defined as resiliency. The inverse of resiliency also called the fraction of the network that can be compromised.
In multi-hop routing, it is commonly well known that choosing short multi-hop paths instead of long multi-hop paths is beneficial. This is because as the length of a multi-hop path (number of hops) increases, the probability of path compromise increases as well. Therefore, for the proposed scheme, we calculate the probability of the link between sensor node  and gateway
and gateway  to be compromised without capturing them directly. Let us assume the following:
to be compromised without capturing them directly. Let us assume the following:
-
(i)
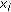 : the probability of node
: the probability of node  to be compromised.
to be compromised. -
(ii)
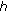 : the number of hops from a sensor node
: the number of hops from a sensor node  to reach the gateway
to reach the gateway 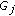 .
.
Therefore, the probability that the given path being compromised  , given that the sensor node
, given that the sensor node  and the gateway
and the gateway  are not compromised, is
are not compromised, is

After establishing the routing algorithm, because the number of sensor nodes in neighborhood is different, the probability of node compromise directly or indirectly will be different. This compromise probability depends on the attacker model. In Figure 4, the effect of increasing, number of hops on link compromise probability is illustrated in terms of node compromise probability  . Since our routing algorithm is based on minimum neighborhood degree, we try to reduce the degree of each node to decrease the indirect link compromise probability and have better resiliency against node capture attack.
. Since our routing algorithm is based on minimum neighborhood degree, we try to reduce the degree of each node to decrease the indirect link compromise probability and have better resiliency against node capture attack.
6.2. Simulations
We assume a network with  sensor nodes is randomly and uniformly deployed in an area of
sensor nodes is randomly and uniformly deployed in an area of  m2. We choose the number of the gateways
m2. We choose the number of the gateways  to cover a considerable area of sensor nodes. The transmission range is varied for each sensor node from 25 m to 100 m to achieve different average node degree
to cover a considerable area of sensor nodes. The transmission range is varied for each sensor node from 25 m to 100 m to achieve different average node degree  , ranging from 2 to 32. The maximum range of each gateway is set to
, ranging from 2 to 32. The maximum range of each gateway is set to  m. The simulations are performed using QualNet, scalable wireless network simulator [44].
m. The simulations are performed using QualNet, scalable wireless network simulator [44].
Through simulations, we observe the number of neighbor nodes which are involved in the routing algorithm and are communicating securely (using allocated symmetric keys). In Figure 5, the secure neighborhood degree is plotted for each sensor node for the proposed network model. About 300 nodes are communicating with just two sensor nodes and about 25 sensor nodes are communicating with 7 other neighbor nodes securely. We run the simulations three times, and the results are almost the same. Therefore, the maximum number of symmetric keys which are required to be dynamically loaded to the sensor nodes is always less than the average number of nodes  for the proposed scheme.
for the proposed scheme.
6.3. Measuring Storage Saving
In this section, the memory storage requirements for sensor nodes and the gateways are analyzed. In the proposed network model, the number of gateways is much less than the number of sensor nodes, that is,  . As each gateway is pre-loaded with
. As each gateway is pre-loaded with  , consequently the memory storage requirement for each gateway is obtained as
, consequently the memory storage requirement for each gateway is obtained as

where  is the key size for public key cryptography.
is the key size for public key cryptography.
On the other hand, each sensor node  is pre-loaded with
is pre-loaded with  . After deployment, each sensor node stores additional symmetric keys to communicate with their neighbors, that is,
. After deployment, each sensor node stores additional symmetric keys to communicate with their neighbors, that is,  , then
, then

where  denotes the size of symmetric key cryptography, and
denotes the size of symmetric key cryptography, and  is the maximum neighborhood degree.
is the maximum neighborhood degree.
It should be noted that since the gateways are tamper proof, the number of keys stored in each sensor node can be further reduced by incorporating the same pair of public and private keys for all the gateways, that is,  and
and  . Therefore, the total memory storage requirement for each sensor node can be written as
. Therefore, the total memory storage requirement for each sensor node can be written as

The proposed scheme requires less memory space than probabilistic schemes based on the work proposed in [11, 14], where those schemes require  bits. As an example, assume that ECC (163-bit) is used for the communication between sensor nodes and the gateway and the SKIPJACK (83-bit) cryptography is used in the communication between each sensor node and its neighbors. Therefore, from (19), the worst case memory requirement for each sensor node is
bits. As an example, assume that ECC (163-bit) is used for the communication between sensor nodes and the gateway and the SKIPJACK (83-bit) cryptography is used in the communication between each sensor node and its neighbors. Therefore, from (19), the worst case memory requirement for each sensor node is  bits. As shown in our simulation results in Figure 5, the maximum node degree in the proposed scheme is 7. However, in the probabilistic schemes, the storage requirement is
bits. As shown in our simulation results in Figure 5, the maximum node degree in the proposed scheme is 7. However, in the probabilistic schemes, the storage requirement is  bits. The scheme proposed in [31] requires
bits. The scheme proposed in [31] requires  bits to be stored in each sensor node for the balanced scheme and
bits to be stored in each sensor node for the balanced scheme and  bits for the unbalanced scheme with connectivity of 67%. Therefore, the proposed approach saves almost 57% of memory storage in comparison with the scheme presented in [31]. Note that the proposed scheme is deterministic and completely connected. As one can deduce from (17), the number of keys stored in each gateway is 1,002 keys. Note that in this work as well as [12, 31] and several previous works reviewed in this paper, it is assumed that gateways are more powerful than the sensor nodes in terms of memory, computation, and communication capabilities. In Table 4, the proposed scheme is qualitatively compared with its counterparts.
bits for the unbalanced scheme with connectivity of 67%. Therefore, the proposed approach saves almost 57% of memory storage in comparison with the scheme presented in [31]. Note that the proposed scheme is deterministic and completely connected. As one can deduce from (17), the number of keys stored in each gateway is 1,002 keys. Note that in this work as well as [12, 31] and several previous works reviewed in this paper, it is assumed that gateways are more powerful than the sensor nodes in terms of memory, computation, and communication capabilities. In Table 4, the proposed scheme is qualitatively compared with its counterparts.
6.4. Communication and Computation Overheads
Inherently, randomized key predistribution schemes (including the basic scheme and its extended schemes reviewed in this paper) suffer from lack of structure because the key ring  is chosen randomly from a key pool. Consequently, the communication complexity is
is chosen randomly from a key pool. Consequently, the communication complexity is  , and increasing
, and increasing  results in a dramatic increase in communication overhead. The number of messages passed in the network is a metric related to the power consumption and communication overhead. It is well known that transmitting is the most costly operation on a sensor node (e.g., the cost of transmitting one bit of data using MICA mote sensor node is approximately equivalent to processing 1000 CPU instructions) [45]. We define the communication overhead as the sum of packets sent and received per cluster in the network. The average number of packets can be estimated as the sum of the following.
results in a dramatic increase in communication overhead. The number of messages passed in the network is a metric related to the power consumption and communication overhead. It is well known that transmitting is the most costly operation on a sensor node (e.g., the cost of transmitting one bit of data using MICA mote sensor node is approximately equivalent to processing 1000 CPU instructions) [45]. We define the communication overhead as the sum of packets sent and received per cluster in the network. The average number of packets can be estimated as the sum of the following.
-
(i)
Packets sent from
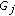 to
to 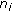 as a message
as a message  in each cluster.
in each cluster. -
(ii)
Packets sent by each sensor node toward the gateway within the cluster as a message
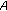 .
. -
(iii)
Unicast encrypted messages (pairwise secret keys) that each gateway sent to the nodes within its cluster
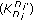 .
.
6.4.1. Cost of Secure Clustering and Pairwise Key Establishment
In Table 3, the number of encryptions and decryptions during the secure clustering and pairwise key establishment is reported. Therefore, the cost of secure clustering, i.e.,  , can be formulated as follows
, can be formulated as follows

where  is the cost of generating an elliptic curve digital signature using private key of gateway
is the cost of generating an elliptic curve digital signature using private key of gateway  ,
,  is the cost of verifying the signature using the public key of gateway
is the cost of verifying the signature using the public key of gateway  by sensor node
by sensor node  ,
,  is the cost of an encryption using public key of gateway
is the cost of an encryption using public key of gateway  by sensor node
by sensor node  , and
, and  is the cost of a decryption using the private key of the gateway
is the cost of a decryption using the private key of the gateway  performed by the gateway
performed by the gateway  .
.
6.5. Compromise Analysis and Key Revocation
Sensor nodes are deployed physically in insecured environments; hence, they are prone to be compromised. When a sensor node is captured, we assume that all information and stored key materials will be exposed to the adversary. In the proposed key management scheme, each sensor node stores the pairwise keys between its potential neighbors. After an adversary captures one of its neighbor nodes, she will be able to decrypt the information coming from other neighbor nodes directly. But other links which are not involved directly in this communication will remain secure. Therefore, the resiliency of the scheme is high because of its deterministic nature.
The problem which remains is the injection of false data into the network by the adversary. In this case, an efficient malicious behavior detection scheme is required to identify the misbehaving nodes and revoke them and their keys from the network. In the distributed and homogeneous WSNs, the resource constraint nature of sensor nodes limits the memory, computation, and communication resources which can be used for revocation. In [46], an efficient misbehaving detection scheme based on artificial immune system (AIS) for distributed sensor networks has been presented.
In clustered WSNs using public key infrastructure, a gateway as a certificate authority (CA) can issue a certificate revocation list (CRL) containing a list of keys to be revoked. Since, in the proposed scheme, node-to-node authentication is considered with the pairwise key allocation, then detecting and reporting misbehaved nodes is possible.
Upon detection of a misbehaving node by the gateway, a digital signature including the IDs of all the pairwise keys stored in that node can be generated and broadcast within the entire cluster as follows:

Note that in the scheme presented in [31] for heterogeneous and hierarchical WSNs, key revocation is not considered. In Table 4, resiliency of the proposed scheme is compared with the counterparts.
6.6. Scalability Analysis of the Proposed Scheme
The main drawback of the pairwise scheme proposed previously for distributed and homogeneous WSNs is scalability. In those networks, if the size of the network increases, the number of keys required to be stored in each sensor node will increase. Note that in the proposed scheme, adding new nodes to the network can be achieved easily by forwarding the required session key-request message to its potential neighbors and then toward the gateway. Upon authenticating the gateway, it can join the network via other nodes securely. Therefore, the proposed scheme is scalable.
7. Conclusions and Future Work
In this paper, we have proposed a new secure clustering scheme for clustered WSNs incorporating public key cryptography. We take advantage of gateway nodes which are powerful and tamper proof to establish/revocate the symmetric keys in each cluster. This key establishment is completed during the bootstrapping and clustering phase assuming that the adversary is present in the field. We have presented an approximation to determine the number of neighbor nodes for each sensor node obtained from the average number of neighbor nodes involved in the routing algorithm toward the gateway. Consequently, we have analyzed the number of keys which are required to be dynamically loaded to each sensor node, and a considerable saving in memory requirements is achieved. High resiliency against node capture and node-to-node authentication is accomplished by the proposed scheme. We note that we have not considered the overhead of the broadcasts from the gateways, as we assumed that they are powerful. However, applying network coding schemes will be considered to reduce these overheads in future works.
References
Xiao Y, Rayi VK, Sun B, Du X, Hu F, Galloway M: A survey of key management schemes in wireless sensor networks. Computer Communications 2007, 30(11-12):2314-2341. 10.1016/j.comcom.2007.04.009
Oliveira L, Wong H, Loureiro A, Dahab R: On the design of secure protocols for hierarchical sensor networks. International Journal of Security and Networks 2007, 2(3):216-227. 10.1504/IJSN.2007.013175
IEEE Std.802.15.4 for Information Technology—Telecommunication and Information Exchage between Systems—Local and Metropolitan Area Networks Specific Requirements Part 15.4: Wireless Medium Access Control (MAC) and Physical Layer (PHY) Specifications for Low-Rate Wireless Personal Area Networks, IEEE, 2006
Westmark V: A definition for information system survivability. In Proceeding of the 37th Hawaii Internal Conference on System Sciences (HICSS '04), 2004. IEEE press; 2086-2096.
Akkaya K, Younis MF: Energy and QoS aware routing in wireless sensor networks. Cluster Computing 2005, 8(2-3):179-188. 10.1007/s10586-005-6183-7
Low CP, Fang C, Ng JM, Ang YH: Efficient load-balanced clustering algorithms for wireless sensor networks. Computer Communications 2008, 31(4):750-759. 10.1016/j.comcom.2007.10.020
Younis MF, Ghumman K, Eltoweissy M: Location-aware combinatorial key management scheme for clustered sensor networks. IEEE Transactions on Parallel and Distributed Systems 2006, 17(8):865-882.
Younis O, Fahmy S: HEED: a hybrid, energy-efficient, distributed clustering approach for ad hoc sensor networks. IEEE Transactions on Mobile Computing 2004, 3(4):366-379. 10.1109/TMC.2004.41
Tian Q, Coyle EJ: Optimal distributed detection in clustered wireless sensor networks. IEEE Transactions on Signal Processing 2007, 55(7):3892-3904.
Deng J, Han YS: Multipath key establishment for wireless sensor networks using just-enough redundancy transmission. IEEE Transactions on Dependable and Secure Computing 2008, 5(3):177-190.
Eschenauer L, Gligor VD: A key-management scheme for distributed sensor networks. In Proceedings of the 9th ACM Conference on Computer and Communications Security (CCS '02), November 2002. ACM; 41-47.
Lu K, Qian Y, Guizani M, Chen H-H: A framework for a distributed key management scheme in heterogeneous wireless sensor networks. IEEE Transactions on Wireless Communications 2008, 7(2):639-647.
Zhang W, Tran M, Zhu S, Cao G: A random perturbationbased scheme for pairwise key establishment in sensor networks. In Proceedings of the 8th ACM Interational Symposium on Mobile Ad Hoc Networking and Computing, (MobiHoc '07), 2007. Edited by: Kranakis E, Belding EM, Modiano E. ACM; 90-99.
Chan H, Perrig A, Song D: Random key predistribution schemes for sensor networks. Proceedings of the IEEE Symposium on Security And Privacy, May 2003 197-213.
Du W, Deng J, Han YS, Varshney PK, Katz J, Khalili A: A pairwise key predistribution scheme for wireless sensor networks. ACM Transactions on Information and System Security 2005, 8(2):228-258. 10.1145/1065545.1065548
Liu D, Ning P, Rongfang LI: Establishing pairwise keys in distributed sensor networks. ACM Transactions on Information and System Security 2005, 8(1):41-77. 10.1145/1053283.1053287
Xue Y, Jürgensen H, Azarderakhsh R, Reyhani-Masoleh A: Key management for wireless sensor networks using trusted neighbors. In Proceedings of IEEE/IFIP International Conference on Embedded and Ubiquitous Computing (EUC '08), 2008. Volume 2. Edited by: Xu C-Z, Guo M. IEEE Computer Society; 228-233.
Ma C, Shang Z, Wang H, Geng G: An improved key management scheme for heterogeneity wireless sensor networks. Proceedings of the 3rd International Conference on Mobile Ad-Hoc and Sensor Networks (MSN '07), 2007 854-865.
Malan D, Welsh M, Smith M: A public-key infrastructure for key distribution in tinyos based on elliptic curve cryptography. Proceedings of 1st Annual IEEE Communications Society Conference on Sensor and Ad Hoc Communications and Networks (IEEE SECON '04), 2004 71-80.
Liu A, Kampanakis P, Ning P: Tinyecc: elliptic curve cryptography for sensor networks (version 0.3). 2007, http://discovery.csc.ncsu.edu/software/TinyECC
Rivest RL, Shamir A, Adleman L: A method for obtaining digital signatures and public-key cryptosystems. Communications of the ACM 1978, 21(2):120-126. 10.1145/359340.359342
Shih W, Hu W, Corke P, Overs L: A public key technology platform for wireless sensor networks. In Proceedings of the 6th ACM conference on Embedded Network Sensor Systems, 2008. ACM; 447-448.
Panja B, Madria SK: An energy and communication efficient group key in sensor networks using elliptic curve polynomial. In Proceedings of the 6th International Conference on Ad-Hoc, Mobile and Wireless Networks (ADHOC-NOW '07), 2007. Springer; 153-171.
Szczechowiak P, Oliveira L, Scott M, Collier M, Dahab R: Nanoecc: testing the limits of elliptic curve cryptography in sensor networks. In Proceedings of European Conference on Wireless Sensor Networks (EWSN '08), 2008. Springer; 305-320.
Čagalj M, Hubaux J-P, Enz CC: Energy-efficient broadcasting in all-wireless networks. Wireless Networks 2005, 11(1-2):177-188. 10.1007/s11276-004-4754-9
Jolly G, Kusçu MC, Kokate P, Younis MF: A lowenergy key management protocol for wireless sensor networks. Proceedings of the 8th IEEE Symposium on Computers and Communications (ISCC '03), 2003 335-340.
Du X, Xiao Y, Guizani M, Chen H-H: An effective key management scheme for heterogeneous sensor networks. Ad Hoc Networks 2007, 5(1):24-34. 10.1016/j.adhoc.2006.05.012
Kausar F, Hussain S, Yang LT, Masood A: Scalable and efficient key management for heterogeneous sensor networks. Journal of Supercomputing 2008, 45(1):44-65. 10.1007/s11227-008-0184-2
Azarderakhsh R, Reyhani-Masoleh A, Abid Z-E: A key management scheme for cluster based wireless sensor networks. In Proceedings of IEEE/IFIP International Conference on Embedded and Ubiquitous Computing (EUC '08), 2008 Edited by: Xu C-Z, Guo M. 222-227.
Johnson D, Menezes A, Vanstone SA: The elliptic curve digital signature algorithm (ECDSA). International Journal of Information Security 2001, 1(1):36-63.
Traynor P, Kumar R, Choi H, Cao G, Zhu S, La Porta T: Efficient hybrid security mechanisms for heterogeneous sensor networks. IEEE Transactions on Mobile Computing 2007, 6(6):663-676.
Brown J, Du X, Nygard K: An efficient public-key-based heterogeneous sensor network key distribution scheme. Proceedings of the 50th Annual IEEE Global Telecommunications Conference (GLOBECOM '07), November 2007 991-995.
Rahman SKMDM, Nasser N, Saleh K: Identity and pairing-based secure key management scheme for heterogeneous sensor networks. Proceedings of the 4th IEEE International Conference on Wireless and Mobile Computing, Networking and Communication (WiMob '08), October 2008 423-428.
Ren K, Yu S, Lou W, Zhang Y: Multi-user broadcast authentication in wireless sensor networks. IEEE Transactions on Vehicular Technology 2009, 58(8):4554-4564.
Khuller S, Raghavachari B, Young N: Balancing minimum spanning trees and shortest-path trees. Algorithmica 1995, 14(4):305-321. 10.1007/BF01294129
Du W, Deng J, Han Y, Chen S, Varshney P: A key management scheme for wireless sensor networks using deployment knowledge. In Proceedings of 23rd Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '04), 2004. Volume 4. IEEE; 586-597.
Ning P, Liu A, Du W: Mitigating DoS attacks against broadcast authentication in wireless sensor networks. ACM Transactions on Sensor Networks 2008, 4(1, article no. 1):1-35.
Aguayo D, Bicket J, Biswas S, Judd G, Morris R: Link-level measurements from an 802.11b mesh network. Proceedings of the Conference on Computer Communications (ACM SIGCOMM '04), September 2004, usa 121-131.
Awerbuch B, Gallager RG: A new distributed algorithm to find breadth first search trees. IEEE Transactions on Information Theory 1987, 33(3):315-322. 10.1109/TIT.1987.1057314
Busch C, Magdon-Ismail M, Sivrikaya F, Yener B: Contention-free MAC protocols for asynchronous wireless sensor networks. Distributed Computing 2008, 21(1):23-42. 10.1007/s00446-007-0053-x
Cristescu R, Beferull-Lozano B: Lossy network correlated data gathering with high-resolution coding. IEEE Transactions on Information Theory 2006, 52(6):2817-2824.
Chang J-H, Tassiulas L: Maximum lifetime routing in wireless sensor networks. IEEE/ACM Transactions on Networking 2004, 12(4):609-619. 10.1109/TNET.2004.833122
Woo A, Tong T, Culler DE: Taming the underlying challenges of reliable multihop routing in sensor networks. In Proceedings of the 1st International Conference on Embedded Networked Sensor Systems (Sensys '03), 2003. Edited by: Akyildiz IF, Estrin D, Culler DE, Srivastava MB. ACM; 14-27.
I. Scalable Network Technologies : QualNet Simulator. http://www.scalable-networks.com/products/qualnet
M. Wireless Sensor Networks : Crossbow. http://www.xbow.com/Products
Drozda M, Schaust S, Szczerbicka H: AIS for misbehavior detection in wireless sensor networks: performance and design principles. In Proceedings of IEEE Congress on Evolutionary Computation, 2007. IEEE; 3719-3726.
Acknowledgments
The authors would like to thank the anonymous reviewers for the careful reading and valuable comments that helped to improve this paper. This research is supported in part by the NSERC Discovery grant awarded to A. Reyhani-Masoleh.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Azarderskhsh, R., Reyhani-Masoleh, A. Secure Clustering and Symmetric Key Establishment in Heterogeneous Wireless Sensor Networks. J Wireless Com Network 2011, 893592 (2011). https://doi.org/10.1155/2011/893592
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/893592

 .
.
 : the function of remaining energy of the sensor node
: the function of remaining energy of the sensor node  , for all
, for all 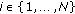 .
.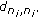 : the distance between sensor nodes
: the distance between sensor nodes 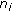 and
and 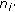 .
.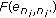 : the error function between sensor node
: the error function between sensor node  and
and 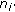 .
.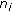 transmits a message with its
transmits a message with its 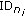 .
.
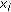 : the probability of node
: the probability of node  to be compromised.
to be compromised.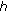 : the number of hops from a sensor node
: the number of hops from a sensor node  to reach the gateway
to reach the gateway 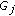 .
.

 ;
;  ;
;  m.
m. to
to 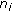 as a message
as a message  in each cluster.
in each cluster. .
.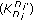 .
.