- Research Article
- Open access
- Published:
Interference-Aware Radio Resource Management for Local Area Wireless Networks
EURASIP Journal on Wireless Communications and Networking volume 2011, Article number: 921623 (2011)
Abstract
Interference-aware multiple access is an enabler to cost-efficient and reliable high data-rate local area wireless access. In this paper, we propose an interference-aware radio resource management scheme where receivers inform about their throughput, interference, and signal levels by means of broadcast messages tied to data reception. In the proposed scheme, the conventional scheduler is extended to interference-aware operation where individual scheduling decisions are based on estimated change in system-level performance. The performance of the proposed scheme is evaluated in system simulations where it is compared to a conventional scheduler and a centralized scheduler (global optimum). The convergence of the proposed scheduler is analyzed and signaling overhead of an example implementation is characterized. The results demonstrate that the proposed scheme enables fair and efficient wireless access in challenging interference scenarios, for example, multiple networks deployed in the same geographical area and sharing a common band.
1. Introduction
As the demand for higher data rates for wireless access continues, new technologies to satisfy it are constantly under development in for example, IMT-Advanced, in future releases of 3GPP Long-Term Evolution (LTE) (see http://www.3gpp.org/), WiMAX (see http://www.wimaxforum.org/), and IEEE 802.11ac. The high growth in data rates brings new challenges and opportunities to system design in the face of harsh interference environment and demanding propagation conditions. As such, higher data rates can be achieved by increasing the bandwidth via flexible and cognitive spectrum use and/or denser network deployments. Costs of denser network deployments can get overwhelmingly high, unless the base stations are made cheaper, the network deployment is made simpler (possibly uncoordinated), and the need for costly infrastructure and network planning is reduced. This all means that there is more and more need for interference management in the lower layers of the system in order to keep the quality of service at a desired level. Smaller cells imply fewer users per cell, which in turn makes local interference awareness feasible and more appealing to implement.
The task of the scheduler in a cellular network is to organize multiple access in the cell such that system performance is maximized. A suitable system performance metric needs to trade-off between two conflicting goals: high spectral efficiency (total system throughput) and fairness. Highest efficiency is achieved when the performance metric is the sum throughput over all served nodes. Such a metric is maximized by granting access only to the nodes that have most favorable channel conditions and leaving for example, cell edge users with poor or no service. A widely used measure of fairness is the so-called Jain's fairness index [1], which is maximized when all users have equal throughput regardless of efficiency, and the corresponding system performance metric would be the minimum of served nodes' throughputs. The total throughput and minimum throughput performance metrics lead to two extreme schedulers where one is maximally efficient but minimally fair, and the other is maximally fair but minimally efficient [2]. A reasonable trade-off between efficiency and fairness is achieved by taking the sum of logarithms of user throughputs as the performance metric. This corresponds to the well-known Proportional Fair (PF) Scheduler [2, 3].
In conventional systems, for example, LTE [4], the scheduler has information on the perceived quality of resource blocks per UE and link direction (channel quality indicator, CQI). This allows the scheduler to react to time-varying interference caused by other schedulers' decisions and by channel fading. A drawback of this approach is that the scheduler has no information on the interference that it inflicts on the neighboring cells, and hence it is only able to maximize own cell performance in a selfish manner. When the network deployment is well planned and strict reuse patterns are used such that interference is minimized, adequate performance can be achieved [4]. In the general case of an arbitrary network, a stable resource usage may be achieved with suitable admission control as shown in [5]. However, in that case fairness is not taken into account. One way of improving the fairness is to incorporate transmitted power to the user utility function. In that approach the user utility increases with throughput but decreases with increased transmitted power. Hence, unfair resource allocations are somewhat discouraged, see for example, [6, 7].
The luxury of interference coordination by network planning and reuse patterns is unfortunately too costly and time-demanding for dense local area network deployments. Moreover, as we show here, fixed frequency reuse may result in suboptimal system performance. By letting the devices locally coordinate the transmissions such that interference is flexibly and adaptively managed, we can significantly boost the system performance. The contributions of this paper are the following.
-
(i)
We propose an interference-aware (IA) scheduling algorithm where scheduling decisions are made based on system performance maximization instead of intracell performance maximization, as in for example, conventional PF scheduler. The proposed scheduler is structurally related to the noninterference aware PF scheduler.
-
(ii)
We propose a signaling framework for TDD systems that enables distributed IA scheduling. In the proposed scheme, the receivers transmit a small broadcast interference report after reception of data, which allows other transmitters to become active on the corresponding resources only in the case when it is beneficial for the overall system performance. We sketch the signaling implementation and characterize the overhead caused.
-
(iii)
We give a simple proof of convergence of the proposed IA scheduler under the assumption of perfect interference information sharing with broadcast messages.
-
(iv)
We evaluate the performance of IA scheduler in numerical examples, where IA scheduler is compared to both PF scheduler and the global optimum transmission schedule obtained by a centralized scheduler having full system-wide information. The performance evaluation is done in system-level simulations where also the nonidealities such as overhead of a practical IA scheduler implementation are taken into account.
This paper is organized as follows: in Section 2 we present a summary of related work. Section 3 presents the system model used in the paper and describes the PF scheduler. The proposed IA scheduler is presented in Section 4, followed by an example implementation and overhead characterization in Section 5. In Section 6, we provide analysis of the convergence of IA scheduler. Numerical results from system simulations are presented in Section 7. Finally, Section 8 concludes the paper.
2. Summary of Related Work
The available gains from intercell interference awareness in cellular networks have been identified in several papers, see for example, [8–10] and the references therein. The analysis done in [10] reveals a very interesting property of such networks in that binary power control (i.e., each link is active on a resource with maximal power, or then idle) is surprisingly close to the case of general power control in terms of system throughput.
A distributed resource allocation scheme for interference aware power control is proposed in [11, 12]. In that scheme, each receiver broadcasts to its neighbors a so-called interference price, which is the rate of change of the users utility with respect to the change in total received interference power. This allows for adaptive power control with the target of optimizing system utility. Under specific constraints on the utility functions, the scheme of [12] is proven to converge to a global maximum. Unfortunately, the interesting case of OFDMA and log-throughput user utility functions does not satisfy the constraints. In [13], an extension to the pricing scheme is proposed that is convergent also in this case.
Another concept employing receiver beaconing is the busy burst OFDMA-TDD [14, 15]. In the busy burst scheme, the receiver beacon does not convey any information on the interference tolerance of the receiver. It merely sounds the channel and the potential transmitters then measures the total busy burst power and compares it to a threshold value determining whether concurrent transmission is allowed.
An approximate solution to interference-aware reuse pattern adaptation between cells is described in [16], where the information on intercell interference coupling is obtained by measuring DL signal strength of neighboring cells at the user equipments (UEs). Based on the measurement data, the base stations form information on inter-cell interference coupling and may select secondary component carriers (subbands) into use when the impact of resulting inter-cell interference is estimated to be low enough. A similar approach to the spectrum sharing problem as in [16] is taken in [17]. Also [18] aims at distributed reuse pattern adaptation in a more simple setting where the interference inflicted on other cells is not estimated, but the total amount of resources used by any of the cells alone is restricted.
In the context of reuse-1 cellular networks, there is a need to coordinate transmissions and limit the reuse of radio resources in order to improve cell edge coverage. On the other hand, contention-based MAC of 802.11 family of standards provides another angle to the problem, where the system performance would benefit from allowing more spatial reuse of radio resources in order to obtain higher areal spectral efficiency. To this end, interference-aware MAC enhancements to 802.11 systems have been proposed in for example, [19, 20]. These works propose added signaling in the form of beacons sent by the receivers that would enable a better MAC protocol achieving higher spectral efficiency.
In this work, we propose a scheme that provides sufficient information to the transmitters in the vicinity of each receiver such that extending the conventional proportional fair scheduler to being proportional fair across the whole system is facilitated. This results in an interference-aware (IA) scheduler for cellular systems. The information is shared by means of short broadcast messages sent by the receivers. This is in contrast to [12, 13] where a single measure of interference price is broadcast and the transmit powers are gradually adapted accordingly. The difference between our scheme and the busy burst concept of [15] is that we have more informative beacons that allow for more precise estimation of interference impact to other receivers. A drawback of this approach is the increased overhead caused by the interference reports. We argue that the higher amount of signaling proposed in this paper is attractive in high data-rate local area networks where the overhead is well justified since the achieved gains are higher. The proposed scheme is capable of adapting the spectral reuse and resource allocations in varying interference situations such that coverage and a fair operating point are maintained.
3. System Model
We assume a time division duplex (TDD) wireless network. The access is frame based, where each radio frame is subdivided into subframes in time domain and into subbands in frequency domain. A combination of a sub-frame and a sub-band is called a resource block (RB). All base stations (BS) and user equipment (UE) are assumed to be synchronized and equipped with good quality radios such that there is no significant interference between RBs. Each frame is partitioned to downlink (DL) access sub-frames and uplink (UL) access sub-frames. The scheduler is allowed to assign RBs to UEs freely while adhering to the constraint on DL and UL transmissions being scheduled on the associated sub-frames. OFDMA/TDD is an example of such a physical layer access scheme.
Each UE is assigned to the BS with the strongest channel gain in its network. The group of UEs together with the serving BS form a cell, and the transmissions in the cell are organized at the BS by the scheduler. A transmitter and a receiver form a communication link, such that each UE and BS pair forms two links (DL and UL).
We assume that there are  communication links operating in the same geographical area. For each link, indexed by
communication links operating in the same geographical area. For each link, indexed by  , data is transmitted and received on a subset of
, data is transmitted and received on a subset of  resources. The channel gain from the transmitting node of
resources. The channel gain from the transmitting node of  th link to the receiving node of
th link to the receiving node of  th link on
th link on  th resource is denoted by
th resource is denoted by  . The transmit power on
. The transmit power on  th link on
th link on  th resource at
th resource at  th frame is
th frame is  . Now the signal to interference plus noise ratio (SINR) of
. Now the signal to interference plus noise ratio (SINR) of  th link on
th link on  th resource,
th resource,  , can be expressed as
, can be expressed as

where  is the noise variance that includes all noise and interference sources other than transmitters of the modeled
is the noise variance that includes all noise and interference sources other than transmitters of the modeled  links, and the sum is taken over interfering links indexed by
links, and the sum is taken over interfering links indexed by  such that it represents the total interference received at the receiving node of
such that it represents the total interference received at the receiving node of  th link. The available set of modulation and coding schemes (MCS) determines a nonconvex mapping from SINR values to throughput and is denoted as
th link. The available set of modulation and coding schemes (MCS) determines a nonconvex mapping from SINR values to throughput and is denoted as  , see for example, [21].
, see for example, [21].
3.1. Proportional Fair (PF) Scheduler
The schedulers' task is to determine which links are active on which resources, and which MCS will be employed in the transmissions. It determines  and MCS's for the
and MCS's for the  th frame, given the observations on the system state made during the
th frame, given the observations on the system state made during the  th frame. Note that the case of a link being not active on a resource is included in the formulation as a special case
th frame. Note that the case of a link being not active on a resource is included in the formulation as a special case  .
.
In general, the transmit powers  may be adapted freely in the constraints given by the hardware and regulations for spectrum use. However, we make the simplifying assumption that the transmit powers are a function
may be adapted freely in the constraints given by the hardware and regulations for spectrum use. However, we make the simplifying assumption that the transmit powers are a function  of the channel gain
of the channel gain  only, such that
only, such that  , with
, with  . Here
. Here  is a maximum power level per resource constrained by the regulations. The function
is a maximum power level per resource constrained by the regulations. The function  may represent any power control algorithm which is independent of the scheduler. Thus the scheduler does not adapt the power levels beyond the binary decision
may represent any power control algorithm which is independent of the scheduler. Thus the scheduler does not adapt the power levels beyond the binary decision  .
.
Assume that the scheduler has knowledge of the observed SINR per link and per resource,  , and also the weighted average link throughput,
, and also the weighted average link throughput,

where  is a forgetting factor. A conventional proportional fair (PF) scheduler is described in Algorithm 1. Each of the
is a forgetting factor. A conventional proportional fair (PF) scheduler is described in Algorithm 1. Each of the  schedulers, indexed by
schedulers, indexed by  , is responsible for a subset of links, denoted by
, is responsible for a subset of links, denoted by  . A common case in a cellular network is that the schedulers are operated at the base stations (BSs), so that the set of schedulers
. A common case in a cellular network is that the schedulers are operated at the base stations (BSs), so that the set of schedulers  corresponds to the BSs and for each BS, the set
corresponds to the BSs and for each BS, the set  contains all uplink and downlink links formed by the BS and the UEs served by it. PF scheduler calculates a scheduling metric
contains all uplink and downlink links formed by the BS and the UEs served by it. PF scheduler calculates a scheduling metric

for each link  on each yet unallocated resource
on each yet unallocated resource  (see line 5 of Algorithm 1), where
(see line 5 of Algorithm 1), where  denotes the throughput already scheduled for link
denotes the throughput already scheduled for link  during this scheduling round. Then the link and resource combination with the maximal metric is allocated for data transmission and
during this scheduling round. Then the link and resource combination with the maximal metric is allocated for data transmission and  is updated (see lines 6–10). The procedure is repeated until all the resources have been allocated. In this manner, all the resources will be scheduled to have a transmission in all cells (provided that there exists a link with data in queue and a positive expected throughput), no matter how much interference the associated transmission generates.
is updated (see lines 6–10). The procedure is repeated until all the resources have been allocated. In this manner, all the resources will be scheduled to have a transmission in all cells (provided that there exists a link with data in queue and a positive expected throughput), no matter how much interference the associated transmission generates.
Algorithm 1: Proportional fair scheduler. Given  and
and  , determine
, determine  .
.
-
(1)
for
 to
to 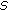 do
do
(2) 
(3) 
(4) while  do
do
(5) 
(6) 
(7) 
(8) 
(9) 
(10) 
(11) end while
-
(12)
end for
4. Interference-Aware (IA) Scheduler
The IA scheduler works with the same basic principle as the PF scheduler, except that neighboring cell links are taken into account in the scheduling metric calculation as well. It is easy to see that PF scheduling metric is equivalent to maximizing the geometric mean of averaged throughputs (or sum of the logarithms of the averaged throughputs) over the links handled by that scheduler. For a rigorous analysis of the PF scheduler, the reader is referred to for example, [3].
In order to extend the same principle to system-wide maximization, we form the IA scheduling metric as the mean of the logarithms of the throughputs of all affected links. In decentralized RRM, the metric calculation is approximated by making the assumption that other schedulers repeat the previous frame's schedules. Hence, the proposed approach is most effective in a somewhat static situation where only incremental changes are needed, for example, when a new user gets active or data queue becomes empty.
The required modification to the PF scheduler (Algorithm 1) is to replace the intra-cell scheduling metric of line 5 with a system-level scheduling metric. The metric is defined as the change in geometric mean of throughput of all involved links when the link under consideration is activated compared to the case when it is idle. This is computed assuming that all the other scheduling decisions are repeated as in the preceding frame. It thus reflects the change in system utility per scheduling decision. In the following, we give a description of the steps taken in IA scheduler while the complete algorithm is summarized later in Algorithm 2.
Algorithm 2: Interference-aware scheduler. Given  ,
,  ,
,  , and
, and  , determine
, determine  .
.
(1)for  to
to  do
do
(2) 
(3)  ,
, 
(4)  ,
, 
(5) while  do
do
(6) for  ,
,  do
do
(7) Evaluate  ,
,  , (4) and (8)
, (4) and (8)
(8) Evaluate  , (10)
, (10)
(9) end for
(10) 
(11) if  then
then
(12) 
(13) 
(14) 
(15) 
(16) 
(17) else
(18) 
(19) end if
(20) end while
-
(21)
end for
Consider now the calculation of IA scheduling metric  of
of  th link on
th link on  th resource. First we need to compute the expected throughput of link
th resource. First we need to compute the expected throughput of link  on resource
on resource  , which is denoted by
, which is denoted by  , (the same as in PF scheduler). In order to compare the geometric mean values of the throughputs obtained when a link is activated or not, we need to define the following link throughput estimates. Let
, (the same as in PF scheduler). In order to compare the geometric mean values of the throughputs obtained when a link is activated or not, we need to define the following link throughput estimates. Let  be the resulting (own) link
be the resulting (own) link  total throughput if it is active on resource
total throughput if it is active on resource  . Similarly, let
. Similarly, let  be the resulting total throughput of link
be the resulting total throughput of link  if it is not active on resource
if it is not active on resource  . The other cell links that are affected by the scheduling decisions in scheduler
. The other cell links that are affected by the scheduling decisions in scheduler  are indexed by
are indexed by  . For those, we define the total link throughput vectors by
. For those, we define the total link throughput vectors by  and
and  for
for  . Here,
. Here,  contains the throughput values of other cell links if link
contains the throughput values of other cell links if link  is active on resource
is active on resource  , and
, and  contains the throughput values of other cell links if there is no transmission on resource
contains the throughput values of other cell links if there is no transmission on resource  by any of the links in
by any of the links in  (the links served by scheduler
(the links served by scheduler  ).
).
The throughput change  of link
of link  for the case when it is active on resource
for the case when it is active on resource  may be estimated as
may be estimated as

where  is the
is the  -indicator function of the event that link
-indicator function of the event that link  was active on resource
was active on resource  in the preceding frame, such that
in the preceding frame, such that  if the resource
if the resource  was in use by link
was in use by link  and
and  otherwise. Now the total link throughput for link
otherwise. Now the total link throughput for link  in case a transmission is scheduled to it on resource
in case a transmission is scheduled to it on resource  is given by
is given by

where  is the current scheduled link throughput that is updated after each scheduling decision. At the beginning of scheduling,
is the current scheduled link throughput that is updated after each scheduling decision. At the beginning of scheduling,  is initialized to the averaged link throughputs,
is initialized to the averaged link throughputs,  . The quantity
. The quantity  remains unchanged with allocations that were also present in the preceding frame. On the other hand,
remains unchanged with allocations that were also present in the preceding frame. On the other hand,  will increase when new resources are allocated.
will increase when new resources are allocated.
Similarly, the mean frame throughput  in case link
in case link  is not active on resource
is not active on resource  is obtained as
is obtained as

Equations (5) and (6) state that the mean frame throughput increases if link  is activated on resource
is activated on resource  and decreases if the link is inactivated on resource
and decreases if the link is inactivated on resource  . In the other cases, the throughput does not change.
. In the other cases, the throughput does not change.
When estimating the mean frame throughputs of other cell links,  and
and  for
for  , we need the following information to be shared among the schedulers: the signal power,
, we need the following information to be shared among the schedulers: the signal power,  , the total interference plus noise power,
, the total interference plus noise power,  , and the average throughput of each link,
, and the average throughput of each link,  , observed in the
, observed in the  th frame. The interference channel gains
th frame. The interference channel gains  from the transmitting node of link
from the transmitting node of link  to the receiving node of link
to the receiving node of link  are estimated from the IA message.
are estimated from the IA message.
In order to estimate the impact of transmission on link  using resource
using resource  to the other cell links, we need to first determine the interference contribution from the links in
to the other cell links, we need to first determine the interference contribution from the links in  to other cell links. This is denoted by
to other cell links. This is denoted by  and is
and is

In case there was no transmission on resource  among the links in
among the links in  , the quantity
, the quantity  will be zero. Now we can write the other cell links' mean frame throughput change for the event that link
will be zero. Now we can write the other cell links' mean frame throughput change for the event that link  is active on resource
is active on resource  as
as

which can be seen to be zero in case link  was active on resource
was active on resource  also in the preceding frame. In practice, the term
also in the preceding frame. In practice, the term  is evaluated based on estimates which might result in a nonpositive denominator. Therefore, in a practical implementation one needs to limit it from below to the noise power
is evaluated based on estimates which might result in a nonpositive denominator. Therefore, in a practical implementation one needs to limit it from below to the noise power  . The other cell link throughputs are then given by
. The other cell link throughputs are then given by

where  is the current estimate of interfered links' throughputs, which are initialized at the reported throughputs
is the current estimate of interfered links' throughputs, which are initialized at the reported throughputs  at the beginning of scheduling.
at the beginning of scheduling.
From equations (9), it can be seen that in case link  was active on resource
was active on resource  also in the previous frame,
also in the previous frame,  reduces to
reduces to  . This follows since there would be no change in the interference at link
. This follows since there would be no change in the interference at link  if link
if link  is active on resource
is active on resource  . Similarly, in case
. Similarly, in case  , the quantity
, the quantity  reduces to
reduces to  .
.
Once the quantities  ,
,  ,
,  , and
, and  for
for  are evaluated, we form the scheduling metric as follows:
are evaluated, we form the scheduling metric as follows:

Once the scheduling metric is evaluated, the IA scheduler takes the same steps as the PF scheduler to activate the link and resource pair with the maximum metric. However, if the maximal utility change is negative for all links on a specific resource, it implies that the system performance would actually degrade if that resource is taken into use. Hence such allocations are not allowed. This distinguishes the IA scheduler from the conventional PF scheduler. In PF scheduler, the network reuses resources even if the generated interference is severe. In contrast, applying IA scheduler results in a natural reuse pattern for the radio resources. The allocation decision is optimal, taking the instantaneous state of all links into account. In practice, not all the interference messages will be heard. Then the decisions will take only local information into account in the form of the state of other links in the vicinity.
Suppose that the maximal utility change was positive, and it occurred for link  on resource
on resource  ; the scheduler updates current estimates of link throughputs as
; the scheduler updates current estimates of link throughputs as  and
and  for
for  . Then the scheduler computes new metrics with the updated link throughput estimates for the remaining unallocated resources and repeats the procedure until all resources have been allocated or no more nonnegative scheduling metrics are found. The interference-aware (IA) scheduler is summarized in Algorithm 2.
. Then the scheduler computes new metrics with the updated link throughput estimates for the remaining unallocated resources and repeats the procedure until all resources have been allocated or no more nonnegative scheduling metrics are found. The interference-aware (IA) scheduler is summarized in Algorithm 2.
5. Example Implementation of IA Scheduler
The main question at this point is whether the trade-off between interference awareness and signaling overhead results in positive gain. There are several factors to be taken into account.
-
(i)
Network Deployment. If the network deployment is such that there is no severe interference, it is clear that there should be smaller gains from interference awareness. This happens especially in the case of very low network load or more isolated cells.
-
(ii)
The Data Rate per Link and the Number of Active Links. If the data rate per link is low, the signaling overhead may turn out to be too large.
-
(iii)
Mobility and Traffic Load. The scheduling interval has to be short in comparison to the rate of change in the interference links.
-
(iv)
Synchronization. IA scheduler as described in this paper clearly assumes a synchronized network. The related signaling would require substantial modifications to operate in an asynchronous network and in this case interference management capability would be limited.
We show that in the context of data intensive local area networks, emerging and next generation wireless systems should favor such signaling-intensive cooperation schemes. The following observations support our view.
-
(i)
Local area network deployments are normally uncoordinated. An example of this is WiFi access points which are typically installed by the end users, without extensive network planning. This implies that there is severe interference and high outage probability is more likely to occur than in wide area networks, thus increasing the gain potential from interference management.
-
(ii)
The cells are likely to shrink in order to provide higher throughputs and spatial reuse of radio resources. This means on the one hand that there are less and less active users per cell, and on the other hand that the cell traffic loads vary significantly both temporally and spatially. Thus the gains that may be achieved by local interference management are high.
-
(iii)
Local area networks exhibit low mobility which makes it simpler to implement signaling for accurate enough interference awareness.
The implementation of IA scheduler requires the following information to be shared between nodes in different cells: the signal power,  , the total interference plus noise power,
, the total interference plus noise power,  , and the average throughput of each receiver,
, and the average throughput of each receiver,  . These will be encoded in a broadcast message, which is transmitted from each receiver after data reception on the same frequency resources as the payload data. This broadcast message is termed an IA message. More specifically, when a transmitter considers allocating a specific resource, we assume that it had listened to the IA messages on that resource in the previous frame. This arrangement is attractive since it benefits from channel reciprocity, is very simple to implement, and implicitly ensures that each potential interferer is able to listen to the IA messages from every potential interference victim. Moreover, the identities of receivers need not be signaled as long as the transmitter is able to infer which of the reports comes from its own cell link. The channel gain to each interfered receiver
. These will be encoded in a broadcast message, which is transmitted from each receiver after data reception on the same frequency resources as the payload data. This broadcast message is termed an IA message. More specifically, when a transmitter considers allocating a specific resource, we assume that it had listened to the IA messages on that resource in the previous frame. This arrangement is attractive since it benefits from channel reciprocity, is very simple to implement, and implicitly ensures that each potential interferer is able to listen to the IA messages from every potential interference victim. Moreover, the identities of receivers need not be signaled as long as the transmitter is able to infer which of the reports comes from its own cell link. The channel gain to each interfered receiver  can be estimated from the broadcast message with sufficient accuracy, provided that the transmit power is known (agreed beforehand, or encoded in the message).
can be estimated from the broadcast message with sufficient accuracy, provided that the transmit power is known (agreed beforehand, or encoded in the message).
5.1. A Frame Structure for IA Scheduler
As a practical example, consider the frame structure sketched in Figure 1. The system operates on a 20 MHz bandwidth. The access is frame based, such that the frame duration is 10 ms. Assume that the scheduling granularity (i.e., resource block) is 4 MHz wide and 1 ms long. Assume further orthogonal frequency division multiple access (OFDMA) with a subcarrier spacing of 30 kHz. The frame is divided into 10 sub-frames of 1 ms duration, each consisting of 29 OFDMA symbols. In a conventional system without IA messages, this would mean 1.15 μ s cyclic prefix. Suppose now that 3 symbols per sub-frame are used for the IA messages. Since the reports are sent in the reverse direction (relative to the data), additional guard period is needed around them. The guard period is needed in order to accommodate propagation delays and devices switching from transmit to receive state and vice versa. For example, in our example we could specify 5 μ s guard periods by shortening the cyclic prefix to 800 ns, which is similar to 802.11 devices where Tx-Rx turnaround can be as fast as 2 μ s and for example, 802.11g OFDM has 800 ns cyclic prefix. Altogether this means that the overhead of the reports is roughly 10% (=3/29) since no extra symbols need to be sacrificed for the extra guard periods. Note that the impact on energy consumption from reversing the transmission direction for 10% of each sub-frame is dependent on the traffic model among other things. For example, a UE that has equal share of UL and DL transmissions would save energy in the UL direction by switching off the power amplifier during reception of IA messages, while in the DL direction the same amount of energy would be lost due to switching the power amplifier on for the transmission of the IA messages.
Assume now that the 20 MHz bandwidth is realized by size 1024 FFT and 665 used sub-carriers. The reports would need to be multiplexed to  raw bits on QPSK modulated sub-carriers of three OFDM symbols. The multiplexing of the reports needs to be very robust to high interference since they need to be decodable at neighboring cells and their received power can have a high dynamic range. First of all, the reports of a given 4 MHz subband used in the data transmission phase are transmitted on the same 4 MHz sub-band. This assures that there are no intra-cell collisions between the reports. The robustness to inter-cell interference could be obtained by for example, fixed frequency reuse where each 4 MHz reporting channel is subdivided into for example, 8 orthogonal reporting channels. This leaves
raw bits on QPSK modulated sub-carriers of three OFDM symbols. The multiplexing of the reports needs to be very robust to high interference since they need to be decodable at neighboring cells and their received power can have a high dynamic range. First of all, the reports of a given 4 MHz subband used in the data transmission phase are transmitted on the same 4 MHz sub-band. This assures that there are no intra-cell collisions between the reports. The robustness to inter-cell interference could be obtained by for example, fixed frequency reuse where each 4 MHz reporting channel is subdivided into for example, 8 orthogonal reporting channels. This leaves  raw bits per IA message. In our system simulations, we assume that the described frame structure with 10% overhead allows for reliable reception of 15-bit IA message at 0 dB SINR, which is anticipated to be a conservative rather than an optimistic assumption. It is also worth remarking that the IA messages are only taken as side information to the scheduler, and as such, lost IA messages do not lead to collapse of the system. In the extreme situation of all IA messages being lost it would lead to a similar scheduling metric as would arise in conventional PF scheduler where only intra-cell links are considered.
raw bits per IA message. In our system simulations, we assume that the described frame structure with 10% overhead allows for reliable reception of 15-bit IA message at 0 dB SINR, which is anticipated to be a conservative rather than an optimistic assumption. It is also worth remarking that the IA messages are only taken as side information to the scheduler, and as such, lost IA messages do not lead to collapse of the system. In the extreme situation of all IA messages being lost it would lead to a similar scheduling metric as would arise in conventional PF scheduler where only intra-cell links are considered.
The scheduling decisions are made in the BS for both DL and UL. Since the UEs are transmitting the IA messages of DL transmissions and the BS (DL transmitter) receives the IA messages, the DL interference CSI is readily available to the scheduler. However, the same does not apply to UL direction where the IA message receiver (UE) is not the same node as the scheduler (BS). This means that the messages need to be forwarded from the UEs to the BS (or, applying contention-based mechanisms in UL MAC). While the exact mechanism of implementing the UL IA message forwarding is out of scope of this paper, we note that there are ways to arrange it. For example, the UL access may be arranged in pairs of two sub-frames which means twice as coarse scheduling granularity. In this case, the reports transmitted between the two sub-frames would be forwarded to the BS in the second sub-frame together with the data. In principle, the message forwarding creates additional overhead but is negligible compared to the IA messages due to the fact that it is intra-cell signaling for which control channels are already present and are operating at higher SINR and spectral efficiency. For simplicity of the system simulations we assume that the BS has acquired the UL interference CSI.
6. Convergence of IA Scheduler
The IA scheduling metric is a system-wide metric. Let us assume that the scheduler has acquired the interference CSI from all receivers on the same band in the form of exact signal power, interference plus noise power, throughput of the corresponding receivers, and also perfectly estimated the interference channel gains to the reporting receivers. If a single scheduler updates the transmission schedule while all other schedulers repeat their schedules from the previous frame, it is straightforward to see that the system-wide performance metric (the geometric mean user throughput) does not decrease due to the fact that an allocation with negative scheduling metric is not allowed. Now suppose further that the schedulers take turns in updating their transmission schedules. The resulting sequence of system-wide performance metrics is nondecreasing and therefore monotonic. Given the fact that the system-wide metric is bounded, it must also converge, since any monotonic sequence that is bounded is also convergent [22]. The proof of the scheduler convergence is given in the Appendix. The method of sequential updates corresponds to the coordinate descent method where multivariate optimization problem is solved by solving a sequence of scalar subproblems, each operating on a selected coordinate (scheduler) while all other coordinates are fixed.
Sequential scheduling update would be very slow in a large network and cannot be easily implemented in practice. This problem can be overcome by randomization whereby in each frame the schedulers make a random decision of whether to repeat the transmission schedule from the previous frame (persist) or to update the schedule. In this case, the resulting sequence of system-wide performance metrics converges with probability one under perfect interference CSI information. The proof of probability one convergence with random scheduler updates is given in the Appendix. The choice of the persistence probability affects the convergence rate of the schedulers and an optimal choice of the parameter depends on the scenario. Basically, it should depend on the amount of other schedulers serving links that are active in the vicinity in order to maximize the probability of successful updates where the system utility increases.
The above states that IA scheduler converges to a local optimum transmission schedule in the case of perfect channel estimates and all IA messages being heard. In the practical case of nonideal information (only local information, non-ideal channel estimation, and so on), the same does not apply. In this case, the scheduler cannot observe the system utility change but will instead have an estimate of it. Each scheduler will then have a slightly different view of the system utility and the required assumption for convergence does not hold.
7. Numerical Examples of System Performance
We assess the performance of the proposed IA scheduler in system-level simulations. In the simulations, we compare IA scheduler to PF scheduler as well as to the optimum transmission schedule given by a centralized scheduler with full knowledge of interference channels. The system-level simulator is a static simulator which simulates the scheduling, link adaptation, and physical layer for 32 frames time interval for 500 random user locations (drops).
The performance of individual users is assessed by user throughput cdf (mean throughput of a user over the frames in a drop), given by  of (2). The overall system fairness is measured using the geometric mean of mean user throughputs over the frames in a drop,
of (2). The overall system fairness is measured using the geometric mean of mean user throughputs over the frames in a drop,  . Intuitively, the geometric mean throughput is low if any of the links are in outage, while a single link with a higher throughput cannot compensate for very low throughput values.
. Intuitively, the geometric mean throughput is low if any of the links are in outage, while a single link with a higher throughput cannot compensate for very low throughput values.
The link adaptation uses CQI in the form of SINR measurement reports that are available for each scheduling resource and chooses the modulation and coding scheme (MCS) that gives the maximum expected throughput from a set of 28 available MCSs. The MCSs are obtained by a combination of either QPSK, 16QAM, or 64QAM modulation, and a puncturing pattern of rate 1/3 mother turbo code, see for example, [21]. The maximum available transmit power is chosen such that the network is clearly in the interference limited regime. Each link has an infinite buffer of data to be transmitted. UL and DL are on separate sub-frames with an equal share of the frame duration (TDD).
7.1. Scenario and Channel Model
The wireless propagation is modeled according to WINNER II channel model for office/indoor scenarios [23]. The model includes path-loss with distance-dependent probability for line of sight (LOS) links and shadowing with wall losses. Frequency selectivity is modeled on top of the slow faded channel gain. We assume that each BS and UE has single antenna. A set of cellular UEs per BS are uniformly distributed over the area. The A1 scenario of WINNER II model contains four rows of offices facing two long corridors with the base stations located in the corridor and user equipment in the offices, see Figure 2.
Simulation scenario. The triangles represent BSs and the UEs are randomly distributed into the square rooms. Each UE connects to either the BS with the strongest channel gain out of the four BSs (case of no CSGs), or the UEs are allowed to connect to either BSs 1 and 4, or 2 and 3 (case of two CSGs).
In a first set of simulations, we compare the scheduler performance to the centralized scheduler and use only four links (1 UE per BS) to limit the complexity of the brute force search. In this scenario, there is no power control such that given a link is active on a resource, its transmit power on that resource is a predetermined constant,  .
.
In a second set of simulations, we consider a larger scenario, where the scenario of Figure 2 represents a single floor in a large scenario of 4 buildings with two floors in each with an average of 12 active UEs are distributed per floor. The buildings are separated with streets where the wireless propagation model for street canyons given in [23] is employed. In the larger scenario, power control is employed in both UL and DL such that  , with the fractionally power controlled power being
, with the fractionally power controlled power being

where  is the net loss of path-loss, shadow fading, and frequency selective fading in decibels and
is the net loss of path-loss, shadow fading, and frequency selective fading in decibels and  is the SNR target in decibels, here set to 26 dBm. Fractional power control is beneficial in reuse-1 networks for better trade-off between mean throughputs and coverage, see [24]. It is also needed in UL for balancing the received power from different UEs so that they would not mask each other due to loss of orthogonality.
is the SNR target in decibels, here set to 26 dBm. Fractional power control is beneficial in reuse-1 networks for better trade-off between mean throughputs and coverage, see [24]. It is also needed in UL for balancing the received power from different UEs so that they would not mask each other due to loss of orthogonality.  is defined as 20 dBm per sub-band of 4 MHz. Total bandwidth is 8 MHz (2 sub-bands) in the smaller scenario and 16 MHz (4 sub-bands) in the larger scenario.
is defined as 20 dBm per sub-band of 4 MHz. Total bandwidth is 8 MHz (2 sub-bands) in the smaller scenario and 16 MHz (4 sub-bands) in the larger scenario.
7.2. Results
In this section, we present the simulation results in three different simulations. First, we take a look at the convergence of the transmission schedules. Secondly, we present the results in a small 4 link scenario and compare the IA scheduler and PF scheduler performance to the optimum transmission schedule obtained by a centralized scheduler with global knowledge. The third simulation case compares both practical implementation and ideal IA scheduler to PF scheduler in a larger scenario with 32 base stations and 96 UEs.
7.2.1. IA Scheduler Convergence
Figure 3 shows a numerical example of the convergence of the transmission schedule. In this example, a 32-cell network with 96 randomly placed UEs was simulated. The same scenario was run with a conventional PF scheduler and IA scheduler. The IA scheduler was simulated under the assumption of ideal interference messaging as well as under the practical signaling scheme described in Section 5 in order to study the impact of nonideal implementation to the performance. The upper figures depict the portion of changed scheduling decisions versus frame index (the amount of resources that were allocated to a different UE, left unallocated, or taken into use, divided by the total amount of resources). The simulation starts with all links inactive at frame zero. In frame one, there is no interference CSI and thus the schedulers take all resources into use, resulting in zero similarity to the preceding frame. The schedulers update the transmission schedules for the next frame independently of each other with probability 0.5. As time evolves the schedulers reach a common understanding of resource usage and there are no further updates to transmission schedules, see Figure 3. In this particular example, this happens in roughly 15 frames for the IA scheduler, both with practical signaling scheme and ideal interference CSI. The lower figures show the geometric mean of ideal link adaptation throughput (the expected throughput in case there would be no link adaptation delay) versus frame index.
IA scheduler convergence in 32 cell indoor office scenario with 96 UEs. Persistence probability is 50%. The upper figures display the percentage of changed scheduling decisions per frame and the lower figures display the mean (over scenario realizations) of geometric mean throughputs. The left-hand side figures are for OSG and right-hand side figures are for 2 CSGs. Ideal IA scheduler converges to a stable transmission schedule. Nonideal IA scheduler shows a small residual of differing scheduling decisions due to imperfect interference CSI. The "PF, orth." curve stands for PF scheduler and orthogonal bands for the two CSGs.OSG2 CSGs
7.2.2. Comparison to Centralized Scheduler Optimum
The throughput distributions in the relatively low interference case of no closed subscriber groups (CSGs) are shown in Figure 4(a), where single floor with 4 DL and UL links is simulated in order to keep the centralized scheduler tractable. Note that single UE per cell implies that the PF scheduler results in each link being active on all the resources with nonzero expected throughput. In this scenario, the UEs are connecting to the BS with the strongest signal, and thus the scenario does not impose a particularly challenging interference situation. It is rather an example of a well-deployed network, where one would expect least gain from the proposed IA scheduler. However, as can be seen from upper figure in Figure 4(a), the system fairness of a conventional PF scheduler is far from optimum. That is, already in the simplest case, a reuse-1 network is not giving the best performance from system fairness point of view. IA scheduler performance is very close to global optimum resource allocation. An interesting observation is that the UL and DL performances differ significantly from each other with PF scheduler, but an interference-aware transmission schedule leads to virtually equal UL and DL performances (for this reason, the UL results are left out of the figure). From the user throughput distribution in the lower figure, we see that PF scheduler is able to provide the peak throughput to a larger amount of links at the expense of cell edge throughput. The step-like behavior of the IA schedulers comes from the fact that each link gets either 1, 2, 3, or 4 resources (each frame consists of two sub-bands and two UL and DL sub-frames). The interference awareness drives the system to high SINR regime, and thus a significant portion of the transmissions employ MCSs from the high end of the available set.
Empirical throughput distributions in the 4-link scenario. In the open subscriber group (OSG) case on the left, the UEs connect to the strongest BS without restrictions, and in the closed subscriber group (2 CSGs) case on the right, the UEs connect to the strongest out of two own network BS. The upper figures display the system geometric mean throughput and lower figures the user throughput distributions. In the optimum centralized and IA scheduler cases, only DL cdf is plotted since the UL cdf was virtually the same. IA scheduler improves the system fairness over PF scheduler significantly. Conventional PF scheduler leads to very poor coverage in the CSG case, while IA scheduler gets rid of the outages. IA scheduler yields a like performance with the global optimum centralized scheduler.OSG2 CSGs
A more challenging interference situation is obtained by dividing the UEs and BSs into two closed subscriber groups (CSGs) operating on a shared band. The UEs of the two CSGs are still distributed evenly over the floor, but are only allowed to connect to own CSG BS, which may be much further away than the closest BS. Figure 4(b) shows the resulting throughput distributions. As expected, the PF scheduler is struggling with coverage due to the very high amount of interference between the two CSGs. Interference awareness is able to get rid of the coverage issue completely and make the shared band operation for two CSGs possible. The difference between the IA scheduler and the global optimum is very small compared to the gain relative to PF scheduler, and we may conclude that very high gain in system utility can be obtained with the proposed distributed scheme. Note that one can estimate a rough upper bound on the performance of a system where the two CSGs use orthogonal bands by scaling the no CSG results of Figure 4(a) by half. It can be seen that the shared band solution with IA scheduler would beat the orthogonal bands PF scheduler by a significant margin.
7.2.3. Performance in Large Scenario and Non-Ideal IA Scheduler
We have also simulated a more practical scenario that includes 4 buildings separated with streets. Each building has two floors with 12 UEs per floor on average, and optionally two CSGs (as in the preceding case). In such a large scenario, the search space gets too large for finding the global optimum transmission schedule by using a brute force algorithm. The simulated IA scheduler algorithm takes into account nonidealities of practical implementation. Specifically, the signaling arrangement discussed in Section 5 is modeled in the simulator. The modeling takes into account the 10% reduction of the effective data rates due to time-multiplexing of the IA messages, and also a 0 dB SINR threshold for reliable IA message reception. The IA messages are further orthogonalized to 8 channels. The non-ideal orthogonality of these signaling channels is taken into account by suppressing other channel transmissions by 50 dB instead of nulling them completely. The channels are assigned to cells in a distributed manner. The system simulation results in the larger scenario are shown in Figures 5, 6, and 7.
SINR distributions in the scenario with 96 UEs and 32 BSs. The figures on the left represent OSG network and the figures on the right represent 2 CSGs network. IA scheduler drives the receiver operating point to high SINR regime in comparison to PF scheduler. The "PF, orth." curve represents the case of PF scheduler with the 2 CSGs on orthogonal bands.OSG2 CSGs
User throughput distributions in the scenario with 96 UEs and 32 BSs. The figures on the left represent OSG network and the figures on the right represent 2 CSGs network. The largest gains from IA scheduler are evident in the lower percentiles of user throughput, while there is also gain in the median throughput. The coverage of PF scheduler with two CSGs on shared band is very poor with 20% DL outage. IA scheduler is able to remedy the situation remarkably. The "PF, orth." curve represents the case of PF scheduler with the 2 CSGs on orthogonal bands, where it can be seen that just orthogonalizing the band between the 2 CSGs and running a PF scheduler is a suboptimal strategy.OSG2 CSGs
Geometric mean throughput distributions in the scenario with 96 UEs and 32 BSs. The figures on the left represent OSG network and the figures on the right represent 2 CSGs network. This system-wide performance metric shows that there is an overall gain of 10% in DL and 30% in the UL when employing IA scheduler in the open subscriber group case. PF scheduler shows large amount of zero geometric mean throughputs in the CSG case due to the fact that zero geometric mean occurs if any of the 96 users is in outage. The superiority of shared-band operation with IA scheduler over orthogonal bands PF scheduler is evident in the case of 2 CSGs.OSG2 CSGs
The SINR distributions for DL and UL transmissions of Figure 5 show that IA scheduler drives the system into higher SINR regime by decreasing the spatial reuse of resources as compared to PF scheduler. High SINR is not necessarily a benefit per se (if it is achieved on a smaller set of resources), but it might be useful if power efficiency is of concern. Specifically, the higher throughput per resource might be advantageous together with optimizing the time domain resource usage and switching the transmitter off in the sub-frames where there is no data scheduled for transmission (DRX/DTX, see [4]).
The cumulative user throughput distributions are shown in Figure 6. Comparing IA scheduler and PF scheduler in case of no CSGs shows that there is roughly 1.5- and 2.5-fold increase in the lower percentiles of DL and UL user throughput distributions when IA scheduler is employed. In the higher percentiles, the situation is the other way around, indicating the relatively unfair resource allocation of PF scheduler. Median throughput is higher with IA scheduler in both DL and UL, but with a higher margin in UL. When there are two CSGs, the coverage achieved with PF scheduler is poor with roughly 20% of DL outage and 5% UL outage. IA scheduler is able to restore the coverage in the CSG case, thus enabling shared band operation. It is interesting to compare the performance of a conventional system that would give orthogonal bands for the two CSGs with PF scheduler to the proposed IA scheduler with shared band operation. The conclusion is that around 40% gain in median user throughputs is available by switching to interference-aware shared-band operation. Comparing the lower percentiles shows that this gain is not in the expense of coverage. On the contrary, IA scheduler gains also in coverage with fifth percentile user throughput increasing of 1.2-fold in DL and 2.6-fold in UL.
Finally, Figure 7 displays the distribution of the geometric mean of the throughput over all 96 UEs in the scenario. In the OSG case, the gain from IA scheduler over PF scheduler is 10% and 30% in the DL and UL, respectively. This shows that even when considering a scenario that is least challenging in the sense of absence of strong interferers, IA scheduler is able to provide gain in system-wide performance over PF scheduler (imperfect interference CSI and 10% signaling overhead are taken into account in the IA scheduler results). When the two CSGs are operating on a shared-band, the significant portion of zero geometric mean throughputs in the PF scheduler case is due to the fact that the geometric mean is taken over 96 users. If any of the 96 users is in outage, the geometric mean throughput will be zero. If we take the more reasonable case of PF schedulers on orthogonal bands for the CSGs as the comparison point to IA scheduler, we see that a roughly 1.5-fold increase in system performance is available by switching to shared band operation and IA scheduling.
The loss from nonidealities in the IA messaging is evident in all of the figures. It is in the order of 10% in the median throughputs. This can be explained by the signaling overhead of 10%. However, the loss is much larger in the low percentiles, indicating that the performance could be significantly improved if a better signaling scheme could be developed.
The results shown in this section support the conclusion that IA scheduler is feasible to implement in practice, providing significant performance gains over a conventional system, especially in scenarios with harsh interference. Moreover, the gain from having interference awareness at the scheduler is significantly higher than the throughput loss due to the signaling overhead.
8. Conclusion
In this paper, we proposed an interference-aware scheduling scheme that allows the individual transmission decisions to be made in the schedulers optimally in the sense of system fairness. We sketched an example implementation and characterized the associated overhead. The proposed scheduler was proven to be convergent.
The scheme is distributed and the scheduler works much like a conventional scheduler, except that the information from other receivers on the shared-radio resources is made available to the scheduler by means of interference-awareness (IA) reports. The performance of the scheme was assessed through system simulations. In a small scenario the performance was found to be close to the optimum attained by a centralized scheduler with full system-wide channel knowledge. Overall, the presented simulation results show that the proposed scheme is able to provide user fairness and coverage in high interference scenarios, where a conventional system would fail to meet any reasonable fairness and coverage constraints. We conclude that by slightly increasing the overhead by providing inter-cell interference signalling, a significant increase in spectral efficiency and fairness may be achieved. Most importantly, the additional overhead is clearly well offset by the obtained gains.
A significant advantage of the proposed scheme is elimination of outage in high-interference local area wireless networks arising from for example, uncoordinated network deployments, closed subscriber groups on a shared band, device-to-device communication underlying cellular band, per-cell flexible UL/DL switching point adaptation, and other strong interference sources.
There are a number of open questions related to IA scheduler that demand further attention. The exact performance of the physical format of IA message needs to be assessed in link-level simulations. This would allow for more realistic trade-off between the reliability of IA message reception and signaling overhead.
An interesting question is that of scalability with the amount of users per cell. In case the amount of UEs per cell grows, it becomes necessary to either time-domain multiplex the UEs over frames or subdivide the resource units to finer granularity. This would mean that the persistence would be partially lost or increased overhead. Another possibility is to cluster multiple links under a single IA message, which would be then sent coherently from the receivers of the corresponding links.
MIMO communication induces yet another interesting area for development of IA scheduler. As it would require a large amount of signaling to enable perfect interference CSI in the MIMO case (estimates of the MIMO interference channels, received interference and signal covariance matrices), there is need for an approximate solution.
The proposed interference management scheme would fit well with device-to-device (D2D) communications underlying cellular network [25]. For maximal spectral efficiency and throughputs, it is beneficial for the D2D links to reuse the cellular UL and DL resources in case the interference can be kept at a tolerable level [26].
References
Jain R, Chiu D, Hawe W: A quantitative measure of fairness and discrimination for resource allocation in shared computer systems. DEC Research Report TR-301 September 1984.
Radunović B, Boudec JYL: Rate performance objectives of multihop wireless networks. IEEE Transactions on Mobile Computing 2004, 3(4):334-349. 10.1109/TMC.2004.45
Kushner HJ, Whiting PA: Convergence of proportional-fair sharing algorithms under general conditions. IEEE Transactions on Wireless Communications 2004, 3(4):1250-1259. 10.1109/TWC.2004.830826
Holma H, Toskala A: LTE for UMTS—OFDMA and SC-FDMA Based Radio Access. John Wiley & Sons, New York, NY, USA; 2009.
Kucera S, Aissa S, Yoshida S: Adaptive channel allocation for enabling target SINR achievability in power-controlled wireless networks. IEEE Transactions on Wireless Communications 2010, 9(2):833-843.
Saraydar CU, Mandayam NB, Goodman DJ: Efficient power control via pricing in wireless data networks. IEEE Transactions on Communications 2002, 50(2):291-303. 10.1109/26.983324
Xiao M, Shroff NB, Chong EKP: A utility-based power-control scheme in wireless cellular systems. IEEE/ACM Transactions on Networking 2003, 11(2):210-221. 10.1109/TNET.2003.810314
Etkin R, Parekh A, Tse D: Spectrum sharing for unlicensed bands. IEEE Journal on Selected Areas in Communications 2007, 25(3):517-528.
Chiang M, Tan CW, Palomar DP, O'Neill D, Julian D: Power control by geometric programming. IEEE Transactions on Wireless Communications 2007, 6(7):2640-2650.
Gesbert D, Kiani SG, Gjendemsj A, Ien GE: Adaptation, coordination, and distributed resource allocation in interference-limited wireless networks. Proceedings of the IEEE 2007, 95(12):2393-2409.
Huang J, Berry RA, Honig ML: Distributed interference compensation for wireless networks. IEEE Journal on Selected Areas in Communications 2006, 24(5):1074-1084.
Schmidt DA, Shi C, Berry RA, Honig ML, Utschick W: Distributed resource allocation schemes: pricing algorithms for power control and beamformer design in interference networks. IEEE Signal Processing Magazine 2009, 26(5):53-63.
Shi C, Berry RA, Honig ML: Distributed interference pricing for OFDM wireless networks with non-separable utilities. Proceedings of the 42nd Annual Conference on Information Sciences and Systems (CISS '08), March 2008 755-760.
Omiyi P, Haas H, Auer G: Analysis of TDD cellular interference mitigation using busy-bursts. IEEE Transactions on Wireless Communications 2007, 6(7):2721-2730.
Ghimire B, Auer G, Haas H: Busy bursts for trading off throughput and fairness in cellular OFDMA-TDD. EURASIP Journal on Wireless Communications and Networking 2009, 2009(10):-14.
Garcia LGU, Pedersen KI, Mogensen PE: Autonomous component carrier selection: interference management in local area environments for LTE-advanced. IEEE Communications Magazine 2009, 47(9):110-116.
Virtej E, Lunden P: Coordination between access points in distributed flexible spectrum use. Proceedings of the 20th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, September 2009 666-670.
Ellenbeck J, Hartmann C, Berlemann L: Decentralized inter-cell interference coordination by autonomous spectral reuse decisions. Proceedings of the 14th European Wireless Conference (EW '08), June 2008 1-7.
Cesana M, Maniezzo D, Bergamo P, Gerla M: Interference aware (IA) MAC: an enhancement to IEEE802.11b DCF. Proceedings of the 58th IEEE Vehicular Technology Conference (VTC '03), October 2003 2799-2803.
Monks J, Bharghavan V, Hwu W-M: A power controlled multiple access protocol for wireless packet networks. Proceedings of the 20th IEEE Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '01), 2001 1: 219-228.
Lembo S, Ruttik K, Tirkkonen O: Modeling BLER performance of punctured turbo codes. Proceedings of the 12th International Symposium on Wireless Personal Multimedia Communications (WPMC '09), September 2009 1-5.
Bibby J: Axiomatisations of the average and a further generalisation of monotonic sequences. Glasgow Mathematical Journal 1974, 15: 63-65. 10.1017/S0017089500002135
WINNER II D1.1.2 : WINNER II channel models. September 2007.
Castellanos CÚ, Villa DL, Rosa C, Pedersen KI, Calabrese FD, Michaelsen PH, Michel J: Performance of uplink fractional power control in UTRAN LTE. Proceedings of the 67th IEEEVehicular Technology Conference (VTC '08), May 2008 2517-2521.
Jänis P, Yu C-H, Doppler K, et al.: Device-to-device communication underlaying cellular communications systems. International Journal of Communications, Network and System Sciences 2009, 2(3):169-178. 10.4236/ijcns.2009.23019
Jänis P, Koivunen V, Ribeiro Ć, Korhonen J, Doppler K, Hugl K: Interference-aware resource allocation for device-to-device radio underlaying cellular networks. Proceedings of the 69th IEEE Vehicular Technology Conference (VTC '09), April 2009, Barcelona, Spain
Author information
Authors and Affiliations
Corresponding author
Appendix
Assume that each link is either active with maximal power or off. Then a transmission schedule of  th scheduler can be represented with variable
th scheduler can be represented with variable  , where
, where  is the number of resource blocks and
is the number of resource blocks and  is the number of links served by
is the number of links served by  th scheduler. The system utility is represented by function
th scheduler. The system utility is represented by function  , which can be evaluated at each scheduler if each scheduler knows the signal power, interference plus noise power, and throughput of other links operating on the same area. Now the convergence of IA scheduler in the case of sequential updates and randomized updates is characterized by the following theorems.Theorem 1. The sequential update rule of current transmission schedules
, which can be evaluated at each scheduler if each scheduler knows the signal power, interference plus noise power, and throughput of other links operating on the same area. Now the convergence of IA scheduler in the case of sequential updates and randomized updates is characterized by the following theorems.Theorem 1. The sequential update rule of current transmission schedules  to next transmission schedules
to next transmission schedules 

 in finite time, that is,
in finite time, that is,  s.t.
s.t.  .Proof. Denote
.Proof. Denote  . Since each scheduler updates its allocation only in case system utility rises, we have
. Since each scheduler updates its allocation only in case system utility rises, we have  . The system utility is clearly bounded from above,
. The system utility is clearly bounded from above,  , since the data rate of each link bounded by the available set of modulation and coding schemes, and the amount of resources is bounded due to finite system bandwidth. Convergence of the resulting sequence of system utilities
, since the data rate of each link bounded by the available set of modulation and coding schemes, and the amount of resources is bounded due to finite system bandwidth. Convergence of the resulting sequence of system utilities  follows from monotone convergence theorem, which states that a monotone increasing sequence that is bounded from above is convergent [22]. Therefore,
follows from monotone convergence theorem, which states that a monotone increasing sequence that is bounded from above is convergent [22]. Therefore,  s.t.
s.t.  . Then also the scheduling decisions will reach the constant
. Then also the scheduling decisions will reach the constant  ,
,  . Theorem 2. The random update rule of the schedulers
. Theorem 2. The random update rule of the schedulers
 , will reach a stable point
, will reach a stable point  with probability one, that is,
with probability one, that is,  s.t.
s.t.  .Proof. The event of a single scheduler updating its transmission schedule such that the system utility increases is denoted by
.Proof. The event of a single scheduler updating its transmission schedule such that the system utility increases is denoted by  . The probability of
. The probability of  is positive, since
is positive, since  , unless the schedules have already converged. The event of a colliding update (more than one scheduler updating simultaneously) is denoted by
, unless the schedules have already converged. The event of a colliding update (more than one scheduler updating simultaneously) is denoted by  and the event of no update by
and the event of no update by  . The sequence of updates is denoted by
. The sequence of updates is denoted by  , where each
, where each  . Define
. Define  as the maximum number of sequential successful updates required to reach a stable transmission schedule from an arbitrary transmission schedule
as the maximum number of sequential successful updates required to reach a stable transmission schedule from an arbitrary transmission schedule  . Necessarily
. Necessarily  since the space of possible transmission schedules is finite by definition. Now the probability of a sequence of successive successful updates of length
since the space of possible transmission schedules is finite by definition. Now the probability of a sequence of successive successful updates of length  is positive. Therefore, the probability of
is positive. Therefore, the probability of  ,
,  , containing such a subsequence converges to one as
, containing such a subsequence converges to one as  . In other words, a stable transmission schedule is reached with probability 1, which completes the proof.
. In other words, a stable transmission schedule is reached with probability 1, which completes the proof.

Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jänis, P., Koivunen, V. & Ribeiro, C.B. Interference-Aware Radio Resource Management for Local Area Wireless Networks. J Wireless Com Network 2011, 921623 (2011). https://doi.org/10.1155/2011/921623
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/921623
 to
to 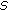 do
do





