- Research
- Open access
- Published:
Mobility management in HetNets: a learning-based perspective
EURASIP Journal on Wireless Communications and Networking volume 2015, Article number: 26 (2015)
Abstract
Heterogeneous networks (HetNets) are expected to be a key feature of long-term evolution (LTE)-advanced networks and beyond and are essential for providing ubiquitous broadband user throughput. However, due to different coverage ranges of base stations (BSs) in HetNets, the handover performance of a user equipment (UE) may be significantly degraded, especially in scenarios where high-velocity UE traverse through small cells. In this article, we propose a context-aware mobility management (MM) procedure for small cell networks, which uses reinforcement learning techniques and inter-cell coordination for improving the handover and throughput performance of UE. In particular, the BSs jointly learn their long-term traffic loads and optimal cell range expansion and schedule their UE based on their velocities and historical data rates that are exchanged among the tiers. The proposed approach is shown not only to outperform the classical MM in terms of throughput but also to enable better fairness. Using the proposed learning-based MM approaches, the UE throughput is shown to improve by 80% on the average, while the handover failure probability is shown to reduce up to a factor of three.
1 Introduction
To cope with the wireless traffic demand within the next decade, operators are underlaying their macro-cellular networks with low-power base stations (BSs) [1]. Such networks are typically referred as heterogeneous networks (HetNets), and their deployment entails a number of challenges in terms of capacity, coverage, mobility management (MM), and mobility load balancing across multiple network tiers [2]. Mobility management, in particular, is essential to ensure a continuous connectivity to mobile user equipment (UE) while maintaining satisfactory quality of service (QoS). Therefore, poor mobility management may lead to handover failures (HOFs), radio link failures, as well as unnecessary handovers, typically referred as ping-pong (PP) events. Such deficiencies result in low resource utilization efficiency and poor user experience. In order to solve such problems, mobility parameters in each cell need to be dynamically optimized according to cell traffic loads, coverage areas of different cells, and velocities of the UE.
In the advent of HetNets, recent studies have demonstrated that HOFs and PPs can be serious problems due small cell sizes [2,3]. MM mechanisms, which have been included in the first release of the long-term evolution (LTE) standard (Rel-8), were originally developed for networks that only involve macrocells [4]. The defined MM procedures for the macrocell-only scenarios have been widely discussed in the literature, e.g., in [5-19]. It has been shown that MM for macrocell-only scenarios yield highly reliable handover execution, where HOFs and PPs can be typically avoided due to large cell sizes [20]. However, the deployment of a large number of small cells (e.g., femtocells, picocells, etc.) increases the complexity of MM in HetNets, since mobile UE may trigger frequent handovers when they traverse the coverage area of a small cell. This leads to less reliable handover execution in HetNets.
While MM carries critical importance for HetNets to minimize HOFs and PPs, mobility load balancing is also crucial to achieve load balancing among different network tiers. In HetNets, the load among tiers is unbalanced due to significant differences in transmit power levels. UE tend to connect to the macrocell even when the path loss conditions between the small cell and the UE are better, because the handover decision is based on the highest reference signal received power (RSRP) measured at a UE [21]. As a remedy to this, the 3rd Generation Partnership Project (3GPP) standardized the concept of cell range expansion to virtually increase a small cell’s coverage area by adding a bias value to its RSRP, which leads to traffic offloading from the macrocell. To enhance the overall system performance, not only cell-specific handover parameter optimization, such as the range expansion bias (REB) value adaptation, but also scheduling and resource allocation must be performed in a coordinated manner across different tiers. A survey of these and various other existing mobility management and load balancing approaches considering such aspects for small cells in LTE-advanced networks is provided in [22].
In this article, a joint MM and UE scheduling approach is proposed using tools from reinforcement learning. The proposed MM approach utilizes parameter adaptation both in the long term and the short term. Hereby, macro- and picocells learn how to optimize their long-term traffic load, whereas in the short-term, the UE association process is carried out based on history and velocity-based scheduling. We propose multi-armed bandit (MAB) and satisfaction-based MM learning techniques as a long-term load balancing approach aiming at improving the overall system throughput while at the same time reducing the HOF and PP probabilities. A context-aware scheduler is proposed as a short-term UE scheduling approach considering fairness.
The rest of the article is organized as follows. Section 3 provides a brief review about recent mobility management works in the literature and summarizes our contribution in this paper. Section 3 describes our system model. In Section 3, the problem formulation for MM is presented. In Section 3, the context-aware scheduler is described. In Section 3, we introduce our learning based MM approaches. Section 3 presents system level simulation results, and finally, Section 3 concludes the article.
2 Related work and contribution
In this section, we first summarize some of the recent studies on mobility management in LTE-advanced HetNets and use these to highlight the challenges and open problems that should be further addressed in the research community. Subsequently, a typical HetNet scenario with macro- and picocells deployed in the same frequency band is considered to describe our contribution in this paper.
2.1 Literature review
The handover process requires a smooth transfer of a UE’s active connection when moving from one cell to another, while still maintaining the guaranteed QoS. The objective is to have mobility procedures resulting in low probability of experiencing radio link failures, HOFs, and PP events. Mobility solutions meeting those objectives are often said to be robust. The enhancement for handover robustness in HetNet LTE networks have been subject to recent interest. In LTE Rel-11, mobility enhancements in HetNets have been investigated through a dedicated study item [2]. In this study item and cited work items therein, mobility performance enhancement solutions for co-channel HetNets are analyzed taking into account mobility robustness improvement. Proposed solutions are related to optimizing the handover procedure by dynamically adapting handover parameters for different cell sizes and UE velocities.
Mobility management techniques for HetNets have been recently investigated in the literature, e.g., [23-28]. In [23], the authors evaluate the effect of different combinations of various MM parameter settings for HetNets. The conclusions are aligned with the HetNet mobility performance evaluations in 3GPP [2], i.e., HetNet mobility performance strongly depends on the cell size and the UE speed. The simulation results in [23] consider that all UE have the same velocity in each simulation setup. Further results on the effects of MM parameters are presented in [24], where the authors propose a fuzzy-logic-based controller. This controller adaptively modifies handover parameters for handover optimization by considering the system load and UE speed in a macrocell-only network.
In [25], the authors evaluate the mobility performance of HetNets considering almost blank subframes in the presence of cell range expansion and propose a mobility based intercell interference coordination scheme. Hereby, picocells configure coordinated resources by muting on certain subframes, so that macrocells can schedule their high-velocity UE in these resources which are free of co-channel interference from the picocells. However, the proposed approach only considers three broad classes of UE velocities: low, medium, and high. Moreover, no adaptation of the REB has been taken into account. In [26], the authors propose a hybrid solution for HetNet MM, where MM in a macrocell is network controlled while UE-autonomous in a small cell. In the scenario in [26], macrocells and small cells operate on different component carriers which allows the MM to be maintained on the macrocell layer while enabling small cells to enhance the user plane capacity. In addition to these approaches, a fairness-based MM solution is discussed in [27]. Here, the cell selection problem in HetNets is formulated as a network wide proportional fairness optimization problem by jointly considering the long-term channel conditions and the distribution of user load among different tiers. While the proposed method enhances the cell-edge UE performance, no results related to mobility performance are presented.
In [28], the authors propose a MAB-based intercell interference coordination approach that aims at maximizing the throughput and handover performance by subband selection for transmission for a small-cell-only network. The proposed approach deals with the trade-off of increasing the subband size for throughput and handover success rate maximization and decreasing the subband size as far as possible to minimize interference. The only parameter which is optimized is the number of subbands based on some signal-to-interference-plus-noise-ratio (SINR) thresholds. While the HOF rate is decreased by the proposed approach, the PP probability is not analyzed. To the best of our knowledge, there is no previous work related to learning-based HetNet MM in the literature, which jointly considers handover performance, load balancing, and fairness.
2.2 Contribution
In this paper, we propose MM approaches for network capacity maximization and HOF reduction, which also maintain user fairness across the network. In Figures 1a,b, we depict the basic idea of the classical MM and the proposed MM approaches, respectively. In the classical MM approach, there is no information exchange among tiers in case of UE handover and traffic offloading might be achieved by picocell range expansion. In the proposed MM approaches, instead, each cell individually optimizes its own MM strategy based on limited coordination among tiers. Hereby, macro and pico BSs learn how to optimize their REB on the long term. On the other hand, on the short term, they carry out user scheduling based on each UE’s velocity and average rate via coordination among the macrocell and picocell tiers. We propose two learning-based MM approaches: MAB and satisfaction-based MM. The major difference between MAB and satisfaction-based learning is that MAB aims at maximizing the overall capacity, while satisfaction-based learning aims at satisfying the network in terms of capacity. The contributions of this article can be summarized as follows:
-
In the proposed MM approaches, we focus on both short-term and long-term solutions. In the long term, a traffic load balancing procedure in a HetNet scenario is proposed, while in the short term, the UE association process is solved.
-
To implement the long-term load balancing method, we propose two learning-based MM approaches by using reinforcement learning techniques: a MAB-based and a satisfaction-based MM approach.
-
The short-term UE association process is based on a proposed context-aware scheduler considering a UE’s throughput history and velocity to enable fair scheduling and enhanced cell association.
3 System model
We focus on the downlink transmission of a two-layer HetNet, where layer 1 is modeled as macrocells and layer 2 as picocells. The HetNet consists of a set of BSs \(\mathcal {K} = \{1,\ldots,K\}\) with a set \(\mathcal M = \{1,\ldots,M\}\) of macrocells underlaid by a set \(\mathcal P = \{1,\ldots,P\}\) of picocells, where \(\mathcal {K} = \mathcal {M} \cup \mathcal {P}\). Macro BSs are dropped following a hexagonal layout including three sectors. Within each macro sector m, \(p\in \mathcal {P}\) picocells are randomly positioned, and a set \(\mathcal U = \{1,\ldots,U\}\) of UE which are randomly dropped within a circle around each picocell p (referred as a hotspot region). UE associated to macrocells are referred as macro UE \(\mathcal {U}(m) = \{1(m),\ldots,U(m)\} \in \mathcal {U}\) and UE served by picocells are referred as pico UE \(\mathcal {U}(p) = \{1(p),\ldots,U(p)\} \in \mathcal {U}\), where \(\mathcal {U}(p) \neq \mathcal {U}(m)\). Each UE i(k) with k∈{m,p} has a randomly selected velocity \(v_{i(k)}\in \mathcal {V}\) km/h and a random direction of movement within an angle of [ 0;2π]. This is a slightly modified version of the mobility model described in Section 5.3.1 case 2 in [2]. The only difference with the 3GPP mobility model is that we do not consider any bouncing circle in our simulations. Hereby, considering a random direction of movement and no bouncing circle enables different types of handover (macro-to-macro and pico(macro)-to-macro(pico). A co-channel deployment is considered, in which picocells and macrocells operate in a system with a bandwidth B consisting of r={1,…,R} resource blocks (RBs). At every time instant t n =n T s with n=[1,…,N] and T s =1 ms, each BS k decides how to expand its coverage area by learning its REB β k ={β m ,β p } with β m ={0;3;6} dB and β p ={0;3;6;9;12;15} dBa. Both macro and pico BSs select their REB to decide which UE i(k) to schedule on which RB based on the UE’s context parameters. These context parameters are defined as the UE’s velocity v i(k), its instantaneous rate ϕ i(k)(t n ) when associated to BS k, and its average rate \(\overline {\phi }_{i(k)}(t_{n})\) defined as
whereby T=N T s is a time window. The instantaneous rate ϕ i(k)(t n ) is given by
with γ i(k)(t n ) being the SINR of UE i(k) at time t n , which is defined as
where p k is the transmit power of BS k, σ 2 is the noise variance, and g i(k),k (t n ) is the channel gain from cell k to UE i(k) associated to BS k. The bandwidth B i(k) in Equation 2 is the bandwidth which is allocated to UE i(k) by BS k at time t n .
3.1 Handover procedure
According to the 3GPP standard, the handover mechanism involves the use of RSRP measurements, the filtering of measured RSRP samples, a handover hysteresis margin, and a time-to-trigger (TTT) parameter. Hereby, TTT is a time window which starts after the handover condition is fulfilled; a UE does not transmit its measurement report to its serving cell before the TTT timer expires. This helps to ensure that ping-pongs are minimized due to fluctuations in the link qualities from different cells. The main steps of a typical handover process in a HetNet scenario are illustrated in Figure 2. First, a UE performs RSRP measurements and waits until the biased RSRP from a target cell (e.g., a picocell) is larger than the biased RSRP from its serving cell (e.g., a macrocell) plus a hysteresis margin (step 1). Hence, a handover is executed if the target cell’s (biased) RSRP (plus hysteresis margin) is larger than the source cell’s (biased) RSRP, i.e., the handover condition for a UE i(k) to BS k is defined as
with \(\{l,k\}\in \mathcal {K}\), m hist [dB] the UE- or cell-specific hysteresis margin, β k (β l ) [dB] is the REB of BS k(l), and P k (i(k))(orP l (i(l))) [dBm] is the i(k)-th (i(l)-th) UE’s RSRP from BS k(l). Even when the condition in (4) is satisfied, the UE waits for a duration of TTT, before sending a measurement report to its serving cell (step 2). If the condition in step 1 is still satisfied after TTT, the UE sends the measurement reports to its serving cell in its uplink (step 3), which finalizes the handover by sending a handover command to the UE in the downlink (step 4). In order to filter out the effects of fast fading and shadowing, a UE obtains each RSRP sample as the linear average over the power contribution of all resource elements that carry the common reference signal within one subframe (i.e., 1 ms) and in a pre-defined measurement bandwidth (e.g., 6 RBs) [2]. This linear averaging is done in layer 1 filter. As illustrated in Figure 3, layer 1 filtering is performed every 40 ms and averaged over five samples. The layer 1 filtered measurement is then updated through a first-order infinite impulse response filter in layer 3 every 200 ms [2].
Processing of the RSRP measurements through layer 1 and layer 3 filtering at a UE [ 2 ].
4 Problem formulation for throughput maximization
In this section, we describe our optimization approach for maximizing the total rate of each cell k as a long-term load balancing process. To provide a better overview, we first present the interaction of the proposed long-term and short-term processes in Figure 4. The long-term load balancing optimization approach is solved by the proposed learning-based MM approaches presented in Section 3 and Section 3. As illustrated in Figure 4, both, MAB and satisfaction-based MM, result in REB β k value optimization and in load balancing ϕ k,tot(t n ). Based on the estimated instantaneous load, the context-aware scheduler selects, in the short term, for each RB a UE by considering its history and velocity as described in Section 3. This results in each UE’s instantaneous rate ϕ i(k)(t n ) and the RB allocation vector α i(k)(t n )=[α i(k),1,…,α i(k),R ] containing binary variables α i(k),r , and indicating whether UE i(k) of BS k is allocated at RB r or not. The inter-relation between the selected context parameters (UE’s history and velocity), the scheduling function, the described optimization formulation, and the rationale behind the short-term and long-term MM approaches can be summarized as follows. Within the proposed MM approach, we carry out load balancing in the long term by optimizing the REB values and carry out history-based UE scheduling in the short term by means of the proposed context-aware scheduler. The combination of both procedures yields the HOF and PP probability reduction via the optimal REB value selection and the proposed context-aware scheduler. Here, the load balancing procedure yielding the optimal REB value incurs wideband SINR enhancement and HOF reduction. The context-aware scheduler on the other hand schedules UE based on the highest estimated achievable rate of each UE according to its instantaneous channel condition and its history, which leads to long-term fairness among UE. Both approaches, i.e., load balancing and history-based scheduling, yield throughput enhancement. Additionally, the velocity-based ranking property of the context-aware scheduler reduces the PP probability since low velocity UE are prioritized over high-velocity UE.
The optimization approach aims at maximizing the total rate ϕ k,tot(t n ) of each cell k in long-term, i.e., for t n =[t 1, …, t N ], through dynamically changing the RB allocation α k (t n ) and REB β k , whereby the total rate is defined as
ϕ i(k),r (t n ) is the instantaneous rate of UE i(k) at RB r. At each time instant t n , each BS k performs the following optimization:
The condition in (12) implies that the total transmitted power over all RBs does not exceed the maximum transmission power of BS k. Since our optimization approach in (6) aims at maximizing the total rate, the last condition (13) dictates that the instantaneous rate is larger than a minimum rate for BS k. Due to the distributed nature of this optimization problem in (6), we will investigate two reinforcement learning techniques in this paper, as will be discussed in Sections 3 and 3.
5 Short-term solution: a context-aware scheduler
The proposed MM approach considers a fairness-based context-aware scheduling mechanism in the short term. At each RB r, a UE i(k)∗ is selected to be served by BS k according to the following scheduling criterion:
where \(\text {sort}_{\min (v_{i(k)})}\) sorts the candidate UE according to their velocity starting with the slowest UE. After the sorting operation, if more than one UE can be selected for RB r, the UE with minimum velocity is selected. The rationale behind introducing a sorting/ranking function for candidate UE according to their velocity is that high-velocity UE will not be favored over slow moving UE. This has two advantages: 1) High-velocity UE might pass through the picocell quickly and should therefore not be favored to avoid PPs, and 2) the channel conditions of low-velocity UE changes slowly which may result, especially for slow-moving cell-edge UE, in poor rates if they are not allocated to many RBs.
The scheduler defined in (14) will allocate many (or even all) resources to a newly handed over UE since its average rate in the target cell is zero. To avoid this and enable a fair resource allocation among all UE in a cell, we propose a history-based scheduling approached as follows. Via the X2-interface, macro- and picocells coordinate, so that once a macro UE i(m) is handed over to a picocell p, the UE’s target cell p and source cell m exchange information. In particular, UE i(m)’s rate history at time instant t n is provided to picocell p in terms of average rate \(\overline {\phi }_{i(m)}(t_{n})\), such that the UE’s (which is named as i(p) after the handover) average rate at picocell p becomes
In (15), a moving average rate is considered from macrocell to picocell, whereas in the classical MM approach, a UE’s rate history is not considered and is equal to zero. In other words, in the classical proportional fair scheduler, the average rate \(\overline {\phi }_{i}(t_{n})\) in (14) is \(\overline {\phi }_{i}(t_{n}) = \overline {\phi }_{i(k)}(t_{n}) = 0\) when a UE is handed over to cell k, whereas we redefine it according to (15), i.e., \(\overline {\phi }_{i}(t_{n}) = \overline {\phi }_{i(p)}(t_{n}+T_{s})\). The proposed MM approach, instead, considers the historical rate when UE i(m) was associated to the macrocell m in the past. The incorporation of a UE’s history enables the scheduler to perform fair resource allocation even in the presence of a sequence of handovers. Since handovers occur more frequently in HetNets due to small cell sizes, such a history-based scheduler leads to fair frequency resource allocation among the UE of a cell. More specifically, UE recently joining a cell will not be preferred over other UE of the cell since their historical average rate will be taken into account.
6 Long-term solution: learning-based mobility management techniques
To solve the optimization approach defined in Section 3, we rely on the self organizing capabilities of HetNets and propose an autonomous solution for load balancing by using tools from reinforcement learning [29]. Hereby, each cell develops its own MM strategy to perform optimal load balancing based on the proposed learning approaches presented in Sections 3 and 3 and schedules its UE according to the context-aware scheduler presented in Section 3. An overview of the inter-relation of the short-term and long-term MM approaches is provided in Algorithm 2 (see Appendix). To realize this, we consider the game \(\mathcal {G}=\{\mathcal {K},\{\mathcal {A}_{k}\}_{k\in \mathcal {K}},\{u_{k}\}_{k\in \mathcal {K}}\}\), in which each cell autonomously learns its optimal MM strategy. Hereby, the set \(\mathcal {K}=\{\mathcal {M}\cup \mathcal {P}\}\) represents the set of players (i.e., BSs), and for all \(k\in \mathcal {K}\), the set \(\mathcal {A}_{k} = \{\beta _{k}\}\) represents the set of actions player k can adopt. For all \(k\in \mathcal {K}\), u k is the utility function of player k. The action definition implies that the BSs learn at each time instant t n to optimize their traffic load in the long term using the cell range expansion process. Each BS learns its action selection strategy based on the MAB or satisfaction-based learning approaches as presented in Sections 3 and 3, respectively.
6.1 Multi-armed bandit-based learning approach
The first learning-based MM approach is based on the MAB procedure, which aims to maximize the overall system performance. MAB is a machine learning technique based on an analogy with the traditional slot machine (one-armed bandit) [30]. When pulled at time t n , each machine/player provides a reward. The objective is to maximize the collected reward through iterative pulls, i.e., learning iterations. The crucial trade-off the player faces at each trial is between exploitation of the action that has the highest expected utility and exploration of new actions to get more information about the expected utility performance of the other actions. The player selects its actions based on a decision function reflecting this exploration-exploitation trade-off.
The set of actions, the learning strategy, and the utility function for our MAB-based MM approach are defined as follows:
-
Actions: \(\mathcal {A}_{k}=\{\beta _{k}\}\) with β m =[0,3,6] dB and β p =[0,3,6,9,12,15,18] dB is the CRE bias. We consider higher bias values for picocells due to their low transmit power. The considered bias values are selected considering the results in [31] and also based on our extensive simulation studies.
-
Strategy:
-
1.
Every BS k learns its optimum CRE bias value on a long-term basis considering its load as defined in (5). This is interrelated with the handover triggering by defining the cell border of each cell. The problem formulation defined in Section 3 optimizes this load in the long term, i.e., over time t n .
-
2.
A UE is handed over to BS k if it fulfills the condition (4).
-
3.
RB-based scheduling is performed based on the context-aware scheduler defined in Section 3.
-
1.
-
Utility Function: The utility function is a decision function in MAB learning and is composed by an exploitation term represented by player k’s mean reward for selecting an action until time t n and an exploration term that considers the number of times an action has been selected so far. Player k selects its action \(a_{j(k)}(t_{n})\in \mathcal {A}_{k}\) at time t n through maximizing a decision function \(d_{k,a_{j(k)}}(t_{n})\), which is defined as
$$ {\footnotesize{\begin{aligned} d_{k,a_{j(k)}}(t_{n}) = u_{k, a_{j(k)}}(t_{n}) + \sqrt{\frac{2\log\left(\sum_{i=1}^{|\mathcal{A}_{k}|} n_{k,a_{i(k)}}(t_{n})\right)}{n_{k,a_{j(k)}}(t_{n})}}, \end{aligned}}} $$((16))where \(u_{k, a_{j(k)}}(t_{n})\) is the mean reward of player k at time t n for action a j(k), \(n_{k,a_{j(k)}}(t_{n})\) is the number of times action a j(k) has been selected by player k until time t n , and |·| represents the cardinality operation.
The decision function in the form as in (16) has been proposed by Auer et al. in [30]. The main advantage of Auer’s solution is that the decision function does not rely on the regret which is the loss due to the fact that the globally optimal policy (which is usually not known in practical wireless networks) is not followed in each learning iteration. It is clear that the regret will increase with time, because the globally optimal policy is usually not known and hence cannot be followed by the player. Thus, the MAB-based strategies need to bound the increase of the regret, at least asymptotically. Auer et al. defined an upper confidence bound (UCB) within which the regret will be present. The UCB considers the player’s average reward and the number of times an action has been selected until t n . Relying on these assumptions, we define our decision function in Equation 16.
During the first \(t_{n}=|\mathcal {A}_{k}|\) iterations, player k selects each action once in a random order to initialize the learning process by receiving a reward for each action. For the following iterations \(t_{n}>|\mathcal {A}_{k}|\), action selection is performed according to Algorithm 1. In each learning iteration, the action \(a^{*}_{j(k)}\) that maximizes the decision function in (16) is selected by player k. Then, the parameters \(s_{k,a_{j(k)}}(t_{n})\), \(n_{k,a_{j(k)}}(t_{n})\), and \(u_{k,a_{j(k)}}(t_{n})\) are updated, where \(s_{k,a_{j(k)}}(t_{n})\) is the cumulated reward of player k after playing action a
j(k) and  is equal to 1 if i=j and zero otherwise.
is equal to 1 if i=j and zero otherwise.

6.2 Satisfaction-based learning approach
The idea of satisfaction equilibrium was introduced in [32], where players having partial or no knowledge about their environment and other players are solely interested in the satisfaction of some individual performance constraints instead of individual performance optimization. Here, we consider the player to be satisfied if its cell reaches a certain minimum level of total rate and if at least 90% of the UE in the cell obtain a certain average rate. The rationale behind considering these satisfaction conditions is to guarantee a minimum rate for each individual UE, while at the same time improving the total rate of the cell.
To enable a fair comparison, the set of players and the corresponding set of actions in the proposed satisfaction-based MM approach are considered to be the same as those in the MAB-based MM approach. The utility function of player k at time t n is defined as the load according to (5). In the satisfaction-based learning approach, the actions are selected according to a probability distribution \(\boldsymbol {\pi }_{k}(t_{n})=\left [\pi _{k,1}(t_{n}),\ldots,\pi _{k,|\mathcal {A}_{k}|}(t_{n})\right ]\). Hereby, π k,j (t n ) is the probability with which BS k chooses its action a j(k)(t n ) at time t n . The following learning steps are performed in each learning iteration:
-
1.
In the first learning iteration t n =1, the probability of each action is equal and an action is selected randomly.
-
2.
In the following learning iterations t n >1, the player changes its action selection strategy only if the received utility does not satisfy the cell, i.e., if the satisfaction condition is not fulfilled.
-
3.
If the satisfaction condition is not fulfilled, the player k selects its action a j(k)(t n ) according to the probability distribution π k (t n ).
-
4.
Each player k receives a reward ϕ k,tot(t n ) based on the selected actions.
-
5.
The probability π k,j (t n ) of action a j(k)(t n ) is updated according to the linear reward-inaction scheme:
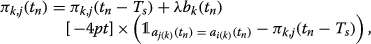 ((17))
((17))whereby
 for the selected action and zero for the non-selected actions. Moreover, b
k
(t
n
) is defined as follows: $$b_{k}(t_{n})=\frac{u_{k,\text{max}} + \phi_{k,\text{tot}}(t_{n})- u_{k,\text{min}}}{2 u_{k,\text{max}}}, $$((18))
for the selected action and zero for the non-selected actions. Moreover, b
k
(t
n
) is defined as follows: $$b_{k}(t_{n})=\frac{u_{k,\text{max}} + \phi_{k,\text{tot}}(t_{n})- u_{k,\text{min}}}{2 u_{k,\text{max}}}, $$((18))where u k,max is the maximum rate in case of single-UE and \({u_{k,\text {min}}= \frac {1}{2} u_{k,\text {max}}}\). Hereby, \(\lambda = \frac {1}{100 t_{n}+T_{s}}\) is the learning rate.
7 Simulation results
The scenario used in the system-level simulations is based on configuration #4b HetNet scenario in [21]. We consider a macrocell consisting of three sectors and P={1,2,3} pico BSs per macro sector, randomly distributed within the macrocellular environment as illustrated in Figure 5. It has to be pointed out that the proposed MM approaches can be applied to any number of macrocells. We are presenting in this section the results for one macrocell (three macro sectors) due to large computation times. In each macro sector, U=30 mobile UE are randomly dropped within a 60-m radius of each pico BS. The rationale behind dropping all UE around pico BSs is to obtain a large number of handover within a short time in order to avoid large computation times due to the complexity of our system level simulations. Each UE i(k) has a randomly selected velocity v i(k) of \({\mathcal {V}= \{3;30; 60; 120\}}\) km/h and a random direction of movement within [ 0;2π]. We consider fast-fading and shadowing effects in our simulations that are based on 3GPP assumptions [21]. Further simulation parameters are summarized in Table 1.
To compare our results with other approaches, we consider a baseline MM approach as defined in [2]. In the baseline MM approach, handover is performed based on layer 1 and layer 3 filtering as described in Section 3. For the baseline MM approach, we consider proportional fair-based scheduling, with no information exchange between macro and pico BSs. This baseline approach is referred to as classical HO approach. In the following, we will compare our proposed MM approaches with this baseline MM approach which is aligned with the handover procedure defined in 3GPP [2].
7.1 UE throughput and sum-rate
Figure 6 depicts the cumulative distribution function (CDF) of the UE throughput for the classical, MAB- and satisfaction-based MM approaches. For the classical approach, we present results for different picocell REB values β p . For the MAB- and satisfaction- based MM approaches, we distinguish between the long-term-only MM approach (with a proportional fair scheduler instead of the proposed context-aware scheduler) and the long-term and short-term MM approach in dashed and solid lines, respectively, to demonstrate the impact of the proposed context-aware scheduler. In the selected scenario, the CRE of picocells does influence the cell-edge (5th%) UE throughput, which is zoomed in Figure 6. This is because in the simulation scenario all UE are dropped within a radius of 60 m around the picocell, so that many macrocell UE are close to the picocell and suffer from intercell interference. Compared to the classical approach, MAB- and satisfaction-based approaches lead to an improvement of up to 39% and 80% for cell-edge UE for the long-term and short-term approaches, respectively. In the case of the long-term-only MM approach, the MAB-based approach yields similar results as the classical approach for cell-edge UE. A similar gain is achieved in terms of average (50th%) UE throughput. Here, the MAB- and satisfaction-based approaches yield 43% and 75% improvement compared to the classical approach. In the case of the long-term only MM approaches, the improvement in average UE throughput is 12% and 37% for the MAB- and satisfaction-based MM approaches, respectively. Hence, the satisfaction-based approach outperforms the other MM approaches in terms of average and cell-edge UE throughput. In case of the cell-center UE throughput, which is defined as the 95th% throughput, the opposite behavior is obtained. In this case, an improvement of 124% and 80% is achieved for the MAB- and satisfaction-based approaches, respectively. The reason is that the satisfaction-based MM approach only aims at satisfying the network in terms of rate and does not update its learning strategy once satisfaction is achieved in the network, i.e., no actions that may lead to improvements are explored. The MAB-based approach on the other hand aims at maximizing the network performance, which is reflected in the improved cell-center UE throughput.
To show the effect of different REB values in case of classical MM, we depict in Figure 7 the cell-edge UE throughput for different number of UE per macrocell. With increasing REB bias value for picocells, the cell-edge UE throughput is enhanced. However, the proposed learning-based MM approaches outperform the classical approach up to five times for 10 UE per macrocell and up to 4.5 times for 50 UE per macrocell. Interestingly, the MAB-based MM yields higher cell-edge UE throughput than the satisfaction-based MM approach for smaller number of UE. This can be interpreted as follows: In a scenario with 10 UE and a bandwidth of 10 MHz, the probability of having unsatisfied UE is very low. Since most of the UE (or even all UE) are satisfied, the satisfaction-based learning approach does not change its strategy to further enhance each UE’s performance, whereas the MAB-based learning procedure adapts its strategy disregarding the satisfaction condition to maximize the UE’s performance. This leads to the fact that the cell-edge UE performance is enhanced, too. With increasing number of UE, the probability of unsatisfied UE’s in the cell increases and the satisfaction-based learning approach adapts its strategy to enhance especially the cell-edge UE performance, i.e., to satisfy all UE in the cell. That is why the cell-edge UE performance is larger for the satisfaction-based MM approach for increasing the number of UE. In addition to the results for different REB values, we present in Figure 8 the sum-rate versus UE density per macrocell for TTT = {40,480} ms values. For both TTT values, the classical approach yields very low sum-rates, while the proposed approaches lead to significant improvement of up to 81% and 85% for TTT values 40 ms and 480 ms, respectively. The proposed MM approaches converge to significantly larger sum-rates than the classical MM approach. Interestingly, the sum-rate performance of the proposed MM approaches depends on the TTT. The reason for this lies in the convergence behavior of the learning algorithms. For smaller TTT values, handover is executed faster and the BS has to adapt its REB strategy to the new cell load before convergence. To demonstrate the statistical properties of the presented results in Figure 8, we present confidence intervals of the sum-rates for a confidence level of 95% in Table 2. It can be seen that the presented sum-rate results lie within the confidence intervals.
Figure 9 depicts the effect of the long-term strategy on the derived REB values. Since the long term is related to the load estimation which impacts the average UE throughput, we depict it over the REB values. In case of the learning-based MM approaches, we would like to emphasize that each BS selects its own REB value according to the selected learning approach. This leads in the simulations to the fact that in the REB optimization process some REB values are favored against other REB values and that a mix of REB value selection for all BSs is achieved, so that the average UE throughput is depicted over mixed REB values. This is due to the fact that based on the self-organizing capability of our proposed learning approaches, the REB values are selected autonomously by each BS according to their learning strategy. Hence, the selection of each REB value is controlled by the learning approach and not by our simulation settings, so that it is not possible to separately present results for each REB value. It can be seen that a fix REB value selection leads to lower average UE throughput than an autonomous REB value selection by each BS, which is the case for the proposed learning-based MM approaches.
To compare the performance of the proposed approaches for different number of picocells per macrocell, Figure 10 plots the sum-rate versus number of pico BSs per macrocell. For the different number of pico BSs, the proposed MM approaches yield gains of around 70% to 80% for TTT = 480 ms.
7.2 HOF and PP probabilities
Mobility management approaches must not only enhance the networks performance in terms of UE throughput and sum-rate but also reduce handover failure rates and PP probabilities. Here, we present results for the HOF probability and PP event probability. We modify our simulation settings by using the same velocity for each UE per simulation, so that we can present results for each velocity separately. Figure 11 depicts the HOF probability for different TTT values. As it can be seen, our proposed learning-based approaches yield, besides the gains in terms of rate, improvements in terms of HOF probability. Compared to the classical MM approach, the proposed methods yield to the same HOF probability for UE at 3 km/h speed. For higher velocities in which more HOFs are expected, the HOF probability obtained by the proposed approaches is significantly lower than in the case of classical MM. Interestingly, the proposed methods lead to almost constant HOF probabilities for velocities larger than 30 km/h. For UE at 120 km/h, the HOF probability of the MAB-based approach is twice the HOF probability of satisfaction-based learning but only one third of the classical approach for TTT = 40 ms. For increasing TTT values, the trend between the proposed MM approaches and the classical MM approach remains similar. This is because the picocell coverage in the classical approach without range expansion is small, and thus the macrocell UE quickly run deep inside the picocell coverage area before the TTT expires, significantly degrading the signal quality of the macrocell UE before the handover is completed. In this case, HOFs are alleviated with smaller TTT values.
Reducing TTT values may decrease the HOF probability but increase PP probability. Hence, HOFs and PPs must be studied jointly. We depict in Figure 12 the PP probability for the same simulation settings as in Figure 11. It can be observed that the number of PPs are reduced with larger TTT values. In addition, for lower velocities, all MM approaches yield similar PP probabilities for all TTT values. For higher velocities, the PP probability is decreased by the proposed MM approaches by up to a factor of two (TTT = 40 ms).
7.3 Convergence behavior of MAB- and satisfaction-based MM
One of the major concerns of learning-based approaches is their convergence behavior in dynamic systems. In Figure 13, we depict the convergence of the proposed learning-based MM approaches in terms of cell-center UE throughput. It can be seen that the MAB-based MM approach converges slower than the satisfaction-based MM approach, but it converges to a larger cell-center UE throughput since it aims at system performance maximization. Hence, depending on the system requirements, either the MAB-based approach can be applied if a large cell-center UE throughput is aimed or the satisfaction-based approach can be preferred if a better cell-edge UE throughput (see Figure 7) and fast convergence is expected.
8 Conclusions
We propose two learning-based MM approaches and a history-based context-aware scheduling method for HetNets. The first approach is based on MAB-based learning and aims at system performance maximization. The second method aims at satisfying each cell and each UE of a cell and is based on satisfaction-based learning. System level simulations demonstrate the performance enhancement of the proposed approaches compared to classical MM method. While up to 80% gains are achieved in average for UE throughput, the HOF probability is reduced significantly by the proposed learning-based MM approaches.
9 Endnote
a We consider lower REB values for macro BSs to avoid overloaded macrocells due to their large transmission power.
10 Appendix
Algorithm 2 presents the interrelation between the short-term and long-term MM approaches.

References
Cisco Visual Networking Index: Global Mobile Data Traffic Forecast Update, 2013-2018. Cisco Public Information (2014).
3GPP, Evolved Universal Terrestrial Radio Access (E-UTRA); Mobility Enhancements in Heterogeneous Networks. Technical Report 3GPP TR 36.839 V11.1.0 (Oct. 2012).
Y Peng, YZW Yang, Y Zhu, in Proc. IEEE Symposium on Personal Indoor and Mobile Radio Communications (PIMRC). Mobility Performance Enhancements for LTE-Advanced Heterogeneous Networks (Sydney, Sept 2012).
H Holma, A Toskala, LTE-Advanced: 3GPP Solution for IMT-Advanced (John Wiley & Sons, Ltd, UK, 2012).
J Aonso-Rubio, in Proc. IEEE Network Operations and Management Symp. Self-optimization for handover oscillation control in LTE, (2010), pp. 950–953.
G Hui, P Legg, in Proc. IEEE Vehic. Technol. Conf. (VTC). LTE handover optimisation using uplink ICIC, (2011), pp. 1–5.
K Kitagawa, T Komine, in Proc. IEEE Int. Symp. Personal Indoor Mobile Radio Commun. (PIMRC). A handover optimization algorithm with mobility robustness for LTE systems, (2011), pp. 1647–1651.
K Ghanem, H Alradwan, in Proc. IEEE Int. Symp. Commun. Syst., Networks and Digital Signal Proc. Reducing ping-pong handover effects in intra EUTRA networks, (2012), pp. 1–5.
H Zhang, X Wen, B Wang, W Zheng, Z Lu, in Proc. IEEE Int. Conf. on Research Challenges in Computer Science, 1. A novel self-optimizing handover mechanism for multi-service provisioning in LTE-Advanced, (2009), pp. 221–224.
T Jansen, I Balan, J Turk, I Moerman, T Kurner, in Proc. IEEE Vehic. Technol. Conf. (VTC). Handover parameter optimization in LTE self-organizing networks, (2010), pp. 1–5.
K Dimou, M Wang, Y Yang, M Kazmi, A Larmo, J Pettersson, W Muller, Y Timner, in Proc. IEEE Vehic. Technol. Conf. (VTC). Handover within 3GPP LTE: design principles and performance, (2009), pp. 1–5.
W Li, X Duan, S Jia, L Zhang, Y Liu, J Lin, in Proc. IEEE Vehic. Technol. Conf. (VTC). A dynamic hysteresis-adjusting algorithm in LTE self-organization networks, (2012), pp. 1–5.
T-H Kim, Q Yang, J-H Lee, S-G Park, Y-S Shin, in Proc. IEEE Vehic. Technol. Conf. (VTC). A mobility management technique with simple handover prediction for 3G LTE systems, (2007), pp. 259–263.
M Carvalho, P Vieira, in Proc. Int. Symp. on Wireless Personal Multimedia Commun.An enhanced handover oscillation control algorithm in LTE Self-Optimizing networks, (2011).
W Luo, X Fang, M Cheng, X Zhou. Proc. IEEE Int. Workshop on Signal Design and Its Applications in Commun, (2011), pp. 193–196.
I Balan, T Jansen, B Sas, in Proc. Future Network and Mobile Summit. Enhanced weighted performance based handover optimization in LTE, (2011), pp. 1–8.
T Jansen, I Balan, S Stefanski, I Moerman, T Kurner, in Proc. IEEE Vehic. Technol. Conf. (VTC). Weighted performance based handover parameter optimization in LTE, (2011), pp. 1–5.
H-D Bae, B Ryu, N-H Park, in Australasian Telecommunication Networks and Applications Conference (ATNAC). Analysis of handover failures in LTE femtocell systems, (2011), pp. 1–5.
Y Lei, Y Zhang, in Proc. IEEE Int. Conf. Computer Theory and Applications. Enhanced mobility state detection based mobility optimization for femto cells in LTE and LTE-Advanced networks, (2011), pp. 341–345.
M. P Wiley-Green, T Svensson, in Proc. IEEE GLOBECOM. Throughput, Capacity, Handover and Latency Performance in a 3GPP LTE FDD Field Trial (FL, USA, Dec. 2010).
3GPP, Evolved Universal Terrestrial Radio Access (EUTRA); Further advancements for E-UTRA Physical Layer Aspects, Technical Report 3GPP TR 36.814 V9.0.0, (Oct. 2010).
D Xenakis, LMN Passas, C Verikoukis, Mobility Management for Femtocells in LTE-Advanced: Key Aspects and Survey of Handover Decision Algorithms. IEEE Comm. Surveys Tutorials. 16(1) (2014).
S Barbera, SPH MMichaelsen, K Pedersen, in Proc. IEEE Wireless Comm. and Networking Conf. (WCNC). Mobility Performance of LTE Co-Channel Deployment of Macro and Pico Cells (France, Apr. 2012).
RBP Munoz, I de la Bandera, On the potential of handover parameter optimization for self-organizing networks. IEEE Trans. Vehicular Technol. 62(5), 1895–1905 (2013).
D Lopez-Perez, I Guvenc, X Chu, Mobility management challenges in 3GPP heterogeneous networks. IEEE Comm. Mag. 50(12) (2012).
KI Pedersen, RPH CMichaelsen, S Barbera, Mobility enhancements for LTE-advanced multilayer networks with inter-site carrier aggregation. IEEE Comm. Mag. 51(5) (2013).
J Wang, JPJ DWLiu, G Shen, in Proc. IEEE Vehic. Technol. Conf. (VTC). Optimized Fairness Cell Selection for 3GPP LTE-A Macro-Pico HetNets (CA, Sept. 2011).
A Feki, V Capdevielle, L Roullet, AG Sanchez, in 11th Int. Symp. on Modeling & Optimization in Mobile, Ad Hoc & Wireless Networks (WiOpt). Handover Aware Interference Management in LTE Small Cells Networks, (2013).
ME Harmon, SS Harmon, Reinforcement Learning: A Tutorial. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.33.2480&rep=rep1&type=pdf.
NC-BP Auer, P Fischer, Finite time analysis for the multiarmed bandit problem. Mach. Learn. 17, 235–256 (2012).
3GPP, Performance Study on ABS with Reduced Macro Power, Technical Report 3GPP R1-113806, (Nov. 2011).
S Ross, B Chaib-draa, in Proc. 19th Canadian Conf. on Artificial Intelligence. Satisfaction equilibrium: achieving cooperation in incomplete information games, (2006).
Acknowledgements
This research was supported in part by the SHARING project under the Finland grant 128010 and by the U.S. National Science Foundation under the grants CNS-1406968 and AST-1443999.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The general ideas presented in this article have been developed by all the authors at high level. MS developed the algorithms presented, implemented them into the system level simulator, and ran simulations. The paper has been revised collaboratively by all authors. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Simsek, M., Bennis, M. & Guvenc, I. Mobility management in HetNets: a learning-based perspective. J Wireless Com Network 2015, 26 (2015). https://doi.org/10.1186/s13638-015-0244-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-015-0244-2




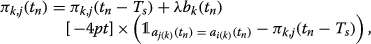
 for the selected action and zero for the non-selected actions. Moreover, b
k
(t
n
) is defined as follows:
for the selected action and zero for the non-selected actions. Moreover, b
k
(t
n
) is defined as follows: 







