- Research
- Open access
- Published:
Cost-effective joint optimisation of BBU placement and fronthaul deployment in brown-field scenarios
EURASIP Journal on Wireless Communications and Networking volume 2020, Article number: 242 (2020)
Abstract
In this work, one proposes a model to evaluate the optimal deployment of Centralised Radio Access Network (C-RAN) architecture elements, i.e. Base Band processing Units (BBUs) and fronthaul links, in a brown-field scenario, in which traditional base stations are already deployed and a physical network is present. The proposed optimisation framework jointly optimises BBU placement and accesses network infrastructures deployment. It clusterises the Remote Radio Heads in the scenario through a Multicommodity Flow approach and solves the minimum cost fronthaul network deployment through a Rooted Delay-Constrained Minimum Spanning Tree approach. Optical fibre and microwave links are considered as fronthaul infrastructures. The proposed optimisation framework is validated through a comparison with a theoretical output for a canonical scenario, being afterwards applied to a real scenario. A cost analysis for different scenario configurations is presented, and trade-offs and guidelines for a cost optimal deployment of C-RAN are provided. The analysis of results for the real scenario of the city of Lisbon and its surrounding areas shows that the delay budget in the fronthaul network highly impacts on capital expenditures as well as on operational ones. It is shown that a larger delay budget enables an annual cost reduction up to 72% in urban areas and 54% in rural ones.
1 Introduction
Network evolution towards 5G involves several solutions and techniques proposed with the general intent of improving users’ quality of experience in a variety of services. This global objective is mapped onto very demanding requirements in terms of expected throughput, latency, scalability and automation.
In order to satisfy traffic growth, mobile operators must significantly increase their network capacity to provide broadband capabilities to users. However, in an intensifying competitive marketplace, high saturation levels, rapid technological changes and declining voice revenues, operators are challenged with the deployment of traditional Base Stations (BSs) as cost is high and return is not high enough. The average revenue per user is already affecting operators’ profitability, and new architectures are being proposed in order to allow them to remain profitable and competitive [1, 2].
The C-RAN architecture splits traditional BSs into a radio unit, called Remote Radio Head (RRH), and a Base Band processing Unit (BBU). This represents an efficient solution in order to overcome the aforementioned problems. As a consequence of splitting a traditional BS into two functional units, C-RAN introduces a new connectivity segment, called ”fronthaul”. In [3], a more in-depth analysis of the C-RAN architecture can be found. The flexibility related to the software implementation of mobile functionalities enables a dynamical management of several network aspects, such as load balancing among BBUs [4], multicell association [5] and efficient Coordinated Multi-Point (CoMP) transmission [6].
Recently, new 5G fronthaul interfaces and requirements have been put forward in terms of maximum supported latency and bandwidth for the fronthaul segment [7]. This work focuses on a C-RAN functional split that corresponds to Option 8 (PHY-RF split) where the RF functionality is in the distributed unit (i.e. RRH) and upper layers are in the central one (i.e. BBU). Moreover, several activities are currently ongoing in the investigation of possible functional split implementations and fronthaul interfaces [8, 9].
The deployment of the physical infrastructures supporting C-RAN architectures is crucial from the operators’ viewpoint, since it affects CAPital EXpenditure (CAPEX) and OPerating EXpenditure (OPEX) and impacts on economic sustainability [10, 11]. Several strategies for the placement of RRHs [12] and BBUs [13] have been proposed. Moreover, models for the estimation of the economic impact from the deployment of C-RANs for different scenarios configurations [14] and deployment strategies [15, 16] have been proposed.
Recently, relevant aspects related to C-RAN deployment have been investigated. In [17], survivability strategies for link and node failures in C-RAN are studied with different optimisation objectives. A novel technique to compute the optimal deployment of BBUs based on machine learning is proposed in [18], with the objective to minimise bandwidth and computing resources consumption. Finally, in [19] millimetre wave wireless fronthaul links are used to support C-RAN migration, but the latency impact is not considered. To the best of our knowledge, the matter of how the future evolution of latency constraints could impact on the possibility to reuse existing infrastructures and require newly deployed ones have not yet been extensively studied.
In this work, one proposes a model to obtain the optimal deployment of BBUs and RRHs in a brown-field scenario, where a physical network is already present and traditional BSs are already deployed. In order to minimise CAPEX, the proposed model considers that optical fibre and microwave links are already deployed as possible fronthaul infrastructures. Furthermore, it can be extended by applying a proper cost and latency modelling to any other technology, such as free space optics or millimetre wave links. The novelty of the proposed optimisation framework is that it jointly optimises BBU placement and access deployment. To achieve an efficient use of the available physical links, cascading links between RRHs are taken into consideration, resulting in a tree-based architecture between a BBU and its served RRHs that minimises the deployment cost. The proposed model is designed to address the C-RAN deployment planning, hence, not considering traffic or delay variations (which are handled at the network management level) and coverage and interference probabilities (since one takes BSs locations as an input, given that it is a brown-field scenario assumption). It is intended to be a tool for the analysis of the influence of different parameters (e.g. delay constraint, size of the area to serve and deployment strategy) on deployment configurations. It enables relative comparisons over many scenarios and deployment configurations, which can be suitable from the operators’ viewpoint in network deployment planning.
In Sect. 2, a formal problem definition is provided, and the system model is presented: an integer linear programming optimisation problem for the minimum cost of deployment is formulated. In Sect. 3, an analysis of the results for a canonical scenario is conducted in order to validate the proposed model, after which three real scenarios, namely urban, suburban and rural, are presented, showing the impact of different factors on C-RAN deployment. Conclusions are presented in Sect. 4.
2 Methods
2.1 Model overview
2.1.1 Problem description
The problem addressed in this work is the optimal deployment of BBU pools and a fronthaul network in urban, suburban and rural scenarios, in which traditional BSs and backhaul infrastructures are already present. One assumes that all BSs sites are converted to RRHs ones. The introduction of the fronthaul implies that network time constraints must incorporate the time for the transportation of data through the fronthaul segment. The delay constraint for transportation represents a key aspect for deployment optimisation, because it has a direct impact on the maximum length of the links between RRHs and BBUs. Additionally, the splitting of the traditional transmission chain into two functional units requires the exchange of radio samples through the fronthaul segment and consequently a high data rate. Thus, link capacity represents another major constraint.
Designing a solution for an urban scenario raises an important requirement: not all locations that could be considered optimal for BBU pool positions are able to host its infrastructure, because operators cannot locate equipment in arbitrary locations. The adopted approach to avoid this problem is to consider a subset of the RRHs locations as the set of feasible positions for the BBUs.
Based on the former considerations, the problem that one addresses is to find which BSs’ positions can be elected as possible BBU pools ones, given a constraint of delay between BBU and RRH, and minimising the number of BBU pools to reduce costs. This problem can be interpreted as the well-known Set Covering Problem, which is known to be NP-complete [20], which has been studied extensively due to its wide applicability in facility location and in wireless networks.
One has to find an optimal deployment of links considering the different technologies available in the service area, delay constraints and links capacity. In order to do this, one uses an integer linear programming (ILP) [21] approach that minimises the total network cost in terms of kilometres of optical fibre and number of microwaves links to be deployed, taking the reuse of existent infrastructures into consideration and considering cascading links among RRHs for the connection towards the serving BBU. A graphical view is given in Fig. 1.
One defines the group of RRHs served by a single BBU as a cluster; hence, one has to find an optimal clusterisation of RRHs to be connected to the serving BBUs, and, on a per-cluster base, a deployment tree connecting a BBU with every served RRH, with the minimum deployment cost and respecting the maximum delay constraint. The clusterisation objective can be obtained by modelling the problem as a Multi-Commodity Flow Problem (MCFP) [22]. Considering the cluster of RRHs served by a BBU as a graph, and using a Rooted Delay-Constrained Minimum Spanning Tree (RDCMST) [23] approach for each cluster adopting the BBU as a root, ensures that each RRH will be connected to a BBU using a series of physical links that introduce a delay lower than the maximum one.
It is important to notice that the adoption of a spanning tree approach allows to use a single link for several connections among the BBUs and their served RRHs, as illustrated in Fig. 1. One assumes that each physical link serves at most one BBU cluster. Figure 1 also shows how the physical links that transport several BBU-RRH connections have higher capacity requirements.
From a high-level perspective, one can summarise the model’s inputs and outputs. The proposed optimisation model takes as input a set of possible positions for the BBUs. Since the objective is the minimisation of cost and the reutilisation of the existing infrastructures, another input is the set of links that are already present in the scenario and that can be reused in order to avoid newly deployed links with a high cost for the operator. The split of the BS calls for high capacity requirements on the fronthaul segment, which are related to the characteristics of the RRH site. The optimisation problem takes the data rate required by each RRH as input, in order to enable possible supporting links for the connection to the BBU. The delay constraint represents a key decision aspect in the design of the network. Technical standards distinguish maximum tolerable latency values for the feasibility of the C-RAN fronthaul [7]. However, fronthaul delay represents a contribution to the latency experienced by users and heterogeneous services (such as ultra-reliable low latency communications in 5G) may imply a lower delay budget for the fronthaul segment. Thus, one considers the maximum delay budget for the fronthaul as a design input parameter. From the operator’s side, the adoption of a lower delay budget intuitively implies higher costs, but, on the other hand, it also makes the deployment ready for the future evolution of technology and network requirements.
As an output, the optimisation model yields the locations in the infrastructure hosting the BBU pools, together with the set of RRHs served by each BBU site. Regarding the connection between RRHs and BBUs, an optimal set of links is given, including the already existing links and newly deployed ones. Moreover, an estimation of the deployment cost of the C-RAN architecture in terms of CAPEX and OPEX is provided as well.
2.1.2 Problem statement
Input parameters In order to model the maximum delay constraint for the communication between a BBU and an RRH, one defines \(\tau _{\mathrm{max}}\) as the one-way maximum delay of the fronthaul segment. The proposed model takes as input the set of RRH sites. Without any loss of validity, one can assume the set of RRH sites to be either coincident with the set of BS sites, i.e. when all the BSs are converted to RRHs, or a proper subset of BS sites, i.e. for hybrid scenarios where only part of the BSs is converted into RRHs. In the following, one assumes that each BS site will be converted to an RRH one, defining:
-
\(N_{\mathrm{RRH}}\): number of RRH sites;
-
\(N_{\mathrm{pBBU}}\): number of possible BBU sites.
Since one looks for BBU positions within the set of RRH sites, but not all RRH sites will be taken as feasible locations for BBUs, one has
Starting from a real scenario, where a backhaul network is already deployed, one has to consider the presence of fibre and microwave links already serving the sites. In order to model link availability, one introduces several matrices that define if fibre/microwave links are already present in the scenario and which kind of links is deployable among RRH sites.
One introduces the sparse and symmetric matrix \(\mathbf {P}_{[N_{\mathrm{RRH}}\times N_{\mathrm{RRH}}]}\) that models the general link presence between couples of RRH sites without caring about the physical medium used and with each element being given by:
One defines the sparse and symmetric matrices \(\mathbf {P}_{\mathbf {f}/\mathbf {m}[N_{\mathrm{RRH}}\times N_{\mathrm{RRH}}]}\) that model the fibre/microwave link presence between couples of RRH sites. One is using \(\mathbf {P}_{\mathbf {f}/\mathbf {m}}\) as a notation to denote two possible matrices \(\mathbf {P}_{\mathbf {f}}\) and \(\mathbf {P}_{\mathbf {m}}\), and this notation is used throughout the paper, with each element as:
One imposes for the introduced matrices
since just one technology (fibre or microwave) is used for the link between RRHs i and j. In the following, one uses the notation \(\veebar\) to denote the logical Exclusive OR operator. This constraint imposes that, in case of availability of redundant links for reliability reasons, only the working one is considered in the C-RAN optimal deployment.
An optimal C-RAN deployment can require the deployment of new fibre or microwave links not already present in the area. However, given two RRH sites, it may not always be possible to connect them, due to operational restrictions, such as the impossibility to deploy fibres or the low capacity of microwave links. The deployment of new links is therefore subject to deployability conditions, which one models using deployability matrices. The sparse and symmetric matrices \(\mathbf {D}_{\mathbf {f}/\mathbf {m} [N_{\mathrm{RRH}}\times N_{\mathrm{RRH}}]}\) model fibre/microwave links deployability between couples of RRH sites, with each element as:
It is important to notice that:
which means that \(\mathbf {D}_{\mathbf {f/m}}\) contains the links that are not already deployed but still deployable.
One introduces the sparse and symmetric matrix \(\mathbf {D}_{[N_{\mathrm{RRH}}\times N_{\mathrm{RRH}}]}\) that models a general link deployability between couples of RRH sites, with each element as:
imposing
to obtain the links that are deployable.
As illustrated in Fig. 1, one considers pedestrian path distance for fibre links and straight-line distance for microwave ones; the former is a simple model for the fact that fibre links are not deployed linearly, rather having to conform with the geographical obstacles and constraints, while the latter models the usual line of sight deployment of radio links. The matrices \(\mathbf {d}_{\mathbf {f/m}[N_{\mathrm{RRH}}\times N_{\mathrm{RRH}}]\left[ \text {km}\right] }\) express the distances between couples of RRH sites connected through fibre/microwave:
-
\(d_{{\mathrm{f}},ij\left[ \text {km}\right] }\): pedestrian path distance between RRHs i to j
-
\(d_{{\mathrm{m}},ij\left[ \text {km}\right] }\): straight-line distance between RRHs i to j
In order to check whether the delay of the connection between BBU and RRH is lower than \(\tau _{\mathrm{max}}\), one needs to take the delay introduced by the links between the considered sites into consideration. Two input matrices fibre/microwave links delay \(\mathbf {T_{\mathrm{f/m}}}_{[N_{\mathrm{RRH}}\times N_{\mathrm{RRH}}]\left[ \upmu {\mathrm {s}}\right] }\) are introduced, where
-
\(T _{{\mathrm{f/m}},ij\left[ \upmu {\mathrm {s}}\right] }\): delay introduced by the link between RRHs i to j using fibre/microwave.
Link capacity is given by matrices \(\mathbf {C}_{\mathbf {f/m}[N_{\mathrm{RRH}}\times N_{\mathrm{RRH}}]\left[ \text {Mbps}\right] }\), expressing the bandwidth available for each fibre/microwave link, where
-
\(C_{{\mathrm{f/m}},ij\left[ \text {Mbps}\right] }\): capacity of the link between RRHs i to j using fibre/microwave.
The main aspect that impacts on the design of C-RAN is CAPEX. The choice between fibre and microwave links is based on the cost of deployment, since different technologies have different costs for the realisation of the links and impact significantly on the initial investment of the operator, i.e. CAPEX. Matrices
 represent the cost of deployment of fibre/microwave links, where
represent the cost of deployment of fibre/microwave links, where
-
 : cost of the link deployment between RRHs i to j using fibre/microwave.
: cost of the link deployment between RRHs i to j using fibre/microwave.
The link deployment cost is related to the presence of the link in the scenario. Trivially, to deploy a totally new link will imply a cost that is significantly higher than to use an already existing one. One assumes that the use of an existing link does not require an increase of CAPEX, therefore
One also has to take BBU deployment-related costs into consideration, which are modelled through vector
 , where
, where
-
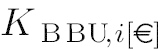 is the deployment cost of a BBU in site i.
is the deployment cost of a BBU in site i.
In this work, one considers the cost of each RRH as constant and defines
 as the cost of an RRH.
as the cost of an RRH.
Output variables Among all possible BBU positions, the proposed model leads to the subset of nodes that is able to serve all RRHs minimising deployment cost and balancing load among BBUs, consequently
where \(N_{\mathrm{BBU}}\): number of elected BBU sites for the optimal deployment.
One of the outputs is the decision if a specific RRH site is elected as a BBU one, represented by vector \(\mathbf {B}_{[N_{\mathrm{pBBU}}\times 1]}\), where
Another output is the assignment of RRHs to BBUs, defining the clustering of RRHs, with matrix \(\mathbf {S}_{[N_{\mathrm{pBBU}}\times N_{\mathrm{RRH}}]}\):
An RRH will be served by one and only one BBU, leading to:
It follows from previous considerations that whenever an RRH is connected to another RRH, the latter becomes a BBU one,
The output variables that represent the usage of fibre/microwave links for optimal deployment are sparse and symmetric matrices \(\mathbf {U}_{\mathbf {f}/\mathbf {m}[N_{\mathrm{RRH}}\times N_{\mathrm{RRH}}]}\), where
and
in order to avoid that both fibre and microwave are chosen for the link between RRHs i and j.
Moreover, one has to impose that
in order to exclude from the final deployment the links that are neither present nor deployable.
One can finally introduce the link usage sparse matrix \(\mathbf {U}_{[N_{\mathrm{RRH}}\times N_{\mathrm{RRH}}]}\), where
with
in order to include into the final deployment both link types.
Internal variables In order to formulate the MCFP, one introduces a 4-dimensional sparse matrix \(\mathbf {U}_{\mathbf {c}[N_{\mathrm{RRH}}\times N_{\mathrm{RRH}}\times N_{\mathrm{pBBU}}\times N_{\mathrm{RRH}}]}\) that relates each link to the cluster that it serves, where
For each pair BBU-RRH (b, r) there is a flow of one unit towards b and the quantity of incoming flow in an intermediate node in the path is equal to the outgoing one; therefore, one has to impose:
A link between two sites can be shared for connecting more than one RRH to the same serving BBU, allowing a more efficient usage of link capacity and reducing deployment costs, but each link serves one BBU cluster at most:
In order to have constraints in (21) affecting the final deployment, one imposes
Additional 4-dimensional sparse matrices \(\mathbf {U}_{\mathbf {c,f/m}[N_{\mathrm{RRH}}\times N_{\mathrm{RRH}}\times N_{\mathrm{pBBU}}\times N_{\mathrm{RRH}}]}\) represent fibre/microwave usage:
Delay matrix \(\mathbf {T }_{[N_{\mathrm{RRH}}\times N_{\mathrm{RRH}}]\left[ \upmu {\mathrm {s}}\right] }\) represents the delay introduced by the link between RRHs i to j:
The RDCMST delay constraint is performed in what follows, imposing that the sum of the links delays in a connection between RRH r and its serving BBU b is lower than \(\tau _{\mathrm{max}}\),
The available capacity matrix \(\mathbf {C}_{\mathbf {A}[N_{\mathrm{RRH}}\times N_{\mathrm{RRH}}]\left[ \text {Mbps}\right] }\) is related to the capacity of fibre/microwave links \(\mathbf {C}_{\mathbf {f/m}\left[ N_{\mathrm{RRH}}\times N_{\mathrm{RRH}}][\text {Mbps}\right] }\) matrices:
The required bandwidth on each link matrix \(\mathbf {C}_{\mathbf {R}[N_{\mathrm{RRH}}\times N_{\mathrm{RRH}}]\left[ \text {Mbps}\right] }\) is the required capacity between RRHs i and j:
The required capacity on a link has to be lower than the available one,
Finally, the link cost matrix
 satisfies:
satisfies:

2.2 Optimisation problem
In this subsection, firstly the different metrics that allow to evaluate the effectiveness of the proposed model are described, and then the mathematical entities and the objective function of the optimisation model are presented.
2.2.1 Performance metrics
Latency Latency is one of the main constraints for the fronthaul, determining the maximum length for the link between an RRH and a BBU. One of the factors that impact on the delay introduced by the fronthaul link is the physical medium adopted to implement it. Fibre links are normally deployed into cable ducts that are constructed in a way to be easily accessible for maintenance (e.g. along streets), while microwave links are deployed taking line of sight radio propagation. In order to calculate the links length, one takes the pedestrian path distance for fibre links and a straight-line for microwave ones.
The roundtrip propagation time for a link is:
where \(\nu _{{\mathrm{f/m}}}\): fibre/microwave propagation speed; \(d_{{\mathrm{f/m}},ij}\) is the fibre/microwave link length.
The different latency contributions, presented in Fig. 2, can be expressed as:
where \(T_{\mathrm{l}}\): link propagation delay, round trip time, \(N_{\mathrm{l}}\): number of links used for the connection between an RRH and a BBU, \(\delta _{\mathrm{S}}\): switching delay
It is worthwhile mentioning that the first term in (32) depends on the distance between RRH sites and represents a variable contribution, while the second one accounts for distance-independent delay such as queuing, switching, optical line termination, line card and processing.
Link capacity The fronthaul link required traffic demand that is needed by the RRH site depends on the number and type of cells that the site possesses. Here, one assumes CPRI [9] as fronthaul interface; thus, the required data rate is calculated as [24]:
where M: number of antennas used at the RRH, S: sampling rate for the RRH, W: sample width for the RRH, F: coding factor for the RRH.
The 2 factor in (33) is introduced to take in-phase and quadrature modulated data into account. It is worthwhile to mention that parameters M, S, W and F are related to the underlying radio access technology, e.g. NR, LTE, UMTS or GSM.
Economical cost A key aspect for the design of C-RAN is represented by CAPEX, which is considered to be related to the deployment of links, BBU pools and RRHs. In a brown-field scenario, a new link increases CAPEX, while the usage of an already deployed one contributes to OPEX. OPEX includes power cost, personnel expenses and site maintenance and rental and is taken as a percentage of the related initial deployment cost (i.e. CAPEX).
The link CAPEX is related to the adopted physical medium, being modelled for fibre as:

where \(k_{\mathrm{f}}\): cost per kilometre of fibre link, \(d_{{\mathrm{f}},ij}\): pedestrian path link length.
The cost of a microwave link
 is not related to distance, being modelled by the cost of equipment.
is not related to distance, being modelled by the cost of equipment.
Another important factor that influences CAPEX is represented by the cost related to the deployment of a BBU. The deployment cost of a BBU pool site is taken as a fix component related to the characteristics of the site, plus a variable one related to the requirements imposed by network design, such as the number of RRHs to be served by the BBU pool, expressed by vector


where \(K_{\mathrm{vBBU},i}\): variable cost of possible BBU site i, \(K_{\mathrm{fBBU},i}\): fix cost of possible BBU site i.
The variable cost of the BBU site is the sum of the costs of the equipment needed to serve each connected RRH:

where \(N_{\mathrm{sRRH},i}\): number of RRHs served by BBU i, \(K_{\mathrm{bRRH}}\): cost associated with the equipment required at BBU pool site to serve a single RRH.
Considering that
one can model the deployment cost of a BBU as:

Finally, considering that one can express the RRHs CAPEX as
 , one can express the total CAPEX as:
, one can express the total CAPEX as:

where the first term represents BBUs-related CAPEX, the second one the links’ CAPEX and the third one is RRHs deployment cost.
2.2.2 Integer linear programming model
In this subsection, one provides the ILP formulation for the problem under consideration. It is worthwhile mentioning that, although an ILP-based approach suffers from scalability issues, it guarantees the optimality of the solution. The objective function is represented by the CAPEX expressed in (39).
Since one is interested in obtaining a cost-optimal deployment, the objective of the ILP can be written as:

Given (38), the first term of the function becomes:

which becomes nonlinear, because \(B_{i}\) and \(S_{ij}\) are output variables. Since (41) can be rewritten as:

and noticing that

one can rewrite (42) as:

where the first term is constant and the second one is variable. Moreover, the term
 in (39) is also constant. Given that a constant contribution can be ignored in the minimisation expressed in (40), one can write the objective function as:
in (39) is also constant. Given that a constant contribution can be ignored in the minimisation expressed in (40), one can write the objective function as:

Furthermore, one can observe that

given (30), can be written as:

Observing that the constraint in (19) can be expressed as
the problem becomes again nonlinear.
In order to avoid this nonlinearity, one extends the MCFP illustrated in (21) to consider microwave and fibre usage matrices \(U_{{\mathrm{cf/m}},ijbr}\) into the optimal flow accommodation.
This requires to add some additional constraints. One has to impose that
and
which means that a single link can be deployed using either fibre or microwave. Moreover, one has to impose that
to force the inclusion of the link into the final deployment.
Therefore, one can finally write the linear objective function:

The above nonlinearity impacts also on the constraint in (26). One can rewrite the RDCMST delay constraint in (26) as:
The involved parameters and variables can be divided into three categories: physical, i.e. all the entities related to the physical constraints and to the infrastructural deployment; network, i.e. entities related to network design decision, such as delay, capacity and BBU-RRHs connections; and economic, i.e. entities related to costs.
The list of input parameters and internal variables required for problem formulation is presented in Table 1.
Moreover, several internal variables are involved in the proposed optimisation model. Analogously to the input parameters, internal variables can be categorised into physical, network and economic variables, as illustrated in Table 2.
The constraints of the problem can be categorised as well into three classes: network (13), (14), (21), (22), (23), (25), (27), (28), (29), (53), physical (4), (8), (16), (17), (19), (49), (50), (51) and economical (30).
The output variables of the optimisation problem are:
 , \(\mathbf {B}\), \(\mathbf {U}\), \(\mathbf {S}\).
, \(\mathbf {B}\), \(\mathbf {U}\), \(\mathbf {S}\).
3 Results and discussion
3.1 Canonical scenario analysis
3.1.1 Canonical scenario description
The canonical scenario adopted for the evaluation of the proposed optimisation model is represented by a hexagonal grid of cells, Fig. 3, considering different configurations with three key parameters \(R_{\mathrm{S}},R_{\mathrm{B}},R_{\mathrm{C}}\) where
-
\(R_{S\left[ \text {km}\right] }\): radius of the service area
-
\(R_{B\left[ \text {km}\right] }\): radius of the BBU area
-
\(R_{C\left[ \text {km}\right] }\): radius of the cell
These three parameters have a different impact on the number of cells and the number of required BBUs. An increase of \(R_{\mathrm{S}}\) implies an increase of the number of cells, while an increase of \(R_{\mathrm{C}}\) reduces the number of cells. \(R_{\mathrm{B}}\) is strictly related to the maximum BBU-RRH delay \(\tau _{\mathrm{max}}\), since the higher is the delay budget the higher is the area covered by a single BBU, intuitively, the lower is the number of BBUs required to serve all RRHs.
Regarding \(R_{\mathrm{S}}\), three values resulting in the three configurations were taken, Fig. 4, and Table 3.
In the following, without loss of generality and in order to obtain a theoretical behaviour comparable with the optimisation model, one considers that all cells are already connected via a network of fibre links. The pedestrian path distance is assumed to be 1.5 times the straight-line one, but a different factor can be assumed without loss of generality for the whole model. One assumes null switching delay, just for the sake of simplicity in the analysis, all RRHs sites as feasible BBU ones, i.e.:
and that all RRHs sites are trisector cells, each one offering LTE 20MHz MIMO 2\(\times\)2 and requiring a link capacity of 2.4 Gbps corresponding to CPRI Option 3 (derived from (33) assuming 4 antennas, 30.72 MHz sample rate, 8 bit per sample, and coding factor 10/8). Since each RRH site hosts three cells, the total required link capacity for the RRH site is 7.2 Gbps. Regarding the available link capacity, one assumes 1.6 Tbps fibre links (corresponding to 40 channels at 40 Gbps in optical wavelength division multiplexed networks) and 100 Gbps capable microwave links.
Moreover, regarding costs, one adopts as reference the values listed in Table 4. CAPEX is calculated according to (39), and OPEX is taken as an annual expenditure of 10% of CAPEX. This assumption is in line with the results obtained in [10] (OPEX equals CAPEX in 10 years).
The optimisation approach CVX [25] combined with Gurobi [26] and MATLAB is used to solve the ILP. For our minimisation problem, CVX and Gurobi compute the gap between the incumbent value and the upper bound, which guarantees the optimal result when the gap reduces to 0. All simulations were run on an HP Server with Intel Xeon CPU E5-4627 and 64 GB RAM.
3.1.2 Theoretical output
The assumptions illustrated in Sect. 3.1.1 allow to formulate the problem of obtaining a theoretical number of required BBUs as a well-known cellular planning one. One can consider the number of required BBU sites as the ratio between the total number of RRH sites in the scenario, \(N_{\mathrm{RRH}}\), and the number or RRHs servable by a single BBU defined as \(N_{\mathrm{sRRH}}\):
where \(N_{\mathrm{BBU}}\) is the number of required BBUs.
Assuming the scenario as a hexagon and that the cell and BBU coverage are hexagons, and given that the area of the hexagon is [27]:
where \(R_{H\left[ \text {km}\right] }\): radius of the hexagon.
one can express \(N_{\mathrm{RRH}}(R_{\mathrm{S}}, R_{\mathrm{C}})\) as a ratio of areas:
where \(A_{Rs\left[ \mathrm {k}\mathrm {m}^{2}\right] }\): area of the service hexagon, \(A_{Rc\left[ \mathrm {k}\mathrm {m}^{2}\right] }\): area of the cell hexagon and similarly
where \(A_{R_B\left[ \mathrm {k}\mathrm {m}^{2}\right] }\) is the area of the BBU coverage, leading to:
3.1.3 Analysis of maximum latency impact
One evaluates the proposed optimisation model considering maximum BBU-RRH delay values spanning from 1.25 up to \(12.5\; \upmu {\mathrm {s}}\), which correspond to maximum BBU-RRH distance (\(R_{\mathrm{B}}\)) values spanning from \(250\; \mathrm {m}\) up to \(2.5 \;\text {km}\).
Figure 5 shows the number of required BBU sites for the three considered configurations and \(R_{\mathrm{C}}=0.25\;\text {km}\). One compares the output of the proposed optimisation model with the expected theoretical behaviour illustrated in Sect. 3.1.2. The obtained results adopting the proposed model are in line with the theoretical output calculated as in (59), with some discrepancies explainable by the discrete nature of the problem. Figure 5 shows that by increasing the maximum delay \(\tau _{\mathrm{max}}\) the number of required BBU sites decreases, which is explainable by observing that an increase of \(\tau _{\mathrm{max}}\) corresponds to an increase of \(R_{\mathrm{B}}\) and therefore an increase of \(N_{\mathrm{sRRH}}\), resulting in a lower number of BBU sites required to cover the whole scenario. The maximum value of the number of BBUs is equal to 19, i.e. 1 BBU per RRH, while the minimum is 1 corresponding to 1 BBU serving all RRHs.
Figure 6 shows the proportional relation between the maximum delay and the number of served RRHs per BBU. Since when increasing maximum delay the number of BBUs decreases, each BBU must serve a higher number of RRHs. The maximum value is trivially reached when just one BBU is deployed, i.e. 19.
Figure 7 shows the trend of CAPEX, calculated according to (39), considering different values of maximum BBU-RRH delay. It can be noticed how low values of \(\tau _{\mathrm{max}}\) require a high CAPEX for the operator, given the higher number of required BBUs; CAPEX remains constant from \(5 \; \upmu \text {s}\) onward, i.e. when the number of BBUs is equal to 1. Moreover, RRHs contribution to CAPEX remains constant, since it is related to the number of RRHs that is constant. Since one assumed an optical network already deployed, there is no contribution of fibre and microwave links because no new links deployment is required.
In the case of OPEX, although negligible, a minor contribution from fibre links is present, due to annual expenditures for the maintenance of the physical network. However, it can be noticed that the economic sustainability of the C-RAN architecture is related mainly to the annual cost of BBUs and RRHs operation, since link OPEX represents less than 1% of the network annual costs. Figure 8 shows that the trend of OPEX is analogous to CAPEX one, since it is mainly influenced by the number of BBU sites. Analogously to CAPEX, RRHs OPEX represents the main contribution when the number of BBUs is equal to 1.
3.1.4 Canonical scenario results overview
Figure 9 shows the number of BBUs as a function of the maximum fronthaul delay and the scenario radius. It highlights that the number of BBU sites is proportional to the scenario size, since the higher is the area to cover the higher is the number of required BBUs. On the other hand, as previously shown, there is an inverse proportional relation between the maximum delay constraint and the number of BBUs, since the higher is \(\tau _{\mathrm{max}}\) the higher is the number of RRHs servable by a single BBU.
3.2 Real scenario analysis
3.2.1 Real scenario description
In this subsection, one analyses the proposed model for a real scenario, i.e. the city of Lisbon and its surroundings. In Fig. 10, one represents the cell sites from a mobile operator covering an area at the north of the Tagus river, spanning for 40 km from the city centre.
Three coverage areas with different radius and density of cell characteristics are considered for the validation of the proposed model: urban (\(R_S = 0.65 \,\hbox {km}\)), suburban (\(R_S = 1.5 \,\hbox {km}\)) and rural (\(R_S = 7 \,\hbox {km}\)). As the proposed approach does not scale well with a large problem size due to ILP modelling limitations, one limits the analysis to 18 RRH sites corresponding to 54 cells. On the other hand, considering 18 RRHs allows a relative comparison with the canonical scenario analysis. In the following, one adopts the reference simulation parameters illustrated in Sect. 3.1.
3.2.2 Analysis of maximum latency impact
One evaluates the proposed optimisation model considering \(\tau _{\mathrm{max}}\) varying in different ranges for the different scenarios: \([0.65,6.5]\; \upmu \text {s}\) for urban, \([1.5,15]\; \upmu \text {s}\) for suburban and \([7,70]\; \upmu \text {s}\) for rural.
In Fig. 11, the results for the different scenarios are illustrated. The results obtained adopting the real scenarios appear to be in line with the canonical one, with some discrepancies explainable by the discrete nature of the problem. It can be noticed that in all three scenarios the maximum number of BBUs, i.e. 18, is not reached for small values of \(\tau _{{\max }}\), which is explainable by the nonregular disposition of RRHs in the scenario and by the presence of very near RRHs used to cover more populated areas. However, Fig. 11 shows that when increasing the maximum delay \(\tau _{\mathrm{max}}\) the number of required BBU sites decreases, as expected.
Figures 12 and 13 show CAPEX and OPEX for the considered scenarios calculated according to (39). Results show that, as in the canonical scenario, there is an inverse relation between maximum delay constraint and costs. CAPEX variation is mainly influenced by the number of BBUs, since RRHs contribution is constant and links initial investment is negligible.
For the three considered scenarios, the maximum CAPEX ranges between 1.32 and 1.54 M€ and is obtained for minimum values of \(\tau _{\mathrm{max}}\), a small variation being related to the different maximum number of BBUs, as shown in Fig. 11. To consider higher \(\tau _{\mathrm{max}}\) values reduce CAPEX to 0.35 M€ for the urban scenario and 0.37 M€ for the suburban and rural ones, thus achieving a reduction of 76% and 74%, respectively.
In the OPEX case, it can be noticed that passing from urban to rural scenarios increases the contribution of links maintenance. In fact, in the rural scenario, physical links OPEX becomes the major contribution to the operating costs for higher values of the maximum delay. Since in rural areas the density of cells is lower, intercell distance is generally higher and longer physical links are required; thus, it requires higher maintenance costs, increasing OPEX contribution. In the suburban case, links’ OPEX becomes equal to the BBUs cost for high values of delay, when only 1 BBU is required. In the rural scenario, the links’ OPEX grows more rapidly and links’ OPEX reaches BBUs’ OPEX for lower values of delay, when BBUs number is still greater than 1, and becomes the highest annual cost contribution when only 1 BBU is taken.
The maximum OPEX ranges between 132 k€ and 155 k€, while the minimum one is equal to 37 k€ in the urban scenario, 41 k€ in the suburban one and 60 k€ in the rural one. Thus, the reduction of OPEX related to \(\tau _{\mathrm{max}}\) is equal to 73% in the urban scenario, 75% in the suburban one and it goes down to 62% in the rural case, which highlights the impact of links maintenance annual cost in rural areas.
The three considered real scenarios are characterised by different sizes of the served area; thus, one can analyse C-RAN costs in terms of expenditure per square kilometre. The urban area requires 0.99 M€/km2 maximum CAPEX, being significantly higher with respect to the suburban scenario 0.22 M€/km2 and the rural one 0.01 M€/km2. Analogously, in the OPEX case the annual expenditure per square kilometre in the urban scenario is equal to 99 k€/km2, 22 k€/km2 in the suburban one and 1 k€/km2 in the rural one.
3.2.3 Microwave deployability impact
In this subsection, one analyses the impact of microwave radio links deployability. The comparison between different scenarios is conducted by adopting different percentages of new deployable microwave radio links with respect to the total number of newly deployable ones.
Figure 14 shows the trend of CAPEX for two different values of \(\tau _{\mathrm{max}}\) , i.e. 3 \(\upmu {\mathrm {s}}\) and 15 \(\upmu {\mathrm {s}}\) in the suburban scenario. For \(\tau _{\mathrm{max}}= 3\; \upmu {\mathrm {s}}\) the possibility to deploy new microwave radio links enables a significant reduction of CAPEX, since it allows to reduce the number of required BBUs. On the other hand, a small increase in microwave radio links deployment cost is required. Microwave links allow to reduce up to 35% CAPEX while requiring an investment equal to 4% of initial CAPEX in microwave links deployment. For \(\tau _{\mathrm{max}} = 15\; \upmu {\mathrm {s}}\), the number of required BBUs is already minimum; therefore, no BBUs-related CAPEX reduction is introduced by microwave links. In this case, for different microwave deployability indexes one can notice a conversion of CAPEX from fibre links investment to microwave one.
4 Conclusion
The Cloud Radio Access Network architecture represents a viable solution to address the problems related to the increase of traffic and also the increase of deployment and operation costs. It splits traditional BSs into Remote Radio Heads and Base Band processing Units, which introduces the front-haul segment of the mobile network, requiring a new approach to the deployment of a network architecture.
This work proposes an optimisation model for the deployment of C-RAN architectures in a brown-field scenario where traditional BSs are already present. The proposed model minimises deployment costs by optimising BBUs placement as well as links deployment. The proposed optimisation framework takes physical, network and economic aspects into account. The clusterisation of RRHs is modelled through a Multicommodity Flow approach. The links deployment reuses existing access infrastructures and interconnects BBUs and RRHs through a Rooted Delay-Constrained Minimum Spanning Tree approach, where the delay constraint is given by the BBU-RRH maximum round trip transmission budget.
The key input parameters considered are cost of links, BBUs and RRHs as well as links’ delay and capacity. The key output parameters are CAPEX, BBU placement, BBU-RRHs connections and physical links setup. For the optimisation, an integer linear programming approach that minimises the CAPEX is considered.
Regarding the sensitivity of the objective function to the input parameters, results show the inverse relation between CAPEX and delay budget. CAPEX grows linearly with the cost of links, BBUs and RRHs; thus, there are no critical values for the calculation of the cost-optimal deployment. This allows to adopt the proposed model as a tool for relative comparisons over many scenarios and deployment configurations that can be suitable from the operators’ viewpoint in network deployment planning.
The evaluation of the proposed model has been done by using a canonical hexagonal grid coverage in order to compare the results obtained from the proposed approach with the theoretical output calculated by adopting a well-known cellular planning approach. The coherence of the results between the two approaches validates the proposed model. Results show an inverse relation between the number of BBU Pools and the maximum accepted fronthaul delay.
Real scenarios represented by the deployment of BSs of a real operator in the city of Lisbon and its suburban area are considered. Moreover, optimal deployments for different maximum delay constraints are compared in order to show the operator’s trade-off between CAPEX and future proof ability of network deployment.
The analysis of urban, suburban and rural real scenarios confirms the inverse relation between delay budget and number of BBUs, which impacts significantly on CAPEX, since RRHs contribution is shown to be constant and links initial investment is negligible. The adoption of different maximum delay constraints in the fronthaul allows a CAPEX reduction between 74% and 76%. Regarding OPEX, results show that to adopt higher values of delay allows a reduction of costs up to 72% in urban areas and 62% in rural ones. The lower reduction with respect to CAPEX is explained by the fact that when passing from urban to rural scenarios the links’ operating costs impact is higher.
The considered scenarios are compared in terms of expenditures per square kilometre. Results show that a dense urban area requires 0.99 M€/km2 CAPEX and 90 k€/km2 OPEX, while moving to rural areas with lower density of customers and cells reduces CAPEX to 0.01 M€/km2 and OPEX to 1 k€/km2.
Finally, the impact of microwave deployability in a suburban scenario has been analysed. Results show that microwave links represent a convenient choice for the operator enabling a reduction of 35% of total CAPEX, while requiring an increase of investment of 4%, when capacity aspects are not at stake.
The main limitation of the proposed approach is represented by the low scalability of the ILP modelling. Since real-world planning problems are commonly larger than the ones considered in this work, future work includes the development of scalable heuristic-based solutions, which can handle a larger problem size. However, it is worthwhile mentioning that such approaches cannot guarantee the optimality of the solution. On the other hand, this work represents a suitable benchmark for the evaluation of the goodness of heuristic-based solutions.
Other future directions include the study of the impact on CAPEX and OPEX of infrastructure sharing among operators, the introduction of computational capacity limitations that may affect the deployment of the BBUs, and node-specific technological constraints that may impose limitations on switching capabilities in the network.
Availability of data and materials
The data sets used in the current study are available from the authors, in an anonymised version, upon request.
Abbreviations
- BBU:
-
Base Band Unit
- BS:
-
Base Station
- C-RAN:
-
Centralised Radio Access Network
- CAPEX:
-
CAPital EXpenditure
- CoMP:
-
Coordinated Multi-Point
- ILP:
-
Integer linear programming
- MCFP:
-
Multi-Commodity Flow Problem
- OPEX:
-
OPerating EXpenditure
- RDCMST:
-
Rooted Delay-Constrained Minimum Spanning Tree
- RRH:
-
Remote Radio Head
References
M. Masoudi, S.S. Lisi, C. Cavdar, Cost-effective migration toward virtualized C-RAN with scalable fronthaul design. IEEE Syst. J. 1–11 (2020). https://doi.org/10.1109/JSYST.2020.2982428
B. Naudts, M. Kind, F. Westphal, S. Verbrugge, D. Colle, M. Pickavet, Techno-economic analysis of software defined networking as architecture for the virtualization of a mobile network, in 2012 European Workshop on Software Defined Networking (2012), pp. 67–72
NGMN - Next Generation Mobile Networks : Suggestions on potential solutions to C-RAN. Technical report (2013)
C. Ran, S. Wang, C. Wang, Optimal load balancing in cloud radio access networks, in 2015 IEEE Wireless Communications and Networking Conference (WCNC), New Orleans, US (2015). https://doi.org/10.1109/WCNC.2015.7127607
L. Ferdouse, A. Alnoman, A. Bulzacki, A. Anpalagan., Energy efficient multiple association in comp based 5g cloud-ran systems, in 2017 IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, Canada (2017). https://doi.org/10.1109/VTCFall.2017.8288049
G. Venkatraman, A. Tolli, J. Kaleva, M. Juntti, JP-CoMP with antenna selection for multi-carrier C-RAN with finite backhaul capacity, in 2017 IEEE International Conference on Communications (ICC), Paris, France (2017). https://doi.org/10.1109/ICC.2017.7996948
3GPP - 3rd Generation Partnership Project: Radio Access Architecture and Interfaces (Release 14), 38.801. Technical report (2016)
IEEE - Institute of Electrical and Electronics Engineers: New Generation Fronthaul Interface. https://standards.ieee.org/develop/wg/NGFI.html. Accessed 20 Mar 2018
CPRI - Common Public Radio Interface: ecpri interface specification v1.2. Technical report (2018)
H. Frank, R.S. Tessinari, Y. Zhang, Z. Gao, C.C. Meixner, S. Yan, D. Simeonidou, Resource analysis and cost modeling for end-to-end 5g mobile networks, in Optical Network Design and Modeling, ed. by A. Tzanakaki, M. Varvarigos, R. Muñoz, R. Nejabati, N. Yoshikane, M. Anastasopoulos, J. Marquez-Barja (Springer, Cham, 2020), pp. 492–503
D. Harutyunyan, R. Riggio, How to migrate from operational lte/lte-a networks to c-ran with minimal investment? IEEE Trans. Netw. Serv. Manag. 15(4), 1503–1515 (2018)
F. Tonini, M. Fiorani, M. Furdek, L. Wosinska, C. Raffaelli, P. Monti, Minimum cost deployment of radio and transport resources in centralized radio architectures, in 2016 International Conference on Computing, Networking and Communications (ICNC), Kauai, US (2016). https://doi.org/10.1109/ICCNC.2016.7440671
F. Musumeci, C. Bellanzon, N. Carapellese, M. Tornatore, A. Pattavina, S. Gosselin, Optimal BBU placement for 5G C-RAN deployment over WDM aggregation networks. J. Lightwave Technol. 34(8), 1963–1970 (2016). https://doi.org/10.1109/JLT.2015.2513101
S.S. Lisi, A. Alabbasi, M. Tornatore, C. Cavdar, Cost-effective migration towards C-RAN with optimal fronthaul design, in 2017 IEEE International Conference on Communications (ICC),Paris, France (2017). https://doi.org/10.1109/ICC.2017.7996772
M.D. Andrade, M. Tornatore, A. Pattavina, A. Hamidian, K. Grobe, Cost models for baseband unit (bbu) hotelling: from local to cloud, in 2015 IEEE 4th International Conference on Cloud Networking (CloudNet), Niagara Falls, Canada (2015). https://doi.org/10.1109/CloudNet.2015.7335306
T.J. Monteiro, L.M. Correia, R. Dinis, Analysis of different cloud-ran implementation strategies in small cells scenarios, in: 2017 IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, Canada (2017). https://doi.org/10.1109/VTCFall.2017.8288045
M. Shehata, F. Musumeci, M. Tornatore, Resilient BBU placement in 5G C-RAN over optical aggregation networks. Photon Netw. Commun. 37(3), 388–398 (2019)
Z. Gao, J. Zhang, S. Yan, Y. Xiao, D. Simeonidou, Y. Ji, Deep reinforcement learning for BBU placement and routing in C-RAN, in 2019 Optical Fiber Communications Conference and Exhibition (OFC) (2019), pp. 1–3
D. Harutyunyan, R. Riggio, S. Kuklinski, T. Ahmed, CU placement over a reconfigurable wireless fronthaul in 5g networks with functional splits. Int. J. Netw. Manag. (2020). https://doi.org/10.1002/nem.2086
R.J. Fowler, M.S. Paterson, S.L. Tanimoto, Optimal packing and covering in the plane are np-complete. Inf. Process. Lett. 12(3), 133–137 (1981). https://doi.org/10.1016/0020-0190(81)90111-3
D. Pallaschke, R. Horst, P.M. Pardalos, Handbook of Global Optimization (Non-convex Optimization and Its Applications 2) (Kluwer Academic Publishers, Dordrecht, 1995)
S. Even, A. Itai, A. Shamir, On the complexity of time table and multi-commodity flow problems, in 16th Annual Symposium on Foundations of Computer Science (1975). https://doi.org/10.1109/SFCS.1975.21
H.F. Salama, D.S. Reeves, Y. Viniotis, The delay-constrained minimum spanning tree problem, in Proceedings Second IEEE Symposium on Computer and Communications (1997). https://doi.org/10.1109/ISCC.1997.616089
P. Chanclou, et al, Optical fiber solution for mobile fronthaul to achieve cloud radio access network, in 2013 Future Network Mobile Summit, Lisbon, Portugal (2013)
M. Grant, S. Boyd, CVX: Matlab Software for Disciplined Convex Programming, version 2.1. http://cvxr.com/cvx (2014)
Gurobi Optimization, L.: Gurobi Optimizer Reference Manual (2020). http://www.gurobi.com
D.P. Agrawal, Q.A. Zeng, Introduction to Wireless and Mobile Systems, 4th edn. (Delmar Learning, Clifton Park, 2015)
Funding
This work was partially supported by the Italian Government under CIPE resolution no. 135 (21 December 2012), project INnovating City Planning through Information and Communication Technologies (INCIPICT).
Author information
Authors and Affiliations
Contributions
The authors have contributed jointly to the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Marotta, A., Correia, L.M. Cost-effective joint optimisation of BBU placement and fronthaul deployment in brown-field scenarios. J Wireless Com Network 2020, 242 (2020). https://doi.org/10.1186/s13638-020-01844-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-020-01844-9

 : cost of the link deployment between RRHs i to j using fibre/microwave.
: cost of the link deployment between RRHs i to j using fibre/microwave.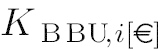 is the deployment cost of a BBU in site i.
is the deployment cost of a BBU in site i.











