- Research
- Open access
- Published:
A secure and privacy-preserving authentication protocol for wireless sensor networks in smart city
EURASIP Journal on Wireless Communications and Networking volume 2021, Article number: 119 (2021)
Abstract
Smart city can improve the efficiency of managing assets and resources, optimize urban services and improve the quality of citizens’ life. Wireless sensor networks (WSNs) can solve many problems in smart city, such as smart transportation, smart healthcare and smart energy. However, security and privacy are the biggest challenges for WSN. Recently, Banerjee et al. proposed a security-enhanced authentication and key agreement scheme for WSN, but their scheme cannot resist offline password guessing attack, impersonation attack, and does not achieve session key secrecy, identity unlinkability, and perfect forward secrecy. In order to fix these flaws, a secure and privacy-preserving authentication protocol for WSN in smart city is proposed. We prove the security of the proposed protocol by using applied pi calculus-based formal verification tool ProVerif and show that it has high computational efficiency by comparison with some related schemes.
1 Introduction
Smart city means to make use of information and communication technology, such as artificial intelligence, Internet of Things and cloud computing, to sense, analyze and integrate the key information of urban operation core system, so as to make intelligent response to various needs including people's livelihood, environmental protection, public safety, urban services, industrial and commercial activities, to create a better city life for mankind and build sustainable communities. Wireless sensor networks (WSNs) are widely used in smart city, such as environmental monitoring, health care, smart grids and surveillance [1,2,3,4]. Through Internet of Things devices, users can access any sensor node in WSN. Therefore, the security of wireless sensor networks is getting more and more attention. Authentication is the first step to ensure the correct transmission of information and the security of WSN. A legitimate user can access a legitimate sensor with user anonymity and receive information from the sensors. Therefore, security and privacy are the biggest challenges for WSN, and many protocols are proposed in the last ten years [5,6,7,8,9,10,11,12,13,14,15,16]. However, these protocols have one or more weaknesses.
In 2004, Watro et al. [9] proposed an authentication protocol for wireless sensor networks based on public key encryption. In order to strengthen the security of the protocol, Das [10] proposed a two-factor authentication protocol using password and smartcard. Khan and Alghathbar [11] proposed a protocol with better performance than Das's protocol. However, the password update phase in their scheme is faulty. Later, Yeh et al. [12] proposed a mutual authentication scheme based on elliptical curve cryptosystem, but it has a higher computation cost. Xue et al. [13] proposed a temporal-credential-based protocol in WSN. However, their scheme cannot resist many attacks, such as stolen smart card attack and impersonation attack. Later, Gope et al. [14] proposed a lightweight two-factor protocol for WSN, but Luo et al. [15] pointed out that their protocol exists several drawbacks and proposed an improved scheme. However, the improved scheme is still insecure. Recently, Turkanović et al. [16] proposed an authentication and key agreement scheme for wireless sensor networks, but Banerjee et al. [17] found that Turkanvic et al.'s scheme cannot resist identity theft attack and eavesdropping attack, and then, Banerjee et al. proposed an improved scheme based on the biometric and smart card.
Banerjee et al. [17] claimed that their scheme can resist various attacks. However, in this paper, we find that their scheme has some weaknesses, it cannot resist offline password guessing attack and impersonation attack and does not achieve session key secrecy, identity unlinkability and perfect forward secrecy. Therefore, we propose a new scheme to overcome the weaknesses of Banerjee et al.’s scheme.
The rest of the paper is structured as follows: Sections 2 and 3 introduce methods and preliminaries. Sections 4 and 5 review the Banerjee et al.'s scheme and present the attacks on their scheme. The proposed scheme, security analysis, results and discussion are given in Sects. 6, 7 and 8. Section 9 is conclusions.
2 Methods
The authentication model for WSN consists of users, sensor nodes and gateway nodes. Sensor nodes collect data from their environment, and users can access and receive data from sensor nodes. Gateway nodes are responsible for authentication between users and sensor nodes. In order to prevent unauthorized users from accessing data stored in sensors nodes, before users access sensor nodes, users and sensors nodes should authenticate each other with the help of gateway nodes and establish session keys to encrypt data transmitted between users and sensors nodes.
The threat assumptions of this model are as follows [18]:
-
The adversary can be a user, any registered user can act as an adversary.
-
The adversary can intercept or eavesdrop on all communication messages in a public channel, thereby capturing any exchanged messages between a user and gateway or sensor.
-
The adversary has the ability to eavesdrop, intercept, modify, or delete the transmitted message.
-
The adversary has the ability to obtain all information stored in users’ smart cards by using the side channel attack [19].
-
An external adversary can also register, login and receive his smart card.
According to above threat assumptions, the proposed protocol for WSN should meet the following security and privacy criteria:
-
Mutual authentication and key agreement: user and sensor node should authenticated each other with the help of gateway node and establish session key.
-
Anonymity and unlinkability: the protocol protects the user’s real identity and the adversary cannot trace the user’s activities.
-
Password friendly: the user can update and change his/her password freely.
-
No password guessing attacks: the protocol can protect the user’s password from guessing attack and ensure the adversary cannot verify whether the password is right or not.
-
No smart stolen/lost attacks: even if the smart card is lost or stolen, the adversary can obtain all information stored in it, but the adversary cannot attack the protocol successfully.
-
Perfect forward secrecy: even if an adversary can compromise long secret keys, he or she still cannot compute the session keys.
-
Known session key security: even if an adversary knows session key, the protocol still safety.
-
No replay attack: the protocol prevents the adversary from replaying the transmission information to attack the protocol successfully.
-
No various known attacks: the protocol can resist various known attacks, such as forgery attacks, impersonation attacks and man-in-the-middle attacks.
3 Preliminaries
In this section, we introduce the elliptic curve cryptosystem, the fuzzy extractor and some notations, which will be used in our protocol.
3.1 Elliptic curve cryptosystem
The elliptic curve cryptosystem (ECC) is widely used to design password-based authentication protocols, which are created by Miller [20] and Koblitz [21], respectively. ECC uses the following formula:
The above equation is ECC on \(F_{p}\). The following conditions must be met in order to ensure safety:
We choose P as a base point on \(F_{p}\), then \(xP = \overbrace {P + \cdots + P}^{x}\), \(xyP\) is a Diffie–Hellman value based on ECC.
3.2 Fuzzy extractor
It is very difficult for users to lose and steal their biological information. In many protocols, the users’ biometric will be taken as an important factor. There is a slight difference in each extraction of biological information, which can be corrected by using fuzzy extraction. The fuzzy extractor consists of two procedures \((Gen,Rep)\) [22, 23]:
where \(B\) is the biometric, and \(B^{*}\) is closed to \(B\). \(Gen\) function returns a string \(\alpha \in \left\{ {0,1} \right\}^{k}\) and a coadjutant string \(\beta \in \{ 0,1\}^{*}\). For each biometric \(B\), \(Gen\) function outputs a key \(\alpha\) and a help data \(\beta\). For each biometric \(B^{*}\), \(Rep\) function recovers a key \(\alpha\) with the help data \(\beta\).
3.3 Notations
The notations used in the paper are shown in Table 1.
4 Brife review of Banerjee et al.'s scheme
The Banerjee et al.'s scheme [17] has six phases: pre-deployment phase, registration phase, login phase, authentication and key agreement phase, password change phase and dynamic node addition phase. We omit the last two phases.
4.1 Pre-deployment
In this phase, the administrator uses the setup server to establish the environment. The setup server chooses identity \(SID_{j}\) for each sensor node \(S_{j}\) and provides a key \(GWNPS_{j}\) shared with the gateway node \(GWN\). The \(GWN\) is also provided with a secret key \(S_{g}\) and stores \(\{ SID_{j} ,\;GWNPS_{j} ,\;S_{g} \}\).
4.2 Registration phase
4.2.1 User registration phase
The user \(U_{i}\) chooses his identity \(UID_{i}\), password \(UPWD_{i}\) and a random number \(r_{i}\) and then calculates \(MID_{i} = h(UID_{i} ||r_{i} )\) and \(MPWD_{i} = h(UPWD_{i} ||r_{i} )\). \(U_{i}\) sends \(\{ MID_{i} ,MPWD_{i} \}\) to the gateway node \(GWN\) through secure channel.
After receiving \(\{ MID_{i} ,MPWD_{i} \}\), \(GWN\) selects secret key \(GWNPU_{i}\) and calculates \(MXIP_{i} = h(MID_{i} ||MPWD_{i} ) \oplus GWNPU_{i}\) and \(X_{i} = h(MID_{i} ||S_{g} )\), and stores \(\{ MXIP_{i} ,X_{i} ,h()\}\) into the smart card \(USC\) and issues it to \(U_{i}\) securely.
After receiving \(USC\), \(U_{i}\) calculates \(GWNPU_{i} = h(MID_{i} ||MPWD_{i} ) \oplus MXIP_{i}\),\(img_{x} = BH(r_{i} \oplus BIO_{i} )\),\(V_{i} = h(GWNPU_{i} ||img_{x} )\) and \(A_{i} = \, h(UID_{i} ||UPWD_{i} \, ) \oplus \, r_{i}\). The user appends \(\{ BH(),V_{i} ,A_{i} \}\) to the \(USC\).
4.2.2 Sensors registration phase
The sensor node \(S_{j}\) chooses a random number \(r_{j}\). \(S_{j}\) calculates \(MX_{j} = h(SID_{j} ||r_{j} ||GWNPS_{j} )\) and \(MY_{j} = r_{j} \oplus GWNPS_{j}\). \(S_{j}\) sends \(\{ SID_{j} ,MX_{j} ,MY_{j} \}\) to \(GWN\) through secure channel.
After receiving \(\{ SID_{j} ,MX_{j} ,MY_{j} \}\), \(GWN\) calculates \(r_{j} = MY_{j} \oplus GWNPS_{j}\) and verifies \(MX_{j} = h(SID_{j} ||r_{j} ||GWNPS_{j} )\). And then calculates \(P_{j} = h(MX_{j} ||S_{g} )\). The \(GWN\) stores \(P_{j}\) securely in its memory and issues \(P_{j}\) to \(S_{j}\). \(S_{j}\) stores \(P_{j}\) securely.
4.3 Login phase
The user \(U_{i}\) inputs \(UID_{i}\), \(UPWD_{i}\) and \(BIO_{i}\). \(USC\) calculates \({\text{r}}_{{\text{i}}} {\text{ = h(UID}}_{{\text{i}}} {||UP}{\text{WD}}_{{\text{i}}} { )} \oplus {\text{ A}}_{{\text{i}}}\), \(img_{x} = BH(r_{i} \oplus BIO_{i} )\), \(MID_{i} = h(UID_{i} ||r_{i} )\), \(MPWD_{i} = h(UPWD_{i} ||r_{i} )\) and \(GWNPU_{i} = h(MID_{i} ||MPWD_{i} ) \oplus MXIP_{i}\). And then \(USC\) verifies \(V_{i} ? = h(GWNPU_{i} ||img_{x} )\). If not, the user \(U_{i}\) re-does it. Otherwise, the smart card \(USC\) chooses a random number \(r_{1}\) and calculates \(M_{1} = h(X_{i} ||GWNPU_{i} ||r_{1} )\) and \(M_{2} = r_{1} \oplus X_{i}\). \(U_{i}\) sends the request message \(\{ MID_{i} ,M_{1} ,M_{2} \}\) to sensor node \(S_{j}\).
4.4 Authentication and key agreement phase
After receiving \(\{ MID_{i} ,M_{1} ,M_{2} \}\), \(S_{j}\) chooses a random number \(r_{2}\) and calculates \(M_{3} = P_{j} \oplus r_{2}\) and \(M_{4} = h(GWNPS_{j} ||M_{2} ||r_{2} )\). \(S_{j}\) sends \(\{ SID_{j} ,MID_{i} ,M_{1} ,M_{2} ,M_{3} ,M_{4} \}\) to \(GWN\).
After receiving \(\{ SID_{j} ,MID_{i} ,M_{1} ,M_{2} ,M_{3} ,M_{4} \}\),\(GWN\) calculates \(X_{i}^{*} = h(MID_{i} ||S_{g} )\), \(r_{1}^{*} = M_{2} \oplus X_{i}\), and \(r_{2}^{*} = M_{3} \oplus P_{j} .\)\(GWN\) verifies \(M_{1} ? = h(X_{i} ||GWNPU_{i} ||r_{1}^{*} )\) and \(M_{4} = h(GWNPS_{j} ||M_{2} ||r_{2}^{*} )\). If both are equal, the \(GWN\) authenticates the user \(U_{i}\) and the sensor node \(S_{j}\) The \(GWN\) chooses a random number \(r_{3}\) and calculates \(M_{5} = r_{3} \oplus h(GWNPS_{j} \oplus r_{2}^{*} )\), \(M_{6} = h(X_{i}^{*} ||GWNPS_{j} ||r_{1}^{*} ||r_{2}^{*} ||r_{3} )\), \(P_{1} = r_{1} \oplus P_{j}\) and \(P_{2} = X_{i}^{*} \oplus h(P_{j} ||r_{2}^{*} ||r_{1}^{*} )\). And then sends \(\{ M_{5} ,M_{6} ,P_{1} ,P_{2} \}\) to \(S_{j}\).
After receiving \(\{ M_{5} ,M_{6} ,P_{1} ,P_{2} \}\),\(S_{j}\) calculates \(r_{1}^{*} = P_{1} \oplus P_{j}\), \(X_{i}^{*} = P_{2} \oplus h(P_{j} ||r_{2}^{{}} ||r_{1}^{*} )\), \(r_{3}^{*} = M_{5} \oplus h(GWNPS_{j} \oplus r_{2}^{{}} )\) and verifies \(M_{6} ? = h(X_{i}^{*} ||GWNPS_{j} ||r_{1}^{*} ||r_{2}^{{}} ||r_{3}^{*} )\). If it is equal, the \(S_{j}\) authenticates the \(GWN\) and then calculates the session key \(SK = h(X_{i}^{*} ||P_{j} ||r_{3}^{*} ||r_{2} ||r_{1}^{*} )\). \(S_{j}\) calculate \(M_{7} = X_{i}^{*} \oplus r_{2}\), \(M_{8} = (P_{j} ||r_{3}^{*} ) \oplus r_{2}\) and \(M_{9} = h(r_{1}^{*} ||r_{2} )\). \(S_{j}\) sends \(\{ M_{7} ,M_{8} ,M_{9} \}\) to \(U_{i}\).
After receiving \(\{ M_{7} ,M_{8} ,M_{9} \}\),\(U_{i}\) calculates \(r_{2}^{*} = X_{i}^{*} \oplus M_{7}\),\((P_{j} ||r_{3}^{*} ) = M_{8} \oplus r_{2}^{*}\) and then verifies \(M_{9} ? = h(r_{1}^{{}} ||r_{2}^{*} )\). If the result is equal, \(U_{i}\) authenticates \(S_{j}\) and then calculates the session key \(SK = h(X_{i}^{{}} ||P_{j} ||r_{3}^{*} ||r_{2}^{*} ||r_{1}^{{}} )\).
5 Security flaws of Banerjee et al.'s scheme
Though Banerjee et al. claimed that their scheme can resist various attacks, in this section, we show that their scheme has some security flaws.
5.1 Identity linkability
In Banerjee et al.’s scheme, because \(MID_{i} = h(UID_{i} ||r_{i} )\) transmitted in public channel and unchanged in each session, the scheme exists the user identity linkability. Further, the adversary may get the user's real identity according to the user's behavior information. That is, the user's anonymity may be broken.
5.2 Offline password guessing attacks
If an adversary can obtain \(\{ MXIP_{i} ,X_{i} ,h(),BH(),V_{i} ,A_{i} \}\) stored in user’s smart card, and \(\{ MID_{i} ,M_{1} ,M_{2} \}\) from the public channel, then he can guess the user’s password \(UPWD\) and computes \({\text{r}}_{{\text{i}}}^{{\prime }} {\text{ = h(UID}}_{{\text{i}}} {||UP}{\text{WD )}} \oplus {\text{A}}_{{\text{i}}} \,\),\(MID_{i}^{{\prime }} = h(UID_{i} ||r_{i}^{{\prime }} )\), \(MPWD_{i}^{{\prime }} = h(UPWD||r_{i}^{{\prime }} )\),\(GWNPU_{i}^{{\prime }} = h(MID_{i}^{{\prime }} ||MPWD_{i}^{{\prime }} ) \oplus MXIP_{i}\), \(r_{1} ^{\prime} = M_{2} \oplus X_{i}\) and verifies whether \(M_{1} = h(X_{i} ||GWNPU_{i}^{{\prime }} ||r_{1}^{{\prime }} )\) or not. If yes, the guessed password is correct. Otherwise, the adversary does it again till to find the correct password.
This attack may success; the reason is that the user’s identity \(UID_{i}\) may easily to be known (e.g., an insider attacker, like the user's colleague) or it is often publicly available, and the password dictionary size is very restricted. Even if the adversary needs to guess \(UID_{i}\) and \(UPWD_{i}\) simultaneously, the time complexity of the above attacking procedure is \({\rm O}(|D_{id} |*|D_{pw} |*(T_{h} ))\), where \(T_{h} \,\) is the running time for hash operation and can guess the correct identity and password quickly [24].
If an adversary can get the user’s password by offline password guessing attack, then he can know \(GWNPU_{i}\) and \(X_{i}\), and he can launch impersonation attack.
5.3 No perfect forward secrecy
Because the session key is \(SK = h(X_{i}^{{}} ||P_{j} ||r_{3}^{{}} ||r_{2}^{{}} ||r_{1}^{{}} )\), if an adversary can obtain the secret key \(S_{g}\) of \(GWN\), then he can compute \(X_{i}^{{}} = h(MID_{i} ||S_{g} )\), \(r_{1} = M_{2} \oplus X_{i}\), \(P_{j} = r_{1} \oplus P_{1}\), \(r_{2} = X_{i}^{{}} \oplus M_{7}\), \((P_{j} ||r_{3}^{{}} ) = M_{8} \oplus r_{2}\). That is, the adversary can compute the session key, since he can get \(\{ MID_{i} , \, M_{2} , \, P_{1} , \, M_{7} , \, M_{8} \}\) from public channels.
5.4 No session key secrecy
If a legal user \(U_{l}\) have pass through the authentication of the sensor node \(S_{j}\), then \(U_{l}\) can know \(P_{j}\). After that, when other user \(U_{i}\) wants to pass through the authentication of the sensor node \(S_{j}\), \(U_{l}\) can get the authentication messages \(\{ MID_{i} , \, M_{2} , \, P_{1} , \, M_{7} , \, M_{8} \}\) from public channels, so \(U_{l}\) can compute \(r_{1} = P_{j} \oplus P_{1}\), \(X_{i} = M_{2} \oplus r_{1}\), \(r_{2} = X_{i}^{{}} \oplus M_{7}\), \((P_{j} ||r_{3}^{{}} ) = M_{8} \oplus r_{2}^{{}}\); therefore, \(U_{l}\) can compute the session key \(SK = h(X_{i}^{{}} ||P_{j} ||r_{3}^{{}} ||r_{2}^{{}} ||r_{1}^{{}} )\) shared between the \(U_{i}\) and \(S_{j}\).
5.5 Impersonation attack
If a legal user \(U_{l}\) have pass through the authentication of the sensor node \(S_{j}\), and obtains \(P_{j}\), then he can impersonate the \(S_{j}\). When other user \(U_{i}\) wants to login onto the sensor node \(S_{j}\), \(U_{l}\) sends \(\{ MID_{i} ,M_{1} ,M_{2} \}\) to \(S_{j}\), \(S_{j}\) sends \(\{ SID_{j} ,MID_{i} ,M_{1} ,M_{2} ,M_{3} ,M_{4} \}\) to \({\text{GWN}}\). When \({\text{GWN}}\) responses the message \(\{ M_{5} ,M_{6} ,P_{1} ,P_{2} \}\), \(U_{l}\) intercepts it, and chooses a random number \(r_{3}^{{\prime }}\), and computes \(r_{1}^{*} = P_{1} \oplus P_{j}\),\(r_{2}^{*} = M_{3} \oplus P_{j}\), \(X_{i}^{*} = P_{2} \oplus h(P_{j} ||r_{2}^{{}} ||r_{1}^{*} )\), the session key \(SK = h(X_{i}^{*} ||P_{j} ||r_{3}^{{\prime }} ||r_{2} ||r_{1}^{*} )\), \(S_{j}\) calculate \(M_{7} = X_{i}^{*} \oplus r_{2} {*}\), \(M_{8} = (P_{j} ||r_{3}^{{\prime }} ) \oplus r_{2} {*}\) and \(M_{9} = h(r_{1}^{*} ||r_{2} {*})\). \(U_{l}\) sends \(\{ M_{7} ,M_{8} ,M_{9} \}\) to \(U_{l}\). Obviously, \(U_{l}\) can compute and verify the correction of the session key SK. However, \(U_{l}\) shares the session key SK with \(U_{l}\), not the sensor node \(S_{j}\).
6 Proposed scheme
There are three entities of our proposed scheme: the user \(U_{i}\), the sensor node \(S_{j}\) and the gateway node \(GWN\). The user and the sensor node can authenticate each other and establish a session key with the help of the gateway node. Our protocol has four phases: initialization phase, registration phase, authentication and key agreement phase and password change phase.
6.1 Initialization phase
The administrator provides an identity \(SID_{j}\) and a secret key \(GWNPS_{j}\) (shared with \(GWN\)) for the sensor node \(S_{j}\) and chooses a prime number \(P\) and an additive group \(G1\), the \(GWN\)’s long secret key \(S_{g} \in Z_{p}\) and computes the \(GWN\)’s public key \(PK_{g} = S_{g} P\), where \(P \in G1\).
6.2 Registration phase
The registration phase is run through the secure channel as shown in Algorithm 1. The user \(U_{i}\) firstly chooses its identity \(UID_{i}\) and password \(UPWD_{i}\) and sends \(\{ UID_{i} \}\) to \(GWN\). After receiving \(\{ UID_{i} \}\), \(GWN\) calculates \(X_{i} = h(UID_{i} ||S_{g} )\). \(GWN\) enters \(\{ X_{i} \}\) into the smart card and sends it to \(U_{i}\) through the secure channel.
\(U_{i}\) imprints the biological information \(BIO_{i}\) and calculates \((\alpha ,\beta ) = Gen(BIO_{i} )\), \(V_{1} = h(UID_{i} ||UPWD_{i} ||\alpha )\) and \(Y_{i} = X_{i} \oplus h(UID_{i} ||\alpha )\).\(U_{i}\) stores \(\{ Y_{i} ,Rep(),V_{1} ,\beta \}\) in the smart card \(USC\).

6.3 Authentication and key agreement phase
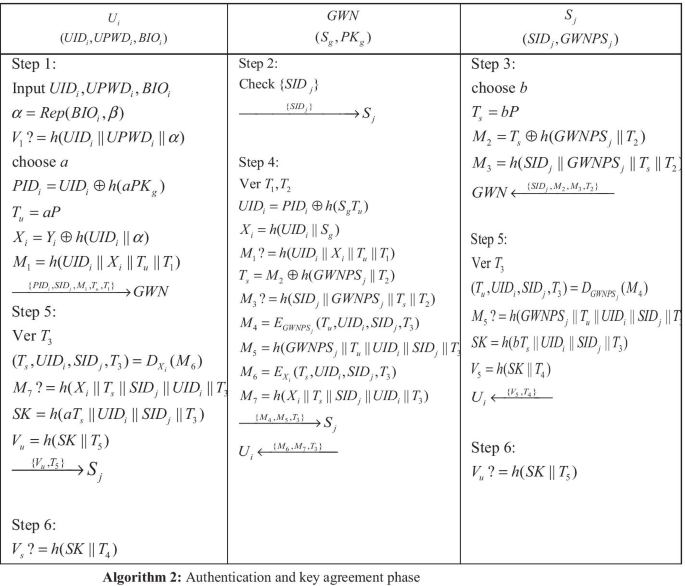
The user, the sensor and the gateway authenticate with each other, and the user and the sensor negotiate session key as shown in Algorithm 2.
-
Step 1 \(U_{i}\) inserts smart card and inputs identity \(UID_{i}\), password \(UPWD_{i}\) and biological information \(BIO_{i}\). The smart card \(USC\) calculates \(\alpha = Rep(BIO_{i} ,\beta )\) and verifies whether \(V_{1} ? = h(UID_{i} ||UPWD_{i} ||\alpha )\) or not. If not, the user re-does it. Otherwise, \(USC\) chooses a random numbers \(a\) and calculates the user's temporary identity \(PID_{i} = UID_{i} \oplus h(aPK_{g} )\), \(T_{u} = aP\), \(X_{i} = Y_{i} \oplus h(UID_{i} ||\alpha )\), and \(M_{1} = h(UID_{i} ||X_{i} ||T_{u} ||T_{1} )\) where \(T_{1}\) is the current timestamp. \(U_{i}\) sends \(\{ PID_{i} ,SID_{j} ,M_{1} ,T_{u} ,T_{1} \}\) to \(GWN\).
-
Step 2 After receiving \(\{ PID_{i} ,SID_{j} ,M_{1} ,T_{u} ,T_{1} \}\), \(GWN\) checks the validity of \(T_{1}\) and \(SID_{j}\) and forwards \(\{ SID_{j} \}\) to the sensor node \(S_{j}\).
-
Step 3 After receiving \(\{ SID_{j} \}\), \(S_{j}\) chooses a random number \(b\) and calculates \(T_{s} = bP\), \(M_{2} = T_{s} \oplus h(GWNPS_{j} ||T_{2} )\) and \(M_{3} = h(SID_{j} ||GWNPS_{j} ||T_{s} ||T_{2} )\) where \(T_{{2}}\) is the current timestamp. \(S_{j}\) sends \(\{ SID_{j} ,M_{3} ,M_{4} ,T_{2} \}\) to the \(GWN\).
-
Step 4 After received the authentication message, \(GWN\) first verifies the timestamp \(T_{{2}}\). If \(T - T_{2} \le \Delta T\) is false where \(T\) is the current timestamp, \(GWN\) refuses the authentication request. Otherwise, \(GWN\) calculates \(UID_{i} = PID_{i} \oplus h(S_{g} T_{u} )\), \(X_{i} = h(UID_{i} ||S_{g} )\) and verifies \(M_{1} ? = h(UID_{i} ||X_{i} ||T_{u} ||T_{g} ||T_{1} )\). If the result is false, \(GWN\) terminates the protocol. Otherwise, \(GWN\) authenticates the user successfully. After that, \(GWN\) calculates \(T_{s} = M_{2} \oplus h(GWNPS_{j} ||T_{2} )\) and verifies \(M_{3} ? = h(SID_{j} ||GWNPS_{j} ||T_{s} ||T_{2} )\). If the result is false, \(GWN\) also terminates the protocol. Otherwise, \(GWN\) authenticates the sensor node \(S_{j}\) successfully. Then, \(GWN\) computes \(M_{4} = E_{{GWNPS_{j} }} (T_{u} ,UID_{i} ,SID_{j} ,T_{3} )\) and \(M_{6} = E_{{X_{i} }} (T_{s} ,UID_{i} ,SID_{j} ,T_{3} )\) and calculates \(M_{5} = h(GWNPS_{j} ||T_{u} ||UID_{i} ||SID_{j} ||T_{3} )\) and \(M_{7} = h(X_{i} ||T_{s} ||SID_{j} ||UID_{i} ||T_{3} )\), where \(T_{3}\) is the current time stamp. \(GWN\) sends \(\{ M_{4} ,M_{5} ,T_{3} \}\) to \(S_{j}\) and \(\{ M_{6} ,M_{7} ,T_{3} \}\) to \(U_{i}\).
-
Step 5 After receiving the message \(\{ M_{4} ,M_{5} ,T_{3} \}\), \(S_{j}\) firstly verifies \(T_{3}\). If \(T^{{\prime }} - T_{3} \le \Delta T\) is false where \(T^{{\prime }}\) is the current timestamp, \(S_{j}\) terminates the protocol. Otherwise, \(S_{j}\) computes \((T_{u} ,UID_{i} ,SID_{j} ,T_{3} ) = D_{{GWNPS_{j} }} (M_{4} )\) and verifies \(M_{5} ? = h(GWNPS_{j} ||T_{u} ||UID_{i} ||SID_{j} ||T_{3} )\). If the result is equal, \(S_{j}\) authenticates \(GWN\) successfully. And then, \(S_{j}\) calculates the session key \(SK = h(bT_{u} ||UID_{i} ||SID_{j} ||T_{3} )\) and \(V_{s} = h(SK||T_{4} )\) where \(T_{4}\) is the current timestamp. \(S_{j}\) sends \(\{ V_{s} ,T_{4} \}\) to \(U_{i}\).
At the same time, when \(U_{i}\) receives \(\{ M_{6} ,M_{7} ,T_{3} \}\) from \(GWN\), \(U_{i}\) firstly verifies \(T_{3}\). If \(T^{{\prime \prime }} - T_{3} \le \Delta T\) is false where \(T^{{\prime \prime }}\) is the current timestamp, \(U_{i}\) terminates the protocol. Otherwise, \(U_{i}\) decrypts \((T_{s} ,UID_{i} ,SID_{j} ,T_{3} ) = D_{{X_{i} }} (M_{6} )\) and verifies \(M_{7} ? = h(X_{i} ||T_{s} ||SID_{j} ||UID_{i} ||T_{3} )\). If the result is false, \(U_{i}\) also terminates the protocol. Otherwise, \(U_{i}\) authenticates \({\text{GWN}}\) successfully and calculates the session key \(SK = h(aT_{s} ||UID_{i} ||SID_{j} ||T_{3} )\) and \(V_{u} = h(SK||T_{5} )\), where \(T_{5}\) is the current timestamp. Then, \(U_{i}\) sends \(\{ V_{u} ,T_{5} \}\) to \(S_{j}\).
Step 6. After receiving \(\{ V_{s} ,T_{4} \}\) and \(\{ V_{u} ,T_{5} \}\), \(U_{i}\) and \(S_{j}\) verifies the freshness of \(T_{4}\) and \(T_{5}\), and verifies the correctness of \(V_{s}\) and \(V_{u}\), respectively. After verification of correctness, \(U_{i}\) and \(S_{j}\) share the session key \(SK\).
6.4 Password change phase
If the user wants to change or update his passwords, \(U_{i}\) inserts \(USC\) in card reader and inputs identity \(UID_{i}\), password \(UPWD_{i}^{old}\) and biological information \(BIO_{i}\). Next, the smart card calculates \(\alpha = Rep(BIO_{i} ,\beta )\) and verifies \(V = h(UID_{i} ||UPWD_{i}^{old} ||\alpha )\). If the result is false, the smart card does not recognize him as a legitimate user. Otherwise, the user inputs new password \(UPWD_{i}^{new}\). The smart card calculates \(V^{new} = h(UID_{i} ||UPWD_{i}^{new} ||\alpha )\) and replaces \(V\) with \(V^{new}\).
7 Security analysis
In the section, we analyze the security of the proposed protocol by using formal and informal security analysis.
7.1 Formal security analysis
We simulate our scheme using ProVerif simulation tool [25], which is widely used for proving the authentication and session key secrecy. We defined three public channels ch1, ch2, ch3. The details of variables and functions are shown in Table 2. The details of process of user authentication are shown in Table 3. The process of sensor authentication is shown in Table 4. The simulation process of gateway is shown in Table 5.
We use the ProVerif to prove our authentication phase. First, the smart card authenticates the user successfully. Second, the gateway node authenticates the user successfully. Third, the sensor node authenticates the gateway node successfully. Fourth, the gateway node authenticates the sensor node successfully. Finally, the user authenticates the gateway node and the sensor node successfully. That is, users, sensors and gateway achieve mutual authentication each other. If the scheme successfully goes on, the user and sensor node will negotiate the same session key. Therefore, our scheme has six time points, and their code is represented in the ProVerif as follows:
-
event SmartcardAccept(user) means the user logins the smart card successfully.
-
event gwnAcceptU(user) means the gateway node authenticates the user successfully.
-
event gwnAcceptS(sensor) means the gateway node authenticates the sensor node successfully.
-
event sensorAccept(GWN) means the sensor node authenticates the gateway node successfully.
-
event userAccept(sensor,GWN) means the user authenticates the gateway node and the sensor node successfully.
-
event Sksuccessful(user,sensor) means user and sensor node get the same session key.
The authentication order of our protocol is as follows:
-
query Ui:user; inj-event(gwnAcceptU(Ui)) = = > inj-event(SmartcardAccept(Ui)).
-
query Ui:user,Gateway:GWN; inj-event(sensorAccept(Gateway)) = = > inj-event (gwnAcceptU(Ui)).
-
query Sj:sensor,Gateway:GWN; inj-event(gwnAcceptS(Sj)) = = > inj-event (sensorAccept(Gateway)).
-
query Ui:user,Sj:sensor,Gateway:GWN; inj-event(userAccept(Sj,Gateway)) = = > inj-event (gwnAcceptS(Sj)).
Our protocol must also protect the session keys (SKus and SKsu). The code is:
-
query attacker(SKsu).
-
query attacker(SKus).
Finally, we use the following code to start the verification:

The simulation authentication result is shown in Fig. 1. The simulation result of the session key is shown in Fig. 2. The result shows that our scheme achieves mutual authentication and the session key security.
7.2 Informal security analysis
7.2.1 Anonymity and unlinkability
In our scheme, the user’s real identity is contained in those parameters \(< PID_{i} , \, M_{4} , \, M_{5} , \, M_{6} , \, M_{7} >\).\(\, PID_{i} \,\) is protected by Diffie–Hellman problem. And the \(\, M_{4}\) and \(\, M_{6}\) are encrypted by \(X_{i}\) and \(GWNPS_{j}\), respectively. The rest of the parameters \(< M_{6} , \, M_{8} >\) are protected by the hash function. So, the adversary cannot know the user’s real identity. Our scheme meets the need of anonymity. The \(PID_{i}\) changes in each session because of the use of the random number and Diffie–Hellman value. So, our scheme is also unlinkability.
7.2.2 Offline password guessing attacks
Assume that an adversary knows the parameters \(\{ Y_{i} ,Rep(),V_{1} ,\beta \}\) stored in the smart card and all messages transmitted in all public channels, but he cannot guess the true password. Since the user’s password is protected by the bio-information and the hash function, the adversary cannot verify the parameter \(V_{1}\). On the other hand, we assume that an adversary knows the legal user’s password and all messages transmitted through the public channel, but do not know the parameters stored in the smart card. However, the adversary cannot login the protocol because he cannot obtain the bio-information. So, our scheme can resist the offline password guessing attacks.
7.2.3 Replay attack
There are two ways to prevent replay attacks: adding timestamps and random numbers. Our scheme uses time stamps to prevent replay attack. In every session, the timestamps are different and the entity checks the fresh of the timestamps.
7.2.4 Impersonation attack and man-in-the-middle attack
In our scheme, the gateway node authenticates the user by the parameter \(M_{1}\). The user authenticates the gateway node by the parameter \(M_{7}\). If an adversary wants to impersonate the legal user, he must know those parameter \(< T_{u} , \, X_{i} , \, T_{s} >\) which \(X_{i}\) is pre-shared with the gateway node. However, \(X_{i}\) is contained in \(Y_{i}\) stored in the smart card securely. Similarly, an adversary cannot impersonate the sensor node because of \(GWNPS_{j}\). If an adversary captures a sensor node, he cannot know the others’ key parameters. So he cannot impersonate other sensor node and the user. Therefore, our scheme resists impersonation attack, and the man-in-the-middle is also invalid.
7.2.5 Perfect forward secrecy
Assume that an adversary knows the user’s password \(UPWD_{i}\), the sensor node’s secret key \(GWNPS_{j}\). Since the session key is \(SK = h(abP||UID_{i} ||SID_{j} ||T_{3} )\), an adversary cannot compute \(abP\) due to Elliptic Curve Diffie–Hellman problem (ECDHP). So he cannot compute the session key.
7.2.6 Known session key security
In our scheme, the adversary cannot compute the session key because of ECDHP. The session key is also different in each session due to two random numbers \(\, a, \, b\). So, if the adversary knows a session key, he cannot know the before and the future session keys.
7.2.7 Sensors capture attack
If an adversary can capture a sensor node \(S_{j}\), then he can obtain the secret key \(GWNPS_{j}\) shared with GWN. However, each sensor node has a different secret key shared with GWN, so the adversary cannot impersonate another sensor node to pass through the authentication with GWN. On the other hand, even if the adversary can know the secret key \(GWNPS_{j}\) of a sensor node \(S_{j}\), he cannot know the user’s \(X_{i} = h(UID_{i} ||S_{g} )\) from the session run. Therefore, the proposed scheme is secure even if the sensor node is captured.
8 Results and discussion
In this section, we will discuss security and performance comparison with some related schemes, such as Fan et al. [1], Yeh et al. [12], Luo et al. [15], Banerjee et al. [17], Choi et al. [26], Park et al. [27] and Challa et al.’s schemes [28].
\(T_{m} \,\) means the time of the point multiplicative operation in ECC, \(\, T_{Rep} \,\) means the running time to performance \(Rep\) which is equal to \(T_{m}\) [29], \(T_{s}\) means the time in symmetric encryption or decryption, \(T_{h}\) means the time of hash operation, and \(T\) is the time or searching the identity in verification table which is related to the number of users. The running time is shown in Table 6 [30].
As shown in Tables 7 and 8, we can know that the proposed scheme achieves both security and computational efficiency.
9 Conclusions
In this paper, we have shown that the recently proposed Banerjee et al.’s protocol cannot resist offline password guessing attack, impersonation attack, and does not achieve session key secrecy, identity unlinkability and perfect forward secrecy. Then, we proposed a secure and privacy-preserving protocol to fix their security flaws. According to the formal security proof and performance comparison with some related schemes, we can know that our protocol achieves both security and computational efficiency and can be used to the smart city. In the future, we will design more secure authentication protocols for smart city applications, such as smart transportation and smart healthcare.
Availability of data and materials
The dataset used and analyzed during the current study is available in the manuscript.
Abbreviations
- WSNs:
-
Wireless sensor networks
- USC:
-
The user’s smart card
- GWN:
-
Gateway node
References
W. Fan, X. Lili, K. Saru, L. Xiong, An improved and provably secure three-factor user authentication scheme for wireless sensor networks. Peer Peer Net. Appl. 11, 1–20 (2018)
V.R. Maneesha, R. Prabha, H. Thirugnanam, R.A. Devidas, R.K. Pathinarupothi, Achieving sustainability through smart city applications: protocols, systems and solutions using IoT and wireless sensor network. CSI Trans ICT 8, 1–18 (2020)
Q. Xie, L. Hwang, Security enhancement of an anonymous roaming authentication scheme with two-factor security in smart city. Neurocomputing 347, 131–138 (2019)
T. Gaber, S. Abdelwahab, M. Elhoseny, A.E. Hassanien, Trust-based secure clustering in WSN-based intelligent transportation systems. Comput. Netw. 146, 151–158 (2018)
S.A. Chaudhry, K. Yahya, F. Al-Turjman, M.H. Yang, A secure and reliable device access control scheme for IoT based sensor cloud systems. IEEE Access 8, 139244–139254 (2020)
S.A. Chaudhry, M.S. Farash, N. Kumar, M.H. Alsharif, PFLUA-DIoT: a pairing free lightweight and unlinkable user access control scheme for distributed IoT environment. IEEE Syst. J. PP, 1–8 (2020)
S.A. Chaudhry, Correcting “PALK: password-based anonymous lightweight key agreement framework for smart grid.” Int. J. Electr. Energy Syst. 125, 106529 (2021)
A. Irshad, M. Usman, S.A. Chaudhry, H. Naqvi, M. Shafiq, A provably secure and efficient authenticated key agreement scheme for energy internet-based vehicle-to-grid technology framework. IEEE Trans. Ind. Appl. 56(4), 4425–4435 (2020)
R. Watro, D. Kong, S. Cuti, C. Gardiner, P. Kruus, P.K. Tiny, Securing sensor networks with public key technology, in Proceedings of the 2nd ACM Workshop on Security of Ad Hoc and Sensor Networks (ACM, 2004), pp. 59–64
M.L. Das, Two-factor user authentication in wireless sensor networks. IEEE Trans. Wireless Commun. 8(3), 1086–1090 (2009)
M.K. Khan, K. Alghathbar, Cryptanalysis and security improvements of ‘two-factor user authentication in wireless sensor networks.’ Sensors 10(3), 2450–2459 (2010)
H.L. Yeh, T.H. Chen, P.C. Liu, T.H. Kim, H.W. Wei, A secured authentication protocol for wireless sensor networks using elliptic curves cryptography. Sensors 11(5), 4767–4779 (2011)
K. Xue, C. Ma, P. Hong, R. Ding, A temporal-credential-based mutual authentication and key agreement scheme for wireless sensor networks. J. Netw. Comput. Appl. 36(1), 316–323 (2013)
P. Gope, T. Hwang, A realistic lightweight anonymous authentication protocol for securing real-time application data access in wireless sensor networks. IEEE Trans. Industr. Electron. 63(11), 7124–7132 (2016)
H. Luo, G. Wen, J. Su, Lightweight three factor scheme for real-time data access in wireless sensor networks. Wirel. Netw. 26(2), 955–970 (2020)
M. Turkanović, B. Brumen, M. Hölbl, A novel user authentication and key agreement scheme for heterogeneous ad hoc wireless sensor networks, based on the Internet of Things notion. Ad Hoc Netw. 20, 96–112 (2014)
S. Banerjee, C. Chunka, S. Sen, R.S. Goswami, An enhanced and secure biometric based user authentication scheme in wireless sensor networks using smart cards. Wirel. Pers. Commun. 107, 1–28 (2019)
L. Yanrong, L. Lixiang, Y. Xing, Y. Yixian, Robust biometrics based authentication and key agreement scheme for multi-server environments using smart cards. PLoS ONE 10(5), e0126323 (2015)
T.S. Messerges, E.A. Dabbish, R.H. Sloan, Examining smart-card security under the threat of power analysis attacks. IEEE Trans. Comput. 51(5), 541–552 (2002)
V.S. Miller, Use of elliptic curves in cryptography, in Conference on the theory and application of cryptographic techniques (Springer, Berlin, 1985), pp. 417–426
N. Koblitz, Elliptic curve cryptosystems. Math. Comput. 48(177), 203–209 (1987)
A.K. Das, A secure and effective biometric-based user authentication scheme for wireless sensor networks using smart card and fuzzy extractor. Int. J. Commun Syst 30(1), 1–25 (2017)
Y. Dodis, L. Reyzin, A. Smith, Fuzzy extractors: how to generate strong keys from biometrics and other noisy data, in International Conference on the Theory and Applications of Cryptographic Techniques (Springer, Berlin, 2004), pp. 523–540
W. Ding, Q. Gu, H. Cheng, W. Ping, The request for better measurement: a comparative evaluation of two-factor authentication schemes, in Proceedings of the 11th ACM on Asia Conference on Computer and Communications Security (2016), pp. 475–486
B. Blanchet, An efficient cryptographic protocol verifier based on prolog rules, in 14th IEEE Computer Security Foundations Workshop (CSFW-14) (2014), pp. 82–96
Y. Choi, Y. Lee, D. Won, Security improvement on biometric based authentication scheme for wireless sensor networks using fuzzy extraction. Int. J. Distrib. Sens. Netw. 4, 1–16 (2016)
Y. Park, Y. Park, Three-factor user authentication and key agreement using elliptic curve cryptosystem in wireless sensor networks. Sensors 16(12), 2123 (2016)
S. Challa, M. Wazid, A.K. Das, N. Kumar, R.A. Goutham, E.J. Yoon, K.Y. Yoo, Secure signature-based authenticated key establishment scheme for future IoT applications. IEEE Access 5, 3028–3043 (2015)
L. Xu, F. Wu, Cryptanalysis and improvement of a user authentication scheme preserving uniqueness and anonymity for connected health care. J. Med. Syst. 39(10), 1–9 (2015)
H.H. Kilinc, T. Yanik, A survey of sip authentication and key agreement schemes. IEEE Commun. Surv. Tutor. 16(2), 1005–1023 (2014)
Acknowledgements
This research was supported by the National Natural Science Foundation of China (Grant Nos. 61702152 and 61702153, URL http://www.nsfc.gov.cn/).
Funding
This research was supported by the National Key R&D Program of China (Grant No. 2017YFB0802000, URL http://www.most.gov.cn/).
Author information
Authors and Affiliations
Contributions
QX, BH and KL have analyzed the security of Banerjee et al.’s scheme and have modeled and designed the protocol. KL and WT wrote the paper. XT and LH proved the authentication and security of the proposed scheme. BH and KL verified the authentication, security and anonymity of the proposed scheme in the latest version 1.95 of ProVerif. QX, BH and KL revised the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xie, Q., Li, K., Tan, X. et al. A secure and privacy-preserving authentication protocol for wireless sensor networks in smart city. J Wireless Com Network 2021, 119 (2021). https://doi.org/10.1186/s13638-021-02000-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-021-02000-7


