Opportunistic routing based on partial CSI in MIMO random ad-hoc networks

Abstract

In this paper we consider opportunistic routing in multiple-input–multiple-output (MIMO) random wireless ad-hoc networks (WANETs). Our analysis uses a proper model of the physical layer together with an abstraction of the higher communication layers. We assume that the nodes are distributed according to a Poisson point process and consider a routing scheme that opportunistically selects the next relay and the number of spatially multiplexed data streams. The routing decisions are based on geographic locations, the channel gains of the neighbor nodes, and the statistical characterization of all other nodes. Unlike the single antenna case, the optimal routing scheme cannot be explicitly expressed. Hence, we propose a smart-routing scheme for MIMO that adapts the number of data streams per user to the channel conditions. The numerical results demonstrate that this scheme outperforms all previously published schemes for this scenario. The findings highlight the importance of channel state information for efficient routing, and the need for an adaptive selection of the number of data streams at each transmitter.

1 Introduction

Wireless ad-hoc networks (WANETs) have grown in popularity primarily because of their simplicity and scalability. WANET technology has been used in many applications, for example in machine-to-machine communication (e.g., [1,2,3]), military communications (e.g., [4]), and disaster recovery in 4G and 5G (e.g., [5, 6]).

WANETs need to transfer messages from their sources to their destinations. Direct transmission from source to destination is undesirable (due to high interference levels as well as shortening of the battery life). Hence, WANETs typically apply multihop routing. In this paper, we study the challenge of multihop routing in multiple-input–multiple-output (MIMO) networks, where each node is equipped with multiple antennas.

We adopt a stochastic geometry approach, without focusing on a specific network structure, using the ubiquitous homogenous Poisson point process (HPPP) for the locations of the nodes (e.g., [7,8,9,10,11]). Several works have considered multihop routing in WANETs using the HPPP model. Most have considered geographic routing (e.g., [12, 13]), since it considerably simplifies the analysis.

In geographic routing, the next hop is selected using knowledge of the geographic locations of the potential relays, where the routing decision at each hop is independent of all other decisions. The most popular geographic routing scheme is nearest neighbor routing (e.g., [12, 14]).

Routing algorithms can be significantly improved when the routing decisions take the instantaneous channel state information (CSI) into account. This type of algorithm is known as opportunistic relaying. Opportunistic relaying (e.g., [15,16,17,18,19,20]) was shown to outperform traditional routing (such as nearest neighbor). To date, however, opportunistic relaying has not been investigated for MIMO multihop networks. MIMO increases the data rate in WANETs by enabling both spatial multiplexing and interference mitigation (e.g., [21]).

A good performance measure for routing schemes is the multiplication of bit rate and link length. Intuitively, this multiplication makes sense since delivering the same link rates to longer link lengths (distance between a transmitter and its next relay) enables faster delivery of the data from their initial sources to their final destinations, as does delivering a higher data rate for a link at the same distance (e.g., doubling the link distances while maintaining the same rates or doubling the link rates while maintaining the same distances will double the network throughput).

Some of these ‘bit rate $\times$ distance’ metrics are based on the outage rate (e.g., the transport-capacity [22] and the progress rate density [23]). An alternative approach assumes that each link achieves the ergodic rate (e.g., the Asymptotic-Density-of-Rate-Progress, ADORP, [18]). The ergodic rate is higher than the outage rate (e.g., [24, 25]) but typically requires a longer delay. The achievability of the ergodic rate in MIMO WANETs was recently discussed in detail [25]. Conveniently, the ergodic rate also lends itself better to analysis. Thus, this work focuses on the ADORP metric.

Recently, in a study that considered single antenna (SISO) WANETs using the ADORP routing performance measure, we derived a routing scheme that maximizes the network throughput based on local knowledge at each node [20]. We also conducted complete network simulations in which messages were routed from sources to destinations and showed that the ADORP provides a good characterization of the capability of the network to deliver messages from sources to destinations.

This paper extends the work on SISO routing [20] to MIMO routing. Using multiple antennas, the network gains two important capabilities: spatial multiplexing (i.e., the ability to transmit multiple data streams in parallel) and interference mitigation (i.e., the ability to combine the signals from different receive antennas such that the effect of the interference from undesired transmissions is lessened). Thus, MIMO can significantly increase the throughput of WANETs.

However, in addition to the selection of the next hop, smart routing in MIMO networks requires decisions on the number of spatially multiplexed data streams and their precoding vectors. Hence, these new capabilities significantly complicate the routing decisions. Each transmitter needs to determine the number of data streams for each transmission (while also selecting the preferred relay). This decision needs to consider the link to the selected receiver, as well as any available information related to the interference at this receiver. In addition, the interference mitigation capability increases transmitter uncertainty, since it becomes more difficult to predict the final impact of the interference on the received signal quality.

Furthermore, although increasing the number of data streams can increase the data rate of the link, it has two shortcomings: increasing the number of data streams reduces the receiver’s ability to mitigate interference and increases the effect of the transmission on other receivers in the network (even when the total transmission power is fixed). Thus, the routing decision in MIMO routing is significantly more challenging than in SISO routing.

A number of works have quantified the gain of MIMO in WANETs, in terms of the transmission-capacity metric over a bipolar network model (e.g., [26,27,28,29,30,31]). The transmission capacity calculates the number of single-hop transmissions possible in a specific area (using simple abstractions of the routing mechanism). However, the transmission capacity evaluates the maximum density of transmitters per unit area while all data streams (regardless of their gain) are constrained to the same outage probability at the same data rate. Some of these studies (e.g., [26, 28, 30]) have shown that if the transmitter density can be sufficiently increased, a single stream is preferable.

An alternative approach considered a network optimization while assuming a fixed stream transmission, i.e., all users transmit an identical number of data streams (e.g., [30, 32]). Thus far, an adaptive selection of the number of streams has not been studied analytically for routing in MIMO WANETs using HPPP modeling.

In this paper, we present a novel routing metric for MIMO WANETs based on local knowledge. The achievable rate over MIMO WANETs depends on the precoder (at the transmitter), the receive weights (at the receiver), and the number of data streams to transmit. We propose a routing scheme that adaptively selects the number of data streams jointly with the selection of the next hop relay. Unlike the single antenna case [20], the routing that maximizes performance in this scenario cannot be explicitly expressed. Instead, we use an approximation that allow us to derive a novel and efficient routing scheme. This scheme has three advantages. It has low computational complexity, it allows each transmitter to send an adaptive number of data streams, and it achieves better performance than previously published schemes.

To demonstrate the superiority of this novel routing scheme, we compare its performance to the popular nearest neighbor routing which has been tested in previous works (e.g., [12, 14]). We also compare this scheme to a single-stream transmission, which has been reported to maximize the transmission capacity (e.g., [26, 28, 30]). We show that unlike the transmission capacity in the bipolar model, when considering the actual routing, the ADORP experiences a significant degradation with single-stream transmission. Thus, the optimization of the number of streams is crucial.

The main contributions of this paper are as follows: (1) We present a novel routing scheme for MIMO WANETs that outperforms currently known schemes. The routing scheme jointly selects the physical layer parameters (the number of data streams) and the network layer parameters (the next hop relay) based on local knowledge and network statistics. (2) We show that adaptive selection of the number of data streams at each node leads to a significant performance gain over the use of identical numbers of data streams for all nodes. (3) We show that HPPP modeling is useful in providing information on the effect of non-neighbor nodes (which are not included in the transmitter’s local knowledge). Note that the analytical characterization of the signal gain in a partial-zero-forcing receiver is also important in itself, since it is applicable to other MIMO scenarios.

The rest of this paper is organized as follows. Section 1 describes methods of the structure of the analyzed WANET. Section 2 presents a performance analysis of the MIMO WANETs. Section 4 presents the novel routing scheme. Section 4 reports the numerical results, and Sect. 5 draws conclusions.

2 Methods

We consider a decentralized WANET over an infinite area, where each node is equipped with multiple antennas. The locations of the nodes are modeled by a homogeneous Poisson point process (PPP), $\Phi$, with density $\lambda$ (i.e., the number of nodes in any area of size A has a Poisson distribution with a mean of $\lambda A$).

2.1 Medium-access-control (MAC)

We use the common slotted ALOHA medium-access-control (MAC) model (e.g., [7, 10, 11, 33]) where each node chooses to be an active transmitter at a given slot with probability $p_{\mathrm {tx}}$, independently of the other nodes¹. Using the thinning property of PPP (e.g., [9]), the locations of the transmitting nodes can be represented by the PPP $\Phi _T$ of density $\lambda p_{\mathrm {tx}}$. The MAC decisions are made locally and independently. Thus, each node does not know which of the other nodes are scheduled to transmit.

2.2 Physical layer (PHY)

Considering a specific time slot, some of the nodes choose to transmit, while all the others are considered receivers. Each node is equipped with N antennas. The received vector at the ith node is given by

$$\begin{aligned} {\mathbf {y}}_i= \sum \limits _{j\in {\mathbb {N}}} r_{i,j}^{-\frac{\alpha }{2}}{\mathbf {H}}_{i,j} {\mathbf {x}}_{j} +{\mathbf {v}}_i \end{aligned}$$

(1)

where $r_{i,j}$ and ${\mathbf {H}}_{i,j}$ are the distance and the channel matrix between the jth transmitter and the ith node, respectively, ${\mathbf {x}}_{j}\in {\mathbb {C}}^{N\times 1}$ is the transmitted symbol vector of transmitter j. The noise vector at the ith node, ${\mathbf {v}}_i$, is assumed to have a proper complex Gaussian distribution with zero mean and ${\mathbb {E}}\{\mathbf{v}_i {\mathbf {v}}_i^H\}=\sigma _v^2{\mathbf {I}}_{N}$. The noise vector, ${\mathbf {v}}_i$, is independent of the transmitted symbol vector, ${\mathbf {x}}_j$. The summation is over ${\mathbb {N}}$, the set of natural numbers. The path loss exponent is denoted by $\alpha$ and satisfies $\alpha >2$. For convenience, all the main network parameters are listed in Table 1.

Table 1 Definitions of parameters and variables

We assume throughout that all entries of the channel matrices, $\{{\mathbf {H}}_{i,j}\}$, are composed of statistically independent and identically distributed (iid) standard complex Gaussian random variables. We also assume that all nodes use identical total transmission power, $\rho$, and equal power allocation for each stream.

Denoting by $K_{j}$ is the number of data streams of the jth transmitter, the transmitted vector, ${\mathbf {x}}_{j}$, is constructed by ${\mathbf {x}}_{j}=\frac{\sqrt{\rho }}{K_j}{\mathbf {F}}_j\mathbf{z}_j$, where ${\mathbf {F}}_j=[{\mathbf {f}}_{j,1},\mathbf{f}_{j,2},...,{\mathbf {f}}_{j,K_j} ]\in {\mathbb {C}}^{N\times K_j}$ is the precoding matrix of the jth transmitter. Each column in $\mathbf{F}$ is a precoding vector for a single data stream (and satisfies $\Vert {\mathbf {f}}_{j,\ell }\Vert =1, \forall \ell$). The details on the selection of the precoding vectors are given below. The data symbols of the jth transmitter are the entries of the vector ${\mathbf {z}}_j=[z_{j,1},z_{j,2},...,z_{j,K_j}]^T$, where all data symbols are independent and identically distributed (iid) standard complex Gaussian random variables with unit variance.

Considering linear receivers, the decision variable of the kth data stream from transmitter j to node i, ${\hat{z}}_{i,j,k}$, is generated by multiplying the received vector ${\mathbf {y}}_{i}$ by the weight vector ${\mathbf {w}}_{i,j,k}\in {\mathbb {C}}^{N \times 1}$, such that ${\hat{z}}_{i,j,k}={\mathbf {w}}_{i,j,k}^H {\mathbf {y}}_{i}$. The vector ${\mathbf {w}}_{i,j,k}$ is the receive weights at node i for the kth stream of the jth transmitter. This weight vector multiplies the received signal at each antenna and hence determines the effective channel gain and the interference mitigation at the receiver. We denote by

$$\begin{aligned} W_{i,j,k,\ell } = |{\mathbf {w}}_{i,j,k}^H {\mathbf {H}}_{i,j} {\mathbf {f}}_{j,\ell }|^2 \end{aligned}$$

(2)

the fading variable between the $\ell$th stream of the jth transmitter and the detector of the kth stream at the ith node.

If node i is interested in the data transmitted by transmitter j, the desired signal power of the kth stream is $S_{i,j,k} = \frac{\rho }{K_j} \cdot r_{i,j}^{-\alpha } W_{i,j,k,k}$ and the power of the interference plus noise to this stream is $J_{i,j,k} = \frac{\rho }{K_j}\cdot r_{i,j}^{-\alpha } \sum \nolimits _{\begin{array}{c} \ell =1\\ \ell \ne k \end{array}}^{K_j} W_{i,j,k,\ell } + \sum \nolimits _{\begin{array}{c} n\in \Phi _T\\ n\ne j \end{array}} \frac{\rho }{K_n}\cdot r_{i,n}^{-\alpha } W_{i,n,k}+\sigma _v^2$, where

$$\begin{aligned} W_{i,n,k} \triangleq \sum \limits _{\begin{array}{c} \ell =1 \end{array}}^{K_n} W_{i,n,k,\ell }. \end{aligned}$$

(3)

The signal-to-interference-plus-noise-ratio (SINR) at node i, for detecting the kth stream of the jth transmitter, is $\text {SINR}_{i,j,k}= \frac{S_{i,j,k}}{J_{i,j,k}}$. Assuming a near-optimal coding scheme and a long enough code word, transmitter j can reliably send information to node i at any rate up to $R_{i,j} = \sum _k R_{i,j,k}$, where the rate contribution per stream is

$$\begin{aligned} R_{i,j,k}= B \cdot \log _2\left( 1+ \text {SINR}_{i,j,k} \right) \end{aligned}$$

(4)

and B is the channel bandwidth. Note that (4) considers independent linear decoding of each data stream, where the signals from all other streams are considered as noise (better performance can be achieved using nonlinear decoding, e.g., successive interference cancelation, but such decoders are out of the scope of this work).

2.3 Routing mechanism

Each message has its source (origin) node and its destination (desired) node. The task of the routing algorithm is to forward messages from their sources to their destinations. A direct long distance transmission has significant drawbacks (e.g., high transmission power and strong interference); thus, multihop routing is preferred.

As stated above, we focus on geographic routing together with opportunistic relaying [15, 20]. Specifically, the routing decisions are performed independently at each node and are based solely on the locations of the nodes and the available CSI.

In opportunistic relaying, a transmitter first selects the next relay based on channel states and relay locations. Afterward, the transmitter searches in its buffer for the message that gains most from the use of this relay. We assume that the message buffer is long enough such that it always contains a message to a destination that is located very close to the line that extends from the source to the selected relay.

Each transmitter only has knowledge of the location of the destination node, the locations of its neighbor nodes, and the channel matrix to each neighbor. We define two nodes to be neighbors if their distance is at most $r_{\mathrm{RZ}}$. Thus, the neighborhood of node j is the set of indices: $\mathcal N_j\triangleq \left\{ i: \Vert {\mathbf {r}}_{i}-{\mathbf {r}}_{j} \Vert \le r_{\mathrm{RZ}} \right\}$ where the vector ${\mathbf {r}}_i$ contains the coordinates of the ith node. We also use the term routing zone to describe the area of all potential neighbors, i.e., the circular area of radius $r_{\mathrm{RZ}}$ that is centered at each node.

Using the notations given above, the local knowledge that is available to each node can be written as the set: ${\mathcal {M}}_j \triangleq \Big \{ ({\mathbf {r}}_i,{\mathbf {H}}_{i,j}):\forall i \in {\mathcal {N}}_j \Big \}$. This local knowledge can be obtained in various ways. For example, the location can be obtained by each node using GPS and then broadcast to its neighbors. As WANETs typically use time division duplexing (TDD), CSI to neighboring nodes can easily be obtained by pilot-based channel estimation (e.g., [36]) and using channel reciprocity (e.g., [37]).

The routing decisions are described by two functions that depend on the available knowledge, ${\mathcal {M}}_j$. The first function is the routing function, $f({\mathcal {M}}_j)$ that denotes the next relay selection of user j, i.e., $f({\mathcal {M}}_j)\in {\mathcal {N}}_j$ is the index of the node selected as the next hop. The second function is the stream number function, $\kappa ({\mathcal {M}}_j)\in \{1,2,...,N\}$ that denotes the number of data streams to transmit by user j (note that the maximum number of data streams is limited by the number of antennas, i.e., $\kappa ({\mathcal {M}}_j)\le N$).

In particular, we show that a good routing approach can be formulated by evaluating a score for each candidate relay and then choosing the candidate with the maximal score. More specifically, to determine the next relay and the number of data streams, the transmitter first calculates a routing metric (score) for each of the candidate relays. We denote the routing metric of candidate i with K data streams at transmitter j with local knowledge ${\mathcal {M}}_j$ by $m(i,{\mathcal {M}}_j,K)$. Then, the routing function $f({\mathcal {M}}_j)$ and the stream number function $\kappa ({\mathcal {M}}_j)$ are chosen as the relay index and number of data streams that maximize the routing metric, e.g.,

$$\begin{aligned} f({\mathcal {M}}_j),\kappa ({\mathcal {M}}_j) =\mathop {argmax}\limits _{i,K} m(i,{\mathcal {M}}_j,K). \end{aligned}$$

(5)

Good choices of routing metrics are discussed below.

2.4 Precoding and receive weight vectors

Since the transmitter’s local knowledge does not include the channel matrices between the selected relay and its interferers, and because the elements of these channel matrices are Gaussian iid, the transmitter has no knowledge of the ‘direction’ of the interferers. More precisely, the transmitter’s knowledge may contain hints as to the interference power, but all the interference vectors with the same norm are equally likely. Thus, local knowledge may improve the selection of the number of streams per transmission. However, given the number of transmitted data streams and the (equal) power allocation per stream, the optimal precoding does not depend on the local CSI, and is given by the eigen-beamformer (EBF).

In EBF, the precoding matrix of the jth transmitter, $\mathbf{F}_j$, is determined by the singular value decomposition (SVD) of the channel matrix to the selected receiver. Thus, if $f(\mathcal M_j)=i$, we use the SVD of ${\mathbf {H}}_{i,j}={\mathbf {U}}_{i,j} \mathbf \Lambda _{i,j}{\mathbf {V}}_{i,j}^H$, and the precoding matrix $\mathbf{F}_j$ is chosen as the first $K_j$ columns of the unitary matrix ${\mathbf {V}}_{i,j}$. Note that the selection of the precoding vectors depends solely on the channel matrix of the desired link and does not include any knowledge about the channels of the interferers.

Given the EBF precoding matrix and assuming that the receiver can estimate the interference covariance matrix, the optimal linear weight vector is the well-known minimal mean square error (MMSE) weight vector. The MMSE vector, $\mathbf{w}_{i,j,k}$, is given by

$$\begin{aligned} {\mathbf {w}}_{i,j,k} = {\mathbf {C}}_{i}^{-1} {\mathbf {H}}_{i,j} {\mathbf {f}}_{j,k} \end{aligned}$$

(6)

where ${\mathbf {C}}_{i}=\sigma _v^2 {\mathbf {I}}_{N}+\sum \limits _{\begin{array}{c} n \end{array}} \frac{\rho }{K_n} r_{i,n}^{-\alpha } {\mathbf {H}}_{i,n} {\mathbf {F}}_n {\mathbf {F}}_n^H {\mathbf {H}}_{i,n}^H$ is the noise plus the interference covariance matrix.

However, the MMSE weight vector, ${\mathbf {w}}_{i,j,k}$, does not allow for the derivation of the closed form performance measure needed for the WANET analysis, or the derivation of good routing schemes. Hence, we also consider a receiver that uses partial zero forcing (PZF). The PZF receiver represents an efficient, low complexity alternative for interference management that is amenable to analysis (e.g., [27, 30]).

The PZF nulls the interference of the most dominant interferers while ignoring the interference from all the other interferers (dominant interferers are selected typically by their distance to the receiver, the received power of the interference, or their effect on the SINR). The choice of the zero-forced interferers explicitly considers the trade-off between interference suppression and the desired signal gain.

We denote by ${\mathcal {N}}_{{\mathrm{ZF}},i,j}^{\mathrm{Inter}}$ the set of zero-forced interferers when node i tries to decode data from transmitter j. We also denote the total number of data streams to be canceled by $T_{i,j}^{{\mathrm{ZF}}}= \sum _{\begin{array}{c} n\in \mathcal N_{{\mathrm{ZF}},i,j}^{\mathrm{Inter}} \end{array}} K_n.$

Further details on the PZF receiver structure are given in ‘Appendix 1.’ Nevertheless, keep in mind that in practice, each receiver uses weight vectors according to (6) and our numerical results present findings for both types of receivers.

2.5 Routing performance

The messages are generated in a homogenous manner in all the nodes of the network. To analyze the maximal network performance, we assume that the message generation rate is high enough and that the nodes are equipped with long enough buffers such that the message buffers of all nodes are rarely empty or full.

We adopt the fast mobility model [20, 38], since it is relatively easy to analyze, and can give at least an upper bound on the achievable performance in real-life networks. This model assumes that small movements in the network will cause enough changes to the network topology such that over a long enough observation time, the network can be considered homogenous (and no node will become a network bottleneck).² It should be noted that the fast mobility model inherently allows for long message delays (Further details can be found in [20]).

While the routing mechanism aims to deliver messages from their sources to their destinations (through several hops), in this work we measure performance by analyzing a single time slot. Thus, the routing performance is assessed in terms of the density of the rate-distance product in the network, termed the Asymptotic-Density-of-Rate-Progress (ADORP) [18]. Due to network homogeneity, each transmitter can be considered a typical transmitter, and the ADORP can be evaluated by choosing one of the receivers as a probe.

Taking transmitter j as the probe transmitter (which can either transmit a new message, or relay a received message from another user) the ADORP is given by:

$$\begin{aligned} {\bar{D}}\big (f(\cdot ),\kappa (\cdot )\big ) \triangleq \lambda p_{\mathrm {tx}}(1-p_{\mathrm {tx}}) {\mathbb {E}}\left\{ r_{f({\mathcal {M}}_j),j}R_{f({\mathcal {M}}_j),j}\right\} \end{aligned}$$

(7)

where $R_{i,j}$ is the achievable rate in the link from transmitter j to node i, the density of active transmitters is $\lambda p_{\mathrm {tx}}$, and $(1-p_{\mathrm {tx}})$ is the probability that the selected relay is indeed listening. (Recall that each transmitter does not know which other nodes are scheduled to transmit at the current time slot.)

Note that if two transmitters decide to transmit to the same receiver, the two packets will be received in an interference-limited manner, i.e., the receiver decodes each message, while considering the other message as noise. Thus, we can consider each message separately, and the interference term for each message includes all other transmitted messages, regardless of their destinations.

In the next section, we analyze the PZF-based receiver performance in MIMO networks.

3 Performance analysis in MIMO networks based on PZF receivers

This section presents the performance analysis of the signal in MIMO networks with PZF receivers. We first apply the chain rule for expectations on (7):

$$\begin{aligned} {\bar{D}}\big (f(\cdot ) ,\kappa (\cdot )\big ) = \lambda B p_{\mathrm {tx}}(1-p_{\mathrm {tx}}) \cdot {\mathbb {E}}_{{\mathcal {M}}_j} \left\{ \sum _{k=1}^{\kappa ({\mathcal {M}}_j)} G_{f({\mathcal {M}}_j),j,\kappa }({\mathcal {M}}_j) \right\} \end{aligned}$$

(8)

where

$$\begin{aligned} G_{i,j,k}({\mathcal {M}}_j) \triangleq {\mathbb {E}}_{W,J|{\mathcal {M}}_j} \left\{ r_{i,j} \log _2\Big (1+\frac{ \frac{\rho }{K_j} r_{i,j}^{-\alpha } W_{i,j,k,k}}{J_{i,j,k}}\Big ) \Big |{\mathcal {M}}_j \right\} \end{aligned}$$

(9)

and ${\mathbb {E}}_{W,J|{\mathcal {M}}_j} \{\cdot \}$ is the expectation with respect to the received signal power and the interference power, given the available local knowledge.

To further simplify (9), we characterize the conditional distribution of the signal fading variables, $W_{i,j,k,k}$. Let $\gamma _{i,j,k}$ to be the kth singular value of ${\mathbf {H}}_{i,j}$, and define:

$$\begin{aligned} Y_{i,j,k}\triangleq & {} \Big | {\mathbf {w}}_{i,j,k}^H {\mathbf {H}}_{i,j} {\mathbf {f}}_{j,k} /\gamma _{i,j,k}\Big |^2=W_{i,j,k,k}/\gamma _{i,j,k}^2 . \end{aligned}$$

(10)

Thus, (9) can be rewritten as:

$$\begin{aligned} G_{i,j,k}({\mathcal {M}}_j) = {\mathbb {E}}_{W,J|{\mathcal {M}}_j} \left\{ r_{i,j} \log _2\Big (1+\frac{\frac{\rho }{K_j} r_{i,j}^{-\alpha } \gamma _{i,j,k}^2 Y_{i,j,k}}{J_{i,j,k}}\Big ) \Big |{\mathcal {M}}_j \right\} . \end{aligned}$$

(11)

The importance of (11) is that it separates the statistical behavior of the signal power and the statistical behavior of the interference power into terms that are statistically independent given ${\mathcal {N}}_{{\mathrm{ZF}},i,j}^{\mathrm{Inter}}$ (the terms $Y_{i,j,k}$ and $J_{i,j,k}$, respectively). This is shown in the following lemma which characterizes the distribution of $Y_{i,j,k}$. Note that this lemma is also applicable to PZF receivers in non-routing scenarios.

Lemma 1

Consider the decoding of the kth data stream from transmitter j, at node i, where the transmitter uses EBF and the receiver uses PZF according to (27). The distribution of $Y_{i,j,k}$ is the same for all k and depends only on $K_j$ and $T_{i,j}^{{\mathrm{ZF}}}$. If $T_{i,j}^{{\mathrm{ZF}}}=0$, then $Y_{i,j,k}=1$. If $1 \le T_{i,j}^{{\mathrm{ZF}}}\le N-K_j$ then $Y_{i,j,k}|T_{i,j}^{{\mathrm{ZF}}},K_j \sim {\mathrm{Beta}}(N-T_{i,j}^{{\mathrm{ZF}}}-(K_j-1),T_{i,j}^{{\mathrm{ZF}}})$, where ${\mathrm{Beta}}(\alpha ,\beta )$ is the beta distribution with shape parameters $\alpha$ and $\beta$. For larger values of $T_{i,j}^{{\mathrm{ZF}}}$, we get $Y_{i,j,k}=0$.

Proof

See "Appendix 2". $\square$

Thus, Lemma 1 provides a complete characterization of the statistics of the signal power, given the local knowledge, the choice of number of streams ($K_j$) and the total number of interferer streams to be canceled ($T_{i,j}^{{\mathrm{ZF}}}$). Because interferers that affect $T_{i,j}^{{\mathrm{ZF}}}$ are completely nulled by the PZF receiver, $J_{i,j,k}$ and $Y_{i,j,k}$ are indeed statistically independent given the set of zero-forced users, $\mathcal N_{{\mathrm{ZF}},i,j}^{\mathrm{Inter}}$.

The optimal routing scheme given the local knowledge is defined by the functions $f(\mathcal \cdot )$ and $\kappa (\cdot )$ that maximize the conditional ADORP (the argument of the expectation in (8)). However, unlike the single antenna case [20], Equation (8) does not lead directly to an optimal routing function. This is because $J_{i,j,k}$ depends on the number of streams selected by each of interfering users. Thus, it is not possible to consider the optimal selection function $\kappa (\cdot )$ that maximizes the expectation in (8) without considering its effect on all other users. Hence, finding the optimal routing is intractable. (By contrast, the single antenna case is much simpler, because it only has one stream).

Thus, the routing task in MIMO is much more challenging than in SISO, since the transmitter needs to jointly select the preferred relay and the number of data streams to transmit. An intuitive routing scheme can implement the popular approach of using identical numbers of data streams for all users. By limiting the set of possible functions, $\kappa (\cdot )$, the resulting ADORP is obviously a lower bound on the achievable ADORP. Hence, we set $\kappa (\cdot )=K$ where K is the number of streams used by all users. We then can find the optimal routing for a given K by explicitly evaluating the expectation in (9) given the local knowledge, ${\mathcal {M}}_j$. (In an additional stage, an offline optimization can find the number of data streams, K that gives the highest ADORP for any set of parameters $\{\alpha , \lambda ,p_{{\mathrm{tx}}},N, \rho \}$.) Note that the conditional distribution of $J_{i,j,k}|{\mathcal {M}}_j$ is known but quite complicated. Yet, the expectation can still be evaluated, for example, through Monte Carlo simulations for a given local knowledge, ${\mathcal {M}}_j$. We dub this approach the fixed statistically optimal (FSO) routing scheme and examine its performance in the numerical results section below.

As mentioned above, the FSO scheme has very high complexity, since evaluating the routing metric through the expectation in (9) is very demanding. Moreover, while the FSO aims at finding the optimal next-hop, the selection of the same number of streams for all links is very limiting.

In the next section we present a novel routing scheme that outperforms the FSO, but only requiring low computational complexity.

4 Smart routing scheme based on local knowledge

This section presents the smart routing (SR) scheme for MIMO multihop routing. The SR scheme is derived through optimization of an approximation to the conditional ADORP given the local knowledge. The derivation of this approximation is described below in several stages.

We start by simplifying the derivation, considering only part of the available knowledge. More specifically, the SR metric for a candidate node i is based solely on part of the routing zone termed the known zone (KZ). The KZ of candidate node i is the largest disk, centered at the tested relay that can fit into the routing zone. Thus, for transmitter j, the radius of the KZ of the ith tested relay is given by:

$$\begin{aligned} r_{{\mathrm{K}},i,j} \triangleq r_{{\mathrm{RZ}}}-r_{i,j}. \end{aligned}$$

(12)

We denote by $N_{{\mathrm{K}},i,j}$ the number of nodes within the KZ of the ith tested relay and by ${\mathcal {K}}_{i,j}$ the local knowledge of the nodes in the KZ of candidate node i:

$$\begin{aligned} {\mathcal {K}}_{i,j} \triangleq \Big \{ ({\mathbf {r}}_n,{\mathbf {H}}_{n,j}):\forall n \in {\mathcal {N}}_j,r_{i,n}\le r_{{\mathrm{K}},i,j} \Big \}. \end{aligned}$$

(13)

Thus, we approximate

$$G_{{i,j,k}} ({\mathcal{M}}_{j} ) \simeq {\mathbb{E}}\left\{ {r_{{i,j}} \log _{2} \left( {1 + \frac{{\frac{\rho }{{K_{j} }}r_{{i,j}}^{{ - \alpha }} W_{{i,j,k,k}} }}{{J_{{i,j,k}} }}} \right)\left| {{\mathcal{K}}_{{i,j}} } \right.} \right\}.$$

(14)

The evaluation of (14) with respect to the distribution of $J_{i,j,k}$ requires the evaluation of each possible combination of transmission decisions of each user in the KZ. This will typically be too complicated so we chose a different treatment for closer users (which can create strong interference) than for all other users.

To do so, we condition the expectation with respect to the user’s transmission decisions and then use the Jensen inequality. To control the computational complexity, we only condition on part of the users in the KZ. We define the SR-L as the SR scheme for which the number of conditioned users is:

$$\begin{aligned} N_{\mathrm {C},i,j} \triangleq \min \{ L,N_{{\mathrm{K}},i,j} \}. \end{aligned}$$

(15)

See Fig. 1 for an illustration of a simple example.

Fig. 1

Local neighborhood of the probe transmitter: each dot represents a node in the network. The red triangle is the probe transmitting node and the green star is the tested relay (node i in this example). The red dashed circle represents the routing zone with radius $r_{{\mathrm{RZ}}}$ centered at the probe transmitter. The distance between the probe transmitter and the tested relay is $r_{i,j}$. The known zone (KZ) of tested relay i is marked by the small blue dotted circle centered at the tested relay with radius $r_{{\mathrm{K}},i,j}$ (12). In this case, the KZ contains a single undesired node; thus, $N_{{\mathrm{K}},i,j}=1$

We also define the vector that contains the decisions of these nodes by ${\mathbf {b}}_{i,j}=[b_1,b_2,\ldots ,b_{N_{\mathrm {C},i,j}}]$. Each element in this vector denotes the transmission decision of a single node (i.e., $b_\ell \in \{0,1\}$) where the nodes are ordered according to their distances from node i. Note that there are $2^{N_{\mathrm {C},i,j}}$ possible vectors of ${\mathbf {b}}_{i,j}$, each having the probability:

$$\begin{aligned} {\mathbb {P}}({\mathbf {b}}_{i,j}={\underline{b}}_{i,j})=\prod _{\ell =1}^{N_{\mathrm {C},i,j}} p_{\mathrm {tx}}^{b_\ell }\cdot (1-p_{\mathrm {tx}})^{1-b_\ell }. \end{aligned}$$

(16)

where ${\underline{b}}_{i,j}=[b_1,b_2,...,b_{N_{\mathrm {C},i,j}}]$. An example of the permutations with $N_{\mathrm {C},i,j}=2$ is given below.

Next, we use the chain rule for expectations and the Jensen inequality to further simplify the approximation³:

$$\begin{aligned} G_{i,j,k}( {\mathcal {M}}_{j})& \simeq {} {\mathbb {E}}\Big \{ {\mathbb {E}} \Big \{ r_{i,j} \log _2\Big (1+\frac{\frac{\rho }{K_j} r_{i,j}^{-\alpha } W_{i,j,k,k}}{J_{i,j,k}}\Big ) \Big | {\mathbf {b}}_{i,j} , {\mathcal {K}}_{i,j} \Big \}\Big \} \\ & \simeq {} {\mathbb {E}}_{{\mathbf {b}}_{i,j}} \Big \{ r_{i,j} \log _2\Big (1+\tfrac{\frac{\rho }{K_j} r_{i,j}^{-\alpha } W_{i,j,k,k}}{{\mathbb {E}}\{J_{i,j,k}|{\mathbf {b}}_{i,j},{\mathcal {K}}_{i,j}\}}\Big ) \Big | r_{i,j},{\mathbf {H}}_{i,j} \Big \}. \end{aligned}$$

(17)

At this stage, we need to consider the receiver operation. As stated above, the receiver typically uses an MMSE receiver. However, to allow for a tractable derivation, we assume a PZF receiver. To optimize the receiver, we need to consider all possible choices of zero-forced users. For simplicity, we consider at most one zero-forced interferer. We denote the number of zero-forced users by $z\in \{0,1\}$. That is, if $z=0$ then $T_{i,j}^{{\mathrm{ZF}}}=0$, and the receiver only uses the EBF. If $z=1$ we assume that the receiver zero-forces a single interferer. As the transmitter has no knowledge of the channel matrices between the interferers and the receiver, it will assume that the receiver zero-forces the nearest active interferer.

Using these approximations, we can evaluate the effect of the interference quite easily. The denominator in the log function in the last line of (17) can be written as:

$$\begin{aligned} {\tilde{J}}_{i,j,k}^z({\underline{b}}_{i,j},{\mathcal {K}}_{i,j}) & \triangleq {} {\mathbb {E}}\{J_{i,j,k}|{\mathbf {b}}_{i,j},{\mathcal {K}}_{i,j}\} \\ &= {} {\bar{J}}_{i}(r_{{\mathrm{K}},i,j})+\sum _{\ell =1}^{N_{{\mathrm{K}},i,j}} r_{i,\ell }^{-\alpha } \cdot e_{\ell ,z}({\underline{b}}_{i,j},N_{\mathrm {C},i,j}) \end{aligned}$$

(18)

where the parameter $e_{\ell ,z}({\underline{b}}_{i,j},n)$ is the activation weight for node $\ell$, given the SR-L parameter, n, the activation parameter, z, and the vector of states of the nodes within the routing zone, ${\underline{b}}_{i,j}$. Recall that the nodes are ordered according to their distances from the ith tested relay, and $r_{{\mathrm{K}},i,j}$ is the radius of the KZ (12). For an activation vector ${\underline{b}}$, the parameter $e_{\ell ,z}({\underline{b}},n)$ is given by:

$$\begin{aligned} e_{\ell ,z}({\underline{b}},n) = {\left\{ \begin{array}{ll} p_{{\mathrm{tx}}} &{} \ell>n \\ 0 &{} \ell \le n, b_\ell =0 \\ 1-z &{} \ell \le n , b_\ell =1, \sum _{k=1}^{\ell -1}b_k=0 \\ 1 &{} \ell \le n , b_\ell =1, \sum _{k=1}^{\ell -1}b_k>0 \\ \end{array}\right. }. \end{aligned}$$

(19)

Stated in words, the first condition in (20) considers the nodes within the KZ that are not taken into consideration while evaluating the SR with parameter L. Hence, in (1819), the expected power of these nodes depends on the ALOHA transmission probability. The second line considers the nodes in the KZ that are assumed to be receivers (with $b_\ell =0$) and hence do not induce interference. The third and fourth lines indicate that all nodes with $b_\ell =1$ interfere with the reception except for the nearest transmitter that will be canceled if $z=1$. We further assume that this nearest interferer transmits N/2 streams⁴. Thus, we assume that in the SR scheme, the PZF scheme ($z=1$) is supported only for $K_j\le N/2$. Note that in the EBF case (i.e., $z=0$) the third and the fourth rows in (20) are identical.

The term $\bar{J}_{i}(r_{{\mathrm{K}},i,j})$ denotes the expected interference of the (unknown) transmitters outside the KZ. The average interference plus noise generated outside of a circle with radius r centered at the ith tested next hop is given by [39, eq. (14)]:

$$\begin{aligned} {\bar{J}}_{i}(r) = \frac{2\pi \lambda }{(\alpha -2)}r^{2-\alpha }{\mathbb {E}}\{W_{i,n,k}\} {\mathbb {E}}\{\tfrac{\rho }{K_j}\} +\sigma _v^2 \end{aligned}$$

(20)

and recall that in our case ${\mathbb {E}}\{W_{i,n,k}\} \mathbb E\{\tfrac{\rho }{K_j}\}=\rho$. It is worth noting that (21) can also be estimated from the received signal at each receiver and then broadcast to the neighbors even without knowing the density, $\lambda$.

To simplify the evaluation of the desired signal power term in the SR metric, we approximate the Beta r.v. $Y_{i,j,k}$ by its mean. For $z=0$ we have $T_{i,j}^{{\mathrm{ZF}}}=0$ and hence we use ${\mathbb {E}}\{Y_{i,j,k}\}=1$. For $z=1$ (PZF receiver), we approximate the desired signal loss by ${\mathbb {E}}\{Y_{i,j,k}\} = \frac{N-T_{i,j}^{{\mathrm{ZF}}}-(K_j-1)}{N-(K_j-1)}$ . By further assuming that $T_{i,j}^{{\mathrm{ZF}}}=N/2$, we can replace this expectation in the PZF case by:

$$\begin{aligned} {\bar{Y}}(N,K_j)\triangleq \frac{0.5 N-(K_j-1)}{N-(K_j-1)} . \end{aligned}$$

(21)

The joint selection of the SR routing function and the SR stream function can be summarized as:

$$\begin{aligned} f_{_{\mathrm{SR}}}({\mathcal {M}}_j) , \kappa _{_{\mathrm{SR}}} ({\mathcal {M}}_j) = \mathop {argmax}\limits _{\begin{array}{c} i\in {\mathcal {N}}_j \\ 1\le K\le N \end{array}} m_{_{\mathrm{SR}}}(i,{\mathcal {M}}_j,K) \end{aligned}$$

(22)

where

$$\begin{aligned} m_{_{\mathrm{SR}}}(i,{\mathcal {M}}_j,K)&\triangleq r_{i,j} \cdot \sum _{k=1}^{K}{\mathbb {E}}_{{\mathbf {b}}_{i,j}}\Big \{ \log _2 \Big (1+\frac{\rho }{K} r_{i,j}^{-\alpha }\gamma _{i,j,k}^2 \\&\nonumber \cdot \max \left\{ \tfrac{1 }{{\tilde{J}}_{i,j,k}^0({\mathbf {b}}_{i,j},{\mathcal {K}}_{i,j})} , \tfrac{{\bar{Y}}(N,K) \cdot {\mathbf {1}}_{\{K \le N/2\}}}{{\tilde{J}}_{i,j,k}^1({\mathbf {b}}_{i,j},{\mathcal {K}}_{i,j})}\right\} \Big |{\mathcal {K}}_{i,j} \Big \} \end{aligned}$$

(23)

and ${\mathbf {1}}_{\{A\}}$ is the indicator function that is equal to 1 if condition A is true. The function $\max \{a,b\}$ in (24) chooses between the EBF receiver or the PZF receiver. The EBF receiver is allowed in all cases, while the PZF receiver is allowed only for $K\le N/2$.

To better explain the routing metric, note that $r_{i,j}$ and $\gamma _{i,j,k}^2$ are obtained from the local knowledge on the tested ith relay, ${\bar{Y}}(N,K_j)$ represents the expected power loss due to PZF and ${\tilde{J}}_{i,j,k}^z({\mathbf {b}}_{i,j},{\mathcal {K}}_{i,j})$ represents the expected interference power for each setting. This latter term is composed of 2 parts (1819). One part is evaluated using local knowledge at the transmitter, while the other part, ${\bar{J}}_{i}(r_{{\mathrm{K}},i,j})$, uses statistical modeling to characterize the expected interference from nodes outside the routing zone.

Recall that the evaluation of ${\bar{J}}_{i}(r_{{\mathrm{K}},i,j})$ is the only part of this work that uses the PPP modeling of the network. Using PPP modeling we can compute the expected interference power from nodes outside a disk, as a function of the disk radius. As mentioned above, this function can also be locally estimated at each node and broadcast to its neighbors.

In words, the SR routing metric, $m_{_{\mathrm{SR}}}(i,\mathcal M_j,K)$, is the score for each candidate node. The SR routing function, $f_{_{\mathrm{SR}}}({\mathcal {M}}_j)\in {\mathcal {N}}_j$ and the SR stream function, $\kappa _{_{\mathrm{SR}}}\in \{1,2,...,N\}$, are the index of the node and the number of data streams that maximize this metric. Note that $r_{i,j}$ and $\gamma _{i,j,k}$ in (24) are known given ${\mathcal {K}}_{i,j}$.

Algorithm 1 illustrates the simplicity of the evaluation of the SR scheme.

To demonstrate the simplicity of this computation, we present a brief example for the case where $L=2$ and the KZ contains 3 nodes (thus $N_{{\mathrm{K}},i,j}=3$). Hence, by (15), $N_{\mathrm {C},i,j}=2$ and ${\mathbf {b}}_{i,j}=[b_1,b_2]$. To evaluate the SR metric in this case, we use the following table:

where the columns correspond to the $2^{N_{\mathrm {C},i,j}}=4$ possible combinations for $b_1$ and $b_2$. In the first combination ($[b_1,b_2]=[0,0]$) both interferers are idle, and the PZF receiver does not cancel any transmitter. Because Node 1 is closer to the tested relay than Node 2, for combinations [1, 0] and [1, 1] the receiver cancels Node 1, and for combination [0, 1] the receiver cancels Node 2.

Clearly, the complexity of the SR can be controlled by the L-parameter. Setting $L=\infty$ allows conditioning on all nodes in the KZ, while for any $L<\infty$ the computational complexity is lower (and bounded). In the numerical results section, we demonstrate the performance of the SR scheme, with parameters $L=1$ and $L=\infty$.

5 Numerical results

This section presents the simulation results that demonstrate the efficiency of the proposed routing schemes. We use two types of simulations. Most of the simulations evaluate a single time slot and assess the ADORP. We also present a complete network simulation, where messages pass from sources to destinations through multiple hops over many time slots.

In all the ADORP simulations, the number of nodes has a Poisson distribution with an average of $N_{\mathrm{nodes}}=200$, and the nodes are uniformly distributed in a disk with an area of size $N_{\mathrm{nodes}}/\lambda$, centered at the probe transmitter. We also used the bias correction in [39]. The transmitted power, $\rho$, was set to $\rho =1$, the thermal noise variance to $\sigma ^2_v = 0.5$ and the node density was $\lambda =2.5$ [nodes/$\hbox {km}^2$]. The radius of the routing zone was set such that the average number of nodes within the routing zone was $\lambda \pi r_{{\mathrm{RZ}}}^2=10$. All the results are averaged over 1000 network realizations.

Figure 2 depicts the normalized ADORP (ADORP/B) as a function of the ALOHA transmission probability, $p_{{\mathrm{tx}}}$, for a system with a path loss exponent of $\alpha =2.7$ and $\alpha =3.3$, where each node is equipped with $N=2$ antennas. This is the only figure in which we present performance when all receivers use the PZF weights (27). (All the other figures present the performance with MMSE receivers.) The figure depicts the performance of the common nearest neighbor (NN) routing, the FSO routing, and the novel SR routing.

Fig. 2

PZF receiver: Normalized ADORP versus ALOHA transmission probability for the SR, FSO and NN schemes, where $N=2, \pi r_{{\mathrm{RZ}}}^2=10$ and $\alpha =\{2.7,3.3\}$

Both the NN and the FSO schemes take the traditional approach of setting an identical number of data streams to all transmitters. For the results in Fig. 2, the optimal number of data streams for each transmission probability was determined through offline optimization. The NN scheme does not use local knowledge and always selects the nearest neighbor to be the next hop.

The FSO scheme (defined at the end of Sect. 2) requires the evaluation of the expectation in (11), which is far from trivial. While this evaluation is not feasible in practical systems, in this numerical study we evaluated this expectation through MC simulations for the given local knowledge, ${\mathcal {M}}_j$. That is, at each step we generated many realizations of a random network around the transmitter, such that the local knowledge was respected and the PPP distribution was used outside the routing zone (e.g., [20]).

Both the SR and the FSO exhibited significant advantages compared to the common NN scheme. Thus, the use of local knowledge contributes significantly to the selection of the next hop. The gain of SR over FSO is small; however, it should be kept in mind that the FSO uses an exact optimization after limiting all users to utilize the same number of data streams. The fact that it outperformed the FSO using an approximated method, shows the importance of the adaptive selection of the number of streams.

Furthermore, the FSO scheme is not practical given its high complexity. By contrast, the SR routing scheme (23) requires much lower computational complexity and yields higher performance.

Figure 3 depicts the normalized ADORP (ADORP/B) as a function of the ALOHA transmission probability, $p_{{\mathrm{tx}}}$, for the same system setup, except for the use of MMSE receivers (6). When using the MMSE receive weights, the achievable performance was higher than for the PZF receiver, and the disparities between the different schemes changed slightly. Again, the SR and FSO routing schemes outperformed the NN, showing the advantage of the use of local knowledge. In this case the difference between FSO and SR was negligible.

Fig. 3

MMSE receiver: Normalized ADORP vs. ALOHA transmission probability for various routing schemes, where $N=2, \pi r_{{\mathrm{RZ}}}^2=10$ and $\alpha =\{2.7,3.3\}$

Figure 4 depicts the normalized ADORP (ADORP/B) as a function of the ALOHA transmission probability, $p_{{\mathrm{tx}}}$, when each node is equipped with $N = 4$ antennas, and a path loss exponent of 2.7 and 3.3. Again, the performance gap between the two versions of the SR scheme, $L=\{1,\infty \}$ was negligible. This again confirms the attractiveness of SR-1.

Fig. 4

MMSE receiver: Normalized ADORP vs. ALOHA transmission probability for various routing schemes, where $N=4, \pi r_{{\mathrm{RZ}}}^2=10$ and $\alpha =\{2.7,3.3\}$

In the $N=4$ case, the maximum performance ratio between the SR scheme and the NN scheme was 1.12 and 1.10 for $\alpha =2.7$ and $\alpha =3.3$, respectively. Compared to Fig. 3, the gain of SR and FSO over NN was much smaller for smaller number of antennas and a lower path loss exponent, $\alpha$.

With a smaller number of antennas, the receiver is more sensitive to interference. This makes it more important that the probe transmitter should be aware of the interference and take it into account. Furthermore, with a large number of antennas, the variations of the desired signal become smaller (also known as channel hardening). Thus, the probability of having a ‘very good’ channel or a ‘very bad’ channel decreases and the advantage of opportunistic routing vanishes.

For a small path loss exponent, more interferers affect the receiver’s performance. Thus, the receiver’s ability to handle interference is not enough, and the transmitter has more incentive to avoid interference using knowledge of the neighbor locations.

Figure 4 also compares our routing schemes to the optimal ADORP with single-stream transmission (which was shown to maximize the transmission capacity; e.g., [26, 28, 30]). This curve is termed $\hbox {FSO}_1$ and its performance was even worse than the NN scheme. This illustrates the importance of the optimization of the number of data streams, which was implemented in all the other curves in this figure. Recall that the SR scheme performs an inherent optimization of the number of data streams, while the FSO and the NN in these simulations require offline optimization.

The optimization of the number of data streams is further illustrated in Fig. 5, which depicts the optimal average number of data streams vs. the ALOHA transmission probability for $N=4$ and $N=8$, when the path loss exponent is $\alpha =3.3$. For the SR-1 scheme, the figure presents the average number of data streams selected by the users in the system, averaged over all Monte Carlo simulations. For the FSO and the NN schemes, the number of data streams is fixed throughout the network. However, to optimize the network, we performed offline optimization: we ran the simulation for each possible number of streams and chose the value that maximized the average ADORP. As can be seen, the average number of data streams decreased as a function the ALOHA transmission probability. This was expected since the number of interferers and the total interferers’ power increase with the transmission probability, and forces the transmission to focus its energy on a smaller number of data streams. Note that the SR scheme enjoys a continuous change in the average number of data streams (and, of a course, a different and optimized choice for each transmitter).

Fig. 5

Selected number of streams vs. ALOHA transmission probability for various routing schemes, where $N=\{4,8\}, \pi r_{{\mathrm{RZ}}}^2=10$ and $\alpha =3.3$

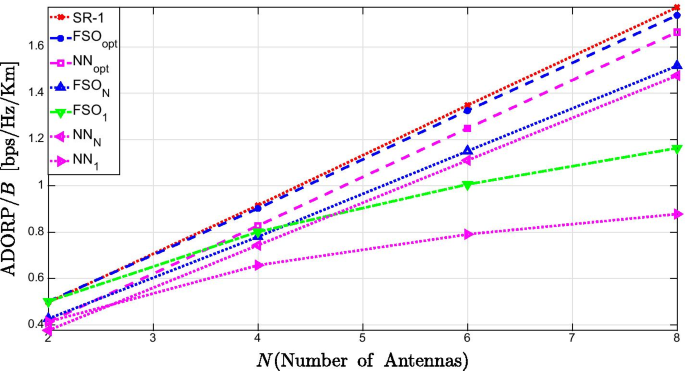
Figure 6 depicts the highest ADORP as a function of the number of antennas, $N\in \{2,3,4,6,8\}$ for a system with a path loss exponent of 2.7 and ALOHA transmission probability, $p_{{\mathrm{tx}}}=0.25$. We compare the SR scheme to the modified version of Louie et al. [26] who found that a single-stream transmission has a superiority of over a full mode transmission in certain scenarios. Specifically, Fig.6 presents the modifications of the FSO scheme and the NN scheme that use fixed stream transmission, and either send 1 or N data streams. Figure 6 shows again the advantage of the adaptive stream transmission that brings the performance gain at very low complexity.

Fig. 6

Normalized ADORP vs. $N=\{2,3,4,6,8\}$ (number of antennas) for a system with $p_{{\mathrm{tx}}}=0.25$, $\pi r_{{\mathrm{RZ}}}^2=10$ and $\alpha =2.7$. The figure depicts the curves of the SR-1 scheme, the optimal FSO scheme ($\hbox {FSO}_{{\mathrm{opt}}}$) and the FSO schemes for FSO with single-stream transmission ($\hbox {FSO}_1$) and full-stream transmission ($\hbox {FSO}_N$), the optimal NN scheme ($\hbox {NN}_{{\mathrm{opt}}}$) and the NN schemes with single-stream transmission ($\hbox {NN}_1$) and full-stream transmission ($\hbox {NN}_N$)

Correspondingly, Fig. 7 presents the optimal number of streams that achieved the best performance in Fig. 6. Inspecting the results in Fig. 7, the SR scheme allows a dynamic selection of the number of data streams, which in average, may be irrational number. However, both the FSO and the NN schemes need to select an integer. In this scenario, the number of data streams used by the NN schemes was half the number of antennas (0.5N) while the novel SR scheme used 0.6N. This increase in the number of data streams is part of the reason for the SR performance advantage. The FSO scheme used approximately the same number of data streams as the SR scheme, but was forced to settle to the nearest integer at each data point.

Fig. 7

Optimal number of streams (highest ADORP from Fig. 6) versus $N=\{2,3,4,6,8\}$ (number of antennas) for a system with $p_{{\mathrm{tx}}}=0.25,\pi r_{{\mathrm{RZ}}}^2=10$ and $\alpha =2.7$. The figure depicts the curves of the SR-1 scheme, the optimal FSO scheme ($\hbox {FSO}_{{\mathrm{opt}}}$) and the optimal NN scheme ($\hbox {NN}_{{\mathrm{opt}}}$)

To further demonstrate the advantages of our novel routing scheme, we performed a complete network simulation in which messages were routed from sources to destinations according to the mechanism described in Subsection II-C (also see in [20]). The simulation included an average of 100 nodes uniformly distributed over a simulation area of $1000\,\hbox {m}^2$ where each node was equipped with two antennas. We considered that each node had a home location and an iid mobility model (e.g., [38]). The mobility model followed a symmetric normal distribution with variance of 2.84m. This represents low mobility that is only sufficient to unravel network bottlenecks. We chose a simulation length that depends on $p_{\mathrm{tx}}$ according to $t_s = 100/p_{\mathrm{tx}} + 8 \cdot 100$ slots. Thus, each simulation was run for a duration of $t_s \cdot T$ seconds, where T was the duration of a time slot. Each message contained 20BT bits where B was the bandwidth.

The simulation utilizes a hybrid automatic repeat request (HARQ) scheme. Thus, if a message is not decoded successfully, the receiver will store the received symbols and wait for another retransmission. Once the routing algorithm decides to send a message again to the same relay, the transmitter will transmit additional parity bits of the same message and will continue with the same approach until the message is successfully decoded. Thus, all messages in this simulation are eventually decoded, and we have no outage events. (The messages are not subjected to any delay constraint.)

The performance was measured by the normalized density of end-to-end rate distance metric (eeR) [18], where we summed the distance-bit product for all successful messages, and divided by the size of the area-time and by the bandwidth. The normalized eeR metric is given by [18, equation (9)]: ${\mathrm{eeR}} \triangleq \frac{1}{T_{\mathrm{T}}A\cdot B}\sum _m L_m M \cdot i_m$ where A is the simulation area, $T_{\mathrm{T}} = t_s \cdot T$ is the simulation time, $M = 20BT$ is the number of bits per message, $i_m$ is the successful delivery indicator, and $L_m$ is the distance between source and destination at the time of message generation. Using the ergodic rate approach, a message is assumed to be successfully decoded if it accumulates mutual information that is equal or larger than K in each of its hops. The summation is over all the messages in the network. Figure 8 depicts the normalized eeR as a function of the ALOHA transmission probability, $p_{\mathrm{tx}}$, for a system with a path loss exponent of 3.3. We used the parameters of the SR to be the smallest known zone (KZ) with $L=1$. Figure 8 shows the eeR performance of the NN scheme and the SR scheme. It also depicts the relevant normalized ADORP for each scheme. As can be seen, the end-to-end performance indeed converged to the normalized ADORP. (The difference is due to the fact that each hop distance of the routing in eeR had a deviation from the line between the transmitter and the destination.) In addition, as expected from the previous results, the SR scheme significantly outperformed the NN scheme. The gains ranged from $12\%$ to $30\%$.

Fig. 8

Density of the normalized end-to-end rate distance metric (eeR) as a function of the ALOHA transmission probability in a full network simulation where each node was equipped with $N=2$. The figure depicts the performance of the SR and the NN routing schemes, for a path loss exponent of $\alpha =3.3$

6 Conclusions

In this paper, we proposed a novel routing scheme for multihop MIMO WANETs. This smart routing (SR) scheme works in a decentralized manner where each decision in each node is based solely on its local knowledge. The SR scheme takes into account both channel state information and geographic knowledge (the location of the nodes), all at low computational complexity.

The proposed approach adaptively selects the number of data streams for each transmission. This adaptive selection was shown to even outperform the ‘optimal’ traditional routing (where the number of data streams is fixed for all transmissions). This combination of robust performance with low implementation complexity makes the SR scheme very attractive for practical routing in MIMO WANETs.

We also presented a performance analysis of PZF receivers in general MIMO networks that can serve to characterize the signal gain.

This work considered the transmission of data streams with equal power. Future work may study the performance improvement when the transmitter optimizes the power allocation between the data streams. Although equal power allocation was shown to be close to optimal in Gaussian noise [40], this was not shown for the multiuser MIMO interference channel. Hence, such study in the context of MIMO routing might yield interesting insights.

Appendices

Appendix 1: Partial-zero-forcing (PZF) receiver structure

This appendix presents the PZF receiver structure. We assume that each receiver knows which nodes transmit at each slot, and can measure their channel matrices and uses this knowledge for interference cancelation. We define ${\mathbf {H}}_{{\mathrm{null}},i,j}$ as the effective channel matrix of receiver i that contains its interferers. Specifically, the columns of $\mathbf{H}_{{\mathrm{null}},i,j}$ are $\{{\mathbf {H}}_{i,n}\mathbf{F}_n\}_{n\in {\mathcal {N}}_{{\mathrm{ZF}},i,j}^{\mathrm{Inter}}}$. The number of columns of ${\mathbf {H}}_{{\mathrm{null}},i,j}$ is $T_{i,j}^{{\mathrm{ZF}}}$ (which is the total number of inter-user streams to be canceled). Thus, the dimensions of ${\mathbf {H}}_{{\mathrm{null}},i,0}$ are $N\times T_{i,j}^{{\mathrm{ZF}}}$.

When trying to decode the kth stream at receiver i, the receiver also nulls the other $(K_j-1)$ streams of the probe transmitter. It is important to note that if $T_{i,j}^{{\mathrm{ZF}}}+K_j>N$, the receiver cannot decode its messages. These $(K_j-1)$ streams induce intra-stream interference. By adding the $(K_j - 1)$ intra-streams, the interfering signals are spanned by the effective channel matrix:

$$\begin{aligned} \tilde{{\mathbf {H}}}_{{\mathrm{null}},k}= \left[ {\mathbf {H}}_{i,j}{\mathbf {F}}_{j,k},{\mathbf {H}}_{{\mathrm{null}},i,j}\right] \end{aligned}$$

(24)

where ${\mathbf {F}}_{j,k}\in {\mathbb {C}}^{N\times (K_j-1)}$ denotes the matrix ${\mathbf {F}}_j$ without its kth column. The projection onto the null space of $\tilde{{\mathbf {H}}}_{{\mathrm{null}},k}$ is given by the matrix:

$$\begin{aligned} {\mathbf {P}}_{i,j,k} = {\mathbf {I}}_{N}- \tilde{{\mathbf {H}}}_{{\mathrm{null}},k} \left( \tilde{{\mathbf {H}}}_{{\mathrm{null}},k}^H\tilde{{\mathbf {H}}}_{{\mathrm{null}},k}\right) ^{-1} \tilde{{\mathbf {H}}}_{{\mathrm{null}},k}^H \end{aligned}$$

(25)

and the normalized PZF weight vector is:

$$\begin{aligned} {\mathbf {w}}_{i,j,k} = \frac{{\mathbf {P}}_{i,j,k} {\mathbf {H}}_{i,j}{\mathbf {f}}_{j,k}}{\Vert {\mathbf {P}}_{i,j,k}{\mathbf {H}}_{i,j}{\mathbf {f}}_{j,k}\Vert }. \end{aligned}$$

(26)

This weight vector satisfies ${\mathbf {w}}^{H}_{i,j,k} {\mathbf {H}}_{i,j} {\mathbf {F}}_{n}={\mathbf {0}}^T$ for $n \in \mathcal N_{{\mathrm{ZF}},i,j}^{\mathrm{Inter}}$ (of course $n\ne j$) and $\mathbf{w}^{H}_{i,j,k} {\mathbf {H}}_{i,j} {\mathbf {f}}_{j,\ell }=0$ for all $\ell \ne k$.

The rank of the projection matrix is $\max \{M,0\}$ where:

$$\begin{aligned} M= N-T_{i,j}^{{\mathrm{ZF}}}-(K_j-1). \end{aligned}$$

(27)

Therefore, if M is not positive, the PZF precoding is not feasible and the receiver is idle for this time slot.

Appendix 2: Proof of Lemma 1

This appendix evaluates $Y_{i,j,k}$ (10) which depends on the desired fading variable, $W_{i,j,k,k}=\left| {\mathbf {w}}^{H}_{j,k} {\mathbf {H}}_{i,j} \mathbf{f}_{j,k}\right| ^2$, using the PZF receiver and BF precoding. In this section we take transmitter 0 as the probe transmitter. We use $Y_{i,0,k}$ to denote the r.v. that describes the desired fading from the probe transmitter at the ith candidate relay. The PZF received vector, ${\mathbf {w}}_{i,0,k}$, depends on $\mathbf{P}_{i,0,k}$ (26) the matrix that projects outside the null space of $\tilde{{\mathbf {H}}}_{{\mathrm{null}},k}$ (25) (the effective channel matrix of the interfering signals). In the first step, we simplify the term of $W_{i,0,k,k}$ into a multiplication of the desired singular value $\times$ scalar. In the second step, we find the distribution of this scalar. We use manipulations from linear algebra.

In the first step, we aim at simplifying $\tilde{\mathbf{H}}_{{\mathrm{null}},k}$ and thus inspect its structure in (25) and use SVD: ${\mathbf {H}}_{i,0} ={\mathbf {U}}_{i,0}\mathbf \Lambda _{i,0} {\mathbf {V}}_{i,0}^H$, in which ${\mathbf {U}}_{i,0}$ and ${\mathbf {V}}_{i,0}$ are unitary matrices. Thus, the matrix $\tilde{{\mathbf {H}}}_{{\mathrm{null}},k}$ (25) can be written as

$$\begin{aligned} \tilde{{\mathbf {H}}}_{{\mathrm{null}},k}&= {\mathbf {U}}_{i,0}\left[ {\mathbf {U}}_{i,0}^H{\mathbf {H}}_{i,0}{\mathbf {F}}_{0,k}, {\mathbf {U}}_{i,0}^H {\mathbf {H}}_{{\mathrm{null}},i,0}\right] = {\mathbf {U}}_{i,0} \left[ {\mathbf {B}}_k ,{\mathbf {G}} \right] \end{aligned}$$

(28)

where we define ${\mathbf {B}}_k \triangleq {\mathbf {U}}_{i,0}^H {\mathbf {H}}_{i,0} {\mathbf {F}}_{0,k}$ and ${\mathbf {G}}\triangleq {\mathbf {U}}_{i,0}^H\mathbf{H}_{{\mathrm{null}},i,0}\in {\mathbb {C}}^{N\times T_{i,j}^{{\mathrm{ZF}}}}$. Since the precoding matrix ${\mathbf {F}}_{0,k}$ is chosen as the $K_j$ left singular vectors of the unitary matrix ${\mathbf {V}}_{i,j}$ without the kth vector, the resulting matrix ${\mathbf {B}}_k$ is a $N\times (K_0-1)$ matrix in which each column only contains a single nonzero element. These nonzero elements are the singular values of the matrix ${\mathbf {H}}_{i,0}$ (given by the diagonal elements of $\mathbf \Lambda _{i,0}$). It should be emphasized once again that ${\mathbf {B}}_k$ does not contain the kth column that corresponds to the kth singular value. For example, matrix ${\mathbf {B}}_2$, for $N=4$ and $K_0=3$, has dimensions of ${\mathbf {B}}_2 \in {\mathbb {R}}^{4 \times 2}$ where all the elements are zero except two elements: $[{\mathbf {B}}_2]_{1,1}=\gamma _{i,0,1}$ and $[\mathbf{B}_2]_{3,2}=\gamma _{i,0,3}$.

Now, setting (),e:tildePspsd,k,e:tildePspsd,k,e:tildePspsd,k,e:tildePspsd,k in ${\mathbf {P}}_{i,0,k}$ (26) the projection matrix onto the null space of $\tilde{\mathbf ,e:Hspsnull,k,e:tildePspsd,kH}_{{\mathrm{null}},k}$ can be rewritten as:

$$\begin{aligned} {\mathbf {P}}_{i,0,k} = {\mathbf {U}}_{i,0} \tilde{{\mathbf {P}}}_{i,k} {\mathbf {U}}_{i,0}^H \end{aligned}$$

(29)

where

$$\widetilde{{\mathbf{P}}}_{{i,k}} \triangleq {\mathbf{I}}_{N} - \left[ {{\mathbf{B}}_{k} ,{\mathbf{G}}} \right]\left[ {\left[ {\begin{array}{*{20}l} {{\mathbf{B}}_{k}^{H} } \\ {{\mathbf{G}}^{H} } \\ \end{array} } \right]\left[ {{\mathbf{B}}_{k} ,{\mathbf{G}}} \right]} \right]^{{ - 1}} \left[ {\begin{array}{*{20}l} {{\mathbf{B}}_{k}^{H} } \\ {{\mathbf{G}}^{H} } \\ \end{array} } \right].$$

(30)

Substituting (29) into the PZF received vector for the kth stream in (27), and noting that

$$\begin{aligned} {\mathbf {P}}_{i,0,k} {\mathbf {H}}_{i,0}{\mathbf {f}}_{0,k}= & {} {\mathbf {U}}_{i,0} \tilde{{\mathbf {P}}}_{i,k} {\mathbf {U}}_{i,0}^H{\mathbf {U}}_{i,0}\mathbf \Lambda _{i,0} {\mathbf {V}}_{i,0}^H{\mathbf {f}}_{0,k} = {\mathbf {U}}_{i,0}\tilde{{\mathbf {P}}}_{i,k} {\mathbf {e}}_{k,N}\cdot \gamma _{i,0,k} \end{aligned}$$

(31)

where we used ${\mathbf {U}}_{i,0}^H{\mathbf {U}}_{i,0} \mathbf \Lambda _{i,0} {\mathbf {V}}_{i,0}^H{\mathbf {f}}_{0,k}=\mathbf \Lambda _{i,0} {\mathbf {V}}_{i,0}^H{\mathbf {f}}_{0,k}=\gamma _{i,0,k} {\mathbf {e}}_{k,N}$, and ${\mathbf {e}}_{k,N}$ is the column vector of length N in which the kth element is 1 and all other elements are 0. Hence, (27) becomes:

$$\begin{aligned} {\mathbf {w}}_{i,0,k} = \frac{{\mathbf {U}}_{i,0}\tilde{{\mathbf {P}}}_{i,k} {\mathbf {e}}_{k,N}}{\sqrt{ {\mathbf {e}}_{k,N}^H\tilde{{\mathbf {P}}}_{i,k} {\mathbf {e}}_{k,N}}} \end{aligned}$$

(32)

where (32) uses basic properties of the projection matrix: $\tilde{{\mathbf {P}}}_{i,k}^H = \tilde{\mathbf{P}}_{i,k}$ and $\tilde{{\mathbf {P}}}_{i,k}^2 = \tilde{{\mathbf {P}}}_{i,k}$.

Substituting the PZF receives weight vector (32) into the desired fading power:

$$\begin{aligned} W_{i,0,k,k}= & {} \left| {\mathbf {w}}^{H}_{i,0,k} {\mathbf {H}}_{i,0} {\mathbf {f}}_{0,k}\right| ^2 = \left| \frac{{\mathbf {e}}_{k,N}^H\tilde{{\mathbf {P}}}_{i,k} {\mathbf {U}}_{i,0}^H}{\sqrt{ {\mathbf {e}}_{k,N}^H\tilde{{\mathbf {P}}}_{i,k} {\mathbf {e}}_{k,N}}} {\mathbf {H}}_{i,0} {\mathbf {f}}_{0,k}\right| ^2 \nonumber \\= & {} \left| \frac{{\mathbf {e}}_{k,N}^H \tilde{{\mathbf {P}}}_{i,k} {\mathbf {e}}_{k,N} \gamma _{i,0,k}}{\sqrt{ {\mathbf {e}}_{k,N}^H\tilde{{\mathbf {P}}}_{i,k} {\mathbf {e}}_{k,N}}} \right| ^2 = \gamma _{i,0,k}^2{\mathbf {e}}_{k,N}^H \tilde{{\mathbf {P}}}_{i,k}{\mathbf {e}}_{k,N}. \end{aligned}$$

(33)

In words, we simplified the term of the desired fading power into a multiplication of the desired singular value, $\gamma _{i,0,k}^2$, times the scalar, ${\mathbf {e}}_{k,N}^H \tilde{{\mathbf {P}}}_{i,k}\mathbf{e}_{k,N}$. This completes the first step of this appendix. In the following, we evaluate the distribution of this latter scalar.

This evaluation is not straightforward because the projection matrix $\tilde{{\mathbf {P}}}_{i,k}$ (30) is not uniformly distributed. (Note that the columns of ${\mathbf {B}}_k$ are deterministic.) Hence, we need to further simplify $\tilde{\mathbf{P}}_{i,k}$. To this end, we use the formula for the inverse of a block matrix

$$\begin{aligned} \Big [ \Big [ \begin{array}{c} {\mathbf {B}}_k^H \\ {\mathbf {G}}^H \\ \end{array} \Big ]&[{\mathbf {B}}_k,{\mathbf {G}}] \Big ]^{-1} = \left[ \begin{array}{cc} {\mathbf {B}}_k^H{\mathbf {B}}_k &{} {\mathbf {B}}_k^H{\mathbf {G}}\\ {\mathbf {G}}^H{\mathbf {B}}_k &{} {\mathbf {G}}^H{\mathbf {G}}\\ \end{array} \right] ^{-1} \nonumber = \Big [ \begin{array}{cc} {\mathbf {C}}+{\mathbf {C}}{\mathbf {B}}_k^H{\mathbf {G}}{\mathbf {E}}^{-1}{\mathbf {G}}^H{\mathbf {B}}_k{\mathbf {C}} &{} -{\mathbf {C}}{\mathbf {B}}_k^H{\mathbf {G}} {\mathbf {E}}^{-1}\\ -{\mathbf {E}}^{-1}{\mathbf {G}}^H{\mathbf {B}}_k{\mathbf {C}} &{} {\mathbf {E}}^{-1}\\ \end{array} \Big ] \end{aligned}$$

(34)

where ${\mathbf {E}} \triangleq {\mathbf {G}}^H{\mathbf {G}} - {\mathbf {G}}^H\mathbf{B}_k({\mathbf {B}}_k^H{\mathbf {B}}_k)^{-1}{\mathbf {B}}_k^H{\mathbf {G}}$ and ${\mathbf {C}}\triangleq ({\mathbf {B}}_k^H{\mathbf {B}}_k)^{-1}$. We use the fact that ${\mathbf {B}}_k{\mathbf {e}}_{k,N}$ is a vector of zeros, and only the element in the position [2, 2] (i.e., ${\mathbf {E}}^{-1}$) is relevant since for the other elements of the matrix we have a multiplication with ${\mathbf {B}}_k{\mathbf {e}}_{k,N}$ or $\mathbf{e}_{k,N}^H{\mathbf {B}}_k^H$. Then, we substitute the last equation into (30). Then, the scalar ${\mathbf {e}}_{k,N}^H \tilde{{\mathbf {P}}}_{i,k}{\mathbf {e}}_{k,N}$ can be written as:

$$\begin{aligned} {\mathbf {e}}_{k,N}^H \tilde{{\mathbf {P}}}_{i,k}{\mathbf {e}}_{k,N}&= {} 1-{\mathbf {e}}_{k,N}^H [{\mathbf {B}}_k,{\mathbf {G}}] \left[ \Big [ \begin{array}{c} {\mathbf {B}}_k^H \\ {\mathbf {G}}^H \\ \end{array} \Big ] [{\mathbf {B}}_k,{\mathbf {G}}] \right] ^{-1} \Big [ \begin{array}{c} {\mathbf {B}}_k^H \\ {\mathbf {G}}^H \\ \end{array} \Big ]{\mathbf {e}}_{k,N} \nonumber \\&= {} 1-{\mathbf {e}}_{k,N}^H {\mathbf {G}} \left( {\mathbf {G}}^H({\mathbf {I}} - {\mathbf {B}}_k({\mathbf {B}}_k^H{\mathbf {B}}_k)^{-1}{\mathbf {B}}_k^H){\mathbf {G}}\right) ^{-1} {\mathbf {G}}^H{\mathbf {e}}_{k,N} \nonumber \\&= {} 1-{\mathbf {e}}_{k,N}^H {\mathbf {G}} \left( {\mathbf {G}}^H \bar{{\mathbf {I}}}_k\bar{{\mathbf {I}}}_k^H{\mathbf {G}}\right) ^{-1} {\mathbf {G}}^H{\mathbf {e}}_{k,N} \end{aligned}$$

(35)

where the $\bar{{\mathbf {I}}}_k$ is the $N \times (N-K_0+1)$ matrix given by

$$\begin{aligned} \bar{{\mathbf {I}}}_k =\left[ \begin{array}{cc} {\mathbf {e}}_{k,K_0} &{} {\mathbf {0}} \\ {\mathbf {0}} &{} {\mathbf {I}} \end{array}\right] . \end{aligned}$$

(36)

and we define $\bar{{\mathbf {I}}}_k$ to satisfy $\bar{\mathbf{I}}_k\bar{{\mathbf {I}}}_k^H={\mathbf {I}} -{{\mathbf {B}}}_k(\mathbf{B}_k^H{\mathbf {B}}_k)^{-1}{{\mathbf {B}}}_k^H$.

Using the fact that ${\mathbf {e}}_{k,N}=\bar{{\mathbf {I}}}_k\bar{\mathbf{I}}_k^H {\mathbf {e}}_{k,N}$, equation (34) can be rewritten as

$$\begin{aligned} {\mathbf {e}}_{k,N}^H \tilde{{\mathbf {P}}}_{i,k}{\mathbf {e}}_{k,N} = 1-&{\mathbf {e}}_{k,N}^H \bar{{\mathbf {I}}}_k\bar{{\mathbf {I}}}_k^H {\mathbf {G}} \left( {\mathbf {G}}^H \bar{{\mathbf {I}}}_k\bar{{\mathbf {I}}}_k^H{\mathbf {G}}\right) ^{-1} {\mathbf {G}}^H\bar{{\mathbf {I}}}_k\bar{{\mathbf {I}}}_k^H{\mathbf {e}}_{k,N}. \end{aligned}$$

(37)

Noting also that $\bar{{\mathbf {I}}}^H_k{\mathbf {e}}_{k,N}=\mathbf{e}_{1,N-K_0+1}$, we define $\tilde{{\mathbf {G}}}\triangleq \bar{\mathbf{I}}_k^H{\mathbf {G}}\in {\mathbb {C}}^{(N-K_0+1)\times T_{{\mathrm{ZF}}}}$ which is the matrix ${\mathbf {G}}$ after puncturing $(K_0-1)$ rows. Eventually, (34) can be written as

$$\begin{aligned} {\mathbf {e}}_{k,N}^H \tilde{{\mathbf {P}}}_{i,k}{\mathbf {e}}_{k,N}= & {} 1- {\mathbf {e}}_{1,N-K_0+1} \tilde{{\mathbf {G}}} (\tilde{{\mathbf {G}}}^H\tilde{{\mathbf {G}}})^{-1} \tilde{{\mathbf {G}}}^H {\mathbf {e}}_{1,N-K_0+1} \\= & {} {\mathbf {e}}_{1,N-K_0+1}^H \tilde{{\mathbf {P}}}_{\tilde{{\mathbf {G}}}} {\mathbf {e}}_{1,N-K_0+1}. \end{aligned}$$

(38)

where the projection matrix

$$\begin{aligned} \tilde{{\mathbf {P}}}_{\tilde{{\mathbf {G}}}} \triangleq {\mathbf {I}}-\tilde{{\mathbf {G}}}(\tilde{{\mathbf {G}}}^H\tilde{{\mathbf {G}}})^{-1} \tilde{{\mathbf {G}}}^H\in {\mathbb {C}}^{(N-K_0+1)\times (N-K_0+1)} \end{aligned}$$

(39)

is uniformly distributed over the space of projection matrices of the same rank. (Recall that the projection matrix $\tilde{\mathbf{P}}_{i,k}$ (30) is not uniformly distributed.)

Substituting (3738) into (33), the normalized fading is defined by

$$\begin{aligned} Y_{i,0,k}= & {} \Big | {\mathbf {w}}_{i,0,k}^H {\mathbf {H}}_{i,0} {\mathbf {f}}_{0,k} /\gamma _{i,0,k}\Big |^2 = \tilde{{\mathbf {e}}}_{1,N-K_0+1}^H \tilde{{\mathbf {P}}}_{\tilde{{\mathbf {G}}}} \tilde{{\mathbf {e}}}_{1,N-K_0+1}. \end{aligned}$$

Using an eigen-decomposition, ${\tilde{\mathbf {P}}}_{\tilde{\mathbf {G}}}={\tilde{\mathbf {U}}}{\tilde{\varvec{\Lambda }}}{\tilde{\mathbf {U}}}^H$ and defining ${\mathbf {d}}\triangleq {\tilde{\mathbf {U}}}^H{tilde{\mathbf {e}}}{1,N-K_0+1}$ we have: $Y_{i,0,k} = {\mathbf {d}}^H {\tilde{\varvec{\Lambda }}}{\mathbf {d}}=\Vert {\tilde{\varvec{\Lambda }}}{\mathbf {d}}\Vert ^2$ where ${\tilde{\varvec{\Lambda }}}$ is a projection to the first M dimensions. Noting that ${\tilde{\mathbf {U}}}$ is uniformly distributed over the space of unitary matrices, vector ${\mathbf {d}}$ is uniformly distributed over the unit sphere. Thus, using [41, IV-C], given $T_{{\mathrm{ZF}}}$, $Y_{i,0,k}$ has a beta distribution, $Y_{i,0,k}|T_{{\mathrm{ZF}}} \sim {\mathrm{Beta}}(M,T_{{\mathrm{ZF}}})$ and its mean is given by $\mathbf {E}\{Y_{i,0,k} |T_{{\mathrm{ZF}}}\}=\frac{M}{N-(K_0-1)}$.