- Research
- Open access
- Published:
Geographical model-derived grid-based directional routing for massively dense WSNs
EURASIP Journal on Wireless Communications and Networking volume 2016, Article number: 17 (2016)
Abstract
This paper presents the grid-based directional routing algorithms for massively dense wireless sensor networks. These algorithms have their theoretical foundation in numerically solving the minimum routing cost problems, which are formulated as continuous geodesic problems via the geographical model. The numerical solutions provide the routing directions at equally spaced grid points in the region of interest, and then, the directions can be used as guidance to route information. In this paper, we investigate two types of routing costs, position-only-dependent costs (e.g., hops, throughput, or energy) and traffic-proportional costs (which correspond to energy-load-balancing). While position-only-dependent costs can be approached directly from geodesic problems, traffic-proportional costs are more easily tackled by transforming the geodesic problem into a set of equations with regard to the routing vector field. We also investigate two numerical approaches for finding the routing direction, the fast marching method for position-only-dependent costs and the finite element method (and its derived distributed algorithm, Gauss-Seidel iteration with finite element method (DGSI-FEM)) for traffic-proportional costs. Finally, we present the numerical results to demonstrate the quality of the derived routing directions.
1 Introduction
With their embedded computation and communication capabilities, wireless sensor networks (WSNs) can extend the senses of human beings to normally inaccessible locations and operate unattended for a long period of time, thus opening up the potential of many new applications [1]. Such applications bring up many challenges in network maintenance since sensors may be unreliable in hazardous situations which prohibit any human intervention to repair or replace malfunctioning sensors. Thus, compared to the cost to access WSNs, advanced developments in manufacturing techniques will make it preferable to deploy a large number of sensors in the region of interest (ROI) in one time, in which sensors can self-organize to operate. However, such a deployment strategy may lead to a massively dense WSN which poses many challenges for efficient algorithm design due to the problem scale and hardware constraints.
For such large-scale networks, the complexity of topological algorithms that model the networks by graphs and then describe network operations by nodes and edges may inevitably increase with the number of nodes and edges, since optimizing, particularly globally, the network performance may require the consideration that all nodes or edges determine the best node or edge to perform a given operation. However, two characteristics of WSNs suggest an alternative approach:
-
1.
WSN applications are usually spatial-oriented, and spatially close nodes tend to perform the same role in networks.
-
2.
Extending the working duration of the whole WSN is more important than keeping each sensor node alive. In other words, it may be preferable to exhaust individual nodes in an attempt to achieve better overall performance.
Therefore, rather than optimizing the performance of individual nodes by micro-controlling node operations, the high role substitutability of WSNs allows networks to be managed via geographical parameters, i.e., use the geographical parameters to locate appropriate sensor nodes to perform assigned tasks. Thus, network operations are described by geographical parameters, not node identities, and the complexity, even when considering global optimization, depends on the ROI, not the number of nodes and edges.
Furthermore, one advantage of geographical approaches is that we may use “distributions” or “vector fields” defined in geographical space to describe network states or operations, and these distributions or vector fields have some nice mathematical properties under massively dense networks, such as differentiability or integrability, which allow many techniques developed in classical mathematical analysis to be applicable. For example, several studies [2–6] have used geographical approaches to analyze WSN routing problems from a macroscopic perspective. Without the complexity of detailed descriptions in micromanaging individual nodes, the geographical descriptions can still provide sufficient information to allow meaningful analysis and optimization at the macroscopic level and the derivation of useful insights.
In this paper, we adopt the geographical model to study the minimum routing cost problems for massively dense WSNs in which the problems are formulated as continuous geodesic problems. We use density distributions to describe how nodes are deployed and routing vector fields for how information are transmitted. The relationship between density distributions and various routing costs may be further analyzed, and the equivalence between geodesic problems and optimum routing vector field problems can be established. We investigate two types of routing costs, position-only-dependent costs which are presented in the preliminary work [7] and traffic-proportional costs. Position-only-dependent costs may be the number of hops, throughput, or transmission energy, and traffic-proportional costs correspond to energy-load-balancing. While the routing problems with position-only-dependent costs can be tackled directly from geodesic problems, routing vector field problems provide a better approach to solve the routing problems with traffic-proportional costs.
Numerically solving continuous geodesic problems or routing vector field problems requires discretizing continuous functions involved in problems in a systematic way and then producing solutions (paths or vectors) at finite locations in the ROI, e.g., equally spaced grid points in the ROI. These numerical solutions at grid points provide the directions to the next forwarding nodes, which can be used as guidance to route information. Thus, the resulting routing algorithms, which we call grid-based directional routing algorithms, are actually the natural outcomes of the numerical approaches of these problems and mainly consist of the following two stages:
-
1.
The ROI is divided into equally spaced grids, and then, each grid point computes its routing direction by numerically solving the continuous geodesic problems or routing vector field problems.
-
2.
A node may use the routing direction of its closest grid point as guidance to determine its next forwarding node.
In this paper, we mainly focus on two numerical approaches for finding the routing direction of each grid point (i.e., the first stage), namely the fast marching (FM) method [8] for position-only-dependent costs and the finite element method (FEM) [9], including its derived distributed algorithm (namely distributed Gauss-Seidel iteration with FEM, DGSI-FEM), for traffic-proportional costs. We then investigate the quality of the derived routing directions via numerical simulations. Note that though the second stage is needed to completely determine a routing path, the study of the second stage is beyond the scope of this paper and we simply use the mechanism adopted in [10] for the second stage to conduct numerical simulations.
The remainder of this paper is organized as follows. After introducing related work in Section 2, we briefly describe the minimum cost routing problem from a macroscopic perspective and the equivalence between geodesic problems and optimum routing vector field problems in Section 3. The minimum routing cost problems with position-only-dependent costs and traffic-proportional costs, including algorithms and numerical results, are then discussed in Sections 4 and 5, respectively. Finally, conclusions are drawn in Section 6. For the sake of convenience, relevant notations introduced in this paper are listed in Table 1.
2 Related work
Mauve et al. [11] argued that, for ad hoc networks, geographical routing scales better than topological routing even given frequently changing network topology. Several approaches are known to be suitable for WSNs, including greedy forwarding (GF) [12], in which each node uses the line segment to the destination to select the optimum forwarding node, and its various remedies [13–15] for the hole problem, in which packets may be trapped in local optima due to the existence of holes. In addition, a global pre-defined trajectory, instead of the local line segment used in GF, may be used to determine the next forwarding node [16].
For massively dense WSNs, several studies have applied analysis techniques developed in the disciplines other than networking to geographical models to analyze the macroscopic behavior of WSNs. For instance, Jacquet [2] analyzed how information traffic may impact the curvature of routing paths from the perspective of geometrical optics. Similarly, Catanuto et al. [5] formulated routing paths as equations of the calculus of variations which state that light follows the path that can be traversed in the least time, i.e., Fermat’s principle. Additionally, Kalantari and Shayman [4] formulated the routing problems of WSNs as equations analogous to Maxwell’s equations in electrostatic theory.
Jung et al. [17] considered spreading network traffic uniformly throughout the ROI using a potential field-based routing scheme in which the potential field is governed by Poisson’s equation via an analogy between physics and network routing problems. Chiasserini et al. [18] used a fluid model to analyze a massively dense WSN in which the media access control and the switch between different operating modes, active and sleep, are considered. Altman et al. [19] analyzed the global optimized routing paths of massively dense networks using the techniques developed in road traffic engineering. Various approaches that work around the scalability problem by creating analogies between various WSN problems and problems in branches of mathematics and physics may be found in [20, 21].
Note that for the approaches mentioned above to be applicable, the massive denseness assumption is required for the validity of some mathematical properties such as continuity or differentiability. In addition to [22] which investigated the relation between the feasibility of such an assumption and node density, Ko [23] provided an operational definition of massively dense networks and then used the definition to derive the upper bound of analysis errors obtained from applying macroscopically derived results to nonmassively dense networks.
3 Minimum cost routing paths
Typically, a routing algorithm is designed with various optimization goals such as minimum total energy consumption or load-balancing. By introducing the transmission cost function \(\mathcal {C} (x_{v},y_{v})\) (i.e., the cost paid by the node v at (x v ,y v ) to transmit one unit amount of information), a routing problem may be formulated as a geodesic problem which minimizes the route cost \(\sum \limits _{v^{\prime } \in \llbracket {P}\rrbracket }\mathcal {C} (x_{v^{\prime }},y_{v^{\prime }})\). That is, a routing problem is to find a path P ∗ to a sink such that:
in which P can be any possible path between a given source node v and any possible sink and ⟦P⟦ denotes the set of nodes on P.
To catch the operations, sensing and networking, we use ρ to represent the amount of information generated by a node located in the ROI (denoted as A) and define the routing vector field, \(\mathbf {D}: A \rightarrow \mathbb {R}^{2}\), in which the direction of D(x,y), called the routing direction and denoted as u f (x,y), points to the next forwarding node of the node at (x,y) and the length |D(x,y)| represents the amount of information transmitted by all nodes at (x,y).
Suppose that the information is conservative; that is, ρ does not consider the information generated and then disappears without being transmitted out, and each node in the ROI relays all the information it received. Thus, for v in A, the net amount of information flowing out of v should be equal to ρ(x v ,y v ). Therefore, we have the following theorem which states that the routing problem may be formulated as a geodesic problem (1) or an optimization problem for the routing vector field incurring the minimum total cost. For the proof please refer to [23].
Theorem 1.
Suppose that the information is conservative for a considered WSN. Hence, ∀v in A, \(\sum \limits _{v^{\prime } \in \llbracket {{P}^{\ast }}\rrbracket }\mathcal {C} (x_{v^{\prime }},y_{v^{\prime }})\) is minimum over all possible paths from v to sinks if and only if \(\sum \limits _{v \,\,\text {in}\, A}\mathcal {C} (x_{v},y_{v})\left |\mathbf {D}(x_{v},y_{v})\right |\) is minimum over all possible vector fields for a given ρ.
In the limit of massively dense networks, routing paths can be considered as continuous lines rather than sequences of discrete nodes [2]. Thus, the geodesic problem (1) may be formulated as the one to find the path P ∗ from (x 0,y 0) to a sink such that:
in which P can be any possible path from (x 0,y 0) to any possible sink and s is the curvilinear coordinate associated with the path P ∗ or P. Similar to Theorem 1, the continuous geodesic problem (2) may be expected to be equivalent to the optimum routing vector field problem for massively dense networks; that is,
Theorem 2.
Suppose that the information is conservative for a considered WSN. Hence, ∀(x 0,y 0) in A, \(\int _{{P}^{\ast }}\mathcal {C} (x(s),y(s))\mathrm {d}s\) is minimum over all possible paths from (x 0,y 0) to sinks if and only if \(\int _{A}\mathcal {C} (x,y)\left |\mathbf {D}(x,y)\right |\mathrm {d}x\mathrm {d}y\) is minimum over all possible vector fields for a given ρ.
Some routing problems can be tackled via geodesic problems; for example, the cost function \(\mathcal {C} (x,y)\) is isotropic (e.g., sensor nodes with omni-directional antennas) and only depends on position. However, Theorem 2 provides an alternative that allows routing problems to be approached via D. One example is that \(\mathcal {C}(x,y)\) is proportional to |D(x,y)|. We will discuss these two types of \(\mathcal {C} {(x,y)}\), respectively, in Sections 4 and 5.
4 Position-only-dependent routing cost
4.1 Cost function and node density
This section considers the cost functions which are isotropic and only depends on position. Reference [24] discussed the relationship between the transmission energy as the cost and the node density ψ. Note that referring to [25], the energy consumption per unit of information is proportional to \({r}^{\alpha _{\textit {rf}}}\phantom {\dot {i}\!}\) in which r is the distance between the sender and receiver and the RF attenuation exponent α rf is typically in the range of 2 to 5. Additionally, the average inter-distance between nodes is proportional to \(1/\sqrt {\psi }\), which leads to \(\mathcal {C}\propto 1/\psi ^{\alpha _{\textit {rf}}/2}\).
As pointed out in [26], while considering the capacity of wireless communications, the throughput of each node at (x,y) cannot be fully utilized and is only proportional to \(1/\sqrt {\psi (x,y)}\) [3]. Therefore, the optimum total throughput at (x,y) can only be proportional to \(\sqrt {\psi (x,y)}\); that is, \(\mathcal {C} \propto 1/\sqrt {\psi }\) corresponds to a network in which the objective is to maximize the throughput.
Several other possible forms of \(\mathcal {C}\) are also listed in [5]. For example, if the objective is to minimize the number of hops, \(\mathcal {C}\) may be taken to be proportional to 1/r, in which communication is constrained between the nearest neighbors. Thus, \(\mathcal {C} \propto \sqrt {\psi }\). In addition, the case that \(\mathcal {C}\) is a constant corresponds to a setting where routing is equally costly at all parts of the network. Thus, the objective is to minimize the length of routes. The relationships between \(\mathcal {C}\) and ψ for the above objectives are summarized in Table 2.
4.2 Grid approximation Dijkstra’s method (GADM)
It is infeasible to directly find the minimum cost routing path under massively dense networks. One possible approach to reduce the problem scale is to divide the ROI into equally spaced grids which compose a grid point network, referring to Fig. 1. We then find the minimum cost path between each grid point and sink (e.g., using Dijkstra’s method) under the grid point network. The routing direction of a grid point will be the direction pointing to the next grid point on the minimum cost path under the grid point network. For the example of Fig. 1, the direction from  to
to  is the routing direction of
is the routing direction of  . Here, we denote
. Here, we denote  as the grid point located at the ith column and the jth row, and say a node belongs to
as the grid point located at the ith column and the jth row, and say a node belongs to
 if its closest grid point in the ROI is
if its closest grid point in the ROI is  ; for example, all nodes in the dark gray region belong to
; for example, all nodes in the dark gray region belong to  . Therefore, a node belonging to
. Therefore, a node belonging to  may use the direction from
may use the direction from  to
to  as guidance to determine the next forwarding node [10].
as guidance to determine the next forwarding node [10].
Grid point network of ROI. The ROI is divided into equally spaced grids which compose a grid point network (grid points are connected by dashed lines).  is the grid point located at the ith column and the jth row. A node is defined as belonging to
is the grid point located at the ith column and the jth row. A node is defined as belonging to  if its closest grid point in the ROI is
if its closest grid point in the ROI is  ; for example, all nodes in the dark gray region belong to
; for example, all nodes in the dark gray region belong to  . The path indicated by the blue solid line is the minimum cost routing path from
. The path indicated by the blue solid line is the minimum cost routing path from  to the grid point which the sink belongs to (indicated by the red circle). The black region represents the hole (the region without enough working sensors)
to the grid point which the sink belongs to (indicated by the red circle). The black region represents the hole (the region without enough working sensors)
Note that the routing direction of  derived by grid approximation Dijkstra’s method (GADM) always points to one of
derived by grid approximation Dijkstra’s method (GADM) always points to one of  s four adjacent grid points. Such a restriction is the main reason that GADM cannot approximate continuous paths well (i.e., the minimum cost routing paths under massively dense networks), which thus yields less optimum routing paths.
s four adjacent grid points. Such a restriction is the main reason that GADM cannot approximate continuous paths well (i.e., the minimum cost routing paths under massively dense networks), which thus yields less optimum routing paths.
4.3 Fast marching (FM) method
4.3.1 Cost map and eikonal equation
Define the cost map T(x,y) as the minimum total routing cost needed from a node at (x,y) to sinks. Assume that T is differentiable. We then have the following theorem for which proof is given in Appendix 1:
Theorem 3.
In addition,
in which s is the curvilinear coordinate associated with the minimum cost path P ∗ and ∥ is the symbol for two parallel vectors.
Note that the a priori differentiability requirement of T may not be possible, e.g., existence of multiple sinks, in which case a weak solution may be considered instead. Refer to [27] for details.
Equation (3) is known as the eikonal equation, illustrating how a high-frequency wave front advances; T(x,y) corresponds to the time which the front takes to arrive at (x,y), and \(1/\mathcal {C}(x,y)\) is the speed of the front at (x,y). Theorem 3 indicates that if T may be solved from (3), the minimum cost path may be derived by following the gradient of T.
4.3.2 Geodesic path via eikonal equation
To solve (3), we adopt the FM method proposed by Sethian [8]. We first divide the definition domain of T into equally spaced grids with a gap size h and then approximate the differential terms by differences. Referring to Fig. 2, the definition domain of T should be large enough to cover the ROI. We distinguish the ROI and the definition domain of T to provide a consistent formula of difference approximation at the boundary of the ROI (via δ i,j introduced in (6)).
\(\tilde {f}_{{i},{j}}\) and  . The definition domain of f (e.g., T or D) is divided into equally spaced grids with a grid size h.
. The definition domain of f (e.g., T or D) is divided into equally spaced grids with a grid size h.  is the grid point located at the ith column and the jth row. \(\tilde {f}_{{i},{j}}\) is the value of f at
is the grid point located at the ith column and the jth row. \(\tilde {f}_{{i},{j}}\) is the value of f at  . The set of grid points, marked by black circles, in A is denoted as
. The set of grid points, marked by black circles, in A is denoted as  . The grid points marked by white circles are not in
. The grid points marked by white circles are not in 
Various difference approximations to the length of gradient may be used. In this paper, the following less diffusive difference approximation to |∇T| [28] is chosen; that is, for  in ROI, (3) is approximated as:
in ROI, (3) is approximated as:
in which:
Here, \(\widetilde {T}_{{i},{j}}\) is the value of T at  , and:
, and:

δ
i,j
is introduced to ensure a consistent difference formula with the grid points not in the ROI. Note that T is undefined for the grid point not in the ROI; thus, if  is not in the ROI, δ
i−1,j
=0 will force \(\Delta ^{-x}_{i,j}T=0\) which corresponds to no information flow from
is not in the ROI, δ
i−1,j
=0 will force \(\Delta ^{-x}_{i,j}T=0\) which corresponds to no information flow from  to
to  .
.
FM iteratively computes \(\widetilde {T}_{{i},{j}}\) starting from sinks via (5). Conceptually, the iteration of FM works as the wave front advances in the ROI. As the front advances in the ROI, Ts and states of the grid points are determined and updated iteratively as illustrated in Figs. 3 and 4: Upwind side: the zone which has been visited by the wave front. The states of grid points in the upwind zone are marked as accepted, and the values of \(\widetilde {T}\)s at these grid points have been determined. Since \( \mathcal {C}(x,y) > 0\), the front moves outward. Thus, the states of the accepted grid point will not be changed. Narrow band: the zone where the wave front is located. The states of grid points in this zone are marked as trial, and FM is determining the values of \(\widetilde {T}\)s at these grid points. Once finished, the grid point with the smallest \(\widetilde {T}\) in this zone will be included in the upwind side and the wave front expands further. Downwind side: the zone which has not been visited by the wave front. The states of grid points in this zone are marked as far away, and the values of \(\widetilde {T}\)s at these grid points have not been determined.
The algorithm of FM is listed in Algorithm 1. Here,  ,
,  , and
, and  are the sets of the grid points in the upwind side, narrow band, and downwind side, respectively, and the neighbor set of
are the sets of the grid points in the upwind side, narrow band, and downwind side, respectively, and the neighbor set of  , denoted as
, denoted as  , is the set of
, is the set of  s adjacent grid points in A, i.e.,
s adjacent grid points in A, i.e.,  .
.

Initially, the entire ROI is the downwind side except the sinks which are marked as accepted with \(\widetilde {T}=0\) (Line 2); then, the wave front begins to expand (Line 3). FM uses (5) to compute the \(\widetilde {T}\)s of the grid points in the narrow band (Line 4). Once finished, the grid point with the smallest \(\widetilde {T}\) in the narrow band is marked as accepted (Lines 6–7). The wave front will then keep expanding (Lines 8–13) while updating the \(\widetilde {T}\)s of the grid points in the narrow band (Line 12) for the next iteration until the entire ROI is the upwind side (Lines 5–14). The state changes of grid points are illustrated in Fig. 4.
After determining \(\widetilde {T}\)s at all grid points by Algorithm 1, we may use \(\widetilde {T}\)s and (4) to derive the routing direction, \(\widetilde {\mathbf {u}_{\text {f}}}_{{i,j}}\), which is the unit tangent vector along the geodesic path from  to the sink. By (4), the vector V=−∇T is tangent to the geodesic path. We may apply the finite difference method to approximate V: for
to the sink. By (4), the vector V=−∇T is tangent to the geodesic path. We may apply the finite difference method to approximate V: for  in the ROI:
in the ROI:
in which \(\widetilde {\mathbf {V}}_{{i},{j_{x}}}\) and \(\widetilde {\mathbf {V}}_{{i},{j_{y}}}\) are the x and y components of \(\widetilde {\mathbf {V}}_{{i},{j}}\), respectively. Note that it is easy to verify that the formula for \(\widetilde {\mathbf {V}}_{{i},{j}}\) in (7) is consistent with the finite difference approximation of ∇T at  . In addition, \(\widetilde {\mathbf {V}}_{{i},{j_{x}}} = 0\) if both
. In addition, \(\widetilde {\mathbf {V}}_{{i},{j_{x}}} = 0\) if both  and
and  are not in the ROI, which corresponds to zero traffic along the x-direction (the similar reasoning may apply to \(\widetilde {\mathbf {V}}_{{i},{j_{y}}}\)). Once \(\widetilde {\mathbf {V}}_{{i},{j}}\) is computed, \(\widetilde {\mathbf {u}_{\text {f}}}_{i,{j}}\) can be determined by \(\widetilde {\mathbf {u}_{\text {f}}}_{{i,j}} = \widetilde {\mathbf {V}}_{{i},{j}}/\left |\widetilde {\mathbf {V}}_{{i},{j}}\right |\).
are not in the ROI, which corresponds to zero traffic along the x-direction (the similar reasoning may apply to \(\widetilde {\mathbf {V}}_{{i},{j_{y}}}\)). Once \(\widetilde {\mathbf {V}}_{{i},{j}}\) is computed, \(\widetilde {\mathbf {u}_{\text {f}}}_{i,{j}}\) can be determined by \(\widetilde {\mathbf {u}_{\text {f}}}_{{i,j}} = \widetilde {\mathbf {V}}_{{i},{j}}/\left |\widetilde {\mathbf {V}}_{{i},{j}}\right |\).
4.4 Numerical results
We first present numerical results, illustrated in Figs. 5 and 6, to compare the effectiveness of GADM and FM. The settings of both scenarios, as summarized in Table 3, are similar except the number of sinks. Furthermore, the cost function \(\mathcal {C}\) considered is a constant; thus, the minimum cost path is the one with the shortest length.
Routing direction and routing paths. Here, the sinks indicated by circles are located at  and
and  , and the black regions represent the holes. a Routing direction \(\widetilde {\mathbf {u_{f}}}\). b Routing paths: the source is close to the grid point
, and the black regions represent the holes. a Routing direction \(\widetilde {\mathbf {u_{f}}}\). b Routing paths: the source is close to the grid point  . c Routing paths: the source is close to the grid point
. c Routing paths: the source is close to the grid point 
If the information is currently routed to a node, denoted as v, belonging to  , we use \(\widetilde {\mathbf {u_{f}}}_{{i},{j}}\) and the following mechanism adopted in [10] to determine the next forwarding node (i.e., the second stage of the grid-based directional routing algorithms).
, we use \(\widetilde {\mathbf {u_{f}}}_{{i},{j}}\) and the following mechanism adopted in [10] to determine the next forwarding node (i.e., the second stage of the grid-based directional routing algorithms).
-
1.
Choose the neighbor nodes within the communication range R c of v which can make positive progress to sink. The progress of the neighbor node v ′ is defined as the inner product of \(\widetilde {\mathbf {u_{f}}}_{{i},{j}}\) and the vector from v to v ′. If there are multiple candidates, choose the one which makes the greatest progress.
-
2.
If no nodes are making positive progress, increase R c by ΔR c .
Note that due to the characteristics of wireless communication [3], it is preferred to use multiple short-range transmissions for optimal power consumption and communication capacity. Therefore, we gradually increase the communication range R c of v in searching for the next forwarding nodes to avoid long distance transmissions. The values of R c and ΔR c are also listed in Table 3.
Figure 5 a depicts the routing directions derived by FM. Figure 5 b, c illustrate the routing paths via the routing directions derived by GADM and FM. The route lengths listed in Table 4 show that FM may derive shorter routing paths than GADM. Note that GADM and FM may result in different routes to bypass the hole for the same source node, as illustrated in Fig. 5 c. Similar results may be found for the second scenario, referring to Fig. 6 and Table 4. In addition, GADM and FM may result in routing to different sinks for the same source node, as illustrated in Fig. 6 c.
The reason that FM outperforms GADM is that the minimum cost path derived under the grid point network may not approximate the actual minimum cost path well. In addition, the routing direction of a grid point  always points to the neighbors of
always points to the neighbors of  (that is, the four adjacent grid points of
(that is, the four adjacent grid points of  in our simulations). Though this problem may be alleviated by extending the neighbor set (for example, adding the diagonal grid points to the neighbor set), the direction restriction (the routing direction always points to one of the neighbors) cannot be removed. On the other hand, (5) used in Algorithm 1 approximates |∇T| well, and the routing direction (via using \(\widetilde {T}\)s and (7)) has no such direction restriction.
in our simulations). Though this problem may be alleviated by extending the neighbor set (for example, adding the diagonal grid points to the neighbor set), the direction restriction (the routing direction always points to one of the neighbors) cannot be removed. On the other hand, (5) used in Algorithm 1 approximates |∇T| well, and the routing direction (via using \(\widetilde {T}\)s and (7)) has no such direction restriction.
Figure 7 illustrates how node density may affect routing paths for the optimization objectives listed in Table 2 with α rf =4. Twenty thousand nodes are randomly deployed according to ψ(x,y)∝(3.5×10−5 y 2+0.02). Note that routing directions are solved (i.e., the first stage of the grid-based directional routing algorithms) using only the macroscopic parameter, ψ, but not the detailed position of each node. Thus, FM derives the same routing directions under the same density distribution regardless of the node positions. The node positions are merely used to determine the next forwarding node (i.e., the second stage) from the routing directions using the approach described earlier in this section.
The results show that routing should utilize the nodes in the sparse area to minimize the number of hops and use the nodes in the dense area to increase the throughput and to avoid long distance transmissions for less energy consumption. Of course, routing should use the straight line to the sink for minimizing the route length.
We also conducted simulations to compare the routing cost of \(\widetilde {\mathbf {u_{f}}}_{{i},{j}}\) obtained from FM and GADM with the optimum routing cost determined by applying a shortest path algorithm to the connectivity graph of the WSN shown in Fig. 7, which basically is a microscopic routing approach. The results illustrated in Fig. 8 reveal that \(\widetilde {\mathbf {u_{f}}}_{{i},{j}}\) obtained from FM may lead to a reasonable routing cost; the average cost is 5 % more than the average optimum cost. On the other hand, \(\widetilde {\mathbf {u_{f}}}_{i,j}\) obtained from GADM may have a routing cost up to 28 % more than the optimum cost. In Fig. 8, the mean of the routing cost is the average cost of all nodes to the sink. The relative mean of FM (or GADM) is defined as the mean of the routing cost of FM (or GADM) divided by the mean of the optimum routing cost.
The relative mean of routing cost of the scenario in Fig. 7: the mean of the routing cost of FM (or GADM) is the average cost of all nodes to the sink using the routing directions derived by FM (or GADM). The relative mean of FM (or GADM) is defined as the mean of the routing cost of FM (or GADM) divided by the mean of the optimum routing cost (OPT)
5 Traffic-proportional routing cost
5.1 Load-balancing routing
This section considers the case in which \(\mathcal {C}(x,y)= \lambda (x,y)^{2}\left |\mathbf {D}(x,y)\right |\); here, λ is the energy cost e, normalized to the initial energy E, for transmitting one unit of information, i.e., λ=e/E. As pointed out in [2], in the context of a massively dense network, routing paths can be considered as continuous lines, instead of sequences of discrete nodes, and D may be considered differentiable. Thus, the fact that information is conservative (i.e., at each location, the net amount of traffic is equal to the amount of information generated) can be formulated as [29]:
Thus, from Theorem 2, if (8) holds, the geodesic problem (2) with \(\mathcal {C}(x,y)=\lambda (x,y)^{2}\left |\mathbf {D}(x,y)\right |\) is equivalent to the optimization problem which finds the vector field D(x,y) to minimize:
Note that the variance of λ|D|, \(\int _{A}\left (\lambda (x,y)\left |\mathbf {D}(x,y)\right |-\overline {\lambda \left |\mathbf {D}\right |}\right)^{2}\mathrm {d}x\mathrm {d}y\), is positive; here, \(\overline {\lambda \left |\mathbf {D}\right |}\) is the average of λ(x,y)|D(x,y)|. Since:
in which area(A) is the area of A; minimizing (9) not only minimizes the difference of each location’s λ|D| but also inherently reduces \(\overline {\lambda \left |\mathbf {D}\right |}\).
Since λ is the normalized communication energy cost per unit of information, λ(x,y)|D(x,y)| is the normalized total communication energy consumption. Thus, it is not difficult to reason that keeping λ|D| the same everywhere in A is equivalent to exhausting the energy of each location in A simultaneously. In other words, the objective of the geodesic problem (2) with \( \mathcal {C}(x,y)=\lambda (x,y)^{2}\left |\mathbf {D}(x,y)\right |\) is to achieve global load-balancing (by minimizing the difference of each location’s λ|D|, i.e., the variance) and reduce the total communication energy consumption (by reducing \(\overline {\lambda \left |\mathbf {D}\right |}\)).
As mentioned in [30], the necessary condition for deriving the minimum value of (9) is the existence of a scalar function Φ called potential that satisfies:
in which J=1/λ 2. In addition, there is no information flow from the outside of A; that is, there is no traffic along the inward pointing normal direction at the boundary of A, denoted as ∂A, which leads to the following boundary condition:
in which \(\hat {\mathbf {n}}\) is the unit inward pointing normal vector to ∂A.
Therefore, the minimum cost routing problem with the cost \( \mathcal {C} (x,y)=\lambda (x,y)^{2}\left |\mathbf {D}(x,y)\right |\) can be transformed into a set of partial differential equations that we call load-balancing routing equations, (8), (10), and (11). We may combine these equations into the following single equation called the weak formulation of the load-balancing routing equations:
in which ν is an arbitrary smooth scalar valued function.
Note that there is no differential term of D in (12), and the a priori differentiability requirement of D is weakened. Thus, the weak formulation allows us to consider irregular problems in which true solutions cannot be continuously differentiable [9], e.g., the problems in which ψ or ρ are jump functions in A. For the sake of brevity, the derivation of (12) is given in Appendix 2.
The relationship between J and the node density distribution ψ may be further established if the transmission energy consumption model is given. For example, we may adopt the energy consumption model in [25], in which the energy consumption per unit of information (denoted as e) is proportional to \(r^{\alpha _{\textit {rf}}}\phantom {\dot {i}\!}\). Here, r is the sender-to-receiver distance and the RF attenuation exponent α rf is typically in the range of 2 to 5. Since the average inter-distance between nodes is proportional to \(1/\sqrt {\psi }\), \(r \propto 1/\sqrt {\psi }\) and hence \( e\propto {\psi}^{-{\alpha}_{rf}/2} \). In addition, suppose that the nodes have an equal amount of initial energy; thus, the initial energy E is proportional to ψ, which leads to:
5.2 Finite element method (FEM) and DGSI-FEM algorithm
Equation (12) can be solved numerically by FEM in which (12) is locally approximated (posed over small partitions called elements of the entire ROI) and a global solution is built by combining the local solutions over these elements [9]. Similarly, referring to Fig. 2, we may divide the ROI into equally spaced grids and then use these grid points to form the elements (i.e., the gray hexagon on the x–y plane illustrated in Fig. 9).
Consider the set of basis functions, μ
i,j
with  , defined on the A such that μ
i,j
has the following properties:
, defined on the A such that μ
i,j
has the following properties:
and

Here, \((x_{i^{\prime }}, y_{j^{\prime }})\) is the position of  We then approximate Φ, J, and ρ, respectively, by:
We then approximate Φ, J, and ρ, respectively, by:



in which \(\widetilde {\Phi }_{{i},{j}}=\Phi (x_{i}, y_{j})\), \( {\overset{\sim }{J}}_{i,j}=J\left({x}_i,{y}_j\right) \), and \(\widetilde {\rho }_{{i},{j}}=\rho (x_{i}, y_{j})\) (i.e., the values of Φ, J, and ρ at the grid point  , respectively). By substituting (15), (16), and (17) into (12), we obtain the following set of linear equations:
, respectively). By substituting (15), (16), and (17) into (12), we obtain the following set of linear equations:

One possible set of candidate functions satisfying (14) are pyramids with peaks at grid points as illustrated in Fig. 9. That is:
Here, \({_{i_{1},j_{1}}}\triangle {^{i_{2},j_{2}}_{i_{3},j_{3}}}\) is the triangle formed by 
 and
and  if all
if all  ,
,  and
and  are in the ROI. If any of these three grid points is not in the ROI, \({_{i_{1},j_{1}}}\triangle {^{i_{2},j_{2}}_{i_{3},j_{3}}}\) is an empty region. That is:
are in the ROI. If any of these three grid points is not in the ROI, \({_{i_{1},j_{1}}}\triangle {^{i_{2},j_{2}}_{i_{3},j_{3}}}\) is an empty region. That is:

With the linear basis functions (19), the coefficients, \(K^{i^{\prime },j^{\prime }}_{i,j}\) and g i,j , in (18) can be derived:

and:
in which δ i,j is defined in (6) and:
Note that it is not difficult to verify that \(K^{i^{\prime },j^{\prime }}_{i,j}=K^{i,j}_{i^{\prime },j^{\prime }}\). For the sake of brevity, the detailed computation of \(K^{i^{\prime },j^{\prime }}_{i,j}\) and g i,j is given in Appendix 3.
The Gauss-Seidel iteration (GSI) may solve (18) for \(\widetilde {\Phi }_{{i},{j}}\) via iteratively updating each \(\widetilde {\Phi }_{{i},{j}}\) in lexicographical order from the most updated \(\widetilde {\Phi }\) value at other grid points until the update change \(\left |\widetilde {\Phi }_{{i},{j}}^{(k)}-\widetilde {\Phi }_{{i},{j}}^{(k-1)}\right | \leq \varepsilon \) for all  That is, \(\widetilde {\Phi }_{{i},{j}}^{(k)}\) are computed sequentially by:
That is, \(\widetilde {\Phi }_{{i},{j}}^{(k)}\) are computed sequentially by:
in which \( \mathcal {O}_{L}(i,j)\) defines the lexicographical order; that is:
In GSI, only one \(\widetilde {\Phi }\) is updated in one iteration (21). We say GSI has gone through one sweep when each \(\widetilde {\Phi }\) has been updated once. \(\widetilde {\Phi }_{{i},{j}}^{(k)}\) is the value of \(\widetilde {\Phi }_{{i},{j}}\) after the kth sweep.
Note that if  and
and  . Thus, only \(\widetilde {\Phi }_{{i},{j-1}}^{(k)}\), \(\widetilde {\Phi }_{{i-1},{j}}^{(k)}\), \(\widetilde {\Phi }_{{i+1},{j}}^{(k-1)}\), and \(\widetilde {\Phi }_{{i},{j+1}}^{(k-1)}\) are needed to compute \(\widetilde {\Phi }_{{i},{j}}^{(k)}\) via (21). In other words, as long as \(\widetilde {\Phi }_{{i},{j-1}}^{(k)}\) and \(\widetilde {\Phi }_{{i-1},{j}}^{(k)}\) are computed, \(\widetilde {\Phi }_{{i},{j}}^{(k)}\) can be computed.
. Thus, only \(\widetilde {\Phi }_{{i},{j-1}}^{(k)}\), \(\widetilde {\Phi }_{{i-1},{j}}^{(k)}\), \(\widetilde {\Phi }_{{i+1},{j}}^{(k-1)}\), and \(\widetilde {\Phi }_{{i},{j+1}}^{(k-1)}\) are needed to compute \(\widetilde {\Phi }_{{i},{j}}^{(k)}\) via (21). In other words, as long as \(\widetilde {\Phi }_{{i},{j-1}}^{(k)}\) and \(\widetilde {\Phi }_{{i-1},{j}}^{(k)}\) are computed, \(\widetilde {\Phi }_{{i},{j}}^{(k)}\) can be computed.
Accordingly, the distributed routing algorithm, DGSI-FEM, is proposed to coordinate sensors to solve \(\widetilde {\Phi }\)s from (18) in parallel using (21). In DGSI-FEM, a nearby node is selected as the grid head for each grid point to compute the value of \(\widetilde {\Phi }\). The grid head of  may update \(\widetilde {\Phi }_{{i},{j}}\) as long as the most updated \(\widetilde {\Phi }_{{i},{j-1}}\) and \(\widetilde {\Phi }_{{i-1},{j}}\) are known; it does not need to wait for the grid heads of all the grid points with lexicographical order less than \(\mathcal {O}_{L}(i,j)\). Note that only these grid heads are involved in the computation of \(\widetilde {\Phi }\)s, resulting in low overhead for a massively dense network. For the sake of brevity, we simply describe the operations of grid points without explicitly mentioning that the operations are actually executed by grid heads.
may update \(\widetilde {\Phi }_{{i},{j}}\) as long as the most updated \(\widetilde {\Phi }_{{i},{j-1}}\) and \(\widetilde {\Phi }_{{i-1},{j}}\) are known; it does not need to wait for the grid heads of all the grid points with lexicographical order less than \(\mathcal {O}_{L}(i,j)\). Note that only these grid heads are involved in the computation of \(\widetilde {\Phi }\)s, resulting in low overhead for a massively dense network. For the sake of brevity, we simply describe the operations of grid points without explicitly mentioning that the operations are actually executed by grid heads.
Since the termination condition is that all the changes made by a sweep fall below a size threshold ε, each grid point needs to know all these changes. To achieve this, DGSI-FEM uses two state packets, PRECISE and DONE, for each grid point, which represent the convergence status and the termination decision, i.e., whether the update changes are small enough and whether the iteration should terminate, respectively. In addition, DGSI-FEM uses two phases (namely, a forward sweep followed by a backward sweep) to propagate the termination decision (via the state packet DONE) and collect the convergence status (via the state packet PRECISE) of all \(\widetilde {\Phi }\)s. Detailed DGSI-FEM is illustrated in Algorithm 2. Note that \(K_{i,j}^{i^{\prime },j^{\prime }}\) and \(\delta _{i^{\prime },j^{\prime }}\) for all  and
and  are known in advance. This may be done by letting each grid point discover its adjacent grid points and, once found, exchange \( {\overset{\sim }{J}}_{i,j} \) with them. Additionally, the algorithms for sending and waiting for messages are depicted in Algorithms 3 and 4, respectively. Both algorithms will check whether the communication counterpart is in the ROI and wait will return 〈0,true〉 if not.
are known in advance. This may be done by letting each grid point discover its adjacent grid points and, once found, exchange \( {\overset{\sim }{J}}_{i,j} \) with them. Additionally, the algorithms for sending and waiting for messages are depicted in Algorithms 3 and 4, respectively. Both algorithms will check whether the communication counterpart is in the ROI and wait will return 〈0,true〉 if not.
After initialization (Lines 1–2), the iteration for  will proceed as follows, referring to Fig. 10 for the sequence diagram of DGSI-FEM iteration:
will proceed as follows, referring to Fig. 10 for the sequence diagram of DGSI-FEM iteration:
Sequence diagram for  in the iteration of DGSI-FEM. For example, in the forward sweep,
in the iteration of DGSI-FEM. For example, in the forward sweep,  and
and  update and then send their \(\widetilde {\Phi }\)s and DONEs to
update and then send their \(\widetilde {\Phi }\)s and DONEs to  After updating \(\widetilde {\Phi }_{{i},{j}}\) and DONE
i,j
,
After updating \(\widetilde {\Phi }_{{i},{j}}\) and DONE
i,j
,  sends \(\widetilde {\Phi }_{{i},{j}}\) and DONE
i,j
to
sends \(\widetilde {\Phi }_{{i},{j}}\) and DONE
i,j
to  and
and  . The dark rectangles drawn on top of the lifelines indicate that grid points are updating \(\widetilde {\Phi }\)s and DONEs (or PRECISEs in the backward sweep)
. The dark rectangles drawn on top of the lifelines indicate that grid points are updating \(\widetilde {\Phi }\)s and DONEs (or PRECISEs in the backward sweep)



-
1.
Forward sweep: iteration direction begins from bottom-left (the grid point with the smallest \(\mathcal {O}_{L}\)) to top-right (the grid point with the largest \(\mathcal {O}_{L}\)).
-
(a)
 waits for \(\widetilde {\Phi }\)s and DONEs, respectively, from the down and left adjacent grid points,
waits for \(\widetilde {\Phi }\)s and DONEs, respectively, from the down and left adjacent grid points, 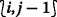 and
and  , which have smaller \(\mathcal {O}_{L}\) values. (Lines 5–9)
, which have smaller \(\mathcal {O}_{L}\) values. (Lines 5–9) -
(b)
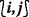 updates \(\widetilde {\Phi }_{{i},{j}}\) by (21). (Line 10)
updates \(\widetilde {\Phi }_{{i},{j}}\) by (21). (Line 10) -
(c)
 updates DONE
i,j
. (Lines 11–19)
updates DONE
i,j
. (Lines 11–19) -
(d)
 sends \(\widetilde {\Phi }_{{i},{j}}\) and DONE
i,j
to the right and top adjacent grid points,
sends \(\widetilde {\Phi }_{{i},{j}}\) and DONE
i,j
to the right and top adjacent grid points, 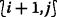 and
and 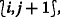 , respectively, which have larger \(\mathcal {O}_{L}\) values. (Lines 20–20)
, respectively, which have larger \(\mathcal {O}_{L}\) values. (Lines 20–20)
-
(a)
-
2.
Backward sweep: iteration direction moves from top-right to bottom-left.
-
(a)
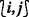 waits for \(\widetilde {\Phi }\)s and PRECISEs from the top and right adjacent grid points, respectively. (Lines 27–29)
waits for \(\widetilde {\Phi }\)s and PRECISEs from the top and right adjacent grid points, respectively. (Lines 27–29) -
(b)
 updates \(\widetilde {\Phi }_{{i},{j}}\) by (21). (Line 30)
updates \(\widetilde {\Phi }_{{i},{j}}\) by (21). (Line 30) -
(c)
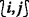 updates PRECISE
i,j
. (Lines 31–33)
updates PRECISE
i,j
. (Lines 31–33) -
(b)
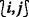 sends \(\widetilde {\Phi }_{{i},{j}}\) and PRECISE
i,j
to the down and left adjacent grid points, respectively. (Lines 34–36)
sends \(\widetilde {\Phi }_{{i},{j}}\) and PRECISE
i,j
to the down and left adjacent grid points, respectively. (Lines 34–36)
-
(a)
Note that  will set PRECISE
i,j
as true if the update made by itself is small enough and the PRECISEs of its top and right grid points are true (Lines 31–33). The PRECISEs collected by the \(\mathcal {O}_{L}\)-initiator, which has no bottom and left adjacent grid points (e.g., the grid point with the smallest lexicographical order), indicate whether the update changes of all \(\widetilde {\Phi }\)s are small enough and are used to determine the termination by the \(\mathcal {O}_{L}\)-initiator.
will set PRECISE
i,j
as true if the update made by itself is small enough and the PRECISEs of its top and right grid points are true (Lines 31–33). The PRECISEs collected by the \(\mathcal {O}_{L}\)-initiator, which has no bottom and left adjacent grid points (e.g., the grid point with the smallest lexicographical order), indicate whether the update changes of all \(\widetilde {\Phi }\)s are small enough and are used to determine the termination by the \(\mathcal {O}_{L}\)-initiator.
In addition,  will set DONE
i,j
as true based on the following rules:
will set DONE
i,j
as true based on the following rules:
-
1.
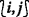 is an \(\mathcal {O}_{L}\)-initiator, and the update changes in the last backward sweep are small enough, i.e., PRECISE
i,j
is true (Lines 11–14), or
is an \(\mathcal {O}_{L}\)-initiator, and the update changes in the last backward sweep are small enough, i.e., PRECISE
i,j
is true (Lines 11–14), or -
2.
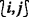 is not an \(\mathcal {O}_{L}\)-initiator, but DONE
i,j−1=true and DONE
i−1,j
=true (Lines 15–19).
is not an \(\mathcal {O}_{L}\)-initiator, but DONE
i,j−1=true and DONE
i−1,j
=true (Lines 15–19).
Note that DONEs are propagated from bottom-left to top-right in the forward sweep, so the termination proceeds from bottom-left to top-right. Thus, the if statement that checks whether the down or left adjacent grid points have terminated is added (Line 6) to avoid infinite waiting when waiting for messages from the down or left adjacent grid points (Line 7).
After \(\widetilde {\Phi }_{{i},{j}}\)s are solved from (18), \(\widetilde {\mathbf {D}}_{{i},{j}}\) may be approximated by the following formulae, which are derived by using (15) to approximate (10):
in which \(\widetilde {\mathbf {D}}_{{i},{j_{x}}}\) and \(\widetilde {\mathbf {D}}_{{i},{j_{y}}}\) are, respectively, the x and y components of \(\widetilde {\mathbf {D}}_{{i},{j}}\). For the sake of brevity, the derivation is given in Appendix 4. Once \(\widetilde {\mathbf {D}}_{{i},{j}}\) is computed, \(\widetilde {\mathbf {u_{f}}}_{{i},{j}}\) can be determined by \(\widetilde {\mathbf {u_{f}}}_{{i},{j}}=\widetilde {\mathbf {D}}_{{i},{j}}/\left |\widetilde {\mathbf {D}}_{{i},{j}}\right |\) and then used as guidance to find the next forwarding nodes for routing information.
5.3 Numerical results
We present several numerical results to demonstrate the effectiveness of DGSI-FEM for different scenarios, namely the ROI with holes, the ROI with a nonuniform information generation rate, and the ROI with a nonuniform density. The simulation settings for these scenarios are listed in Table 5. Twenty thousand sensors are randomly deployed based on the density distribution ψ and generate information based on ρ except for the sink which will consume all the information generated. Similarly, routing directions are solved using only the macroscopic parameters, ψ and ρ, but not the detailed position of each node. The node positions are merely used to determine the next forwarding node from the routing directions. In addition, the energy consumption per unit of information is proportional to \(r^{\alpha _{\textit {rf}}}\phantom {\dot {i}\!}\) with α rf =2 and thus J=ψ 4 as indicated in (13).
The routing directions obtained by DGSI-FEM are depicted as arrows in Fig. 11. The arrows provide the routing guidance for load-balancing. For example, Fig. 11 a reveals that information may be forwarded in a direction which deviates from a straight line to the sink to bypass the holes in advance. Thus, unlike many hole-bypassing algorithms [15, 31–33], using routing directions may alleviate the excess energy consumption of the boundary sensors.
Routing direction. All ROIs are square regions divided into 37×37 grids. Sinks which will consume all the information generated are marked as circles, and the arrows represent the routing directions, \(\widetilde {\mathbf {u_{f}}}\)s. a Uniform ψ and ρ: the black regions represent the holes. b Uniform ψ and nonuniform ρ: the sensors in the gray region generate ten times more information than other sensors. c Nonuniform ψ and uniform ρ: the gray region has 50 % higher sensor density than the white region. d Nonuniform density and uniform ρ: the gray region has 30 % lower sensor density than the white region
The routing directions shown in Fig. 11 b indicate that, to achieve load-balancing, information may be forwarded to the sensors outside the high- ρ region and then to the sink, instead of being delivered straight to the sink by the sensors in the high- ρ region. Particularly, some nodes around the bottom-right corner of the high- ρ region may forward packets in the opposite direction to the sink in order to avoid using nodes in the high- ρ region. Note that the sensors in the high- ρ region generate more events and potentially have more loading.
The routing directions shown in Fig. 11 c, d indicate that the information traffic tends to flow into the high-density regions and bypass the low-density regions to achieve load-balancing. Similar to Fig. 11 b, Fig. 11 d depicts that some nodes along the bottom-left boundary of the low-density region may forward packets in the opposite direction to the sink in order to avoid using nodes in the low-density region. In the last two scenarios, the ρs are uniform; thus, the sensors in the high-density (or low-density) region generate fewer (or more) events and potentially have less (or more) loading.
We then conducted simulations to compare the energy consumption of the routing directions obtained from DGSI-FEM with that of a microscopic routing algorithm, namely greedy perimeter stateless routing (GPSR) [31]. We used the approach described in Section 4.4 to route the information via the routing directions. Note that GPSR normally works as GF [12]; that is, the next forwarding node will be the one closest to the destination among the current sender’s neighbors. However, if GF fails to find the node making any progress in delivering information, the node to the left in a planar subgraph of the connectivity graph of the WSN will be selected as the next forwarding node until GF recovers. The planarization used here is RNG [34].
We also conducted comparative simulations for another microscopic routing algorithm, namely geographical and energy aware routing (GEAR) [35], which attempts to achieve load-balancing by considering both the distance to the sink and the energy consumption. If a node has neighbors closer to the sink, GEAR will choose among these neighbors the one with the smallest weighted sum of the distance to the sink and the energy consumed as the next forwarding node; otherwise, the neighbor with the smallest weighted sum is the next forwarding node.
Figure 12 depicts the means and standard deviations of the energy consumption of DGSI-FEM and GEAR, normalized to the energy consumption of GPSR. Referring to Fig. 11 a, DGSI-FEM may forward information in a direction which deviates from a straight line to the sink to bypass the holes in advance, while our GPSR implementation uses the left-hand rule to forward information, thus resulting in excess energy consumption along the holes. Hence, DGSI-FEM may achieve better load-balancing with less energy consumption than GPSR for the ROI with holes.
The relative statistics of energy consumption of the scenarios in Fig. 11: the relative mean (or standard deviation) of DGSI-FEM (or GEAR) is defined as the mean (or standard deviation) of the routing energy consumption of DGSI-FEM (or GEAR) divided by the mean (or standard deviation) of the routing energy consumption of GPSR. a The relative mean of the energy consumption. b The relative standard deviation of the energy consumption
Furthermore, GPSR is degenerated to GF for the ROIs without holes and thus exhibits a lower average energy consumption for the scenarios shown in Fig. 11 b–d. On the other hand, DGSI-FEM will avoid the nodes in the high- ρ and low-density region and utilize the nodes in the high-density region for load-balancing. Thus, the routing paths will bypass the high- ρ and low-density regions or bend into the high-density region.
In addition, though GEAR strives to achieve load-balancing by considering the distance and energy factors, the best next forwarding node is still a local optimum; thus, GEAR provides less effective load-balancing than does DGSI-FEM. The standard deviation results in Fig. 12 b indicate that the routing directions solved by DGSI-FEM can effectively achieve load-balancing, particularly for the ROIs having holes.
6 Conclusions
This paper studies the minimum routing cost problems for massively dense WSNs via the geographical model, which leads to the grid-based directional routing algorithms. The minimum routing cost problems are formulated as continuous geodesic problems under massively dense WSNs, and the grid-based directional routing algorithms are the natural outcomes of numerically solving these problems; numerical solutions of the geodesic problems provide the directions to the next forwarding nodes at equally spaced grid points in the ROI, and these directions can be used as guidance to route information.
We first consider the position-only-dependent costs (e.g., hops, throughput, or energy) and investigate two numerical approaches, GADM and FM. GADM uses Dijkstra’s method to determine the minimum cost path (under the grid point network). However, GADM may yield less optimum routing paths due to the direction restriction. On the other hand, by introducing the cost map T, the geodesic problem can be transformed into the eikonal equation and then solved by FM. Note that the geodesic problem considered here is to find a continuous curve which has the minimum cost from a given source to a sink. Our numerical results show that FM is more suitable than GADM for approximating the continuous curves and thus yields a path with less routing cost. The routing cost comparison results shows that FM has a routing cost 5 % more than the optimum cost, and GADM may have a routing cost 28 % more than the optimum cost.
We then consider the traffic-proportional costs which correspond to energy-load-balancing. By the equivalence between geodesic problems and optimum routing vector field problems, we transform the geodesic problem into a set of equations with regard to the routing vector field, which can be more easily tackled. We propose a distributed algorithm, i.e., DGSI-FEM, for solving the routing vector field via FEM and present the numerical results to demonstrate the quality of the derived routing directions. The routing energy consumption results show that routing directions may effectively achieve load-balancing than the microscopic routing algorithms, GPSR, and GEAR, particularly for the ROIs with holes.
Many aspects of this paper, the problems studied and the approaches taken, are the application of the existing work, e.g., minimum cost routing paths [23], cost function and node density [5, 24, 26], geodesic path via eikonal equation [27], fast marching method [8, 28], load-balancing routing equations [2, 24, 29, 30], and finite element method [9]. However, these works either do not specifically focus on the network routing problems or only theoretically analyze the routing problems without providing routing algorithms. The main contribution of this paper is to propose a systematic framework to develop low overhead routing algorithms for massively dense WSNs, i.e., coordinate sensor nodes themselves to solve the routing directions using these existing techniques and then route the information with the routing directions. In addition, there have existed numerous strategies for solving geodesic paths and PDEs. We believe this paper will open up a potential research direction toward the development of routing algorithms via investigation of the appropriateness of these strategies for implementation on WSNs.
7 Appendix 1: proof of theorem 3
For the sake of convenience, we use the position vector x to represent the position (x,y). Consider T(x) and for any dx, i.e., a small change of x:
by the Taylor expansion [29]. Let the cost of the straight line from x to x+dx be ΔT ′; then:
Since T is the minimum cost:
Thus, choosing dx = small multiple of ∇T:
On the other hand, consider x and x+dx along a minimum cost path. We have:
and then by (22):
in which θ is the angle between ∇T and dx. Therefore, \(\left |\nabla T\right | \geq \mathcal {C}\), and (3) is proved.
Furthermore, consider x and x+dx along a minimum cost path. It is also clear from (3) and (23) that θ=0. Since both x and x+dx are on a minimum cost path, dx and thus ∇T are tangent to the minimum cost path.
8 Appendix 2: weak formulation of the load-balancing routing equations, (8), (10), and (11)
Multiply (8) by an arbitrary smooth scalar valued function ν and integrate it over the ROI; then:
By the product rule of a scalar valued function and a vector field:
we have:
and hence:
By divergence theorem, we obtain:
By substituting (10) and the boundary condition (11) into the above equation, we have the weak formulation (12).
9 Appendix 3: values of \(K^{i',j'}_{i,j}\) and g i,j
Referring to Fig. 9, for the element centered at  (i.e., the gray hexagon), denoted H
i,j
as the set of vertices, that is:
(i.e., the gray hexagon), denoted H
i,j
as the set of vertices, that is:

and T i,j as the set of the triangles forming the element, that is:
Similar to (15), we approximate ν by:

By substituting (15) and the above equation into (12), (12) becomes:

By reordering the summation and integral of the above equation, we then have:

Since ν is arbitrary, \(\widetilde {\nu }_{{i,j}}\) are arbitrary. Therefore, the above equation leads to:

By reordering the summation and integral of the above equation, we obtain:

Define:
and:
Then (24) can be written as (18).
From (19):
and:
Note that if  and
and  the element centered at
the element centered at  and the element centered at
and the element centered at  do not overlap; therefore, it is not difficult to verify that:
do not overlap; therefore, it is not difficult to verify that:
In addition, if (x,y) in \( {}_{i_1}{,}_{j_1}{\triangle}_{i_3,{j}_3}^{i_2,{j}_2}\in {T}_{i_1,{j}_1} \), (x,y) is located within the elements centered at 
 and
and  and \( J\left(x,y\right)=\sum_{k=1}^3{\overset{\sim }{J}}_{i_k,{j}_k}{\mu}_{i_k,{j}_k}\left(x,y\right) \) by (16) and (19). For example, for (x,y) in \(_{i,j}\triangle ^{i+1,j}_{i+1,j-1}\):
and \( J\left(x,y\right)=\sum_{k=1}^3{\overset{\sim }{J}}_{i_k,{j}_k}{\mu}_{i_k,{j}_k}\left(x,y\right) \) by (16) and (19). For example, for (x,y) in \(_{i,j}\triangle ^{i+1,j}_{i+1,j-1}\):
Thus:
Note that referring to Fig. 9, \( \int {_{_{i,j}\triangle ^{i+1,j}_{i+1,j-1}}}\mu _{i,j}\mathrm {d}y\mathrm {d}x\) is the volume of the triangular pyramid formed by the vertex (x i ,y j ,μ i,j (x i ,y j )) and \(_{i,j}\triangle ^{i+1,j}_{i+1,j-1}\); here, the volume is h 2/6, since μ i,j (x i ,y j )=1 and the area of \(_{i,j}\triangle ^{i+1,j}_{i+1,j-1}\) is h 2/2. The same argument can be used to compute the rest of two integrals in the above equation. Thus, referring to (20) and (6):
Here, δs are added to check whether the vertices of \(_{i,j}\triangle ^{i+1,j}_{i+1,j-1}\) are in the ROI.
Similarly, this integral computation can apply to other \(\vartriangle \)s in T i,j , and we have:
for i,j △i 2,j 2 i 1,j 1∈T i,j . By denoting:
we then have:
Now we compute \(K^{i^{\prime },j^{\prime }}_{i,j}\)s for  We first consider
We first consider  Referring to (25), the only \(\vartriangle \)s for both ∂μ
i,j
/∂x≠0 and ∂μ
i+1,j
/∂x≠0 are \(_{i,j}\triangle ^{i,j+1}_{i+1,j}\) and \(_{i,j}\triangle ^{i+1,j}_{i+1,j-1}\), and there is no \(\vartriangle \) for both ∂μ
i,j
/∂y≠0 and ∂μ
i+1,j
/∂y≠0. Therefore:
Referring to (25), the only \(\vartriangle \)s for both ∂μ
i,j
/∂x≠0 and ∂μ
i+1,j
/∂x≠0 are \(_{i,j}\triangle ^{i,j+1}_{i+1,j}\) and \(_{i,j}\triangle ^{i+1,j}_{i+1,j-1}\), and there is no \(\vartriangle \) for both ∂μ
i,j
/∂y≠0 and ∂μ
i+1,j
/∂y≠0. Therefore:
The same argument can be used to compute \(K^{i^{\prime },j^{\prime }}_{i,j}\)s for the rest of  in H
i,j
, and we have:
in H
i,j
, and we have:
Note that as mentioned earlier, \(K^{i^{\prime },j^{\prime }}_{i,j} = 0\) if  and
and  Thus, together with \(K^{i+1,j-1}_{i,j}= 0\) and \(K^{i-1,j+1}_{i,j}= 0\), we have:
Thus, together with \(K^{i+1,j-1}_{i,j}= 0\) and \(K^{i-1,j+1}_{i,j}= 0\), we have:

To compute g i,j , we use (17) to expand g i,j as follows:

If  and
and  the element centered at
the element centered at  and the element centered at
and the element centered at  do not overlap; therefore, it is not difficult to verify from (19) that \(\mu _{i^{\prime },j^{\prime }} \mu _{i,j} = 0\). Hence:
do not overlap; therefore, it is not difficult to verify from (19) that \(\mu _{i^{\prime },j^{\prime }} \mu _{i,j} = 0\). Hence:

In addition, it is obvious that if \( \vartriangle \notin {T}_{i,j} \), \(\int _{\vartriangle }\mu _{i^{\prime },j^{\prime }} \mu _{i,j}\mathrm {d}y\mathrm {d}x=0\). We only need to compute the integral over the region \( \vartriangle \in {T}_{i,j} \).
We first consider the integral over \(_{i,j}\triangle ^{i+1,j}_{i+1,j-1}\):

The computation of each integral of the above equation is carried out as follows:
Hence:

By denoting:
we then have:

The same computation can be carried out for the rest of △s in T i,j , and we have:
10 Appendix 4: values of \(\widetilde {\mathbf {D}}_{{i},{j}}\)
By (10) and (15) together with the boundary condition (11):
Here, D
x
is the x component of D and (x
i
,y
j
) is the position of 
Note that (x
i
+Δx,y
j
) is located within the elements centered at  and
and  . Thus:
. Thus:
From (19), μ i,j+1(x i +Δx,y j )=0 and μ i+1,j−1(x i +Δx,y j )=0. Thus:
From (19):
and:
Thus:
Similarly:
Hence:
Therefore:
Similarly:
References
IF Akyildiz, W Su, Y Sankarasubramaniam, EE Cayirci, A survey on sensor networks. IEEE Commun. Mag.40(8), 102–114 (2002).
P Jacquet, in Proceedings of the 5th ACM International Symposium on Mobile Ad Hoc Networking and Computing. Geometry of information propagation in massively dense ad hoc networks (ACMRoppongi Hills, Tokyo, Japan, 2004), pp. 157–162.
P Gupta, PR Kumar, The capacity of wireless networks. IEEE Trans. Inform. Theory. 46(2), 388–404 (2000).
M Kalantari, M Shayman, in 2004 IEEE International Conference on Communications, vol. 7. Routing in wireless ad hoc networks by analogy to electrostatic theory (IEEE PressParis, France, 2004), pp. 4028–4033.
R Catanuto, G Morabito, S Toumpis, in Proceedings of the 3rd International Symposium on Wireless Communications Systems. Optical routing in massively dense networks: practical issues and dynamic programming interpretation (ACMValencia, Spain, 2006).
E Hyytiä, J Virtamo, in Proceedings of the 10th ACM Symposium on Modeling, Analysis, and Simulation of Wireless and Mobile Systems. On optimality of single-path routes in massively dense wireless multi-hop networks (ACMChania, Crete Island, Greece, 2007), pp. 28–35.
J-Y Li, R-S Ko, in Proceedings of the 28th Edition of the International Conference on Information Networking. Grid-based directional minimum cost routing for massively dense wireless sensor networks (IEEE PressPhuket, Thailand, 2014), pp. 136–141.
JA Sethian, Fast marching methods. SIAM Rev. 41(2), 199–235 (1999). doi:10.1137/S0036144598347059.
TI Zohdi, A Finite Element Primer for Beginners: The Basics. SpringerBriefs in Applied Sciences and Technology (Springer, New York, 2014).
R-S Ko, Analyzing the redeployment problem of mobile wireless sensor networks via geographic models. Wirel. Commun. Mob. Comput.13(2), 111–129 (2013). doi:10.1002/wcm.1099.
M Mauve, J Widmer, H Hartenstein, A survey on position-based routing in mobile ad-hoc networks. IEEE Netw.15(6), 30–39 (2001).
GG Finn, Routing and addressing problems in large metropolitan-scale internetworks. Research ISI/RR-87-180, Information Sciences Institute (1987).
I Stojmenovic, X Lin, Loop-free hybrid single-path/flooding routing algorithms with guaranteed delivery for wireless networks. IEEE Trans. Parallel Distrib. Syst.12(10), 1023–1032 (2001).
I Stojmenovic, M Russell, B Vukojevic, in Proceedings of the 2000 International Conference on Parallel Processing. Depth first search and location based localized routing and QoS routing in wireless networks (IEEE Computer SocietyToronto, Canada, 2000), pp. 173–180.
Q Fang, J Gao, LJ Guibas, Locating and bypassing holes in sensor networks. Mobile Networks and Applications. 11(2), 187–200 (2006).
D Niculescu, B Nath. Trajectory based forwarding and its applications (ACMSan Diego, CA, USA, 2003), pp. 260–272.
S Jung, M Kserawi, D Lee, J-KK Rhee, Distributed potential field based routing and autonomous load balancing for wireless mesh networks. IEEE Commun. Lett.13(6), 429–431 (2009).
C-F Chiasserini, R Gaeta, M Garetto, M Gribaudo, D Manini, M Sereno, Fluid models for large-scale wireless sensor networks. Perform. Eval.64(7–8), 715–736 (2007).
E Altman, P Bernhard, A Silva, in Proceedings of the 7th International Conference on Ad-hoc, Mobile and Wireless Networks. The mathematics of routing in massively dense ad-hoc networks (SpringerSophia-Antipolis, Frances, 2008), pp. 122–134.
S Toumpis, in The 2006 Workshop on Interdisciplinary Systems Approach in Performance Evaluation and Design of Computer & Communications Systems. Optimal design and operation of massively dense wireless networks: or how to solve 21st century problems using 19th century mathematics (ACM PressPisa, Italy, 2006).
S Toumpis, Mother nature knows best: a survey of recent results on wireless networks based on analogies with physics. Comput. Netw.52(2), 360–383 (2008).
M Haghpanahi, M Kalantari, M Shayman, in Proceedings of the 28th IEEE Conference on Global Telecommunications. Implementing information paths in a dense wireless sensor network (IEEE PressHonolulu, Hawaii, USA, 2009), pp. 5412–5418.
R-S Ko, Macroscopic analysis of wireless sensor network routing problems. Adhoc & Sensor Wireless Networks. 13(1–2), 59–85 (2011).
R-S Ko, A distributed routing algorithm for sensor networks derived from macroscopic models. Comput. Netw.55(1), 314–329 (2011).
F Zhao, L Guibas, Wireless Sensor Networks: An Information Processing Approach (Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, 2004).
S Toumpis, L Tassiulas, Optimal deployment of large wireless sensor networks. IEEE Trans. Inform. Theory. 52(7), 2935–2953 (2006).
G Peyré, M Péchaud, R Keriven, LD Cohen, Geodesic methods in computer vision and graphics. Foundations and Trends in Computer Graphics and Vision. 5(3–4), 197–397 (2010). doi:10.1561/0600000029.
E Rouy, A Tourin, A viscosity solutions approach to shape-from-shading. SIAM J. Numer. Anal.29(3), 867–884 (1992). doi:10.1137/0729053.
JE Marsden, AJ Tromba, Vector Calculus, 5th edn. (W. H. Freeman, New York, 2003).
M Kalantari, M Shayman, in IEEE Wireless Communications and Networking Conference. Design optimization of multi-sink sensor networks by analogy to electrostatic theory (IEEE PressLas Vegas, NV USA, 2006), pp. 431–438.
B Karp, HT Kung, in Proceedings of the 6th Annual International Conference on Mobile Computing and Networking. GPSR: greedy perimeter stateless routing for wireless networks (ACMBoston, MA, US, 2000), pp. 243–254.
P Bose, P Morin, I Stojmenovic, J Urrutia, Routing with guaranteed delivery in ad hoc wireless networks. Wirel. Netw.7(6), 609–616 (2001).
W-J Liu, K-T Feng, Greedy routing with anti-void traversal for wireless sensor networks. IEEE Trans. Mobile Comput.8(7), 910–922 (2009).
GT Toussaint, The relative neighbourhood graph of a finite planar set. Pattern Recogn.12(4), 261–268 (1980).
Y Yu, R Govindan, D Estrin, Geographical and energy aware routing: a recursive data dissemination protocol for wireless sensor networks. Technical Report UCLA/CSD-TR-01-0023, Computer Science Department, UCLA (2001).
Acknowledgements
This research was supported by Ministry of Science and Technology of Taiwan, under Grant MOST 104-2221-E-194-008. The authors gratefully acknowledge this support.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Li, JY., Ko, RS. Geographical model-derived grid-based directional routing for massively dense WSNs. J Wireless Com Network 2016, 17 (2016). https://doi.org/10.1186/s13638-015-0492-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-015-0492-1





 , and the black regions represent the holes. a Routing direction
, and the black regions represent the holes. a Routing direction  . c Routing paths: the source is close to the grid point
. c Routing paths: the source is close to the grid point 




 and is nonzero only within the element centered at
and is nonzero only within the element centered at  (i.e., the gray hexagon). In addition, (x
i
,y
j
) is the position of
(i.e., the gray hexagon). In addition, (x
i
,y
j
) is the position of 

 waits for
waits for 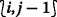 and
and  , which have smaller
, which have smaller 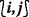 updates
updates  updates DONE
i,j
. (Lines 11–19)
updates DONE
i,j
. (Lines 11–19) sends
sends 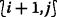 and
and 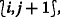 , respectively, which have larger
, respectively, which have larger 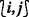 waits for
waits for  updates
updates 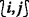 updates PRECISE
i,j
. (Lines 31–33)
updates PRECISE
i,j
. (Lines 31–33)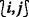 sends
sends  is an
is an  is not an
is not an 

