- Research
- Open access
- Published:
Pursuit-evasion games: a tractable framework for antijamming games in aerial attacks
EURASIP Journal on Wireless Communications and Networking volume 2017, Article number: 69 (2017)
Abstract
We solve a communication problem between a UAV and a set of receivers, in the presence of a jamming UAV, using differential game theory tools. We propose a new approach in which this kind of games can be approximated as pursuit-evasion games. The problem is posed in terms of optimizing capacity, and it is solved in two ways: firstly, a surrogate function approach is used to approximate it as a pursuit-evasion game; secondly, the game is solved without that approximation. In both cases, Isaacs equations are used to find the solution. Finally, both approaches are compared in terms of relative distance and complexity.
1 Introduction
The jamming problem in wireless links has received a lot of attention in research. The expansion of wireless communications has been responsible for that. A field of interest in this area is related to communications between unmanned aerial vehicles (UAVs), whose communications must be wireless and hence vulnerable to jamming attacks. This is an area of research where different attack/defense strategies have been proposed. A wide variety of techniques are used, such as spectral channel surfing and spatial positioning of the nodes [27], game theory tools [12, 13, 25, 26], or the use of a honeypot node [4]. A general survey of jamming techniques is presented in [20].
In case that the jammer and communicating nodes are mobile, the attack can be modeled as a zero-sum, non-cooperative differential game [1]. There are several tools dedicated to analyze this kind of games, especially for two-player games [8, 11]. There are specific solutions for some multi-player games, such as [3, 19, 24]. The main tools used are the Hamilton-Jacobi-Bellman-Isaacs equations, which are difficult to solve to obtain an analytical solution. In some specific games, the game can be solved using only Isaacs equations [8], which greatly simplify the analysis. However, Isaacs equations are not very known, and in this work, we also relate them to Bellman and Pontryagin methods, showing that Isaacs equations are a particularization of them for pursuit-evasion games. The main advantage of Isaacs equations relies on the fact that they provide a method that uses a set of steps to find the solution to the game.
Another contribution of this work is posing the problem of pursuit-evasion in terms of capacity, which none of the cited works do. This approach allows us to study the problem from the communications point of view: our target is to optimize the communications capacity, which to the best of our knowledge, has not been done yet. We approximate the communications capacity by a linear function, and it turns out that solving the game using that function becomes unpractical. We also solve the pursuit-evasion game—without taking into account the communications capacity—and we show that both problems have very similar solutions. Hence, we show that it is possible, under certain circumstances, to approximate the hard capacity problem by an easier pursuit-evasion game, which could be solved either analytically—as we do—or using numerical methods, as in [9].
This work also expands a previous one [18]. In both works, we study the case in which there is one UAV trying to communicate with receiver nodes while another UAV trying to jam the communications. The problem is modeled using differential game theory. The receivers can be static or dynamic, but their exact position is unknown. On [18], our main contribution was posing the problem in terms of optimizing capacity, and under some hypotheses, approximating it as a pursuit-evasion game using Isaacs’ tools, which allowed obtaining a new approach in which communications-related problems can be solved using well-known pursuit-evasion game tools. In this work, we deepen the theoretical bases for our approach and we also solve the capacity game posed without using the surrogate function approach. Both approaches give very similar solutions but very different computational complexity. Hence, in this work, our main contribution is to validate our primal approach, as well as to solve the game with less hypotheses, that allows comparing of both solutions.
The article is organized as follows: the main results and discussions are found in Sections 2 to 6. In Section 2, we give a brief introduction to differential game theory and present Isaacs equations. Then, in Section 3, we describe the jamming problem that we pose and obtain the expression for total system capacity. After, in Section 4, we solve the game posed in Section 3 approximating it as a pursuit-evasion game. Next, in Section 5, the capacity game is solved. Both game results are compared in Section 6. Finally, the main conclusions are outlined in Section 7.
2 General framework of differential games
2.1 Introduction to game theory
Game theory [1] is a branch of mathematics that deals with interactions among multiple decision makers called players. A player tries to optimize her own objective function, which generally depends on the actions of other players, which means that a player cannot optimize her objective function independently of the rest of players.
In this paper, we will center in non-cooperative, dynamic, zero-sum games. Non-cooperative games model the actions of agents trying to maximize their own objective function. In these games, the solution concept that is used is a Nash equilibrium, named after the mathematician John Nash who introduced and proved this concept [16, 17]: a Nash equilibrium is such that none of the players can improve her payoff by a unilateral move.
A game is dynamic if a player takes different decisions over time [5]. In these games, the objective function of the players depend on a state which changes with time. Also, each player makes various actions, which are collected by her strategy, which is a function of time.
In the case of dynamic games, the time interval over which the game takes place can be finite, that is, t∈ [ 0,t f ], or infinite, when t∈ [ 0,∞): that causes games to be of finite or infinite horizon. Also, it is possible that this time is discrete or continuous; in the second case, the game is usually called differential game.
Finally, a game is called zero-sum if the sum of the objective functions of the players can be made zero after appropriate positive scaling and/or translation that do not depend on the decision variables of the players (i.e., their actions or controls) [1].
2.2 Introduction to differential games
A differential N player game, with N players and where  is the players set, has the following elements:
is the players set, has the following elements:
-
A continuous time interval, t∈ [ 0,t f ], where t f is the final time of the game. This interval denotes the duration of the evolution of the game, which can be finite in case that t f <∞ or infinite otherwise. In this work, we will study finite horizon games.
-
A trajectory space, denoted by
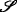 , which is an infinite set whose elements are the permissible state trajectories, denoted as {x(t),0≤t≤t
f
}. For each fixed t∈ [ 0,t
f
], x(t)∈S
0, where S
0 is a subset of a finite-dimensional vector space. The trajectories x(t) describe the state of each player in each time instant.
, which is an infinite set whose elements are the permissible state trajectories, denoted as {x(t),0≤t≤t
f
}. For each fixed t∈ [ 0,t
f
], x(t)∈S
0, where S
0 is a subset of a finite-dimensional vector space. The trajectories x(t) describe the state of each player in each time instant. -
An action space for each of the N players, denoted by
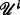 , which is an infinite set defined for each
, which is an infinite set defined for each 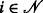 . The elements of this set are the permissible controls of player i. There exists a set
. The elements of this set are the permissible controls of player i. There exists a set  so that for each fixed t∈ [ 0,t
f
], u
i
(t)∈S
i. The controls will be functions of the time, and the game solution searches for the optimal control function for each one of the players that drive the game to a Nash equilibrium situation.
so that for each fixed t∈ [ 0,t
f
], u
i
(t)∈S
i. The controls will be functions of the time, and the game solution searches for the optimal control function for each one of the players that drive the game to a Nash equilibrium situation. -
A differential equation, called the dynamics equation, which defines how the states vary with time as a function of the players’ controls, states, and time. Its solution describes the state trajectory of the game as a function of controls and initial state (i.e., x 0). Its form will be:
$$ \frac{d x(t)}{dt}=f(t,x(t),u_{1}(t),\ldots,u_{N}(t)), x(0)=x_{0} $$(1) -
A set-valued function η i(t) which determines the information that is available to player i at time t. There are two main information patterns [1]:
-
1.
Open-loop pattern, if η i(t)={x 0},t∈ [ 0,t f ]. The player can only access the initial state of the game.
-
2.
Closed-loop perfect state (CLPS) information, if η i(t)=x(s),∀s∈ [ 0,t]. The player has access in every stage of the game, to the current, past, and initial states.
-
1.
-
Two functionals for each player, \(G^{i}:S^{0} \rightarrow \mathbb {R}, L^{i}:[\!0,t_{f}]\times S^{0}\times S^{1}\times...\times S^{N} \rightarrow \mathbb {R}\), defined for each
 , so that the cost functional of player i, denoted by π
i(x(t),u
1(t),...,u
N
(t)), is well defined. Its form is:
$$ \begin{aligned} \pi^{i}&(x(t),u_{1}(t),..., u_{N}(t))\\=& \int_{0}^{t_{f}} L^{i}(t,x(t),u_{1}(t),...,u_{N}(t)) dt + G^{i}(x(t_{f})) \end{aligned} $$(2)
, so that the cost functional of player i, denoted by π
i(x(t),u
1(t),...,u
N
(t)), is well defined. Its form is:
$$ \begin{aligned} \pi^{i}&(x(t),u_{1}(t),..., u_{N}(t))\\=& \int_{0}^{t_{f}} L^{i}(t,x(t),u_{1}(t),...,u_{N}(t)) dt + G^{i}(x(t_{f})) \end{aligned} $$(2)This cost functional is the objective function. L i is called the running cost, and G i is the terminal cost, the former being the cost incurred while the game is being played and the latter being the cost that adds up in a particular terminal state.
2.3 Standard methods for solving differential games
In order to solve a differential game, the information structure η i(t) plays a key role in the solution procedure used [28, pp 22–32]. Mainly, two approaches are followed: the maximum principle of optimal control, developed by Pontryagin [21], is used to solve open-loop games, whereas the principle of dynamic programming by Bellman [2] is used to solve closed-loop, perfect state information games.
If the information structure follows an open-loop pattern, each player can only access the initial state of the game, and this information allows each player to know the optimal trajectories of the others. Hence, the controls become a function of initial state and time. The solution to this problem uses the maximum principle of Pontryagin and is characterized using the following theorem [28, pp 24–25]:
Theorem 1
A set of strategies \(\{u_{i}^{*}(t)\), for i∈N} provides an open-loop Nash equilibrium solution to the game in Section 2.2, being {x ∗(t),t∈ [ 0,t f ]} as the corresponding state trajectory, if there exist m costate functions \(\Lambda ^{i}(t):[\!0,t_{f}] \rightarrow \mathbb {R}^{m}\), for i∈N, such that the following relations are satisfied:
-
\(\begin {aligned}[t]u_{i}^{*}(t)=& \arg \max _{u_{i}} \{ L^{i}(t,x^{*}(t),u_{1}^{*}(t),...,u_{N}^{*}(t)) \\ &+\Lambda ^{i}(t) f(t,x^{*}(t),u_{1}^{*}(t),...,u_{N}^{*}(t)) \}\end {aligned}\)
-
\(\dot {x^{*}}(t)=f(t,x^{*}(t),u_{1}^{*}(t),...,u_{N}^{*}(t))\), x ∗(0)=x 0
-
\(\dot {\Lambda ^{i}}(t)=-\frac {\partial }{\partial x^{*}} \{L^{i}(t,x^{*}(t),u_{1}^{*}(t),...,u_{N}^{*}(t))+\Lambda ^{i}(t) f(t,x^{*}(t),u_{1}^{*}(t),...,u_{N}^{*}(t)) \}\)
-
\(\Lambda ^{i}(t_{f})=\frac {\partial }{\partial x^{*}} \{G^{i}(x^{*}(t_{f})) \}\)
for i∈N
This theorem could also be used to obtain solutions under closed-loop information structure; however, the partial derivative with respect to x in the costate equations would receive contributions from dependence of the others N−1 players’ strategies on the current value of x, which complicates the solution. Another problem is that there are, in general, an uncountable number of solutions, due to information non-uniqueness.
In order to avoid these problems, closed-loop perfect state (CLPS) information structure is used. The solution to this problem uses Bellman’s dynamic programming principle and is characterized using the following theorem [28, p 28]:
Theorem 2
A set of strategies \(\{u_{i}^{*}(t)\), for i∈N} provides a feedback Nash equilibrium solution to the game in Section 2.2, if there exist continuously differentiable functions \(V^{i}(t,x):[\!0, t_{f}] \times \mathbb {R}^{m} \rightarrow \mathbb {R}, i \in N\), satisfying the following set of partial differential equations:
-
\(\begin {aligned}[t] -\frac {\partial V^{i}(t,x)}{\partial t}=&\max _{u_{i}} \{L^{i}(t,x^{*}(t),u_{1}^{*}(t),...,u_{N}^{*}(t)) \\ &+\frac {\partial V^{i}(t,x)}{\partial x} f(t,x^{*}(t),u_{1}^{*}(t),...,u_{N}^{*}(t)) \} \end {aligned}\)
-
V i(t f ,x)=G i(x)
for i∈N
Observe that the expression from Theorem 1 can be obtained from the optimality system in Theorem 2 in the case where the value function is smooth. If the value function is not smooth, weak derivatives or derivative in the distribution sense can be used as well.
2.4 Pursuit-evasion games
Let us particularize the expressions in Section 2.2 for a two-player, zero-sum, pursuit-evasion game. Being two-player means that there are N=2 players, called pursuer and evader, respectively. The pursuer tries to catch the evader, whereas the evader seeks to flee from the pursuer. Their controls will be called ϕ(t) and ψ(t), and the dynamics equation will be provided by the concrete setup of the game. The state vector will be called x(t). Both players will have the same cost functional with opposite sign, and hence, the rewards add up zero, and thus, the game will be zero-sum. That means that the gains of one player are the losses of the other. This payoff function is given by the following functional, which comes from (2):
In a pursuit-evasion game, final and running costs are G=0 and L=1, respectively; thus, the payoff function will be π=t f , where t f stands for capture or termination time. Pursuer tries to minimize the capture time and evader tries to maximize it.
The game outcome obtained if both players implement their optimal strategy will be called value function V(x)=π[ x(t),ϕ ∗(t),ψ ∗(t)], where ϕ ∗ denotes the optimum value of ϕ and ψ ∗ is the optimum value of ψ, for any state x(t) in the state space. The gradient of the value function will be denoted as ∇V. Lastly, the concrete setup of the system will provide the dynamic equation, which will be expressed in the following form: \(\dot {x}=f\left (x(t),\phi (t),\psi (t)\right)\).
Finally, a key element of the solution procedure is the Hamiltonian, which is built using the dynamics equation, the gradient of the value function, and the running cost of the game as follows:
where ∇V T is the transposed of the vector ∇V.
2.5 Isaacs’ approach
Apart from the methods described in Section 2.3, another approach can be used to solve certain kind of games: Isaacs’ equation [8]. This method can be used to solve open-loop games, which satisfy the following conditions:
-
The game is two players, zero-sum, and pursuit-evasion type. Being a pursuit-evasion game implies that final time is free (i.e., to be optimized), but this condition can be relaxed [8, p. 34].
-
The Hamiltonian is separable on its controls [8, p. 35].
If these hypotheses are satisfied, the Hamiltonian satisfies the following conditions along the optimal trajectories:
1. H(x, ∇V,ϕ,ψ ∗)≤H(x, ∇V, ϕ ∗,ψ ∗)≤H(x,∇V,ϕ ∗,ψ)
2. H(x,∇V,ϕ ∗,ψ ∗)=0
The first condition means that any unilateral deviation by the pursuer leads to a smaller Hamiltonian value (and any unilateral deviation by the evader leads to a larger Hamiltonian value), which is the Nash equilibrium definition. The second condition means that when both players use their optimal controls, the Hamiltonian is zero.
The method used by Isaacs has the following steps:
-
First, the system states must be defined, and a dynamics equation that relates states with controls must be obtained. This dynamics equation will have the following form:
$$ \frac{d x(t)}{dt}=f(x(t), \phi(t), \psi(t)) $$(5) -
Secondly, the Hamiltonian must be built and optimized. This is done using Isaacs “main equation 1,” which is the Hamiltonian:
$$ \max_{\psi} \min_{\phi} \sum_{i} V_{x_{i}} f_{i} + L=0 $$(6)where \(V_{x_{i}}\) stands for the partial derivative, that is, \(V_{x_{i}}=\frac {\partial V}{\partial x_{i}}\), and f i is the ith component of f(x(t),ϕ(t),ψ(t)) Eq. (5). This expression must be solved in order to obtain the optimal controls. These are substituted into the Hamiltonian to obtain the optimal Hamiltonian, denoted by H ∗.
-
Thirdly, the optimal trajectories are obtained using a backward procedure in which the retrogressive path equations (RPE) play a key role. These equations are a function of retro-time τ, which is the time-to-go, obtained using the following variable change:
$$ \tau=t_{f}-t $$(7)where t f is the termination time of the game. Intuitively, τ is a backward time: it goes from final time t f until initial time t=0. Hence, initial conditions in τ will be final conditions in time.
There will be two different RPEs. The first kind depends on the states and are obtained from the dynamics in Eq. (5). These RPEs have the following form:
$$ \frac{d x(t)}{dt}=f(x(t),\phi(t),\psi(t))=-\frac{d x(\tau)}{d\tau}=\mathring{x(\tau)} $$(8)where x ̈ denotes the derivative of x with respect to retro-time τ and x(τ)=x(t)| t=τ . That means that these RPEs are obtained changing the sign of the dynamic equation.
The second kind of RPEs depend on the gradient of the value function. Along the optimal trajectory, the following adjoint equation holds:
$$ \frac{d}{dt}\nabla V[\!x(t)]=-\frac{\partial}{\partial x} H(x,\nabla{V},\phi^{*},\psi^{*}) $$(9)Using Eq. (7), the adjoint equation becomes:
$$ \frac{d}{d\tau}\nabla V[\!x(\tau)]=\frac{\partial}{\partial x} H(x,\nabla{V},\phi^{*},\psi^{*}) $$(10)Hence, the RPEs related to the gradient are also related to the left-hand side of the “main equation” (ME) (6), according to this expression [8, p. 82]:
$$ \mathring{V_{k}}=\frac{\partial H}{\partial x_{k}}=\frac{\partial ME}{\partial x_{k}} $$(11)where x k refers to the states.
-
In order to solve the RPEs, initial conditions in retro-time are needed. The terminal surface is defined as a manifold, denoted by h, which is parametrized using n−1 variables (where n is the number of states). Each of these variables will be called s i ,i∈1,...,n−1. These will be initial conditions in τ (in time t, they are final condition), and they are obtained using the following expression:
$$ \frac{\partial G}{\partial s_{k}}=\sum_{i} V_{x_{i}} \frac{\partial h}{\partial s_{k}} $$(12)where G is the final cost of the game considered, h the terminal manifold, and s k the variables used to describe this manifold.
-
Once those final conditions in time are obtained, the RPEs are integrated in order to find out the optimal trajectories and the optimal controls for the posed game. However, these trajectories will be function of final time conditions, but we only know initial time conditions. In order to solve this problem, the final time t f must be obtained in order to get a system of equations that may allow us to obtain these final conditions in time from the initial ones. In doing this, the following vectorial identity is used, where s are the final conditions, initial state x 0 are the initial conditions, and T are the trajectories obtained after integrating the RPEs. The solutions of this equation system are the final conditions, depending on initial ones; by substituting these values on the trajectories equations, the dependency on initial conditions appears.
$$ T(\tau, s)=T(t_{f}-t, s)=T(t_{f}, s)=x_{0} $$(13)
2.6 Comparison of Isaacs with Bellman and Pontryagin approaches
Isaacs’ method described above is closely related to Pontryagin approach to solve games. If we compare Theorem 1 with Isaacs equations, it is possible to see that the first point of the theorem corresponds to Isaacs’ main equation 1 (6), the second one is the dynamics equation as appears in Eq. (5), and the third point is the adjoint equation which Isaacs includes in Eq. (9). Pontryagin uses costate functions, that he calls Λ(t), which can be identified with the gradient of the value function ∇V that Isaacs uses. Also, the final conditions on costate functions from Pontryagin and gradient of the value function that Isaacs used are obtained through partial derivatives of the final cost, as in Eq. (12) and the fourth point of Theorem 1.
Hence, it is possible to see that Isaacs equations are actually a particularization of Pontryagin’s method, for the concrete case that the game is zero-sum and two players and that controls are separable. Thus, it can be used to obtain open-loop solution to games that fall into this category.
Isaacs method is also related to Bellman method. Let us start from Hamilton-Jacobi-Bellman (HJB) equation, which comes from the first point in Theorem 2, using the definition of Hamiltonian from Eq. (4):
Isaacs’ main equation [8, p. 67] can be seen as a particular case, when \(\frac {\partial V}{\partial t}=0\), and hence, H ∗=0. Also, the game must be two players, zero-sum, and pursuit-evasion type, and its Hamiltonian must be separable on its controls.
Thus, if V, the game value function, does not depend explicitly on time, and these conditions are satisfied, Isaacs approach becomes also a particularization of Bellman equation (as it was expected: even the basis of their equations, Isaacs’ “Tenet of transition” [8] and Bellman’s “Principle of Optimality” [2], are very similar). This condition is also satisfied, according to [7, p. 36], when the optimal control problem that is being solved is time-invariant and the final time is free, i.e., needs to be optimized. This is extended to differential games [1, p 223]: a game is time-invariant if time does not appear explicitly as a variable in dynamics equation, running and terminal costs, and termination condition. In that case, partial derivative of value function with respect to time will be zero.
The drawbacks that arise when using Pontryagin’s method to solve closed-loop games (Section 2.3) would also affect Isaacs equations. Hence, they are usually only employed to solve open-loop games. Yet, as it is described in [1, pp 345-350], the solutions to some pursuit-evasion games are usually first obtained in open-loop strategies and then synthesized to feedback strategies, provided that both exists. Hence, in pursuit-evasion games, open-loop and feedback solutions are related. Bellman approach provides a sufficiency condition for saddle-point strategies, but his main drawback is that the value function V is generally not known ahead of time. In order to overcome this, Pontryagin method is used in order to obtain a set of necessary conditions for an open-loop representation of the feedback solution: if both open-loop and feedback equilibria exist, Pontryagin will lead to the desired solution. Hence, in these games, it is usual obtaining an open-loop representation of the solution, which then can be synthesized to obtain the feedback strategy. This is the main contribution of Isaacs method: obtaining open loop solution for games that fall into the category of pursuit-evasion, thus providing a simpler method than Bellman’s equation.
3 Problem description
3.1 Capacity approximation
In this section, we pose a capacity game. Let us suppose that there are two UAVs and a high number of receivers, which can be static or dynamic. The communicator tries to communicate with the receivers, whereas the jammer tries to jam this communication. Thus, both players have opposite objectives, and hence, a zero-sum game between them is posed.
The total capacity in this scenario can be computed as the sum of the different capacities at each receiver. Considering a free-space propagation model, orthogonal modulation, and using Shannon’s capacity formula, the total capacity per bandwidth unit of the system depends on the signal to interference plus noise ratio (SINR) as follows:
In the expression before, P c and P j are the communicator and the jammer transmission fixed power, respectively; d c,r i and d j,r i are the euclidean distances between the communicator or the jammer and receiver i, respectively, considering that there are N receivers; and N 0 is the noise floor power. The jammer sends a signal that is seen as interference by the communicator and the receivers: this jamming is referred to as trivial jamming [3]. The effectiveness of the jamming will be measured using the SINR. We consider that jamming is effective when SINR falls below a certain level threshold S I N R min .
In order to optimize the expression in Eq. (15), it would be necessary to know the position of each receiver in every time instant (and their dynamics if they were mobile). If there is no knowledge about receiver positions, a different approach is required. Let us suppose that receivers and UAVs move in the \(\mathbb {R}^{3}\) Cartesian space; thus, in every time instant, the position is defined by the vector (x,y,z). Let us assume that both UAVs move on the same plane (i.e., they have constant z-coordinate) and that all mobile receivers also move on the same plane, being ε the distance between the plane of receivers and the UAVs plane. This situation is shown in Fig. 1.
We assume that the communication channel is interference-limited [10, 22], that is, the jamming power is much higher than thermal noise. That means that \(\frac {P_{j}}{d_{j,ri}^{2}} \gg N_{0}\). Hence, the SINR can be approached by the SIR—that is, we neglect the noise term in Eq. 15. If the receiver positions in the plane are considered to be a random vector S=(S x ,S y ), with arbitrary probability density function p i (S x,i ,S y,i ), the game payoff can be computed as the mathematical expectation of the SIR as follows:
where d S i =d S y,i d S x,i , and \(d_{c,ri}^{2}(S)=(x_{c}-S_{x,i})^{2}+(y_{c}-S_{y,i})^{2}+\epsilon ^{2}\) and \(d_{j,ri}^{2}(S)=(x_{j}-S_{x,i})^{2}+(y_{j}-S_{y,i})^{2}+\epsilon ^{2}\) are, respectively, the distance between the communicator or the jammer and receiver i, whose plane coordinates are (S x,i ,S y,i ). If the random variables S i are considered to be independent and identically distributed (i.i.d.), assuming that receivers follow a uniform distribution over a square region in the interval [−D,D] in coordinates X and Y and assuming that this square region is much larger than the zone in which UAVs move and also much larger than ε, as it is shown in [18], the expression in Eq. (16) is approximated as:
where r=(y c −y j )2+(x c −x j )2. Hence, the capacity depends on r, the squared norm of the vector pointing from the communicator to the jammer. The jammer wants to minimize capacity and that means trying to be spatially close to the communicator, whereas the communicator tries to maximize capacity and that means being spatially as far as possible from the jammer.
3.2 Hyperbolic arcsine linearization
The expression in Eq. (17) can be further simplified linearizing the hyperbolic arcsine term. In order to do so, let us consider the following expression:
where K is a constant, that, in Eq. (17), is:
We want to fit this function using a linear expression, that is:
where m is the slope of the line and b is the intercept. In order to approximate this function, we must obtain the optimal parameters m and b that satisfy the optimization problem:
That is, we want to minimize the squared error between the original function and the fit, considering that the distance between players r is between 0 and D. Minimizing in a grid over K, b, and m and adjusting the results in the least squared sense, we obtain the following expressions:
Finally, the relative error is computed using m(K) and b(K) from (22) as:
The relative error obtained in our simulations is always inferior to 1% and is monotone decreasing with K. Hence, applying the expressions in Eqs. (22), (20), and (19) to simplify Eq. (17) yields the following simplified, linear expression for the capacity:
whose slope and intercept are:
4 Pursuit-evasion game of two UAVs
4.1 Introduction
In this section, the two-person, zero-sum, pursuit-evasion game that appears when approximating the problem described in Section 3 will be solved using Isaacs’ method, described in [8, Chap. 4], as a pursuit-evasion game, with running cost L=1. The solution to the capacity game involves that the jammer tries to be close to the communicator and the communicator tries to be far away from the jammer. This is also the idea in pursuit-evasion games, yet in these games, the payoff is not in terms of capacity, but in terms of capture time (Section 2), and hence, the running cost is L=1 in these games. In this case, we are using a surrogate function approach, which gives an approximation of the solution.
We consider each UAV to have a constant acceleration, that will be F p for the pursuer and F e for the evader. A friction limit will be used, for the speed not to grow unbounded, denoted by k p and k e for the pursuer and evader, respectively. Therefore, the maximum speed will be F/k. This setup is an extension to Isaacs “isotropic rocket” game [8, pp. 105–116], but considering that pursuer and evader have the same dynamics: constant acceleration and bounded speed.
4.2 Dynamics of the UAVs
Each player control variable will be their heading angle with respect to y-axis, which will be noted ϕ for the pursuer and ψ for the evader. Considering that there are eight states, which will be the position (x and y coordinates) and the velocities (u and v, which are the velocity components) of the pursuer and evader, the dynamics are:
4.3 Game solution
We have already posed and solved this game in [18] using Isaacs’ equations. The optimal control and trajectories obtained depend on the final conditions of the game.
In order to determine these final conditions, we must define the terminal surface (i.e., the surface where the pursuer captures the evader), which we will call h. By considering that the capture distance is l, the surface capture will be the ball whose center is the evader position: when the pursuer enters that ball, the game ends and capture occurs. Hence, the termination surface will be the sphere in which the distance between the pursuer and the evader equals l, the capture distance. It can be parameterized using n−1 variables (where n is the number of states) as follows, where we recall that s i are the final time condition variables:
In [18], it was shown that the optimal controls are:
where s 5 is the final heading angle of each player, which is the same for both of them. Hence, both optimal controls are constant and equal to both players.The same solution is obtained in the original setup [8, p. 109], though the dynamics are different in this setup.
Finally, the optimal trajectories were obtained in [18]:
where y p , v p , y e , and v e have similar expressions, but sin(s 5) is replaced by cos(s 5), s 1 by s 2, s 3 by s 4, and s 6 by s 7.
4.4 Analytical solution to the system
The equations in Eq. (29) give the optimal trajectories for both players, depending on the parameters used to describe the terminal sphere and the retro-time τ, which are unknown. Since initial conditions are known (i.e, initial positions and speeds of both players), it is possible to obtain these parameters by equaling the equations in Eq. (29) to the initial conditions and particularized to t=0, that is, τ=t f −t=t f .
This system, is nonlinear and trigonometric and may be hard to solve. To simplify its resolution, we apply the same procedure that Isaacs used [8, pp. 110–111]: the final time t f is obtained from the initial conditions and game parameters by squaring and adding these two identities and by using that cos2(α)+ sin2(α)=1:
where Δ x=x p −x e , Δ y=y p −y e and:
The resulting expression, which is in Eq. (32), only depends on known initial conditions and game parameters, and hence, it is a nonlinear function of τ. By solving for τ, that is, g(τ)=0, the τ obtained will be the final time of the game, that is, τ=t f .
Once that t f has been obtained, it can be replaced in the system in Eq. (29). If this system is particularized for the initial time conditions, doing the following variable change, w 1= cos(s 5),w 2= sin(s 5), yields a linear system which can be solved using standard techniques (recall that \(w_{1}^{2}+w_{2}^{2}=1\)). An illustration of these steps is shown in Algorithm 1.

4.5 Optimization solution to the system
The technique proposed in the section before to solve the equations system in Eq. (29) has a big drawback: due to the exponentials involved in the system, the solution is not always found by the computer. A different approach can be done in order to obtain the final conditions from the initials, based on searching an optimum of a cost function.
We do a search over a two-dimensional surface: since we know the initial conditions of the game, the trajectories can be computed numerically using the expressions in Eq. (26). To do so, a Runge-Kutta method is used to solve the differential equations that control the dynamics of the UAVs. Only two parameters are needed to obtain these trajectories: the final time t f and the final heading angle s 5.
After numerically obtaining the trajectories, congruency is checked: in final time, capture occurs and heading angle corresponds to s 5. If both conditions happen, then the point is a candidate to be a solution to the game.
We implement this approach in order to obtain the game solution. The numerical ODE solver chosen is a Runge-Kutta one, based on Dormand-Prince (4, 5) pair [6]. The duple (s 5, t f ) that is considered the solution is chosen as the duple where capture happens, that is, final distance between players is equal or smaller than capture distance l, and which has the smaller absolute error between the final heading angle obtained in the trajectories and the introduced a priori in the duple. The final heading angle can be obtained from Eq. (27) as:
where x e,f , x p,f , y e,f and y p,f are the final points in the trajectories numerically obtained.
Finally, we put these conditions in a cost function which we minimize. Its form is:
where k 1, k 2, and k 3 are constants; d f is the final distance between players, computed using the trajectories values; l is capture distance; s 5 is the final heading angle supposed a priori; and \(\hat {s_{5}}\) is the final heading angle, computed with the trajectories using Eq. (33).
The first term is an analytic and smooth approximation for the Heaviside step function, when k 1=1. The parameter k 2 controls how sharp the transition will be in d f =l: larger values of k 2 give a sharper transition, closer to the ideal but non-smooth step function.
For adequate values of the constants k 1, k 2, and k 3, it is possible to get the cost function that we need. If d f >l, the exponential argument is negative and hence small, so the first term is approximately k 1. If \(k_{1} > k_{3} |s_{5}-\hat {s_{5}}|\), then, the value tends to be k 1. This is the case where capture does not occur.
If capture occurs, d f <l, and hence, the exponential argument is positive. For sufficiently high values of k 2, the first term of the cost function vanishes, and hence, the cost function tends to be \(k_{3} |s_{5}-\hat {s_{5}}|\). This means that when capture occurs, the cost is proportional to the absolute error between heading angles, as we intended.
Hence, the cost function defined in Eq. (34) will be used for the two dimensional search proposed. We consider that the constants are k 1=1, k 2=500, and k 3=1. The non-convex algorithm Simultaneous Optimistic Optimization (SOO) details can be found in [14, 15]. This algorithm is used in order to obtain the game solution—i.e., final heading angle, which is the control, and time of capture, which is the payoff of the game. An illustration of these steps is found in Algorithm 2.

4.6 Hybrid solution to the system
An intermediate approach between the analytical and the optimization methods proposed in the previous sections can also be considered. It consists in simplifying the two-dimensional optimization method by computing the right t f using Eq. (31). Hence, in this case, we first obtain the final time analytically, by numerically solving Eq. (31), and afterwards, we perform a minimization of the cost function defined in Eq. (34) over the final heading angle s 5.
This approach needs less iterations of the optimization algorithm, and hence, it is faster at the cost of having to solve numerically the expression shown in Eq. (31) in order to obtain the optimum final time. An illustration of these steps is found in Algorithm 3.

4.7 Simulation 1: comparison between analytical, optimization, and hybrid solution approaches
In this section, the three methods proposed in Sections 4.4, 4.5, and 4.6 are implemented and compared. In order to do so, a grid has been defined over the initial position conditions, taking the following values: x e,0,y e,0∈{1,6,11}, x p,0,y p,0∈{−10,−5,0}. Each one of these four initial conditions can take three possible values on the grid, and hence, it has 81 points. The rest of the parameters are u e,0=v e,0=1, u p,0=v p,0=−1, v m a x,e =1, v m a x,p =2, F e =F p =1, l=1, D=100, N=100, P j =1.11, and P c =1, using a SINR threshold of S I N R min =1 in the receivers for communications to be considered successful.
The non-convex optimization algorithm implementation used [14, 15] in the optimization and hybrid methods stops when a fixed number of iterations have been done, regardless of whether a solution was found or not. In order to study how the iteration number affects to solution obtaining, we run the algorithm three times for optimization method (using {103,104,105} iterations) and for the hybrid approach (using {102,103,104} iterations).
A point is considered to be a valid solution after iterating if its cost from Eq. (34) is smaller than a threshold. Since the cost will be smaller than one if and only if capture happens, we set 0.9 as threshold. In order to compare the different methods, we define the relative distance between the solutions given by each method as:
where ||x||2 is the Euclidean norm of vector x; \(\hat {x}\) is the solution vector that the analytical method provides—its two components are final heading angle and final time, \(\hat {x}=(t_{f}, s_{5});\) and \(\tilde {x}\) is the solution vector that either optimization or hybrid method gives. Hence, this is a relative measure of how far are the solutions: a smaller value means that solutions found are close between the methods tested. Our simulations show that for the hybrid method, this relative distance is always inferior to 0.05%; for the optimization approach, it is always below 3.5%.
Finally, Table 1 presents the results obtained with each method. It is possible to see that the hybrid method yields the highest number of solutions found, being able to find all the solutions for the proposed grid points. The second best solution is the analytical method, and the worse in number of solutions found is the optimization approach.
Comparing all the approaches, it is possible to see that the hybrid method yields better performance than the optimization method. The drawback is that it needs to solve a nonlinear expression for final time, but it achieves a solution with a smaller relative distance and it takes less iterations—which means less computation cost and time. Finally, analytical method is the fastest, but due to the nonlinearity of the system to be solved, a solution is not always achieved—in the proposed grid, though, that happened only once.
5 Capacity game of two UAVs
5.1 Introduction
In this section, Isaacs’ method, described in [8, Chap. 4], will be used to solve the linear approximation of the capacity game described in Section 3. The running cost L will be considered to be linear Eq. (24):
where r=(y c −y j )2+(x c −x j )2, A and B are constants whose expressions are in Eq. (25). The final cost G will be considered to be zero. As in Section 4, we consider each UAV to have a constant acceleration and a friction limit. Again, this setup is an extension to Isaacs “isotropic rocket” game [8, pp. 105–116], but considering that pursuer and evader have the same dynamics and using a different running cost.
5.2 Dynamics of the UAVs
We consider the player to have the same control variable as in the previous section, which will be their heading angle with respect to y-axis. Hence, there will be eight states, as in the previous case, and the dynamics of pursuer and evader are the same as in Eq. (26).
5.3 Control optimization
Building the Hamiltonian using Isaacs “main equation” [8, p. 67] yields:
Using that controls are separable:
The optimization problems in Eq. (36) is solved using the same approach as in Section 4.3, and the Hamiltonian Eq. (36) becomes:
5.4 Retrogressive path equations
The sixteen retrogressive path equations (RPE) are obtained using the same expressions in Eqs. (8) and (11). The eight equations that depend on the dynamics equation are the following:
were x ̈ denotes derivative of x with respect to τ.The eight RPEs that depend on the gradient of the value function are obtained through derivation of the Main Eq. (37) with respect to each state variable. The resulting RPEs are:
These second group of RPEs are different from the ones obtained in the game solved before because of using a different running cost.
5.5 Final conditions
We consider that the capture distance is l and that the surface capture will be the ball whose center is the evader position and whose radius is l. Its parametrization can be found in Eq. (27). Using Eqs. (27) and (12), taking into account that the final cost G is zero, the final conditions obtained are:
From Eq. (40), the two first equations and the fifth show that in the terminal sphere, \(-V_{x_{p}}=V_{x_{e}}=\lambda \sin (s_{5})\) and \(-V_{y_{p}}=V_{y_{e}}=\lambda \cos (s_{5})\), where λ is an auxiliary variable. Also, from the rest of equations in Eq. (40) and that \(\rho _{p}=\sqrt {V_{u_{p}}^{2}+V_{v_{p}}^{2}}\) and \(\rho _{e}=\sqrt {V_{u_{e}}^{2}+V_{v_{e}}^{2}}\), in the terminal manifold, ρ e =ρ p =0. Substituting all that in Eq. (37) yields:
Manipulating Eq. (41) gives the following result for λ:
where the value of r was substituted. The expression in the denominator can be simplified: if final speeds of pursuer and evader are called, respectively, v f,p and v f,e , we have that:
Replacing and manipulating in Eq. (42), taking into account that cos2(s 5)+ sin2(s 5)=1 yields the following expression for λ:
5.6 RPEs integration
Let us start integrating the equations in Eq. (39). The four equations for \(V_{x_{e}}\), \(V_{y_{e}}\), \(V_{x_{p}}\), \(V_{y_{p}}\) are solved using the initial condition found in the previous section, and it yields:
where λ is defined as in Eq. (44). The other four RPEs in Eq. (39) are solved by replacing the values of \(V_{x_{e}}, V_{y_{e}}, V_{x_{p}},V_{y_{p}}\) that are in Eq. (45) and using the initial conditions (in retro time) from Eq. (40).
The optimal controls can be obtained now: since \(\rho _{p}=\sqrt {V_{u_{p}}^{2}+V_{v_{p}}^{2}}\) and \(\rho _{e}=\sqrt {V_{u_{e}}^{2}+V_{v_{e}}^{2}}\), substituting into the integrated RPE equations yield the following expressions for the controls:
where:
It is possible to see that the optimal controls in Eq. (46) are neither constant nor equal for both players, as it happened in the problem in the previous section (see Eq. 28). In this case, trajectories of both players are coupled, and the game is still open loop: optimal trajectories and controls, though coupled, can be obtained from initial conditions of the game.
The complex expressions for the controls in Eq. (46) causes that obtaining a closed expression for speeds and trajectories is hard. Also, since the controls depend on λ and λ depends on the final conditions in Eq. (44), if there are no closed expressions for the trajectories, the approach followed in Section 4.4 cannot be used to obtain the final conditions using the initial conditions: for this game, we have no analytical solution procedure. Hence, in order to solve this game, a similar approach to the one described in Section 4.5 will be used.
5.7 Simulation 2:optimization approach solution to capacity game
In order to extend the approach proposed in Section 4.5 to this capacity game, the same grid used there for the initial conditions will be used here, that is, x e,0,y e,0∈{1,6,11}, x p,0,y p,0∈{−10,−5,0}. The rest of the parameters are as follows: u e,0=v e,0=1, u p,0=v p,0=−1, v m a x,e =1, v m a x,p =2, F e =F p =1, l=1, D=100, N=100, P j =1.11 and P c =1, using a SINR threshold of S I N R min =1 in the receivers for communications to be considered successful.
The control equations in Eq. (46) will be used to numerically solve the system in Eq. (26) and hence obtain the trajectories. The numerical solver used is not the same that was described in Section 4.5, since the ODE system might become stiff, and hence, a different method is required in order to be time-efficient. In this case, a variable-step, variable-order solver based on the numerical differentiation formulas of orders 1 to 5 is used, combined with Gear’s method [23].
The non-convex optimization algorithm used will be the same that was used in previous section (SOO). The search will be performed over three dimensions, since there are three initial parameters to be obtained: final heading angle and final time (s 5 and t f respectively), and the final difference of speeds, \(\phantom {\dot {i}\!}v_{f,p}-v_{f_{e}}\), which is required to solve Eq. (44). The number of iterations chosen are {103,104,105}.
Finally, the cost function will be adapted from Eq. (34) as:
where the first two terms are the same than in Eq. (34) and the third one is due to the final difference of speeds, where Δ v f corresponds to the final difference of speeds introduced a priori, whereas \(\hat {\Delta v_{f}}\) corresponds to the final difference of speeds in the trajectories numerically obtained. Hence, this cost function tries to minimize the error between final heading angle and final difference of speeds, as well as adding a term if capture does not happen. In this simulation, k 1=k 3=k 4=1 and k 2=500, and the threshold in cost function Eq. (48) to consider a point valid is 0.9 again. An illustration of the steps followed in this method can be found in Algorithm 4.

Also, an approximation of this method will be tested. If final time t f is sufficiently high for both players to be able to accelerate until they reach their speed limits, it is possible to approximate the final difference of speeds as follows:
Using this approximation allows to reduce the dimensionality of the search to two dimensions, which means a smaller computational cost and time because we only search for final heading angle and final time. The cost function used will be Eq. (48). Considering the final conditions triplet (s 5,t f ,Δ v), we use the relative distance in Eq. (35) as the error metric, where \(\hat {x}\) is the triplet of final conditions obtained with the optimization approach and \(\tilde {x}\) is the triplet of final conditions obtained with the \(\hat {\Delta v}\) approximation, in which Δ v follows the expression in Eq. (49). Our simulations show that this error is always smaller than 1.5%, and hence, \(\hat {\Delta v}\) approximation is validated. An illustration for the steps followed in this approximation can be found in Algorithm 5.

The results obtained can be observed in Table 2 and are similar to the ones in Table 1 for the optimization approach. It is important to note that this game requires more iterations than the one in Table 1, and hence, the computational cost and time to solve this capacity game increases with respect to the one in the previous section. Also, we see that \(\hat {\Delta v}\) approximation is less computationally costly: it yields more solutions with the same number of iterations.
6 Comparison between games proposed
In Section 3, the main problem was posed is a UAV tries to communicate with some receivers, whereas another UAV tries to jam that communication. Two different approaches were used to solve the problem: a surrogate function approach in Sections 4 and 5; the game was solved in terms of capacity.
In this section, the trajectories and controls obtained in both approaches will be compared. Since the simulations done in the sections before were run on the same grid of initial conditions for both games, it is straightforward to compare the results.
First, in Fig. 2, it is possible to see two trajectories solved using different approaches for the same initial conditions, the first with a small relative distance and the second with a high relative distance between trajectories. Solutions for the game with running cost L=1 were obtained with hybrid method, whereas for game with running cost L=A+B r, we use the optimization approach. It is possible to see that for the game with running cost L=1, the controls are constant, whereas for the game with running cost L=A+B r, they are nearly constant. This small difference causes speeds and trajectories to be slightly different.
Comparison of controls and trajectories obtained for games with running cost L=1 and L=A+B r. The initial grid conditions are x e,0=1, y e,0=1, x p,0=0, y p,0=−5 for case 1 and x e,0=6, y e,0=1, x p,0=−10, y p,0=0 for case 2. The rest of the parameters are described in Section 5.7. The continuous blue line is the evader and the dashed red line is the pursuer when L=1, whereas the dotted blue line is the evader and the dash-dot red line is the pursuer when L=A+B r. On the trajectories representation, the circles represent initial positions (blue for evader, red for pursuer) and black ellipses represent the terminal surface. It is possible to see that differences in control are small in case 2, and that means that trajectories are quite similar, but in case 1, the control differences are bigger, and hence, trajectories vary more. (a) Controls (case 1). (b) Trajectories (case 1). (c) Controls (case 2). (d) Trajectories (case 2)
Secondly, a quantification of how much different the controls and trajectories are can be found in Table 3. The metric used is relative error in controls, which is computed as follows for the control of each player:
where α 1 is the heading angle in the case where running cost L=A+B r and α 2 is the heading angle when L=1. Since heading angle evolves with time in the first case, the relative error is computed along the whole trajectory for all the grid points of initial conditions on which both methods reach a solution, and this vector of relative errors is analyzed in Table 3. The methods compared are the hybrid method when L=1 and for the case when L=A+B r, both the optimization approach and the \(\hat {\Delta v}\) approximation are considered. In the first case, after computing the empirical cumulative distribution function (CDF), more than 90% of the errors are below 0.5%, whereas in the second case, more than 90% of the errors are below 1%, as can be observed in Fig. 3. Hence, it is possible to approach the second game by the first one, without getting an excessive error.
Comparison of empirical CDF for relative error between the game with L=1 and the game with L=A+B r, using Eq. 50. For the game with L=1, we used the hybrid approach. For the case when L=A+B r, we used the optimization approach (blue continuous lines) and the \(\hat {\Delta v}\) approximation (red dashed lines). It is possible to see that in both cases, the CDF of the error shows that more than 90% of the cases are below a relative error of ζ=1%. (a) Evader. (b)Pursuer
7 Conclusions
We propose a new approach for solving games in scenarios with stochasticity (i.e., scenarios in which there is some randomness), which consists in solving a pursuit-evasion game instead of a capacity one using an approximation. A concrete application to a jamming game has been studied.
The steps we have followed are the following:
-
The communications maximum capacity has been computed in the environment we have posed. We showed that this capacity can be approximated as a linear function of the squared distance between players.
-
The game was solved as a standard pursuit-evasion game, using a surrogate function approach. This game was solved using three different approaches (analytical, optimization, and hybrid).
-
The game was also solved using the total system capacity as the payoff, as a zero-sum game. This is be the exact solution to the game we posed. We used two approaches (optimization and \(\hat {\Delta v}\) approximation).
-
Both games solutions were compared and it was shown that both yield very similar results, having a very small relative error. Hence, the capacity game can be accurately approached as a standard pursuit-evasion one and be efficiently solved.
References
T Basar, GJ Olsder, Dynamic noncooperative game theory, vol. 23 (SIAM, 1999).
R Bellman, Dynamic programming, 1st edn. (Princeton University Press, Princeton, 1957). http://books.google.com/books?id=fyVtp3EMxasC&pg=PR5&dq=dynamic+programming+richard+e+bellman&client=firefox-a#v=onepage&q=dynamic%20programming%20richard%20e%20bellman&f=false.
S Bhattacharya, T Basar, in American Control Conference (ACC), 2010. Game-theoretic analysis of an aerial jamming attack on a UAV communication network (IEEE, 2010), pp. 818–823. http://ieeexplore.ieee.org/abstract/document/5530755/.
S Bhunia, X Su, S Sengupta, F Vázquez-Abad, in Distributed Computing and Networking. Stochastic model for cognitive radio networks under jamming attacks and honeypot-based prevention (Springer, 2014), pp. 438–452. https://books.google.es/books?hl=es&lr=&id=fwC6BQAAQBAJ&oi=fnd&pg=PA438&dq=+Stochastic+model+for+cognitive+radio+networks+under+jamming+968+attacks+and+honeypot-based+prevention+(Springer,+2014),+pp.+438%E2%80%93452&ots=Z5sfxArnn2&sig=1QojbKt3KqWOvm9ESqQEDWrr53c.
A Bressan, Noncooperative differential games.a tutorial, (Department of Mathematics, Penn State University, 2010). https://www.math.psu.edu/bressan/PSPDF/game-lnew.pdf.
JR Dormand, PJ Prince, A family of embedded runge-kutta formulae. J. Comput. Appl. Math.6:, 19–26 (1980).
HP Geering, Optimal control with engineering applications, vol. 113 (Springer, 2007). http://www.springer.com/br/book/9783540694373.
R Isaacs, Differential games: a mathematical theory with applications to warfare and pursuit, control and optimization (Courier Corporation, 1999). https://books.google.es/books?hl=es&lr=&id=XIxmMyIQgm0C&oi=fnd&pg=PA1&dq=differential+games+Isaacs&ots=WhR34ML8_v&sig=hVOwUrKJ8YnHQo7Q7u3YeGLofQ0.
S Karaman, E Frazzoli, in Algorithmic foundations of robotics IX. Incremental sampling-based algorithms for a class of pursuit-evasion games (Springer, 2010), pp. 71–87. http://link.springer.com/chapter/10.1007/978-3-642-17452-0_5.
WC Lee, Mobile Communications Design Fundamentals (John Wiley & Sons, Inc., 1992). http://dl.acm.org/citation.cfm?id=530392.
J Lewin, Differential games: theory and methods for solving game problems with singular surfaces (Springer Science & Business Media, 2012). https://books.google.es/books?hl=es&lr=&id=w9PiBwAAQBAJ&oi=fnd&pg=PR15&dq=Differential+games:+theory+and+methods+for+solving+game+problems+with+singular+surfaces&ots=5Izby-1Qcm&sig=jBHfcVJFB1hQHEapn28M12YQ95I.
H Li, Z Han, Dogfight in spectrum: Combating primary user emulation attacks in cognitive radio systems, part i: Known channel statistics. Wirel. Commun. IEEE Trans.9(11), 3566–3577 (2010).
H Li, Z Han, Dogfight in spectrum: combating primary user emulation attacks in cognitive radio systems, part ii: Unknown channel statistics. Wirel. Commun. IEEE Trans.10(1), 274–283 (2011).
R Munos, in Advances in Neural Information Processing Systems 24 (NIPS). Optimistic optimization of a deterministic function without the knowledge of its smoothness (Granada, 2011), pp. 783–791. https://papers.nips.cc/paper/4304-optimistic-optimization-of-a-deterministic-function-without-the-knowledge-of-its-smoothness.pdf.
R Munos, From bandits to monte-carlo tree search: The optimistic principle applied to optimization and planning. Foundations and Trends in Machine Learning. 7(1), 1–129 (2014).
JF Nash, et al., Equilibrium points in n-person games. Proc. Nat. Acad. Sci. USA. 36(1), 48–49 (1950).
J Nash, Non-cooperative games. Annal math., 286–295 (1951). http://www.jstor.org/stable/1969529.
J Parras, J Del Val, S Zazo, J Zazo, S Valcarcel Macua, in Statistical Signal Processing (SSP), 2016 IEEE Workshop on. A new approach for solving anti-jamming games in stochastic scenarios as pursuit-evasion games (IEEE, 2016), pp. 1–5.
A Pashkov, S Terekhov, A differential game of approach with two pursuers and one evader. J. Optim. Theory Appl.55(2), 303–311 (1987).
K Pelechrinis, M Iliofotou, SV Krishnamurthy, Denial of service attacks in wireless networks: The case of jammers. Commun. Surv. Tutorials, IEEE.13(2), 245–257 (2011).
LS Pontryagin, Mathematical theory of optimal processes (CRC Press, 1987). https://books.google.es/books?hl=es&lr=&id=kwzq0F4cBVAC&oi=fnd&pg=PR11&dq=mathematical+theory+of+%C3%B3ptimal+processes&ots=3nv3Yylc_f&sig=l_ywT5P3uudBZKH4nZW8rttd9Vo.
TS Rappaort, Wireless communications: principles and practice (Prentice-Hall, 2002). https://nyu.pure.elsevier.com/en/publications/wireless-communications-principles-and-practice-3.
LF Shampine, MW Reichelt, The matlab ode suite. SIAM J. Sci. Comput.18(1), 1–22 (1997).
S Shankaran, DM Stipanović, CJ Tomlin, in Advances in Dynamic Games. Collision avoidance strategies for a three-player game (Springer, 2011), pp. 253–271.
W Wang, S Bhattacharjee, M Chatterjee, K Kwiat, Collaborative jamming and collaborative defense in cognitive radio networks. Pervasive Mobile Comput.9(4), 572–587 (2013).
B Wang, Y Wu, K Liu, TC Clancy, An anti-jamming stochastic game for cognitive radio networks. Sel. Areas Commun. IEEE J.29(4), 877–889 (2011).
W Xu, T Wood, W Trappe, Y Zhang, in Proceedings of the 3rd ACM workshop on Wireless security. Channel surfing and spatial retreats: defenses against wireless denial of service (ACM, 2004), pp. 80–89.
DW Yeung, LA Petrosjan, Cooperative stochastic differential games (Springer Science & Business Media, 2006). http://link.springer.com/chapter/10.1007/0-8176-4501-2_7.
Acknowledgements
This work was supported in part by the Spanish Ministry of Science and Innovation under the grant TEC2013-46011-C3-1-R (UnderWorld), the COMONSENS Network of Excellence TEC2015-69648-REDC, and by an FPU doctoral grant to the fourth author.
Competing interests
The authors declare that they have no competing interests.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Parras, J., Zazo, S., del Val, J. et al. Pursuit-evasion games: a tractable framework for antijamming games in aerial attacks. J Wireless Com Network 2017, 69 (2017). https://doi.org/10.1186/s13638-017-0857-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-017-0857-8
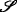 , which is an infinite set whose elements are the permissible state trajectories, denoted as {x(t),0≤t≤t
f
}. For each fixed t
, which is an infinite set whose elements are the permissible state trajectories, denoted as {x(t),0≤t≤t
f
}. For each fixed t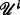 , which is an infinite set defined for each
, which is an infinite set defined for each 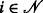 . The elements of this set are the permissible controls of player i. There exists a set
. The elements of this set are the permissible controls of player i. There exists a set  so that for each fixed t
so that for each fixed t , so that the cost functional of player i, denoted by π
i(x(t),u
1(t),...,u
N
(t)), is well defined. Its form is:
, so that the cost functional of player i, denoted by π
i(x(t),u
1(t),...,u
N
(t)), is well defined. Its form is:


